导航增强系统能够确保全球导航系统(GNSS)在恶劣环境下提供正常PNT服务。随着GNSS在特殊复杂环境中如城市、峡谷、室内、森林等的扩展,用户对首次定位时间、抗干扰以及完好性、连续性和可用性等提出了越来越苛刻的要求。为此,各GNSS除了加大卫星升级和信号体制改进的力度外,还建立了各种地基和天基增强系统[1-2]。
利用LEO卫星作为导航增强卫星正在逐渐成为一种趋势。传统的导航增强系统都是采用的GEO卫星,例如美国的WAAS、欧盟的EGNOS和我国的BDS等[3],这些系统通过GEO卫星作为通信媒介,提供差分校正值和完好性数据[4]。虽然GEO卫星仅需要少量的卫星就可以向全球用户发播增强信息,但是其轨道资源有限。随着星载GNSS测定轨技术的成熟和辅助加速度计在摄动力测定中的应用,LEO卫星定轨精度优于分米级[5]。在已经建成的“铱”系统导航增强GPS系统中,LEO卫星首先完成与GPS系统时的精确同步,然后播发类似GPS信号的直接序列扩频信号。与传统的GEO增强卫星相比,较低的轨道有利于改善地面信号强度和用户终端的抗干扰能力,此外,GNSS-LEO的高低轨星间链路也很好地改进GNSS系统完好性的监测能力[6]。
LEO增强卫星自身的广播电文参数,是实现其星基增强的一项基本设计指标。目前,广播星历参数设计主要是针对中高轨卫星,主要有两大类,一是基于轨道根数型的GPS广播星历,另一类是基于轨道状态型的GLONASS广播星历[7-8]。对低轨卫星的广播星历参数设计相对较少。文献[9]研究了基于轨道根数型小偏心率低轨卫星参数拟合理论,数据来源于某星载GPS接收机定位,数据拟合误差在100 m量级。该方法简单有效、计算速度快,但是拟合时间太短、拟合精度不高。文献[10]参照GPS广播星历15参数拟合法的特点,根据约1000 km高度的卫星轨道特征设计了一套针对低轨卫星的星历25参数拟合法,其2 h轨道弧段的均方差小于10 m,其局部弧段拟合误差小于25 m,但是参数较多。相对于GPS广播星历,基于轨道状态型的GLONASS广播星历参数个数更少,意义更直观简单,易于理解和应用,具有可拓展性,能为卫星轨道变化快的导航系统星历参数设计提供重要的参考意义[11]。本文借鉴中高轨卫星的轨道状态型广播星历,对低轨卫星的星历进行了研究。
针对低轨卫星的短期动力学特性,提出了一组针对LEO的轨道状态型21参数广播星历。在地心地固系下,除了考虑中心引力和J2项之外,对其他摄动力主项,采用二次多项式和周期项模型分别进行3方向投影分量的综合摄动力补偿。该方法既保留了GLONSS型广播星历的无奇点特性,又能够利用较少的星历参数拟合,得到高精度的拟合结果。采用STK复杂力模型下仿真的500~1200 km高度的低轨卫星轨道数据和GRACE-A卫星的实测精密轨道数据,分析了20~40 min拟合时段的星历拟合。20 min时段的拟合结果表明,1000 km高度圆轨道的拟合用户距离误差(FURE)精度优于0.03 m。
1 低轨卫星受力和短期变化特征与中高轨卫星轨道相比,低轨卫星受到的轨道摄动力更大也更复杂,尤其是大气阻力的建模精度较差。
1.1 LEO摄动力分析表 1计算了不同高度的LEO卫星所受主要摄动力的加速度量级[12-13]。可知,除了最大的摄动源即地球扁率J2的摄动外,低轨卫星所受主要摄动力为大气阻力、日月引力摄动和其他非球形引力摄动主项。对于500~1200 km高度的低轨卫星,大气阻力影响是显著的,大气密度模型误差可能会对拟合结果产生一定影响。许多文献分析和比较了不同大气密度模型的表现,结论是这些模型的统计精度大约为15%,在最近20 a内密度模型没有突破性进展,选择中等复杂程度的密度模型是比较合理的[13]。本文采用最常用的Harris-Priester密度模型。表 1中加速度量级的单位为km/s2, 卫星面质比单位为0.01 m2/kg。
| 摄动力 | 轨高/km | |||
| 600 | 800 | 1000 | 1200 | |
| J2 | 10-5 | 10-5 | 10-6 | 10-6 |
| 大气阻力(最大) | 10-7 | 10-8 | 10-9 | 10-10 |
| 大气阻力(最小) | 10-8 | 10-9 | 10-10 | 10-11 |
| 日月引力摄动 | 10-8 | 10-8 | 10-8 | 10-8 |
 |
10-8 | 10-8 | 10-9 | 10-9 |
| 太阳光压 | 10-10 | 10-10 | 10-10 | 10-10 |
| 动力学固体潮 | 10-10 | 10-10 | 10-10 | 10-10 |
| 地球反照压 | 10-11 | 10-11 | 10-11 | 10-11 |
| 相对论效应 | 10-11 | 10-11 | 10-11 | 10-11 |
| 金星引力摄动 | 10-14 | 10-14 | 10-14 | 10-14 |
1.2 LEO卫星摄动力短期变化特征
为同时保证卫星位置拟合精度和用户计算的简便,各摄动加速度的取舍及其在地心地固系下的表达方式需要确定。其中,最大项是扁率摄动,其力模型简单,可以直接采用;其次是力模型计算复杂的大气阻力和日月引力摄动等,通常的简化处理方式是针对其短期内的摄动加速度变化规律,采用简单的数学函数进行模型逼近。对于20 min的轨道积分,更小量级的摄动力则可以忽略。
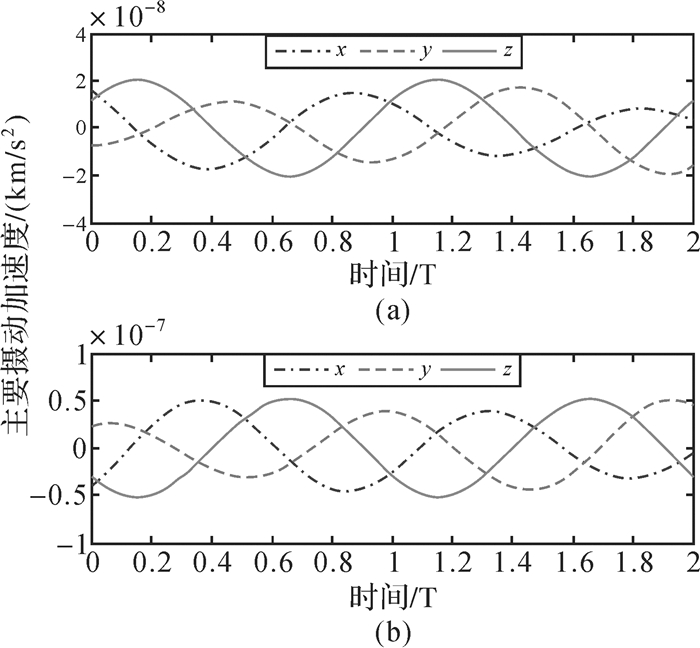
图 1给出了两个轨道周期(2T)内大气阻力和日月引力摄动加速度之和在ECEF坐标系下的变化特性。试验采用的卫星高度为1000 km(图 1(a))和600 km(图 1(b)),偏心率为0.001,计算大气阻力采用的卫星有效面质比为0.01 m2 /kg。可以看出,短时段内,这两项摄动加速度的综合变化具有一定的趋势性和明显的与轨道周期相关的混频变化特征,可以考虑用二次多项式和周期项来分别吸收趋势变化和短周期变化。
|
| 图 1 低轨卫星的主要摄动加速度短期波动变化(两个轨道周期) Fig. 1 The short term fluctuation of main perturbation acceleration of LEO satellites |
2 LEO广播星历参数设计
GLONASS型广播星历是通过对地心地固坐标系(ECEF)下的力模型进行数值积分来计算卫星位置的[14-15]。由于星历更新较快、轨道弧段短,摄动力仅考虑了对轨道影响较大的摄动主项。
令卫星的状态向量为ECEF下的位置和速度向量,即X=[RT ṘT]T,状态微分方程为
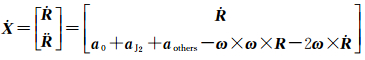 (1)
(1)
式中,牛顿加速度主项a0、aJ2和aothers分别为ECEF下的地球中心引力加速度、地球扁率摄动加速度和其他摄动力主项;随后的两项是由于在非惯性系下描述二阶时间导数而引进的牵连加速度主项,分别为离心加速度和科里奥利加速度向量,其中,ω=[0 0 ωe]T为地球自转角速度向量,ωe为平均地球自转角速度。
2.1 标准9参数星历模型若令摄动力主项aothers为常向量,则式(2)为标准的9参数GLONASS星历模型,即状态向量为X=[RT ṘT aothersT]T。将9参数星历模型直接应用于低轨卫星,根据带有初值条件的状态微分方程
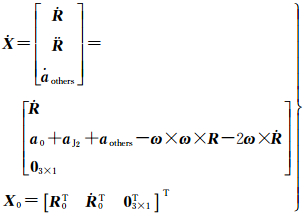 (2)
(2)
通过最小二乘平差方法即可以拟合出式(2)中的星历参数X0的最佳估值[16]。用户获得t0时的星历参数X0,利用Runge-Kutta四阶积分器进行数值积分,即可得到有效期内任意时刻的ECEF下的卫星位置和速度向量。
2.2 改进的21参数星历模型标准的GLONASS广播星历是针对高度20 000 km左右的中轨卫星设计的星历模型。在该模型中,由于中高轨卫星在星历有效期(30 min)内的摄动力主项aothers具有慢变特性,可令其为常向量[17]。但是,低轨卫星轨道周期短(100 min左右),相同时段内的摄动加速度比中高轨卫星变化快,且更加复杂,同时具有慢变趋势性和短周期震荡性。因此,需要增加参数才能高精度地逼近和表征摄动力主项aothers,如以高阶多项式和傅里叶级数的数学函数表达式。
本文在LEO摄动主项的短期变化基础上,综合考虑参数个数、拟合精度以及用户卫星位置速度的计算复杂度等,提出采用二次多项式和基于轨道半周期的三角函数来逼近大气阻力和日月引力等在3个分量上的摄动加速度之和。即
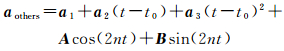 (3)
(3)
式中,a1、a2、a3、A、B为二次多项式系数和三角函数幅值的常向量,n为卫星的平均运动角速度。
若令aothers的参数向量为y=[a1T a2T a3T AT BT]T,则状态微分方程为
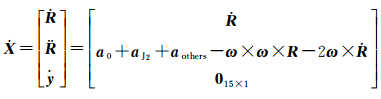 (4)
(4)
则有改进的21个状态参数的LEO广播星历表示法
式中,R0、Ṙ0为历元时刻t0(取拟合时段中间时刻)的位置和速度向量,y=[a1T a2T a3T AT BT]T为历元时刻t0的附加力模型参数向量。
2.3 LEO的星历拟合精度指标URE是计算星历和钟差误差对定位影响的一个重要评价指标[18]。URE的来源主要是外推的轨道和钟差误差,此外还包括星历参数拟合和钟参数拟合的拟合误差。
这里仅分析星历参数拟合的单项影响,故称为拟合URE(FURE)。FURE仅与轨道高度有关,其计算公式为[19-20]
 (5)
(5)
式中,ΔR、ΔT和ΔN分别为卫星径向、沿迹和外法向位置分量的拟合误差;AR、AT和AN是分别对应3方向的贡献因子。对于中高轨卫星,通常径向分量的拟合误差ΔR是贡献主项;但是随着轨道降低,其他两方向的影响将逐渐增大。以1000 km高的LEO为例,ΔR、ΔT和ΔN的贡献因子分别为0.595、0.696和0.402,对FURE贡献量级相当。
3 拟合试验和分析将设计的21参数的星历模型用于500~1200 km高度圆轨道低轨卫星的星历拟合。轨道仿真从2015年8月14日开始共计7 d。首先对卫星在地心惯性系(ECI)下进行复杂力模型下的轨道外推,摄动力包括21×21的地球非球形摄动、大气阻力摄动、第三体引力摄动和光压摄动等,其中计算大气阻力摄动的大气密度模型采用Harris-Priester密度模型;进而采用IERS发布的地球定向参数将外推轨道转换到ECEF坐标系下。仿真数据中,卫星轨道倾角为45°,偏心率为0.001,卫星面质比为0.01;按照拟合时段和数据点间隔进行分组,历元时刻取每组的中间时刻。
参数解算采用最小二乘平差,迭代终止条件为迭代前后两次单位权方差的相对变化小于0.001。参数初值中,位置和速度向量取拟合时段中间时刻的卫星位置和速度,其他参数均设为0;采用Runge-Kutta四阶积分器,分别向前和向后数值积分。
40/30/20 min的星历拟合的成功率均为100%,除极少数拟合迭代次数为5之外,均为4次迭代收敛。
3.1 拟合参数个数的影响目前GNSS导航星的星历拟合精度要求是优于0.1 m,甚至0.05 m。在拟合精度满足要求的前提下,星历参数个数越少,越有利于参数发播。为了讨论拟合参数选取的合理性,对比了4种参数集的表征方法和轨道拟合精度,其中后3种的周期项均相同,即
9参数集:附加摄动加速度参数为常向量。
18参数集:附加摄动加速度参数为线性多项式+周期项。
21参数集:附加摄动加速度参数为二次多项式+周期项。
24参数集:附加摄动加速度参数为三次多项式+周期项。
表 2和图 2给出了20 min拟合时段的4组参数集的拟合精度统计。显然,9参数星历模型直接用于LEO卫星的拟合误差太大,不能满足导航要求;星历参数越多,拟合精度越高;若满足低至500 km轨高的0.1 m拟合精度要求,至少需要21个参数。此外,相同参数个数情况下,轨道越高,摄动力数学表征效果越好,拟合精度越高。
| 轨高/km | 拟合精度 | 参数个数 | |||
| 9参数 | 18参数 | 21参数 | 24参数 | ||
| 参数集 | |||||
| {R0, Ṙ0, aothers} | {R0, Ṙ0, a1, a2, A, B} | {R0, Ṙ0, a1, a2, a3, A, B} | {R0, Ṙ0, a1, a2, a3, a4, A, B} | ||
| 500 | R | 128.301 | 2.899 | 0.415 | 0.052 |
| T | 332.536 | 2.922 | 0.421 | 0.052 | |
| N | 6.0247 | 0.232 | 0.040 | 0.006 | |
| FURE | 87.918 | 0.533 | 0.077 | 0.010 | |
| 1000 | R | 306.895 | 1.239 | 0.161 | 0.018 |
| T | 180.032 | 1.274 | 0.162 | 0.018 | |
| N | 4.909 | 1.228 | 0.019 | 0.003 | |
| FURE | 61.457 | 0.232 | 0.023 | 0.003 | |

|
| 图 2 FURE的RMS随参数个数变化 Fig. 2 RMS of FURE varies with the number of parameters |
3.2 拟合时段和数据间隔的影响
图 3和表 3给出了不同拟合时段和数据间隔条件下1000 km高的21参数LEO星历拟合的精度情况。图 3对比了15/30/60 s 3种数据间隔的R/T/N 3分量的残差统计,表 3为40/30/20 min 3种拟合时段的FURE的RMS统计。可以看出:

|
| 图 3 拟合数据间隔、时长对拟合残差RMS的影响 Fig. 3 Impact of sample rate and fitting arc on the RMS of fitting residuals |
| 拟合时段/min | 15 s间隔 | 30 s间隔 | 60 s间隔 | ||||||||
| max | min | mean | max | min | mean | max | min | mean | |||
| 40 | 2.761 | 2.341 | 2.494 | 2.528 | 2.154 | 2.289 | 3.307 | 2.900 | 3.039 | ||
| 30 | 0.423 | 0.368 | 0.382 | 0.389 | 0.340 | 0.353 | 0.522 | 0.464 | 0.477 | ||
| 20 | 0.028 | 0.023 | 0.025 | 0.026 | 0.022 | 0.023 | 0.035 | 0.030 | 0.031 | ||
(1) 数据间隔对径向R、沿迹T和外法向N的位置分量拟合误差影响不显著。对于相同拟合时段,拟合误差在同一个数量级。对于20 min的数据拟合,R和T方向误差相当,可保持在0.17 m以内;N方向误差最小,在0.02 m以内。
(2) 拟合时段越短,FURE精度越高。对于30 s间隔的40/30/20 min的数据拟合,FURE的RMS最大值分别为2.528 m、0.389 m和0.026 m。因此,从优于0.1 m的拟合精度要求来说,LEO的星历拟合时段,应该取为20 min。
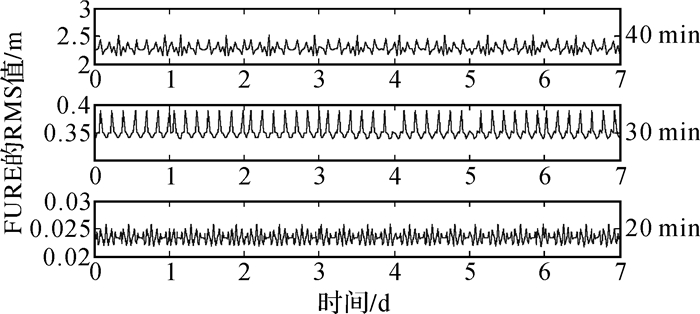
图 4是40/30/20 min FURE的RMS时序图(数据间隔为30 s)。7 d共计504组的数据拟合表明,拟合精度的时序平稳性较好;20 min的拟合时段下,21参数广播星历的FURE精度优于3 cm;拟合时间每增加10 min,FURE增大约一个量级。
|
| 图 4 40/30/20 min数据FURE的RMS分布 Fig. 4 RMS distribution of the 40/30/20 min data FURE |
3.3 轨道高度的影响
采用数据间隔为30 s、拟合时段为20 min的21参数的星历拟合,图 5反映了FURE与LEO轨道高度的变化关系。显然,轨道高度越高,大气阻力摄动影响越小,轨道拟合精度越高。当轨道高度在500 km以上时,LEO的拟合精度均能优于8 cm;若要求拟合精度在5 cm以内,则轨道高度应高于700 km。

|
| 图 5 FURE误差随轨道高度变化 Fig. 5 FURE error varies with orbit altitude |
3.4 GRACE-A卫星数据拟合试验
为验证真实轨道的数据拟合,采用GRACE-A卫星2010年3月15日—19日共5 d的卫星精密轨道数据。该卫星设计轨道高度约500 km,由于大气阻力影响,2010年3月,其轨道高度衰减为440~485 km。
利用21参数的LEO星历模型进行10 min和20 min的星历拟合,如图 6所示。由于GRACE-A卫星高度稍微低于设计星历参数的最佳适用卫星高度,实际数据的拟合精度略低,且精度平稳性也较差,20 min星历拟合的FURE平均值为0.084 m,10 min星历拟合的FURE平均值为0.007 m。因此,若采用高度较低的卫星,可适当缩短拟合时段,提高星历更新频率。

|
| 图 6 GRACE-A卫星轨道数据FURE的RMS统计 Fig. 6 Statistics FURE of RMS of GRACE-A satellite orbit |
4 结论
基于LEO的主要摄动力量级,分析了低轨卫星在短时段内的摄动运动变化特性,提出了基于21个扩展状态参数的轨道状态型LEO广播星历模型。
基于21参数广播星历的拟合试验分析表明:①LEO卫星的星历拟合时段宜控制在20 min,数据间隔取30 s;②当圆轨道低轨卫星高度大于700 km时,FURE精度在5 cm以内,当轨道高度降低至500 km时,FURE的精度也能优于0.1 m;③若需要得到更高精度的结果,可采用24参数星历模型或者缩短拟合时间。
与现有的基于轨道根数型星历模型(如GPS)相比,设计的广播星历能够避免根数奇点引起的拟合算法的病态性问题,且参数可拓展性强,可考虑在低轨卫星增强系统中采用或备份发播。
| [1] | 李康, 巩冠峰, SABATINIR. GPS地基增强系统简介及其性能仿真验证[J]. 电光与控制 , 2013, 20 (8) : 89–94. LI Kang, GONG Guanfeng, SABATINI R. Introduction of GPS Ground Based Augmentation System and Performance Simulation[J]. Electronics Optics&Control , 2013, 20 (8) : 89 –94. |
| [2] | YANG Yuanxi, LI Jinlong, XU Junyi, et al. Contribution of the Compass Satellite Navigation System to Global PNT Users[J]. Chinese Science Bulletin , 2011, 56 (26) : 2813 –2819. DOI:10.1007/s11434-011-4627-4 |
| [3] | 周祖渊. 全球卫星导航系统的构成及其比较[J]. 重庆交通大学学报(自然科学版) , 2008, 27 (S1) : 999–1004. ZHOU Zuyuan. On Composition of Global Satellite Navigation System and Its Comparison[J]. Journal of Chongqing Jiaotong University (Natural Science) , 2008, 27 (S1) : 999 –1004. |
| [4] | 赵爽. 国外卫星导航增强系统发展概览[J]. 卫星应用 , 2015 (4) : 34–35. ZHAO Shuang. The Overview of Foreign Navigation Augmentation Satellite System Development[J]. Satellite Application , 2015 (4) : 34 –35. |
| [5] | 郭金运, 孔巧丽, 常晓涛, 等. 低轨卫星精密定轨理论与方法. 北京:测绘出版社[M]. 2014 . GUO Jinyun, KONG Qiaoli, CHANG Xiaotao, et al. Precise Orbit Determination of Low-earth-orbit Satellite. Beijing:Surveying and Mapping Press[M]. 2014 . |
| [6] | 李广侠, 田世伟. 卫星通信与导航增强. 北京:中国通信学会[M]. 2013 . LI Guangxia, TIAN Shiwei. Satellite Communication and Navigation Enhancement. Beijing:China Institute of Communication[M]. 2013 . |
| [7] | 崔先强, 焦文海, 贾小林, 等. GPS广播星历参数拟合算法[J]. 测绘学院学报 , 2004, 21 (4) : 244–246. CUI Xianqiang, JIAO Wenhai, JIA Xiaolin, et al. The Fitting Algorithm of GPS Broadcast Ephemeris Parameters[J]. Journal of Institute of Surveying and Mapping , 2004, 21 (4) : 244 –246. |
| [8] | 黄华. 导航卫星广播星历参数模型及拟合算法研究. 南京:南京大学[M]. 2012 . HUANG Hua. Research on the Broadcast Ephemeris Parameters Model and Its Fitting Algorithm. Nanjing:Nanjing University[M]. 2012 . |
| [9] | 柳青松, 刘峰, 巨涛. 小偏心率低轨卫星的星历参数拟合法[J]. 航天器工程 , 2010, 19 (4) : 17–22. LIU Qingsong, LIU Feng, JU Tao. Ephemeris Parameters Fitting Method for Low Eccentricity LEO Satellite[J]. Spacecraft Engineering , 2010, 19 (4) : 17 –22. |
| [10] | 马开锋, 彭碧波, 洪樱. 基于卫星轨道特征的低轨卫星星历参数拟合法[J]. 大地测量与地球动力学 , 2007, 27 (1) : 85–90. MA Kaifeng, PENG Bibo, HONG Ying. LEO Satellite Ephemeris Parameters Fitting Method Based on Orbit Character of Satellite[J]. Journal of Geodesy and Geodynamics , 2007, 27 (1) : 85 –90. |
| [11] | 肖琴琴, 崔先强, 贾小林, 等. GPS广播星历参数及拟合算法的性能比较[J]. 大地测量与地球动力学 , 2014, 34 (1) : 92–95. XIAO Qinqin, CUI Xianqiang, JIA Xiaolin, et al. Performance Comparison of GPS Broadcast Ephemeris Parameters and Their Fitting Algorithms[J]. Journal of Geodesy and Geodynamics , 2014, 34 (1) : 92 –95. |
| [12] | 张志. 航天飞行器GPS定位技术研究. 西安:西北工业大学[M]. 1995 . ZHANG Zhi. Research of GPS Technology for Aerospace Vehicles. Xi'an:Northwestern Polytechnical University[M]. 1995 . |
| [13] | MONTENBRUCK O, GILL E. Satellite Orbits:Models, Methods and Applications[J]. Applied Mechanics Reviews , 2002, 55 (2) : 2504 –2510. |
| [14] | 葛奎, 王解先. GLONASS卫星位置计算与程序实现[J]. 测绘与空间地理信息 , 2009, 32 (2) : 137–140. GE Kui, WANG Jiexian. Calculation of GLONASS Satellite Station and the Realization of Program[J]. Geomatics&Spatial Information Technology , 2009, 32 (2) : 137 –140. |
| [15] | 葛茂荣, 过静珺, 葛胜杰. GLONASS卫星坐标的计算方法[J]. 测绘通报 , 1999 (2) : 2–4. GE Maorong, GUO Jingjun, GE Shengjie. Calculation of the Coordinates of GLONASS Satellite[J]. Bulletin of Surveying and Mapping , 1999 (2) : 2 –4. |
| [16] | 杜兰. GEO卫星精密定轨技术研究. 郑州:信息工程大学[M]. 2006 . DU Lan. A Study on the Precise Orbit Determination of Geostationary Satellites. Zhengzhou:Information Engineering University[M]. 2006 . |
| [17] | 路余, 杜兰, 张中凯, 等. 增强型轨道列表星历及其在北斗混合星座中的应用[J]. 宇航学报 , 2015, 36 (7) : 804–810. LU Yu, DU Lan, ZHANG Zhongkai, et al. Enhanced Orbit Catalogue Ephemeris and Its Application in BeiDou Mixed Constellation[J]. Journal of Astronautics , 2015, 36 (7) : 804 –810. |
| [18] | 郭睿, 周建华, 胡小工, 等. 一种地球静止轨道卫星的快速恢复定轨方法[J]. 测绘学报 , 2011, 40 . GUO Rui, ZHOU Jianhua, HU Xiaogong, et al. A New Strategy of Rapid Orbit Recovery for the Geostationary Satellite[J]. Acta Geodaetica et Cartographica Sinica , 2011, 40 . |
| [19] | 张中凯, 杜兰, 刘利, 等. GEO广播星历参数设计的无奇点根数法[J]. 测绘学报 , 2014, 43 (5) : 452–457. ZHANG Zhongkai, DU Lan, LIU Li, et al. Parameter Design of GEO Broadcast Ephemeris Based on the Nonsingular Orbital Elements[J]. Acta Geodaetica et Cartographica Sinica , 2014, 43 (5) : 452 –457. DOI:10.13485/j.cnki.11-2089.2014.0076 |
| [20] | ZHOU Shanshi, CAO Yueling, ZHOU Jianhua, et al. Positioning Accuracy Assessment for the 4GEO/5IGSO/2MEO Constellation of COMPASS[J]. Science China Physics, Mechanics and Astronomy , 2012, 55 (12) : 2290 –2299. DOI:10.1007/s11433-012-4942-z |




