2. 江苏省资源环境信息工程重点实验室,江苏 徐州 221008
2. Key Laboratory of Resources and Environmental Information Engineering of Jiangsu Province, China University of Mining and Technology, Xuzhou 221008, China
水汽是描述大气状况的基本特征参数,大气中的水汽含量只占全球水循环系统总量的百分之一左右,却是其中时空变化最快的活跃因子。大气水汽分布及其变化特征的观测,对于研究气候变化有着重要意义。常规的大气水汽探测手段如无线电探空,观测间隔一般为12 h,时间并不连续,且观测站点相隔一般都在200~300 km。地基微波辐射计在有浓云时穿透能力下降,特别是有降水发生时更会产生较大误差。这些都限制了高时空分辨率、高精度的水汽信息获取。地基GPS水汽层析技术补充了常规观测方法的不足,可以获取高时空分辨率,探测精度1~2 mm[1]的水汽资料。
地基GPS水汽层析技术由文献[2]首先提出,它给出了水汽层析方程的水平、垂直约束条件以及层析区域垂直方向分层的理论依据。而在层析区域网格划分方面,文献[3-4]对垂直方向分层及其分辨率进行了专门的研究。通过层析结果与数值天气预报模型[5]以及探空数据[6]的比对,证实层析技术的可靠性,而层析结果与这两个系统之间存在的差异性[7]是由于观测站网形的几何结构不同造成的。长期研究还表明层析模型在垂直分辨率[8-10]以及探测高层水汽(4000 m以上)[11]方面有着局限性。目前可以通过增加COSMIC(掩星)数据[12]、地面气象观测数据[13-14]等来改善层析在垂直分辨率上的不足。
水汽层析技术的原理是通过地基GPS网络以及高精度GPS数据处理软件获取湿延迟观测值,湿延迟和倾斜路径上的水汽含量(slant water vapor,SWV)之间可以进行转换,用于区域水汽场重建。将地基GPS网天顶方向上的空间,在水平和垂直方向上离散化为包含水汽信息的体素;通过SWV构建层析方程组就可以解算出体素内的水汽参数。而包含湿延迟观测值的GPS信号穿过对流层时,受到对流层的折射影响,GPS信号要发生弯曲和延迟,其中信号的弯曲量很小[15],由此引起的路径总延迟(slant total delay,STD)可以忽略[16]。所以在进行GPS水汽层析时,一般将信号传播路径简化为某历元时刻,卫星位置到GPS接收机天线位置的空间直线路径。
建立层析观测方程组是层析技术的核心。构建方程组就要确定每条GPS信号穿过对流层离散化后的体素位置,获取信号穿过这些体素的截距长度,由体素的位置坐标和对应体素内信号长度确定方程的系数矩阵。传统算法[17]是求出信号路径与层析区域内所有面的交点,通过求出两点之间的距离确定对应体素内信号路径的长度。传统算法无法准确地找出层析区域内和信号相交的平面,而需要对所有平面求交后才能判定,增加了不必要的计算量,而当层析区域增大时,每条信号的求交运算也都会相应增加。
针对传统方法存在的上述问题,本文提出了一种投影面算法。该算法在体素大小确定后,即使扩大层析区域也不会增加任何计算量,而且可以准确找出层析区域内与信号相交的平面进行求交运算,避免了计算的冗余。新算法同时采用代数重构算法(algebraic reconstruction technique,ART)进行层析反演,并根据水汽层析的特性对方程组进行分组,通过按次序分组将迭代值投影到各组超平面,提高了反演的迭代速度和精度。本文采用香港卫星定位参考站网(SatRef)提供的GPS信号数据进行试验。采集9个香港参考站不同时段的观测数据,结果表明投影面算法的计算速度更快、计算量更小并且不受层析区域大小影响。
1 投影面算法投影面算法主要包括基于投影面辅助的直线遍历体素和分组投影ART两部分,直线遍历体素算法减少了计算求交平面的数量,而分组投影ART则提高了层析反演的迭代速度以及结果精度。
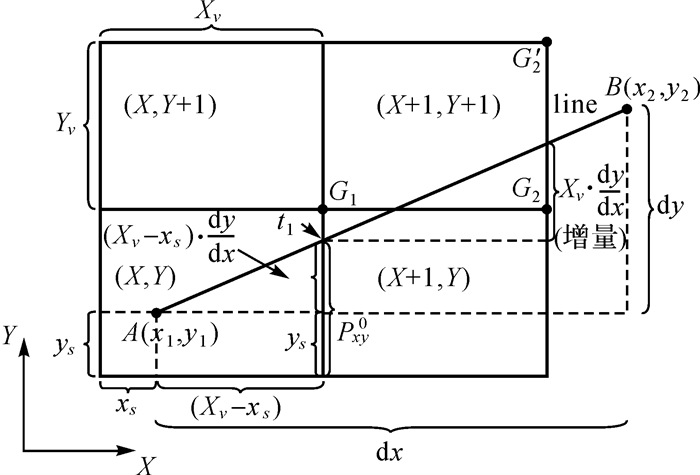
1.1 基于投影面辅助的直线遍历体素投影面算法利用二维空间中像素的遍历算法[18-19]作为辅助,完成三维空间内的体素遍历。如图 1所示,像素遍历即找出直线AB经过的所有像素,设Xv为像素边长,该边与X轴平行,Yv对应与Y轴平行的像素边长。直线AB端点坐标差的绝对值为dx=|x1-x2|、dy=|y1-y2|。起点A所在的像素坐标为X=[x1/Xv]、Y=[y1/Yv],“[ ]”表示向上取整运算,同理终点B所在体素坐标也可以计算出。下面讨论图中Yv/Xv大于dy/dx,且像素路径沿X轴、Y轴正向增加的情况。
|
| 图 1 直线遍历像素 Fig. 1 Line traverse pixels |
首先定义某一点高度为该点与起点A所在像素底边的垂线距离;Gi定义为当前像素右上角点、ti是过Gi点的竖线与直线AB的交点。从起点A(x1, y1)所在的当前像素(X, Y)开始判断直线经过的像素,当直线AB位于当前像素(X, Y)右上角G1点之上时,直线必然经过与当前像素相邻的(X, Y+1)和(X+1, Y+1)。并且(X+1, Y+1)像素就是下一步的当前体素;而若如图 1所示情况,当直线AB在G1点之下时,直线AB经过当前像素右边的(X+1, Y),选择该像素并作为下一步的当前像素,至于此时直线是否还经过(X+1, Y+1)则需进一步判断。因此算法在每一步遍历时分两种路径:直线在参照点Gi之上:(X, Y)→(X, Y+1)→(X+1, Y+1)和直线在参照点之下:(X, Y)→(X+1, Y)。
当判定直线穿过像素的路径后,当前像素变为路径上最后一个到达的像素。再按照上述的方法在下一个单元确定直线穿过像素的路径。判断直线与参照点之间的上下关系,是二维直线像素遍历的关键。从起点像素底边算起,G1点的高度是Yv,而直线AB与过G1点竖线交点t1的初始高度为
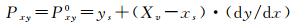 (1)
(1)
通过t1的高度与Yv大小比较,可判定直线与参照点G1的位置关系。当Pxy0大于Yv则说明直线在G1之上,反之Pxy0小于Yv则直线在G1点之下。(X+1, Y)是第2步遍历的当前像素, 则其右上角G2点高度与t2点高度分别是Yv和Pxy0+Xv·(dy/dx)。之后每一步直线与参照点对应垂线交点ti的高度都会增加一个增量Xv·(dy/dx)。若(X+1, Y+1)是当前像素,则用G′2点所在高度(2·Yv)与t2点高度(Pxy=Pxy0+Xv·(dy/dx))比较;Gi高度HGi可用通式(2)表示、ti点高度Hti可用通式(3)表示
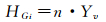 (2)
(2)
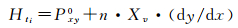 (3)
(3)
式中,n表示大于或等于0的整数;Pxy0是初始高度t1;对应起点体素右上角点G1。通过参照点Gi高度与对应ti点高度可以判定直线经过像素的路径,最终完成所有像素遍历到达终点B。
上面是讨论Yv/Xv大于dy/dx的情况,还有7种情况与其类似,这7种情况对应的参照点Gi高度是Xv或Yv的整数倍,而对应的ti点高度则各不相同。表 1是直线在二维平面内遍历像素的8种情况分类及对应ti点高度的通式。
| 分类 | ti点高度Hti通式 |
| (Yv/Xv) > (dy/dx), x1 < x2, y1 < y2 | 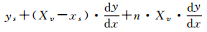 |
| (Yv/Xv) > (dy/dx), x1 < x2, y1 > y2 | 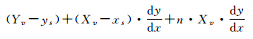 |
| (Yv/Xv) > (dy/dx), x1 > x2, y1 < y2 | 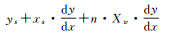 |
| (Yv/Xv) > (dy/dx), x1 > x2, y1 > y2 | 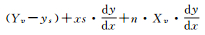 |
| (Yv/Xv) < (dy/dx), y1 < y2, x1 < x2 | 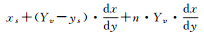 |
| (Yv/Xv) < (dy/dx), y1 < y2, x1 > x2 | 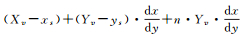 |
| (Yv/Xv) < (dy/dx), y1>y2, x1 > x2 | 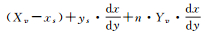 |
| (Yv/Xv) < (dy/dx), y1>y2, x1 < x2 | 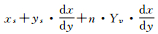 |
三维空间直线遍历体素的投影面算法的思想和二维空间直线的像素遍历一致。如图 2,设三维空间直线AB起点和终点坐标分别是(x1, y1, z1)和(x2, y2, z2),均匀分割的体素在X、Y、Z轴方向的边长分别是Xv、Yv、Zv。直线AB端点坐标差的绝对值为dx=|x1-x2|、dy=|y1-y2|、dz=|z1-z2|。三维空间直线的投影面辅助算法可分为3种情况;分别对应主轴为X轴、Y轴、Z轴的情况。3类情况是关于坐标轴对称的。下面以X轴作为主坐标轴来描述算法步骤。
当Yv/Xv>dy/dx并且Zv/Xv>dz/dx时,X轴判定为主坐标轴。下面空间直线的遍历分两大类情况讨论,第1类,当沿直线从A点所在当前体素(X, Y, Z)穿过下一个体素时,X坐标总是增加或减少一个体素单元;若此时算法判定Y和Z坐标只有其中一个坐标变化(增加或减少一个体素单位)或者不变化,则由二维直线遍历像素算法的扩展就可以解决。Y和Z坐标不变化的情况很简单,这里详细描述Y和Z坐标只有其中一个坐标变化的情况,算法思想是由XY平面和XZ平面的二维直线遍历像素算法获得空间直线遍历体素的位置。如图 2(a)所示,X轴为主轴,直线起点A在体素(X, Y, Z)中。直线AB与体素的交点1、2、3,分别在角a、b、c对应的平面上。将直线AB和体素分别投影到XY和XZ平面,在对应的投影面用二维直线的像素遍历算法分别计算投影直线经过像素的路径。图 2(b)中直线AB在XY平面投影为A1B1,由二维直线遍历像素算法可知A1B1经过像素的路径为:(X, Y)→(X+1, Y)。图 2(c)中直线在XZ平面投影为A2B2,其经过像素路径为:(X, Z)→(X, Z+1)→(X+1, Z+1)。两个投影平面路径的当前像素和终点像素分别对应相同的体素,XY平面的路径实际上应该是(X, Y)→(X, Y)→(X+1, Y),由于前两步路径所在像素相同,所以并未反映在二维投影中。如图 2(a)所示,参照两个投影面的路径可以得到三维空间直线AB经过体素的路径为:(X, Y, Z)→(X, Y, Z+1)→(X+1, Y, Z+1)。
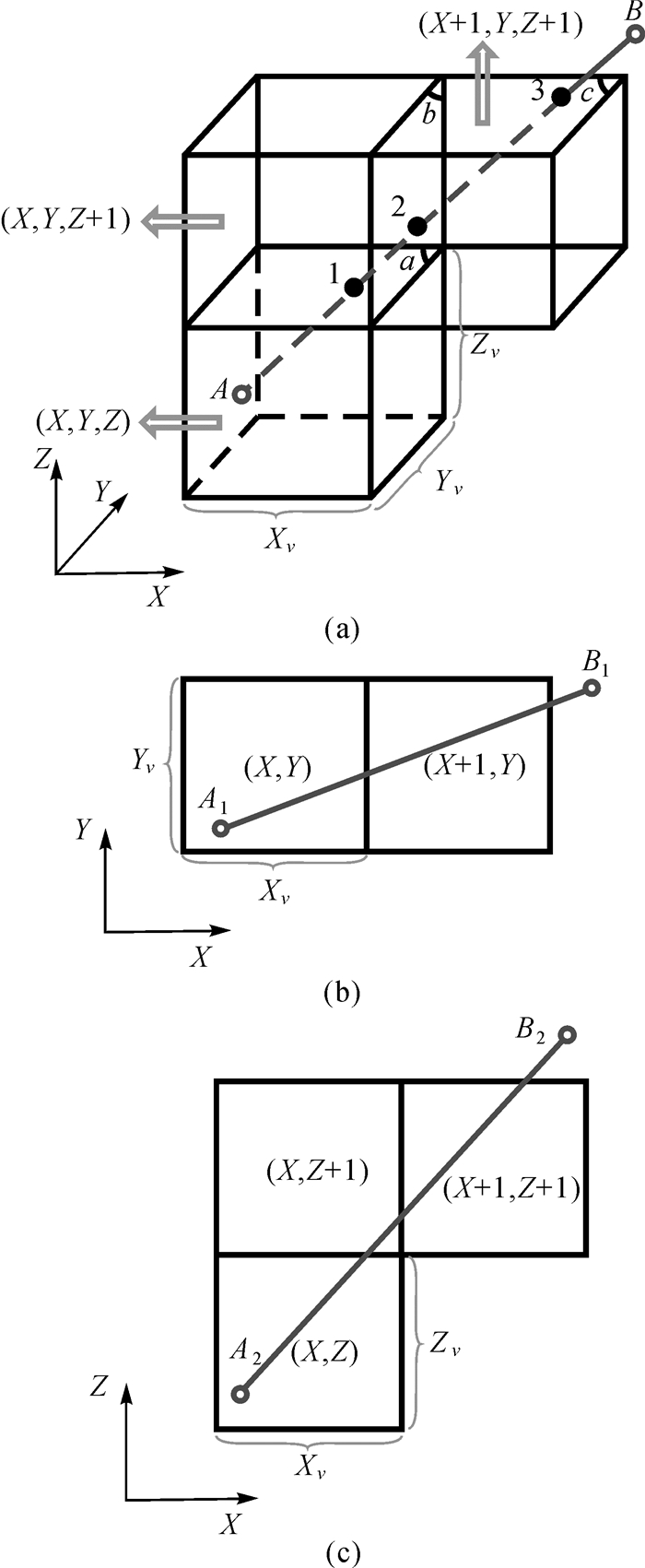
|
| 图 2 第1类空间直线遍历体素 Fig. 2 First type of line traverse voxel |
第2类情况是当Y和Z坐标在一步之内都变化(增加或减少)。如图 3(a)所示,直线穿过角a、b、c、d所在平面的交点为1、2、3、4。可知当前体素(X, Y, Z)和完成一次遍历后,到达的下个当前体素是(X+1, Y+1, Z+1)。图 3(b)中二维直线遍历像素算法可知A1B1经过像素的路径为(X, Y)→(X, Y+1)→(X+1, Y+1)。图 3(b)中直线经过像素路径为(X, Z)→(X, Z+1)→(X+1, Z+1)。第2类情况中,必然经过的体素为:当前体素(X, Y, Z)、(X, Y+1, Z+1)和下一个当前体素(X+1, Y+1, Z+1);而从(X, Y, Z)到达(X, Y+1, Z+1)存在两种不同的选择,因此存在两种不同的路径从当前体素到达下一个当前体素, 路径L1:(X, Y, Z)→(X, Y+1, Z)→(X, Y+1, Z+1)→(X+1, Y+1, Z+1)和路径L2:(X, Y, Z)→(X, Y, Z+1)→(X, Y+1, Z+1)→(X+1, Y+1, Z+1)。两条路径的区别在第2个遍历的体素上,直线是经过体素(X, Y+1, Z)还是(X, Y, Z+1),通过本文提出的投影面辅助方法可以找出正确的路径。当遇到第2类情况时,需判断(X, Y+1, Z)和(X, Y, Z+1)哪一个是直线穿过的体素。此时将图 3(a)投影到两个次轴Y、Z组成的YZ平面上。如图 3(d)所示,通过二维直线遍历体素算法可知投影直线A3B3经过的路径为:(Y, Z)→(Y+1, Z)→(Y+1, Z+1),而体素(X, Y+1, Z)和(X, Y, Z+1)在YZ平面上投影为(Y+1, Z)、(Y, Z+1);与对应的正确路径对比可发现并没有经过像素(Y, Z+1),因此路径2是错误的,去除体素(X, Y, Z+1),正确的路径为L1。

|
| 图 3 第2类空间直线遍历体素 Fig. 3 Second type of line traverse voxel |
1.1.1 求交平面计算优化
采用投影面辅助直线遍历体素算法, 可以准确获取信号穿过的平面, 虽然同传统算法相比, 计算量有所减小,但还是需要较多的计算量。因此对该算法进行优化,从而进一步减少计算量。投影面算法在获取观测方程系数即体素内信号截距长度时,除起点所在体素内的截距需要单独计算外,其他分为两大类情况。首先按照信号穿过的体素坐标中的Z坐标进行分层,第1类情况如图 4(a)所示,体素的Z坐标不重复,体素(X, Y, Z)与(X, Y, Z+1)内的信号截距长度一样,都是信号穿过体素底面和顶面两个交点之间的长度,因此该情况无论直线穿过多少体素,只需计算一次截距长度。第2类情况,Z坐标值重复,将Z坐标数值相同的,按照遍历顺序分为一组,每组除必定穿过的对应体素的起始面(底面)和最终面(顶面)外,还需确定信号穿过的侧面。如图 4(b),直线遍历体素顺序为(X, Y, Z)→(X-1, Y, Z)→(X-1, Y, Z+1)→(X-1, Y+1, Z+1)→(X-2, Y+1, Z+1),按照情况可分组为(X, Y, Z)→(X-1, Y, Z)以及(X-1, Y, Z+1)→(X-1, Y+1, Z+1)→(X-2, Y+1, Z+1)。第1组中,对应底面与顶面分别为z1=(Z-1)·Zv和z3=Z·Zv,其下标表示直线穿过该平面的次序,(X, Y, Z)与(X-1, Y, Z)不同的坐标为X1=X与X2=X-1,则穿过的侧面可通过式(4)计算
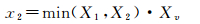 (4)
(4)
式中,min(X1, X2)表示取X1与X2中较小的数值,Xv为体素与X轴平行的边长。
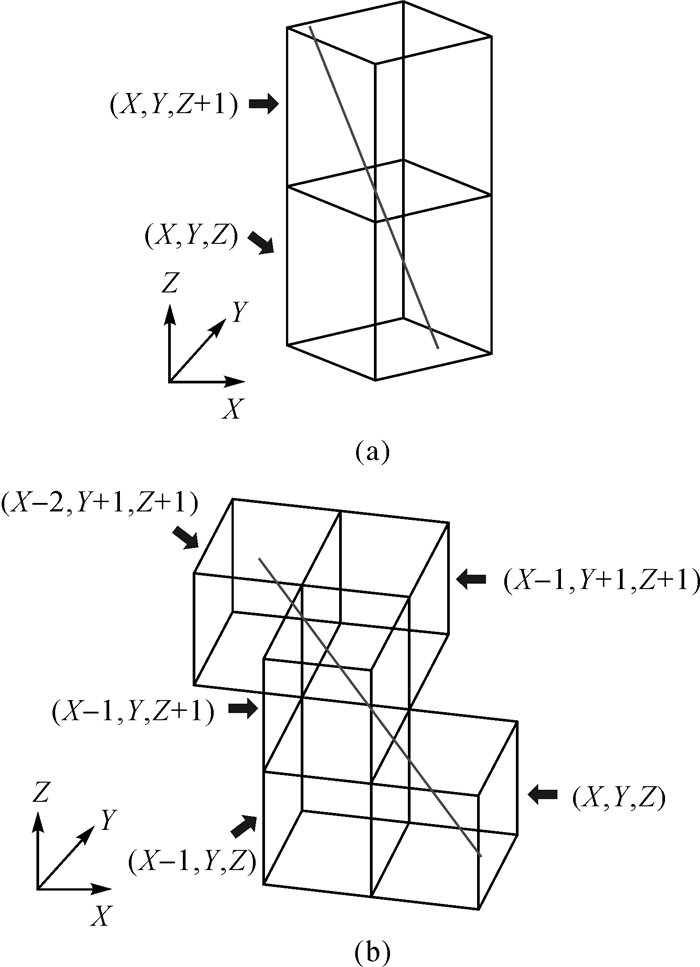
|
| 图 4 计算截距长度的方法 Fig. 4 Method for calculating the length of the ray across voxels |
同理第2组有3个体素,共穿过2个侧面。对照上述方法可知,第1个侧面为y4=Y·Yv,第2个侧面为x5=(X-2)·Xv。第2组底面为第1组的顶面,无需计算,其顶面为z6=(Z+1)·Zv。因此第2类情况,可以通过直线方程与平面方程z1、x2、z3、y4、x5、z6进行求交运算,获取交点坐标后,计算体素内截距长度,而无需对图 4(b)中相关的10个平面全部进行求交运算。由于香港参考站位置密集,层析区域较小,因此层析区域内的信号高度角普遍较高,信号穿过的体素多属于第1种情况,使用本文的方法可以显著提高计算速度。
1.2 分组投影ART代数重构算法的基本原理是从给定的初值x0出发(上标表示迭代次数),通过式(5)将x0按顺序依次投影到方程代表的超平面H上,通过连续的投影,到达所有超平面的交点位置,该位置表示方程组的解
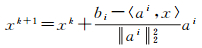 (5)
(5)
由于卫星星座测站分布等引起的层析方程组解算病态问题,需要增加约束条件(如水平、垂直约束方程组)减小方程条件数以及避免解的多值性。观测方程组与约束方程组构成了GNSS水汽层析方程组
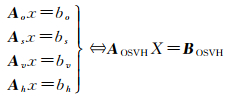 (6)
(6)
式中,Ao、As、Av、Ah分别对应观测、辅助观测、垂直约束、水平约束方程组的系数矩阵,则[Ao As Av Ah]T构成了GNSS水汽层析方程组系数矩阵AOSVH,[bo bs bv bh]T构成等式右端BOSVH,AOSVH和BOSVH的下标OSVH表示4类方程组的排列顺序。其中观测方程组是由式(7)离散化后构成的
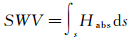 (7)
(7)
式中,s表示信号路径;Habs表示绝对湿度。
代数重构算法进行迭代计算时,方程的投影次序会对最终迭代解的精度和迭代收敛速度造成影响。本节按照4类方程组的可靠性进行分组,将信息量大的观测方程组排在第一组,使解的结果偏向观测方程组提供的信息,有利于精确、高效地重建层析区域;辅助观测方程组和垂直约束方程组虽然都具有较高的精度,但一般包含信息量较少,不利于获取准确的全局信息,这两种方程组的排列顺序根据它们获取信息方式和数量不同可以调换分组顺序;水平约束方程组的加入,虽然可以恢复没有信号穿过体素块内的水汽参数,但在一定程度上降低了层析结果的精度,因此放在最后。分组投影ART算法将方程组按照OSVH顺序进行排序,并利用式(5)进行迭代求解,在满足停止条件后获得最终的迭代解。
2 地基GPS信号处理实例与分析 2.1 试验方案本节利用投影面算法对GPS数据进行处理, 绘制信号穿过体素的射线图。对应2014年3月25日,UTC 6时的层析区域范围为113.841°E-114.425°E,22.07°N-22.618°N,层析最高层为10 km。选取香港卫星定位参考站网(SatRef)9个测站30 min的观测数据,数据采样间隔5 min。研究区域沿东西及天顶方向划分为4×4×10共160个体素。香港9个参考站的层析网格划分和GPS信号遍历体素示意图。
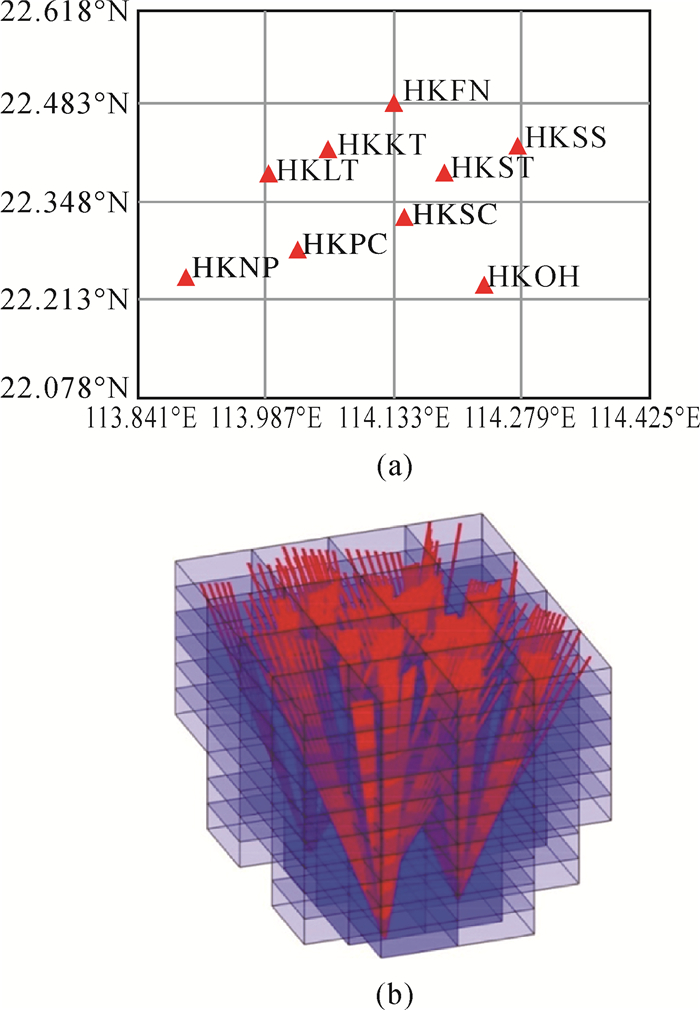
|
| 图 5 GPS信号处理 Fig. 5 GPS network for traversing voxel |
由于在不同时段, GPS信号接收数量不同, 而GPS信号的密集程度以及分布情况对层析区域大小和位置有所影响。在信号密度较低时(信号和区域内体素的比例)应适当缩小层析区域,而当信号密度较高时,可扩大层析区域来获取更多的水汽信息。图 6对应2014年3月25日,UTC 0时(图 6(a))、6时(图 6(b))、12时(图 6(c))GPS信号遍历俯视图。黑框实线内的区域位置大小是相同的,但随着时间的变化,理想的层析区域(黑色虚线方框内区域)发生了变化。UTC 0时由于该时段接受卫星信号较少,层析区域较小。UTC 6时和UTC 12时,由于这两个时段接收的卫星信号较多且分布均匀,所以相应的层析区域扩大。
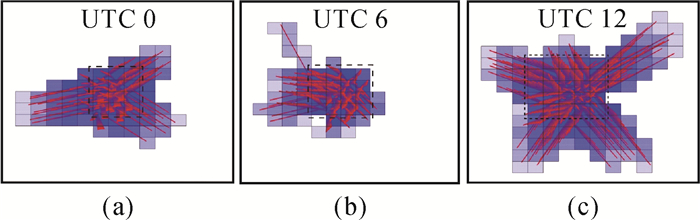
|
| 图 6 GPS信号分布俯视图 Fig. 6 Ground-based GPS signal distribution in the looking-down perspective |
2.2 投影面算法对计算求交平面速度的分析
为验证投影面算法的速度,将其与传统算法在图 6所示的3个时段的求交计算进行比较。表 2通过同时存在于3个时段层析区域内的一条模拟信号,利用传统算法和投影面算法计算其求交平面数量以及所需计算时间,证明了投影面算法随层析区域扩大并不影响其速度也不会增加计算量,而传统算法会随层析区域的扩大而增加计算量和计算时间。
| 算法 | 一条信号计算量(求交平面个数) | 一条信号计算速度/s | |||||
| UTC 0 | UTC 6 | UTC12 | UTC 0 | UTC 6 | UTC12 | ||
| 传统算法 | 19 | 20 | 22 | 0.725 | 0.801 | 0.861 | |
| 投影面算法 | 4 | 4 | 4 | 0.186 | 0.186 | 0.186 | |
表 3通过对3个时段所有层析区域内GPS信号,在两种算法下计算的求交平面个数和计算速度进行比较,证明了投影面算法与传统算法相比,具有更快的计算速度,并且通过1.1.1节提出的对求交平面分类的优化方法,减少了求交平面的数量。
| 算法 | 所有信号计算量(求交平面个数) | 所有信号计算速度/s | |||||
| UTC 0 | UTC 6 | UTC12 | UTC 0 | UTC 6 | UTC12 | ||
| 传统算法 | 9215 | 16 420 | 18 216 | 330.582 | 618.506 | 683.216 | |
| 投影面算法 | 892 | 2169 | 2495 | 32.119 | 77.811 | 89.493 | |
2.3 投影面算法对水汽反演精度的分析
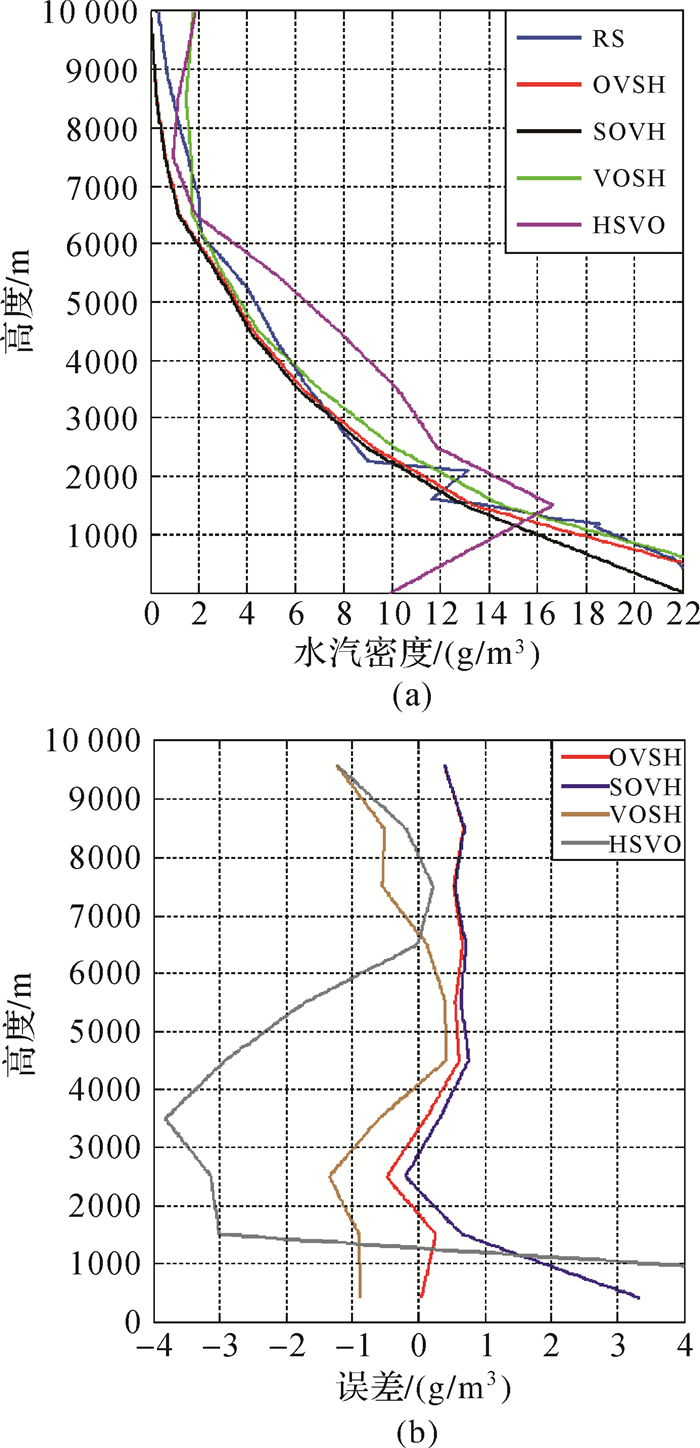
试验按照1.2节提出的分组表示方法,选择OVSH、VOSH、SOVH、HSVO 4种不同分组方案,利用2014年3月25日,UTC 0时HKKP气象站数据与4种方案计算的对应体素内水汽参数进行比较分析,证明了分组投影ART算法的合理性。图 7(a)是4种方案与探空数据(RS)拟合的水汽廓线对比,从图中可以看出投影面算法采用的OVSH与RS数据的水汽廓线基本一致,拟合水汽廓线最大误差出现在2130 m(0.853 2 g/m3),主要原因是水汽在1500~2500 m之间出现违反指数递减规律的波动。图 7(b)是不同方案计算的各层平均水汽值同对应RS数据做差获得的误差曲线图,方案OVSH对应的误差曲线基本在0附近波动,而其他几个方案则误差较大,HSVO方案由于迭代结果偏向前3组约束方程提供的先验信息,导致层析结果与实际不符,SOVH与VOSH层析误差也有较大波动,从层析结果来看,方程组的顺序对层析反演精度具有重要影响。
|
| 图 7 水汽层析结果 Fig. 7 Results of Water Vapor Tomography |
图 8是各组方案的RMSE曲线图,横轴表示迭代次数,反映迭代收敛速度;纵轴表示RMSE,反映迭代结果的精度。结合表 4各方案RMSE以及迭代次数,可以看出与水汽廓线对应,OVSH的RMSE值最小(0.486 8 g/m3),HSVO的精度最低(3.799 5 g/m3)。本次试验采用的垂直约束方程组V利用经验模型获取,精度较低。而辅助观测方程组S是利用Rinex met获取的地表气象数据,精度较高。因此采用SOVH方案使结果偏向S提供的信息时,要比偏向V的VOSH方案精度高。而HSVO解算结果精度最低,主要是由于H组成的约束条件自身含有较大误差,但其迭代次数只有26次,因为先进行迭代的HSV方程组包含水汽信息更全面,使迭代结果更易快速收敛,但无法保证结果的精度。

|
| 图 8 不同方案RMSE值 Fig. 8 RMSE for different schemes |
| 分组方案 | OVSH | SOVH | VOSH | HSVO |
| RMSE/(g/cm3) | 0.486 8 | 0.708 9 | 0.996 8 | 3.799 5 |
| 迭代次数 | 38 | 41 | 47 | 26 |
3 结论
本文通过对直线遍历体素时的辅助投影面以及迭代计算时投影到超平面的顺序进行研究,根据水汽层析的特性提出了投影面算法。与传统算法相比,利用1.1.1节优化方法,投影面算法在计算求交平面时,计算速度更快、计算量更小,并且不受层析区域大小影响,计算效率上的优势会随着层析区域的扩大而更加明显,随着各国GPS网的加密与建设,GPS水汽层析的区域势必会进一步扩大,本文提出的直线遍历体素算法可以高效地获取层析的系数矩阵,为今后进行实时大区域地基GPS水汽层析做好准备。而在水汽层析反演计算方面,新算法通过分组排序的方式,使迭代解的结果偏向观测方程组提供的可靠信息,提高了ART算法的精度,反演结果与HKKP提供的探空数据具有良好的一致性。试验分析发现优先对包含完备信息的方程组(如约束方程组)进行迭代计算,虽然可以达到快速收敛的目的,但若该组方程误差较大,先验信息不准确,其结果也会偏向误差较大的方程提供的信息,最终降低解算的结果。由于ART算法本质是通过逐个迭代方程获得迭代解,因此除按照方程组性质进行分组外,对分组后每个层析方程的排序也是今后需要研究的问题之一。
| [1] | JIANG P, YE S R, LIU Y Y, et al. Near Real-time Water Vapor Tomography Using Ground-based GPS and Meteorological Data:Long-term Experiment in Hong Kong[J]. Annales Geophysicae , 2014, 32 (8) : 911 –923. DOI:10.5194/angeo-32-911-2014 |
| [2] | FLORES A, RUFFINI G, RIUS A.4D Tropospheric Tomography Using GPS Estimated Delays[C]//Proceedings of the IEEE 1999 International Geoscience and Remote Sensing Symposium, 1999.Hamburg:IEEE, 1999, 1:675-677. |
| [3] | SHRESTHA S M.Investigations into the Estimation of Tropospheric Delay and Wet Refractivity Using GPS Measurements[R].Calgary, Alberta:University of Calgary, 2003. |
| [4] | HOYLE V A.Data Assimilation for 4-D Wet Refractivity Modelling in a Regional GPS Network[R].Calgary, Alberta:University of Calgary, 2005. |
| [5] | PANY T, PESEC P, STANGL G. Atmospheric GPS Slant Path Delays and Ray Tracing through Numerical Weather Models:A Comparison[J]. Physics and Chemistry of the Earth, Part A:Solid Earth and Geodesy , 2001, 26 (3) : 183 –188. DOI:10.1016/S1464-1895(01)00044-8 |
| [6] | BI Yanmeng, MAO Jietai, LI Chengcai. Preliminary Results of 4-D Water Vapor Tomography in the Troposphere Using GPS[J]. Advances in Atmospheric Sciences , 2006, 23 (4) : 551 –560. DOI:10.1007/s00376-006-0551-y |
| [7] | TROLLER M, LEUENBERGER D, BROCKMANN E, et al. GPS-tomography:Results and Analyses of the Operational Determination of Humidity Profiles over Switzerland[J]. Geophysical Research Abstracts , 2007, 9 : 11 –18. |
| [8] | BENDER M, RAABE A. Preconditions to Ground Based GPS Water Vapour Tomography[J]. Annales Geophysicae , 2007, 25 (8) : 1727 –1734. DOI:10.5194/angeo-25-1727-2007 |
| [9] | BOCK O, DOERFLINGER E, MASSON F, et al. GPS Water Vapor Project Associated to the ESCOMPTE Programme:Description and First Results of the Field Experiment[J]. Physics and Chemistry of the Earth , 2004, 29 (2-3) : 149 –157. DOI:10.1016/j.pce.2004.01.014 |
| [10] | PERLER D, GEIGER A, HURTER F. 4D GPS Water Vapor Tomography:New Parameterized Approaches[J]. Journal of Geodesy , 2011, 85 (8) : 539 –550. DOI:10.1007/s00190-011-0454-2 |
| [11] | CHAMPOLLION C, MASSON F, BOUIN M N, et al. GPS Water Vapour Tomography:Preliminary Results from the ESCOMPTE Field Experiment[J]. Atmospheric Research , 2005, 74 (1-4) : 253 –274. DOI:10.1016/j.atmosres.2004.04.003 |
| [12] | XIA P, CAI C, LIU Z. GNSS Troposphere Tomography Based on Two-step Reconstructions Using GPS Observations and COSMIC Profiles[J]. Annales Geophysicae , 2013, 31 (10) : 1805 –1815. DOI:10.5194/angeo-31-1805-2013 |
| [13] | ROHM W, BOSY J. The Quality of Meteorological Observations and Tropospheric Delay from EPN/IGS Permanent Stations Located in the Sudety Mountains and in the Adjacent Areas[J]. Acta Geodynamica et Geomaterialia , 2007, 4 (4) : 145 –152. |
| [14] | VEDEL H, HUANG Xiangyu. Impact of Ground Based GPS Data on Numerical Weather Prediction[J]. Journal of the Meteorological Society of Japan , 2004, 82 (1B) : 459 –472. DOI:10.2151/jmsj.2004.459 |
| [15] | 丁金才. GPS气象学及其应用[M]. 北京: 气象出版社, 2009 . DING Jincai. GPS Meteorology and Its Applications[M]. Beijing: China Meteorological Press, 2009 . |
| [16] | BEVIS M, BUSINGER S, HERRING T A, et al. GPS Meteorology:Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research:Atmospheres , 1992, 97 (D14) : 15787 –15801. DOI:10.1029/92JD01517 |
| [17] | 刘春华.三维投影矩阵的刻画及迭代重建的加速研究[D].太原:中北大学, 2008. LIU Chunhua.The Study of Building Three-dimensional Projection Matrix and Accelerate Iterative Image Reconstruction[D].Taiyuan:North University of China, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10110-2008142732.htm |
| [18] | BRESENHAM J E. Algorithm for Computer Control of a Digital Plotter[J]. IBM Systems Journal , 1965, 4 (1) : 25 –30. DOI:10.1147/sj.41.0025 |
| [19] | AMANATIDES J, WOO A. A Fast Voxel Traversal Algorithm for Ray Tracing[J]. Eurographics , 1987, 87 (3) : 10 . |


