病态问题是大地测量数据处理中经常会遇到的棘手问题,广泛存在于GPS快速定位[1-2]、GPS水汽层析、卫星重力延拓[3]及InSAR形变监测等领域。当模型出现病态时,观测数据的微小变化常常会造成难以估计的巨大变化,估值极不稳定,很难得到可靠的参数估计。这种情况下,测量数据处理常用的最小二乘估计虽然仍是无偏估计,但已不是最优估计[4]。针对病态问题,学者们提出了一系列改善估计质量的有偏估计方法[5-7],如岭估计法、截断奇异值法、Tikhonov正则化法等,其中应用最广泛的是Tikhonov正则化法。
Tikhonov正则化法通过正则化参数和正则化矩阵作用于原病态矩阵来改善矩阵的病态性,得到参数更为可靠的稳定解。其中正则化参数与正则化矩阵的确定至关重要,正则化参数起到平衡病态矩阵与正则化矩阵的作用,反映了正则化矩阵的权重大小,正则化矩阵则是对病态矩阵的修正。国内外学者针对正则化法的研究多集中于正则化参数的选取上,提出了许多有效的正则化参数确定方法,如岭迹法、GCV(广义交叉核实)法[8]、L曲线法[9-10]、方差分量估计法[11]等,但针对正则化矩阵的研究较少。一些学者提出将参数的后验协方差阵的逆矩阵作为正则化矩阵[12],则正则化矩阵可视为待定参数的权重,但是待定参数并非观测值,也没有实际意义上的权重。也有一些学者提出利用未知参数的先验信息的确定正则化矩阵,如在卫星定位和重力场反演中,有的利用了模糊度参数的特性[13],有的利用了反映位系数统计规律的Kaula规则[14],这些方式多针对参数包含先验信息的情形。处理病态问题常用的岭估计法中,正则化矩阵为单位阵,即稳定泛函为参数的二范约束的正则化法的特例。岭估计法在改善矩阵病态性的同时也过多地引入了偏差,降低了解的可靠性。因此,正则化矩阵的有效形式仍需进一步研究。本文通过分析岭估计的方差与偏差,提出基于较小奇异值特征向量构造正则化矩阵的方法,在有效减小方差的同时,减少偏差的引入,得到更可靠的稳定解。
1 解算病态问题的正则化方法对于经典测量观测模型
 (1)
(1)
其最小二乘估计及估计的协方差为
 (2)
(2)
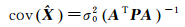 (3)
(3)
由于权矩阵P可进行单位化,为了方便推导,设权矩阵P为单位阵,对系数矩阵A进行奇异值分解可得[15]
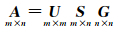 (4)
(4)
协方差矩阵的迹是各参数估计的方差之和,可以整体反映参数估计方差的大小,由式(3)和式(5)得到最小二乘估计的整体方差为
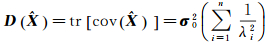 (6)
(6)
式(5)中,λ1>λ2>…>λn为设计矩阵的奇异值,若方程病态,则λ1远大于λn,λn为接近于零的较小值。由式(6)可以看出,较小的奇异值会对估计的方差造成严重影响,估计方差被较小的奇异值严重放大,这导致最小二乘估计极不可靠,已无法得到参数的准确估值。
为了提高估计的稳定性,Tikhonov正则化方法在经典最小二乘平差准则的基础上加入稳定泛函约束条件,并引入正则化因子调节两部分的平衡,使不适定问题转化为适定问题。正则化准则表示为[7]
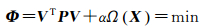 (7)
(7)
式中,Ω(X)称为稳定泛函,起到稳定化的作用;α为正则化参数,起着平衡准则函数中两部分的作用。Ω(X)的选择常常提示出问题的特性[7],不同的病态问题可能具有不同类型的稳定泛函。目前大地测量领域中一般取Ω(X)=XTRX[16],其中R为对称非负定,称为正则化矩阵。则正则化准则可表示为
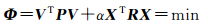 (8)
(8)
Ω(X)的不同形式通过正则化矩阵R的不同形式来反映,在参数包含先验信息时,文献[17]建议依据参数的先验信息采用选权拟合的方法确定R。对于单频GPS的快速定位,文献[13]提出先对法方程矩阵进行奇异值分解,利用奇异值分解后的矩阵构建R,该方法利用了GPS定位位置参数与模糊度参数的不同特性。
在参数不包含先验信息时,大地测量中常将稳定泛函取为参数的二范约束,即取R=I,正则化准则即为
 (9)
(9)
平差的结果为
 (10)
(10)
这就是常用的岭估计法。这时稳定泛函为Ω(X)=XTRX=XTX。
正则化法是一种有偏估计方法,其在改善法方程病态性的同时不可避免地引入了偏差[15],在法方程病态性得到有效改善的情况下,偏差的引入却降低了参数估计的可靠性。目前,针对正则化方法的研究主要集中于正则化参数的选取上,而对正则化矩阵的研究较少。良好的正则化矩阵可有效改善矩阵的病态性,最大程度地减少偏差的引入,使病态问题解算具有更高的可靠性,正则化矩阵的选取对病态问题的解算具有重要意义。
2 正则化矩阵的构造方法研究 2.1 岭估计方差与偏差分析岭估计法可看作是正则化矩阵为单位阵的正则化方法,可有效减小参数估计的方差,改善解的稳定性。依据协方差传播律可得岭估计协方差计算公式为[18-19]
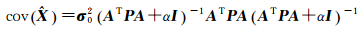 (11)
(11)
协方差矩阵迹可以在整体上反映估计量方差大小,由协方差公式可得矩阵迹为
 (12)
(12)
对方阵ATPA进行特征值分解可得
 (13)
(13)
式中,特征值Λi=λi2,即法方程系数矩阵的特征值是观测方程系数矩阵奇异值的平方,而特征值Λi的特征向量即是λi的右奇异向量。将式(13)代入式(12)可得
 (14)
(14)
岭估计为有偏估计,其偏差计算公式为[15]
 (15)
(15)
对式(15)进行特征值分解化简并求迹得
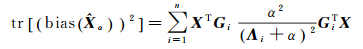 (16)
(16)
由式(14)可见,岭估计通过修正法方程矩阵的特征值来减小估计的方差,提高解的稳定性。由于正则化矩阵为单位阵,正则化参数对各特征值均进行修正,修正程度均为正则化参数α。由式(16)可知,岭估计在降低估计方差的同时也引入了偏差,偏差大小与正则化参数和正则化矩阵息息相关,在正则化参数确定时,正则化矩阵影响正则化法对特征值的修正作用,可使正则化法对特征值有选择的修正,进而调节偏差的引入。
由于模型病态,设计矩阵的条件数较大,最大特征值与最小特征值之间相差几个数量级,而正则化参数α多为远小于最大特征值的较小值,由式(14)和式(16)可见对较大特征值的修正不会有效降低估计的方差,反而更多地引入了偏差。因此有选择性地使正则化法仅对较小的特征值进行修正,可有效降低参数估计的方差,同时减少正则化法对偏差的引入。
2.2 基于小奇异值特征向量构造正则化矩阵由式(6)可以看出,参数的估计方差可以看作是各特征值引起的方差分量之和,其中特征值越小,对方差影响越大,引起的方差分量越大。因此,病态性的影响主要体现在较小的特征值对方差的放大。由于Λi=λi2,特征值对方差的影响可表示为奇异值对标准差的影响
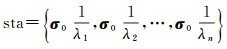 (17)
(17)
由式(17)可见,奇异值越小,对标准差的影响越大,其标准差分量在集合中占的比重也越大,病态矩阵的奇异值中常会出现多个较小的奇异值,因此这些较小的奇异值引起的标准差分量之和占据了标准差的绝大部分。依据病态矩阵较大奇异值与较小奇异值差值较大的特性,设定小奇异值标准差分量之和占标准差比重达到95%以上时,这些奇异值为影响严重的小奇异值,应对其进行正则化以缓解对标准差的影响,判定条件可表示为
 (18)
(18)
奇异值矩阵S中,λ1>λ2>…>λk>…>λn,λk为判定小奇异值的分界值,选取小奇异值对应的特征向量构造正则化矩阵
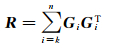 (19)
(19)
构造新正则化矩阵后的正则化方法可表示为
 (20)
(20)
 (21)
(21)
将新正则化矩阵代入式(14)可得正则化法的方差矩阵迹为
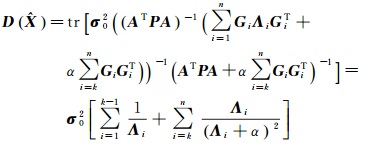 (22)
(22)
将新正则化矩阵代入式(16)得正则化法偏差计算公式
 (23)
(23)
由式(22)可以得出,基于较小奇异值特征向量构造的正则化矩阵,可使正则化法仅对法方程矩阵较小的特征值进行修正,保持较大特征值不变,有效降低了参数估计的方差。比较式(16)与式(23)可以得出,式(23)恒小于式(16),新正则化法较岭估计法减少了偏差的引入。因此,基于较小奇异值特征向量构造正则化矩阵是理论上可行的正则化矩阵构造方法,可有效降低正则化估计的方差,减少偏差,提高参数估计的稳定性和可靠性。
观测方程的病态性多是由于观测条件较差或过度地参数化所引起的,由于观测信息不足以估计所有参数,造成部分参数的估计方差较大,估计不稳定。对观测方程的系数矩阵进行奇异值分解,分析病态性在特征向量的空间影响可知,病态性对估计方差的影响集中体现在较小的奇异值对方差的放大上,较大的奇异值未对方差造成不良影响。通过选择较小的奇异值对应的特征向量,构造正则化矩阵,可对较小的奇异值进行补充修正,由于奇异值分解将信息不足部分集中体现在较小的奇异值上,对较小奇异值的补充修正可更高效地降低方差,而保留信息充足的较大的奇异值部分可减少信息的损坏,进而减少估计的偏差,因此相比于岭估计法的无差别补充,降低方差更高效,引入的偏差更少。
2.4 新正则化法与截断奇异值法的比较分析截断奇异值法是基于奇异值分解技术的病态方程的一种直接解法,其原理是将较小的奇异值删除,保留较大的奇异值进行解算。
设截断参数为k,将式(5)中S较大的奇异值求逆,较小的奇异值取0得
 (24)
(24)
则病态方程的截断奇异值解法为
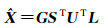 (25)
(25)
由式(25)可得截断奇异值法协方差矩阵迹计算公式为
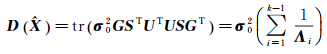 (26)
(26)
截断奇异值法的偏差计算公式为
 (27)
(27)
 (28)
(28)
比较式(22)与式(26)可以得出,新正则化法与截断奇异值法均是通过处理病态矩阵的小奇异值来降低参数估计的方差;而不同之处在于,新正则化法是对较小的奇异值进行修正,而截断奇异值法是将较小的奇异值删除。由式(22)可以看出新正则化法在正则化参数调节下,其改善方差的效果与截断奇异值法相近。比较式(23)与式(28)可知,式(23)恒小于式(28),这表明对小奇异值修正引入的偏差要始终小于删除小奇异值引入的偏差,因而,新正则化法引入的偏差要小于截断奇异值法。此外,由式(26)和式(28)可以看出,截断奇异值法在截掉小奇异值后,其方差下降量和偏差引入量也已固定不可调节,而新正则化法可通过正则化参数进行调节,这表明在小奇异值的选择上,新正则化的可选空间更大,稳定性更高。因此,新正则化法相比于截断奇异值法具有一定的优势。
3 算例分析 3.1 算例1采用文献[20]模拟病态问题算例,法方程矩阵的条件数为1.285 5×105,严重病态。未知参数真值为X=[1 1 1 1 1]T,在观测值中加入N(0, 0.25)的随机噪声。对法矩阵进行奇异值分解并计算奇异值标准差分量,由图 1可以看出,后两个奇异值引起的标准差分量之和达到标准差的99%,因此,选取后两个奇异值对应的特征向量构造正则化矩阵。分别采用岭估计法、截断奇异值法和构造正则化矩阵的正则化法进行平差解算。确定正则化参数的方法主要有岭迹法、GCV法和L曲线法,但针对不同问题,还没有一种方法能够一致地优于另一种,将3种方法确定的正则化参数分别计算出来作为参考,由于岭迹法确定的岭参数具有很大的主观性,在选取岭参数的时候,岭参数值保留在了小数点后一位。

|
| 图 1 奇异值标准差分量 Fig. 1 Standard deviation components |
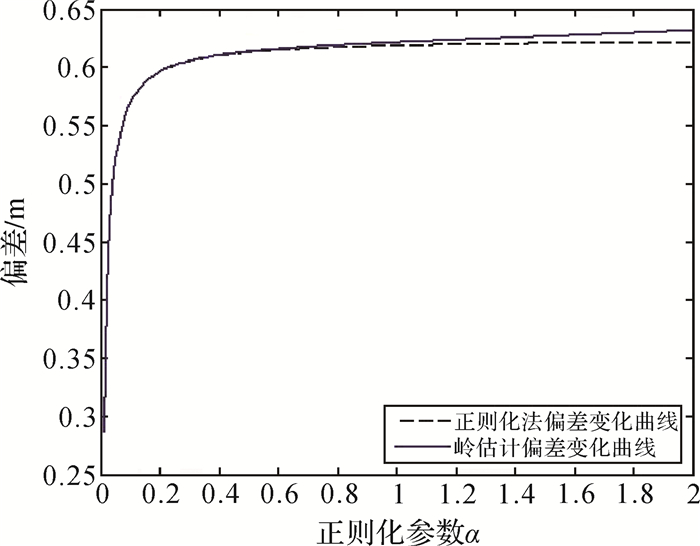
由表 1可以得出,由于设计矩阵的病态性,经典最小二乘估计方差较大,估计极不稳定,已得不到正确的参数估值。岭估计法、新正则化法以及截断奇异值法均可有效改善估计的稳定性,是有效的病态问题解算方法。其中新正则化法和岭估计法相比于截断奇异值法可靠性更高,参数估值更接近于真值。在正则化参数由相同方法确定时,新正则化法的估计结果优于岭估计法。由图 2和图 3可以看出,新正则化法的方差变化曲线与岭估计法的方差变化曲线基本一致,而偏差变化曲线的增幅要小于岭估计法。因此,基于较小奇异值特征向量构造正则化矩阵可使正则化法解算效果优于岭估计法,是一种行之有效的正则化矩阵构造方法。
| 参数 | 真值 | LS估计 | 截断奇异值法 | 岭迹法α=0.4 | L曲线法α=0.533 9 | |||
| 岭估计 | 新正则化法 | 岭估计 | 新正则化法 | |||||
| 参数值 | 1 | -3.723 9 | 1.183 8 | 1.095 4 | 1.107 7 | 1.110 2 | 1.126 5 | |
| 1 | 3.296 5 | 0.434 3 | 0.446 4 | 0.443 5 | 0.444 9 | 0.441 2 | ||
| 1 | 1.469 9 | 0.831 3 | 0.817 0 | 0.832 5 | 0.811 5 | 0.832 2 | ||
| 1 | 10.367 3 | 0.601 2 | 0.746 2 | 0.752 5 | 0.706 6 | 0.715 0 | ||
| 1 | -0.130 6 | 1.291 3 | 1.284 8 | 1.286 8 | 1.285 2 | 1.288 0 | ||
| ∑|ΔX| | 0 | 17.988 3 | 1.608 2 | 1.370 6 | 1.365 9 | 1.432 3 | 1.426 1 | |

|
| 图 2 方差变化曲线 Fig. 2 Variance curves |
|
| 图 3 偏差变化曲线 Fig. 3 Bias curves |
3.2 算例2
采用文献[12]空间测边网算例,算例中包含9个已知点、两个未知点,未知点的模拟真值为(0,0,0)和(7,10,-5)。通过19个等精度观测确定两个未知点的坐标。根据观测值构造法方程,参数初值取为(0.5,-0.5,0.5)与(7.5,9.5,-5.5)时,法矩阵的条件数为4 164.15,属于病态问题。分别采用岭估计法、截断奇异值法和新正则化法进行平差解算。应用正则化参数确定方法确定正则化参数。对法矩阵进行奇异值分解并计算奇异值标准差分量。由图 4可知,后3个较小奇异值引起的标准差分量之和达到标准差的96%,因此,选取后3个较小的奇异值对应的特征向量构造正则化矩阵。

|
| 图 4 奇异值标准差分量 Fig. 4 Standard deviation components |
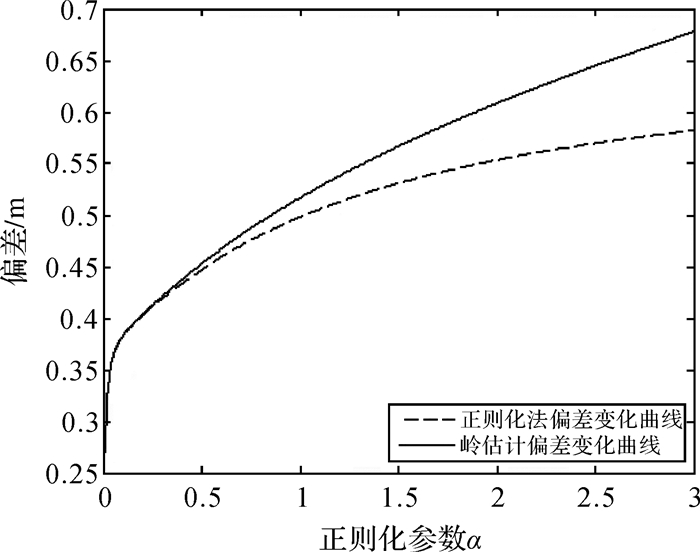
由表 2可以得出与表 1相同的结论,由于模型的病态性,经典最小二乘估计已不是一个良好的估计。岭估计法、新正则化法以及截断奇异值法可有效提高估计精度。对采用相同方法确定正则化参数的岭估计和新正则化法估计结果进行比较发现整体上新正则化法的估计结果优于岭估计法。在正则化参数由GCV法确定时,截断奇异值法的估计结果优于新正则化法和岭估计法,而正则化参数由岭迹法和L曲线法确定时,新正则化法和岭估计法的估计结果更优。因此,在正则化参数合理确定时(GCV法确定的正则化参数在本算例中非最优),新正则化法的估计结果要优于岭估计法和截断奇异值法。由图 5和图 6可以看出,新正则化法的方差变化曲线与岭估计法的方差变化曲线基本一致,而偏差变化曲线的增幅要小于岭估计法,这表明基于较小奇异值特征向量构造正则化矩阵,可有效降低估计方差,减少偏差引入,是行之有效的正则化矩阵构造方法。
| 参数 | 真值 | LS估计 | 截断奇异值法 | 岭迹法α=0.5 | GCV α=0.045 4 | L曲线α=0.200 7 | L曲线α=0.801 0 | ||||
| 岭估计 | 新正则化法 | 岭估计 | 新正则化法 | 岭估计 | 新正则化法 | ||||||
| 参数值 | 0 | 0.068 7 | -0.028 9 | 0.060 3 | 0.018 9 | 0.062 4 | 0.058 3 | 0.056 5 | 0.008 0 | ||
| 0 | -0.255 0 | -0.191 7 | -0.091 4 | -0.058 8 | 0.035 2 | 0.038 5 | -0.018 2 | -0.089 0 | |||
| 0 | -5.755 9 | 0.465 4 | 0.752 4 | 0.748 7 | 0.739 8 | 0.739 5 | 0.841 7 | 0.687 5 | |||
| 7 | 7.004 5 | 7.067 7 | 7.084 8 | 7.061 3 | 7.058 8 | 7.056 6 | 7.069 2 | 7.062 5 | |||
| 10 | 14.271 1 | 9.464 3 | 10.124 0 | 10.120 2 | 10.795 8 | 10.795 4 | 10.417 9 | 9.966 6 | |||
| -5 | -5.417 8 | -5.425 4 | -5.232 4 | -5.227 2 | -5.059 3 | -5.058 7 | -5.138 5 | -5.275 4 | |||
| ∑|ΔX| | 0 | 10.773 2 | 1.715 1 | 1.345 5 | 1.235 3 | 1.751 5 | 1.747 2 | 1.542 4 | 1.155 8 | ||

|
| 图 5 方差变化曲线 Fig. 5 Variance curves |
|
| 图 6 偏差变化曲线 Fig. 6 Bias curves |
4 结语
岭估计法是正则化矩阵为单位阵的正则化方法的特例。通过对岭估计的方差与偏差进行分析得到,岭估计对病态矩阵的各奇异值均进行修正,以减小方差,提高解的稳定性。由于矩阵的奇异性,较大奇异值与较小奇异值之间相差几个数量级,而正则化参数多为较小值,修正大奇异值对减小估计方差效果不明显,却更多地引入了偏差,降低了解的可靠性。通过选取较小奇异值特征向量构造正则化矩阵,调节正则化法对奇异值的修正作用,使正则化法仅对较小的奇异值进行修正,可有效降低参数估计的方差,减少偏差的引入,提高正则化估计的可靠性。与截断奇异值法的比较分析可知,新正则化法是对较小的奇异值进行修正,而截断奇异值法是将较小的奇异值删除。对小奇异值修正引入的偏差要始终小于删除引入的偏差,因而新正则化法引入的偏差小于截断奇异值法。因此,构造正则化矩阵的正则化法相比于截断奇异值法具有一定的优势。
| [1] | GUI Qingming, HAN Songhui. New Algorithm of GPS Rapid Positioning Based on Double-k-type Ridge Estimation[J]. Journal of Surveying Engineering , 2007, 133 (4) : 173 –178. DOI:10.1061/(ASCE)0733-9453(2007)133:4(173) |
| [2] | LI Bofeng, SHEN Yunzhong, FENG Yanming. Fast GNSS Ambiguity Resolution as an Ill-posed Problem[J]. Journal of Geodesy , 2010, 84 (11) : 683 –698. DOI:10.1007/s00190-010-0403-5 |
| [3] | SAVE H, BETTADPUR S, TAPLEY B D. Reducing Errors in the GRACE Gravity Solutions Using Regularization[J]. Journal of Geodesy , 2012, 86 (9) : 695 –711. DOI:10.1007/s00190-012-0548-5 |
| [4] | 崔希璋, 於倧俦, 陶本藻, 等. 广义测量平差[M]. 新版 武汉: 武汉测绘科技大学出版社, 2001 . CUI Xizhang, YU Zongchou, TAO Benzao, et al. Generalized Surveying Adjustment[M]. New Ed Wuhan: Wuhan Technical University of Surveying and Mapping Press, 2001 . |
| [5] | 朱建军. 岭估计的一种新的算法[J]. 测绘信息与工程 , 1997 (3) : 22–25. ZHU Jianjun. A New Algorithm for Ridge Estimate[J]. Journal of Geomatics , 1997 (3) : 22 –25. |
| [6] | HANSEN P C. The Truncated SVD as a Method for Regularization[J]. BIT Numerical Mathematics , 1987, 27 (4) : 534 –553. DOI:10.1007/BF01937276 |
| [7] | TIKHONOV A N, ARSENIN V Y. Solutions of Ill-posed Problems[M]. JOHN F, trans New York: Halsted Press, 1997 . |
| [8] | GOLUB G H, HEATH M, WAHBA G. Generalized Cross-validation as a Method for Choosing a Good Ridge Parameter[J]. Technometrics , 1979, 21 (2) : 215 –223. DOI:10.1080/00401706.1979.10489751 |
| [9] | HANSEN P C. Analysis of Discrete Ill-posed Problems by Means of the L-curve[J]. SIAM Review , 1992, 34 (4) : 561 –580. DOI:10.1137/1034115 |
| [10] | HANSEN P C. The Use of the L-curve in the Regularization of Discrete Ill-posed Problems[J]. SIAM Journal on Scientific Computing , 1993, 14 (6) : 1487 –1503. DOI:10.1137/0914086 |
| [11] | 戴吾蛟, 冯光财, 朱建军. 一种基于Helmert方差分量估计的岭参数确定方法[J]. 大地测量与地球动力学 , 2006, 26 (4) : 30–33. DAI Wujiao, FENG Guangcai, ZHU Jianjun. A Method for Selecting Ridge Parameter Based on Helmert Variance Components Estimation[J]. Journal of Geodesy and Geodynamics , 2006, 26 (4) : 30 –33. |
| [12] | 王振杰, 欧吉坤, 柳林涛. 一种解算病态问题的方法--两步解法[J]. 武汉大学学报(信息科学版) , 2005, 30 (9) : 821–824. WANG Zhenjie, OU Jikun, LIU Lintao. A Method for Resolving Ill-conditioned Problems:Two Step Solution[J]. Geomatics and Information Science of Wuhan University , 2005, 30 (9) : 821 –824. |
| [13] | 王振杰, 欧吉坤, 柳林涛. 单频GPS快速定位中病态问题的解法研究[J]. 测绘学报 , 2005, 34 (3) : 196–201. WANG Zhenjie, OU Jikun, LIU Lintao. Investigation on Solutions of Ill-conditioned Problems in Rapid Positioning Using Single Frequency GPS Receivers[J]. Acta Geodaetica et Cartographica Sinica , 2005, 34 (3) : 196 –201. |
| [14] | 徐新禹, 李建成, 王正涛, 等. Tikhonov正则化方法在GOCE重力场求解中的模拟研究[J]. 测绘学报 , 2010, 39 (5) : 465–470. XU Xinyu, LI Jiancheng, WANG Zhengtao, et al. The Simulation Research on the Tikhonov Regularization Applied in Gravity Field Determination of GOCE Satellite Mission[J]. Acta Geodaetica et Cartographica Sinica , 2010, 39 (5) : 465 –470. |
| [15] | SHEN Yunzhong, XU Peiliang, LI Bofeng. Bias-corrected Regularized Solution to Inverse Ill-posed Models[J]. Journal of Geodesy , 2012, 86 (8) : 597 –608. DOI:10.1007/s00190-012-0542-y |
| [16] | 朱建军, 田玉淼, 陶肖静. 带准则参数的平差准则及其统一与解算[J]. 测绘学报 , 2012, 41 (1) : 8–13. ZHU Jianjun, TIAN Yumiao, TAO Xiaojing. United Expression and Solution of Adjustment Criteria with Parameters[J]. Acta Geodaetica et Cartographica Sinica , 2012, 41 (1) : 8 –13. |
| [17] | 欧吉坤. 测量平差中不适定问题解的统一表达与选权拟合法[J]. 测绘学报 , 2004, 33 (4) : 283–288. OU Jikun. Uniform Expression of Solutions of Ill-posed Problems in Surveying Adjustment and the Fitting Method by Selection of the Parameter Weights[J]. Acta Geodaetica et Cartographica Sinica , 2004, 33 (4) : 283 –288. |
| [18] | XU Peiliang, SHEN Yunzhong, FUKUDA Y, et al. Variance Component Estimation in Linear Inverse Ill-posed Models[J]. Journal of Geodesy , 2006, 80 (2) : 69 –81. DOI:10.1007/s00190-006-0032-1 |
| [19] | 徐天河, 杨元喜. 均方误差意义下正则化解优于最小二乘解的条件[J]. 武汉大学学报(信息科学版) , 2004, 29 (3) : 223–226. XU Tianhe, YANG Yuanxi. Condition of Regularization Solution Superior to LS Solution Based on MSE Principle[J]. Geomatics and Information Science of Wuhan University , 2004, 29 (3) : 223 –226. |
| [20] | 王振杰, 欧吉坤. 用L-曲线法确定岭估计中的岭参数[J]. 武汉大学学报(信息科学版) , 2004, 29 (3) : 235–238. WANG Zhenjie, OU Jikun. Determining the Ridge Parameter in a Ridge Estimation Using L-curve Method[J]. Geomatics and Information Science of Wuhan University , 2004, 29 (3) : 235 –238. |


