2. 中国测绘科学研究院GIS所, 北京 100830
2. Institute of GIS, Chinese Academy of Surveying and Mapping, Beijing 100830, China
建筑物是大比例尺城市地图的核心要素,对地图表达的效果具有重要影响。建筑物的合并作为大比例尺地图综合的难点之一,一直是国内外制图综合领域的研究热点,出现了不同的方法和策略:凸包演化方法[1-2]、扫描扩展搜索[3]及类似的基于数学形态学的方法适用于图像数据,即栅格数据,对矢量格式的数据处理需要借助矢栅转换的过程才能完成,合并过程略显繁复。合并结果在形状上可能产生较大弯曲且精度问题会对合并结果产生影响;基于缓冲区的面合并方法[4]是对多边形建立外侧缓冲区,根据缓冲区的相交情况来实现合并的。但在实际应用中,对矢量多边形建立缓冲区及其求交运算效率不高,难以用于大范围数据处理中。而基于Delaunay三角网的方法通过对研究区域进行三角剖分,借助三角网来识别多边形的空间关系,辅助完成多边形的合并。Delaunay三角剖分算法以其强大的空间邻近探测和分析功能,引起了制图专家的重视并将其应用到地图自动综合中[5-8]。目前使用Delaunay三角网进行建筑物的合并方面的探索主要有:文献[10-11]介绍了二维空间中约束Delaunay三角网剖分结构, 借助此结构可以进行形式化条件检索,用于支持邻近多边形的搜索和合并。但该方法没有具体指出搜索和合并操作的具体内容。文献[12-13]探索使用三角网结构模型对包括建筑物在内的地理要素进行邻近关系的搜索。文献[14]使用三角网表达建筑物之间的空间拓扑关系,以网中的最短边作为处理标准实现建筑物多边形的合并。文献[15]提出了利用Delaunay三角网生成拓扑信息的思路,并指出可以根据多边形之间的最小距离来判断是否聚合。但最小距离作为聚合标准并不能取得最好的效果。文献[16-17]把三角网和城市形态学等相结合进行建筑物的聚类和综合。文献[18]把Agent技术与TIN技术、聚类技术相结合的算法(ABTM),这使得算法的智能性得到很大提高,但是对建筑物中空白区域无法进行处理。
借助Delaunay三角网进行面综合为建筑物合并提供了一种解决思路,但纵观这些研究成果,仍存在一些不足:文献[9-10]重点介绍了使用三角网对空间进行分割所要建立的数据模型,以及使用这些数据模型对面状目标的空间关系进行研究,未具体介绍应用三角网进行面目标合并的过程。文献[14-15]中使用Delaunay三角网来确定建筑物之间的邻近关系,进而进行合并。但文献[14]指出由于狭长三角形的存在,采用的是Delaunay三角形的最短边和阈值进行比较。类似的,文献[15]采用的是多边形之间的最小距离。这两种取极小值的方式会夸大聚类结果,不够合理。文献[10-11]在探索邻近关系时使用的是两多边形之间三角形的平均长度,但是在对面进行合并时探讨的是一般面目标的合并,并未顾及到建筑物作为一种特殊的面,具有直角化的特征,合并结果丢失了这一特征。
仔细探索大量实际数据,建筑物面往往具有成群分布(密集)、形状规则(直角化特征) 、坐落有序(多有平行边)等特点。本文研究发现使用建筑物的边线建立约束Delaunay三角网,建筑物都被三角网所覆盖,建筑物通过三角形进行连接,它们之间的空隙由三角形所填充。构建的三角网具有无重叠、无缝隙的全覆盖的特点。为此,对于距离较近的建筑物,连接它们的三角形往往具有良好的几何形态特征。据此,针对之前研究的不足,本文对Delaunay三角网中的三角形提出了6种度量参数,从多种角度对三角形进行分类过滤以确定建筑物的空间邻近关系。同时,借助保留下来的三角形识别出建筑物的桥接部分,并对桥接部分的进行直角化处理。最后,通过桥接部分和建筑物面的融合实现建筑物的合并,保持了合并结果的直角化特征。
1 合并原理 1.1 建筑物合并建筑物的合并主要分为两种。一种是拓扑邻近的合并,即建筑物之间具有共边的情况,删除公共边即可实现合并。这种实现比较简单,常用的方式是对建筑物构建拓扑,将拓扑中同时具有左右多边形的弧段删除掉,即可实现拓扑邻近建筑物的合并。
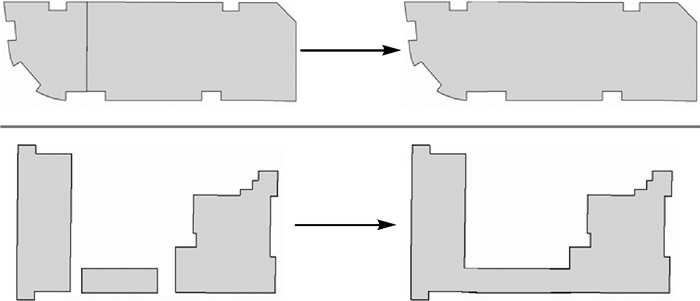
另外一种是对视觉邻近的建筑物合并。视觉邻近是指原始建筑物之间的距离较小,当比例尺变换为某一更小尺度下时,它们之间的距离看上去也会随之变得更小。有时在地图图面上无法观察到,出现建筑物部分重叠的冲突现象。这种情况下,需要填充建筑物之间的缝隙,使建筑物合并为一个整体从而消除空间冲突。本文主要研究视觉邻近建筑物的合并。
|
| 图 1 建筑物合并 Fig. 1 Building aggregation |
1.2 C-Delaunay三角网
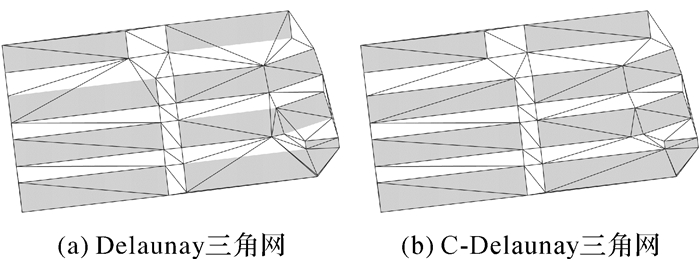
Delaunay三角网是对空间的一种特殊剖分,具备多种优异特性:如邻近性、最优性、区域性、凸多边形性等。C-Delaunay是在构建三角网的过程中,要求指定的边必须作为三角形的边存在,不能够被穿越。由于实际生产中的线、面数据也隐含着边界不被穿越的要求,使用C-Delaunay三角网对空间的划分更加理想,在实际生产活动中的应用也更广泛[14]。图 2(a)、(b)分别是用建筑物构建的Delaunay三角网和C-Delaunay三角网,后者保留了建筑物的边线信息更合理。
|
| 图 2 建筑物构建的三角网 Fig. 2 Triangulation built with buildings |
1.3 基于C-Delaunay的建筑物合并
三角网的优良性质对于建筑物面合并是非常重要的。使用建筑物面建立C-Delaunay,得到的三角网边界轮廓为一个凸多边形,包含所有建筑物。三角形单元遍布了整个数据区域,实现无重叠、无缝隙的覆盖。相互连接的三角形很好地表达了空间对象间的邻近特性,本文将其应用在对需要合并建筑物对象的定性探测上。
如前所述,当地图比例尺发生变化时(缩小时),要对距离较近的建筑物之间的空隙进行填充。在这一过程中,三角网可以精确地描述数据表达的目标边界,且容易进行长度、面积等几何计算。本文将三角网的这个优势应用在对合并过程的定量控制上。通过大量研究,本文提出了三角形形态的6种度量特征,依此对三角形进行过滤,进而自动获得桥接多边形,实现建筑物的合并。6种特征具体如下。
1.3.1 位置特征考量三角形内心在建筑物面内部或外部。三角形的内心点一定在其内部,可以代表其位置。合并过程中关注的是位于面外的三角形。因此对三角形逐一取内心点,判断是否位于建筑物几何面内。
1.3.2 属性特征考量三角形3个顶点连接的建筑物个数。三角形每个顶点至少关联一个建筑物。对每个顶点赋予其关联的建筑物面要素的唯一ID。依据顶点ID的情况,三角形可以分为3类:①Ⅰ类三角形:只连接一个建筑物面;②Ⅱ类三角形:连接两个建筑物面;③Ⅲ类三角形:连接3个建筑物面的。
当建筑物面共边时,需要预先进行合并;当不同的建筑物仅仅相交于一个点时,点的ID值选择存在二义性,这时取任一ID,同时作特殊标记。
1.3.3 关联特征考量邻接三角形的个数。三角形通过边关联的情况可以分为4种:①A类三角形:仅有一个边关联;②B类三角形:有两条边关联三角形;③C类三角形:3条边都有关联三角形;④孤立的三角形。
在对三角网进行过滤过程中,当对不符合要求的三角形作了特殊标记后,关联规则可以变形为另一种形式,同时需要考虑所关联的三角形的标记状态或所属的保留集合。
1.3.4 高度特征考量三角形的高度。单个三角形高度规则如下:Ⅰ类三角形存在两顶点是建筑物边线上紧相邻的两点时,取此边上的高,否则取任意一个边上的高;Ⅱ类三角形取ID值相同两顶点组成的边上的高;Ⅲ类三角形取3边高度平均值。对于三角形集合,取所有或部分三角形的平均高度。当三角形的个数不足个数阈值时,取所有三角形的平均高;否则,排除最大和最小的1/5高度值,对剩余的求平均值,以排除极值情况。
1.3.5 角度特征考量三角形是锐角还是钝角。在三角网的边界部分会出现狭长的钝角三角形,关联的是距离较远的建筑物,通过角度规则可以过滤掉。
1.3.6 边长特征考量三角形边的平均长度。连接距离较近建筑物的三角形平均边长较小;而连接距离较远建筑物的三角形平均边比较大,通过边长规则可以过滤掉。
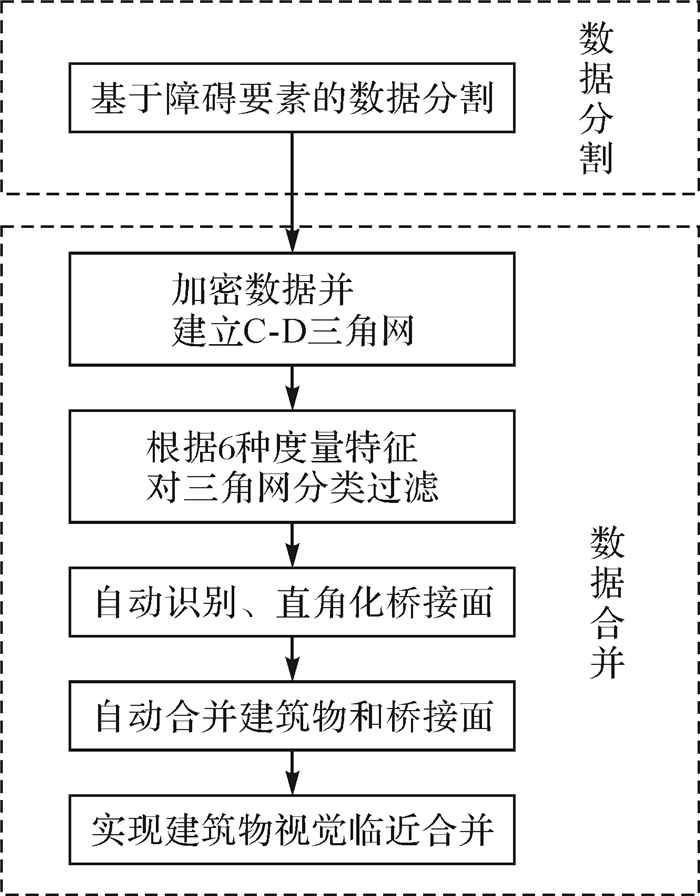
2 合并方法 2.1 合并过程本文通过对大量、多尺度、多地区现实数据的分析及试验,提出如图 3所示的合并过程。
|
| 图 3 建筑物合并流程 Fig. 3 Blueprint for building aggregation |
2.2 合并方法 2.2.1 加密数据,建立C-Delaunay三角网
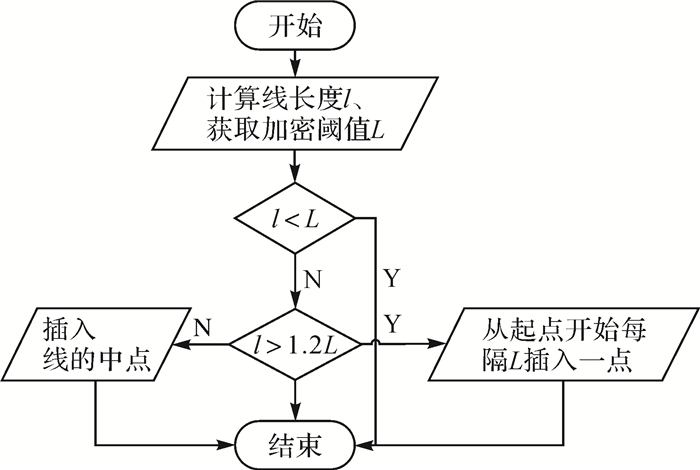
(1) 确定加密阈值,对建筑物数据进行加密。借助三角网进行建筑物面的合并时,三角网是探测建筑物面邻近关系以及进行连接的关键所在。为了使三角形保持良好的几何形态,加密建筑物面的边线是非常重要的一步。加密阈值的选择需要综合考虑建筑物之间的距离和目标比例尺的大小。阈值过小会造成加密点冗余,降低处理效率。阈值过大不能保证三角网的良好形态。假设加密阈值为L,要加密线的长度为l,本文设计的加密算法如图 4所示。
|
| 图 4 边线数据加密算法流程 Fig. 4 Densification algorithm flow chart |
(2) 建立约束Delaunay三角网。使用加密后的点集,以建筑物边为限制边条件,建立约束Delaunay三角网的方法已经有很多研究,这里不再赘述。
2.2.2 根据6种度量参数对三角形进行过滤操作过滤操作的主要步骤如下:
(1) 位置特征过滤。排除建筑物面内的三角形,保留面外的。
(2) 属性特征过滤。排除3边均不是或只有一条是建筑物边的Ⅰ类三角形,保留Ⅱ类三角形,预留两边是建筑物边的Ⅰ类三角形和Ⅲ类三角形以备修复。
(3) 边长特征过滤。排除平均边长大于阈值的三角形,保留平均边长小于阈值的三角形。
(4) 角度特征过滤。保留钝角对边是建筑物边的钝角三角形,预留其余的钝角三角形以备修复;保留包含建筑物边界边的锐角三角形,预留不含边界边的锐角Ⅱ类三角形以备修复。
(5) 修复预留的钝角三角形。当钝角三角形存在两条非建筑物边,且他们关联的三角形处于保留状态时,把该三角形放回保留集。
(6) 高度特征过滤。对保留集中的三角形聚类,计算每一个三角形分组的平均高度,排除大于阈值的三角形集合,保留小于阈值的三角形集合。
(7) 修复预留的Ⅰ、Ⅱ、Ⅲ类三角形。考量预留Ⅱ、Ⅲ类三角形标记状态下的关联特征,若属于B类三角形则放回保留集。考虑预留的Ⅰ类三角形的非建筑物边是否关联了保留状态的三角形,若是则放回保留集。
图 5中星状标记的三角形展示了几种修复的情况。图(a)中的Ⅲ类三角形,3边关联的三角形都是保留状态。图(b)中的Ⅰ类三角形,顶点是同一边线上的连续3点且唯一的关联三角形是保留状态。图(c)中的钝角三角形,两边关联的三角形是保留状态。

|
| 图 5 特殊特征的三角形 Fig. 5 Special triangles |
对过滤操作的结果有两种形式表示:一是用集合分别存储排除和保留的三角形;二是对三角形作标记,true表示保留,false表示排除。标记的方式可以快速查询三角形的排除保留状态,而集合的方式能快速确定每一步过滤操作的对象。考虑到具体应用的需求,本文采用两种方式结合的方法。
2.2.3 自动提取、直角化桥接多边形对过滤结果进行分堆,求出外边界形成桥接部分。分堆结果为一个三角形的是无效部分。定义如下符号:R-保留三角形集合;S-已处理三角形集合;E-当前桥接边界边集合;T-当前种子三角形集合;seedTri-当前种子三角形;提取桥接多边形的过程如下:①得到2.2.2中过滤操作得到的保留三角形集合R;②判断R中的三角形是否都已经处理过,如果都处理过进入步骤⑥,否则取R中任一未处理过的三角形放入到T中,进入步骤③;③从T中移出一个三角形,作为seedTri放入S中,取seedTri三边关联的三角形,进入步骤④,当T为空时,进入步骤⑤;④如果seedTri的边没有关联三角形或者关联的三角形不属于R时,将这个边放入到E中,如果三边关联的三角形都已处理过时返回步骤③,否则将未处理过的关联三角形放入到T中返回步骤③;⑤对E中的边,按照点的关联关系进行连接,即为一个桥接多边形的外轮廓,完成一个桥接多边形的搜索,清空E,返回步骤②;⑥确定最后一个桥接多边形的轮廓,结束搜索,即得到所有的桥接多边形。
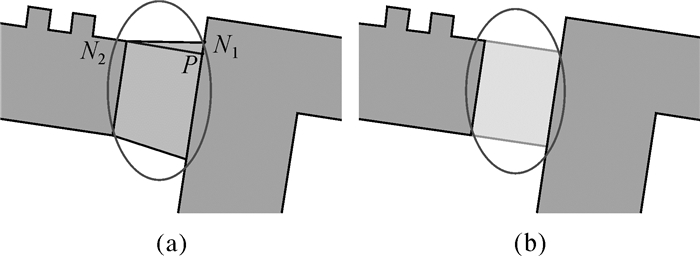
桥接多边形由三角形得到,难以保证结果的直角化特征。目前有少数文献[20-21]对建筑物进行直角化处理,本文通过对桥接部分进行处理来维持直角化特征。基本原理如下:得到的桥接部分的轮廓边线有两种:一种是和建筑物的公共边,是原始建筑物边线的一部分;另一种是连接视觉邻近的建筑物的非公共边,直角化调整的是后者。根据左右三角形的位置属性特征区分公共边和非公共边;非公共边的两端点分别与两条公共边相连接,过一个端点可向另一端点关联的公共边作垂线,如果垂点在公共边上,则称该端点为短顶点,另一端点为长顶点。直角化处理:①对桥接部分Q,根据两侧三角形的位置属性特征,识别出它的非公共边L;②确定L的长顶点N1、短顶点N2,过N2向N1关联的公共边作垂线,计算垂点P位置;③确定N1、N2与P所形成的边角三角形T;④从桥接部分Q中切除T。如图 6所示,图(a)是未直角化的桥接部分,图(b)是直角化后的桥接部分。
|
| 图 6 直角化处理 Fig. 6 Rectangularity of bridge polygon |
2.2.4 合并桥接部分和建筑物
通过相邻关系进行聚类,自动识别关联在一起的建筑物面和桥接面。对每一组聚类结果进行拓扑邻近合并。聚类过程中保留原始建筑物的ID信息,这样能够通过一定的准则,来维护合并后结果建筑物的属性,如保留面积最大或者周长最长建筑物的属性。
3 试验与分析本文在NewMap WJ-Ⅲ地图工作站底层开发接口的支撑下,使用C、C++语言进行二次开发,生成了相关程序模块。对多样性的数据进行试验,实现了基于C-Delaunay三角网分类的建筑物自动化合并处理,验证了本文所提方法的正确性和实用性。
3.1 试验平台和数据试验采用的计算机配置为:操作系统为Windows7(x64),CPU为I7-3770型号,主频是3.2 GHz,内存16 GB,固态硬盘1024 GB。试验数据样本有两个,试验区1是成都市60 km2(中心城区)、原始比例尺为1:2000数据,将其合并综合至1:5000和1:1万比例尺。试验区2是邯郸市30 km2(含城区和农村地区)、原始比例尺为1:500数据,将其合并综合至1:5000和1:1万比例尺。
3.2 结果分析图 7显示的是部分试验结果:图(a)为原始数据,图(b)为合并结果。从合并结果中可以看出空间邻近多边形得到了合理的合并并保持了直角化特征;此外,还进行了一组对比试验:图(c)是原始建筑物;图(d)是使用传统三角网方式进行合并的结果;图(e)是使用文献[22]中缓冲区方法得到的结果;图(f)是使用本文方法合并并直角化后得到的结果。通过对比可以看出,图(f)、(e)虽然能正确识别出建筑物的邻近关系并进行合并,但是并不能保持建筑物的直角化特征。

|
| 图 7 合并效果对比图 Fig. 7 Comparison chart |
另外,本文还对实现方法的效率进行了测试分析,如表 1所示。试验1-4统计的是自动化合并所需要的时间。试验5-6由于数据保密性等原因,统计的是建筑物综合处理(合并、选取、化简)的时间。从图中可以看出:建筑物自动化合并的时间远远短于人工处理的时间,能够满足实际生产的需要;同时也发现,试验1-2使用的是形状规则、分布整齐是城区。试验3-4是形状破碎的农村数据,因此。试验3-4消耗的时间是不与其数据范围成比例的。即自动合并的时间和数据范围、数据的具体情况、比例尺等都有密切关系。
| 试验序号 | 数据范围/km2 | 原始比例尺 | 目标比例尺 | 运行时间 | 备注 |
| 1 | 6 | 1:500 | 1:5 000 | 15.37 s | 自动合并 |
| 2 | 6 | 1:500 | 1:10 000 | 20.08 s | 自动合并 |
| 3 | 36 | 1:500 | 1:5 000 | 200.27 s | 自动合并 |
| 4 | 36 | 1:500 | 1:10 000 | 241.22 s | 自动合并 |
| 5 | 651 | 1:2000 | 1:5 000 | 4.5 h | 自动综合 |
| 6 | 651 | 1:2000 | 1:10 000 | 7.5 h | 自动综合 |
4 结 论
建筑物的合并综合本质包含两个子过程:一是邻近关系识别,确定哪些建筑物应该合并在一起;二是对确定了邻近关系的建筑物实施合并操作。三角网结构在表达空间对象邻近关系时具有定性、定量的优势:既可以确定建筑物是否相邻,又可以通过对网中三角形的分析、量测和计算确定相邻的具体情况。通过对多样性真实数据的试验和分析,证明合并结果合理,效率能够满足生产实践的要求。该方法已应用于多个城市的数据缩编项目中,并取得了良好的效果。
基于三角网分类的建筑物合并操作是针对不同建筑物之间缝隙的填充,下一步的研究将是通过观察建筑物外部自身凹陷部分三角形的特点,来建立一定的过滤规则,完成这一部分空隙的填充,实现建筑物合并和化简的一体化实现。
| [1] | 王光霞, 杨培. 数学形态学在居民地街区合并中的应用[J]. 测绘学院学报 , 2000, 17 (3) : 201–206. WANG Guangxia, YANG Pei. Application of Mathematic Morphology in Uniting Blocks of Residential Area[J]. Journal of Institute of Surveying and Mapping , 2000, 17 (3) : 201 –206. |
| [2] | 王辉连, 武芳, 张琳琳, 等. 数学形态学和模式识别在建筑物多边形化简中的应用[J]. 测绘学报 , 2005, 34 (3) : 269–276. WANG Huilian, WU Fang, ZHANG Linlin, et al. The Application of Mathematical Morphology and Pattern Recognition to Building Polygon Simplification[J]. Acta Geodaetica et Cartographica Sinica , 2005, 34 (3) : 269 –276. |
| [3] | 郭仁忠, 艾廷华. 制图综合中建筑物多边形的合并与化简[J]. 武汉测绘科技大学学报 , 2000, 25 (1) : 25–30. GUO Renzhong, AI Tinghua. Simplification and Aggregation of Building Polygon in Automatic Map Generalization[J]. Journal of Wuhan Technical University of Surveying and Mapping , 2000, 25 (1) : 25 –30. |
| [4] | 郭建忠, 谢明霞, 李柱林. 基于线缓冲区分析的街区合并方法[J]. 地理与地理信息科学 , 2011, 27 (6) : 111–112. GUO Jianzhong, XIE Mingxia, LI Zhulin. Block Aggregation Based on Line Buffer Analysis[J]. Geography and Geo-Information Science , 2011, 27 (6) : 111 –112. |
| [5] | 何宇兵.地学制图综合中多边形对象的合并算法研究与应用[D].杭州:浙江大学, 2007. HE Yubing.Study and Application of Algorithm for Polygon Aggregation in Geo-Cartographic Generalization[D].Hangzhou:Zhejiang University, 2007. |
| [6] | 齐琳.D-TIN并行构建方法及其在地图综合中的应用研究[D].南京:南京师范大学, 2011. QI Lin.Delaunay Triangulation Parallel Construction Method and Its Application in Map Generalization[D].Nanjing:Nanjing Normal University, 2011. http://cdmd.cnki.com.cn/article/cdmd-10319-1011248229.htm |
| [7] | 张巧凤.应用Delaunay三角网进行城市居民地和路网自动综合理论和方法研究[D].太原:太原理工大学, 2005. ZHANG Qiaofeng.The Method and Theory Research on Automated Map Generalization of City Settlement and Road Network Applying Delaunay Triangulation Network[D].Taiyuan:Taiyuan University of Technology, 2005. http://cdmd.cnki.com.cn/article/cdmd-10112-2005148447.htm |
| [8] | REGNAULD N.Spatial Structures to Support Automatic Generalisation[C]//Proceedings of the 22nd International Cartographic Conference.A Coruña:[s.n.], 2005. |
| [9] | 艾廷华. Delaunay三角网支持下的空间场表达[J]. 测绘学报 , 2006, 35 (1) : 71–76. AI Tinghua. A Spatial Field Representation Model Based on Delaunay Triangulation[J]. Acta Geodaetica et Cartographica Sinica , 2006, 35 (1) : 71 –76. |
| [10] | 艾廷华, 郭仁忠. 支持地图综合的面状目标约束Delaunay三角网剖分[J]. 武汉测绘科技大学学报 , 2000, 25 (1) : 35–41. AI Tinghua, GUO Renzhong. A Constrained Delaunay Partitioning of Areal Objects to Support Map Generalization[J]. Journal of Wuhan Technical University of Surveying and Mapping , 2000, 25 (1) : 35 –41. |
| [11] | 艾廷华, 郭仁忠, 陈晓东. Delaunay三角网支持下的多边形化简与合并[J]. 中国图象图形学报 , 2001, 6 (7) : 703–709. AI Tinghua, GUO Renzhong, CHEN Xiaodong. Simplification and Aggregation of Polygon Object Supported by Delaunay Triangulation Structure[J]. Journal of Image and Graphics , 2001, 6 (7) : 703 –709. |
| [12] | JONES C B, WARE J M. Proximity Search with a Triangulated Spatial Model[J]. The Computer Journal , 1998, 41 (2) : 71 –83. DOI:10.1093/comjnl/41.2.71 |
| [13] | JONES C B, WARE J M, EYNON C D. Triangulated Spatial Models and Neighbourhood Search:An Experimental Comparison with Quadtrees[J]. The Visual Computer , 1999, 15 (5) : 235 –248. DOI:10.1007/s003710050175 |
| [14] | 童小华, 熊国锋. 建筑物多边形的多尺度合并化简与平差处理[J]. 同济大学学报(自然科学版) , 2007, 35 (6) : 824–829. TONG Xiaohua, XIONG Guofeng. Aggregation, Simplification and Adjustment of Building Polygon Objects in Multi-scale Map Generalization[J]. Journal of Tongji University (Natural Science) , 2007, 35 (6) : 824 –829. |
| [15] | 黄继风. 基于Delaunay三角网的城市多边形合并算法[J]. 计算机工程与设计 , 2004, 25 (7) : 1220–1222. HUANG Jifeng. Urban Polygon Aggregation Algorithms Based on Delaunay Trigonometry Network[J]. Computer Engineering and Design , 2004, 25 (7) : 1220 –1222. |
| [16] | LI Z, YAN H, AI T, et al. Automated Building Generalization Based on Urban Morphology and Gestalt Theory[J]. International Journal of Geographical Information Science , 2004, 18 (5) : 513 –534. DOI:10.1080/13658810410001702021 |
| [17] | YAN Haowen, WEIBEL R, YANG Bisheng. A Multi-parameter Approach to Automated Building Grouping and Generalization[J]. Geoinformatica , 2008, 12 (1) : 73 –89. DOI:10.1007/s10707-007-0020-5 |
| [18] | 钱海忠, 武芳, 谭笑, 等. 基于ABTM的城市建筑物合并算法[J]. 中国图象图形学报 , 2005, 10 (10) : 1224–1233. QIAN Haizhong, WU Fang, TAN Xiao, et al. The Algorithm for Merging City Buildings Based on ABTM[J]. Journal of Image and Graphics , 2005, 10 (10) : 1224 –1233. |
| [19] | 邵春丽, 胡鹏, 黄承义, 等. DELAUNAY三角网的算法详述及其应用发展前景[J]. 测绘科学 , 2004, 29 (6) : 68–71. SHAO Chunli, HU Peng, HUANG Chengyi. The Expatiation of Delaunay Algorithms and a Promising Direction in Application[J]. Science of Surveying and Mapping , 2004, 29 (6) : 68 –71. |
| [20] | 刘鹏程, 艾廷华, 邓吉芳. 基于最小二乘的建筑物多边形的化简与直角化[J]. 中国矿业大学学报 , 2008, 37 (5) : 699–704. LIU Pengcheng, AI Tinghua, DENG Jifang. Simplification and Rectangularity of Building-polygon Based on Least Squares Adjustment[J]. Journal of China University of Mining & Technology , 2008, 37 (5) : 699 –704. |
| [21] | 刘鹏程, 艾廷华, 胡晋山. 一种基于条件极值的建筑多边形直角化的方法[J]. 测绘与空间地理信息 , 2008, 31 (5) : 12–14. LIU Pengcheng, AI Tinghua, HU Jinshan. Rectangularity of Building Polygon Based on Condition-Extremum[J]. Geomatics & Spatial Information Technology , 2008, 31 (5) : 12 –14. |
| [22] | BADER M, WEIBEL R.Detecting and Resolving Size and Proximity Conflicts in the Generalization of Polygonal Maps[C]//Proceedings of the 18th International Cartographic Conference.Stockholm:[s.n.], 1997. |


