在地形图中,居民地要素占据较多内容,其化简应该考虑整体结构和个体表达上的特点。整体结构与地理上下文环境密切相关,多受地形影响而呈现一定的聚集分布模式[1]。例如河谷地形环境下,居民地要素沿道路或河流方向呈阵型排列,山地丘陵则在鞍部等平坦地区散列式分布,而城镇地区则聚集成街区。在个体表达上,居民地要素的形状结构是按照建筑师、规划师意志生成的,特征可控。在大尺度城市空间中,居民小区内的建筑通常在形状上保持一致,有较强的模式化;而在中尺度空间下,其分布也能表现出区域性,如北方农村地区的房屋仍保留传统四合院型建筑风格,在形状结构也具有相似性。
传统的居民地要素化简,在整体上通常采用典型化的化简方法,能保持整体的群落结构特征,但其过程并没有充分考虑对个体目标形状特征的分析[2-3]。而对单一目标化简,主要考虑几何形态、拓扑关系及语义属性。例如文献[4-5]提出了在形状简化和定位精度等限制条件下,基于最小二乘平差模型的建筑物多边形化简方法;文献[6]在保证拓扑一致性前提下引入优化技术对建筑物轮廓点集进行化简;文献[7]中提出了多边形差分组合的思想,通过对子图形的分解和组合来表达建筑物形状结构实现化简;文献[8]建立三角网分析多边形外侧凹部结构特征,提出基于凹部层次结构的建筑物渐进式化简方法;文献[9]以邻近四点组合为基本处理单元,通过判别其凹凸结构类型并区别处理实现化简。这类化简方法主要思路是对细小弯曲识别,并进行删除、填充、夸大、拟合和直角化等操作,其过程只是针对单一的多边形结构特征,往往牺牲统一性区域特点。
地图综合是两个空间表达集合之间的映射实施过程,通过尺度变换对图形进行深加工。在传统手工综合中,制图人员通过阅读地图对地理空间形成初步的理解和认知,基于这种认知,往往会有意识地对相似的图形用同样的结果表示,保持综合后的规整性。在数字化制图自动综合中,文献[10]提出结构识别是综合中的关键过程,其后进一步指出结构分析是自动综合中的首先步骤,其中包括单一目标结构和群目标结构[11]。一些学者也对此展开了研究:文献[12]按左右转角方向对建筑物的形状进行编码,并以字母符号作为模板进行形状匹配,实现了农村建筑物的化简;文献[13]通过链码和形状数来描述形状,提出了原型模板匹配的建筑物化简方法;文献[14]提出了基于模式识别的街区块轮廓化简方法,文献[15]又进一步提出了数学形态学和神经网络等理论在模式识别中的综合应用;文献[16]提出轮廓曲线的傅里叶描述算子,可较好地应用于空间形状检索和模板匹配,同时文献[17]利用该算子的层次结构组织,实现了多尺度表达和渐进式传输。该类研究的核心在于对形状整体性特征的定量化描述和结构模式的自动化识别,而居民地要素的化简操作也旨在对目标形状进行抽象概括得到更精练的图形表达,其过程需要保持主体结构特征,同时顾及区域的群落结构和分布模式。基于此思路,本文考虑到居民地要素的人为可控性,其在一定的区域范围内也存在着相对稳定的模式化表达,从空间认知的角度可抽象提炼出几类模板,因此尝试将这种具有统一结构特征的模板作为其化简后的表达结果,提出基于模板匹配的居民地化简方法。
1 模板库构建和形状相似性度量基于模板匹配的居民地化简,旨在用一套具有典型代表性的模块去替换待处理的居民地目标来实施化简,其过程主要面临两个问题:如何构建模板库以及如何度量居民地和模板之间的相似度。
1.1 模板库构建模板反映了目标集合所具有的基本特征,它能够抽象出目标之间的相似性,而忽略单一个体的微小细节。在居民地化简过程中,模板能够描述与之形状相似的目标集的主体结构特征,忽略细小弯曲,达到综合目的;同时,形状相似的目标集合在综合后用同一模板表达,也更能突出体现群体的一致性、规整性,反映出区域特征。模板作为目标的化简结果,其选择的合适与否直接关系到综合的好坏。文献[12]根据一定区域内建筑物具有相似性的特点,通过对特定综合区域的建筑物形状的抽象与提炼,得到可以代表该区域建筑物的几类模板;文献[13]针对丹麦的农村房屋格局,利用一系列的英文字母(IFPGELUOT)构建模板库。本文考虑地图综合的要求,在构建模板库时主要考虑以下原则:
(1) 象征性。人们认知空间实体时,通常会与文字、动物或日常生活用品等事物联系起来,这些事物具有形状表达的象征意义,易于交流和理解[18]。在尺度缩小过程中,目标表达的重心也从位置信息的精确性向图形的抽象化和象征性转移,以便更符合人们的认知过程和感受习惯。因此,在模板库的构建时,需要考虑引入一些典型象征性的模板,如E、F、L、T等文字字符,突出表达地物的象征性意义。示例模板如图 1(a)所示(见文末)。

|
| 图 1 基于象征性和形态概括性构建的模板 Fig. 1 The templates based on symbolism and abstraction |
(2) 形态概括性。形态概括是地图综合中的基本原则,在较小尺度下,居民地要素侧重于整体结构表达,通过形状碎部的取舍,得到更高层次的形态概括,因此模板库的构建中,需要满足形态概括性原则。结合居民地目标的直角化特点[19],同时考虑到在化简时也可以直接以最小外接矩形(MBR)作为综合结果[20],因此将矩形作为模板中的基本图元,是重要的模板之一。对于较为复杂的居民地目标,其边界也多由垂直线段构成,其多边形亦可以看作一系列外接矩形的分解组合结果[7],因此可以尝试将多个矩形图元组合来构建模板库。该类模板中,同一模板中矩形图元大小和长宽比保持一致,可概括细小弯曲;同时,模板具有正交化特点,有较规范的结构模式,能有意识的保持形状对称性,体现人工地物的建筑特点。示例模板如图 1(b)所示。
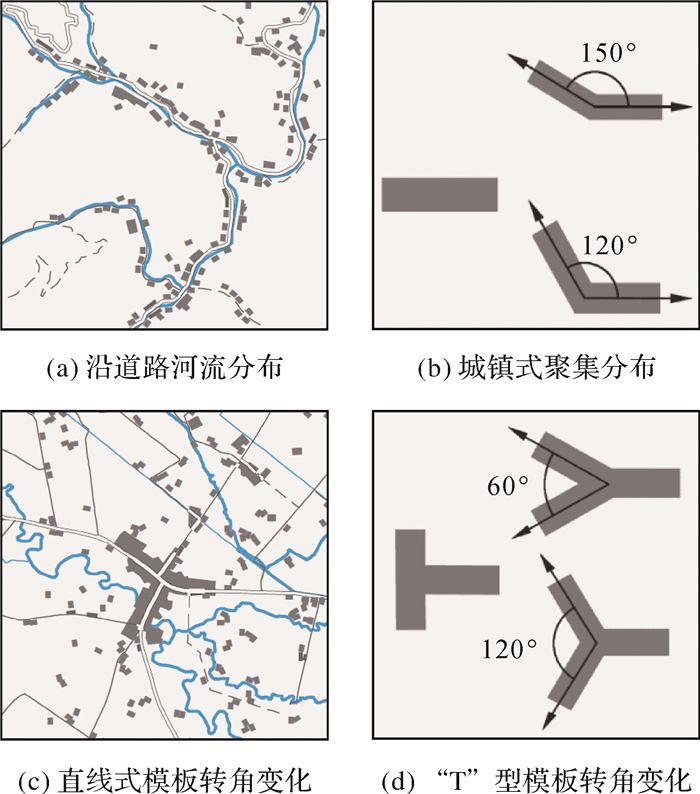
(3) 区域环境特征。居民地作为人工地物,其表达构成的人文环境特征,不但可以反映出地形地貌,同时也能揭示了区域规划、经济发展等宏观背景信息。在同一区域出现结构相似的一类建筑物,应提炼出相应的模板。例如河谷地貌下,居民地沿河流聚合成直线或弧线式分布[21-22],形态上保持狭长且转折的群落结构特征,因此需要针对性的抽象出模板。对于一些特征较显著的独立建筑物,同样应该提炼出模板。例如城镇地区,道路建设能够划分出明显的发展经济带,建筑物的分布也能体现出这种典型的区域特点,因此也需要构建相应的模板。在图 2(b)、(d)中,分别将I、T型模板变化一定角度,构建出新的模板,以更好地适用居民地要素沿着道路河流或其他经济带分布,体现出区域环境特征(见文末)。
|
| 图 2 基于区域环境特征构建的模板 Fig. 2 The templates based on the characteristics of regional environment |
模板能反映出特定的语义含义或区域特征,而蕴含同一语义含义或区域特征的模板则是多样化的。这类似于书法,每个人的字迹都不一样,但都代表着同一个字。因此在构建模板库时,模板的长宽比和角度变化值可根据数据特点进行灵活调整,以保证模板库的丰富,如长宽比可选择1∶1、1∶2、1∶3等,角度变化值可包括60°、120°、150°等。
1.2 基于转角函数的形状相似性度量基于上述原则构建模板库后,接下来需要寻找有效的度量方式计算居民地目标与模板之间相似性,通过形状的相似性度量,即可找到“最相似”的模板作为居民地目标化简后的结果。形状的定性化描述是其相似性度量的前提,包括骨架线、弯曲度、距等基于区域的描述算子和形状数、傅里叶变换、转角函数等基于轮廓边界的表示方法。区域描述算子计算量小,然而容易受噪音影响,且单一算子相似性度量精度不高[23]。轮廓边界的表示方法以字符串或函数近似拟合形状,可较好分析形状的结构特征。但基于形状数的相似性结果离散程度高、区别度不大,导致在模板匹配中存在多个最相似的模板[13];傅里叶变换通过高阶多项式函数逼近形状轮廓,又较难适应于具有直角化的居民地。转角函数表示形状边界上切角对弧长的变化关系,形状之间的相似性可通过切角的差异来度量。针对居民地要素的化简,考虑到其轮廓具有节点少、几何转折明显且无连续弯曲,因此切角变化波动小,相似性度量较为稳定,适合采用转角函数表达形状。方法具体描述如下[24]:
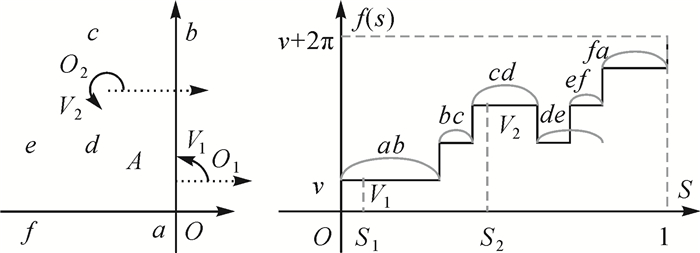
对于多边形A,其边界上的任意点O沿参考方向(如x轴)的切角为v,转角函数f(s)即表示切角沿A边界逆或逆时针相对于弧长s的变化关系。如图 3所示,弧段

|
| 图 3 多边形的转角函数表示 Fig. 3 The turn function of a polygon |
从其定义可知,转角函数可将二维的居民地形状转换为一维的函数表达。对于多边形A、B,分别记其转角函数为fA(s)、fB(s),其形状差异可利用函数组成的Lp空间距离来度量,定义距离Lp(A, B)为
 (1)
(1)
公式(1)表明多边形A、B相似度越高,则Lp(A, B)值越小。然而,Lp(A, B)对多边形旋转角度和边界起始点的选择都较为敏感。通常采用旋转多边形和移动边界起始点位置的方法来求Lp(A, B)最小值,并作为其相似性S(A, B)的计算结果[25]。若将起始点O沿多边形A边界移动一定距离t,则新的转角函数可表达为fA(s+t);若将多边形旋转一定角度θ后,则新的转角函数为fA(s)+θ。因此,选择L2距离,修改式(1)可得到形状相似度的计算公式
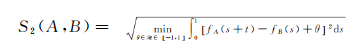 (2)
(2)
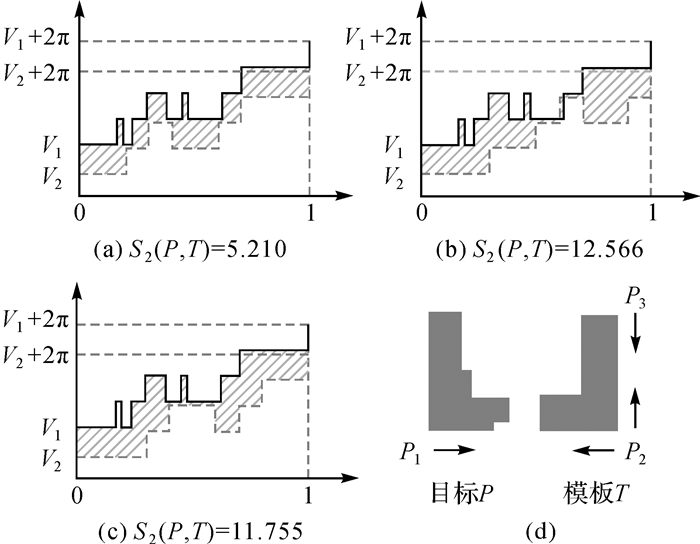
由公式(2)分析可知,多边形的缩放、平移等并不会影响相似性的计算;对于镜像形状,也可以通过改变切角沿边界的移动方向来控制。例如图 4中实线表示目标P从点P1按逆时针的转角函数,虚线表示模板T的转角函数,其中(a)、(b)、(c)分别表示从点P2按顺时针、点P3按顺时针、P2按逆时针结果,由此看出,不同起始点和计算方向,其相似度也不相同。通过比较,图(a)相似度值计算结果最小,即模板T从P2点按顺时针方向与目标P从P1按逆时针方向计算时可较好的匹配,这与视觉认知结果相一致。
|
| 图 4 基于转角函数的相似性距离计算 Fig. 4 Similarity measure based on the angle function |
相似度值表示模板与目标之间的形状特征差异,具有相对意义,因此旋转角度θ值并不会影响匹配结果。例如将图 4中模板T旋转某一角度后,计算与目标P的相似度,在(a)、(b)、(c)中切角值V2都会改变,即相似度都会改变,但仍可比较得出图(a)相似度最小。对于t值,其取值范围为[-1, 1],即起始点可以在多边形A和B的边界上都可任意移动。由于模板是简略化的表达、节点数较少,因此可以选定目标上的任意点作为起始点,而通过遍历模板上所有的转角节点作为起始点,比较各节点相似值,取其最小值即该模板与目标之间的相似度。
2 基于模板匹配的居民地化简在本文中,尝试通过建立一系列具有典型代表性的模板来象征性、概括化表达居民地要素综合化简后的结果。由于居民地形状尺寸各不相同,而模板形状大小的缩放并不会影响其结构变化,因此可通过缩放动态派生出与居民地目标面积相同或接近的模板,既可以顾及综合前后面积变化,又不会影响模板匹配时的相似性计算。模板位置和方向同样会影响匹配化简结果,因此参考重心位置和最小外接矩形(MBR)长边方向来确定,可以保持视觉中心位置不变,满足综合要求[26]。
对化简操作质量的评价,通常从点数、周长、面积等几何统计量和形状结构特征等方面进行。本文从形状认知的角度出发,侧重于形状结构特征的定量化分析,同时通过缩放也可保持周长、面积变化的稳定,因此本文主要以匹配后模板和原目标重叠区域面积占原目标面积的百分比作为匹配度,来评价化简操作,匹配度越高,则化简效果越好。该指标可以反映出位置、方向、形状结构等方面变化。
为了保证综合效果,对匹配度低的目标应放弃化简操作,需要采用其他方法处理或针对性构建出新的模板。在最小匹配度阈值选择时,也应考虑到居民地的特点。对于面积较小的居民地,其分支弯曲更为破碎,同时形状结构简单,模式性较强,因此选择较小的匹配度阈值,可以保证匹配效果较好;面积较大则反之。例如图 5中化简目标A时,匹配度较高的模板2(94.4%)缩放后出现0.2 mm短边,无法满足图示规范要求,而匹配度较小的模板1(88.9%)则可以满足要求;化简目标B时,利用模板1匹配则删除分支弯曲力度过大,而模板2缩放后也未出现短边,满足综合要求。试验中,小面积居民地目标的最小匹配度阈值可设定为80%,而大面积街块的匹配度设定为85%,该阈值的设定也体现了模板具有尺度性。

|
| 图 5 目标尺寸对匹配精度的影响 Fig. 5 The effect of target size on the matching accuracy |
基于上述分析,本文提出基于模板匹配的居民地要素化简方法。首先根据数据特点,按照象征性、形态概括性和区域环境特点等原则构建相应的模板库,针对每一个待化简居民地目标,其主要步骤如下:
(1) 计算目标面积,缩放模板库派生出与之面积相同或相近的动态模板,并确定最小匹配度阈值。
(2) 利用公式(2)计算目标和所有动态模板之间的相似度,并按相似度值对其排序。
(3) 计算目标重心和最小外接矩长边方向,并平移、旋转模板,使其重心和长边方向与目标一致。
(4) 依序计算匹配度,判断匹配度是否大于最小匹配阈值,若是则停止计算,化简有效;若不存在模板的匹配度大于阈值,则化简无效。该过程如图 6所示。
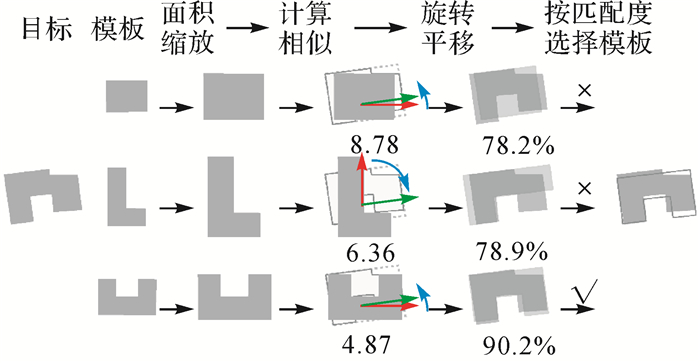
|
| 图 6 基于模板匹配的居民地要素化简过程 Fig. 6 Building simplification based on the template matching method |
3 试验与分析
本文采用转角函数作为形状度量算子度量居民地目标和模板之间的相似程度。为了论证该算子的有效性,本文从1∶5万地形图选择一批典型的居民地目标,并构造出相应的模板,利用转角函数计算每个目标和所有模板之间的相似度及匹配度,结果如表 1所示。

|
表 1中,不同模板与目标之间的匹配结果差异较大,其匹配度和相似度两个指标也随之变化。本文选择其中3个目标,分析匹配度和相似度之间的相关性,结果如图 7所示。该结果反映出匹配度和相似度之间呈高度负相关(相关系数-1<r<-0.7),表明基于转角函数计算出模板与目标之间相似度值越低,匹配程度则越高。同时,对所有的目标,与之“最”相似的模板,其匹配度也最高,符合视觉认知。因此,基于转角函数的形状相似性度量能较好地解决居民地目标和模板之间关系匹配的问题。
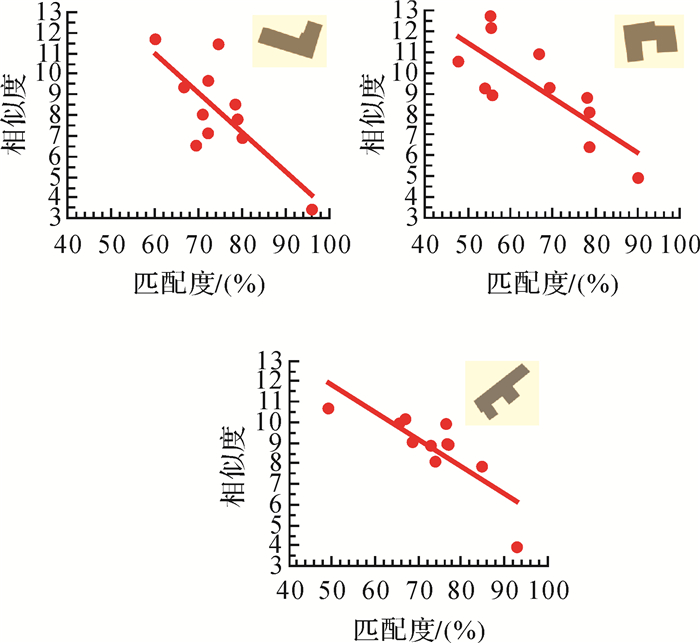
|
| 图 7 匹配度与相似度之间的相关性分析 Fig. 7 Correlation analysis between matching degree and similarity degree |
进一步,本文利用真实数据对居民地模板匹配化简方法进行试验。试验数据集选自地处我国一、二阶梯分界线的四川省中部地区,区域特征显著,包括1056个面状居民地目标及道路、水系等基础要素。试验数据原始比例尺为1∶5万,目标比例尺为1∶10万,对于化简后面积值小于25 mm2的居民地其匹配化简阈值选为80%,而面积值大于或等于25 mm2则匹配化简阈值选为85%。试验中基于上述构建模板库的基本原则,并结合该区域居民地直角化和沿地形转角的特征,构建了33个模板进行匹配化简(如图 8)。在试验中未对目标进行选取操作,化简前后结果对比如图 9所示。

|
| 图 8 针对试验所构建的模板库 Fig. 8 Devising templates referenced to this experiment |
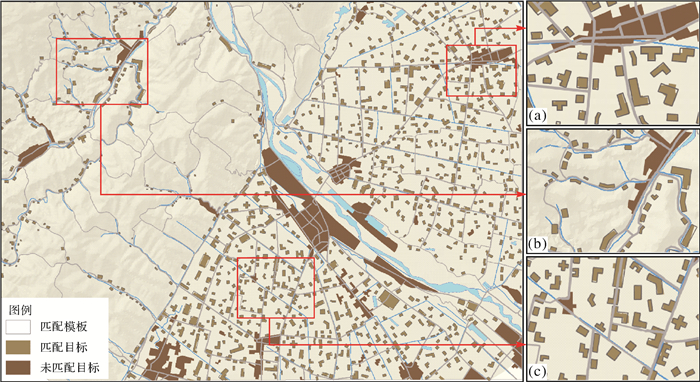
|
| 图 9 基于模板匹配的居民地化简结果 Fig. 9 Buildings before and after simplification based on the template matching method |
从结果可知,试验区域内的绝大多数目标都进行了有效的化简操作,而小部分的大面积街区则化简无效,其数量为44,模板匹配化简方法有效率为95.8%。图 9(a)城区大面积街区由于其形状结构复杂,未能成功匹配化简,而周边小面积的目标都得到了较好的化简;图 9(b)山地地区居民地要素呈散列式分布,沿道路河流分布有一定的角度变化,化简后总体趋势得到了较好的保持;而在图 9(c)中,居民地目标形状结构多样化,通过构建一些抽象概括性的模板,如字母、符号、图案等,也能对其进行有效的化简。该方法通过缩放模板,可以保证综合前后的面积均衡。
同时,本文按山地和盆地两种不同的区域环境,对所有目标的匹配度进行了统计,分布情况如图 10所示。在山地地区,目标的匹配度集中分布在95%~97.5%,占据了总数的50%,匹配度大于85%的目标数比例达到94.7%;在盆地地区,目标的匹配度则在85%~97.5%内分布较为均衡,而匹配度大于85%的目标数比例为83.2%。分析原因是在山地地区,居民地目标表达相对独立,呈散列式分布,多为直角型形状或沿道路、河流成转角型,其面积较小且形状较为规整,因此其匹配效果较好;而在盆地地区,1∶5万地形图上面状居民地表达成块状房屋,甚至是大面积城市街区,其面积较大且形状较为复杂多样化,因此存在部分目标不能找到合适的模板进行匹配化简。因此,本文所提出的方法比较适应于表达相对独立、面积值较小的居民地目标,如中比例尺下散列式农村居民地、大比例上独立表示的房屋或小街块等;而对形状结构复杂的聚集型大面积街区则需要通过传统的处理细小弯曲方法进行化简。
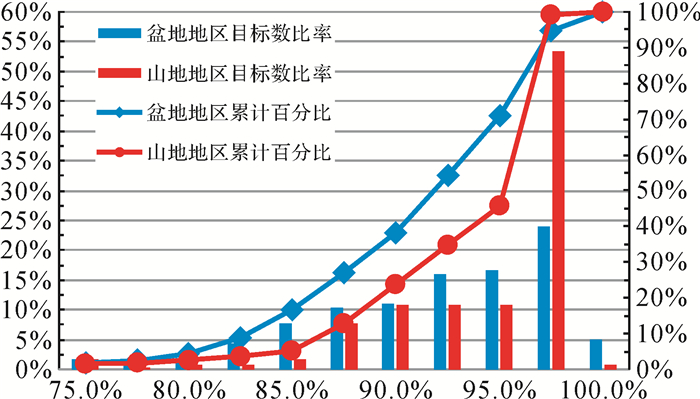
|
| 图 10 目标匹配度的分布情况 Fig. 10 The distribution of target matching degree |
4 结 论
居民地化简是地图综合中的经典问题之一,其要素在整体分布上能体现出较强的区域环境特征,在个体表达也具有典型模块化特点。传统的化简方法中,无论是基于群落模式的典型化方法,还是处理细小弯曲的化简方法,都无法统一区域性和个体表达之间的关系。本文介绍了一种模板匹配的化简方法,其基本思想是充分考虑地图综合的要求,从象征性、形态概括性和区域环境特征3个原则构建一批模板,来抽象表达居民地要素。该过程中居民地和模板之间的形状相似性度量是关键问题之一,本文考虑居民地具有节点较少、几何转折明显且切角变化波动小等特点,利用转角函数作为形状描述算子来计算其与模板之间的相似性。结合真实数据进行试验,分析表明该方法能较好地保持居民地形状的结构特征,同时兼顾了综合前后的面积均衡,适用于表达相对独立、面积值较小的居民地目标的,具有较强的可靠性和实用性,可规模化应用于中小比例尺综合实践。但是,本文提出的模板匹配化简方法不能处理结构复杂的街区,需要结合传统化简方法进行处理;同时,模板库的完备性对化简的结果有直接的影响,在后续工作中仍需要作进一步的补充和丰富。
| [1] | REGNAULD N, MCMASTER R B. A Synoptic View of Generalisation Operators[M]//MACKANESS W A, RUAS A, SARJAKOSKI L T. Generalisation of Geographic Information:Cartographic Modelling and Applications. Amsterdam:Elsevier, 2007:37-66. |
| [2] | LI Zhilin, YAN Haowen, AI Tinghua, et al. Automated Building Generalization Based on Urban Morphology and Gestalt Theory[J]. International Journal of Geographical Information Science , 2004, 18 (5) : 513 –534. DOI:10.1080/13658810410001702021 |
| [3] | REGNAULD N. Contextual Building Typification in Automated Map Generalization[J]. Algorithmica , 2001, 30 (2) : 312 –333. DOI:10.1007/s00453-001-0008-8 |
| [4] | SESTER M. Generalization Based on Least Squares Adjustment[C]//International Archives of Photogrammetry and Remote Sensing. Amsterdam:International Society for Photogrammetry & Remote Sensing, 2000:931-938. |
| [5] | 刘鹏程, 艾廷华, 邓吉芳. 基于最小二乘的建筑物多边形的化简与直角化[J]. 中国矿业大学学报 , 2008, 37 (5) : 699–704. LIU Pengcheng, AI Tinghua, DENG Jifang. Simplification and Rectangularity of Building-polygon Based on Least Squares Adjustment[J]. Journal of China University of Mining & Technology , 2008, 37 (5) : 699 –704. |
| [6] | HAUNERT J H, WOLFF A. Optimal and Topologically Safe Simplification of Building Footprints[C]//Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York:ACM, 2010:192-201. |
| [7] | 郭仁忠, 艾廷华. 制图综合中建筑物多边形的合并与化简[J]. 武汉测绘科技大学学报 , 2000, 25 (1) : 25–30. GUO Renzhong, AI Tinghua. Simplification and Aggregation of Building Polygon in Automatic Map Generalization[J]. Journal of Wuhan Technical University of Surveying and Mapping , 2000, 25 (1) : 25 –30. |
| [8] | 陈文灏, 龙毅, 沈婕, 等. 利用约束D-TIN进行建筑物多边形凹部结构识别与渐进式化简[J]. 武汉大学学报(信息科学版) , 2011, 36 (5) : 584–587, 592. CHEN Wenhao, LONG Yi, SHEN Jie, et al. Structure Recognition and Progressive Simplification of the Concaves of Building Polygon Based on Constrained D-TIN[J]. Geomatics and Information Science of Wuhan University , 2011, 36 (5) : 584 –587, 592. |
| [9] | 许文帅, 龙毅, 周侗, 等. 基于邻近四点法的建筑物多边形化简[J]. 测绘学报 , 2013, 42 (6) : 929–936. XU Wenshuai, LONG Yi, ZHOU Tong, et al. Simplification of Building Polygon Based on Adjacent Four-point Method[J]. Acta Geodaetica et Cartographica Sinica , 2013, 42 (6) : 929 –936. |
| [10] | BRASSEL K E, WEIBEL R. A Review and Conceptual Framework of Automated Map Generalization[J]. International Journal of Geographical Information System , 1998, 2 (3) : 229 –244. |
| [11] | STEINIGER S, WEIBEL R. A Conceptual Framework for Automated Generalization and Its Application to Geologic and Soil Maps[C]//Proceedings of XXⅡ International Cartographic Conference. A Coruña:The International Cartographic Association, 2005. |
| [12] | RAINSFORD D, MACKANESS W. Template Matching in Support of Generalization of Rural Buildings[M]//RICHARDSON D E, VAN OOSTEROM P. Advances in Spatial Data Handling. Berlin:Springer, 2002:137-151. |
| [13] | 刘鹏程, 艾廷华, 胡晋山, 等. 基于原型模板形状匹配的建筑多边形化简[J]. 武汉大学学报(信息科学版) , 2010, 35 (11) : 1369–1372. LIU Pengcheng, AI Tinghua, HU Jinshan, et al. Building-polygon Simplification Based on Shape Matching of Prototype Template[J]. Geomatics and Information Science of Wuhan University , 2010, 35 (11) : 1369 –1372. |
| [14] | WANG Zeshen, LEE D. Building Simplification Based on Pattern Recognition and Shape Analysis[C]//Proceedings of the 9th International Symposium on Spatial Data Handling. Beijing:[s.n.], 2000:58-72. |
| [15] | 王辉连, 武芳, 张琳琳, 等. 数学形态学和模式识别在建筑物多边形化简中的应用[J]. 测绘学报 , 2005, 34 (3) : 269–276. WANG Huilian, WU Fang, ZHANG Linlin, et al. The Application of Mathematical Morphology and Pattern Recognition to Building Polygon Simplification[J]. Acta Geodaetica et Cartographica Sinica , 2005, 34 (3) : 269 –276. |
| [16] | AI Tinghua, CHENG Xiaoqiang, LIU Pengcheng, et al. A Shape Analysis and Template Matching of Building Features by the Fourier Transform Method[J]. Computers, Environment and Urban Systems , 2013, 41 : 219 –233. DOI:10.1016/j.compenvurbsys.2013.07.002 |
| [17] | LIU Pengcheng, LI Xingong, LIU Weibo, et al. Fourier-based Multi-Scale Representation and Progressive Transmission of Cartographic Curves on the Internet[J]. Cartography and Geographic Information Science , 2015 . DOI:10.1080/15230406.2015.1088799 |
| [18] | 艾廷华, 帅赟, 李精忠. 基于形状相似性识别的空间查询[J]. 测绘学报 , 2009, 38 (4) : 356–362. AI Tinghua, SHUAI Yun, LI Jingzhong. A Spatial Query Based on Shape Similarity Cognition[J]. Acta Geodaetica et Cartographica Sinica , 2009, 38 (4) : 356 –362. |
| [19] | 郭庆胜. 以直角方式转折的面状要素图形简化方法[J]. 武汉测绘科技大学学报 , 1999, 24 (3) : 255–258. GUO Qingsheng. The Method of Graphic Simplification of Area Feature Boundary as Right Angle[J]. Journal of Wuhan Technical University of Surveying and Mapping , 1999, 24 (3) : 255 –258. |
| [20] | WILSON J P, FOTHERINGHAM A S. The Handbook of Geographic Information Science[M]. New York: John Wiley & Sons, 2008 : 222 -238. |
| [21] | ZHANG Xiang, AI Tinghua, STOTER J, et al. Building Pattern Recognition in Topographic Data:Examples on Collinear and Curvilinear Alignments[J]. GeoInformatica , 2013, 17 (1) : 1 –33. DOI:10.1007/s10707-011-0146-3 |
| [22] | REGNAULD N, EDWARDES A, BARRAULT M. Strategies in Building Generalisation:Modelling the Sequence, Constraining the Choice[C]//ICA Workshop on Progress in Automated Map Generalization. Ottawa:ICA, 1999. |
| [23] | 郝燕玲, 唐文静, 赵玉新, 等. 基于空间相似性的面实体匹配算法研究[J]. 测绘学报 , 2008, 37 (4) : 501–506. HAO Yanling, TANG Wenjing, ZHAO Yuxin, et al. Areal Feature Matching Algorithm Based on Spatial Similarity[J]. Acta Geodaetica et Cartographica Sinica , 2008, 37 (4) : 501 –506. |
| [24] | ARKIN E M, CHEW L P,HUTTENLOCHER D P,et al. An Efficiently Computable Metric for Comparing Polygonal Shapes[C]//Proceedings of the First Annual ACM-SIAM Symposium on Discrete Algorithms. Philadelphia, PA:Society for Industrial and Applied Mathematics, 1990:129-137. |
| [25] | LATECKI L J, LAKAMPER R. Shape Similarity Measure Based on Correspondence of Visual Parts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2000, 22 (10) : 1185 –1190. DOI:10.1109/34.879802 |
| [26] | LI Zhilin. Algorithmic Foundation of Multi-scale Spatial Representation[M]. Boca Raton, FL: Taylor & Francis Group, CRC Press, 2006 : 188 -189. |



