2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079 ;
3. 武汉市测绘研究院, 湖北 武汉 430022 ;
4. 南京师范大学地理科学学院, 江苏 南京 210023
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China ;
3. Wuhan Geomatics Institute, Wuhan 430022, China ;
4. School of Geographic Science, Nanjing Normal University, Nanjing 210046, China
线状地图要素图形的简化和移位都有可能产生线与其周边地图要素之间的空间冲突。通常情况下,这两种操作都是独立执行,执行完后,再进行空间冲突识别,并想办法解决空间冲突。线图形简化算法有很多,例如:Douglas-Peucker算法、Li-Openshaw算法等,为了解决线图形简化过程中产生的空间冲突问题,很多学者进行了有益的探讨[1-6]。但是线简化后,有时还需要进行移位处理,这有可能再次产生空间冲突。为了提高解决空间冲突的数据处理效率,把这两个阶段的空间冲突处理操作协同起来应该是一个比较好的解决方案。当前,道路及其周边建筑物之间空间冲突的解决方法是国内外学者的重要研究对象,为了维护好线状要素的形状特征,目前使用的主要移位算法是Snake算法和Beam算法[7-11];线状地图要素与其周边地图目标之间的空间冲突处理方法,主要以街区的建筑物群为研究对象[12-15]。为了解决离散的建筑物群的移位问题,有的学者采用了几何计算方法、最优化方法或有限元方法[16-21]。这些模型或算法为我们的研究提供了很好的理论基础和经验。文献[9]提出了地图线目标的4种不同受力计算方式以及道路网的分区划分方法,在利用Beam算法解决线要素之间的空间冲突时能顾及地图目标间的空间关系;文献[10]针对Snake算法在道路网移位中的不足,分别从道路形态特征保持、道路受力传播范围控制和道路网整体拓扑关系保持3个方面对Snake算法进行了改进,并取得了不错的移位效果;文献[12, 15]提出了基于场论分析的建筑物群的移位算法,用“等势线”模型来表达建筑物群在街道拓宽后产生移位的现象,并在此基础上建立多源力作用下的移位场模型,实现了顾及上下文条件的多边形目标群移位。本文试图把线的图形简化和移位等图形变化与线周边空间目标(例如:建筑物)的移位统一在一个协同处理模型中,把所有操作统一到顶点移位操作上,并保持空间目标的形状和排列等基本特性。
1 协同处理的基本思想线的图形综合主要涉及图形简化、移位等操作,这些图形操作往往会产生空间冲突,例如:地图综合中常见的道路与其周边建筑物之间的空间冲突。当道路图形简化时可能会产生如图 1(a)所示的空间冲突;当道路移位时也可能产生如图 1(b)所示的空间冲突。当然,道路符号化后也有可能产生空间冲突,如图 1(c)所示。

|
| 图 1 道路图形简化、移位和符号化产生的空间冲突 Fig. 1 Spatial conflicts caused by linear graphic simplification, displacement and symbolization |
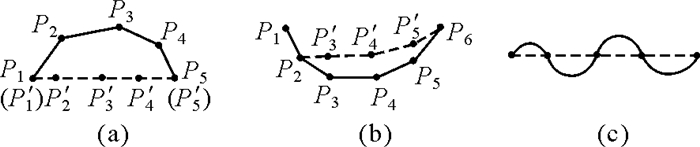
线图形简化和移位这两种操作都可以简化为空间目标顶点的移位。如图 2所示,图 2(a)说明当实线简化为虚线时,P′2点可以认为是从P2点移位到此,同样图 2(b)说明当实线移位后,可认为是有关顶点发生移位,例如从P3点移位到P′3点。当一条线简化后,可以把整条线划分为多个如图 2(a)这样的多边形单元,如图 2(c)所示。线移位操作中应当遵循相应的制图规则,例如:线的形状尽量得到保持;道路周边的建筑物群分布规律尽可能得到维护。在线状地图要素移位过程中,线的形状能保持的比较好的方法是Snake移位算法等。因而,本文试图以Snake算法为基础,在顾及有关约束的前提下,把线图形简化与其周边建筑物群移位和道路移位协同在一起。
|
| 图 2 空间目标顶点的移位 Fig. 2 Displacement of spatial objects vertexes |
Snake移位算法中需要有初始移位向量来计算受力[7-8],可以把道路图形简化的顶点移位、道路与其周边建筑物之间的空间冲突区域看作是移位模型中初始移位向量的计算条件,然后建立道路与其周边建筑物之间的邻近关系连接,最后把关联在一起的道路和建筑物中心看作一个线状网络进行协同移位操作,这种邻近关系的连接起到了传播移位的作用。
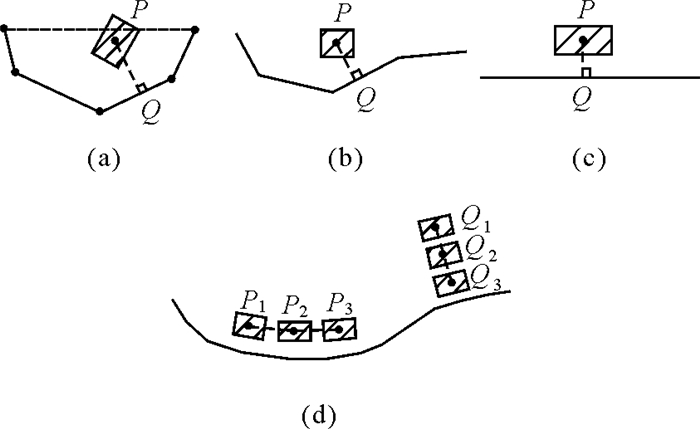
2 移位传播路径的构建协同处理方法中除了把线图形简化转化为顶点移位外,还需要把它和线移位结合在一起,把线图形简化产生的空间冲突、线与其他要素之间的空间冲突等都看成是产生移位的初始力量来源,这些力量协同地对整个移位传播路径起作用。因此,一个非常重要的任务是构建一个线与其周边地物的邻近关联图,这个关联图就是一种移位传播路径。因为线图形简化和移位都可能产生次生空间冲突,所以需要确定线图形简化和移位所波及的空间范围,并在此基础上建立邻近关联图。下面以道路及其周边建筑物为例说明移位传播路径的构建方法。道路图形简化后,可能产生如图 1(a)所示的空间冲突,判断方法是:如图 3(a)所示,虚线是简化后的直线段,它和实线围成了一个多边形(简称:偏差多边形),通过判断建筑物多边形是否与该多边形有交集来确定空间冲突是否存在。若存在空间冲突,就需要从建筑物的中心点到原始图形(图 3(a)的实线)建立最短距离线,如图 3(a)的直线段PQ。同样,当一条道路需要移位时,也需要判断这条道路的移位是否会与其周边建筑物产生新的冲突,若有可能产生新的冲突,则建立建筑物中心点到道路的最短距离线,如图 3(b)中的直线段PQ。若道路的符号化产生如图 1(c)所示的空间冲突,也需要建立类似的直线段PQ,如图 3(c)所示。另外一个重要的考虑因素是:道路旁边的建筑物群有时有沿线分布(或排列)特征,若移位操作破坏这些空间特征就违反了相应的制图规则,移位过程中需要协同处理这些问题,而MST(最小生成树)是表达这种空间特征的较好方法[8, 19],把MST作为一种移位传播路径,在移位过程中可以尽量保持这种线状排列,如图 3(d)所示。
|
| 图 3 建筑物与道路的邻近关联关系和建筑物群的沿线分布特征 Fig. 3 Neighborhood relations between buildings and roads and alignment of buildings along roads |
为了建立移位传播路径,需要设置判断空间冲突的几个阈值。设建筑物之间需要考虑排列方式的可识别距离为d1;设道路符号化和移位的影响范围为d2。道路与其周边建筑物群移位传播路径的整个构建过程如下:
(1) 获取道路图层和建筑物图层,并设置参数d1和d2。
(2) 对道路进行图形简化,并建立如图 2(c)所示的偏差多边形,判断周边建筑物多边形与这些偏差多边形是否有交集,若有,则建立有关建筑物中心点到原始道路的最短距离线,得到图层C1。对图形简化后的道路建立左右侧缓冲区,宽度为d2,判断缓冲区多边形是否与不在偏差多边形内的建筑物多边形相交,若相交,则建立该建筑物中心点到该条简化后的道路的最短距离线,同时在该道路上插入相应的顶点,得到一个移位传播路径C2图层,若所有建筑物判断完,则形成落入不同缓冲区的不同建筑物群。
(3) 以落入不同偏差多边形或不同缓冲区的建筑物群为基础,以d1为搜索半径,搜索移位传播可能影响到的其他建筑物,把这些搜索到的建筑物目标添加到相应的建筑物群中,并再次搜索,直至无新建筑物被搜索到。检查建筑物子群间是否有重叠,若有,则合并相互间有重叠目标的子群。
(4) 以不同的建筑物子群为对象,建立其MST,形成建筑物之间的邻近连接关系。随后,判断MST中的边是否与道路相交,若相交,则删除该边。若某个建筑物子群的MST中某一边长大于该子群内目标的最大初始移位向量的模或设定的阈值,则删除该边,避免不受影响的建筑物也参与运算。从而,得到建筑物之间的移位传播路径图层C3。
(5) 图形简化后的道路有自然的连接关系,可以直接把存在空间冲突的道路作为移位传播路径,设为图层C4。
(6) 合并图层C1、C2、C3和C4,得到移位传播路径图层。
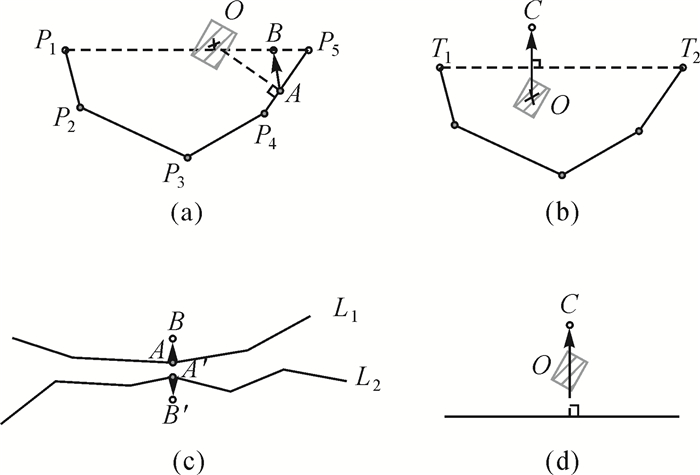
3 初始移位向量的计算在整个协同处理方法中,Snake移位模型是一个基础,该模型的初始移位向量可依据不同空间冲突类型来计算。当出现图 3(a)所示的空间冲突类型时,初始移位向量的计算见图 4(a)和图 4(b),其中,建筑物的中心点为O,图 4(a)中O点不在偏差多边形内,初始移位向量是AB,B点是线简化后A点的位置,可以根据距离等比例法计算,先按照线简化前A点在曲线段P1P2P3P4P5的位置计算A点分别到端点P1和P5的曲线长度,然后依据它们的长度比值计算B点在直线段P1P5上的位置。而图 4(b)中的O点在偏差多边形内,初始移位向量是OC,该向量垂直于直线段T1T2,OC向量模的计算如下
|
| 图 4 初始移位向量的计算 Fig. 4 Calculation of Initial displacement vectors |
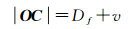 (1)
(1)
式中,Df为建筑物相对直线段T1T2的最远距离;v为建筑物应偏离道路中心线的距离。
当道路之间发生空间冲突时,如图 4(c)所示,A和A′是计算出的线L1和L2之间最近的两个点,它们的初始移位向量分别为AB和A′B′,B、A、A′和B′在同一条线上,AB和A′B′可以依据L1和L2的符号宽度和L1与L2应保持的距离来计算。假设L1和L2同等重要,可移位,那么L1和L2可以相对AA′的中点向外移位,A和A′移位向量的最小模可用公式(2)来计算。假设L1和L2不同等重要,L1更为重要且不可移位,那么L2可以相对A点向外移位,A和A′移位向量的最小模可用式(3)来计算。
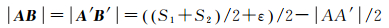 (2)
(2)
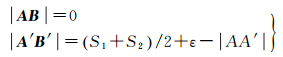 (3)
(3)
式中,S1和S2分别为L1和L2的符号宽度;ε为地图上图形之间可以辨识的最小距离阈值(常设为图上0.2 mm)。
当符号化后的道路与其周边建筑物产生空间冲突时,如图 4(d)所示,初始移位向量OC的模如下
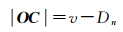 (4)
(4)
式中,Dn为建筑物相对道路中心线的最近距离;v为建筑物应偏离道路中心线的距离,其值的计算见下式
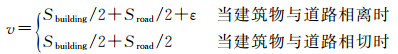 (5)
(5)
式中,Sbuilding和Sroad分别为建筑物边界和道路的符号宽度;ε含义同上。
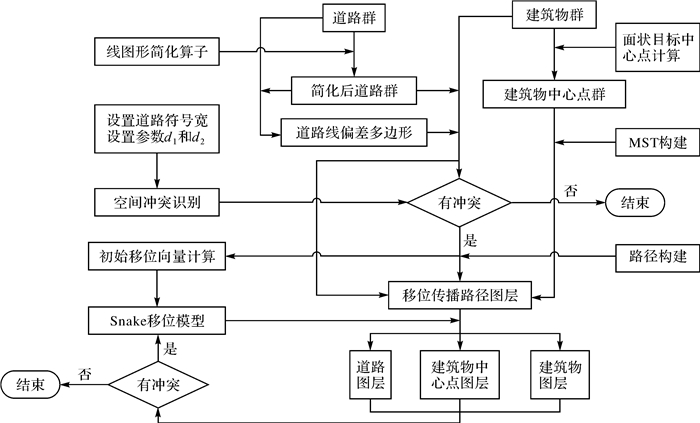
4 算法流程和试验 4.1 数据处理流程计算好初始移位向量后,就需要在已建好的移位传播路径上用Snake移位模型进行移位处理,整个协同方法的数据处理流程见图 5。在整个流程中,建筑物是面状目标,只可整体移位;道路是线状目标,同等重要,都可移位。
|
| 图 5 协同方法的数据处理流程 Fig. 5 Data processing procedure of the collaborative method |
4.2 试验过程
为了有较为完整的试验环境,选择在AE10.0的基础上用C#设计并实现本文所提出的方法。在该试验中,道路等级相同,因此,在移位的优先级上遵循的规则是:若道路与道路之间有冲突,则同时移位;若道路与建筑物之间有冲突,则移位建筑物;若建筑物与建筑物之间有冲突,则同时移位。整个试验的数据处理过程如下。
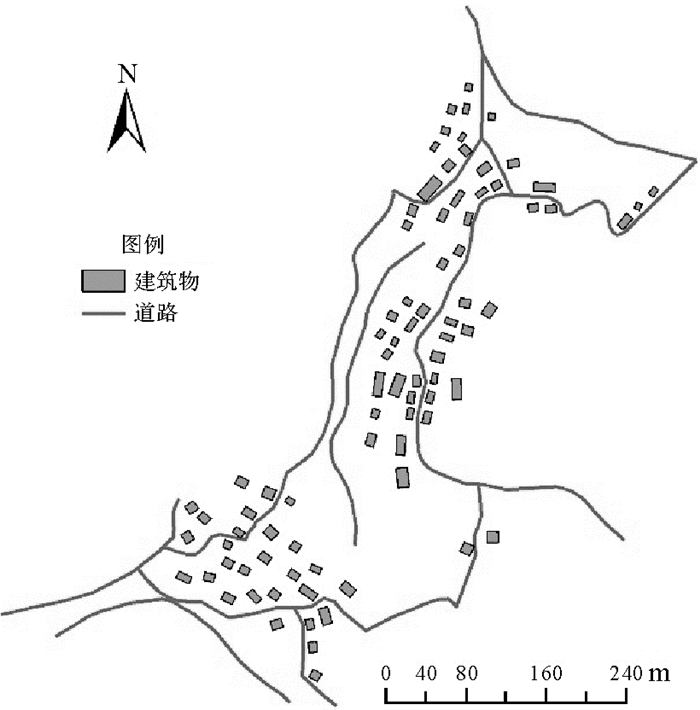
(1) 获取试验数据。以一幅1∶1万地形图上的一小块数据为试验对象,包括83个建筑物以及21条同等级的道路,目标比例尺设置为1∶2.5万。为避免因比例尺缩小造成建筑物群太过拥挤,在试验之前已经进行了适当的选取工作,试验数据见图 6。
|
| 图 6 原始试验数据 Fig. 6 Raw experimental data |
(2) 图形简化。直接用ArcGIS的线图形简化Douglas-Peucker算法生成图形简化后的道路图层。为了更全面显示试验过程中可能会遇到的各种情况,检验算法的有效性,这里将图形简化容差特意设置得比较大,设为2 mm(图上距离)。
(3) 参数设置与计算。参数d1=0.68 mm,d2=0.72 mm(图上距离),这两个参数可分别参照式(6)和式(7)中第1个等式计算。
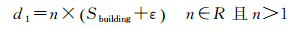 (6)
(6)
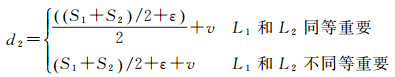 (7)
(7)
式中,Sbuilding和ε的含义同上;S1和S2分别为道路L1和L2的符号宽度;v的含义和具体设置参照式(5)。文中根据建筑物之间的邻近距离分布情况将d1中n设置为2,当比例尺增大时,n的值也会相应地增大。该值是一个近似值,用于判断移位过程中是否需要考虑邻近建筑物之间的相互影响。假设两条同等重要的道路几乎重合并且道路与其周边建筑物距离非常近,如图 7(a)所示,d2的计算见图 7(b),图中虚线代表符号化后的道路或建筑物的轮廓。

|
| 图 7 道路同等重要下参数(d2)的计算 Fig. 7 Computation of parameter (d2) with roads being equally important |
(4) 初始移位向量计算。采用前文所提出的方法进行空间冲突探测并计算初始移位向量。在计算初始移位向量的过程中,需要确定原始道路上的点移位后在简化线上的对应点,确定的方法有多种,本文选择距离等比例法。
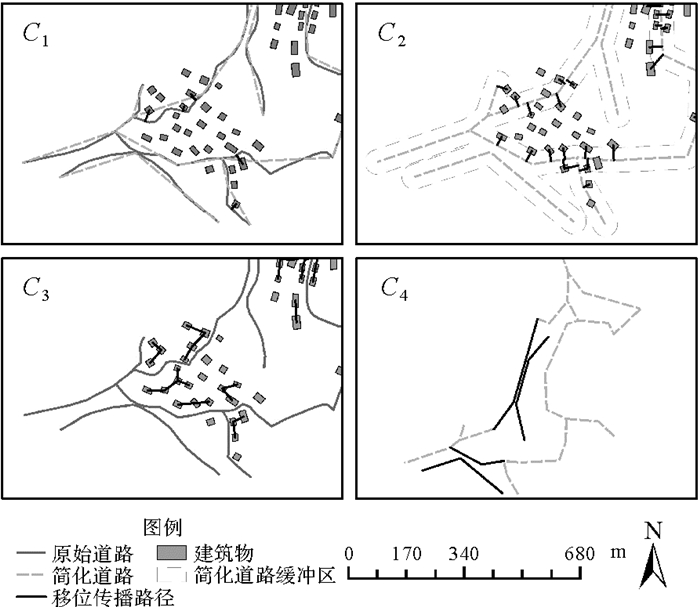
(5) 移位传播路径的建立和修正。根据前述方法构建移位传播路径时需要对C3图层中的MST进行修正。修正方法是:确认每个建筑物子群中最大初始移位向量的模,并与1.5倍的建筑物间容许距离值进行比较,选取较大的一个值作为修正阈值,将该子群的MST中大于该阈值的边删除,其作用是减少建筑物之间不必要的移位传播。最终的移位传播路径见图 8。
|
| 图 8 移位传播路径 Fig. 8 Paths of displacement propagation |
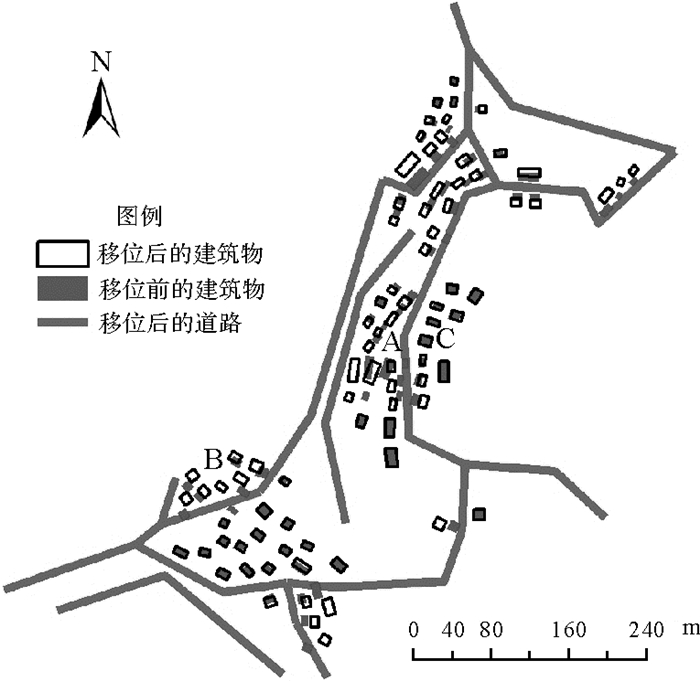
(6) Snake算法移位与冲突再探测。用Snake移位算法进行移位处理,随后,需要对移位结果进行迭代式空间冲突探测和移位,直至无空间冲突为止。移位后的结果见图 9,从视觉显示的角度看,移位后的结果图明显比移位前清晰一些。
|
| 图 9 移位后的试验图 Fig. 9 Experimental map after displacement |
4.3 特殊情况处理
Snake移位模型有两个非常重要的形状参数α和β。在移位过程中,两个参数值设置得越大,线要素移位变形越小。道路是自然的连续要素,其可变形性应当小于连接建筑物质心的MST。在此次试验中,通过人机交互获得道路的α和β值,并对建筑物之间和建筑物与道路之间连线的α和β设置了相对较小的值,经过试验发现,当它们分别约为道路的α和β值的1/100左右时,移位效果比较理想。
对于有初始移位向量的建筑物,在Snake模型中可以使用置大数法[9]进行赋值。但是,当一个子群中相连接的两个或两个以上的建筑物均有初始移位向量时,为了保持建筑物之间的空间关系,首先对具有最大初始移位向量的建筑物进行移位,其相连建筑物由于移位传播的原因也会发生移位,若在此过程中该相连建筑物已移出偏差多边形,则继续进行下一步操作,否则重新计算其初始移位向量进行赋值,重复该步骤。
当一个子群中建筑物的数量较少(小于等于4个)且彼此间都有受力时,使用Snake算法移位会出现移位后,子群内建筑物之间的相对位置变化不大,但整个子群发生较大偏移,违反制图规则。此时,可以根据局部区域内各个建筑物的综合受力情况直接进行移位,这样,一方面可以提高移位的效率,另一方面可以避免建筑物的移位量过大。
5 结果分析该论文中的试验结果的相关统计信息见表 1,其中,P/L表示建筑物与道路之间的冲突,P/P表示建筑物之间的冲突,L/L表示道路之间的冲突。根据我国地形图制图的相关标准,对于地物符号化后出现的压盖、符号间应保留的空隙等情况引起的地物要素位移,位移值一般不超过0.5 mm,特殊情况下最大位移值不应超过1 mm(GB/T12343.1-2008)。试验中,道路顶点的移位距离均保持在0.5 mm以内;建筑物中移位距离超过0.5 mm的有15个,其中有9个处于偏差多边形中,考虑到文中图形简化容差被有意设置为一个较大值,这些建筑物的移位距离也会相应地增大,其余6个分布在图 9中的A区和B区,这两个区域中的建筑物密度较大,已无法在有限的范围内提供足够的移位空间,需要配合其他综合操作(如选取)才能解决。此外,从结果可以看到,对齐分布的建筑物群在移位前后的重心连线变化很小,如图 9中C区左侧的6个建筑物,说明该算法在移位中能够较好地保持空间关系。
| 初始冲突个数 | 建筑物顶点移位距离/mm | 道路顶点移位距离/mm | ||||||||
| P/L | P/P | L/L | 最大值 | 最小值 | 平均值 | 最大值 | 最小值 | 平均值 | ||
| 49 | 24 | 8 | 0.70 | 0.02 | 0.31 | 0.16 | 0.01 | 0.08 | ||
这里把已有的常用的解决空间冲突的方法简称为“常规方法”,在这些常规方法中线简化[2-6]、道路移位[7-10]、建筑物移位[12-17]以及空间冲突探测[9-16]都是独立执行的。以线简化阶段中空间冲突的解决为例,文献[1]先用Douglas-Peucker算法进行线简化,然后采用几何方法探测空间冲突,并通过点移位来解决这些空间冲突。在这个过程中,空间冲突可能需要多次探测,并进行移位处理。但是,本文所提出的协同方法在探测空间冲突的同时建立移位传播路径,在传播路径上使用Snake算法进行移位,明显减少了空间冲突的探测次数,在一定程度上提高了地图综合数据处理的效率。
6 结 论本文以Snake算法为基础,通过把线图形简化转换为线上的点移位,并利用地图目标之间的邻近关系,使得地图目标的移位统一在一个线性网络中,避免了多次次生空间冲突的探测。研究表明,该算法能有效地协同解决线图形简化、移位和符号化所产生的不同类型的空间冲突问题,同时较好地保持有关地图目标的空间特征。但是,在研究中发现,当建筑物群非常密集时,往往需要进行选取才能解决这类空间冲突问题。如何把选取或其他地图综合操作与移位操作进行协同,是下一步需要研究的内容。
| [1] | MULLER J C. The Removal of Spatial Conflicts in Line Generalization[J]. Cartography and Geographic Information Systems , 1990, 17 (2) : 141 –149. DOI:10.1559/152304090783813817 |
| [2] | LI Zhilin, OPENSHAW S. Algorithms for Automated Line Generalization Based on a Natural Principle of Objective Generalization[J]. International Journal of Geographical Information Systems , 1992, 6 (5) : 373 –389. DOI:10.1080/02693799208901921 |
| [3] | 郭庆胜. 线状要素图形综合的渐进方法研究[J]. 武汉测绘科技大学学报 , 1998, 23 (1) : 52–56. GUO Qingsheng. Study on Progressive Approach to Graphic Generalization of Linear Feature[J]. Journal of Wuhan Technical University of Surveying and Mapping , 1998, 23 (1) : 52 –56. |
| [4] | SAALFELD A. Topologically Consistent Line Simplification with the Douglas-Peucker Algorithm[J]. Cartography and Geographic Information Science , 1999, 26 (1) : 7 –18. DOI:10.1559/152304099782424901 |
| [5] | GUO Qingsheng, BRANDENBERGER C, HURNI L. A Progressive Line Simplification Algorithm[J]. Geo-Spatial Information Science , 2002, 5 (3) : 41 –45. DOI:10.1007/BF02826387 |
| [6] | 朱鲲鹏, 武芳, 王辉连, 等. Li-Openshaw算法的改进与评价[J]. 测绘学报 , 2007, 36 (4) : 450–456. ZHU Kunpeng, WU Fang, WANG Huilian, et al. Improvement and Assessment of Li-Openshaw Algorithm[J]. Acta Geodaetica et Cartographica Sinica , 2007, 36 (4) : 450 –456. |
| [7] | BURGHARDT D, MEIER S. Cartographic Displacement Using the Snakes Concept[C]//FÖRSTNER W, PLVMER L. Semantic Modeling for the Acquisition of Topografic Information from Images and Maps. Basel:Birkhaeuser Verlag, 1997:59-71. |
| [8] | BADER M. Energy Minimization Methods for Feature Displacement in Map Generalization[D]. Zürich:University of Zürich, 2001. |
| [9] | 武芳, 侯璇, 钱海忠, 等. 自动制图综合中的线目标位移模型[J]. 测绘学报 , 2005, 34 (3) : 262–268. WU Fang, HOU Xuan, QIAN Haizhong, et al. A Model for Road Network Displacement in Automated Map Generalization[J]. Acta Geodaetica et Cartographica Sinica , 2005, 34 (3) : 262 –268. |
| [10] | 吴小芳, 杜清运, 胡月明, 等. 基于改进Snake模型的道路网空间冲突处理[J]. 测绘学报 , 2008, 37 (2) : 223–229. WU Xiaofang, DU Qingyun, HU Yueming, et al. Disposal of Spatial Conflict between the Roads Networks Based on Improved Snake Model[J]. Acta Geodaetica et Cartographica Sinica , 2008, 37 (2) : 223 –229. |
| [11] | LIU Yuangang, GUO Qingsheng, SUN Yageng. A Complete Solution of Cartographic Displacement Based on Elastic Beams Model and Delaunay Triangulation[C]//Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Suzhou:ISPRS Technical Commission IV Symposium, 2014, XL-4:163-168. |
| [12] | 艾廷华. 基于场论分析的建筑物群的移位[J]. 测绘学报 , 2004, 33 (1) : 89–94. AI Tinghua. A Displacement of Building Cluster Based on Field Analysis[J]. Acta Geodaetica et Cartographica Sinica , 2004, 33 (1) : 89 –94. |
| [13] | 何津, 费立凡. 解决图形冲突的受限变形所涉及的数学原则--以道路与建筑物的关系为例[J]. 武汉大学学报(信息科学版) , 2007, 32 (4) : 326–330. HE Jin, FEI Lifan. Mathematical Methods Involved in Constrained Reshaping for Solving Graphic Conflicts between Streets and Buildings[J]. Geomatics and Information Science of Wuhan University , 2007, 32 (4) : 326 –330. |
| [14] | 费立凡, 何津. 解决街道与建筑物图形冲突的移位模型研究[J]. 武汉大学学报(信息科学版) , 2007, 32 (6) : 540–543. FEI Lifan, HE Jin. Displacement Models for Solving Graphic Conflicts between Streets and Buildings[J]. Geomatics and Information Science of Wuhan University , 2007, 32 (6) : 540 –543. |
| [15] | 周启, 艾廷华, 张翔. 面向多重空间冲突解决的移位场模型[J]. 测绘学报 , 2013, 42 (4) : 615–620. ZHOU Qi, AI Tinghua, ZHANG Xiang. A Displacement Field Model to Resolve Multiple Spatial Conflicts[J]. Acta Geodaetica et Cartographica Sinica , 2013, 42 (4) : 615 –620. |
| [16] | RUAS A. A Method for Building Displacement in Automated Map Generalisation[J]. International Journal of Geographical Information Science , 1998, 12 (8) : 789 –803. DOI:10.1080/136588198241509 |
| [17] | HØJHOLT P. Solving Space Conflicts in Map Generalization:Using a Finite Element Method[J]. Cartography and Geographic Information Science , 2000, 27 (1) : 65 –74. DOI:10.1559/152304000783548028 |
| [18] | HARRIE L. An Optimisation Approach to Cartographic Generalisation[D]. Sweden:Lund University, 2001. |
| [19] | BADER M, BARRAULT M, WEIBEL R. Building Displacement over a Ductile Truss[J]. International Journal of Geographical Information Science , 2005, 19 (8-9) : 915 –936. DOI:10.1080/13658810500161237 |
| [20] | LONERGAN M, JONES C B. An Iterative Displacement Method for Conflict Resolution in Map Generalization[J]. Algorithmica , 2001, 30 (2) : 287 –301. DOI:10.1007/s00453-001-0011-0 |
| [21] | WARE J M, JONES C B, THOMAS N. Automated Map Generalization with Multiple Operators:A Simulated Annealing Approach[J]. International Journal of Geographical Information Science , 2003, 17 (8) : 743 –769. DOI:10.1080/13658810310001596085 |


