高精度的遥感信息提取是遥感图像处理和应用的关键。传统的中低空间分辨率遥感信息提取,主要采用像元分类方法。基于像元光谱特征的硬分类不考虑相邻像元之间的空间相关性和尺度因素,或者即使有些分类算法融合了纹理特征,其本质上考虑了像元之间的空间相关性和影像特征的尺度因素,但是纹理分析的尺度或窗口大小往往采用人为给定,缺少对纹理特征尺度的定量分析,在遥感像元模式识别的自适应尺度选择上存在一定的主观性和盲目性。
随着高空间分辨率遥感的发展,像元之间的空间相关性不断增强,传统的遥感图像像元光谱分类方法面临着更大的挑战,高空间分辨率遥感像元分类的精度更是难以达到实际应用的需求。在这种背景下,“对象级”或者“面向对象遥感影像分析”(geo-object-based image analysis,GeOBIA)方法逐渐受到重视,并被誉为是遥感(RS)和地理信息系统(GIS)之间的桥梁。基于GeOBIA的“对象级”遥感影像分析主要是将影像划分成均质的影像对象,不仅能够表达影像区域的光谱特征,还能表达丰富的空间和上下文特征等语义信息,从而避免了分类中的椒盐效应,使光谱相似的地类区分成为可能[1-2]。在这个过程中,多尺度分割是“对象级”遥感影像分析的基础和关键,直接关系到后续的变化信息提取与分析[3-4],但是如何选择合适的分割尺度参数依旧是一个挑战[5]。
实际上,无论是遥感像元分类,还是面向对象遥感分类,二者的实质是相同的,只是分类的客体从单个的规则的像素变成了连续的不规则的影像对象区域,分类所依据的特征由单纯的光谱或者纹理分类变成了多特征(不仅包括光谱或者纹理,还包括形状、尺度上下文关系等)协同的模式分类。在这两种分类中,尺度选择的不同会带来不同的分类效果和精度,前者体现为影像数据源的空间分辨率不同或者纹理分析采用的计算窗口大小不同[6-8],后者体现为多尺度分割采用的尺度参数不同[9-10]。正是由于尺度选择是否合适会极大地影响遥感信息提取的精度,遥感模式分类的最佳尺度选择成为遥感研究的关键科学问题和技术问题。
然而,由于尺度概念内涵本身的复杂性及尺度处理方法的复杂性,遥感处理与分析中的尺度选择一直是困扰遥感学界的难题。本文在系统总结遥感模式分类中的尺度问题的基础上,论述了将空间统计学应用于遥感模式分类尺度选择的理论基础和可行性,并以面向对象的高分辨率遥感影像农田提取为例,进行了将空间统计学应用于面向对象影像分析最佳尺度估计的实例验证。
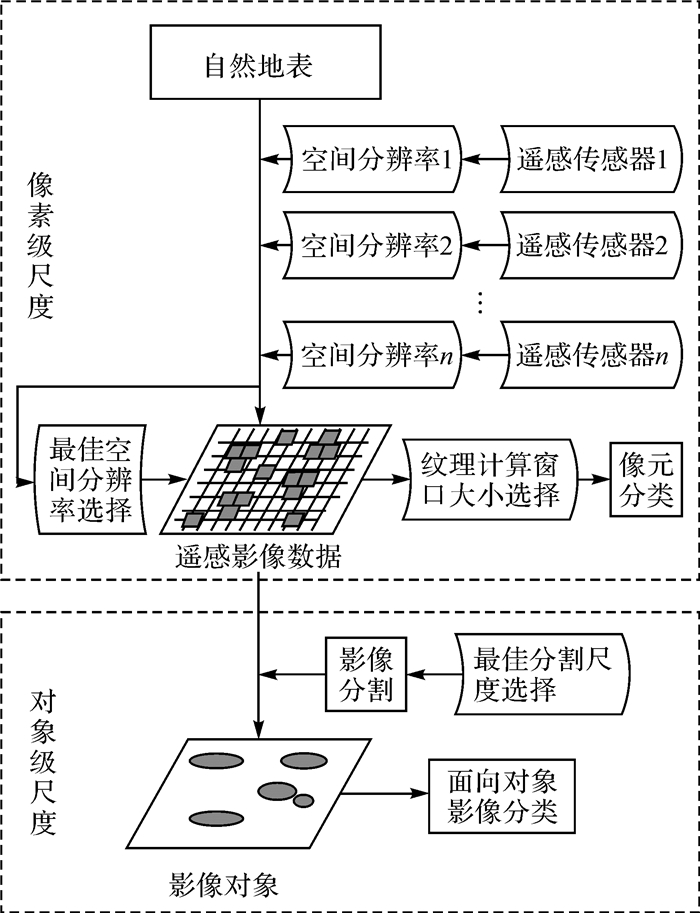
1 遥感模式分类中的尺度问题及其空间统计学理论基础尺度是一个广泛使用的术语,在一般科学研究领域,尺度主要指研究的范围或者详细程度[11]。文献[12-13]对尺度概念的总结相对较为全面,可以扩展到地学其他研究领域,它们定义了4种与空间现象有关的尺度:制图尺度,指地图比例尺;观测尺度或地理尺度,即研究区域的空间扩展;量测尺度或分辨率,指空间数据集中最小的可区分部分,如遥感影像像素大小;运行尺度或操作尺度,指地学现象发生的空间环境范围。文献[8]和文献[14]将上述地学尺度的一般含义应用在遥感领域,结合面向对象遥感分析技术和影像理解的思想,从遥感数据处理、应用和分析的角度,提出了“像素-影像对象-格局”三层次的遥感尺度内涵,并将其与遥感信息处理与分析具体环节相结合,初步分析了各个层次尺度研究的重点。在此三层次的遥感尺度内涵基础上,本文针对前两个层次,结合遥感模式分类具体问题,提出了如图 1所示的遥感分类中像素级与对象级尺度研究框架。
|
| 图 1 遥感分类中像素级与对象级尺度研究框架 Fig. 1 Schematic map of scale issues in pixel and object based remote sensing image classification |
在地学尺度的一般范畴里,合适的尺度本质上是恰好能反映地物间空间相关性是否存在的一个临界点[15],因而空间统计学方法被认为是遥感处理与分析中尺度问题研究的一个重要途径[4, 15],且已被应用于面向遥感像元分类的最佳空间分辨率选择[7-8, 14]以及面向对象遥感分析多尺度分割的尺度参数选择中[15-16]。
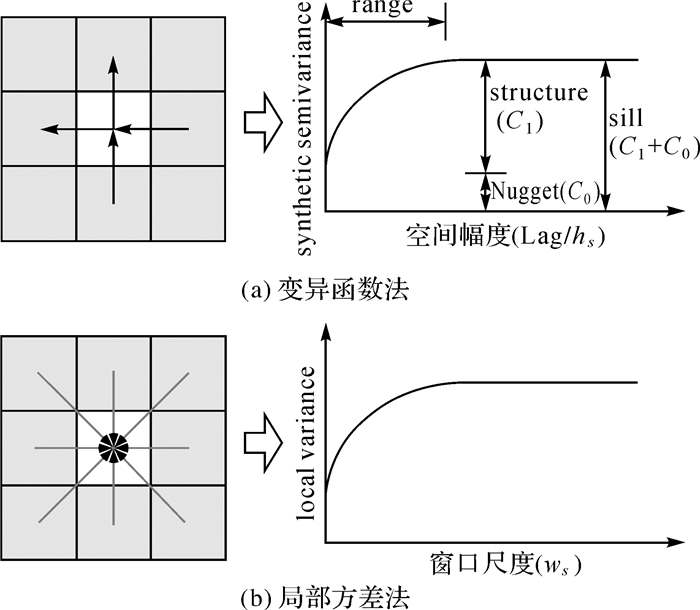
对于像元级尺度和遥感像元分类而言,尺度是与分辨率有内在联系的[14],空间分辨率的大小反映了空间细节水平以及和背景环境的分离能力[17]。对这种空间细节水平的描述,实质就是对地物空间相关性尺度依赖关系的描述,最简单也最有效果的方法就是经典地统计学中的变异函数方法(也称半方差方法),其在遥感影像尺度问题中得到应用的理论前提就是空间统计学中空间依赖性理论,即空间上相邻近的地物之间的相似性程度要强于空间上相距较远的地物[18],也就是强调在短距离之内观察值比远距离的观察值更要相似,即方差较小[19]。变异函数方法通过绘制地物属性值随空间幅度变化的方差图(semivariogram)来反映尺度变化[20],方差图中几个明显的断点就是影像上的景观在不同尺度水平下的表现结果[21],并以此来确定基于地物类别的景观研究所应采用的最佳分辨率。一个典型变异函数曲线如图 2(a)所示,根据影像数据统计计算确定的变程Range成为最佳空间分辨率选择的依据,合适的空间分辨率就是这个恰好能反映像元间空间相关性是否存在的自相关阈值范围。
|
| 图 2 半方差和局部方差计算过程 Fig. 2 Schematic diagrams for the computation of semivariance and local variance |
基于这个基本思想,文献[15]提出利用局部方差图(LAVariogram)来近似替代semivariogram,二者的区别仅仅在于变异函数法考虑了地物自相关的方向性,而局部方差方法则综合计算了各个方向的方差,因而局部方差方法方法相当于是变异函数法的多方向综合后的计算结果,因而二者的空间统计学思想基础在一定程度上是相似的。这种理解与文献[17]提出的在一定计算窗口下局部方差随影像空间分辨率变化的最大值对应的空间分辨率能更好地反映地物尺寸的思路殊途同归,都最终在方差曲线变程或地物自相关空间阈值上找到出路,因为大量实际统计计算表明当空间幅度计算间隔数量足够多的情况下,LAVariogram的形态和走势与多方个向下综合平均半方差曲线synthetic semivariogram基本一致(其示意图如图 2所示)。换句话说,两种理解的实质都是最终将最佳空间分辨率(或地物尺寸)归结到了地物空间自相关的阈值。
将上述遥感影像尺度问题的空间统计学理解扩展到面向对象影像分析中,虽然尺度分析的对象由离散的规则的像元变为连续的形状不规则的影像对象,但尺度问题的本质依旧是空间统计学的空间自相关或者尺度依赖思想。在面向对象影像分析中,目前学术界还没有对对象级尺度概念进行明确的界定。根据影像对象的定义,对象级尺度是指影像对象(对象细节)在空间跨度上的大小;而从影像对象提取(影像分割)算法的角度,对象级尺度主要对应了多尺度分割算法中的尺度参数。其中前者体现了对象级尺度在理论上的定义,后者体现了对象级尺度在方法技术上的定义。因此对象级尺度研究的焦点目前主要集中在多尺度分割的尺度优选问题上。
关于对象级尺度选择方法的研究,在模式识别领域,主要进行了多尺度聚类分割过程中的尺度参数(带宽参数)选择的研究,如文献[22]对均值漂移(mean-shift)聚类分割算法的属性带宽参数自动选择进行了研究,但同时指出这种方法对多变量聚类(多波段影像分割)的效果缺乏实际意义[23]。此外也有研究对聚类过程中的带宽参数选择进行了研究,但其试验数据为现实生活中很少出现的离散的模拟数据[24]。目前,图像处理领域也对多尺度分割的尺度参数选择问题进行了探讨,目前研究的思路主要分为两大类:一类是基于大量尺度分割结果进行监督或非监督分割评价进行的尺度优选,另一类是基于空间统计学计算的尺度预估计[15-16]。前者的实质是一种分割后的评价,而不是分割前的估计,无疑这种方法进行大量分割和评价要耗费大量的计算资源,普适性和自动化程度欠佳。后者的基于空间统计学计算的尺度预估计思想与地学空间数据分析领域提出的基于方差和频率计算的连续数据离散化处理的思想[25-26]有相通之处,只不过地学空间数据分析领域更多地关注属性数据的离散化,而遥感数据的分割是同时基于空间和属性信息的离散化处理,且遥感数据对应自然地表,遥感影像分割要顾及面积最小的地物类别也能准确划分,故影像分割的离散化过程中只能关注方差较小的部分以避免过度分割。总体上来说,遥感影像的分割尺度参数的确定应该是基于原始影像上全局或者局部特征的一种统计估计,因此空间统计学方法无论从空间统计学的科学思想基础,还是在算法计算效率等方面,都是解决面向对象影像分析尺度问题的根本且可行的方法。
2 基于空间统计学的面向对象影像分析分割尺度估计遥感影像是一种特殊的空间数据,具有空间数据的两大基本特征,即空间特征和属性特征,因此,不同于一般非空间数据聚类,遥感影像的分割可以依据空间特征和属性特征进行。同时,考虑到遥感目标识别或信息提取的地学应用目标,许多分割算法将分割斑块(在面向对象影像分析中被称作影像对象)的大小也作为分割的主要参数,而在空间统计学意义上,影像对象的大小则是地物空间自相关在二维空间上的表现,因此影像对象的大小的尺度估计最终仍可归结到空间特征的尺度估计。
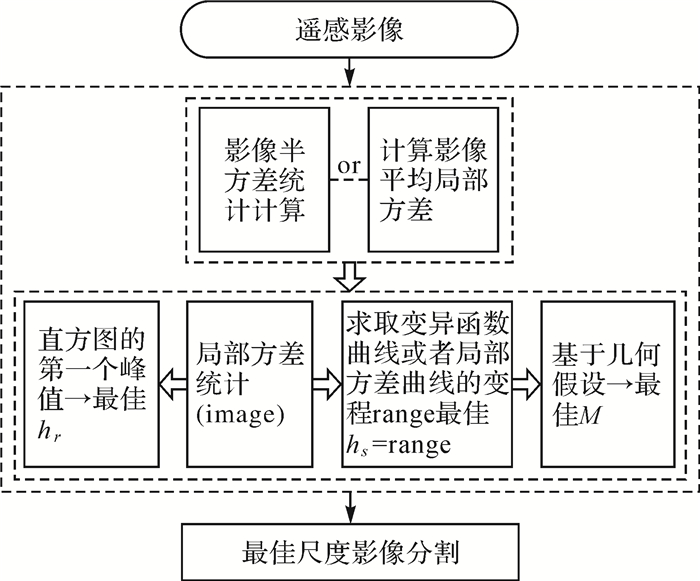
在此分析基础上,将影响遥感影像多尺度分割的尺度分割参数概括为空间属性分割参数hs、光谱属性分割参数hr和影像对象面积阈值参数M。其中,空间属性分割参数hs的实际含义是分割过程中像元在空间域的距离阈值,对应实际计算窗口的尺寸;光谱属性分割参数hr的实际含义是分割过程中像元在属性域的属性阈值,对应两类别间的灰度特征差值;影像对象面积阈值参数M的实际含义是分割斑块合并的阈值,即分割后最小斑块的像元数目。这3个参数是基于空间数据的一般属性提出的,几乎可以部分或者全部地应用于所有遥感影像分割算法中。进而,基于上文提出的遥感模式分类中的尺度问题的空间统计学理论基础,提出如图 3所示的基于数据驱动的面向对象影像分析中的分割尺度自适应估计方法。详细的计算过程及原理见参考文献[14-17]。
|
| 图 3 数据驱动的分割尺度自适应估计方法示意图 Fig. 3 Workflow of data driven optimal segmentation parameter estimation based on spatial statistics |
3 面向对象高分辨率遥感影像农田提取实例 3.1 试验数据及面向对象农田提取技术流程
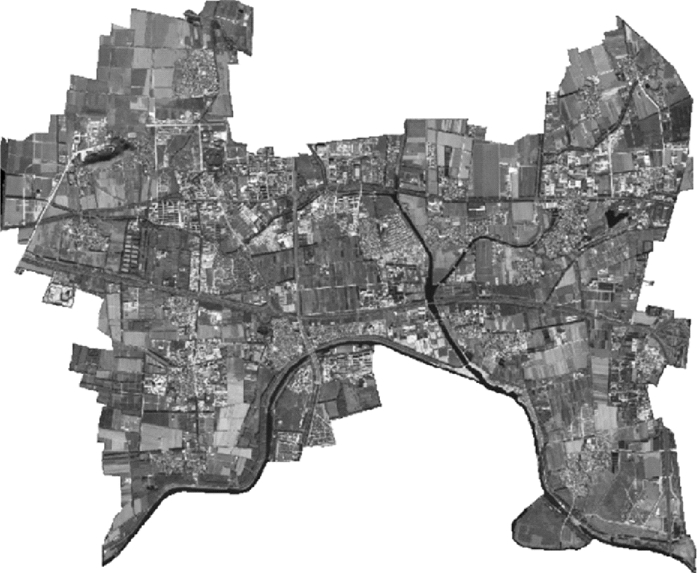
本文以北京市昌平区的小汤山镇作为试验区。小汤山镇位于北京北部,农业生产较为多样化,绿色农业和设施农业占一定的比例。如图 4所示,研究区试验数据为SPOT-5卫星假彩色合成影像(图 4为假彩色合成显示),成像时间为2007年10月16日,包括4个多光谱波段(空间分辨率为10 m)和一个全色波段(空间分辨率为2.5 m)。
|
| 图 4 研究区及试验影像 Fig. 4 SPOT-5 image of the study area |
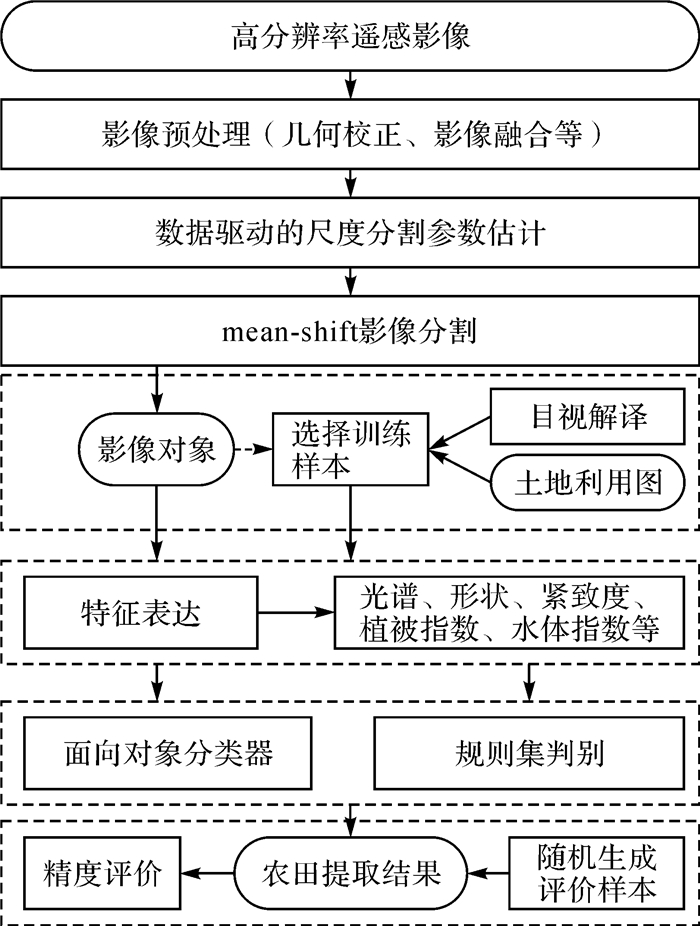
在2002年土地利用矢量图的辅助下,本文首先对原始数据进行了精度优于1个像元的几何校正。由于HSV(hue-saturation-value)影像融合方法能更好地保持地物的纹理和细节信息,对几何校正后的影像数据进行了基于HSV的影像融合,融合后影像的大小为4855×3955像素,覆盖面积约38 km2。本文试验采用的面向对象农田提取方法流程如图 5所示。
|
| 图 5 基于尺度估计的面向对象农田提取流程图 Fig. 5 Workflow of GeOBIA based cropland extraction |
3.2 尺度分割参数估计
根据上文提出的空间统计学尺度估计方法,本文采用研究区融合影像农田子区随计算间隔变化的变异函数值来确定最佳空间属性参数。这里的计算间隔,对应了在水平方向和垂直方向上像元点对之间的空间距离,变异函数方差计算则是像元点对光谱值差异在全局影像遍历基础上的平均计算。关于变异函数及综合半方差变差的详细计算原理和公式,见参考文献[16]。理论上最佳空间属性参数的阈值应为地物属性(即遥感影像的光谱值)自相关空间阈值,即变异函数曲线的变程,该变程常常采用一定数学模型如球状模型或指数模型等拟合求出。但实际计算中影像变异函数曲线并非严格平稳,抖动比较严重,而且从面向对象信息提取的角度讲,过大的计算间隔(或过大的空间属性参数)常常会导致分割单元过大且过于概括,故文献[16]提出用综合半方差随计算间隔变化的变化差异作为近似变程的指示,即计算综合半方差随计算间隔变化的变差,将变差值首次小于零时对应的计算间隔作为近似变程,即理论上的最佳空间属性参数。
通过计算农田子区的变异函数值(如图 6(a)所示),本文采用综合半方差变差计算来进行最佳属性空间分割参数的选择。其计算间隔i对应的综合半方差变差计算公式如下
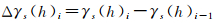 (1)
(1)
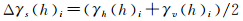 (2)
(2)
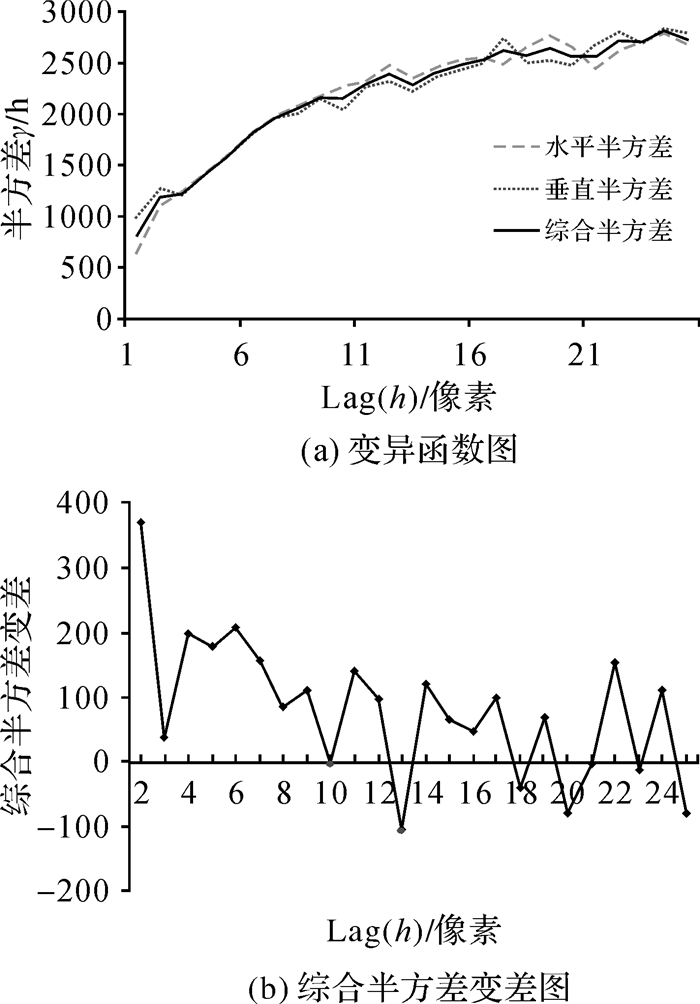
式中,Δγs(h)i表示计算间隔i对应的综合半方差变差;γs(h)i表示计算间隔i对应的综合半方差,它等于计算间隔i对应的水平方向半方差γh(h)i与计算间隔i对应的垂直半方差γv(h)i的平均值。图 6(b)给出了综合半方差变差随计算间隔变化的变化曲线图,当统计计算间隔取10,综合半方差变差为-3.7,当统计计算间隔取13,综合半方差变差为-106.6。进而从理论上,确定适合于研究区影像分割的空间属性参数取10和13都较为合适。
|
| 图 6 研究区面向对象分析空间属性分割参数估计 Fig. 6 Spatial attribute parameter pre-estimation of the experimental image for GeOBIA |
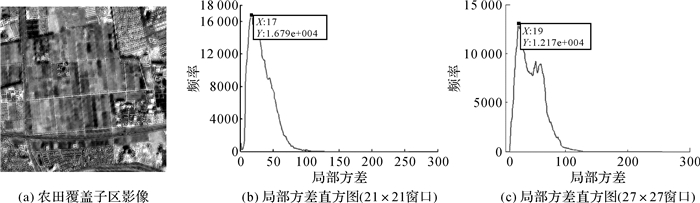
在上述空间属性参数预测基础上(空间属性参数取10,对应21×21的计算窗口;空间属性参数取13,对应27×27的计算窗口),计算了典型农田覆盖区子影像(图 7(a),大小为800×800像素)的局部方差影像,对该局部方差影像进行直方图统计,直方图的第一个峰值对应的局部方差值(记为LV*)可以作为最佳属性参数的指示,因为光谱属性分割参数hr的实际含义是分割过程中对应两类别像元间的灰度特征差值,故hr取LV*的平方根,即hr=(LV*)1/2。从统计学意义上讲,短波红外波段所携带的信息量一般较大,且该波段是植被提取的关键波段[27],为了减少计算量,这里的子影像局部方差只计算了短波红外波段,计算结果见图 7(b)和图 7(c)。根据图 7的计算结果及文献[15]提出的方法,计算出了当空间属性参数取10和13时,局部方差影像直方图峰值出现的位置分别为17和19,进而最佳属性分割参数阈值分别为√17和√19,这里四舍五入均取为4。
|
| 图 7 典型农田覆盖区子影像局部方差直方图 Fig. 7 Histograms of Local Variance image (window size=21) |
根据文献[15]提出的方法,基于目标几何特性假设,当地物形状相对较为规则时,最小斑块的面积为以hs为边长的正方形面积的一半来计,即最佳合并斑块阈值M=hs2/2。进而最终确定当空间属性参数取10及空间属性参数取13时,本试验农田子区合并斑块阈值的最佳取值分别为50和85。
3.3 农田提取结果及分析结合农田提取研究目的并通过目视解译和土地利用图的辅助,确定研究区土地覆盖类型为C1农田、C2建筑用地、C3暗目标及C4林地。考虑到各类别内部的光谱可变性,根据其光谱差异,C1农田又被划分为C11高覆盖度农田、C12低覆盖度农田和C13未耕种农田3个子类;C2建筑用地又被划分为C21居民区、C22水泥地面、C23暗色调建筑区和C24高亮色调建筑区;C3暗目标又被划分为C31阴影和C32水体。
为了进一步验证上文提出的基于空间统计学面向对象尺度估计方法的有效性,本文将VC++实现的mean-shift分割结果导入eCognition Developer 8.0面向对象影像分析软件,进行了系列尺度面向对象农田提取试验,面向对象分类采用的分类器为最近邻分类器。由于这3个尺度分割参数中,M的变化对分割结果的影响最为剧烈,且M的确定是在空间属性参数hs估计的基础上实现的,故本文只对农田提取精度随M的变化情况进行分析,即M的取值从25取到200,间隔为25,共进行了8个尺度的农田提取试验。为了保证不同尺度间分类结果的可比性,训练样本在各个尺度间保持了一致,但由于当M取值200的时候,影像对象的尺寸都比较大,影像对象的个数相对较少,因此试验中能获取的样本数量有限,分别是:C11,16个;C12,14个;C13,12个;C21,8个;C22,6个;C23,5个;C24,9个;C31,8个;C32,8个;C4,15个。在整个原始融合影像上采用每隔400行和400列生成精度验证样本点共751个用于面向对象分类精度评价。评价样本的类别按照训练样本选择的方法确定,其中:C1,330个;C2,190个;C3,129个;C4,102个。分类过程中采用的特征包括光谱特征、灰度共生矩阵纹理(GLCM)和归一化差值植被指数(NDVI)。
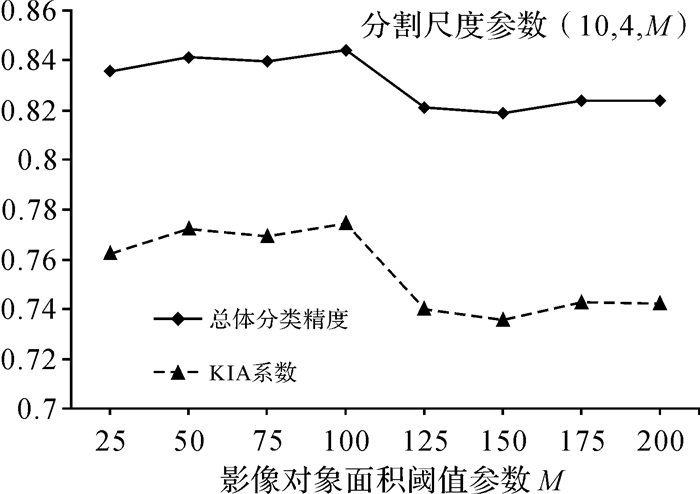
图 8显示了最近邻分类所得到的随着M取值变化的总体分类精度及KIA系数的变化趋势。在系列分类中,M为50时,分类精度为84.15%,仅仅略低于系列分类精度的最高值,M取100时,分类精度84.42%。这两个尺度等于或非常接近于本文利用空间统计学方法进行尺度估计得到的理论最佳尺度(分别为50和85)。文献[15]已经证明通过空间统计学预测的理论最佳尺度,能最大限度地保证斑块间的异质性和斑块内的均质性,这是两个影响分类精度的关键因素。本文的系列分类结果也进一步证明了本文提出的基于空间统计学的尺度估计方法在面向对象信息提取中能保证一定的分类精度,因而这种尺度估计方法是可行且有效的。
|
| 图 8 面向对象分类精度随尺度变化趋势图 Fig. 8 Classification accuracies |
表 1给出了最高分类精度(当尺度参数取(10,4,100))对应的面向对象分类混淆矩阵。表 1显示在分类中农田和林地存在一定程度的误分类,这是由于这两种地物本身的光谱特征就比较相似且不易区分。图 9给出了当尺度参数取(10,4,25)、(10,4,50)、(10,4,100)和(10,4,200)时的面向对象分类结果。将图 9中的一些细节放大,还可以看出当M取值为50和100时,不仅分类精度高,分类结果的破碎性也一定程度上得到了抑制,斑块的完整性相对较好。
| 类别 | C1农田 | C2建筑用地 | C3暗目标 | C4林地 | 总数 |
| C1农田 | 294 | 4 | 4 | 39 | 341 |
| C2建筑用地 | 6 | 169 | 9 | 1 | 185 |
| C3暗目标 | 0 | 16 | 111 | 2 | 129 |
| C4林地 | 30 | 0 | 5 | 60 | 95 |
| 未分类 | 0 | 1 | 0 | 0 | 1 |
| 总数 | 330 | 190 | 129 | 102 | 751 |
| 生产者精度/(%) | 89.10 | 88.95 | 86.04 | 58.82 | |
| 用户精度/(%) | 86.21 | 91.35 | 86.04 | 63.16 | |
| 总体精度/(%) | 84.42 | ||||
| KIA | 0.774 7 |
4 结 论
尺度选择问题一直是影响遥感信息提取精度的关键问题之一。本文论述了利用空间统计学方法解决遥感影像模式分类中的尺度问题的理论基础及可行性,并以面向对象农田提取为例,针对面向对象提取中最优分割尺度预测问题,基于变异函数方法进行了尺度优选试验,并以面向对象农田提取的多尺度分类为应用案例,进行了上述理论可行性及有效性的验证。试验结果证明了基于空间统计学理论方法进行面向对象信息提取尺度预测的有效性,该方法虽然难以估计绝对最佳尺度参数,但是通过该方法估计出的最佳尺度参数能从理论上接近最优,进而能在一定程度上保证面向对象信息提取的精度。此外,以往分割后评价的尺度选择方法会占用大量计算资源且耗费大量时间,本文提出的方法是完全数据驱动的方法,基本不需要先验知识的参与,一定程度上提高了面向对象信息提取的效率和自动化程度。

|
| 图 9 多尺度面向对象分类结果图 Fig. 9 Multi-scale supervised nearest neighbor classification results |
此外,需要说明几点:为进一步优化尺度选择的效果,在尺度参数估计时充分注意参考子影像的选取要有代表性,在计算能力允许的前提下,选择多个参考子区,综合求出折中的参数也是改进最终分类精度的可行途径;在今后的研究中,结合空间统计学理论方法,面向不同类型的地物或景观格局,实现分割前最优尺度分割参数的选择,并进行多个最优尺度的信息综合,更有效提高面向对象遥感影像处理与分析的精度和自动化程度,更深入地研究遥感尺度聚合问题的地学规律及实质,也将成为今后研究的重点。
| [1] | 温奇, 李苓苓, 刘庆杰, 等. 基于视觉显著性和图分割的高分辨率遥感影像中人工目标区域提取[J]. 测绘学报 , 2013, 42 (6) : 831–837. WEN Qi, LI Lingling, LIU Qingjie, et al. A Man-made Object Area Extraction Method Based on Visual Saliency Detection and Graph-cut Segmentation for High Resolution Remote Sensing Imagery[J]. Acta Geodaetica et Cartographica Sinica , 2013, 42 (6) : 831 –837. |
| [2] | 李亮, 舒宁, 王凯, 等. 融合多特征的遥感影像变化检测方法[J]. 测绘学报 , 2014, 43 (9) : 945–953. DOI:10.13485/j.cnki.11-2089.2014.0138 LI Liang, SHU Ning, WANG Kai, et al. Change Detection Method for Remote Sensing Images Based on Multi-features Fusion[J]. Acta Geodaetica et Cartographica Sinica , 2014, 43 (9) : 945 –953. DOI:10.13485/j.cnki.11-2089.2014.0138 |
| [3] | 冯文卿, 张永军. 利用多尺度融合进行面向对象的遥感影像变化检测[J]. 测绘学报 , 2015, 44 (10) : 1142–1151. DOI:10.11947/j.AGCS.2015.20140260 FENG Wenqing, ZHANG Yongjun. Object-oriented Change Detection for Remote Sensing Images Based on Multi-scale Fusion[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (10) : 1142 –1151. DOI:10.11947/j.AGCS.2015.20140260 |
| [4] | 李慧, 唐韵玮, 刘庆杰, 等. 一种改进的基于最小生成树的遥感影像多尺度分割方法[J]. 测绘学报 , 2015, 44 (7) : 791–796. DOI:10.11947/j.AGCS.2015.20140060 LI Hui, TANG Yunwei, LIU Qingjie, et al. An Improved Algorithm Based on Minimum Spanning Tree for Multi-scale Segmentation of Remote Sensing Imagery[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (7) : 791 –796. DOI:10.11947/j.AGCS.2015.20140060 |
| [5] | 慎利, 唐宏, 王世东, 等. 结合空间像素模板和Adaboost算法的高分辨率遥感影像河流提取[J]. 测绘学报 , 2013, 42 (3) : 344–350. SHEN Li, TANG Hong, WANG Shidong, et al. River Extraction from the High Resolution Remote Sensing Image Based on Spatially Correlated Pixels Template and Adboost Algorithm[J]. Acta Geodaetica et Cartographica Sinica , 2013, 42 (3) : 344 –350. |
| [6] | CHEN D, STOW D A, GONG P. Examining the Effect of Spatial Resolution and Texture Window Size on Classification Accuracy:An Urban Environmental Case[J]. International Journal of Remote Sensing , 2004, 25 (11) : 2177 –2192. DOI:10.1080/01431160310001618464 |
| [7] | MING Dongping, DU Jinyang, ZHANG Xiyu, et al. Modified Average Local Variance for Pixel-level Scale Selection of Multi-band Remote Sensing Images and Its Scale Effect on Image Classification Accuracy[J]. Journal of Applied Remote Sensing , 2013, 7 (1) : 073565 –1. DOI:10.1117/1.JRS.7.073565 |
| [8] | MING Dongping, YANG Jianyu, LI Longxiang, et al. Modified ALV for Selecting the Optimal Spatial Resolution and Its Scale Effect on Image Classification Accuracy[J]. Mathematical and Computer Modelling , 2011, 54 (3-4) : 1061 –1068. DOI:10.1016/j.mcm.2010.11.036 |
| [9] | BELGIU M, DRĂGUT L. Comparing Supervised and Unsupervised Multiresolution Segmentation Approaches for Extracting Buildings from Very High Resolution Imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing , 2014, 96 : 67 –75. DOI:10.1016/j.isprsjprs.2014.07.002 |
| [10] | CASTILLA G, HERNANDO A, ZHANG Chunhua, et al. The Impact of Object Size on the Thematic Accuracy of Landcover Maps[J]. International Journal of Remote Sensing , 2014, 35 (3) : 1029 –1037. DOI:10.1080/01431161.2013.875630 |
| [11] | GOODCHILD M, QUATTROCHI DA. Introduction:Scale, Multiscaling, Remote Sensing, and GIS[M]//QUATTROCHI D A, GOODCHILD M F. Scale in Remote Sensing and GIS.Boca Raton:Lewis Publishers, 1997:1-12. |
| [12] | LAM N S N, QUATTROCHI DA. On the Issues of Scale, Resolution, and Fractal Analysis in the Mapping Sciences[J]. The Professional Geographer , 1992, 44 (1) : 88 –98. DOI:10.1111/j.0033-0124.1992.00088.x |
| [13] | CAO C, LAM N S N. Understanding the Scale and Resolution Effects in Remote Sensing and GIS[M]//QUATTROCHI D A, GOODCHILD M F. Scale in Remote Sensing and GIS.Boca Raton:Lewis Publishers, 1997:57-72. |
| [14] | 明冬萍, 王群, 杨建宇. 遥感影像空间尺度特性与最佳空间分辨率选择[J]. 遥感学报 , 2008, 12 (4) : 529–537. MING Dongping, WANG Qun, YANG Jianyu. Spatial Scale of Remote Sensing Image and Selection of Optimal Spatial Resolution[J]. Journal of Remote Sensing , 2008, 12 (4) : 529 –537. |
| [15] | MING Dongping, LI J, WANG Junyi, et al. Scale Parameter Selection by Spatial Statistics for GeOBIA:Using Mean-shift Based Multi-scale Segmentation as an Example[J]. ISPRS Journal of Photogrammetry and Remote Sensing , 2015, 106 : 28 –41. DOI:10.1016/j.isprsjprs.2015.04.010 |
| [16] | MING Dongping, CI Tianyu, CAI Hongyue, et al. Semivariogram-based Spatial Bandwidth Selection for Remote Sensing Image Segmentation with Mean-shift Algorithm[J]. IEEE Geoscience and Remote Sensing Letters , 2012, 9 (5) : 813 –817. DOI:10.1109/LGRS.2011.2182604 |
| [17] | WOODCOCKCE, STRAHLERA H. The Factor of Scale in Remote Sensing[J]. Remote Sensing of Environment , 1987, 21 (3) : 311 –332. DOI:10.1016/0034-4257(87)90015-0 |
| [18] | LLOYD CD, ATKINSON PM. Scale and the Spatial Structure of Landform:Optimizing Sampling Strategies with Geostatistics[C]//Proceedings of the 3rd International Conference on GeoComputation. Bristol:University of Bristol, 1998. |
| [19] | MATHERON G. Principles of Geostatistics[J]. Economic Geology , 1963, 58 (8) : 1246 –1266. DOI:10.2113/gsecongeo.58.8.1246 |
| [20] | GARDNER R H. Pattern, Process, and the Analysis of Spatial Scales[M]//PETERSON D L, PARKER V T. Ecological Scale:Theory and Applications. New York:Columbia University Press, 1998:17-34. |
| [21] | O'NEILL R V, TURNER S J, CULLINAN V I, et al. Multiple Landscape Scales:An Intersite Comparison[J]. Landscape Ecology , 1991, 5 (3) : 137 –144. DOI:10.1007/BF00158061 |
| [22] | COMANICIU D, RAMESH V, MEER P. The Variable Bandwidth Mean Shift and Data-driven Scale Selection[C]//Proceedings of the 8th IEEE International Conference on Computer Vision, 2001. Vancouver:IEEE, 2001:438-445. |
| [23] | LI Xiangru, HU Zhanyi, WU Fuchao. A Note on the Convergence of the Mean Shift[J]. Pattern Recognition , 2007, 40 (6) : 1756 –1762. DOI:10.1016/j.patcog.2006.10.016 |
| [24] | LI Xiangru, WU Fuchao, HU Zhanyi. Convergence of a Mean Shift Algorithm[J]. Journal of Software , 2005, 16 (3) : 365 –374. DOI:10.1360/jos160365 |
| [25] | CAO Feng, GE Yong, WANG Jinfeng. Optimal Discretization for Geographical Detectors-based Risk Assessment[J]. GIScience & Remote Sensing , 2013, 50 (1) : 78 –92. |
| [26] | CAO Feng, GE Yong, WANG Jinfeng. Spatial Data Discretization Methods for GeoComputation[J]. International Journal of Applied Earth Observation and Geoinformation , 2014, 26 : 432 –440. DOI:10.1016/j.jag.2013.09.005 |
| [27] | PEÑA-BARRAGÁN J M, NGUGI M K, PLANT R E, et al. Object-based Crop Identification Using Multiple Vegetation Indices, Textural Features and Crop Phenology[J]. Remote Sensing of Environment , 2011, 115 (6) : 1301 –1316. DOI:10.1016/j.rse.2011.01.009 |


