因人为或自然因素导致的滑坡、地面沉降、泥石流等地质灾害已经严重影响生命安全和财产安全,特别是因大范围工程施工或地下水过度抽取而引发的地表形变带来的影响已不容忽视[1]。GPS因其具有高时间分辨率、可获得高精度三维形变等优点已被广泛应用于形变监测等领域[2]。另一种空间对地观测技术——InSAR,因其几乎不受天气影响继而可获得大范围、高精度厘米级甚至毫米级形变也备受青睐[3]。然而在实际应用中两种技术均存在先天不足,例如GPS的空间分辨率低、建站成本高,而InSAR仅能反映出视线(LOS)向相对形变量等。能否将GPS和InSAR进行集成和融合,以综合各自优势反演高精度多维形变场是值得关注和研究的问题[3-4]。
在融合GPS和InSAR监测结果解算多维形变场方面已有众多成果[5-11]。2002年,文献[5]使用Markov随机场理论及模拟退火法,建立了GPS与InSAR解算地表形变的函数模型,基于能量函数最小原则获得最优解,并较好应用于冰岛Reykjanes Peninsula地区。此方法计算时间长,解算结果并不能保证全局最优。2006年,文献[6-7]简化了能量方程求解算法,通过对方程求导,获得地表形变的最优解,但此方法仍有解算参数不稳定的情况。2008年,文献[8]用直接解法将GPS的水平形变插值,结合降轨InSAR获得的LOS向形变获取垂向形变,此方法的水平形变对GPS插值结果依赖性强。文献[9]于2012年研究了InSAR及GPS两类观测量的方差分量估计确定权比,解算三维形变场。2013年,文献[10]基于目标函数是凸二次函数的特点,利用BFGS方法巧妙地避免了局部最优解。但以上方法仅基于一种InSAR观测数据。
基于上述背景,本文采用一种简洁有效的融合方法,即利用GPS插值南北向形变场及升降轨InSAR两类观测数据获取形变区的三维形变场,并以西安市为例,验证融合方法。西安市位于汾渭盆地,该地区因过度抽取承压水和大面积施工建设而导致的地表形变一直备受关注,而精确获取西安市地表多维形变场对认识其复杂的地质环境尤为重要。以往文献更多关注西安市地面沉降[12-13],而鲜有大范围反演多维形变场。考虑到南北向形变对InSAR观测量的不敏感性,本文基于ALOS PALSAR(PALSAR)和EnviSat ASAR(ASAR)两种数据源和GPS观测数据,首先由GPS观测信息,获取研究区域南北向形变场,结合西安地区2009-2010年两种InSAR数据源提取的LOS向年形变速率,解算出该区域东西向和垂向形变速率场(形变场),并通过同期水准数据对比,其垂向形变精度呈毫米级。
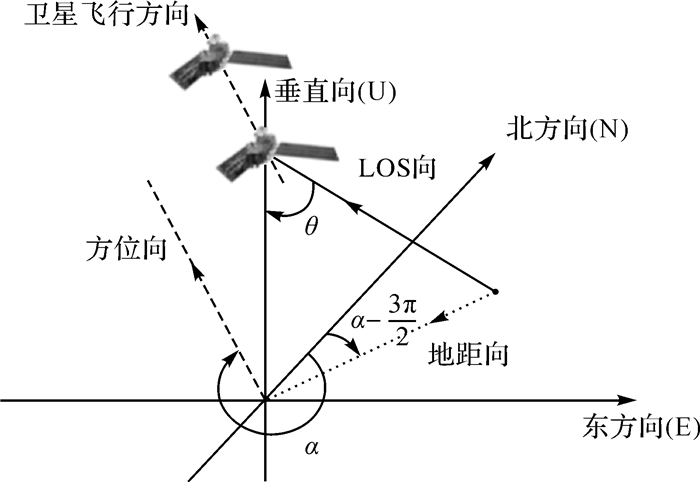
1 形变速率场解算原理 1.1 GPS和InSAR融合策略InSAR观测量仅反映了实际形变矢量在LOS向的投影大小[14],为得到多维形变场,首先分析N、E、U方向形变量与LOS向形变量之间关系。假设dNth、dEst、dUp为地表形变在地平坐标系下坐标轴方向的分解量,dLOS为LOS向形变量,根据图 1可建立如下关系式[15-16]
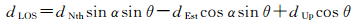 (1)
(1)
式中,dLOS靠近卫星方向为+;dNth、dEst、dUp指向N、E、U方向为+;α为卫星飞行方向方位角;θ为入射角。
理论上,在没有任何先验信息情况下,解算三维形变量dNth、dEst和dUp至少需要3种数据源。目前国际上常用数据来源于ALOS PALSAR、EnviSat ASAR和TerraSAR,其传感器参数如表 1所示。
| 传感器 | |||
| ALOS PALSAR | EnviSat ASAR | TerraSAR | |
| 方位角 | -10.158 | -168.034 | 190.671 |
| 入射角 | 38.737 | 22.806 | 28.618 |
将表 1中参数代入式(1),得到
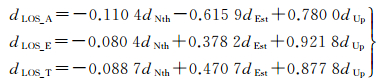 (2)
(2)
式中,dLOS_A、dLOS_E、dLOS_T分别为PALSAR、ASAR、TerraSAR观测的LOS向形变,将上述方程整理成误差方程形式
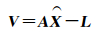 (3)
(3)
式中,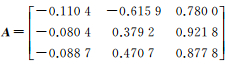
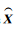
然而,如对于线性方程组Ax=l,A的条件数度量了x对l误差或不确定度的敏感性,其数学定义为:A范数与A逆范数的乘积,如A的条件数较大,l的微小变化就能引起x较大的改变,接近1时为良好条件矩阵,数值稳定性好。式(3)的系数阵条件数为130.2,已呈现一定程度的病态,故直接解算会带来N、E、U形变分量解的不稳定。考虑到InSAR观测量对南北向形变不敏感,为此有学者提出忽略南北向形变[12, 14],如此可以减少一维参数,改善方程性质。
在实际应用中,一方面大部分研究区域不足3种数据源,另一方面对于南北向具有较大形变的情况,忽略其形变将在一定程度上影响其余两方向的解算精度。顾及到GPS结果平面精度高,如果用GPS点在南北向内插结果dNthGPS代替InSAR南北方向的形变量dNth,然后用ASAR和PALSAR数据解算其余两方向形变,可望能在一定程度上改善解算精度,于是有
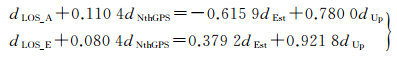 (4)
(4)
此时,系数矩阵条件数1.71与式(3)的系数阵条件数130.2相比降低了两个数量级,方程解较为稳定。
1.2 InSAR形变速率场解算InSAR解算结果为形变矢量在LOS向的投影,且是与参考像素的相对值。由于不同数据源选择的参考像素一般不同,并且参考像素的形变量不为零值,因此其解算的LOS向形变场与真实形变场之间存在着系统偏差,即参考点的形变量,如此在进行融合解算之前需先确定此偏差常数[17]。如将形变场中GPS点形变量代替所在像素的形变,存在下列方程
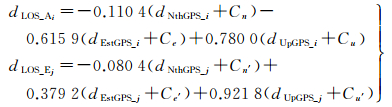 (5)
(5)
式中,dNthGPS_i、dEstGPS_i、dUpGPS_i为PALSAR形变场GPS点所在像素的绝对形变量;dLOS_Ai为i像素PALSAR形变场的LOS向观测量;dNthGPS_j、dEstGPS_j、dUpGPS_j为ASAR形变场GPS点所在像素j的绝对形变量;dLOS_Ej分别是ASAR在j像素的LOS向形变量;CN、CE、CU和CN′、CE′、CU′分别是PALSAR和ASAR两种数据源的参考点在N、E、U方向的形变量。用DLOS_A、DLOS_E表示PALSAR和ASAR的系统偏差组合
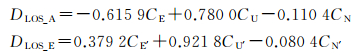 (1)
(1)
分析式(5),两种InSAR数据源解算的形变场中均有n个GPS点,可列2n个方程解算2个未知数。为避免GPS点可能含粗差,采用抗差估计方法[18-19],即可降低精度低GPS点的权重,从而获得最佳估值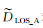
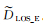
由于GPS水平观测值精度较高,可插值GPS的南北向观测量至InSAR相同的时空分辨率,结合PALSAR、ASAR数据源的LOS向观测结果可解算东西和垂向形变场,即
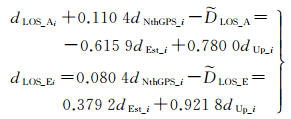 (6)
(6)
式中,左边为已知量,右边为未知参数。其他参数与式(5)中参数代表含义相同。如此可以解算每个像素的东西向和垂向形变量。
2 形变速率场解算试验西安位于中国西北部的渭河盆地,地面沉降最早发现于1959年,随后因地面承压水过度抽取导致地面沉降快速发展,在1996年部分地面最大年沉降速率达到191 mm[13],随后黑河引水,沉降速率有所减缓,而后因大面积建筑施工,沉降中心转移至南郊和西郊[12, 20]。
2.1 数据准备西安地区有20个同期观测的GPS点及11个水准点,分布情况如图 2所示。解算出GPS点在3个方向的年形变速率和水准点的垂向形变速率。在众多内插方法中,Kriging插值基于测量点间基于测量点间统计关系,可预测表面模型并精度较高,成为地学统计中常用方法之一。因此,采用选取线性变异函数的Kriging插值,将GPS点的南北和东西向形变量插值到InSAR格网。
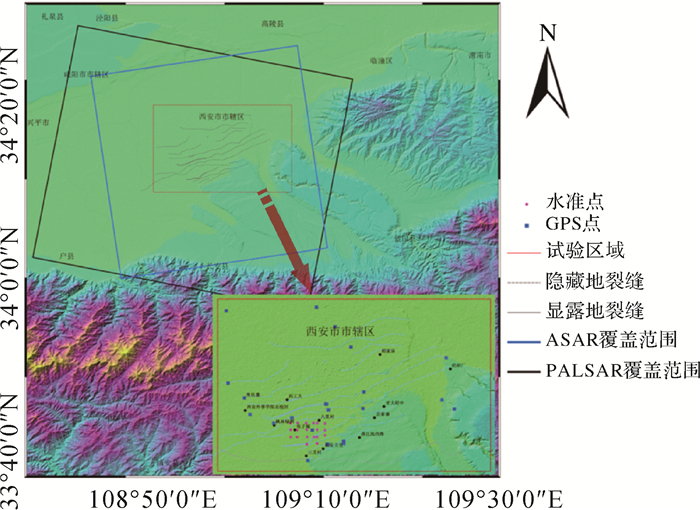
|
| 图 2 西安市地质背景及GPS点和水准点分布 Fig. 2 Xi’an geological background and the distribution of GPS points and levelling points |
关于InSAR数据源,现有17景C波段的ASAR降轨数据,时间跨度2009-01-03-2010-09-25,空间基线阈值为280 m,选择34个干涉对采用小基线和stacking[21]方法提取LOS向年形变速率,干涉图分布及解算形变结果如图 3(a)、(c)所示。另外,有12景L波段的PALSAR升轨数据,时间跨度2009-02-04-2010-12-26,选择2010-02-07作为参考影像,空间基线阈值为2500 m,选择36个干涉对用小基线和stacking方法解算LOS向年形变速率,结果如图 3(b)、(d)所示。根据形变场及GPS点分布情况选择研究范围,其像素大小为717×1317,像元分辨率为22.56×2.56 m,统一坐标基准及空间分辨单元,并将相干性低于0.3的失相干区域进行Kriging插值,结果如图 3(e)、(f)所示。
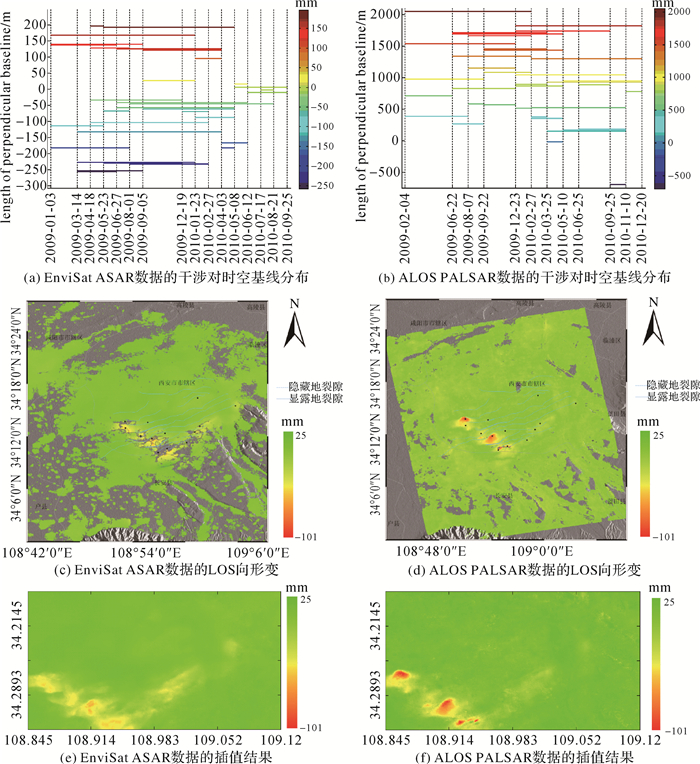
|
| 图 3 InSAR干涉图时空基线及形变结果 Fig. 3 Temporal and spatial baselines of interferograms and deformation results of InSAR |
2.2 试验部分
为计算西安市多维绝对形变量,需先解算组合系统偏差,然后结合GPS内插结果得出东西向和垂向形变量。以水准观测作为真值,比较解算精度。
2.2.1 系统偏差解算根据式(5),结合表 2观测数据,得系统偏差组合估值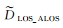
| 点号 | XJ01 | XJ02 | XJ03 | XJ04 | XJ06 | XJ07 | XJ08 | XJ09 | XJ10 | XJ12 | XJ13 | XJ15 | XJ17 | XJ18 | XJA1 | XJA2 | XJA3 | XJA4 | XJA5 | XJA6 |
| North | -8.5 | -29.4 | -10.6 | -5.4 | -2.8 | -8.7 | -7 | -10.6 | -7.1 | -7.2 | -11 | -6.5 | -4.3 | -1.6 | -15.6 | -9.6 | -0.2 | -9.9 | -10 | -7.1 |
| East | 30.7 | 34.8 | 34.9 | 31.4 | 33 | 31.8 | 33.2 | 30.3 | 32.2 | 39.5 | 35.1 | 32.2 | 48.2 | 39.6 | 25.9 | 35.7 | 36.3 | 32.1 | 31.9 | 31.1 |
| Up | -13.4 | -44.9 | -22.6 | -15.8 | -17.3 | -2.2 | -12.5 | -52.3 | 8.2 | -44.7 | -1.3 | 3.9 | -8.9 | -30.2 | -147.9 | -7.8 | -11.5 | -11.3 | -4.4 | -10.1 |
| ENVI_LOS | 2 | -24.1 | -22.5 | -2.1 | -4.1 | 3 | 3.5 | -28.1 | 4.5 | 4.5 | 0.5 | 2.1 | 2.3 | -10.4 | -17.4 | 0.7 | -0.7 | -33 | 3.3 | -3.2 |
| ALOS_LOS | -1 | -28.5 | -21.6 | 2.7 | -2.6 | 4.9 | 5.3 | -28.1 | -3.2 | -2.5 | 5.6 | -0.1 | 0.6 | -7.1 | -90.2 | 3.6 | 5.4 | -10.6 | 8 | 3.2 |
2.2.2 三维形变场提取
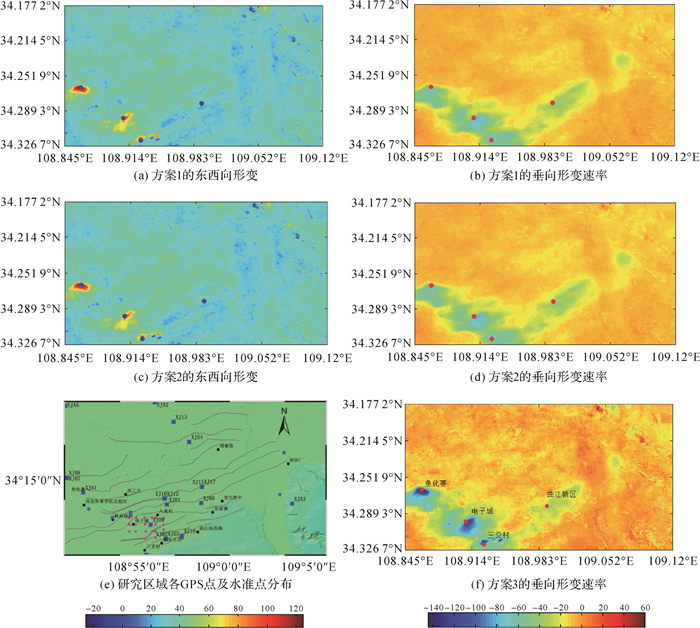
获取系统偏差估值后,结合GPS与InSAR解算结果提取东西向和垂向年形变速率。此时,为验证本文所提出方法的有效性,分别采用3种方案进行解算。方案1:将GPS点南北向观测量内插,结合升降轨InSAR的LOS向观测量解算东西和垂向形变量;方案2:忽略南北向形变,即,将方案1中GPS点南北向形变置为零,解算东西和垂向形变量;方案3:将GPS点南北向和东西向观测量内插解算两方向形变场,选用相干性较好的PALSAR解算垂向形变。
由方案1及方案2均可解算东西向和垂向形变场,方案3可解算垂向形变场。最后将同期水准观测量作为真值,分析其在垂向的精度,结果如表 3所示。
| 点号 | 经度E/(°) | 纬度N/(°) | 水准年速率 | 观测量 | 误差 | |||||
| 方案1 | 方案2 | 方案3 | 方案1 | 方案2 | 方案3 | |||||
| s3 | 108.923 4 | 34.213 36 | -12 | -11 | -5 | -8 | 1 | 7 | 4 | |
| s4 | 108.930 7 | 34.213 22 | -13 | -11 | -6 | -8 | 2 | 7 | 5 | |
| s5 | 108.934 3 | 34.213 31 | -9 | -10 | -5 | -8 | -1 | 4 | 1 | |
| s6 | 108.941 9 | 34.212 94 | -7 | -10 | -5 | -6 | -3 | 2 | 1 | |
| s7 | 108.941 9 | 34.206 33 | -9 | -10 | -5 | -9 | -1 | 4 | 0 | |
| s8 | 108.934 1 | 34.206 83 | -22 | -21 | -11 | -9 | 1 | 11 | 13 | |
| s10 | 108.924 1 | 34.206 97 | -22 | -23 | -12 | -9 | -1 | 10 | 13 | |
| s15 | 108.924 4 | 34.199 83 | -28 | -25 | -12 | -18 | 3 | 16 | 10 | |
| s16 | 108.931 0 | 34.199 86 | -20 | -18 | -9 | -18 | 2 | 11 | 2 | |
| s17 | 108.933 9 | 34.199 81 | -21 | -17 | -8 | -16 | 4 | 13 | 5 | |
| s18 | 108.941 9 | 34.201 50 | -11 | -11 | -5 | -13 | 0 | 6 | -2 | |
| 均方误差 | - | - | - | - | - | - | 2 | 9 | 7 | |
分析表 3及诸图可以看出:
(1) 方案1由于充分顾及了南北向形变场,不仅提取了东西向形变场,其垂向形变场精度也在毫米级,误差最大值4 mm,均方差2 mm,明显高于其他方案。方案2忽略南北向形变,虽也解出了东西向形变,但其垂直形变精度降低,水准点上误差最大值达16 mm,均方差9 mm。方案3尽管也顾及了南北向的形变场,但由于东西向形变场由GPS结果内插得到,降低了监测精度,因此垂向形变场解算精度也受到了影响。
(2) 对比分析方案1与方案2发现,图 5中两方案结果,因形变量较大并统一了形变范围,并不能直观看出两者区别。但是与水准结果相比,方案1提取的垂直分量结果明显更接近水准观测量,这也进一步证实了西安市南北向形变不可直接忽略。

|
| 图 4 研究区域GPS点插值结果 Fig. 4 Interpolation results of GPS points in north-south and west-east directions |
|
| 图 5 3种方案解算的形变速率结果 Fig. 5 Deformation rate results resolved by three schemes |
(3) 方案1与方案3的结果对比说明了尽管GPS的平面精度较高,但是内插降低精度,其结果并不会与研究区域形变特征严格符合,如此,所提取的E、U两方向的形变量精度不如两系统联合解算得到的结果精度。
因此,考虑到InSAR观测量对南北向不敏感的特点,而研究区域南北形变又不可忽略时,需要借助外界数据或者寻求其他算法改正南北向形变量。
3 形变速率场结果分析西安市垂向形变分析。2009-2010年均形变速率最大的地区达到了101 mm,呈V字型分布的沉降区,有4个沉降中心:鱼化寨、电子城、三爻村、曲江新区,前3个沉降中心均位于高新技术开发区,开发区自1991年以来,建区累计面积已达到15.20 km2,竣工面积9.10 km2。曲江新区为陕西文化产业示范区,自2005年建成以来,核心区域面积达51.2 km2。因此,大面积的建筑施工造成了地层压密或地表形变,除此之外,无施工建设的区域也有较小范围的沉降。图中也显示形变区基本上位于地裂缝两侧之间。因此形变主要是施工建设的影响,地裂缝的存在破坏了地层形变的连续性。
西安市东西向形变分析。从图 5(a)所示的东西向形变速率场可以清晰识别出高新开发区3个形变中心,即鱼化寨、电子城和三爻村,其中,鱼化寨在东西向形变速率达到120 mm,远远大于其在垂向的60 mm的下沉速率,因此在关注垂直形变的同时,水平形变也需要给予充分的重视,这很可能是施工建设导致地层倾斜在东方向的表现。电子城则有小部分区域向东移动,主要还是以垂直运动为主。
西安市南北向形变分析。图 4(a)南北向形变场由GPS点插值得到,其精度完全取决于GPS点精度及插值模型与实际形变的符合程度。整个研究区域均是向南运动,图中显示XJA1所在的三爻村年形变速率最大,为25 mm,另一个形变中心位于鱼化寨,形变量超过15 mm。
西安形变场整体分析。西安位于渭河盆地,此盆地在整体上表现出一种不连续的逆时针旋转特征,并因东部甘青块体向东挤压、北部鄂尔多斯地块左旋、南部和东部的华北和华南地块的不协调SE向伸展,渭河盆地表现出向东南方向运动[22],但局部地层表面受建筑物压力,而表现出非均匀性运动。
4 结 论三维形变场的提取有助于灾害机理的反演,InSAR技术尽管能提供高精度的形变监测信息,但只能提供LOS向的形变场,难以满足实际需求。考虑到InSAR观测量对南北向形变不敏感,而当南北向形变又不可被忽视的情况下,对现有的GPS南北向监测成果进行插值,进一步与不同数据源的InSAR监测数据进行融合解算,可望能获得整个研究区域的高精度三维形变场。
本文验证了GPS与InSAR融合达到较好反演效果,同时,从条件数的角度验证了函数模型较为稳定,计算出西安市2009-2010年间在三维绝对形变场,并且4个沉降中心主要分布在西安市的东南和西南方向,呈V字型分布,东西向形变集中在高新开发区,形变量之大应引起足够重视。
| [1] | LANARI R, MORA O, MANUNTA M, et al. A Small-baseline Approach for Investigating Deformations on Full-resolution Differential SAR Interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing , 2004, 42 (7) : 1377 –1386. DOI:10.1109/TGRS.2004.828196 |
| [2] | 王小亚, 朱文耀, 符养, 等. GPS监测的中国及其周边现时地壳形变[J]. 地球物理学报 , 2002, 45 (2) : 198–209. WANG Xiaoya, ZHU Wenyao, FU Yang, et al. Present-time Crustal Deformation in China and Its Surrounding Regions by GPS[J]. Chinese Journal of Geophysics , 2002, 45 (2) : 198 –209. |
| [3] | MASSONNET D, FEIGL K L. Radar Interferometry and Its Application to Changes in the Earth's Surface[J]. Reviews of Geophysics , 1998, 36 (4) : 441 –500. DOI:10.1029/97RG03139 |
| [4] | TRALLI D M, BLOM R G, ZLOTNICKI V, et al. Satellite Remote Sensing of Earthquake, Volcano, Flood, Landslide and Coastal Inundation Hazards[J]. ISPRS Journal of Photogrammetry and Remote Sensing , 2005, 59 (4) : 185 –198. DOI:10.1016/j.isprsjprs.2005.02.002 |
| [5] | GUDMUNDSSON S, SIGMUNDSSON F, CARSTENSEN J M. Three-dimensional Surface Motion Maps Estimated from Combined Interferometric Synthetic Aperture Radar and GPS Data[J]. Journal of Geophysical Research , 2002, 107 (B10) : ETG 13-1 –ETG 13-14. DOI:10.1029/2001JB000283 |
| [6] | SAMSONOV S V, TIAMPO K F. Analytical Optimization of a DInSAR and GPS Dataset for Derivation of Three-dimensional Surface Motion[J]. IEEE Geoscience and Remote Sensing Letters , 2006, 3 (1) : 107 –111. DOI:10.1109/LGRS.2005.858483 |
| [7] | SAMSONOV S V, TIAMPO K F, RUNDLE J B. Application of DInSAR-GPS Optimization for Derivation of Three-dimensional Surface Motion of the Southern California Region Along the San Andreas Fault[J]. Computers & Geosciences , 2008, 34 (5) : 503 –514. |
| [8] | 罗海滨, 何秀凤, 刘焱雄. 利用DInSAR和GPS综合方法估计地表3维形变速率[J]. 测绘学报 , 2008, 37 (2) : 168–171. LUO Haibin, HE Xiufeng, LIU Yanxiong. Estimation of Three-dimensional Surface Motion Velocities Using Integration of DInSAR and GPS[J]. Acta Geodaetica et Cartographica Sinica , 2008, 37 (2) : 168 –171. |
| [9] | HU Jun, LI Zhiwei, SUN Qian, et al. Three-dimensional Surface Displacements from InSAR and GPS Measurements with Variance Component Estimation[J]. IEEE Geoscience and Remote Sensing Letters , 2012, 9 (4) : 754 –758. DOI:10.1109/LGRS.2011.2181154 |
| [10] | 胡俊, 李志伟, 朱建军, 等. 基于BFGS法融合InSAR和GPS技术监测地表三维形变[J]. 地球物理学报 , 2013, 56 (1) : 117–126. HU Jun, LI Zhiwei, ZHU Jianjun, et al. Measuring Three-dimensional Surface Displacements from Combined InSAR and GPS Data Based on BFGS Method[J]. Chinese Journal of Geophysics , 2013, 56 (1) : 117 –126. |
| [11] | HU Jun, LI Zhiwei, DING Xiaoli, et al. Resolving Three-dimensional Surface Displacements from InSAR Measurements:A Review[J]. Earth-Science Reviews , 2014, 133 : 1 –17. DOI:10.1016/j.earscirev.2014.02.005 |
| [12] | QU Feifei, ZHANG Qin, LU Zhong, et al. Land Subsidence and Ground Fissures in Xi'an, China 2005-2012 Revealed by Multi-band InSAR Time-series Analysis[J]. Remote Sensing of Environment , 2014, 155 : 366 –376. DOI:10.1016/j.rse.2014.09.008 |
| [13] | 张勤, 赵超英, 丁晓利, 等. 利用GPS与InSAR研究西安现今地面沉降与地裂缝时空演化特征[J]. 地球物理学报 , 2009, 52 (5) : 1214–1222. ZHANG Qin, ZHAO Chaoying, DING Xiaoli, et al. Research on Recent Characteristics of Spatio-temporal Evolution and Mechanism of Xi'an Land Subsidence and Ground Fissure by Using GPS and InSAR Techniques[J]. Chinese Journal of Geophysics , 2009, 52 (5) : 1214 –1222. |
| [14] | 胡俊. 基于现代测量平差的InSAR三维形变估计理论与方法[D]. 长沙:中南大学, 2013. HU Jun. Theory and Method of Estimating Three-dimensional Displacement with InSAR Based on the Modern Surveying Adjustment[D]. Changsha:Central South University, 2013. |
| [15] | WRIGHT T J, PARSONS B E, LU Zhong. Toward Mapping Surface Deformation in Three Dimensions Using InSAR[J]. Geophysical Research Letters , 2004, 31 (1) : L01607 . DOI:10.1029/2003GL018827 |
| [16] | 查显杰, 傅容珊, 戴志阳. 用D-InSAR技术测量地面形变位移三分量[J]. 地球物理学进展 , 2005, 20 (4) : 997–1002. ZHA Xianjie, FU Rongshan, DAI Zhiyang. Measuring Three Components of Surface Deformation Displacement Using D-InSAR Technique[J]. Progress in Geophysics , 2005, 20 (4) : 997 –1002. |
| [17] | 葛大庆. 区域性地面沉降InSAR监测关键技术研究[D]. 北京:中国地质大学(北京), 2013. GE Daqing. Research on the Key Techniques of SAR Interferometry for Regional Land Subsidence Monitoring[D]. Beijing:China University of Geosciences (Beijing), 2013. |
| [18] | 杨元喜. 抗差估计理论及其应用[M]. 北京: 八一出版社, 1993 . YANG Yuanxi. Theory and Application of Robust Estimation[M]. Beijing: Bayi Press, 1993 . |
| [19] | 杨元喜, 宋力杰, 徐天河. 大地测量相关观测抗差估计理论[J]. 测绘学报 , 2002, 31 (2) : 95–99. YANG Yuanxi, SONG Lijie, XU Tianhe. Robust Parameter Estimation for Geodetic Correlated Observations[J]. Acta Geodaetica et Cartographica Sinica , 2002, 31 (2) : 95 –99. |
| [20] | 赵超英, 张勤, 丁晓利, 等. 基于InSAR的西安地面沉降与地裂缝发育特征研究[J]. 工程地质学报 , 2009, 17 (3) : 389–393. ZHAO Chaoying, ZHANG Qin, DING Xiaoli, et al. InSAR Based Evaluation of Land Subsidence and Ground Fissure Evolution at Xi'an[J]. Journal of Engineering Geology , 2009, 17 (3) : 389 –393. |
| [21] | BERARDINO P, FORNARO G, LANARI R, et al. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing , 2002, 40 (11) : 2375 –2383. DOI:10.1109/TGRS.2002.803792 |
| [22] | 何红前. 渭河盆地地裂缝成因机理研究[D]. 西安:长安大学, 2011. HE Hongqian. Study on the Formation Mechanism of Ground Fissures in Weihe Basin[D]. Xi'an:Chang'an University, 2011. |