2. 北斗导航应用技术河南省协同创新中心, 河南 郑州 450001
2. Beidou Navigation Technology Collaborative Innovation Center of Henan, Zhengzhou 450001, China
因单频GPS接收机成本低廉、功耗低、体积小、重量轻以及所需存储空间小等优势[1],在当前卫星导航与定位领域得到了广泛应用。尤其对星载GPS用户而言,卫星上的资源有限、空间紧凑,搭载单频接收机无疑可以节省资源、降低卫星成本。因而研究星载GPS单频精密定轨技术对于精度要求较高又需节省资源单频用户而言具有重要的意义。
使用单频GPS观测量进行LEO(low earth orbit)卫星精密定轨的关键是如何有效地消除或削弱电离层延迟的影响[2-6]。目前,不少学者开展了地面单频GPS数据处理方面的研究工作并取得了丰硕的成果[7-10]。相比地面用户,LEO卫星一般处于电离层较为活跃的区域,其GPS观测量只受到部分电离层的影响,因而地面获得的高精度电离层薄层模型不能直接应用于LEO卫星单频定轨。文献[11]提出使用Chapman经验函数计算“电离层比例因子”的方法进行电离层改正,但该方法计算Chapman函数值时未考虑电子密度峰值高度随太阳活动、经纬度、昼夜变化、季节等的变化。为消除上述因素的影响,文献[12]提出将IRI2007模型(International Reference Ionosphere 2007)确定的F2层电子密度峰值剖面高度(F2-layer peak height,hmF2)作为Chapman函数的电子密度峰值高度[13-14]。但文献[15]表明,由于IRI2007模型电子密度峰值高度与电离层薄层高度之间采用的标准不一致,通常它们之间存在系统性偏差,因此直接采用IRI2007模型计算电子密度峰值高度会影响电离层延迟最终的改正效果。目前IRI工作组已将IRI2007模型更新为IRI2012模型[16],且该模型延续了IRI2007模型确定hmF2的基本原理,对电子密度峰值高度确定的标准没有发生变化。
为消除上述系统性偏差的影响,本文提出将电离层薄层高度作为约束条件对IRI2012模型确定的电子密度峰值高度均值进行参数约束估计,从而得到了一种改进的电离层模型。经Swarm卫星单频精密定轨试验验证,使用改进的电离模型能够明显改善单频定轨精度,可以满足一般LEO卫星用户的应用需求。
1 算法模型星载GPS码和相位的基本观测方程[17]为
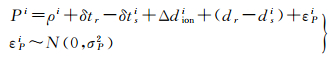 (1)
(1)
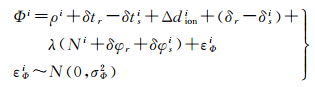 (2)
(2)
式中,Pi和Φi分别为第i颗GPS卫星的码和载波观测值;ρi为LEO卫星到GPS卫星之间的几何距离;δtr和δtsi分别为接收机钟差和卫星钟差;dr和dsi分别为接收机和卫星端的码硬件延迟;δr和δsi分别为接收机和卫星端的相位硬件延迟;δφr和δφsi分别为接收机和卫星端的初始相位;λ和Ni为载波波长和整周模糊度;εPi和εΦi分别为码和载波观测噪声(包含多路径效应),其相应的方差为σP2和σΦ2;Δdion为电离层延迟改正。据式(1)和式(2)可知,电离层延迟改正的精度直接影响单频定轨的精度,下面就LEO卫星电离层改正问题开展研究,首先介绍了传统的电离层改正模型,在此基础上,提出了一种改进的电离层改正模型。
1.1 传统电离层模型目前,在单频LEO精密定轨中,电离层延迟改正主要采用文献[11]提出的“电离层比例因子法”,即
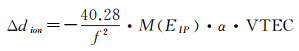 (3)
(3)
式中,f为载波频率;M(EIP)为电离层映射函数;VTEC为垂向总电子含量,可通过全球电离层格网模型计算获得;α为电离层比例因子,其计算方法[11]如下
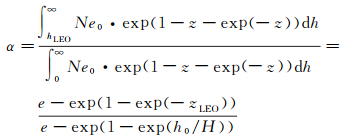 (4)
(4)
式中,zLEO=(hLEO-h0)/H;H为标高,在常用的标高变化范围内,标高对Chapman模型的影响相对较小,通常取H=100 km;h0表示电子密度峰值高度,通常为固定的经验常数值,如450 km;hLEO表示LEO卫星距地面的高度,如图 1所示。
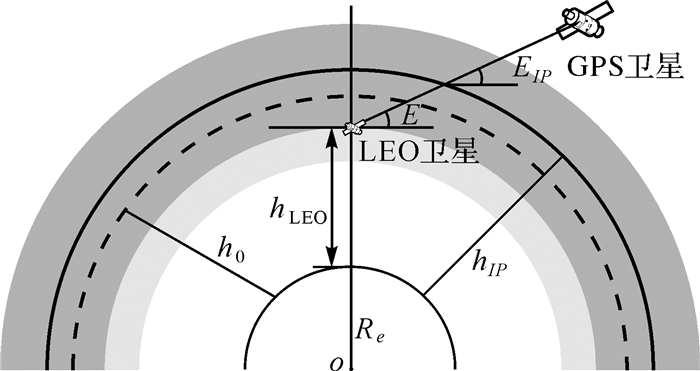
|
| 图 1 电离层比例因子法几何示意图 Fig. 1 Geometric sketch for the method of ionosphere scale factor |
电离层映射函数M(EIP)的计算方法[11]如下
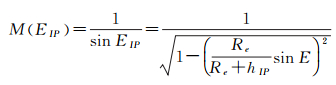 (5)
(5)
式中,Re为地球半径;E为LEO卫星处的高度角;EIP为电离层薄层穿刺点处的高度角;hIP为去除电离层底部至LEO卫星之间电离层影响后得到的电离层薄层高度,如图 1所示,其计算方法[11]如下
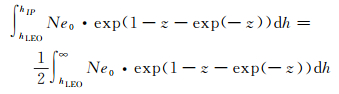 (6)
(6)
传统电离层模型将电子密度峰值高度固定为经验常数值能够有效获得LEO卫星电离层延迟改正,但是电子密度峰值高度会受太阳活动、经纬度、昼夜变化、季节等因素的影响,将其固定为常数不能正确反映其时空变化特性,进而影响电离层延迟改正值精度。为此可在传统电离层模型基础上,引入IRI2012模型来确定电子密度峰值高度。IRI2012模型是IRI工作组根据大量的电离层观测资料和多年积累的电离层研究成果开发的全球电离层经验模型[16, 18],该模型充分考虑了太阳活动、经纬度、昼夜变化、季节等因素对电子密度峰值高度的影响。IRI2012模型电子密度峰值高度计算方法[19]如式(7)所示
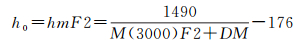 (7)
(7)
式中,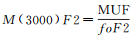
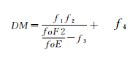
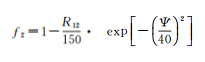
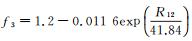
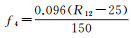
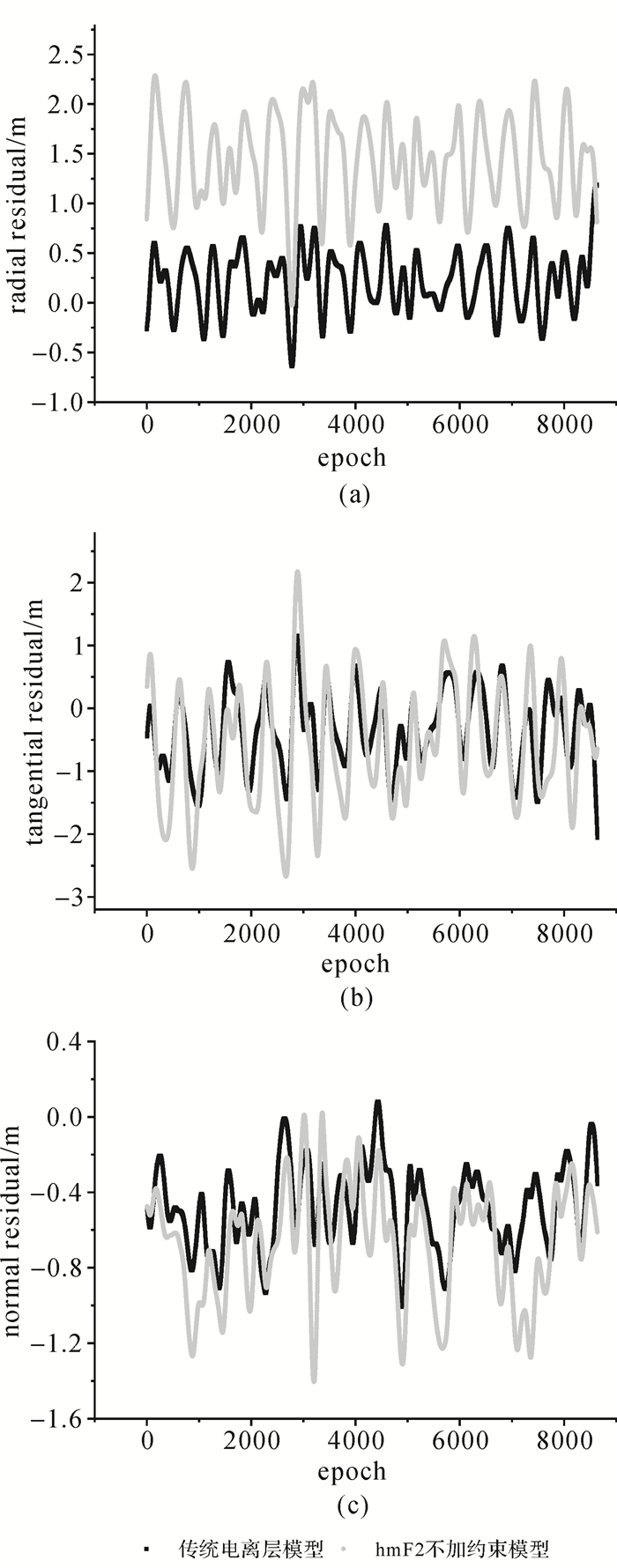
理论上,使用IRI2012模型计算电子密度峰值高度考虑了更多外界因素的影响,能够更好地反映其时空变化特性,其最终的定轨精度会有所提高,但本文采用2014年11月6日Swarm-A卫星实测数据进行试验计算,结果表明:与传统电离层模型相比,直接使用IRI2012模型计算电子密度峰值高度后,LEO卫星径向和法向的定轨精度反而明显下降,如图 2所示。根据文献[15]可知,其主要原因是由于电离层薄层模型的薄层高度和IRI2012模型确定电子密度峰值高度之间采用的标准不一致而引入的系统性偏差,从而导致电离层改正的精度降低。
|
| 图 2 轨道径向、切向和法向残差序列图 Fig. 2 Residual sequence for orbit radial, tangential and normal |
为避免因电子密度峰值高度的选择标准不一致而引起的精度损失,本文提出将电离层薄层高度作为约束条件对IRI2012模型确定的电子密度峰值高度均值进行参数约束估计。在实际定轨过程中,增加如式(8)所示的条件方程
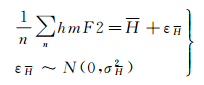 (8)
(8)
式中,n为观测量个数;H为待估参数,其初始值一般选取电离层薄层高度;εH为H的噪声;σH2为相应的方差。
2 试验及结果分析为验证上文改进的电离层模型的有效性,选取Swarm卫星2014年年积日310-312连续3 d的观测数据进行试验。Swarm卫星于2013年11月22日发射,是欧空局(European Space Agency,ESA)首个用于测量来自地球核心、地幔、地壳、海洋、电离层等区域磁场信息的对地观测卫星。该卫星由A、B、C 3颗小卫星组成,其中A和C卫星为运行在高度450 km、倾角为87.4°的极轨道成对卫星;B卫星运行在高度530 km、倾角88°的极轨道[20]。由于Swarm卫星为极轨卫星,每天频繁地经过赤道和两极地区,其GPS观测量受电离层的影响情况更为复杂,更便于验证本文电离层改正模型的稳定性和可靠性;同时,3颗Swarm卫星的轨道不同,也可以分析电离层改正模型对不同轨道的改正效果。
以如下两种方案进行Swarm卫星精密定轨,两种方案都采用约化动力学法[21]进行精密定轨,基本数据处理策略相同,仅在电离层延迟改正处理上有所区别。
方案1:采用传统的电离层模型,将电子密度峰值高度选为450 km。
方案2:采用本文提出的改进的电离层模型。
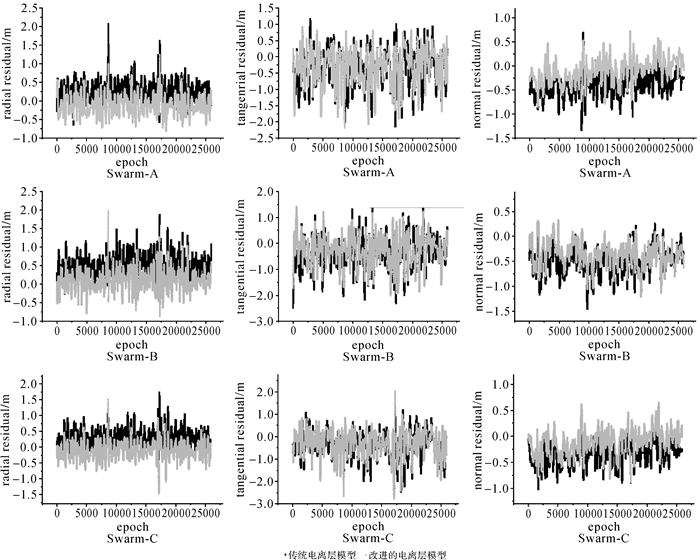
根据上述两种方案,本文对3颗Swarm卫星分别进行处理分析,并将最终定轨结果与ESA标准轨道[20]进行比较。图 3给出了两种方案在轨道径向(R)、切向(T)和法向(N)的残差序列图。表 1给出了精密定轨数据的处理策略。表 2给出了在轨道径向(R)、切向(T)和法向(N)的均值和均方根误差(root mean square, RMS)统计情况。
|
| 图 3 Swarm卫星轨道径向、切向和法向残差序列 Fig. 3 Residual sequence for Swarm satellite orbit radial, tangential and normal |
| 类别 | 详细描述 |
| 观测量 | C1、L1观测量,10 s采样间隔 |
| 高度截止角/(°) | 5 |
| GPS卫星轨道及钟差 | CODE最终轨道及5 s采样间隔钟差产品 |
| 垂向总电子含量 | CODE全球电离层格网模型 |
| 电离层映射函数 | 改进的薄层模型(MSLM) |
| 地球重力场模型 | EGM2008 120×120 |
| N体摄动力 | 太阳、月球以及其他行星摄动(JPL DE450) |
| 潮汐摄动 | 固体潮汐和极潮(IERS 2010);海洋潮汐(FES2004) |
| 太阳光压和大气阻力 | 通过经验加速度参数吸收 |
| 卫星轨道状态参数 | 6个初始轨道根数+3个常数经验加速度参数 |
| 接收机钟差 | 历元待估参数 |
| 载波相位模糊度 | 每个模糊度弧段、每颗卫星1个 |
| 经验加速度 | 每6 min估计一组 |
| 天线相位中心改正 | igs08.atx |
| 卫星 | 统计类型 | 径向(R) | 切向(T) | 法向(N) | |||||
| 传统电离层模型 | 改进的电离层模型 | 传统电离层模型 | 改进的电离层模型 | 传统电离层模型 | 改进的电离层模型 | ||||
| A | 均值 | 0.25 | -0.11 | -0.39 | -0.33 | -0.38 | -0.11 | ||
| RMS | 0.39 | 0.29 | 0.71 | 0.66 | 0.46 | 0.28 | |||
| B | 均值 | 0.51 | 0.09 | -0.40 | -0.28 | -0.49 | -0.37 | ||
| RMS | 0.61 | 0.33 | 0.75 | 0.67 | 0.57 | 0.45 | |||
| C | 均值 | 0.28 | -0.12 | -0.40 | -0.32 | -0.35 | -0.11 | ||
| RMS | 0.43 | 0.33 | 0.76 | 0.70 | 0.42 | 0.27 | |||
(1) 与传统电离层模型相比,改进的电离层模型对3个方向定轨精度均有不同程度的提高,尤其是对轨道径向和法向的精度改善最为明显,A、B、C卫星的径向分别改进了25.6%、45.9%、23.3%,平均提高了31.6%;法向分别改进了39.1%、21.1%、35.7%,平均提高了32.0%。
(2) 通过分析两种方案定轨结果可知,Swarm-B卫星采用传统电离层模型的定轨精度略低于其他两颗卫星,其原因可能是Swarm-B卫星的轨道高度高于CODE全球电离层格网模型高度450 km,导致电离层的映射函数不适应当前轨道高度,进而造成轨道精度的下降。但使用本文改进的电离层模型后,Swarm-B卫星的定轨精度提高程度最为明显。
(3) 从图 3和表 2可以明显看出,采用传统电离层模型进行定轨存在明显的系统性偏差,A、B、C卫星的径向系统性偏差分别为0.25 m、0.51 m、0.28 m;切向的系统性偏差分别为-0.40 m、-0.40 m、-0.39 m;法向的系统性偏差分别为-0.35 m、-0.49 m、-0.38 m。在采用改进的电离层模型后,对轨道3个方向的系统性偏差都有不同程度的降低,径向和法向的改善效果最为显著,分别平均降低了65.0%和54.7%。
(4) 对比图 3和图 2可以看出,对IRI2012模型计算的电子密度峰值高度均值进行参数约束估计后,削弱或消除了因电离层薄层高度与IRI2012模型电子密度峰值高度的选择标准不一致而引入的误差。
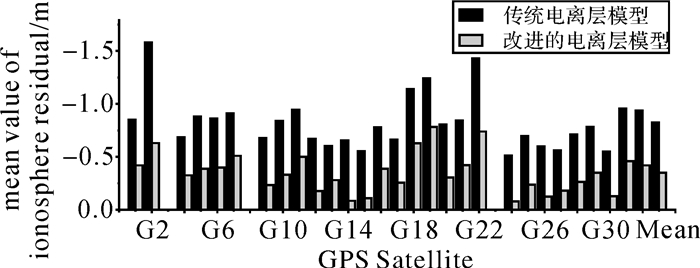
为了进一步分析改进的电离层模型的有效性,本文将ESA通过双频观测量解算获得的斜向电离层延迟改正作为参考值进行分析验证,该电离层延迟计算结果扣除了接收机频间通道时延的影响[22]。图 4给出了Swarm-C卫星2014年年积日310传统电离层模型、改进的电离层模型与参考值之间的残差统计情况,纵坐标表示各GPS卫星所对应的电离层残差的均值。从图 4可以看出,相比传统电离层模型,改进的电离层模型与电离层参考值更为吻合,进一步说明了改进的电离层模型优于传统电离层模型。
|
| 图 4 传统电离层模型、改进的电离层模型与参考值之间残差的均值 Fig. 4 Mean of ionosphere residual between traditional ionospheric model, improved ionospheric model and the reference ionosphere |
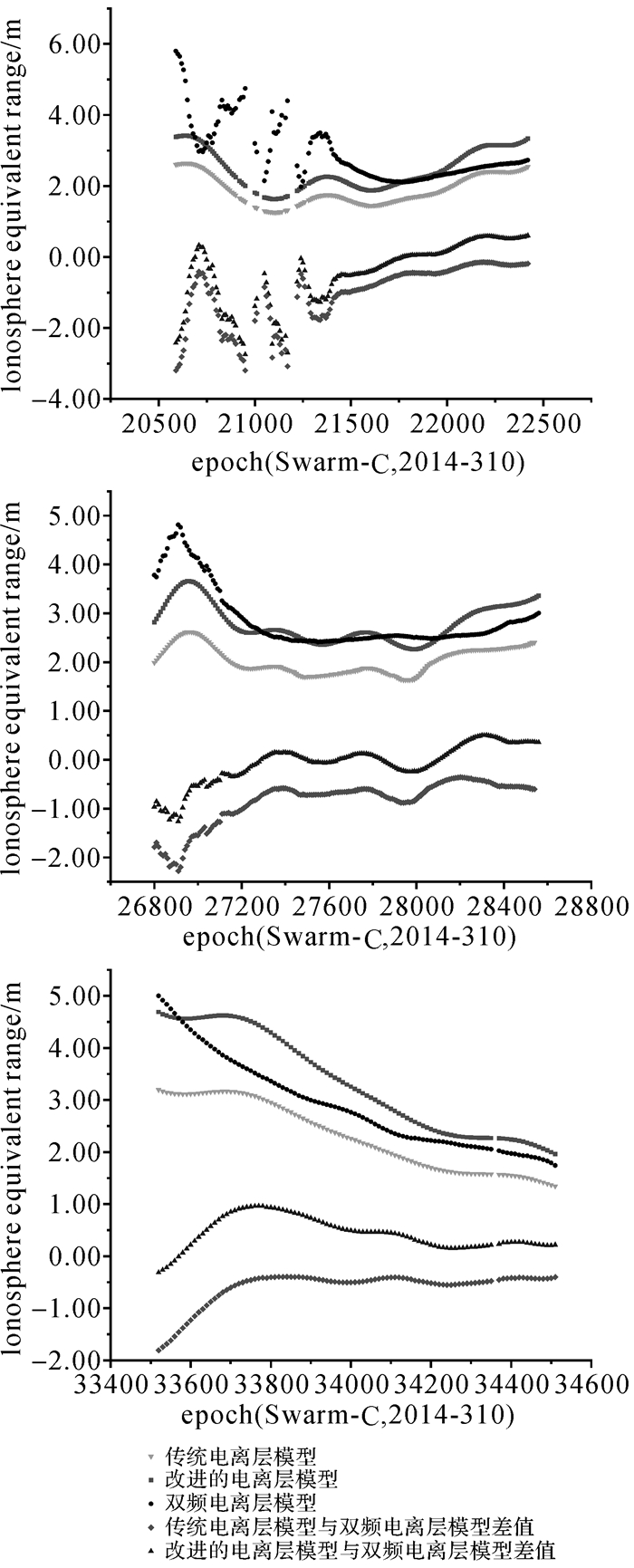
图 5给出了Swarm-C卫星对22号GPS卫星3个跟踪弧段的电离层延迟改正对比情况,从图中可以看出,改进的电离层模型与传统的电离层模型变化趋势较为一致,但两者之间存在系统性差异,表明电子密度峰值高度会对LEO卫星电离层延迟改正造成系统性影响。
|
| 图 5 传统电离层模型、改进的电离层模型与参考值之间残差序列 Fig. 5 Ionosphere residual between traditional ionospheric model, improved ionospheric model and the reference ionosphere |
3 结 论
对于LEO卫星单频精密定轨,电离层延迟的有效改正是其关键。本文针对传统“电离层比例因子法”中电子密度峰值高度确定方法不完善,提出采用IRI2012模型确定电子密度峰值高度,并在实际定轨过程中将电离层薄层高度作为约束条件对电子密度峰值高度的均值进行参数约束估计,得到了一种改进的电离层改正模型。该模型既考虑了电子密度峰值高度与电离层薄层高度的一致性,又顾及了电子密度峰值高度的空间和时间特征,为解决单频LEO单频定轨中的电离层延迟改正提供了一种新的途径。利用Swarm卫星星载GPS数据分析表明:采用改进的电离层模型Swarm卫星的径向、切向和法向定轨精度均有不同程度的提高,尤其是对径向和法向精度改善最为明显,平均提高约31.6%和32.0%;改进后的电离层模型对轨道的系统性偏差也有较大幅度的改善,Swarm卫星的径向和法向系统性偏差分别平均降低了65.0%和54.7%。总体上,采用改进的电离层模型进行LEO卫星单频精密定轨具有更高的精度和可靠性。
需要说明的是,虽然使用改进的电离层模型定轨精度有显著提高,但是与ESA标准轨道相比,最终的定轨结果依然残存部分较强随机噪声,主要原因有两方面:首先是受CODE全球电离层格网模型本身精度的影响,特别是当LEO卫星经过电离层活跃地段或者IGS站稀疏地段,其精度难以保证;其次受IRI2012模型的精度影响,IRI2012模型是在大量电离层观测资料的基础上建立的经验模型,其精度受观测资料的分布和时间跨度等因素的影响,在不同地区其符合程度不同。
| [1] | 谢世杰, 鲁和平. GPS接收机性能之我见[J]. 测绘通报 , 2000 (12) : 32–34. XIE Shijie, LU Heping. My Viewpoint of GPS Receiver Performance[J]. Bulletin of Surveying and Mapping , 2000 (12) : 32 –34. |
| [2] | MONTENBRUCK O. Kinematic GPS Positioning of LEO Satellites Using Ionosphere-free Single Frequency Measurements[J]. Aerospace Science and Technology , 2003, 7 (5) : 396 –405. DOI:10.1016/S1270-9638(03)00034-8 |
| [3] | BOCK H, JÄGGI A, DACH R, et al. GPS Single-frequency Orbit Determination for Low Earth Orbiting Satellites[J]. Advances in Space Research , 2009, 43 (5) : 783 –791. DOI:10.1016/j.asr.2008.12.003 |
| [4] | 胡国荣, 欧吉坤, 崔伟宏. 星载单频GPS接收机低轨卫星几何法定轨研究[J]. 天文学报 , 2000, 41 (3) : 278–288. HU Guorong, OU Jikun, CUI Weihong. A Research on Geometric Orbit Determination for GPS-based Single-frequency Receivers Aboard Low Earth Satellites[J]. Acta Astronomica Sinica , 2000, 41 (3) : 278 –288. |
| [5] | 刘洋, 易东云, 王正明. 基于单频GPS接收机的低轨卫星准实时定轨算法研究[J]. 航天控制 , 2005, 23 (4) : 32–34, 40. LIU Yang, YI Dongyun, WANG Zhengming. The Algorithm Research of Norm-real-time Orbit Determination of LEO Satellites Based on Single-frequency GPS Receiver[J]. Aerospace Control , 2005, 23 (4) : 32 –34, 40. |
| [6] | 郭向, 张强, 赵齐乐, 等. 基于单频星载GPS数据的低轨卫星精密定轨[J]. 中国空间科学技术 , 2013, 33 (2) : 41–46. GUO Xiang, ZHANG Qiang, ZHAO Qile, et al. Precise Orbit Determination for LEO Satellites Using Single-frequency GPS Observations[J]. Chinese Space Science and Technology , 2013, 33 (2) : 41 –46. |
| [7] | 张小红, 李星星, 郭斐, 等. GPS单频精密单点定位软件实现与精度分析[J]. 武汉大学学报(信息科学版) , 2008, 33 (8) : 783–787. ZHANG Xiaohong, LI Xingxing, GUO Fei, et al. Realization and Precision Analysis of Single-frequency Precise Point Positioning Software[J]. Geomatics and Information Science of Wuhan University , 2008, 33 (8) : 783 –787. |
| [8] | 涂锐, 黄观文, 凌晴. GPS单频精密单点定位的研究实现[J]. 测绘科学 , 2011, 36 (3) : 68–69. TU Rui, HUANG Guanwen, LING Qing. Precise Point Positioning of GPS Single frequency[J]. Science of Surveying and Mapping , 2011, 36 (3) : 68 –69. |
| [9] | 姜卫平, 邹璇, 唐卫明. 基于CORS网络的单频GPS实时精密单点定位新方法[J]. 地球物理学报 , 2012, 55 (5) : 1549–1556. JIANG Weiping, ZOU Xuan, TANG Weiming. A New Kind of Real-time PPP Method for GPS Single Frequency Receiver Using CORS Network[J]. Chinese Journal of Geophysics , 2012, 55 (5) : 1549 –1556. |
| [10] | 阮仁桂, 吴显兵, 冯来平, 等. 同时估计电离层延迟的单频精密单点定位方法[J]. 测绘学报 , 2012, 41 (4) : 490–495. RUAN Rengui, WU Xianbing, FENG Laiping, et al. Single-frequency Precise Point Positioning with Simultaneous Ionospheric Delay Estimation[J]. Acta Geodaetica et Cartographica Sinica , 2012, 41 (4) : 490 –495. |
| [11] | MONTENBRUCK O, GILL E. Ionospheric Correction for GPS Tracking of LEO Satellites[J]. The Journal of Navigation , 2002, 55 (2) : 293 –304. |
| [12] | BILITZA D, REINISCH B W. International Reference Ionosphere 2007:Improvements and New Parameters[J]. Advances in Space Research , 2008, 42 (4) : 599 –609. DOI:10.1016/j.asr.2007.07.048 |
| [13] | 郑磊, 李征航, 刘万科. 用星载单频GPS数据实时定轨的电离层延迟改正[J]. 大地测量与地球动力学 , 2010, 30 (3) : 118–121. ZHENG Lei, LI Zhenghang, LIU Wanke. Correction of Ionospheric Delay for Real-time Orbit Determination by Using On-board Single-frequency GPS Data[J]. Journal of Geodesy and Geodynamics , 2010, 30 (3) : 118 –121. |
| [14] | 屈小川, 李征航, 龚晓颖. 星载单频GPS数据的电离层延迟改正方法分析[J]. 北京航空航天大学学报 , 2012, 38 (2) : 252–256. QU Xiaochuan, LI Zhenghang, GONG Xiaoying. Analysis on Ionospheric Delay Correction Method of Space-borne Single-frequency GPS Data[J]. Journal of Beijing University of Aeronautics and Astronautics , 2012, 38 (2) : 252 –256. |
| [15] | 温晋, 万卫星, 丁锋, 等. 电离层垂直TEC映射函数的实验观测与统计特性[J]. 地球物理学报 , 2010, 53 (1) : 22–29. WEN Jin, WAN Weixing, DING Feng, et al. Experimental Observation and Statistical Analysis of the Vertical TEC Mapping Function[J]. Journal of Geophysics , 2010, 53 (1) : 22 –29. |
| [16] | BILITZA D, ALTADILL D, ZHANG Yongliang, et al. The International Reference Ionosphere 2012-A Model of International Collaboration[J]. Journal of Space Weather and Space Climate , 2014, 4 : A07 . DOI:10.1051/swsc/2014004 |
| [17] | KLEUSBERG A, TEUNISSEN P J G. GPS for Geodesy[M]. Berlin: Springer, 1996 . |
| [18] | BILITZA D, MCKINNELL L A, REINISCH B, et al. The International Reference Ionosphere Today and in the Future[J]. Journal of Geodesy , 2011, 85 (12) : 909 –920. DOI:10.1007/s00190-010-0427-x |
| [19] | BILITZA D. International Reference Ionosphere (1990)[J]. Planetary and Space Science , 1992, 40 (4) : 544 . |
| [20] | VAN DEN IJSSEL J, ENCARNAÇÃO J, DOORNBOS E, et al. Precise Science Orbits for the Swarm Satellite Constellation[J]. Advances in Space Research , 2015, 56 (6) : 1042 –1055. DOI:10.1016/j.asr.2015.06.002 |
| [21] | 田英国, 郝金明, 刘伟平, 等. 星载GNSS低轨卫星精密定轨快速解算方法[J]. 大地测量与地球动力学 , 2014, 34 (1) : 157–160. TIAN Yingguo, HAO Jinming, LIU Weiping, et al. A Rapid Solution Method on Precise Orbit Determination of LEOs Using GNSS[J]. Journal of Geodesy and Geodynamics , 2014, 34 (1) : 157 –160. |
| [22] | Swarm Expert Support Laboratories. Swarm L2 TEC Product Description (SW-TR-GFZ-GS-0007)[EB/OL]. (2014-08-27)[2014-11-20]. https://earth.esa.int/documents/10174/1514862/Swarm_Level-2_TEC_Product_Description. |


