2. 中国科学院大学, 北京 100049 ;
3. 山东大学空间科学研究院, 山东 威海 264209
2. University of Chinese Academy of Sciences, Beijing 100049, China ;
3. Institute of Space Science, Shandong University, Weihai 264209, China
文献[1]提出可以利用GPS反射信号进行海洋测高研究,开创了利用GPS 反射信号遥感海平面的先河。此后经过20多年的发展,GNSS测高技术已成为一种高精度水面高监测技术,并发展成为GNSS 遥感技术领域的一个重要分支,是目前国内外遥感和海洋测高领域研究的热点问题之一。
与卫星雷达测高和验潮站等传统观测技术相比,GNSS-R测高的优势在于它能利用已有的GNSS系统多星信号给出高时空分辨率的水面高信息。在水面高监测方面,国内外学者利用GNSS-R设备获取的试验数据,开展了大量研究,取得了许多丰硕的成果[2-4]。近几年来,GNSS-R被广泛地应用于多个领域。除了测高方面的应用,结合海面和海浪对电波的散射特性,它还可以用来获取平均海面高、海冰[5]、海面风场[6-7]、浪高和海面盐度等信息。此外,GNSS-R技术也成功应用于研究土壤湿度[8-9]、陆地植被覆盖、积雪厚度[10]以及地球动力学[11]等方面。随着空间技术的发展,星载GNSS-R逐渐成为可能,并以其低成本、高时空分辨率、较短的重访周期等优点,逐渐凸显出其在测高与遥感方面的重要价值,成为一项非常有发展前景的新型遥感技术。目前,美国国家宇航局NASA和欧空局ESA拟分别开展Cyclone GNSS[12](http://cygnss-michigan.org) 和GEROS-ISS[13] (GNSS Reflectometry, Radio Occultation and Scatterometry onboard the International Space Station, http://www.gfz-potsdam.de/en/section/gps-galileo-earth-observation/projects/geros-iss)卫星任务,以期获得高时空分辨率的全球中尺度海洋信息。随着GNSS-R技术的发展,不断优化GNSS-R数据处理算法,将有助于提高GNSS-R水面高观测精度和数据利用效率,进而拓展GNSS-R的应用范围。
根据试验中采用GNSS接收机观测量类型的不同[14],通常将GNSS-R测高分为干涉GNSS-R(iGNSS-R)[15-17]和传统GNSS-R (cGNSS-R)[18-21]。iGNSS-R主要是利用反射信号与直射信号功率波形相关性,测得时间延迟,然后计算得到天线到水面的垂直距离。cGNSS-R则主要利用接收机所给出的直射信号与反射信号载波相位数据,通过固定模糊度和解算接收机钟差等方式,来确定两者之间的传播路径延迟,进而计算出天线至水面的高度。与传统卫星测高和验潮站技术相比,GNSS卫星数量较多、信号连续、星座空间分布等优点可满足高时空分辨率水面高度测量需要。文献[22]在Crater湖面上利用iGNSS-R设备,实现了1 Hz厘米级精度的GNSS-R水面高测量。欧空局(ESA)、德国地学中心(GFZ)和西班牙加泰罗尼亚空间研究所(IEEC)各自研制了iGNSS-R设备[23-26],我国中科院空间中心[27]和北京航空航天大学[28]也分别自主研发了iGNSS-R接收机。
iGNSS-R涉及复杂的多普勒时延算法,设备和数据处理方法通常较为复杂;而cGNSS-R系统主要配置两套不同极化特性的天线,设备和数据处理方法较为简便,可借鉴现有GNSS定位算法,实现高精度的距离解算。文献[18]基于GPS单差相位组合观测量,利用每20 min的观测数据,依据最小二乘原理解算得到了一组天线到水面高度、模糊度和钟差等参数,测高精度大约为±4 cm。该文献所提出的算法并非逐历元解算,数据结果时间分辨率不高。虽然较高精度的水面高测量已经能够实现,但是在寻求简化仪器和提高时空分辨率等方面仍有待提升。目前的情况与文献[15]所认为监测海洋中小尺度现象(如海洋涡流)时需要中高纬度1 cm精度的高时空分辨率测高数据仍有一定的差距。
本文在文献[18]的研究基础上,进一步拓展实现了逐历元单差解算算法,并将逐历元双差算法也应用到了GNSS-R测高数据处理中。利用本文所提出的改进算法,可以提高cGNSS-R水面高测量的时间分辨率,对于水面实时变化监测具有至关重要的作用。试验结果显示,改进的逐历元cGNSS-R算法在时间分辨率和测高精度上可与iGNSS-R达到同等水平。
1 逐历元GNSS-R测高单差和双差算法图 1为cGNSS-R测高几何关系示意图。在GNSS-R测高中,右旋极化(RHCP)天线朝上安置用于接收GNSS卫星直射信号,而左旋极化(LHCP)天线朝下安置用于接收经水面反射的GNSS信号。其中,两个天线的相位中心在同一铅垂线上。GNSS天线和反射点之间的距离远小于GNSS卫星到天线距离,故卫星的高度角可近似等于反射角余角。

|
| 图 1 cGNSS-R测高关系示意图 Fig. 1 Schematic view on the geometry of ground-based GNSS-R altimetry |
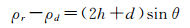 (1)
(1)
式中,ρr是反射信号的路径长度;ρd是直射信号的路径长度;h为水面到反射接收机相位中心的垂直距离;d是直射天线与反射天线相位中心之间的垂直距离;θ为GNSS卫星的高度角。由于直射天线的位置可由长时间观测进行精密单点定位准确计算得到,天线间距d由实测得到,故h的解算结果反映了水面高的变化,ρr和ρd之差也可由同历元的载波相位观测量相减[30]获得
 (2)
(2)
式中,ρr1(ti)和ρd1(ti)分别表示在ti时刻卫星1的信号分别到反射天线和直射天线的路径长度;λ1表示GPS L1的波长;L1r1(ti)为反射接收机得到的来自卫星1的L1相位观测量;L1d1(ti)为直射接收机得到的来自卫星1的L1相位观测量;c为光速;δtrd(ti)为直射接收机和反射接收机钟差之差;Nr1为反射接收机与卫星1相位观测量的模糊度;Nd1为直射接收机与卫星1相位观测量的模糊度。如果在一个弧段内载波相位观测值没有发生周跳,整周模糊度(Nr1-Nd1)的值将保持不变,因此可以利用一弧段的所有观测值求解单差模糊度。
首先,利用来自两颗卫星的时间间隔较长的3个历元观测值,利用最小二乘原理,估计整周模糊度、h以及接收机钟差。然后,通过多组观测值可以解算出该弧段内一系列整周模糊度和的值。进而,依据时间序列和模糊度的整数特性,固定整周模糊度。最后,利用准确的整周模糊度,重新解算接收机钟差项和h。值得注意的是,在此处要求是较大间隔的3 s是避免方程的奇异性。在确定了Nr1-Nd1之后,h和δtrd(ti)这两个时变量仍然需要进行求解。考虑到在不同的历元δtrd(ti)会发生变化,故每个历元至少需要两颗卫星的观测值,才能解算出h和δtrd(ti)。
将式(1)代入式(2),可获得基于L1相位观测量确定h和δtrd(ti)的关系式
 (3)
(3)
式中,N1代表Nr1-Nd1;N2代表Nr2-Nd2;θ1和θ2分别为卫星1和卫星2的高度角;L1r2(ti)为反射接收机给出的来自卫星2的L1相位观测量;L1d2为直射接收机给出的来自卫星2的L1相位观测量。
再将式(2)在卫星1和卫星2之间做差得到双差载波相位观测量组合,双差计算可消除cδtrd(ti)以及其他与几何位置等相关误差。最终可得
 (4)
(4)
式中,N1-N2值在同一弧段保持不变,可通过同一弧段的数据来预先确定。再由此式可以直接求出值
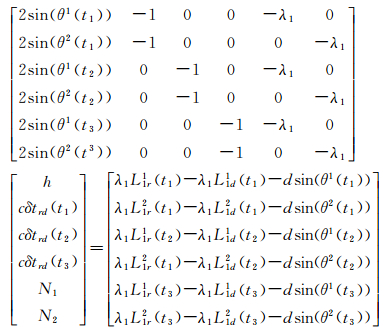 (5)
(5)
在实际数据处理中,先选取同一时间段来自两颗GPS卫星的连续观测数据,并进行单差观测量组合,再从其中选取3个历元的观测值,组成式(5),解算出h、3个历元的cδr、N1和N2,得到一组N1与N2的浮点解,然后根据解算结果确定模糊度浮点解N1与N2,利用式(3)逐历元解算出h和cδtrd。为避免解算过程中法方程的病态性,计算中,3个历元之间应该相隔600 s以上
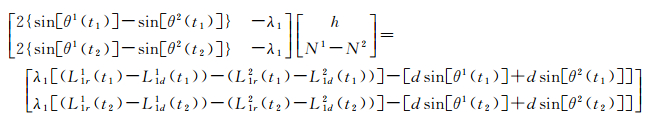 (6)
(6)
对于双差观测值组合,可从连续观测数据中选取两个历元的观测值,按照式(6)求解出h和N1-N2,并得到一组N1与N2的浮点解,将其固定,再利用式(4)逐历元解算出h。
在解算出h之后,若发现存在跳变,则可以依据式(1)和式(2)结合高度角等相关信息,将之修复。
单差方法是在接收机间求一次差,削弱了卫星星历、电离层延迟、对流层延迟等误差的影响。利用上述逐历元单差算法可将测高结果提高至1 s的时间分辨率。双差方法是在单差的基础上在卫星间进行差分,接收机钟的相对钟差也被消去,可大大减少未知数的个数,从而大幅度减少数据处理的工作量。
2 试验与结果为验证上述算法的可靠性和准确性,于2015年5月31日,在武汉市东湖落雁景区清河桥上进行了GNSS-R水面高监测试验。当GNSS-R接收机位于北半球某一位置时,考虑到GNSS卫星星座空间分布特性,在接收机的北方向上一定的范围内存在反射点盲区,如图 2所示。GNSS反射点盲区的分布与接收机地理位置以及架设的高度有关,试验中,将GNSS-R测高系统安置在桥南侧。由于桥体位置的限制,仅能接收到来自方位角70°-230°之间的卫星信号,如图 3(a)所示,试验中,卫星截止高度角为10°,直射和反射接收机共同时记录了约7 h的观测数据,包括码观测和载波相位观测量。为检核GNSS-R水面高解算结果的精度,湖面到LHCP天线相位中心的垂直距离已用电子全站仪精确测得,为5.92 m。

|
| 图 2 GNSS-R反射点空间分布 Fig. 2 Distribution of the reflected points 注:由5月31日试验当天的GNSS卫星精密轨道和接收机架设的地理位置在接收机高度角设为10°的情况下计算得到,方位角(330°, 30°)间存在反射点盲区。 |

|
| 图 3 武汉东湖清河桥地图(a)及东湖2015年5月31日试验天线安装图(b) Fig. 3 Location of the GNSS-R experiment (a) and photo-shot of GNSS-R device (b) |
根据上节提出的逐历元单双差算法,解算出反射接收天线相位中心到湖面的垂直距离h。图 4为计算流程,首先利用Bernese 5.2 高精度GNSS数据处理软件解算出朝上天线相位中心的精确坐标,再结合GNSS精密星历计算出卫星的方位角,选择出方位角在70°-230°之内且观测时长大于10 min的数据,检查在同一时间段内是否有两颗以上卫星的观测值,利用编辑后的观测数据,采用两种不同的算法(单差和双差)分别解算出水面高度值。

|
| 图 4 GNSS-R测高数据处理流程图 Fig. 4 Flowchart of ground-based GNSS-R algorithm to estimate the reflected water level |
图 5给出了反射点到天线的水平距离与卫星高度角的关系,由图可知,在6 m仪器高情况下,当卫星的高度角大于10 °时,反射点到天线的水平距离将小于40 m。

|
| 图 5 反射点到天线的水平距离与卫星高度角的关系 Fig. 5 Observation radius (the horizontal distance between antennae and reflected points) varies with the satellite elevation angle |
由以上编辑条件,选取了3段采样间隔为1 s的观测弧段,分别是:PRN 26 和 PRN 32 GPS卫星同步观测27 min的数据,PRN 16 和PRN 32 GPS卫星同步观测26 min的数据以及PRN 09 和 PRN 19 GPS卫星同步观测17 min的数据。再利用本文提出的分别基于L1、L2单差和双差观测量组合,利用不同策略解算h值。图 6分别显示了利用3段数据解算出的h随时间的变化情况。其中红色、黑色、蓝色和绿色的点分别表示基于L1单差观测值组合(L1-SD)、L2单差观测值组合(L2-SD)、L1双差观测值组合(L1-DD)和L2双差观测值组合(L2-DD)解算的结果。从图 6可知,GNSS-R估算反射天线相位中心至水面的高度在5.92 m左右,与全站仪观测结果相吻合。表 1中列出了相应的对比统计结果,GNSS-R测高结果与全站仪的实测结果约有1 cm的系统性偏差。将各个时段解算结果与全站仪测量值进行比较,标准偏差大致在±2~±4 cm。L1-SD、 L1-DD解算的h值较L2-SD和L2-DD的解算值相对平滑稳定一些,这主要是由于L1载波观测值具有更高的精度和稳定性造成的。

|
| 图 6 利用PRN 26和PRN 32、PRN 16和PRN 32、PRN 09和PRN 19卫星的观测数据解算出的h估值序列 Fig. 6 Time series of estimated reflector height at 1 s sampling using L1 and L2 carrier phase measurements from satellites PRN 26 and PRN 32, PRN 16 and PRN 32, PRN 09 and PRN 19 |
| PRN26&PRN32 | PRN16&PRN32 | PRN09&PRN19 | ||||||
| 平均值/m | 均方误差/cm | 平均值/m | 均方误差/cm | 平均值/m | 均方误差/cm | |||
| L1-单差 | 5.918 | 2.4 | 5.944 | 2.7 | 5.952 | 3.5 | ||
| L1-双差 | 5.932 | 2.6 | 5.918 | 1.5 | 5.925 | 2.4 | ||
| L2-单差 | 5.928 | 3.3 | 5.938 | 2.4 | 5.947 | 4.0 | ||
| L2-双差 | 5.950 | 4.1 | 5.938 | 2.4 | 5.929 | 2.8 | ||
| 平均值 | 5.932 | 3.1 | 5.935 | 2.3 | 5.938 | 3.2 | ||
GNSS-R数据处理中,周跳会严重影响天线至水面高度h解算的准确性。图 7给出了利用PRN09和PRN19两颗卫星的观测数据解算得到h的时间序列。其中,蓝线表示周跳修复前的情况,红线表示周跳修复后的情况。周跳修复前,高度解算值存在一个明显的跳跃。根据这个跳跃的大小和高度角,将出现跳跃的数据段的整周模糊度调整一周,再由调整后的整周模糊度重新计算后段数据结果,完成单差周跳修复。
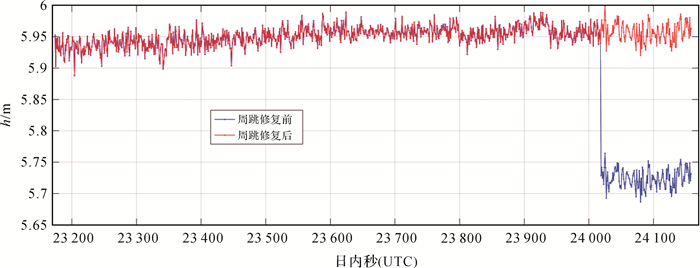
|
| 图 7 PRN09和PRN19周跳修复 Fig. 7 Cycle slip of PRN09 and PRN19 |
3 结 论
GNSS-R海洋测高的发展为获取更为全面的高精度海面高信息和定量研究全球气候变化提供了一种全新的技术手段。由于GNSS-R测高能同时给出多个GNSS信号反射点处的水面高信息,因此,与传统的验潮站和卫星雷达测高技术相比,其具有时空分辨率高的特点。利用GNSS-R观测资料,可实现海洋中小尺度动力环境现象、海潮和洋流的监测以及减弱海潮反演中的混频效应。此外,传统验潮站的测量结果中包含了板块垂直运动的影响,而利用GNSS-R技术测得的水面高是在地心参考框架内解算的,故GNSS-R测高可准确给出水面高度的绝对变化信息。
现有cGNSS-R算法是利用每20 min观测数据,计算一个水面高度值,其不足之处在于,观测数据利用效率不高,时间分辨率较低。为解决这一问题,本文提出了一种改进的逐历元cGNSS-R测高算法,以实现1 Hz的水面高监测。另外,在此改进算法的基础上,实现了利用双差组合算法,逐历元解算水面高。试验结果表明,上述两种算法都可实现高精度、高时空分辨率水面高测量,其精度可达±2~±4 cm,为下一步实现高时空分辨率的水面高监测以及水体相关信息反演提供了基本理论和实践基础。
随着北斗、GLONASS和Galileo等GNSS系统的逐步建成和完善,可实现利用多系统反射信号联合测高,进一步提升水面高度测量的时空分辨率和精度。
| [1] | MARTIN-NEIRA M. A Passive Reflectometry and Interferometry System (PARIS):Application to Ocean Altimetry[J]. ESA Journal , 1993, 17 : 331 –355. |
| [2] | 刘经南, 邵连军, 张训械. GNSS-R研究进展及其关键技术[J]. 武汉大学学报(信息科学版) , 2007, 32 (11) : 995–960. LIU Jingnan, SHAO Lianjun, ZHANG Xunxie. Advances in GNSS-R Studies and Key Technologies[J]. Geomatics and Information Science of Wuhan University , 2007, 32 (11) : 995 –960. |
| [3] | NOGUÉS-CORREIG O, RIBÓ S, ARCO J C, et al. The Proof of Concept for 3-cm Altimetry Using the Paris Interferometric Technique[C]//Proceedings of International Geoscience and Remote Sensing Symposium. Honolulu, HI:IEEE, 2010:3620-3623. |
| [4] | CARRENO-LUENGO H, PARK H, CAMPS A, et al. GNSS-R Derived Centimetric Sea Topography:An Airborne Experiment Demonstration[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 2013, 6 (3) : 1468 –1478. DOI:10.1109/JSTARS.2013.2257990 |
| [5] | KOMJATHY A, MASLANIK J, ZAVOROTNY V U, et al. Sea Ice Remote Sensing Using Surface Reflected GPS Signals[C]//Proceedings of IEEE 2000 International Geoscience and Remote Sensing Symposium. Honolulu, HI:IEEE, 2000:2855-2857. |
| [6] | ZAVOROTNY V U, VORONOVICH A G. Scattering of GPS Signals from the Ocean with Wind Remote Sensing Application[J]. IEEE Transactions on Geoscience and Remote Sensing , 2000, 38 (2) : 951 –964. DOI:10.1109/36.841977 |
| [7] | ZUFFADA C, ELFOUHAILY T, LOWE S. Sensitivity Analysis of Wind Vector Measurements from Ocean Reflected GPS Signals[J]. Remote Sensing of Environment , 2003, 88 (3) : 341 –350. DOI:10.1016/S0034-4257(03)00175-5 |
| [8] | KATZBERG S J, TORRES O, GRANT M S, et al. Utilizing Calibrated GPS Reflected Signals to Estimate Soil Reflectivity and Dielectric Constant:Results from SMEX02[J]. Remote Sensing of Environment , 2005, 100 (1) : 17 –28. |
| [9] | CHEW C, SMALL E E, LARSON K M. An Algorithm for Soil Moisture Estimation Using GPS-Interferometric Reflectometry for Bare and Vegetated Soil[J]. GPS Solutions , 2015 . DOI:10.1007/s10291-015-0462-4 |
| [10] | JIN Shuanggen, NAJIBI N. Sensing Snow Height and Surface Temperature Variations in Greenland from GPS Reflected Signals[J]. Advances in Space Research , 2014, 53 (11) : 1623 –1633. DOI:10.1016/j.asr.2014.03.005 |
| [11] | SHUM C K, LEE H, ABUSALI P A M, et al. Prospects of Global Navigation Satellite System (GNSS) Reflectometry for Geodynamic Studies[J]. Advances in Space Research , 2011, 47 (10) : 1814 –1822. DOI:10.1016/j.asr.2010.07.026 |
| [12] | RUF C S, GLEASON S, JELENAK Z, et al. The CYGNSS Nanosatellite Constellation Hurricane Mission[C]//Proceedings of International Geoscience and Remote Sensing Symposium. Munich:IEEE, 2012:214-216. |
| [13] | WICKERT J, ANDERSEN O, BEYERLE G, et al. Innovative Remote Sensing Using the International Space Station:GNSS Reflectometry with GEROS[C]//Proceedings of IEEE International Geoscience Remote Sensing Symposium. Québec City:IEEE, 2014. |
| [14] | CAMPS A, PARK H, DOMÈNECH E V I, et al. Optimization and Performance Analysis of Interferometric GNSS-R Altimeters:Application to the PARIS IoD Mission[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 2014, 7 (5) : 1436 –1451. DOI:10.1109/JSTARS.2014.2320873 |
| [15] | MARTIN-NEIRA M, CAPARRINI M, FONT-ROSSELLO J, et al. The PARIS Concept:An Experimental Demonstration of Sea Surface Altimetry Using GPS Reflected Signals[J]. IEEE Transactions on Geoscience and Remote Sensing , 2001, 39 (1) : 142 –150. DOI:10.1109/36.898676 |
| [16] | RUFFINI G, SOULAT F, CAPARRINI M, et al. The Eddy Experiment:Accurate GNSS-R Ocean Altimetry from Low Altitude Aircraft[J]. Geophysical Research Letters , 2004, 31 (12) : L12306 . |
| [17] | ZAVOROTNY V U, GLEASON S, CARDELLACH E, et al. Tutorial on Remote Sensing Using GNSS Bistatic Radar of Opportunity[J]. IEEE Geoscience and Remote Sensing Magazine , 2014, 2 (4) : 8 –45. DOI:10.1109/MGRS.2014.2374220 |
| [18] | LÖFGREN J S, HAAS R, JOHANSSON J M. High-rate Local Sea Level Monitoring with a GNSS-based Tide Gauge[C]//Proceedings of International Geoscience and Remote Sensing Symposium. Honolulu, HI:IEEE, 2010:3616-3619. |
| [19] | LÖFGREN J S, HAAS R, JOHANSSON J M. Monitoring Coastal Sea Level Using Reflected GNSS Signals[J]. Advances in Space Research , 2011, 47 (2) : 213 –220. DOI:10.1016/j.asr.2010.08.015 |
| [20] | LÖFGREN J S, HAAS R. Sea Level Observations Using Multi-System GNSS Reflectometry[C]//Proceedings of the 17th NKG General Assembly. Göteborg:NKG, 2014. |
| [21] | MARTIN-NEIRA M, COLMENAREJO P, RUFFINI G, et al. Altimetry Precision of 1 cm over a Pond Using the Wide-lane Carrier Phase of GPS Reflected Signals[J]. Canadian Journal of Remote Sensing , 2002, 28 (3) : 394 –403. DOI:10.5589/m02-039 |
| [22] | TREUHAFT R N, LOWE S T, ZUFFADA C, et al. 2-cm GPS Altimetry over Crater Lake[J]. Geophysical Research Letters , 2001, 28 (23) : 4343 –4346. DOI:10.1029/2001GL013815 |
| [23] | RUFFINI G, CAPARRINI M, CHAPRON B, et al. Oceanpal:An Instrument for Remote Sensing of the Ocean and Other Water Surfaces Using GNSS Reflections[J]. Elsevier Oceanography Series , 2003, 69 : 146 –153. DOI:10.1016/S0422-9894(03)80025-9 |
| [24] | DUNNE S, SOULAT F, CAPARRINI M, et al. Oceanpal®, A GPS-reflection Coastal Instrument to Monitor Tide and Sea-state[C]//Proceedings of Europe Oceans. Brest, France:IEEE, 2005, 2:1351-1356. |
| [25] | CAPARRINI M, EGIDO A, SOULAT F, et al. Oceanpal®:Monitoring Sea State with a GNSS-R Coastal Instrument[C]//Proceedings of IEEE International Geoscience and Remote Sensing Symposium. Barcelona:IEEE, 2007:5080-5083. |
| [26] | NOGUES-CORREIG O, GALI E C, CAMPDERROS J S, et al. A GPS-Reflections Receiver That Computes Doppler/Delay Maps in Real Time[J]. IEEE Transactions on Geoscience and Remote Sensing , 2007, 45 (1) : 156 –174. DOI:10.1109/TGRS.2006.882257 |
| [27] | 孙剑. GNSS-R海洋反射接收机的控制设计及实现[D] 北京:中国科学院空间科学与应用研究中心, 2010. SUN Jian. Design and Realization of Control System for the GNSS-R Receiver[D]. Beijing:Center for Space Science and Applied Research, Chinese Academy of Sciences, 2010. |
| [28] | 杨东凯, 刘宪阳, 李伟强. GNSS-R延迟映射接收机相关器设计[J]. 遥测遥控 , 2008, 29 (6) : 17–21. YANG Dongkai, LIU Xianyang, LI Weiqiang. Design of Correlator of GNSS-R Delay Mapping Receiver[J]. Journal of Telemetry, Tracking, and Command , 2008, 29 (6) : 17 –21. |
| [29] | 杨东凯, 张其善. GNSS反射信号处理基础与实践[M]. 北京: 电子工业出版社, 2012 . YANG Dongkai, ZHANG Qishan. GNSS Reflected Signal Processing:Fundamentals and Applications[M]. Beijing: Publishing House of Electronic Industry, 2012 . |
| [30] | 段举举, 沈云中. GPS/GLONASS组合静态相位相对定位算法[J]. 测绘学报 , 2012, 41 (3) : 825–830, 917. DUAN Juju, SHEN Yunzhong. An Algorithm of Combined GPS/GLONASS Static Relative Positioning[J]. Acta Geodaetica et Cartographica Sinica , 2012, 41 (3) : 825 –830, 917. |


