2. 国家测绘地理信息局卫星测绘应用中心, 北京 100048 ;
3. 山东科技大学测绘科学与工程学院, 山东 青岛 266590
2. Satellite Surveying and Mapping Application Center, NASG, Beijing 100830, China ;
3. College of Geomatics, Shandong University of Science and Technology, Qingdao 266590, China
月球重力场是研究月球的基本物理量,可用来研究月球构造、演化过程和确定绕月卫星精密轨道。绕月卫星受到的摄动力众多,主要包括太阳光压、月球非球形摄动、三体引力等。月球重力场是绕月卫星的主要摄动力场,高精度的月球重力场模型是确定绕月卫星精密轨道的关键。
1998年美国发射的Lunar Propector(LP)绕月卫星,初期轨道高度是100 km,扩展任务阶段轨道平均高度降到30 km。LP获得的多普勒数据的精度为0.2 mm/s,采样间隔为10 s。联合之前的测月跟踪数据和LP任务获得的所有观测数据,解算得到了月球重力场模型LP165P[1-2]。
2007年日本的SELENE探月计划发射了3颗绕月卫星,其中高轨的一颗中继卫星可为主星转发多普勒信号,实现了第1次直接观测月球背面重力场[3-4]。使用SELENE多普勒观测数据、差分VLBI数据和之前已有的测月数据,解算了SGM系列月球重力场模型。其中精度较高的SGM100i与初期解算的SGM100h相比,定轨误差已经降至几十米[4]。
2011年美国发射的GRAIL卫星计划,包括两颗相同的月球探测器GRAIL-A和GRAIL-B,运行在50 km高度的近圆形月球极轨道上,通过Ka频段在两个月球探测器之间进行高精度距离变化率测量,利用这些测量数据来解算月球重力场。由GRAIL观测数据解算的超高阶GRAIL月球重力场模型有:GL0420A、GRGM660-PRIM、GL0660B、GL0990C和GL0990D。GRAIL系列月球重力场模型较之前的月球重力场模型,模型分辨率得到极大提高,在2~10阶次模型改正精度达2个量级,而高阶次可以达到4个量级以上。与SGM100i比较,最明显的不同在两极和背面的较小环形区域,在这些区域,GL0660B的重力信息表达更精细,与地形的相关性也更高。
在GRAIL任务之前,人们对月球重力场的探索大部分局限于月球的正面,通过Lunar Propector任务,月球背面不能被直接观测到。直到SELENE任务,月球背面的重力场第1次被直接观测到,但月球背面有效阶次只在前70阶。通过GRAIL任务采集到的双星间距离变率精度达到0.03 μm,重力场空间频谱信号的强度提高了4个数量级,其解算的GL0660B重力场模型在330阶之前与地形相关性达到95%,空间分辨率大大提高的同时低阶位系数也得到改善。本文主要在利用GL0660B新模型进行分析比较,从而得到前所未发现的认识和结论。首先分析GL0660B模型可靠性,进而使用其分析月球不同高度上的重力场特性;并且比较不同模型空间频谱特性,利用GEODYN定轨软件[5]计算了不同高度卫星所表现出的轨道变化规律,最后分析GL0660B月球重力场模型对绕月卫星轨道的影响。
1 GL0660B模型质量分析月球重力场球谐函数展开模型位系数的阶方差可以反映重力场空间频谱信号的强度[6]。计算公式如下
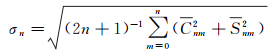 (1)
(1)
式中,Cnm、Snm是正则化位系数,n和m分别是阶和次。在阶方差分析中常用Kaula准则,它近似描述了重力场模型位系数统计规律,与阶数n的平方成反比
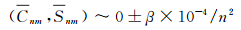 (2)
(2)
式中,β为经验常数。Kaula约束的作用,一是在缺乏月球背面数据情况下解算时,克服求解不稳定性,二是解算时平滑高阶系数。解算不同月球重力场模型时取的值一般不相同。在解算SGM100i时使用的β为3.6;在用GRAIL数据前期解算GRGM540a和GRGM660PRIM时,仅在大于330阶时用到宽松的Kaula约束,β为25;在解算GL0660B时没有用Kaula约束,β的值越小,表示约束越严格[3]。
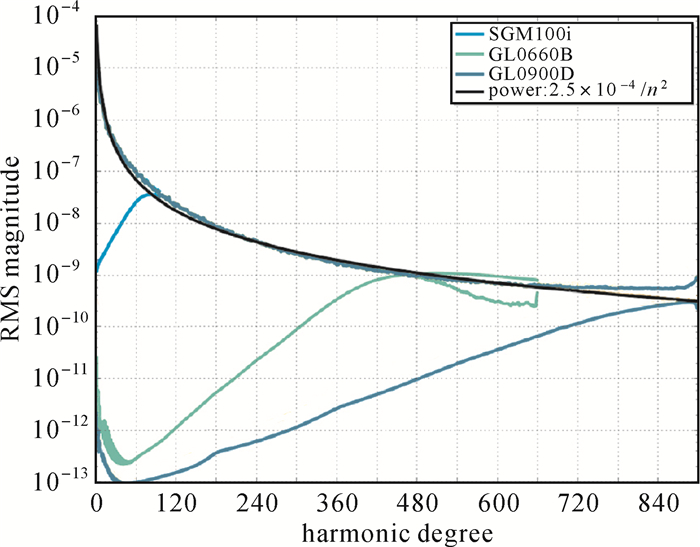
图 1中分别绘制了SGM100i、GL0660B和GL0900D等3个模型的位系数阶方差和误差阶方差曲,Kaula曲线为2.5×10-4/n2。SGM100i在30阶之后开始偏离Kaula曲线。GL0660B和GL0900D在30阶至180阶也偏离Kaula曲线,但之后与Kaula曲线吻合得较好。SGM100i、GL0660B和GL0900D在100阶之前阶方差差别不大,但GL0660B和GL0900D与之前的模型相比,不仅在阶次上大大提升,其误差阶方差也有3个量级的明显改善。GL0660B和GL0900D相比,阶方差基本一致,但误差阶方差曲线略有不同,前者位系数(30~660阶)误差略大。从图中可以看出加入月球背面高精度直接观测数据对重力场的解算起了重要作用,GRAIL系列模型分辨率得到极大提高。
|
| 图 1 不同月球重力场模型阶方差和误差阶方差的比较 Fig. 1 Comparison of degree sigma error and degree variance of lunar gravity models |
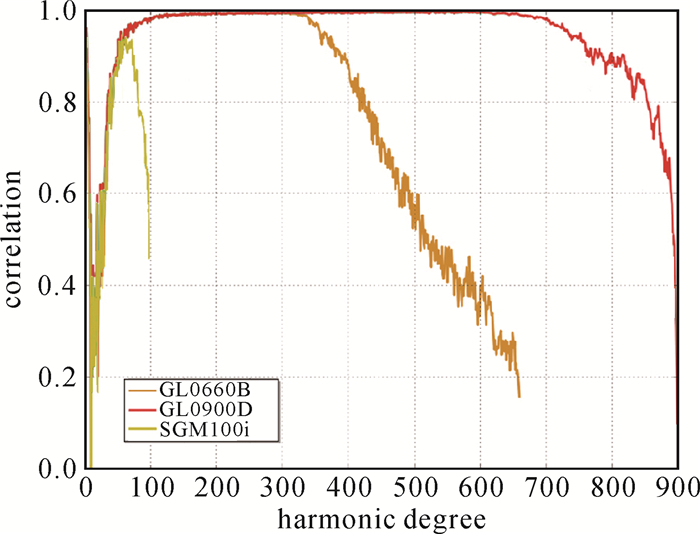
月球上除了质量瘤等独特构造区域,月球重力场的高阶重力信号与地形应该有很高的相关性[8]。高阶重力场位系数与地形相关程度是月球重力场模型质量的一种评价标准。图 2描述了SGM100i、GL0660B和GL0900D模型位系数与LOLA地形模型位系数的相关性。
|
| 图 2 重力场模型位系数与月球地形模型LOLA地形模型位系数相关性 Fig. 2 Comparison of lunar gravity model coefficients and LOLA topography model |
在50~70阶SGM100i相关系数高达0.9左右,从80阶往后相关性急剧降低,到后面几乎没有相关性。GL0660B和GL0900D位系数与地形相关系数在60阶之前与SGM100i几乎一致,之后80~330曲线变化比较平稳,稳定在0.95以上,GL0660B在330阶之后有较明显的下降趋势,GL0900D在660阶之后开始下降。在2~20阶几个模型的地形相关系数曲线几乎一致,数值变化巨大,几乎不相关或负相关,这是由于月球表面存在质量瘤所导致的过度补偿所致[9]。
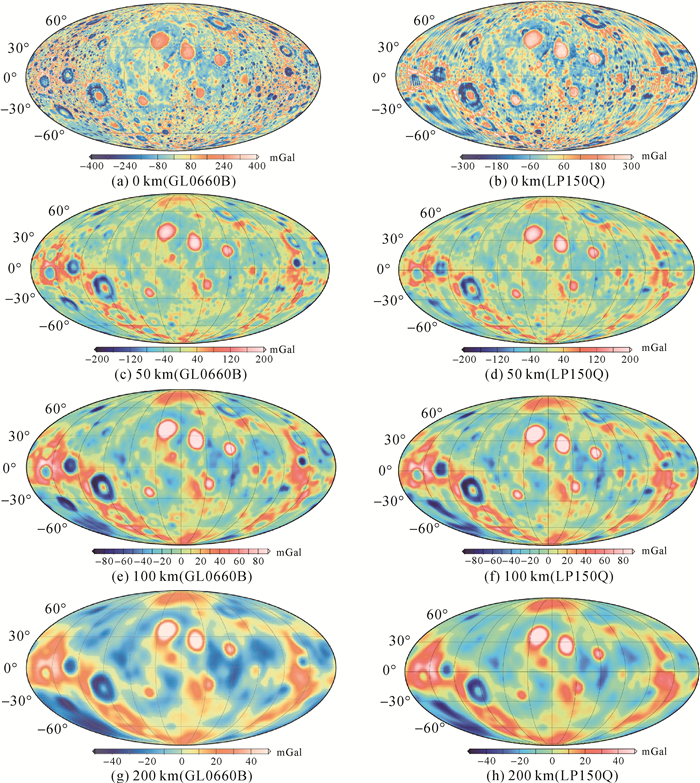
2 GL0660B不同高度处月球重力异常特征分析本文主要应用GL0660B模型在不同高度处重力异常分布进行分析,并与LP150Q重力异常的分布情况进行比较。图 3(a)、(c)、(e)、(g)分别给出了月球上空0 km、50 km、100 km和200 km处由GL0660B模型得到的重力异常分布图。图 3(b)、(d)、(f)、(h)分别给出了月球上空0 km、50 km、100 km和200 km处由LP150Q模型得到的重力异常分布图。采用月固坐标系,坐标系原点O为月心,参考平面为月球赤道面,OX轴通过月面上的中央湾指向地球平均位置,OZ轴沿月球平均自转轴方向,坐标系为右手坐标系。图 3中横坐标为经度,纵坐标为纬度,90°W-90°E为月球正面,其余区域为月球背面。
|
| 图 3 GL0660B和LP150Q模型在不同高度的重力异常 Fig. 3 Gravity anomaly of GL0660B and LP150Q at different heights |
图 3中月球正面的5个主要质量瘤[10]:静海(Imbrium)、澄海(Serenitatis)、危海(Crisium)、湿海(Humorum)、酒海(Nectaris)清晰可见。质量瘤是质量过度集中而形成的,在质量瘤内部,变化平缓,重力异常值都在300 mGal(1 Gal=0.01 m/s2)以上。在质量瘤的边缘,重力异常值快速下降变为负值,形成了重力异常峭壁。每一个质量瘤正好与月球表面大型撞击盆地区域相对应,具有强烈的地形负相关性。质量瘤对低轨绕月飞行器有着明显的影响。一般认为这种现象的形成是火山岩流入盆地所致[1, 4]。质量瘤重力异常的骤变对于绕月低轨卫星有着巨大的影响。
GL0660B使用了高精度全月面的直接观测数据,对月球表面尤其是背面月球重力信息(图 3(a))表达更为精细,从图中可以看出,背面的实际地形和重力异常环形特征符合得很好,如东方海(Orientale)、赫兹斯朋坑(Hertzsprung)、克罗列夫坑(Korolev)、阿波罗坑(Apollo)、莫斯科海(Moscoviense)、门捷列夫(Mendeleev)等,上述地区也均为质量瘤存在区域[2]。月球背面质量瘤与正面质量瘤有显著的不同,正重力异常环与负重力异常环交替包裹,形成正-负-正的重力异常包裹环。
图 3给出了GL0660B模型在0 km、50 km、100 km、200 km处重力异常的分布图,从中可看出,重力异常值随高度逐渐减小,对不同轨道高度绕月卫星轨道的影响。由图 3(c)和表 1的数据统计结果可看出,200 km高度处重力异常比100 km、50 km处的重力异常减少较大,重力异常随轨道高度逐渐衰减,其衰减遵循(a/r)n+2(其中,a为月球的平均半径;n为重力场模型的阶数;r为绕月卫星离月心的距离)[11]。在50 km处重力异常分布的平均值和方差分别为1.80 mGal和43.54 mGal,在100 km处重力异常的平均值和方差分别为1.36 mGal和27.21 mGal,在200 km处下降为0.91 mGal和14.94 mGal。重力异常在随高度衰减的同时,全月球不同高度处的重力异常变化也随高度增加趋于平滑。几个典型质量瘤的重力场信号的衰减也很明显,但其边界的重力异常骤变较为明显。
| 高度/km | 最小值/mGal | 最大值/mGal | 平均值/mGal | 方差/mGal | |||||||
| GL0660B | LP150Q | GL0660B | LP150Q | GL0660B | LP150Q | GL0660B | LP150Q | ||||
| 0 | -686.84 | -492.38 | 1354.08 | 855.99 | 2.83 | 2.95 | 131.02 | 95.52 | |||
| 50 | -177.42 | -176.08 | 210.92 | 210.80 | 1.80 | 1.76 | 43.54 | 42.23 | |||
| 100 | -102.07 | -102.21 | 150.08 | 150.03 | 1.36 | 1.32 | 27.21 | 27.05 | |||
| 200 | -43.19 | -44.31 | 83.25 | 83.21 | 0.91 | 0.87 | 14.94 | 14.94 | |||
图 4显示了GL0660B与LP150Q在0 km、50 km、100 km和200 km高度处重力异常差的分布。GL0660B与LP150Q之间在月球正面差异较小,在月球背面的差异比较明显。可以看出,两个模型在50 km高度处的差值大部分在50 mGal以内,而在200 km高度处的差值在10 mGal以内。GL0660B模型不同高度处的高精度的月球背面重力异常可以为嫦娥四号月球背面落月探测提供参考依据。

|
| 图 4 GL0660B与LP150Q在不同高度处重力异常差分布 Fig. 4 Differences of Gravity anomaly between GL0660B and LP150Q at different height |
3 绕月卫星轨道的变化特征分析
探月工程中,人们更为关心月球重力场对绕月卫星轨道的摄动问题[12]。重力异常反映了月球重力场的特征,下面通过对绕月卫星轨道的变化分析,能更深刻地表征月球重力场的性质。
选用GL0660B模型,给出其在轨道高度为50 km和200 km的变化。选取卫星初始轨道是倾角90°的圆轨道。我国探月计划“嫦娥工程”的卫星轨道设计也为经过极地的低圆轨道,这里进行的模拟计算可以为探月后续卫星提供一定的参考。针对GL0660B模型,用到的动力学模型主要有[13-14]地球中心项引力、N体摄动、地球非球形摄动、固体潮摄动、大行星的摄动、太阳光压摄动、相对论效应等。选用的时间系统为UTC,选用J2000.0地心天球坐标系,用JPL DE421历表计算日月等天体的位置。计算的轨道积分弧段为1 a,间距为60 s,选用不同的采样间隔在精度上差异不大,选用间距为60 s可节省计算时间。
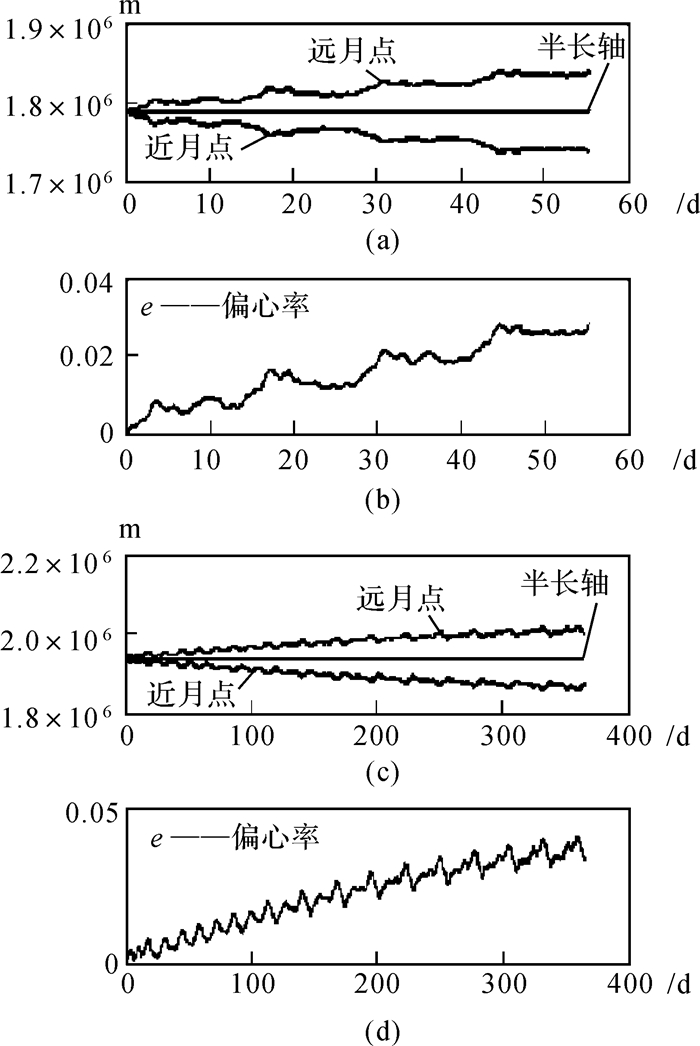
图 5主要反映在不同高度绕月卫星表现出的变化特征。其中,图 5(a)和(c)分别为轨道50 km和200 km远月点、近月点的变化,图 5(b)和(d)分别为轨道50 km和200 km偏心率的变化。当卫星轨道高度为50 km时,在无外界推动力的条件下卫星可飞行55 d,然后会因为近月点距离小于月球半径,卫星会撞击月球表面。当在200 km的轨道高度运行时,卫星可在无外界推动力的情况下飞行1 a以上。从图 5中可以看出离心率随时间的变化,会有复杂的短周期和长周期项,其长周期项与时间成近似线性关系,离心率的增长速度会影响近月点和远月点距离的增长速度,对绕月卫星的离心率的微小助力的调整可有效减缓近月点距离的增加。
|
| 图 5 不同轨道高度绕月卫星表现出的轨道特征 Fig. 5 Different lunar satellite orbit characters |
图 5中不同轨道高度处表现出远月点、近月点和偏心率的差异应该是质量瘤的存在产生的摄动影响。与地球的不同之处主要是月球内部横向质量分布不均匀,存在一定数量的质量瘤,这使得绕月卫星轨道变得复杂。由上一节的月球重力异常分析可以看到,卫星在50 km高度处受到质量瘤影响非常大,其重力异常达到200 mGal,这对轨道产生了明显的影响,造成轨道离心率不断地变动。
4 结 论相对于现有的月球重力场模型,GL0660B是较为可靠的模型,能够很好地反映月球外部重力场的中、长波特性,在330阶之前与月球地形相关性很高。通过重力异常图可看出从月面至高度50 km到200 km,重力异常衰减迅速。月球质量瘤对50 km低轨卫星影响巨大,随着轨道高度增加,对应质量瘤中心的重力异常值衰减都在100 mGal以上。不同的月球重力场模型都能够反映出月球外部重力场的大部分主要特征,GL0660B反映的更为精细,但到200 km以上的外部空间,GL0660B模型与LP150Q模型所得到的重力异常平均值之差为0.04 mGal。对不同高度处的轨道变化特征的分析表明绕月卫星离心率随时间的逐渐变化,会有复杂的短周期变化和长周期项变化趋势,而且不同轨道高度处受质量瘤的摄动影响不同,远月点、近月点和偏心率的变化也存在差异。这些可以为我国探月计划“嫦娥工程”后面的发射计划提供一定的参考依据。
| [1] | KONOPLIV A S, ASMAR S W, CARRANZA E, et al. Recent Gravity Models as a Result of the Lunar Prospector Mission[J]. Icarus , 2001, 150 (1) : 1 –18. DOI:10.1006/icar.2000.6573 |
| [2] | KONOPLIV A S, BINDER A B, HOOD L L, et al. Improved Gravity Field of the Moon from Lunar Prospector[J]. Science , 1998, 281 (5382) : 1476 –1480. DOI:10.1126/science.281.5382.1476 |
| [3] | NAMIKI N, IWATA T, MATSUMOTO K, et al. Farside Gravity Field of the Moon from Four-way Doppler Measurements of SELENE (Kaguya)[J]. Science , 2009, 323 (5916) : 900 –905. DOI:10.1126/science.1168029 |
| [4] | GOOSSENS S, MATSUMOTO K, LIU Q, et al. Lunar Gravity Field Determination Using SELENE Same-beam Differential VLBI Tracking Data[J]. Journal of Geodesy , 2011, 85 (4) : 205 –228. DOI:10.1007/s00190-010-0430-2 |
| [5] | ROWLANDS D D, MARSHALL J A, MCCARTHY J, et al. GEODYN Ⅱ System Description. Vols.1-5[R]. Contractor Report, Hughes STX Corp. Greenbelt, MD:[s.n.], 1997. |
| [6] | KAULA W M. Theory of Satellite Geodesy:Applications of Satellites to Geodesy[M]. London: Blaisdell, 1966 . |
| [7] | LEMOINE F G, GOOSSENS S, SABAKA T J, et al. High-degree Gravity Models from GRAIL Primary Mission Data[J]. Journal of Geophysical Research:Planets , 2013, 118 (8) : 1676 –1698. DOI:10.1002/jgre.20118 |
| [8] | NEUMANN G A, ZUBER M T, SMITH D E, et al. The Lunar Crust:Global Structure and Signature of Major Basins[J]. Journal of Geophysical Research:Planets , 1996, 101 (E7) : 16841 –16863. DOI:10.1029/96JE01246 |
| [9] | MULLER P M, SJOGREN W L. Mascons:Lunar Mass Concentrations[J]. Science , 1968, 161 (3842) : 680 –684. DOI:10.1126/science.161.3842.680 |
| [10] | HEISKANEN W A, MORITZ H. Physical Geodesy[M]. San Francisco: Freeman, 1967 . |
| [11] | LIU Lin, WANG Jiasong. An Analytic Solution of the Orbital Variation of Lunar Satellites[J]. Chinese Astronomy and Astrophysics , 1998, 22 (3) : 328 –351. DOI:10.1016/S0275-1062(98)00044-7 |
| [12] | KONOPLIV A S, PARK R S, YUAN D N, et al. The JPL Lunar Gravity Field to Spherical Harmonic Degree 660 from the GRAIL Primary Mission[J]. Journal of Geophysical Research:Planets , 2013, 118 (7) : 1415 –1434. DOI:10.1002/jgre.20097 |
| [13] | ANDREWS-HANNA J C, ASMAR S W, HEAD Ⅲ J W, et al. Ancient Igneous Intrusions and Early Expansion of the Moon Revealed by GRAIL Gravity Gradiometry[J]. Science , 2013, 339 (6120) : 675 –678. DOI:10.1126/science.1231753 |
| [14] | ASMAR S W, KONOPLIV A S, WATKINS M M, et al. The Scientific Measurement System of the Gravity Recovery and Interior Laboratory (GRAIL) Mission[J]. Space Science Reviews , 2013, 178 (1) : 25 –55. DOI:10.1007/s11214-013-9962-0 |
| [15] | SMITH D E, ZUBER M T, NEUMANN G A, et al. Initial Observations from the Lunar Orbiter Laser Altimeter (LOLA)[J]. Geophysical Research Letters , 2010, 37 (18) : L18204 . DOI:10.1029/2010GL043751 |
| [16] | ARNOLD D, BERTONE S, JÄGGI A, et al. GRAIL Gravity Field Determination Using the Celestial Mechanics Approach[J]. Icarus , 2015, 261 : 182 –192. DOI:10.1016/j.icarus.2015.08.015 |
| [17] | 孙玉, 常晓涛, 郭金运, 等. 由SGM100i质量分析看SELENE的贡献[J]. 测绘科学 , 2012, 37 (2) : 176–178. SUN Yu, CHANG Xiaotao, GUO Jinyun, et al. Contribution of SELENE for Lunar Gravity Field Recovery from Quality Analysis of SGM100i[J]. Science of Surveying and Mapping , 2012, 37 (2) : 176 –178. |
| [18] | LI Peijia, HU Xiaogong, HUANG Yong, et al. Orbit Determination for Chang'E-2 Lunar Probe and Evaluation of Lunar Gravity Models[J]. Science China Physics, Mechanics and Astronomy , 2012, 55 (3) : 514 –522. DOI:10.1007/s11433-011-4596-2 |
| [19] | JIN Shuanggen, ARIVAZHAGAN S, ARAKI H. New Results and Questions of Lunar Exploration from SELENE, Chang'E-1, Chandrayaan-1 and LRO/LCROSS[J]. Advances in Space Research , 2013, 52 (2) : 285 –305. DOI:10.1016/j.asr.2012.11.022 |
| [20] | 丰海, 李建成, 李大炜, 等. 月球Airy均衡状态与月壳厚度估计[J]. 测绘学报 , 2012, 41 (4) : 543–548. FENG Hai, LI Jiancheng, LI Dawei, et al. Airy Isostasy on the Moon:Implications for Crustal Thickness[J]. Acta Geodaetica et Cartographica Sinica , 2012, 41 (4) : 543 –548. |
| [21] | 孙雪梅, 李斐, 鄢建国, 等. Slepian函数在月球局部重力场分析中的适用性分析[J]. 测绘学报 , 2015, 44 (3) : 264–273. DOI:10.11947/j.AGCS.2015.20130728 SUN Xuemei, LI Fei, YAN Jianguo, et al. An Analysis of the Applicability of Slepian Function in Analyzing Lunar Local Gravity Field[J]. Acta Geodaetica et Cartographica Sinica , 2015, 44 (3) : 264 –273. DOI:10.11947/j.AGCS.2015.20130728 |


