2. 广西精密导航技术与应用重点实验室, 广西 桂林 541004
2. Guangxi Key Laboratory of Precision Navigation Technology and Application, Guilin 541004, China
随着科技的发展与社会的进步,人类对各大卫星导航系统(GNSS)提供实时精密单点定位(real time precise point positioning,RTPPP)服务有着迫切的需求。当采用超快产品实现RTPPP功能时,需要配套使用高精度的轨道和钟差数据[1-3]。自2007年GPS采用新一代卫星(Block IIR-M)发射后,超快卫星轨道的预报精度得到了大幅提升,可以满足RTPPP定位精度需求[4-5];而超快速钟差在24 h内的预报精度仍一直处于3 ns量级,同时国际全球卫星定位导航服务组织(The International GNSS Service,IGS)发布的IGU产品(包含观测部分(IGU-O)和预报部分(IGU-P))会滞后3 h,故其难以满足RTPPP的定位精度需求[4-6]。因此,为了尽可能地满足RTPPP服务的需求,对超快星历钟差预报精度的改进工作具有重要意义[7-8]。
就钟差数据成分而言,卫星钟差数据由趋势项成分、周期项成分和随机项成分组成,然而由于星载原子钟易受太空星体引力与外界环境的影响,卫星钟差数据呈现高度非线性特点[5, 9-11]。在传统谱分析模型中,趋势项成分常可以采用一次项线性直线或二次项曲线进行拟合,周期项成分可以采用谱分析技术进行分析,而随机项成分可以采用混沌理论、神经网络和时间序列模型等技术进行建模研究[5, 9-10, 12-20]。另外,就钟差数据特征而言,由于各颗卫星钟差数据存在钟跳频繁现象[5, 19, 21],导致钟差预报精度由于拟合数据长度降低或预报模型参数估计精度降低而变得较差。因此,这些客观因素与主观因素相结合,最终使得卫星钟差的高精度预报工作相对较难。
目前,IGS采用传统的谱分析模型来预报卫星钟差,而IGU-P在24 h范围内的预报精度一直控制在3 ns以内[6]。故针对IGU-P预报精度不高的问题,文献[4-5]提出了一种对IGU-O数据的最后5个历元重新拟合趋势项的方法来改进起点偏差,并取得了较好的预报效果。
在基于中位数法(median of absolute deviation,MAD)精确探测粗差和钟跳的基础上,本文提出了一种针对GPS IIR-M型卫星超快速钟差预报的高精度修正方法。首先,采用趋势项用一次项线性直线拟合的谱分析模型、趋势项用二次项曲线拟合的谱分析模型和文献[21]的自适应动态模型进行钟差建模预报;其次,对3个模型预报数据的第一个值分别与IGU-O的最后一个钟差历元做差,依据差值是否在IGU-O差分序列范围内进而判断出精度修正值的大小与方向,并最终运用修正值分别对3个模型的预报值进行精度修正。最后,分别对比3个模型在不采用和采用精度修正两种情况下的预报精度,从而充分验证本文精度修正方法改进功能的有效性和稳定性。
1 IGS超快速钟差预报高精度修正方法 1.1 传统谱分析模型因卫星钟差数据钟跳现象频繁,故对钟差数据的质量检测显得非常重要[5, 22]。本文采用MAD法对钟差频率数据进行粗差和钟跳的探测,其表达式如下
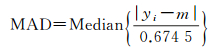 (1)
(1)
式中,m为钟差频率数据的中间数,即
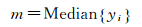 (2)
(2)
当卫星超快速钟差观测频率数据yi>(m+n*MAD)或yi<(m-n*MAD)时(本文将n值统一设置为3),可以判断其为异常点。一般经验认为短期内(1 h内)钟跳或者粗差最多发生一次,故可根据异常点是否连续,来判断其为粗差点或钟跳点[21]。
目前,IGS机构采用传统谱分析模型进行卫星钟差数据建模预报[5]。而谱分析模型存在两种形式,一种是趋势项采用一阶线性直线拟合的谱分析模型,另一种是趋势项采用二阶曲线拟合的谱分析模型。其表达式如下
 (3)
(3)
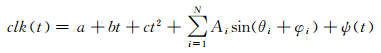 (4)
(4)
式(3)为趋势项采用一阶线性直线拟合的谱分析模型,式(4)为趋势项采用二阶曲线拟合的谱分析模型。两个公式中,a为钟差相位系数,又称钟差预报起点;b和c分别为钟速和钟漂系数;t为历元时刻;N为显著周期项数目;Ai、θi和φi分别为最小二乘正弦拟合函数的幅值、角度和相位;ψ(t)为钟差随机项成分。因为ψ(t)幅值较小且对钟差预报精度影响非常有限,故本文不对该随机项作额外研究。
就目前实时钟差产品而言,IGS提供的IGU产品是世界上精度最高且性能最稳定的产品之一,若仅仅采用上述的传统谱分析模型对超快星历钟差数据进行建模预报,其效果与IGU-P产品差不多,因而有必要从根本上对该模型的预报数据进行精度修正。
1.2 文献[21]的自适应动态预报方案设计针对钟差数据趋势项阶数难以确定及钟跳现象普遍存在的问题,文献[21]根据钟差数据不同的趋势项拟合阶数特性、不同的数据修复方式和不同的数据截取方式,有针对性地提出多种备选预报方案,从而组建成自适应动态预报模型[21]。文献[21]选取多个IGU文件依次迭代采用备选方案进行预报,并统计平均预报精度,选取精度最高的预报方案作为该颗卫星接下来需要预报的IGU文件的预报方案[21]。因最佳方案的选取可以提前确定,因而该方法可以大量减少计算量和提高效率。该最佳方案筛选和预报示意图大致如图 1所示。
图 1中,从IGU文件到预报方案这个过程中需要经过一系列的数据预处理操作。主要包括MAD法精确探测粗差和钟跳、对钟跳发生前的数据进行修复或者删除,以及消除粗差对钟差数据序列的影响等。备选方案与该预报流程的具体信息可参考文献[21]。
1.3 预报数据精度修正方案设计尽管IGS的IGU-P预报精度相对较高,但因无法满足RTPPP定位精度要求而受到科研工作人员的广泛关注。因而本文提出的精度修正方案对于提升其预报精度和提高RTPPP的定位精度具有重要参考价值。
起点偏差可以解释为IGU-P起始预报点精度与零点之间存在或多或少的偏差,因而有必要对钟差预报数据进行精度修正[4-5]。MAD法依靠钟差一阶差分后的频率数据序列可以有效探测出粗差和钟跳的位置,故本文试图对预报数据的第一个值与IGU-O最后一个观测数据进行一次差分操作来探测出精度修正的方向与大小。
本文提出的预报数据精度修正方法的公式设计如下
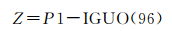 (5)
(5)
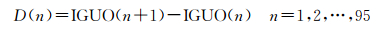 (6)
(6)
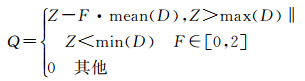 (7)
(7)
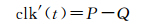 (8)
(8)
式(5)中,P1为IGU文件在所选预报模型下的第一个预报值;IGUO为IGU的观测数据部分;则Z是第一个预报值与IGU观测数据部分最后一个历元的差值。式(6)的序列D为IGU钟差观测数据的一阶差分序列,因IGU-O采样间隔为15 min,24 h共计96个数据,故序列D含有95个差分数据。式(7)为预报数据精度修正值Q的计算公式,F为精度修正放大倍数,取值范围F∈[0, 2],当Z>max(D)或者Z<min(D)时,即差值Z的大小在差分序列D范围之外时,就可以认为预报数据存在一定偏差而需要对其进行精度修正,否则偏差Q值为0。式(8)中,P为预报值,clk′(t)为对所选方案预报数据的精度修正结果[21-22]。
1.4 预报方案流程假设方案1为趋势项采用一阶线性直线拟合的谱分析模型;方案2为趋势项采用二阶曲线拟合的谱分析模型;方案3为文献[21]的自适应动态模型。
结合前面的改进策略与介绍,本文提出的高精度钟差预报修正算法流程具体如下:
(1) 读取IGU文件,获取相应的IGU-O数据和IGU-P数据。
(2) 对IGU-O数据运用MAD法精确探测粗差与钟跳位置。
(3) 方案1和方案2均采用对粗差进行剔除的操作,而对钟跳影响不考虑的策略,方案3的具体处理策略请参考文献[21]。
(4) 在上一步策略下,进行各个方案的趋势项拟合、频谱分析周期项,确定拟合系数并获取预报数据。
(5) 对上一步3个方案的预报数据作两种处理操作。第1种处理策略:不作任何精度修正;第2种处理策略:对3个方案的预报数据分别进行本文提出的精度修正操作。结合IGU-P本身的预报数据,总共可以得到7组预报数据;
(6) 对上一步的7组预报数据分别与对应预报时刻的下一个IGU文件中IGU-O数据做差,获取7组预报精度数据并保存[8];
(7) 进入下一个IGU文件建模预报,程序跳至第1步,直到所选取的文件结束,跳出该循环;
(8) 统计各个文件7组预报精度数据的平均值。
2 试验仿真结果与分析为充分体现本文方法可以独立对GPS IIR-M型卫星超快速钟差预报数据进行精度修正的作用,试验仿真数据从IGS网站(ftp://cddis.gsfc.nasa.gov)上下载,下载文件从igu18492_18.sp3到igu18500_06.sp3,共19个超快星历文件(所选文件中,Block IIR-M卫星共7颗,分别为PRN05、PRN07、PRN12、PRN15、PRN17、PRN29和PRN31)。仿真试验设计上,对这19个IGU文件分别按照前述3个方案进行建模预报,具体处理过程参考前面的预报流程。需要说明的是,IGU文件分为IGU-O部分和IGU-P部分,各占24 h,因而第1个IGU文件的IGU-P数据的参考真值应该是第2个IGU文件对应时刻的观测部分数据。最后将3个预报方案下不采用和采用本文提出的精度修正方法下产生的6组预报数据,以及IGU-P前24个历元数据分别与对应时刻上的IGU-O数据做差,得到短期预报6 h内3个预报方案方法下的7组超快速钟差预报精度数据。
对同一颗卫星的钟差预报精度采用均方根误差(RMS)进行计算,RMS计算公式有
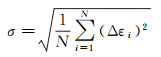 (9)
(9)
式中,N为预报历元总数,本文中N为24;Δεi为钟差预报值与相应的IGU-O参考真值之差。本文方法相对IGU-P产品的提升精度记为
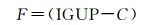 (10)
(10)
故平均精度提升幅度百分比的计算公式如下
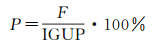 (11)
(11)
式中,F为预报方案较IGU-P产品的提升精度大小;P为提升幅度百分比;IGUP为IGU-P的预报精度;C为本文中各个方案预报的平均精度。
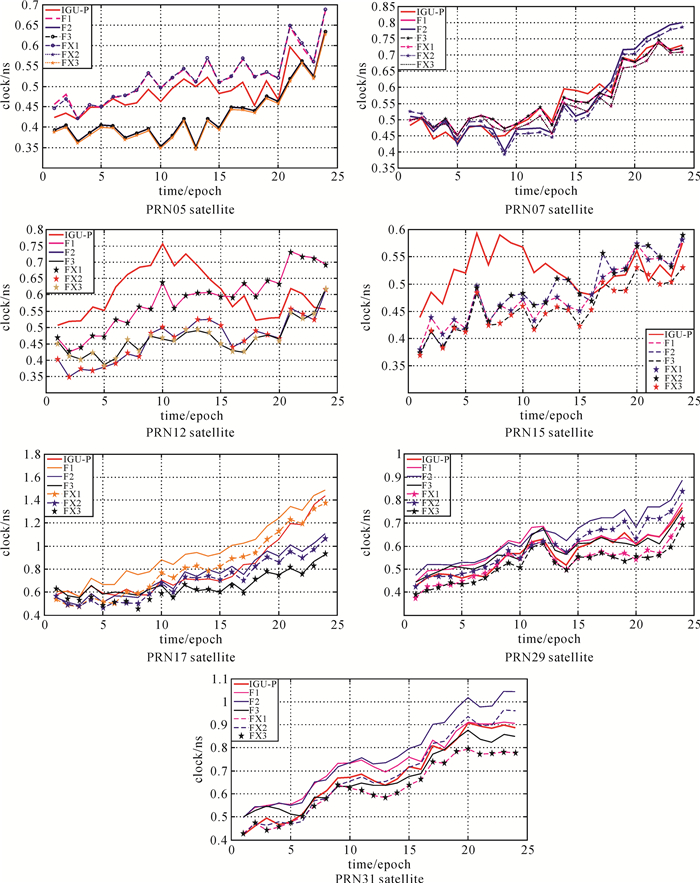
图 2为GPS IIR-M型7颗卫星在19个IGU文件迭代预报过程中的统计平均精度曲线图。表 1为GPS IIR-M型7颗卫星在19个IGU文件中超快速钟差预报6 h的统计平均精度表。图 2和表 1中各符号的含义如下:A为IGU-P;F1为方案1;F2为方案2;F3为方案3;FX1为附加精度修正的方案1;FX2为附加精度修正的方案2;FX3为附加精度修正的方案3;P1为F1提升精度百分比;P2为F2提升精度百分比;P3为F3提升精度百分比;PX1为FX1提升精度百分比;PX2为FX2提升精度百分比;PX3为FX3提升精度百分比。表 1为IIR-M型各颗卫星超快速钟差预报6 h的统计平均精度表,单位为10-9 s。
|
| 图 2 GPS IIR-M型卫星的钟差预报统计平均精度 Fig. 2 Six hours of prediction results for the 7 GPS IIR-M satellites |
| 10-9 s | ||||||||
| PRN05 | PRN07 | PRN12 | PRN15 | PRN17 | PRN29 | PRN31 | 平均水平 | |
| A | 0.494 | 0.569 | 0.609 | 0.525 | 0.839 | 0.577 | 0.698 | 0.616 |
| F1 | 0.525 | 0.570 | 0.590 | 0.482 | 0.981 | 0.605 | 0.740 | 0.642 |
| P1/(%) | -6.39 | -0.25 | 3.21 | 8.18 | -16.87 | -4.90 | -6.10 | -3.30 |
| F2 | 0.437 | 0.574 | 0.469 | 0.489 | 0.762 | 0.655 | 0.788 | 0.596 |
| P2/(%) | 11.61 | -0.92 | 23.00 | 6.86 | 9.17 | -13.63 | -13.01 | 3.30 |
| F3 | 0.437 | 0.570 | 0.468 | 0.458 | 0.672 | 0.586 | 0.683 | 0.553 |
| P3/(%) | 11.61 | -0.25 | 23.14 | 12.82 | 19.92 | -1.54 | 2.02 | 9.68 |
| FX1 | 0.526 | 0.556 | 0.588 | 0.482 | 0.864 | 0.539 | 0.636 | 0.599 |
| PX1/(%) | -6.60 | 2.24 | 3.55 | 8.18 | -2.91 | 6.58 | 8.77 | 2.83 |
| FX2 | 0.431 | 0.566 | 0.469 | 0.489 | 0.719 | 0.607 | 0.709 | 0.570 |
| PX2/(%) | 12.74 | 0.43 | 23.04 | 6.86 | 14.34 | -5.32 | -1.71 | 7.20 |
| FX3 | 0.431 | 0.556 | 0.468 | 0.458 | 0.645 | 0.524 | 0.636 | 0.531 |
| PX3/(%) | 12.74 | 2.24 | 23.25 | 12.82 | 23.17 | 9.11 | 8.77 | 13.16 |
(1) 方案1在PRN07、PRN15、PRN29和PRN31 4颗卫星的预报精度方面优于方案2,但是整体平均精度提升百分比却低于方案2。一方面说明配备Rb原子钟的IIR-M多数卫星在被分析的时段内其趋势项可以用一阶线性直线拟合,少数卫星可以用二次项曲线拟合;另一方面,相同类型原子钟在不同卫星上呈现出不同的趋势项阶数,说明钟差数据易受卫星运行环境的影响。
(2) 在不添加本文精度修正的3个方案中,方案3(F3)不论是在单颗卫星预报上,还是整体精度提升上,其精度都是最高的。这充分说明文献[21]采用的自适应动态模型对于超快速钟差的建模预报具有显著优势,也侧面论证了超快速钟差的时变特性和非线性特性。
(3) 在添加本文精度修正的3个预报方案中,除了PRN15号卫星外,其余各颗卫星相应模型的预报精度均优于不添加本文精度修正算法的对应模型,且使得添加本文修正算法的3个模型(FX1、FX2和FX3)在原有预报精度(F1、F2和F3)上可以分别提高6.13%、3.9%和3.48%,充分论证本文精度修正算法可以独立提升预报模型的精度。
(4) PRN15号卫星因为没有满足本文精度修正方法的判决条件,故其添加精度修正算法的预报曲线与不添加修正的曲线相重合。
(5) 个别卫星预报精度曲线中方案3(F3)的曲线与方案1(F1)或者方案2(F2)存在重合的情况。因为方案3为自适应动态模型,该模型中存在多种备选预报子模型,固然存在方案1和方案2的子预报模型。当自适应动态模型在筛选最佳预报模型时,如果方案1或方案2一直被选取为最佳预报方案时就会出现上述情况。
(6) 相对IGU-P的统计平均预报精度(0.616 ns),其他6种预报方法的统计平均预报精度分别为0.642 ns(F1)、0.596 ns(F2)、0.553 ns(F3)、0.599 ns(FX1)、0.570 ns(FX2)和0.531 ns(FX3)。
尽管本文提出的精度修正方法对3个方案的预报精度分别提升了6.13%、3.9%和3.48%,提升幅度有限,但是该精度修正方法却可以独立于选用的模型而提升精度,这个独立提升预报精度的作用对于我国iGMAS网站提升4系统(GPS、BDS、GLONASS、Galileo)中超快速钟差预报产品的精度具有重要参考意义。
3 总结与展望本文提出了一种针对GPS IIR-M型卫星超快星历钟差预报的高精度修正方法。首先,采用趋势项用一次项线性直线拟合的谱分析模型、趋势项用二次项曲线拟合的谱分析模型和文献[21]的自适应动态模型进行钟差建模预报;其次,分别对3个方案的预报数据进行精度修正。最后,分别对比3个方案在不采用和采用精度修正两种情况下的预报精度,从而充分验证本文提出的精度修正方法可以独立于所采用的模型而提升精度的有效性和稳定性。结合本文,笔者还需要对以下问题做作一步研究:
(1) 尽管本文提出的精度修正方法对IIR-M型卫星具有显著且稳定有效的改进作用,但是针对IIR和IIF型卫星的改进策略仍然需要作进一步研究。
(2) 本文提出的精度修正方法具有很好的改进效果,然而如何对观测数据降噪以保证IGU-O差分序列更加真实地反映精度的大小和方向,是今后研究工作的重要内容。
(3) 本文MAD法中的n值统一设置为3,至于n值对探测结果和预报精度的影响程度以及如何自适应调整n值,需要作一步研究。
(4) 本文精度修正方法存在一定的适用条件,当超快速钟差观测部分数据最后一个历元存在粗差或者钟跳时,对应的精度修正方法需要作进一步研究。
| [1] | 高成发, 高旺, 何帆. GPS实时精密单点定位理论研究与测试分析[J]. 东南大学学报(自然科学版) , 2013, 43 (S2) : 230–234. GAO Chengfa, GAO Wang, HE Fan. Research and Testing of GPS Real-Time Precise Point Positioning[J]. Journal of Southeast University (Natural Science Edition) , 2013, 43 (S2) : 230 –234. |
| [2] | 易重海, 陈永奇, 朱建军, 等. 一种基于IGS超快星历的区域性实时精密单点定位方法[J]. 测绘学报 , 2011, 40 (2) : 226–231. YI Zhonghai, CHEN Yongqi, ZHU Jianjun, et al. An Approach to Regional Real Time Precise Point Positioning Based on IGS Ultra-Rapid Orbit[J]. Acta Geodaetica et Cartographica Sinica , 2011, 40 (2) : 226 –231. |
| [3] | GAO Yang, CHEN Kongzhe. Performance Analysis of Precise Point Positioning Using Real-time Orbit and Clock Products[J]. Journal of Global Positioning Systems , 2004, 3 (1-2) : 95 –100. |
| [4] | HUANG Guanwen, ZHANG Qin, XU Guochang. Real-Time Clock Offset Prediction with an Improved Model[J]. GPS Solutions , 2014, 18 (1) : 95 –104. DOI:10.1007/s10291-013-0313-0 |
| [5] | 黄观文. GNSS星载原子钟质量评价及精密钟差算法研究[D]. 西安:长安大学, 2012. HUANG Guanwen. Research on Algorithms of Precise Clock Offset and Quality Evaluation of GNSS Satellite Clock[D]. Xi'an:Chang'an University, 2012. |
| [6] | 李征航, 黄劲松. GPS测量与数据处理[M]. 第2版 武汉: 武汉大学出版社, 2010 . LI Zhenghang, HUANG Jinsong. GPS Surveying and Data Processing[M]. 2nd ed Wuhan: Wuhan University Press, 2010 . |
| [7] | 黄观文, 张勤, 王继刚. GPS卫星钟差的估计与预报研究[J]. 大地测量与地球动力学 , 2009, 29 (6) : 118–122. HUANG Guanwen, ZHANG Qin, WANG Jigang. Research on Estimation and Prediction of GPS Satellite Clock Error[J]. Journal of Geodesy and Geodynamics , 2009, 29 (6) : 118 –122. |
| [8] | 于合理, 郝金明, 刘伟平, 等. 一种卫星钟差精度评估方法[J]. 海洋测绘 , 2014, 34 (2) : 11–13. YU Heli, HAO Jinming, LIU Weiping, et al. Method of Accuracy Assessment of Satellite Clock Error[J]. Hydrographic Surveying and Charting , 2014, 34 (2) : 11 –13. |
| [9] | 唐桂芬, 许雪晴, 曹纪东, 等. 基于通用钟差模型的北斗卫星钟预报精度分析[J]. 中国科学:物理学力学天文学 , 2015, 45 (7) : 079502. DOI:10.1360/SSPMA2015-00121 TANG Guifen, XU Xueqing, CAO Jidong, et al. Precision Analysis for Compass Satellite clock Prediction Based on a Universal Clock Offset Model[J]. Scientia Sinica Physica, Mechanica & Astronomica , 2015, 45 (7) : 079502 . DOI:10.1360/SSPMA2015-00121 |
| [10] | 黄观文, 张勤, 许国昌, 等. 基于频谱分析的IGS精密星历卫星钟差精度分析研究[J]. 武汉大学学报(信息科学版) , 2008, 33 (5) : 496–499. HUANG Guanwen, ZHANG Qin, XU Guochang, et al. IGS Precise Satellite Clock Model Fitting and Its Precision by Using Spectral Analysis Method[J]. Geomatics and Information Science of Wuhan University , 2008, 33 (5) : 496 –499. |
| [11] | SENIOR K, RAY J R, BEARD R L. Characterization of Periodic Variations in the GPS Satellite Clocks[J]. GPS Solutions , 2008, 12 (3) : 211 –225. DOI:10.1007/s10291-008-0089-9 |
| [12] | 王宇谱, 吕志平, 陈正生, 等. 卫星钟差预报的小波神经网络算法研究[J]. 测绘学报 , 2013, 42 (3) : 323–330. WANG Yupu, LV Zhiping, CHEN Zhengsheng, et al. Research on the Algorithm of Wavelet Neural Network to Predict Satellite Clock Bias[J]. Acta Geodaetica et Cartographica Sinica , 2013, 42 (3) : 323 –330. |
| [13] | 王颖, 徐波, 杨旭海. 一种利用泛函网络进行导航卫星钟差预报的方法研究[J]. 宇航学报 , 2012, 33 (10) : 1401–1406. WANG Ying, XU Bo, YANG Xuhai. Research on the Navigation Satellite Clock Error Prediction Using Functional Network[J]. Journal of Astronautics , 2012, 33 (10) : 1401 –1406. |
| [14] | 郑作亚, 党亚民, 卢秀山, 等. 附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J]. 天文学报 , 2010, 51 (1) : 95–102. ZHENG Zuoya, DANG Yamin, LU Xiushan, et al. Prediction Model with Periodic Item and Its Application to the Prediction of GPS Satellite Clock Bias[J]. Acta Astronomica Sinica , 2010, 51 (1) : 95 –102. |
| [15] | 崔先强, 焦文海. 灰色系统模型在卫星钟差预报中的应用[J]. 武汉大学学报(信息科学版) , 2005, 30 (5) : 447–450. CUI Xianqiang, JIAO Wenhai. Grey System Model for the Satellite Clock Error Predicting[J]. Geomatics and Information Science of Wuhan University , 2005, 30 (5) : 447 –450. |
| [16] | 郑作亚, 陈永奇, 卢秀山. 灰色模型修正及其在实时GPS卫星钟差预报中的应用研究[J]. 天文学报 , 2008, 49 (3) : 306–320. ZHENG Zuoya, CHEN Yongqi, LU Xiushan. An Improved Grey Model for the Prediction of Real-time GPS Satellite Clock Bias[J]. Acta Astronomica Sinica , 2008, 49 (3) : 306 –320. |
| [17] | DAVID W. Characterization, Optimum Estimation, and Time Prediction of Precision Clocks[J]. IEEE Transaction on Geoscience and Remote Sensing , 1987, 34 (6) : 647 –653. |
| [18] | VERNOTTE F, DELPORTE J, BRUNET M, et al. Uncertainties of Drift Coefficients and Extrapolation Errors:Application to Clock Error Prediction[J]. Metrologia , 2001, 38 : 325 –342. DOI:10.1088/0026-1394/38/4/6 |
| [19] | 韩敏. 混沌时间序列预测理论与方法[M]. 北京: 中国水利水电出版社, 2007 . HAN Min. The Prediction Theory and Method of Chaotic Time Series[M]. Beijing: China Water Conservancy and Hydropower Press, 2007 . |
| [20] | 许雪晴. 地球定向参数高精度预报方法研究[D]. 上海:中国科学院上海天文台, 2012. XU Xueqing. Researches on High Accuracy Prediction Methods of Earth Orientation Parameters[D]. Shanghai:Shanghai Astronomical Observatory, Chinese Academy of Sciences, 2012. |
| [21] | 何成文, 蔡成林. 基于自适应动态法的iGMAS北斗超快速钟差预报[C]//第七届中国卫星导航学术年会论文集. 长沙:[s.n.],2016. HE Chengwen, CAI Chenglin. Prediction of iGMAS Ultra-rapid Ephemeris Clock Error Based on Adaptive Dynamic Method[C]//Proceedings of the 7th China Satellite Navigation Conference. Changsha:[s.n.],2016. |
| [22] | 郭海荣. 导航卫星原子钟时频特性分析理论与方法研究[D]. 郑州:信息工程大学, 2006. GUO Hairong. Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellites[D]. Zhengzhou:Information Engineering University, 2006. |