2. 钱学森空间技术实验室, 北京100094 ;
3. 中国科学院测量与地球物理研究所, 湖北 武汉 430077 ;
4. 北京卫星导航中心, 北京 100049
2. Qian Xuesen Laboratory of Space Technology, Beijing 100094, China ;
3. Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China ;
4. Beijing Satellite Navigation Center, Beijing 100049, China
GOCE卫星[1]于2009年3月17日发射升空,2013年11月11日降落,提供的梯度数据观测点数超过1亿。围绕如何利用该颗卫星的数据进行引力场反演,受到了学者们的广泛关注[2-6],官方也陆续发布了10多个GOCE引力场模型,所采用的方法主要包括直接法、时域法和空域法[4, 7]。
不同于重力卫星CHAMP和GRACE所提供的高低卫卫跟踪和低低卫卫跟踪数据,GOCE所提供的梯度数据可直接表示为引力位的显式表达,因此非常易于建立观测方程,也非常适合构建相应的边值问题,并最终通过调和分析来得到相应的引力位系数。早在GOCE卫星论证初期,文献[8]讨论了{Γzz},{Γxz,Γyz},{Γxx-yy,2Γxy}的频谱特性,并给出了其二维傅里叶表示。文献[9]提出超定问题的准解理论,并讨论在GOCE数据处理上应用的可能性。文献[10]利用超定边值问题的准解理论,给出了引力梯度边值问题的准解和相应的球谐分析方法。文献[11]总结讨论了各类广义边值问题的最小二乘解,也给出了引力梯度作为边界条件下的解。文献[12]系统总结分析了卫星重力梯度张量的各类调和分析方法,如球面调和分析、广义轮胎调和分析、点质量调和分析、最小二乘配置调和分析。文献[13]利用不变量构建了相应的边界条件,建立了从不变量进行球谐分析的一整套方法。文献[14]推导了利用卫星梯度数据进行地球重力场求解的最小二乘法、调和分析法和最小二乘配置法的数学模型。尽管对于引力梯度的边值问题,多篇文献讨论了有关的计算方法,但将其应用于实际GOCE梯度数据处理并解算得到引力位模型的文献却并不多。文献[6]通过不变量的线性化方法得到边界条件,文献[15]则是通过坐标变换得到边界条件。从计算角度看,显然利用边值问题相对于最小二乘算法来解算位系数更易于实施,这里主要的核心问题是如何构建边界条件。
对于GOCE观测数据而言,径向梯度并不是直接的观测量,而接近径向的分量Vzz的精度低于Vxx和Vyy[16],这就为构建关于径向梯度的边界条件时如何保证其精度提出了挑战。如何在某种最优的条件下给出径向梯度的计算方法对处理GOCE实际数据是至关重要的。
文献[16]对GOCE的引力梯度观测值采用新的组合方法,有效提高了Vzz方向分量的精度,并据此对东京地震所引起的重力变化进行了讨论;文献[17]采用同样的组合[16]对南极冰川的质量变化进行了讨论。由此自然产生了这样的问题:能否得到径向梯度Vrr的最优组合?此外上述文献优化组合的前提是假设Vxx、Vyy和Vzz相互独立,但没有给出为何能作此假设。即便如此,上述文献所使用的组合方法也并不是最优的方法。
本文的目的是研究如何从GOCE梯度数据来最优地组合出径向梯度分量Vrr。第1部分是对径向梯度的计算方法进行介绍,并深入分析其误差传播规律。第2部分是对如何构建优化组合因子进行阐述,并计算得到有关因子。第3部分通过模拟数据验证上述组合因子的优越性,然后通过实际数据计算验证本文算法;最终对本文所采用的方法及其在GOCE数据处理中需要注意的问题进行了总结。
1 径向扰动梯度的构建 1.1 径向梯度的计算及其误差传播GOCE观测的梯度分量在梯度仪观测坐标系下给出,用Vij(ij=xx,yy,zz,xy,xz,yz)表示。为了得到地固坐标系下的值,可按下式进行坐标转换
 (1)
(1)
式中,R为梯度仪坐标系和地固坐标系之间的转换矩阵。由于低频误差的存在,且V12、V23精度太差无法使用,上述的坐标变换一般基于扰动分量来进行,即首先计算出梯度观测值相对参考值的差异并作低频滤波处理,然后再进行坐标变换,其中V12和V23的观测值由参考引力位计算值代替。若只考虑径向扰动梯度,现利用各坐标轴与地球径向的夹角,在非全张量观测的情况下可得到式(2)[15]
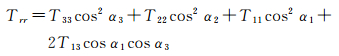 (2)
(2)
式中,Tij(ij=xx,yy,zz,xz)表示扰动梯度;T=V-U;V为实际的地球引力位;U为参考引力位;α1、α2、α3分别表示梯度坐标系x、y、z方向同地球径向之间的夹角。此时误差传播公式如下
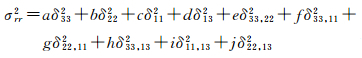 (3)
(3)
式中
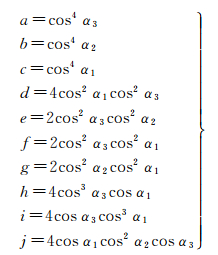 (1)
(1)
σii2(i=1,2,3)表示扰动梯度张量对角分量T11、…T22、T33的观测误差方差;σ132表示扰动梯度张量非对角分量T13的误差方差;σii,jj2(i=1,2,3;j=1,2,3;i≠j)表示扰动梯度张量对角分量之间的协方差;σii,132(i=1,2,3)表示扰动梯度张量对角分量Tii(i=1,2,3)与非对角分量T13之间的协方差。
根据文献[15],可知z方向和地球径向十分接近,夹角最大值小于1.5°。利用2010年1月1日-2010年3月1日的姿态观测数据,可得表 1。
| 项名 | 绝对值均值 | 项名 | 绝对值均值 |
| a | 9.999 4E-01 | f | 8.891 1E-05 |
| b | 2.877 6E-07 | g | 3.086 0E-08 |
| c | 4.620 5E-09 | h | 2.232 4E-02 |
| d | 1.778 2E-04 | i | 1.629 7E-06 |
| e | 1.000 6E-04 | j | 1.132 6E-06 |
由表 1可知,若各分量方差及协方差相等,则σrr2的大小主要受z方向梯度观测精度的影响,其余量的影响总和小于2.3%。但实际中各分量的方差及各分量之间的协方差并不相等,根据文献[16],在观测频带内有
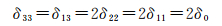 (4)
(4)
事实上,直接评估测量带宽内的误差是十分困难的,由于较少文献给出各分量之间的协方差信息,为了进一步验证σrr2的误差主要受z方向观测误差的影响,现对各分量之间的相关性作如下评估。
第1步,利用FIR向前向后带通滤波器对原始GOCE梯度数据(EGG_NOM2)相对于EIGEN5C前300阶次计算值的差值进行带通滤波处理,滤波通带为0.005~0.1 Hz,原始数据的时间段为2010年1月1日-2010年3月1日,最终得到测量通带内的观测值。采用带通滤波器的目的是消除低频误差的影响;采用参考引力位的目的是消除趋势项信息[18]。
第2步,利用滤波后的残差值计算出各量之间的相关系数,统计结果见表 2。
| 相关系数 | T11 | T22 | T33 | T13 |
| T11 | 1.000 0 | 0.070 8 | -0.139 4 | 0.005 5 |
| T22 | 0.070 8 | 1.000 0 | -0.112 8 | -0.003 9 |
| T33 | -0.139 4 | -0.112 8 | 1.000 0 | -0.009 8 |
| T13 | 0.005 5 | -0.003 9 | 0.006 7 | 1.000 0 |
由表 2可知,测量带宽内的梯度信号各分量间表现出弱相关,之所以相关原因是上述各量并不是原始的独立观测量,而是各种观测量的组合量[19],特别是姿态观测数据的使用。然而尽管非独立,上述各量之间的相关性并不强,相关系数的最大绝对值小于0.15,与T13有关的相关系数更是小于0.01。事实上,上述各量的相关性主要是由姿态观测数据的使用造成的,文献[20-21]随着姿态数据的高精度处理,其影响已经被很好地扣除,上述文献及文献[16-17]均将各分量看作独立分布。而从本文的计算可知,尽管各分量间不是严格的独立分布,但各量之间在测量带宽内的相关性较弱,由此也可得出上述各量之间的协方差要远小于各量的方差,因此式(3)中与协方差有关的项是小项,这也更加表明最终σrr2的大小主要由σ33来决定。值得强调的是,上述结论主要适用于GOCE测量带宽内,对于全频带,由于受低频有色噪声的影响,上述结论会有所不同。
1.2 最优组合因子的选取由以上分析可知,T33的精度直接影响着Trr的计算精度。在独立分布的前提下,文献[16]采用下式来重新计算得到T33
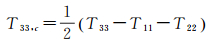 (5)
(5)
这使得T33,c的精度相比于T33提高了1.64倍,误差降低了40%[17]。这也将导致Trr精度的提升。事实上,该种组合并不是最优的组合。本文通过建立如下的极值问题来找出最优的比例因子
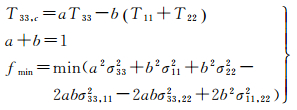 (6)
(6)
其解为
 (7)
(7)
式中,σii2(i=1,2,3)表示对应分量的方差信息;σii,jj2(i,j=1,2,3)表示对应分量之间的协方差信息。只要已知各量的误差方差及其相互之间的协方差,均可按式(7)得到最优组合因子。若各分量观测误差独立分布,解可简化为
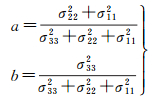 (8)
(8)
若按式(4),则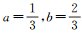
 (9)
(9)
若采用式(1),可用T33,c来代替T33。由此可知,如果各量之间为等精度观测,可得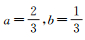
为了验证上节结论,现通过建立如下的边值问题来进行讨论
 (10)
(10)
式中,f由式(9)计算得到。该边值问题的求解可参见文献[15]
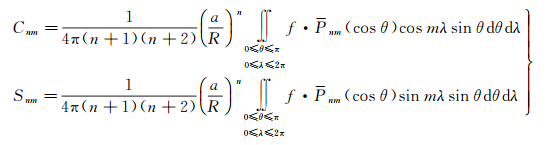 (11)
(11)
式中,Cnm、Snm表示n阶m次的引力位模型系数;Pnm为n阶m次的正规化勒让德函数;a表示地球长半轴;R表示S所在的球面的半径。
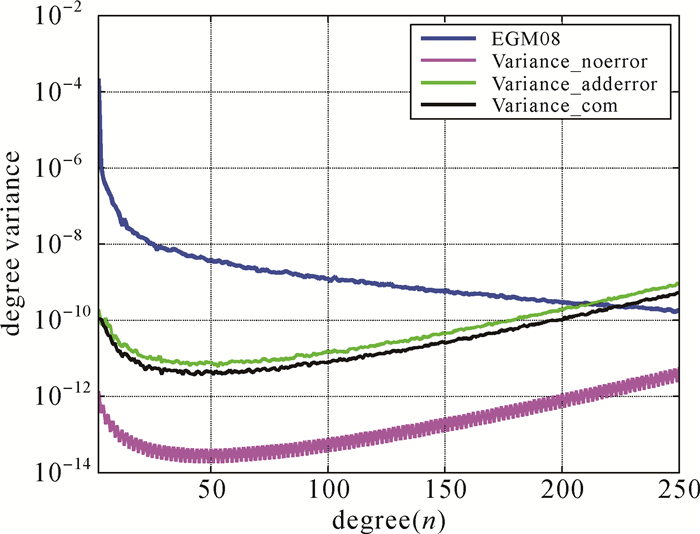
2.1 模拟数据分析首先利用EGM08模型[22]前250阶完整阶次在GOCE卫星的平均轨道高度上按经纬度25′×25′等间隔模拟出梯度张量六分量,坐标系选为地方指北坐标系,将上述模拟值作为观测值;然后按正态分布模拟随机噪声,各分量噪声均值为0,方差相对比例同式(4),其中δ0为1mE。最后构建如式(10)所示的边值问题进行引力场恢复,参考引力位为EIGEN5C。图 1给出了最终结果同引力位EGM08模型的阶方差,可视为真误差。
|
| 图 1 误差阶方差 Fig. 1 Degree variations to EGM08 |
图 1中所有结果是直接计算得到的结果而未作迭代计算,Variance_noerror表示不添加误差利用Tzz恢复得到的引力位模型的误差阶方差;Variance_adderror表示添加误差后直接利用Tzz恢复得到的引力位模型的误差阶方差;Variance_com表示添加误差后利用本文所提出的组合因子重新计算Tzz,然后利用新的Tzz恢复得到的引力位模型的误差阶方差。由该图可知,由于观测误差的存在,引力位模型恢复的精度下降明显;采用组合算法的结果相对于不采用组合算法,精度有明显提升。
2.2 实际数据计算结果分析本节主要采用实际的GOCE引力梯度数据来验证本文所述方法的优越性。如前所述,原始的梯度数据含有大量级的低频误差,必须首先对其进行处理。本文采用FIR带通滤波器进行零相位滤波[23]来处理低频噪声,参考引力位为EIGEN5C前300阶;接着采用本文所述的优化方法来重新计算梯度坐标系下的Tzz,并进一步得到Trr;然后对其数据进行格网化,方法采用反距离加权算法[24-25];最终通过解算如式(10)所述的边值问题计算得到引力位模型。该计算所采用的梯度数据为GOCE卫星Level 2所提供的EGG_NOM2,轨道数据由SST_PSO_2提供,时间段为2009年11月1日-2012年8月1日。
论文采用两种方法来恢复得到引力位,第1种是对滤波后的扰动梯度数据直接进行坐标变换,得到地方指北坐标系下的径向引力梯度数据,然后通过求解边值问题得到引力位模型,结果令为EGMQLSTTrr,可视为传统方法;第2种方法是通过论文提出的优化组合因子得到Tzz,并进一步地得到Trr,然后通过求解边值问题得到引力位模型,结果令为EGMQLSTTrrCom。为了对模型的精度进行评估,现选用两个引力位模型进行对比分析:一是EGM08模型,该模型的研制采用了多种类型的观测数据,是当前精度最高的引力位模型之一;另外一个模型是EGMD4,该模型是官方利用直接法恢复得到的第4组GOCE引力场模型,所采用数据的时段为2009年11月1日-2012年8月1日,与本文所采用数据的时间段相同。图 2、图 3分别给出了引力位模型EGMQLSTTrr、EGMQLSTTrrCom相对于EGM08模型的阶方差和大地水准面累积差异信息;图 4、图 5则分别给出了引力位模型EGMQLSTTrr、EGMQLSTTrrCom相对于EGMD4模型的阶方差和大地水准面累积差异信息。
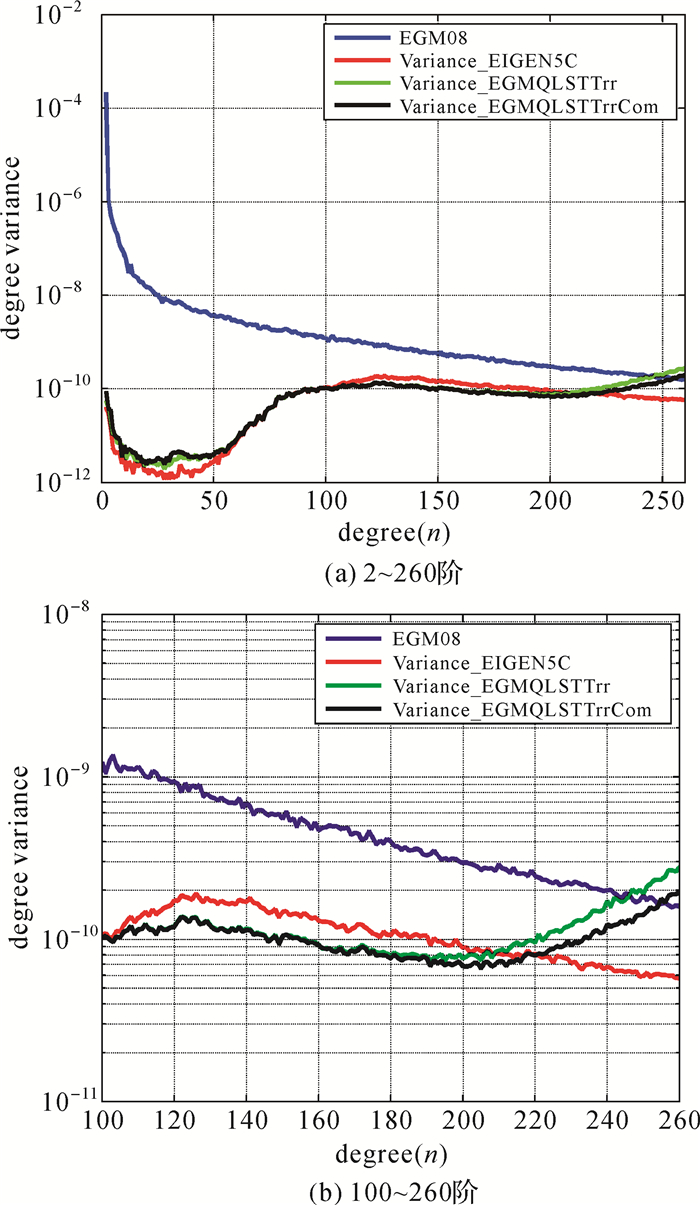
|
| 图 2 与EGM08的差异阶方差 Fig. 2 Degree variance differences between EIGEN5C, EGMQLSTTrr, EGMQLSTTrrCom and EGM08 |
|
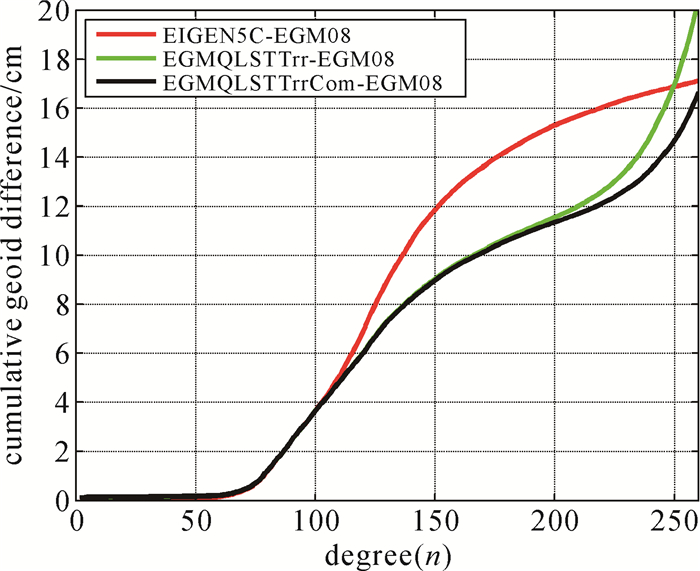
| 图 3 与EGM08大地水准面累积差异 Fig. 3 Cumulative geoid differences between EIGEN5C, EGMQLSTTrr, EGMQLSTTrrCom and EGM08 |

|
| 图 4 与EGMD4的差异阶方差 Fig. 4 Degree variance differences between EIGEN5C, EGMQLSTTrr, EGMQLSTTrrCom and EGMD4 |

|
| 图 5 与EGMD4的累积大地水准面差异 Fig. 5 Cumulative geoid differences between EIGEN5C, EGMQLSTTrr, EGMQLSTTrrCom and EGMD4 |
若将EGM08模型看作真值,由图 2(a)可知,EGMQLSTTrrCOM的有效阶数超过250阶,优于EGMQLSTTrr;由图 2(b)可知,相对于参考引力位模型EIGEN5C,EGMQLSTTrr在100~210阶精度有明显改进,EGMQLSTTrrCom则在100~220阶有明显改进,而在190~260之间的阶数,EGMQLSTTrrCom精度明显高于EGMQLSTTrr。由图 3可知,在200阶时,EGMQLSTTrr、EGMQLSTTrrCom大地水准面的精度优于EIGEN5C大约4 cm,而在200阶以后,EGMQLSTTrrCom精度明显优于EGMQLSTTrr,在250阶时,前者优于后者2 cm,在260阶时大约优于3.5 cm。由于采用了相同的观测数据,因此上述结果表明采用本文所提出的优化因子能够提高GOCE数据处理的精度,特别是对于引力场模型高阶项恢复的精度。
若将官方所发布的模型EGMD4看作真值,由图 4可知,EGMQLSTTrr、EGMQLSTTrrCom在阶数80~230明显优于参考引力位模型EIGEN5C。若按大地水准面的精度,根据图 5可知,在200阶时EGMQLSTTrr、EGMQLSTTrrCom精度相当,优于EIGEN5C大约7 cm;从180阶开始,EGMQLSTTrrCom逐渐优于EGMQLSTTrr,在250阶时精度可高约2 cm,而在260阶时,精度可高约近4 cm。上述结果与图 2、图 3的结果一致,均显示了采用优化因子计算径向梯度的优越性。
3 结 论本文从引力梯度张量观测误差及协方差统计特性出发,建立了计算径向梯度的优化方法。通过模拟数据,验证了该算法能明显地改善径向梯度相应的边界条件。
采用本文所给出的优化方法处理GOCE实际数据,得到了相应的重力场模型。与不采用优化方法所得的模型相比,优化处理后的模型在计算大地水准面时(至250阶)精度可提高约2 cm。
本文方法的前提是已知各分量的方差信息和协方差信息,而这往往是比较困难的。事实上,本文所需要知道的并不是各分量方差和协方差分量的绝对量值,而是各量的相对比例。本文采用的是文献[16]所给出的方差相对比例值(用式(4)表示),实际上也可通过迭代计算[26],利用验后方差分量估计来得到各分量的方差和协方差信息。
最后关于GOCE引力梯度观测数据进行一些说明。由于引力梯度数据在低频部分是不准确的,因此如何处理引力梯度数据的低频部分是很重要的课题,多篇文献对此进行了讨论与研究[23, 27]。若能够有效结合GOCE低频误差的处理方法和本文所述的优化方法,则可更好地提高GOCE梯度数据处理的精度。总之,由于径向梯度具有丰富的地球物理意义,因此本文的工作不仅能有助于提高GOCE重力场模型的恢复精度,而且对许多地球物理问题的研究也会有一定的帮助。
| [1] | BALMINO G, RUMMEL R, VISSER P, et al. Gravity Field and Steady-State Ocean Circulation Mission[R]. The Four Candidate Earth Explorer Core Missions. Noordwijk:ESA Publications Division, 1999. |
| [2] | REGUZZONI M, TSELFES N. Optimal Multi-step Collocation:Application to the Space-Wise Approach for GOCE Data Analysis[J]. Journal of Geodesy , 2009, 83 (1) : 13 –29. DOI:10.1007/s00190-008-0225-x |
| [3] | PAIL R, BRUINSMA S, MIGLIACCIO F, et al. First GOCE Gravity Field Models Derived by Three Different Approaches[J]. Journal of Geodesy , 2011, 85 (11) : 819 –843. DOI:10.1007/s00190-011-0467-x |
| [4] | PAIL R, GOIGINGER H, SCHUH W D, et al. Combined Satellite Gravity Field Model GOCO01S Derived from GOCE and GRACE[J]. Geophysical Research Letters , 2010, 37 (20) : L20314 . |
| [5] | YI Weiyong. An Alternative Computation of A Gravity Field Model from GOCE[J]. Advances in Space Research , 2012, 50 (3) : 371 –384. DOI:10.1016/j.asr.2012.04.018 |
| [6] | YU Jinhai, WAN Xiaoyun. Recovery of the Gravity Field from GOCE Data by Using the Invariants of Gradient Tensor[J]. Science China Earth Sciences , 2013, 56 (7) : 1193 –1199. DOI:10.1007/s11430-012-4427-y |
| [7] | RUMMEL R, GRUBER T. Product Acceptance Review (PAR)-Level 2 Product Report[R]. Noordwijk:ESA, 2012. |
| [8] | RUMMEL R, VAN GELDEREN M. Spectral Analysis of the Full Gravity Tensor[J]. Geophysical Journal International , 1992, 111 (1) : 159 –169. DOI:10.1111/gji.1992.111.issue-1 |
| [9] | 朱灼文, 于锦海. 超定大地边值问题的准解[J]. 中国科学(B辑) , 1992, 35 (6) : 697–708. ZHU Zhuowen, YU Jinhai. Pseudo-Solution on Geodetic Overdetermined Boundary Value Problems[J]. Science in China (Series B) , 1992, 35 (6) : 697 –708. |
| [10] | 罗志才. 利用卫星重力梯度数据确定地球重力场的理论和方法[D]. 武汉:武汉测绘科技大学, 1996. LUO Zhicai. The Theory and Methodology for Determining the Earth's Gravity Field Using Satellite Gravity Gradiometry Data[D]. Wuhan:Wuhan Technical University of Surveying and Mapping, 1996. |
| [11] | VAN GELDEREN M, RUMMEL R. The Solution of the General Geodetic Boundary Value Problem by Least Squares[J]. Journal of Geodesy , 2001, 75 (1) : 1 –11. DOI:10.1007/s001900000146 |
| [12] | 吴星. 卫星重力梯度数据处理理论与方法[D]. 郑州:信息工程大学, 2009. WU Xing. Theory and Methods of Satellite Gradiometry Data Processing[D]. Zhengzhou:Information Engineering University, 2009. |
| [13] | 于锦海, 赵东明. 引力梯度不变量与相关边界条件[J]. 中国科学D辑:地球科学 , 2010, 53 (5) : 781–790. DOI:10.1007/s11430-010-0014-2 YU Jinhai, ZHAO Dongming. The Gravitational Gradient Tensor's Invariants and the Related Boundary Conditions[J]. Science China Earth Sciences , 2010, 53 (5) : 781 –790. DOI:10.1007/s11430-010-0014-2 |
| [14] | 刘晓刚. GOCE卫星测量恢复地球重力场模型的理论与方法[D]. 郑州:信息工程大学, 2011. LIU Xiaogang. Theory and Methods of the Earth's Gravity Field Model Recovery from GOCE Data[D]. Zhengzhou:Information Engineering University, 2011. |
| [15] | WAN Xiaoyun, YU Jinhai. Derivation of the Radial Gradient of the Gravity Based on Non-full Tensor Satellite Gravity Gradients[J]. Journal of Geodynamics , 2013, 66 (2) : 59 –64. |
| [16] | FUCHS M, BOUMAN J, BROERSE T, et al. Observing Coseismic Gravity Change from the Japan Tohoku-Oki 2011 Earthquake with GOCE Gravity Gradiometry[J]. Journal of Geophysical Research , 2013, 118 (10) : 5712 –5721. |
| [17] | BOUMAN J, FUCHS M, IVINS E, et al. Antarctic Outlet Glacier Mass Change Resolved at Basin Scale from Satellite Gravity Gradiometry[J]. Geophysical Research Letters , 2014, 41 (16) : 5919 –5926. DOI:10.1002/2014GL060637 |
| [18] | 赫尔默特·莫里兹. 高等物理大地测量学[M]. 宁津生, 管泽霖, 译. 北京:测绘出版社, 1984:194-198. MORITZ H. Advanced Physical Geodesy[M]. NING Jinsheng, GUAN Zelin, Trans. Beijing:Surveying and Mapping Press, 1984:194-198. |
| [19] | ESA. GOCE Level 1b Products User Handbook[R]. GOCE-GSEG-EOPG-TN-06-0137. Noordwijk:ESA, 2008. |
| [20] | RUMMEL R, YI Weiyong, STUMMER C. GOCE Gravitational Gradiometry[J]. Journal of Geodesy , 2011, 85 (11) : 777 –790. DOI:10.1007/s00190-011-0500-0 |
| [21] | YI Weiyong, RUMMEL R, GRUBER T. Gravity Field Contribution Analysis of GOCE Gravitational Gradient Components[J]. Studia Geophysica et Geodaetica , 2013, 57 (2) : 174 –202. DOI:10.1007/s11200-011-1178-8 |
| [22] | PAVLIS N K, HOLMES S A, KENYON S C, et al. An Earth Gravitational Model to Degree 2160:EGM2008[C]//Presented at the 2008 General Assembly of the European Geosciences Union. Vienna:[s.n.], 2008. |
| [23] | 万晓云, 于锦海, 曾艳艳. GOCE引力梯度的频谱分析及滤波[J]. 地球物理学报 , 2012, 55 (9) : 2909–2916. WAN Xiaoyun, YU Jinhai, ZENG Yanyan. Frequency Analysis and Filtering Processing of Gravity Gradients Data from GOCE[J]. Chinese Journal of Geophysics , 2012, 55 (9) : 2909 –2916. |
| [24] | 徐新禹. 卫星重力梯度及卫星跟踪卫星数据确定地球重力场的研究[D]. 武汉:武汉大学, 2008. |
| [25] | 钟波. 基于GOCE卫星重力测量技术确定地球重力场的研究[D]. 武汉:武汉大学, 2010. |
| [26] | 万晓云, 于锦海. 极地空白对GOCE引力场恢复的影响[J]. 测绘学报 , 2013, 42 (3) : 317–322. WAN Xiaoyun, YU Jinhai. Influence of Polar Gaps on Gravity Field Recovery Using GOCE Data[J]. Acta Geodaetica et Cartographica Sinica , 2013, 42 (3) : 317 –322. |
| [27] | SCHUH W D. The Processing of Band-limited Measurements; Filtering Techniques in the Least Squares Context and in the Presence of Data Gaps[J]. Space Science Reviews , 2003, 108 (1-2) : 67 –78. |



