2. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan 430079, China
目前全球采用的高程系统有两种:一种是以大地水准面为基准面的正高系统,另一种是以似大地水准面为基准面的正常高系统。无论是采用正高系统,还是采用正常高系统,许多国家和地区的高程基准都属于局部高程基准,而且大多是利用区域平均海面来确定,从而使各个国家或地区建立的高程基准之间存在差异。如何建立全球统一的高程基准以及确定局部高程基准与全球高程基准之间的垂直偏差,是近半个世纪来最活跃的一个研究领域并有望实现。局部高程基准面与(似)大地水准面之间的垂直偏差是实现区域高程基准与全球高程基准统一的基础数据。
大地水准面是统一全球高程基准最适宜的参考面。早先,将水准椭球的正常位U0作为全球基准重力位[1],但由正常重力位U0所描述的基准面与全球平均海面有较大差异;随后又提出基于大地边值问题求解大地水准面重力位[2-3],但在求解边值问题时假设大地水准面外部无质量,并采用球近似简化计算,由此产生的误差影响可达分米甚至米级;随着卫星测高技术的发展与卫星重力探测计划CHAMP(challenging mini-satellite payload )、GRACE(gravity recovery and climate experiment)和GOCE(gravity and ocean circulation explorer)的实施,目前已经可以提供厘米级精度的平均海面高数据[4-6]与高精度的全球重力场模型[7]。因此,有学者提出联合高精度全球重力场模型和海面高模型来确定大地水准面重力位[8-10]。此时的大地水准面是Gauss-Listing定义的经典大地水准面,是与平均海面在全球范围内最佳拟合的等位面,大地水准面重力位等于一个格网化全球平均海面高模型所有格网中心点重力位的均值[11]。
我国采用的高程基准为1985国家高程基准,是由青岛验潮站1952-1979年观测的黄海平均海面利用移动平均处理得到。如果已知青岛高程零点的精确地心坐标,可以直接利用重力场模型求得该点的重力位,并将此作为我国高程基准重力位。但是,青岛高程零点的精确位置信息难以确定,我们只能获得其他地面点的位置与高程信息,即GPS/水准数据。因此,需要利用GPS/水准数据,反过来确定我国高程基准重力位[12-14]。例如,文献[15-16]联合重力场模型与GPS/水准数据分别从位理论以及高程异常差的角度确定我国1985国家高程基准重力位及我国高程基准与全球高程基准之间的垂直偏差。
本文联合重力场模型EGM2008与全国均匀分布的649个GPS/水准数据,利用异常位法、正常高反算法以及高程异常差法,求得我国1985国家高程基准与全球高程基准之间的垂直偏差,并通过加权方法改善计算结果,最后用两种方法对垂直偏差的合理性与正确性进行验证。
1 1985高程基准与全球高程基准垂直偏差 1.1 确定全球高程基准重力位W0大地水准面是全球高程基准最适宜的参考面,利用全球重力场模型、海面高模型可以确定全球平均海面重力位,加入海面地形模型改正后可以计算大地水准面重力位,大地水准面是重力等位面,可定义为
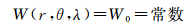 (1)
(1)
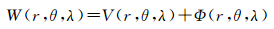 (2)
(2)
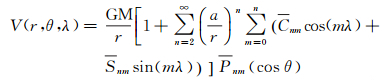 (3)
(3)
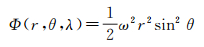 (4)
(4)
式中,(r,θ,λ)为海面P点的地心球坐标,可以根据卫星测高实际观测海面高的位置经纬度和大地高(φ,λ,h)转换得到;GM是全球重力场模型所使用的地心引力常数;a为椭球的长半轴;ω为地球自转角速度;Cn,m和Sn,m为n阶m次规格化重力位球谐系数;Pn,m(·)为规格化缔合勒让德函数。
1.2 1985国家高程基准与全球高程基准垂直偏差本文利用重力场模型联合GPS/水准数据基于异常位法、正常高反算法和高程异常差法分别计算我国高程基准与全球高程基准垂直偏差。
1.2.1 异常位法异常位法建立在Molodensky理论基础上,如图 1所示。P点为地面点,Q点为与P点对应的似地球表面点,P0点位于似大地水准面上,Q0点位于水准椭球上,PQ=P0Q0=ζ。根据Molodensky理论,Q点正常位等于P点重力位WP=UQ,P点正常高等于Q点椭球高,此时大地水准面重力位与参考椭球面正常重力位相等W0=U0,经过验潮站的平均海面与大地水准面重合,即WD=W0=U0。但实际与假设不一致,P0点(即为当前局部基准零点D)与全球基准存在偏差,即WD≠W0≠U0,因此WP≠UQ。如不考虑Q点与Q0点正常重力值之间的差异,P、Q点重力位差与P0、Q0点之间的重力位差相等,即ΔW=WP-UQ=WD-U0。

|
| 图 1 Molodensky理论示意图 Fig. 1 Schematic diagram of Molodensky theory |
我国高程基准重力位为
 (5)
(5)
我国高程基准与全球高程基准垂直偏差为
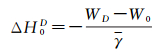 (6)
(6)
正常高反算的方法是基于高程系统与大地位数间的关系来确定的。首先联合重力场模型与GPS/水准数据计算地面点P的实际重力位WP;其次,利用P点正常高HP*与平均正常重力γP计算P点与高程起算面的大地位数即重力位差CD
 (7)
(7)
式中,平均正常重力为
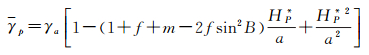 (8)
(8)
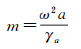 (9)
(9)
式中,f为椭球扁率; γa为椭球赤道处的正常重力;HP*为P点的正常高;a为参考椭球的长半轴;B为P点的大地纬度。从而,得到我国高程起算点的重力位WD为
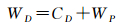 (10)
(10)
我国高程基准与全球高程基准垂直偏差为式(6)。
1.2.3 高程异常差法重力场模型可以确定全球似大地水准面高ζ,GPS/水准数据可以得到该点在局部高程基准下的高程异常值ζ′,则局部高程基准与全球高程基准之间的基准差为
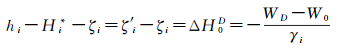 (11)
(11)
利用重力场模型确定的似大地水准面高为
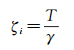 (12)
(12)
该式成立的前提条件是参考椭球与(似)大地水准面有同样的位,与地球有同样的质量,否则的话ζi和T都要加一个常数[17],忽略参考椭球与地球质量的差异,只考虑参考椭球与(似)大地水准面位的差异
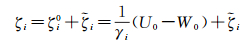 (13)
(13)
式中,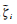
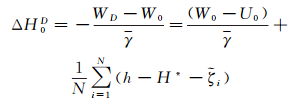 (14)
(14)
最终确定我国高程基准重力位为
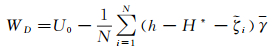 (15)
(15)
我国高程基准与全球高程基准垂直偏差为式(6)。
2 计算结果及分析 2.1 全球高程基准重力位利用高分辨率、超高阶(2190阶)重力场模型EIGEN-6C4(European improved gravity model of the Earth by new techniques)与EGM2008以及高精度全球30′×30′海面高模型MSS(mean sea surface),DNSC08 (Danish National Space Center)、DTU10 (Technical University of Denmark )、DTU13计算平均海面重力位,加入相应海面地形MDT(mean dynamic topography)改正后得到大地水准面重力位,计算结果如表 1所示。
| m2s-2 | |||||
| EGM | MSS/MSS+MDT | max | min | average | STD |
| EGM2008 | DNSC08MSS | 62 636 900.731 6 | 62 636 820.174 6 | 62 636 856.834 5 | 7.814 5 |
| DNSC08MSS+MDT | 62 636 861.808 1 | 62 636 854.534 1 | 62 636 858.159 3 | 1.114 9 | |
| DTU10 MSS | 62 636 900.726 1 | 62 636 819.748 9 | 62 636 856.412 2 | 7.919 3 | |
| DTU10 MSS+MDT | 62 636 861.815 5 | 62 636 854.589 2 | 62 636 858.188 4 | 1.098 2 | |
| DTU13 MSS | 62 636 900.726 1 | 62 636 819.748 9 | 62 636 856.412 2 | 7.919 3 | |
| DTU13 MSS+MDT | 62 636 861.465 0 | 62 636 854.951 5 | 62 636 858.188 9 | 0.968 8 | |
| EIGEN-6C4 | DNSC08MSS | 62 636 903.826 4 | 62 636 817.195 1 | 62 636 856.830 0 | 7.812 1 |
| DNSC08MSS+MDT | 62 636 861.405 7 | 62 636 854.931 7 | 62 636 858.157 5 | 1.034 2 | |
| DTU10 MSS | 62 636 903.820 9 | 62 636 816.769 4 | 62 636 856.407 7 | 7.916 9 | |
| DTU10 MSS+MDT | 62 636 861.578 4 | 62 636 854.818 9 | 62 636 858.183 4 | 1.039 2 | |
| DTU13 MSS | 62 636 903.820 9 | 62 636 816.769 4 | 62 636 856.407 7 | 7.916 9 | |
| DTU13 MSS+MDT | 62 636 861.543 1 | 62 636 854.877 2 | 62 636 858.196 7 | 0.998 6 | |
| average | mean sea level | 62 636 902.275 3 | 62 636 818.401 1 | 62 636 856.550 7 | 7.883 2 |
| geoid | 62 636 861.602 6 | 62 636 854.783 8 | 62 636 858.179 0 | 1.042 3 | |
从表 1中可知,利用不同重力场模型与海面高模型确定的平均海面重力位均值为62 636 856.550 7 m2s-2,加入海面地形改正后确定的大地水准面重力位均值为62 636 858.179 0 m2s-2,与文献[18-20]的计算结果一致。重力场模型与海面高模型的选取对重力位的确定有不同程度的影响。当海面高模型相同时,基于不同重力场模型 (EIGEN-6C4、EGM2008)计算的平均海面重力位之间约有0.05 m2s-2(约5 mm)的差异;当重力场模型相同时,基于不同海面高模型(DNCS08S、DTU10、DTU13) 计算的平均海面重力位之间约有0.4 m2s-2(约4 cm)的差异[10]。同上,大地水准面重力位受重力场模型差异的影响约为0.002 m2s-2(约0.2 mm),受海面高模型差异的影响约为0.03 m2s-2(约3 mm)。重力场模型EIGEN-6C4与EGM2008的选取对重力位的影响较海面高模型DNCS08、DTU10、DTU13的选取对重力位的影响低一个量级[10]。
2.2 我国1985国家高程基准与全球高程基准垂直偏差本文联合重力场模型EGM2008与全国均匀分布的649个GPS/水准数据,分别利用异常位法、正常高反算法以及高程异常差法,计算我国1985国家高程基准与全球高程基准之间的垂直偏差ΔH0D,计算结果如表 2所示,本文计算结果与文献[14-15, 21]计算结果一致。计算结果显示高程异常差法精度最高,正常高反算法次之,异常位法精度最差。理论上利用3种不同方法计算的垂直偏差数值应一致,但利用以上3种方法计算的垂直偏差之间最大差异为0.152 6/0.152 5 m,已达分米级(如表 2所示)。由于利用3种方法确定我国高程基准与全球高程基准之间的垂直偏差时均受重力场模型与公式截断误差的影响,且各GPS点椭球高精度较一致,因此该差异主要来自于水准数据正常高。而我国水准点正常高的获取采用的是传统的逐站传递的方式传递高程,存在传递累积误差,水准点距离高程原点越远或测站数越多累积误差越大,正常高值精度越差越不可靠,因此需要选取合理的权值来减弱低精度水准数据(正常高)对计算我国高程基准与全球高程基准之间的垂直偏的影响,使分别利用3种方法获得我国高程基准与全球高程基准之间的垂直偏差值趋于一致。本文权值的选取采用两种方法,一种是以GPS/水准点距离青岛原点的距离的倒数定权,即pi=1/D,另一种方式是根据高程倒数定权,即pi=1/H,其中D以千米为单位,H以米为单位,计算结果如表 2所示,分别为我国高程基准与全球平均海面、全球大地水准面的垂直偏差
| m | ||||
| 异常位法 | 正常高反算法 | 高程异常差法 | 最大差值 | |
| Pi=1 | 0.157 7±0.865 | 0.210 2±0.361 | 0.310 3±0.240 | 0.152 6 |
| Pi=1/D | 0.296 0±0.876 | 0.266 9±0.365 | 0.324 5±0.241 | 0.057 6 |
| Pi=1/H | 0.287 7±0.875 | 0.286 3±0.369 | 0.326 4±0.241 | 0.040 1 |
| Pi=1 | 0.324 0±0.865 | 0.376 5±0.361 | 0.476 5±0.240 | 0.152 5 |
| Pi=1/D | 0.462 2±0.876 | 0.433 1±0.365 | 0.490 7±0.241 | 0.057 6 |
| Pi=1/H | 0.453 9±0.875 | 0.452 5±0.369 | 0.492 6±0.241 | 0.040 1 |
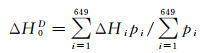 (1)
(1)
表 2上部为我国高程基准与全球平均海面间的垂直偏差,下部为我国高程基准与全球大地水准面间的垂直偏差。加权后基于3种不同的方法计算的我国高程基准与全球高程基准(全球平均海面/全球大地水准面)垂直偏差趋于一致,当权值取1/D时相互之间最大差异为0.057 6 m/0.057 6 m (约0.6 m2s-2);当权值取1/H时相互之间最大差异为0.040 1 m/0.040 1 m (约0.4 m2s-2),相较不加权时的0.152 6 m/0.152 5 m(约1.5 m2s-2)提高了一个量级,证明垂直偏差计算误差与距离和正常高存在高相关性,同时证明加权的必要性与权值选取的合理性。
本文采用两种方法来进一步验证加权后计算的垂直偏差ΔH0D的合理性与正确性。基于高程异常差法计算的垂直偏差精度最高且与异常位法、正常高反算法加权后计算的结果趋于一致,且加权前后对其计算的垂直偏差数值无影响,验证时不考虑该方法。验证方法1依据几何正常高与物理正常高差值理论值为0,即m=H-(WD-WP)/γ=0来验证,验证结果如表 3所示。由于受重力场模型误差的影响,使物理正常高与几何正常高存在一定差异,但加权后m值均保持在亚厘米级,因此本文加权的方法合理的减弱了低精度水准数据(正常高)对计算我国高程基准重力位WD的影响,从而减弱了低精度水准数据(正常高)对计算我国高程基准与全球高程基准之间的垂直偏ΔH0D的影响。
| m | |||||||||
| 权值 | 异常位法 | 正常高反算法 | |||||||
| 均值 | 最大值 | 最小值 | 标准差 | 均值 | 最大值 | 最小值 | 标准差 | ||
| Pi=1 | -0.080 | 1.098 | -1.105 | 0.361 | 0.000 | 1.028 | -1.046 | 0.361 | |
| Pi=1/D | 0.040 | 0.964 | -0.965 | 0.361 | 0.017 | 0.983 | -0.989 | 0.361 | |
| Pi=1/H | 0.036 | 0.960 | -0.969 | 0.361 | 0.035 | 0.958 | 0.970 | 0.361 | |
验证方法2依据理论是我国青岛高程原点重力位为一常数,尽管会随着数据选取区域大小以及数量多少在一定范围有所波动,但变化值应较小,因此计算的我国高程基准与全球高程基准垂直偏差值波动也应较小。本文将GPS/水准点与青岛高程原点(120°19′ E,36°05′ N,72.260)之间的距离D与该点正常高H依据不同的阈值划分,计算我国高程基准与全球高程基准(全球平均海面/全球大地水准面)之间的垂直偏差变化情况,计算结果如表 4所示。
| m | ||||||||||||
| 阈值范围 | 异常位法 | 正常高反算法 | 异常位法 | 正常高反算法 | ||||||||
| 不加权 | 加权 | 不加权 | 加权 | 不加权 | 加权 | 不加权 | 加权 | |||||
| D | <1000 km(188) | 0.412 7 | 0.379 5 | 0.292 1 | 0.305 8 | 0.578 9 | 0.545 7 | 0.458 3 | 0.471 9 | |||
| <1500 km(342) | 0.426 3 | 0.396 8 | 0.288 9 | 0.301 2 | 0.592 4 | 0.563 0 | 0.455 1 | 0.467 4 | ||||
| <2000 km(474) | 0.363 6 | 0.373 0 | 0.268 4 | 0.290 2 | 0.529 7 | 0.539 1 | 0.434 6 | 0.456 4 | ||||
| <2500 km(541) | 0.273 4 | 0.336 9 | 0.248 1 | 0.281 3 | 0.439 5 | 0.503 1 | 0.414 2 | 0.447 5 | ||||
| <3000 km(580) | 0.228 9 | 0.320 3 | 0.226 8 | 0.273 3 | 0.395 0 | 0.486 5 | 0.392 9 | 0.439 4 | ||||
| <3500 km(629) | 0.170 7 | 0.300 7 | 0.216 1 | 0.268 9 | 0.336 8 | 0.466 8 | 0.382 2 | 0.435 0 | ||||
| <4000 km(649) | 0.157 7 | 0.296 0 | 0.210 2 | 0.266 9 | 0.324 0 | 0.462 2 | 0.376 5 | 0.433 1 | ||||
| 最大差值 | 0.255 0 | 0.100 8 | 0.081 9 | 0.038 9 | 0.183 9 | 0.100 8 | 0.081 8 | 0.038 8 | ||||
| H | <200 m(204) | 0.300 9 | 0.285 3 | 0.309 4 | 0.288 4 | 0.467 1 | 0.451 4 | 0.475 6 | 0.454 6 | |||
| <500 m(297) | 0.321 4 | 0.286 9 | 0.294 6 | 0.288 2 | 0.487 5 | 0.453 1 | 0.460 8 | 0.454 3 | ||||
| <1000 m(383) | 0.362 5 | 0.288 6 | 0.276 3 | 0.287 6 | 0.528 7 | 0.454 7 | 0.442 5 | 0.453 7 | ||||
| <2000 m(516) | 0.385 6 | 0.289 8 | 0.260 2 | 0.287 0 | 0.551 7 | 0.456 0 | 0.426 3 | 0.453 2 | ||||
| <3000 m(551) | 0.338 8 | 0.289 2 | 0.233 3 | 0.286 6 | 0.505 0 | 0.455 3 | 0.399 5 | 0.452 7 | ||||
| <4000 m(592) | 0.267 1 | 0.288 3 | 0.207 4 | 0.286 2 | 0.433 2 | 0.454 5 | 0.373 5 | 0.452 3 | ||||
| <5000 m(649) | 0.157 7 | 0.287 7 | 0.210 2 | 0.286 3 | 0.324 0 | 0.453 9 | 0.376 5 | 0.452 5 | ||||
| 最大差值 | 0.227 9 | 0.004 5 | 0.102 0 | 0.002 2 | 0.227 7 | 0.004 6 | 0.102 1 | 0.002 3 | ||||
结果显示,加权后我国高程基准与全球高程基准垂直偏差随阈值的变化较不加权时变化较小,进一步验证权值的选取以及加权后计算的垂直偏差的合理性与正确性。当变量为距离D时,加权前后异常位法计算的我国高程基准与全球平均海面垂直偏差数值之间最大差异由0.255 0 m (约2.6 m2s-2)改善为0.100 8 m(约1 m2s-2);正常高反算法由0.081 90 m(约0.8 m2s-2)改善为0.039 8 m (约0.4 m2s-2)。当变量为正常高H时,加权前后异常位法计算的垂直偏差数值之间最大差异由0.227 9 m (约2.3 m2s-2cm)改善为0.004 5 m (约0.05 m2s-2);正常高反算法由0.102 0 m (约1 m2s-2)改善为0.002 2 m (约0.02 m2s-2)。我国高程基准与全球大地水准面垂直偏差数值随阈值的变化而波动的范围加权后也明显减小,当阈值为D时垂直偏差最大波动值分别由0.183 9 m (约1.8 m2s-2) 改善为0.100 8 m (约1 m2s-2);由0.081 8 m (约0.8 m2s-2)改善为0.038 8 m (约0.4 m2s-2);当阈值为H时,垂直偏差最大波动值分别由0.227 7 m (约2.3 m2s-2)改善为 0.004 6 m (约0.05 m2s-2);由0.102 1 m (约1 m2s-2) 改善为0.002 3 m (约0.02 m2s-2)。两者相比当权值为pi=1/H时比pi=1/D时计算的垂直偏差精度更高。
综上所述,取加权后分别利用异常位法、正常高反算法与高程异常差法计算的垂直偏差的均值作为我国高程基准与全球高程基准的垂直偏差,计算结果如表 5所示。我国85高程基准高于平均海面0.298 0 m,高于全球大地水准面0.464 2 m。
| m | ||||
| 异常位法 | 正常高反算法 | 高程异常差法 | 垂直偏差平均值 | |
| Pi=1/D | 0.296 0 | 0.266 9 | 0.324 5 | 0.298 0 |
| Pi=1/H | 0.287 7 | 0.286 3 | 0.326 4 | |
| Pi=1/D | 0.462 2 | 0.433 1 | 0.490 7 | 0.464 2 |
| Pi=1/H | 0.453 9 | 0.452 5 | 0.492 6 | |
3 结 论
利用不同重力场模型(EGM2008、EIGEN-6C4)和海面高模型(DNSC08、DTU10、DTU13)计算了平均海面重力位均值为62 636 856.550 7 m2s-2,加入相应的海面地形模型改正后计算的大地水准面重力位均值为62 636 858.179 0 m2s-2。
分别利用3种不同的方法确定了我国1985国家高程基准与全球高程基准(全球平均海面/全球大地水准面)之间的垂直偏差,其中高程异常差法精度最高,正常高反算法次之,异常位法精度最差。利用以上3种方法计算的垂直偏差之间存在差异,最大差异为0.152 6 m/0.152 5 m(约1.5 m2s-2)。该差异主要来自于正常高,本文采取合理的加权的方法来减弱低精度正常高数据对计算垂直偏差的影响。改善结果为,当Pi=1/D时最大差异为0.057 6 m /0.057 6 m (约0.6 m2s-2);当Pi=1/H时最大差异为0.040 1 m/0.040 1 m (约0.4 m2s-2)。
两种验证方法计算表明:加权后计算的m=H-(WD-WP)/γ值更趋于0,且加权后计算的垂直偏差受外界影响明显小于加权前。
如果将3种方法计算的6组垂直偏差数据取均值作为我国高程基准与全球高程基准的垂直偏差,可以得到我国85高程基准高于全球平均海面0.298 0 m,高于全球大地水准面0.464 2 m。
| [1] | HIPKIN R. Defining the Geoid by W=W0≡U0:Theory and Practice of a Modern Height System[C]//TZIAVOS I N. Proceedings of the 3rd Meeting of the International Gravity and Geoid Commission. Thessaloniki:[s.n.], 2003:367-377. |
| [2] | RUMMEL R, TEUNISSEN P. Height Datum Definition, Height Datum Connection and the Role of the Geodetic Boundary Value Problem[J]. Bulletin Géodésique , 1988, 62 (4) : 477 –498. DOI:10.1007/BF02520239 |
| [3] | HECK B, RUMMEL R. Strategies for Solving the Vertical Datum Problem Using Terrestrial and Satellite Geodetic Data[M]//SüNKEL H, BAKER T. Sea Surface Topography and the Geoid. New York:Springer, 1990:116-128. |
| [4] | ANDERSEN O B, KNUDSEN P. DNSC08 Mean Sea Surface and Mean Dynamic Topography Models[J]. Journal of Geophysical Research:Oceans , 2009, 114 (C11) : C11001 . DOI:10.1029/2008JC005179 |
| [5] | ANDERSEN O, KNUDSEN P, STENSENG L. The DTU13 MSS (Mean Sea Surface) and MDT (Mean Dynamic Topography) from 20 Years of Satellite Altimetry[M]//RIZOS C. International Association of Geodesy Symposia. Berlin:Springer, 2015:1-10. |
| [6] | 金涛勇, 李建成, 姜卫平, 等. 基于多源卫星测高数据的新一代全球平均海面高模型[J]. 测绘学报 , 2011, 40 (6) : 723–729. JIN Taoyong, LI Jiancheng, JIANG Weiping, et al. The New Generation of Global Mean Sea Surface Height Model Based on Multi-altimetric Data[J]. Acta Geodaetica et Cartographica Sinica , 2011, 40 (6) : 723 –729. |
| [7] | PAVLIS N K, HOLMES S A, KENYON S C, et al. The Development and Evaluation of the Earth Gravitational Model 2008(EGM2008)[J]. Journal of Geophysical Research:Solid Earth , 2012, 117 (B4) : B04202 . |
| [8] | ARDALAN A, GRAFAREND E, KAKKURI J. National Height Datum, the Gauss:Listing Geoid Level Value w0 and Its Time Variation w0 (Baltic Sea Level Project:Epochs 1990.8, 1993.8, 1997.4)[J]. Journal of Geodesy , 2002, 76 (1) : 1 –28. DOI:10.1007/s001900100211 |
| [9] | ČUNDERLÍK R, TENZER R, MIKULA K. Realization of WHS Based on Gravity Field Models Free of Dependencies on Local Vertical Datums[M]//RIZOS C, WILLIS P. Earth on the Edge:Science for a Sustainable Planet. Berlin:Springer, 2014, 139:551-559. |
| [10] | ČUNDERLÍK R, MINARECHOVÁ Z, MIKULA K. Realization of WHS Based on the Static Gravity Field Observed by GOCE[M]//MARTI U. Gravity, Geoid and Height Systems. Switzerland:Springer International Publishing, 2014:211-220. |
| [11] | 晁定波, 申文斌, 王正涛. 确定全球厘米级精度大地水准面的可能性和方法探讨[J]. 测绘学报 , 2007, 36 (4) : 370–376. CHAO Dingbo, SHEN Wenbin, WANG Zhengtao. Investigations of the Possibility and Method of Determining Global Centimeter-level Geoid[J]. Acta Geodaetica et Cartographica Sinica , 2007, 36 (4) : 370 –376. |
| [12] | GRIGORIADIS V N, KOTSAKIS C, TZIAVOS I N, et al. Estimation of the Reference Geopotential Value for the Local Vertical Datum of Continental Greece Using EGM08 and GPS/Leveling Data[M]//MARTI U. Gravity, Geoid and Height Systems. Switzerland:Springer International Publishing, 2014:249-255. |
| [13] | KOTSAKIS C, KATSAMBALOS K, AMPATZIDIS D. Estimation of the Zero-height Geopotential Level WoLVD in a Local Vertical Datum from Inversion of Co-Located GPS, Leveling and Geoid Heights:A Case Study in the Hellenic Islands[J]. Journal of Geodesy , 2012, 86 (6) : 423 –439. DOI:10.1007/s00190-011-0530-7 |
| [14] | TENZER R, VATRT V, ABDALLA A, et al. Assessment of the LVD Offsets for the Normal-Orthometric Heights and Different Permanent Tide Systems-a Case Study of New Zealand[J]. Applied Geomatics , 2011, 3 (1) : 1 –8. DOI:10.1007/s12518-010-0038-5 |
| [15] | 焦文海, 魏子卿, 马欣, 等. 1985国家高程基准相对于大地水准面的垂直偏差[J]. 测绘学报 , 2002, 31 (3) : 196–200. JIAO Wenhai, WEI Ziqing, MA Xin, et al. The Origin Vertical Shift of National Height Datum 1985 with Respect to the Geoidal Surface[J]. Acta Geodaetica et Cartographica Sinica , 2002, 31 (3) : 196 –200. |
| [16] | 郭海荣, 焦文海, 杨元喜. 1985国家高程基准与全球似大地水准面之间的系统差及其分布规律[J]. 测绘学报 , 2004, 33 (2) : 100–104. GUO Hairong, JIAO Wenhai, YANG Yuanxi. The Systematic Difference and Its Distribution between the 1985 National Height Datum and the Global Quasigeoid[J]. Acta Geodaetica et Cartographica Sinica , 2004, 33 (2) : 100 –104. |
| [17] | 海斯卡涅W A, 莫里兹H. 物理大地测量学[M]. 卢福康, 胡国理, 译. 北京:测绘出版社, 1979:74-78. HEISKANEN W A, MORITZ H. Physical Geodesy[M]. LU Fukang, HU Guoli, Trans. Beijing:Surveying and Mapping Press, 1979:74-78. |
| [18] | BURŠA M, KOUBA J, KUMAR M, et al. Geoidal Geopotential and World Height System[J]. Studia Geophysica et Geodaetica , 1999, 43 (4) : 327 –337. DOI:10.1023/A:1023273416512 |
| [19] | BURŠA M, KOUBA J, MVLLER A, et al. Determination of Geopotential Differences between Local Vertical Datums and Realization of a World Height System[J]. Studia Geophysica et Geodaetica , 2001, 45 (2) : 127 –132. DOI:10.1023/A:1021860126850 |
| [20] | BURŠA M, KENYON S, KOUBA J, et al. The Geopotential Value W0 for Specifying the Relativistic Atomic Time Scale and a Global Vertical Reference System[J]. Journal of Geodesy , 2007, 81 (2) : 103 –110. DOI:10.1007/s00190-006-0091-3 |
| [21] | 翟振和, 魏子卿, 吴富梅, 等. 利用EGM2008位模型计算中国高程基准与大地水准面间的垂直偏差[J]. 大地测量与地球动力学 , 2011, 31 (4) : 116–118. ZHAI Zhenhe, WEI Ziqing, WU Fumei, et al. Computation of Vertical Deviation of Chinese Height Datum from Geoid by Using EGM2008 Model[J]. Journal of Geodesy and Geodynamics , 2011, 31 (4) : 116 –118. |


