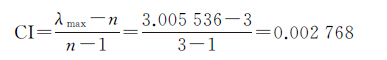居民地是人类活动的中心场所,在政治、经济和文化等方面都有重要意义[1]。居民地是地图上最重要的要素之一,在地图上的面积载负量占有较大的比例,所以居民地自动综合的质量,直接影响着地图的科学性和使用价值。居民地自动综合最基本的方法是选取,即从大量的居民地中选取一部分,这一部分居民地既能符合地图用途和地图比例尺的需求,又能反映制图区域地理特点,还要满足地图主题的需要。
目前,居民地选取方法多以点群形式来讨论,主要有空间比率算法、分布系数算法、重力模型算法[2]以及圆增长算法[3],这些方法可以保证综合后专题信息的正确性,但是仍可能导致几何信息的错误传输;基于遗传算法的选取方法[4],从全局最优化的角度进行选取,能够较好地保持密度分布特征;基于Circle原理的选取方法[5-8],考虑到保持居民地的集群特征,以居民地自身的形状和周围相关的居民地要素作为重要性指标进行居民地选取;基于Kohonen网络的选取方法[7],能够有效保持点群目标空间分布的特征,但只考虑了点与点之间相对位置所构成的点群空间特征的保持;基于Voronoi图的选取方法[8-10],顾及居民地的属性特征和几何分布,较好地保持了居民地信息传输的正确性。上述方法主要考虑了居民地自身及其与周围居民地之间的几何关系,但居民地选取往往除了需要考虑自身及周围同类要素因素之外,如能考虑其与其他种类要素(如道路等)的关联关系,并加以定量描述,则选取结果将会更加符合实际需求。
层次分析法(AHP)是一种定性和定量相结合的、系统化、层次的分析方法[11]。基于上述考虑,本文结合居民地行政等级、面积大小和位置特征等因素对居民地重要性的影响,把层次分析法引入居民地自动综合中来,利用影响单个居民地重要性的因素(包括来自道路网等不同要素集的影响因素)来构建其重要性层次结构模型,通过比较和计算,可得出这些属性的影响居民地重要性的权重,定量地描述这些属性之间的相互关系,然后利用开方根模型计算出新编图上居民地的数量,最终据此完成居民地的选取。该方法将决策者的思维过程条理化、数量化,便于计算,容易被人们所接受,同时所需的定量化数据较少,对涉及居民地重要性的因素及其内在关系分析得更为透彻、清楚。
同时,大比例尺居民地综合主要以合并和典型化为主,中小比例尺中,居民地综合主要以选取为主。因此,本方法主要针对中小比例尺居民地综合展开。
1 影响居民地重要性因素选取是制图综合最重要和最基本的方法。它主要解决选取多少,选取哪些和怎么选取的问题[12]。通过构建居民地层次结构模型,利用层次分析法定量计算出地图上单个居民地的重要性程度,以解决选取哪些的问题,再通过开方根模型进行定额选取来解决选取多少的问题。
居民地在地图上的取舍,是居民地制图综合的一个极其重要的任务。居民地的取舍主要是依赖于居民地的主要标志及其总的价值意义[13]。制图人员根据居民地的重要性进行选取,优先选取重要的居民地。居民地是否重要,则是通过居民地的行政等级、位置特征、面积大小等属性反映。居民地的大小,行政等级等属性在地图上都很直观地显示出来,专家在进行选取的时候很容易就凭借这些属性选取出重要的居民地,同时,在选取的时候,还需要考虑到居民地的位置特征的影响。居民地的位置特征在地图上也是可以通过人眼来识别出来的,在计算机中,则需要通过居民地与其他地物之间进行空间分析来判定居民地的位置特征重要性。
1.1 居民地的面积居民地面积的大小在地图上是居民地取舍的最直观的影响因素,制图员在进行选取的时候一般都会舍弃面积较小的居民,保留面积较大的居民地。计算居民地面积的方法一般采用解析法,其数学模型如下
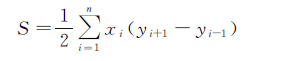 (1)
(1)
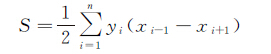 (2)
(2)
式中,当i=1时,i-1=n;i=n时,i+1=1;xi-1、xi、xi+1表示居民地的横坐标;yi-1、yi、yi+1表示居民地的纵坐标。
1.2 居民地的行政等级居民地面积不是决定其重要性的唯一因素。居民地的行政等级对居民地的取舍有最重要、最明显的影响。若行政等级越高,则选取的可能性也就越大;而行政等级越低,舍弃的可能性也就越大[14]。
根据居民地要素的行政级别体系,可将其划分为省级行政区、地级行政区、县级行政区和乡级行政区等。省级行政区包括省、自治区、直辖市、特别行政区4类;在省级行政区下包括副省级市、地级市、自治州等;在地级行政区下又包括市辖区、县、县级市等;在县级行政区下包括乡、镇等;最后是以村为主的行政等级。
综上所述,本文将居民地按其行政级别进行了划分,并对其进行数值化(表 1)。
| 行政等级名称 | 等级 |
| 直辖市/省/自治区/特别行政区 | 6 |
| 副省级市 | 5 |
| 地级市/自治州 | 4 |
| 市辖区/县/县级市/自治县 | 3 |
| 乡/镇 | 2 |
| 村 | 1 |
以上行政等级都是指其政府所在地,而非一般意义上的居民地。另外,某些特殊的居民地(某些反映政治、经济地域重要性的居民地)则应该单独标记出来并设置较高的等级。
1.3 居民地的位置特征除了居民地面积、等级外,还需要突出居民地的位置特征,特别是处在道路关键节点、交通枢纽等区域的居民地,其重要性会更加显著。居民地要素的位置重要性特征可以地图上的其他要素(如道路网、水系等)凸显出来,如一个居民地要素处于道路交通枢纽的位置,则其重要性程度较大,反之,居民地为独立地物,周围无道路网与之相连或相邻,则其重要性程度相对较小。若居民地要素处于较为重要的水系附近,则其重要性程度也为重要。因此,在判断居民地要素位置特征重要性时,需要通过其相关联的其他地物要素来计算出居民地要素的重要性程度。考虑到文本试验数据为北方某地区的居民地要素,其水系相对较少,因此本文主要介绍道路网对居民地位置特征的影响,水系对居民地位置特征的影响,其原理与方法同道路网对居民位置特征的影响相类似,本文就不再专门介绍。
在地图上,道路与居民地是具有强关联关系的制图要素[15-16]。居民地的位置特征重要性主要以道路网为依据,一个居民地连接的道路越多,则表明该居民地为重要的交通枢纽,应该保留。将道路网与居民地进行空间关系分析,在属性中增加邻近道路加权来描述居民地对象状态,计算公式为
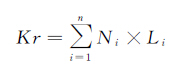 (3)
(3)
式中,Kr为最终的道路等级加权;Ni为邻近道路中到的第i级道路数量;Li为第i级道路对应的权重数。
获取的流程如下:①根据道路编码将道路进行等级化分类;②设定一定阈值对居民地要素生成缓冲区;③进行缓冲区分析记录与缓冲区相交的道路;④对记录进行统计分析,即统计相交道路中各等级道路数量,然后根据加权计算公式计算该居民地的道路等级加权。
基于缓冲区分析的居民地重要性判断,是通过空间分析获取空间信息来补充居民地属性信息不足的一种方法,该方法能够在当前地理要素信息表达模式下,通过空间分析获取尽可能多的居民地空间信息,综合评价居民地的重要性,对于提高居民地的选取准确性具有一定的意义。
居民地的取舍主要是依赖于居民地的重要性程度,影响居民地重要性程度的因素包括很多,如居民地的行政等级、位置特征、面积大小等。在没有确定统一尺度下,人们对于事物的认识总是通过两两比较来进行的,层次分析法计算的重要性是以影响因子两两作对比,然后构建判断矩阵计算其权值,这与人在判断物体重要性的时候也是通过两两对比的方式判断哪一个因素影响程度更大相符合,而且制图综合的人为主观性比较强,在进行对地物进行取舍的时候也是要考虑影响该地物要素的重要性因子,然后再判断是否进行取舍。因此通过层次分析法构建的判断矩阵计算出的权重对于居民地的重要性来说,更符合人的认知方式。
2 层次分析法原理层次分析法是把复杂的问题按其主次或者支配关系分组而形成有序的递阶层次结构,使之条理化;然后根据对一定客观现实的判断就每一层次的相对重要性给予定量表示,利用数学方法确定表达每一层中所有元素的相对重要性权值;最后通过分析排序结果来解决所考虑的问题的一种决策思维方式[17]。一般情况,一个层次分析结构模型可用图 1表示。
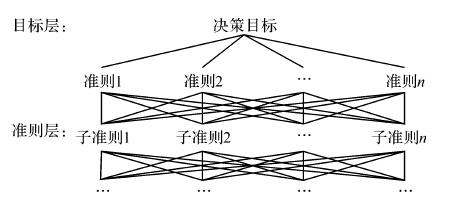
|
| 图 1 层次分析结构模型 Fig. 1 The model of hierarchical structure |
层次分析的基本计算过程有:构造判断矩阵、计算权重系数、一致性检验等[18]。
2.1 构造判断矩阵对准则层的影响因子,根据相对重要性,依据经验和知识进行两两对比,构造判断矩阵,相对重要性标度采用1~9分别表示重要性相同、较重要、明显重要、强烈重要、极端重要等。构建的判断矩阵B=(aij)m×n,其中:aij=1/aji。
2.2 计算权重系数对于判断矩阵B,计算满足Bx=λmaxx的最大特征根λmax和特征向量x,x的分量即为相应元素的权值。判断矩阵最大特征值和特征向量一般采用和积法来求解。
2.3 一致性检验为了检验判断矩阵的有效性,需要进行一致性检验。一致性指标CI为
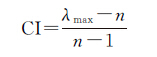 (4)
(4)
当判断矩阵具有完全一致性时,λmax=n,即CI=0。 为了检验矩阵是否具有满意的一致性,需将CI与平均随机一致性指标RI(表 2)进行比较。
对于一、二阶判断矩阵,只是形式上的,因此定义一、二阶判断矩阵总是完全一致的,当时n>2,计算一致性比例CR
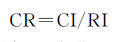 (5)
(5)
若CR><0.1时,判断矩阵满足一致性标准,否则需对判断矩阵进行调整。
3 试验与分析以北方某地区1∶100 000的地图数据为例,对本文方法进行验证。图 2(a)为1∶100 000居民地与交通图,图 2(b)为1∶100 000面状居民地要素图。
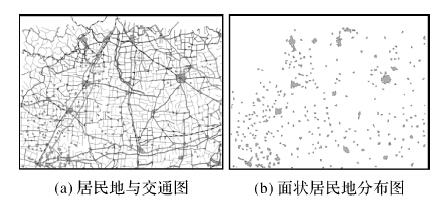
|
| 图 2 某地区试验数据图 Fig. 2 The experimental data of some district |
3.1 基于层次分析法的居民地自动选取步骤
本文采用层次分析法进行居民地自动选取的具体步骤如下:
3.1.1 数据标准化为了消除变量不同量纲差异的影响,原始数据通常都需要进行标准化处理。从居民地属性信息中提取出居民地的行政等级,位置特征、面积大小等信息,构造属性数据矩阵:X=(xij),在计算之前先对数据标准化处理,得到矩阵
 (6)
(6)
式中,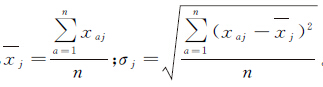
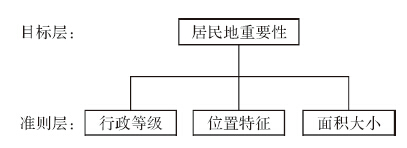
根据上述分析,建立如图 3所示的层次分析模型。
|
| 图 3 居民地重要性层次析分析模型 Fig. 3 The analytic hierarchy model of habitation importance |
如图 3所示,目标层的居民地重要性为A,准则层的居民地的行政等级、位置特征及居民地的面积大小分别用B1、B2、B3表示。在进行居民地的选取时,需要考虑准则层的因素对居民地重要性的影响。居民地的行政等级对居民地要素的取舍有最重要,最明显的影响。在同一行政等级下的居民地要素,则需要考虑其位置特征和面积大小的影响。当居民地要素处于相对重要的交通枢纽时,即便其相对面积较小,其重要性相对较大,在选取时应予以保留。因此,居民地的行政等级的要比位置特征重要一点,位置特征要比面积大小重要一点,根据层次分析法判断矩阵的构造原理及其重要性数值的含义,居民地重要性判断构造矩阵见表 3。
3.1.1 计算权值
计算判断矩阵B的特征向量为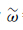
由式(4)计算一致性指标
由于n=3,从随机一致性指标表中得RI=0.58,因此可以计算出一致性比例CR=0.004 772<0.1,因此认为判断矩阵具有满意的一致性,不需要对其进行调整。
3.1.5 计算单个居民地的重要性
因此单个居民地的重要性为:S=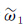
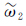
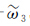
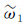

采取层次分析法计算出居民地的重要性排序后,本文采用开方根模型来确定居民地选取的个数,开方根模式由德国制图学家特普费尔(F. Topfer)提出的一种建立在经验规律上的数学模型[19-20]。开方根模式的公式为
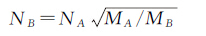 (7)
(7)
式中,NA为资料图要素数量;NB新编图上选取要素的数量;MA资料图比例尺分母;MB新编图比例尺分母。
利用开方根模型计算出新编地图上居民地要素的个数,然后按照层次分析法计算的居民地的重要性进行选取,得到新编地图上的居民地。
原比例尺地图上居民地的个数为307,由式(7)计算出新编地图上的居民地应选取的数量见表 4。
| 地图比例尺 | 居民地数量 |
| 1∶100 000 | 307 |
| 1∶250 000 | 194 |
本文采用层次分析法和基于面积选取方法对试验数据分别进行了选取,结果如图 4所示。
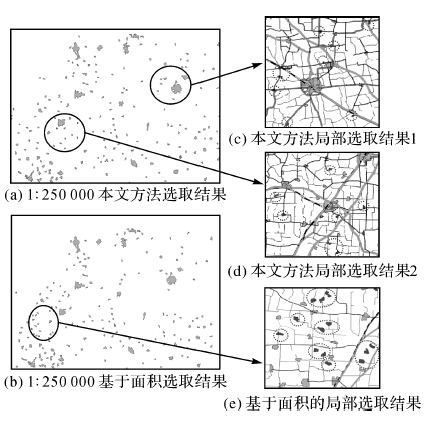
|
| 图 4 居民地自动选取结果对比图 Fig. 4 The comparison diagram of habitation auto-selection |
其中,图 4(a)是采用层次分析法选取的结果,图 4(b)是基于面积选取的结果,图 4(c)、4(d)、4(e)为局部选取结果图(其中圈出的居民地为两种方法部分选取结果的不同之处)。
从整体形态上看,本文方法选取的结果分布密度较为均匀,如图 4(a)所示,而面积法的选取结果部分地区过于密集,有些区域过于稀疏,整体密度分布不均匀,如图 4(b)所示。
从细节上看,本文方法选取的居民地要素顾及了居民地所处位置的重要性程度,保留了即便面积相对较小,但处于交通枢纽位置的居民地要素,如图 4(c)、4(d),而基于面积的选取的结果中保留了较多的居民地面积相对较大,但其位置不重要的居民地要素,如图 4(e)所示。
3.2 试验分析(1) 居民地的选取实质上是多种原因相互关联相互制约的过程,本文方法将这些因素构建层次关联,用数学的方法定量描述出它们之间的关系,用于评价居民地的重要性程度,选取的结果顾及多种因素的相互影响。
| 本文方法 | 面积法 | |
| 选取(143+51) | 删除(51+62) | |
| 选取(143+51) | 143(两方法均选取) | 51(本方法选取,面积法删除) |
| 删除(51+62) | 51(本方法删除,面积法选取) | 62(两方法均删除) |
从1∶100 000比例尺的原始数据(数量为307)新编到1∶250 000比例尺时,地图上居民地选取的数量为194个,删除的居民地要素为113个,其中有143组居民地数据使用两种方法选取的结果相同,有62组居民地要素都删除,有51组居民地数据选取的结果不同,(选取数量对比见表 5)。其中选取的143组居民地数据的行政等级、面积大小和行政等级均相对较大,选取的结果一致;而对于51组选取结果不同的数据,因为本文方法选取的居民地要素顾及要居民地要素的行政等级和所处的位置重要性程度,保留了即便面积相对较小,但其行政等级和位置相对重要的居民地,而基于面积的选取保留了较多的居民地面积相对较大,而其位置不重要的居民地要素。
从本文方法与面积法产生歧义的51组不同选取结果中提取如表 8所示的典型数据进行分析,从部分居民地重要性(表 6)和部分居民地局部特征(图 5)可以看出:对于选取结果相同的143组居民地要素(如表 6中的“廊坊市”和“高碑店市”),其影响居民地重要性的因子值相对来说均较大,因此毫无疑问是应该选取的;对于不同的51组居民地数据,采用层次分析法选取的结果(如表 6和图 5中的“易县”、“张坊镇”)对于面积相对较小的居民地要素,由于考虑到居民地的行政等级和位置特征等因素的影响,在选取时予以保留;对比表 6中后6组数据可以看出,当行政等级一致时,居民地的位置特征重要性的对居民地选取的影响要比居民地面积大小的影响程度大,如“大十三里”和“磁家务”这两个居民地所处于重要的交通枢纽位置,即便其面积相对较小,在进行选取的时候应该予以保留,由表 6中的后4组居民地要素数据可以看出,居民地要素的面积相对较大,然后其行政等级和位置特征均不重要,因此在选取的时候应该删除。
| 名称 | 行政等级 | 位置特征 | 面积大小 | 重要性 | |
| 本文方法 | 面积法 | ||||
| 廊坊市 | 4 | 13.1 | 23 698 514 | 1 | 1 |
| 高碑店市 | 4 | 8.4 | 13 108 008 | 3 | 4 |
| 易县 | 3 | 2.1 | 324 847.1 | 21 | 300 |
| 张坊镇 | 2 | 4 | 561 483.1 | 33 | 234 |
| 大十三里 | 1 | 1.6 | 551 834.8 | 117 | 242 |
| 磁家务 | 1 | 1.3 | 554 648.1 | 127 | 239 |
| 芦村 | 1 | 0.2 | 730 313.7 | 274 | 128 |
| 流井 | 1 | 0.2 | 625 189.1 | 282 | 193 |
| 南连 | 1 | 0 | 795 083.8 | 297 | 108 |
| 尚垡 | 1 | 0 | 706 103 | 299 | 142 |
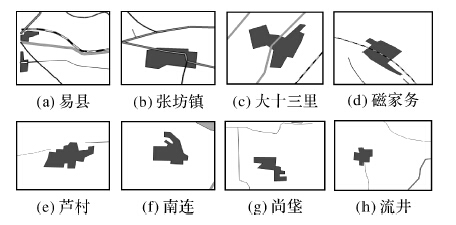
|
| 图 5 部分居民地局部位置特征图 Fig. 5 The partial location characteristic of part habitation |
综上所述,本文方法综合考虑到居民地行政等级、位置特征、面积大小等因素之间的关联,选取的结果较好地保留了一些位置特殊(如交通枢纽处)但面积相对较小的居民地,删除了一些面积相对较大,但是行政等级和位置不重要的居民地。
(2) 考虑到面积法的选取参数过于单一,本文将基于层次分析法的居民地自动选取的结果与人工综合选取的结果进一步作了对比,对比结果如图 6所示。

|
| 图 6 自动选取结果与人工综合选取结果对比 Fig. 6 The result comparison between auto-selection and human generalization |
从图 6的对比来看,采用本文方法选取的结果在整体形态和分布密度上与人工综合选取的结果保持了较高的一致性。从细节上看,本文选取的结果与人工综合选取的结果仍存在一些差异,由1∶100 000的资料图到1∶250 000的新编图,居民地要素选取的个数为194,其中有23组居民地要素的选取结果不同(图中圆圈为部分选取结果不同的居民地要素),人工综合选取时,虽然也综合考虑到居民地要素的行政等级、面积大小、位置特征等因子的影响,但人为主观性较强,对于部分居民地要素的重要性程度的决策判断与基于层次分析法定量计算的重要性程度有细微的差别。但就图 6中两种选取的结果的整体对比而言,采用层次分析法的居民地自动选取方法与人工综合结果是整体符合的,能够较好地反映制图专家的作业经验。
4 总 结居民地的选取主要是解决两个问题:一是选取多少的问题,二是选取哪些的问题。影响居民地选取的因素是相互关联相关约束的,以往的方法主要考虑了居民地自身及其与周围居民地之间的几何关系。但居民地选取往往除了需要考虑自身及周围同类要素因素之外,如能考虑其与其他种类要素(如道路、水系等)的关联关系,并加以定量描述,则选取结果将会更加符合实际需求。本文采用层析分析法,将这些影响居民地重要性的因素构建层次结构模型,并计算出其对应的权重,综合评价地图上居民地要素的重要性程度。通过计算可以看出将层次分析法应用于居民地重要性计算中的权值分配是切实可行的。该方法定量地计算出地图上居民地的重要性程度,较好地解决了居民地选取中选取哪些的问题。利用开方根模型进行的定额选取是根据选取前后地图比例尺和原地图上的居民地数量计算出新编地图上的居民地个数,能够有效地解决选取多少的问题,完成居民地的自动选取,选取结果基本符合选取原则。
| [1] |
王家耀.
普通地图制图综合原理[M]. 北京: 测绘出版社, 1992 .
WANG Jiayao. Principles of Cartographic Generalization of Map[M]. Beijing: Surveying and Mapping Press, 1992 . |
| [2] | LANGRAN G E, POIKER T K. Integration of Name Selection and Name Placement[C]//Proceedings of the 2nd International Symposium on Spattat Data Handling. Seattle: [s.n.],1986:50-64. |
| [3] | MARC V K, RENE V O. Efficient Settlement Selection for Interactive Display[C]//Proceedings of Auto-Carto 13: ACSM/ASPRS Annual Convention Technical Papers. Seattle: [s.n.],1997:287-296. |
| [4] |
邓红艳, 武芳, 钱海忠, 等. 基于遗传算法的点群目标选取模型[J].中国图象图形学报,2003, 8 (8) : 970 –976 .
DENG Hongyan, WU Fang, QIAN Haizhong, et al. A Model of Point Cluster Selection Based on Genetic Algorithms[J]. Journal of Image and Graphics,2003, 8 (8) : 970 –976 . |
| [5] |
钱海忠, 武芳, 邓红艳. 基于CIRCLE特征变换的点群选取算法[J].测绘科学,2005, 30 (3) : 83 –85 .
QIAN Haizhong, WU Fang, DENG Hongyan. A Model of Point Cluster Selection with Circle Characters[J]. Science of Surveying and Mapping,2005, 30 (3) : 83 –85 . |
| [6] |
钱海忠, 刘颖, 张琳琳, 等. 基于圆特征的地图要素自动综合算法研究[J].海洋测绘,2005, 25 (1) : 14 –17 .
QIAN Haizhong, LIU Ying, ZHANG Linlin, et al. Map Generalization Algorithm Research Based on Circle Characters[J]. Hydrographic Surveying and Charting,2005, 25 (1) : 14 –17 . |
| [7] |
蔡永香, 郭庆胜. 基于Kohonen网络的点群综合研究[J].武汉大学学报(信息科学版),2007, 32 (7) : 626 –629 .
CAI Yongxiang, GUO Qingsheng. Points Group Generalization Based on Konhonen Net[J]. Geomatics and Information Science of Wuhan University,2007, 32 (7) : 626 –629 . |
| [8] |
艾廷华, 刘耀林. 保持空间分布特征的群点化简方法[J].测绘学报,2002, 31 (2) : 175 –181 .
AI Tinghua, LIU Yaolin. A Method of Point Cluster Simplification with Spatial Distribution Properties Preserved[J]. Acta Geodaetica et Cartographica Sinica,2002, 31 (2) : 175 –181 . |
| [9] |
闫浩文, 王家耀. 基于Voronoi图的点群目标普适综合算法[J].中国图象图形学报,2005, 10 (5) : 633 –636 .
YAN Haowen, WANG Jiayao. A Generic Algorithm for Point Cluster Generalization Based on Voronoi Diagrams[J]. Journal of Image and Graphics,2005, 10 (5) : 633 –636 . |
| [10] |
郭庆胜.
地图自动综合理论与方法[M]. 北京: 测绘出版社, 2002 .
GUO Qingsheng. Theory and Method of Automatic Map Generalization[M]. Beijing: Surveying and Mapping Press, 2002 . |
| [11] | SAATY T L. The Analytic Hierarchy Process. The Analytic Hierarchy Process[M]. New York: McGraw Hill, 1980 . |
| [12] |
盛文斌. 散列式居民地的自动选取研究[D]. 郑州:信息工程大学, 2010. SHENG Wenbin.Research on Automated Selection of Hash-style Habitation[M]. Zhengzhou: Information Engineering University, 2010. |
| [13] |
王辉连. 居民地自动综合的智能方法研究[D]. 郑州:信息工程大学, 2005. WANG Huilian.Research on Intelligent Method for Automatic Generalization of Habitation[D]. Zhengzhou: Information Engineering University, 2005. |
| [14] |
温婉丽. 基于知识的居民地地图自动综合的研究[D]. 西安: 长安大学, 2006. WEN Wanli.Research on Automatic Generalization of Habitation Based on Knowledge[D]. Xi'an: Chang'an University, 2006. |
| [15] | GUO Min, QIAN Haizhong, WANG Xiao, et al. A New Road Network Selection Approach Based on the Importance Criteria of Spatial Interactive Relationship[C]//Proceedings of the 21st International Conference on Geoinformatics. Kaifeng, China: IEEE, 2013:1-5. |
| [16] |
王红, 李霖, 张晓通, 等. 数字地图制图中居民地和道路关系处理[J].辽宁工程技术大学学报(自然科学版),2010, 29 (1) : 40 –43 .
WANG Hong, LI Lin, ZHANG Xiaotong, et al. Handling of Relationship between Residents and Roads in Digital Cartography[J]. Journal of Liaoning Technical University (Natural Science),2010, 29 (1) : 40 –43 . |
| [17] |
邬伦, 刘瑜, 张晶, 等.
地理信息系统--原理、方法和应用[M]. 北京: 科学出版社, 2001 .
WU Lun, LIU Yu, ZHANG Jing, et al. Geographic Information System: Theory, Method and Application[M]. Beijing: Science Press, 2001 . |
| [18] |
朱长青, 史文中.
空间分析建模与原理[M]. 北京: 科学出版社, 2006 .
ZHU Changqing, SHI Wenzhong. Modeling and Principle of Spatial Analysis[M]. Being: Science Press, 2006 . |
| [19] |
何宗宜.
地图数据处理模型的原理与方法[M]. 武汉: 武汉大学出版社, 2004 .
HE Zongyi. Elements and Methods of Model for Cartographical Data Processing[M]. Wuhan: Wuhan University Press, 2004 . |
| [20] |
王桥, 吴纪桃. 制图综合方根规律模型的分形扩展[J].测绘学报,1996, 25 (2) : 104 –109 .
WANG Qian, WU Jitao. Fractal Transformation of Square Root Model in Cartographic Generalization[J]. Acta Geodaetica et Cartographica Sinica,1996, 25 (2) : 104 –109 . |