拓扑关系是指拓扑变换下的拓扑不变量,对于空间数据处理和空间分析具有重要的意义。拓扑关系描述方法一直是国内外研究的热点。目前,拓扑关系描述主要有基于逻辑的公理化拓扑理论和传统的数学拓扑两大类方法,其中最有代表性的是RCC(区域连接演算)形式化模型[1-2]和4IM(四交集模型)/9IM(九交集模型)[3-4],另外还有许多学者提出的改进方法[5-7]。其中,点集拓扑法建立在点集拓扑理论基础之上,具有简洁和完备的特点,并且具有维度无关性,广泛应用于拓扑关系描述。
空间带洞面状对象是一类常见的空间对象,其拓扑关系描述方法也有一些成果。4IM/9IM区分了8种面/面拓扑关系[3-4],基于Voronoi图的拓扑关系描述模型区分了18种面/面拓扑关系[7],虽然上述3种拓扑关系模型能够区分一些拓扑关系,但是对带洞拓扑关系的描述仍不够详细,基于Voronoi图的拓扑关系描述模型还存在计算相对复杂的问题。文献[8]将空间带洞对象A和B的拓扑关系描述为:A的整体和B的整体、A的整体和B的每一个洞、A的每一个洞和B的整体、A的每一个洞和B的每一个洞之间的拓扑关系,然而,对于具有多个空洞的对象,该方法较为复杂。此外,简单面目标与带孔洞面目标间的拓扑关系[9-12]、带双洞区域与简单区域间的拓扑关系[13-14]、凹形区域和带单洞区域间的拓扑关系的拓扑关系[15]、双嵌套区域与简单区域间的拓扑关系[16]、互相包含洞的区域与简单区域间的拓扑关系[17],也有一些研究进展。然而,上述研究限制了洞的个数,并没有针对带任意多个洞的面状对象。文献[18]提出了一种扩充矩阵的维数,研究内部带有空洞的复杂不确定区域间的拓扑关系,但是并没有证明拓扑关系完备性。文献[19-20]提出了D9交集模型,研究带洞面状对象之间拓扑关系,然而,D9交集模型需要反复编码和解码,较为复杂。
综上所述,空间带洞面状对象之间的拓扑关系描述已经有一些研究成果,但是仍存在拓扑关系描述不够详细、拓扑关系描述和计算复杂度较高等诸多问题。为此,本研究针对带任意多个洞的面状对象之间的拓扑关系描述问题展开论述。
1 基于点集拓扑理论的带洞面状对象描述 1.1 集合的内部、边界和外部定义基于点集拓扑理论,给出拓扑空间给定集合的内部、外部和边界的定义[21]。
定义1:设X是一个拓扑空间,A⊂X。如果A是点x∈X的一个邻域,即存在X中的一个开集V使得x∈V⊂A,则称点x是集合A的一个内点。集合A的所有内点构成的集合称为集合A的内部,记为Ao。
定义2:设X是一个拓扑空间,A⊂X。点x∈X,如果满足条件:在x的任何一个邻域U中,U∩A=φ,则称x是集合A的一个外部点。集合A的全体外部点构成的集合称为集合A的外部,记为A-。
定义3:设X是一个拓扑空间,A⊂X。点x∈X,如果满足条件:在x的任何一个邻域U中既有A中的点又有A-中的点,即既有U∩A≠φ又有U∩A-≠φ,则称x是集合A的一个边界点。集合A的全体边界点构成的集合称为集合A的边界,记为∂A。
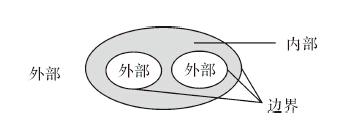
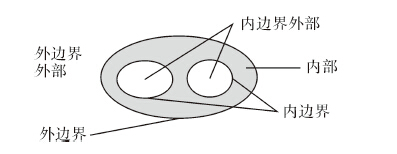
1.2 带洞面状对象定义及性质带洞面状对象为二维空间中的平面,有1个外边界、0到多个内边界组成,每个内边界形成面上的空洞,组成面的任何两个边界都不相交。边界用环来表达,其中,外边界称为外环,内边界称为内环。基于点集拓扑理论,描述了带洞面状对象的内部、边界和外部(图 1)。
|
| 图 1 带洞面状对象的内部、边界和外部 Fig. 1 Interior,boundary and exterior of region with holes |
本研究涉及的带洞面状对象可以包含多个洞,且满足以下性质。
性质1:带洞面状对象是一个二维连通闭子集,其内部为内边界和外边界之间的区域。
性质2:带洞面状对象的内环严格在外环的内部,即内环的边界与外环的边界不能出现相交、相切或者包含等情况。
性质3:带洞面状对象的内环之间不相交。
图 2中显示了3种无效的带洞的面状对象,其中,图 2(a)中空间对象内部不连通,不满足性质1;图 2(b)中内环与外环相切,不满足性质2;图 2(c)中内环与内环相交,不满足性质3。

|
| 图 2 无效的带洞面状对象 Fig. 2 Invalid regions with holes |
2 带洞面状对象间的拓扑关系模型 2.1 简单面状对象拓扑关系描述
9IM是基于点集拓扑理论,广泛应用于拓扑关系描述的一种模型。如果空间对象A和B的内部、边界和外部分别用Ao、∂A、A-和Bo、∂B、B-表示,则9IM的表现形式如式(1)所示
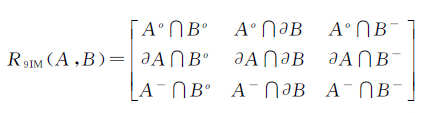 (1)
(1)
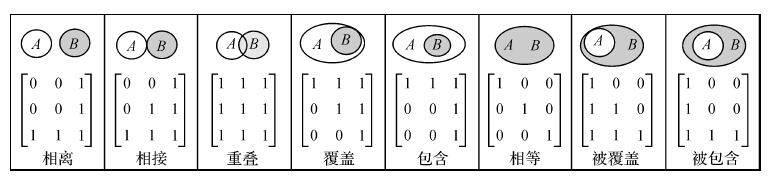
式中,元素的取值可以为{0,1},分别表示{空集,非空集}。简单面/面之间存在8种拓扑关系:{相离,相接,重叠,覆盖,包含,相等,被覆盖,被包含}。图 3描述了简单面/面之间的8种拓扑关系,并给出了相应的9IM矩阵。
|
| 图 3 简单面/面空间拓扑关系描述 Fig. 3 Representation of spatial topological relationship between simple regions |
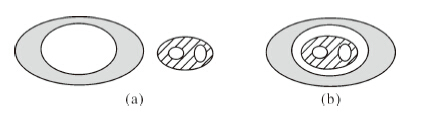
虽然9IM模型能够较好地描述简单对象间的拓扑关系,但是对于复杂对象间的拓扑关系,9IM模型的区分能力则比较有限。图 4中列出了两种拓扑关系,但是9IM都描述为相离关系。由于描述能力的限制,9IM无法区分图 4(a)和图 4(b)的拓扑关系。
|
| 图 4 9IM无法区分的两种相离关系 Fig. 4 Two disjoint topological relations that cannot be distinguished by 9IM |
2.2 25交集模型及其性质
由于9IM无法细致地描述带洞面状对象之间的拓扑关系,究其原因主要是9IM模型主要面向简单空间对象,而带空洞面状对象远比简单对象复杂。为了研究带洞面状对象的拓扑关系,有必要对带洞面状对象进一步细分。与简单面状对象相比,带洞面状对象外部分为相互独立的两部分:外边界之外的部分和内边界之内的部分;带洞面状对象边界也可以分为相互独立的两部分:外边界和内边界。因此,笔者将带洞面状对象分为5部分:内部、外边界、内边界、外边界外部、内边界外部(图 5)。
|
| 图 5 带洞面状对象的空间剖分 Fig. 5 Identification of region with holes using point set topology |
为了克服9IM在描述带洞面状对象拓扑关系方面存在问题,本研究提出一种25IM(25 intersection model,25交集模型),即5×5的矩阵模型。如果带洞面状对象A和B的内部、外边界、内边界、外边界外部、内边界外部分别用Ao、∂AE、AI、A-E、A-I和Bo、∂BE、∂BI、B-E、B-I表示,则25IM可以表示为式(2)
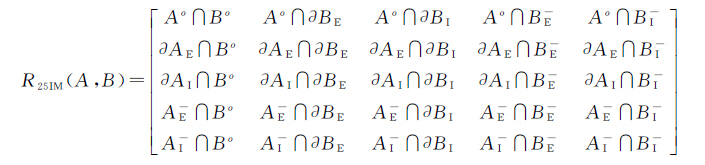 (2)
(2)
式中,元素的取值为{0,1},分别表示{空集,非空集}。如果元素的值即可以取0,也可以取1,则标记为“*”。
25IM能够细致地表达带洞面状对象之间的拓扑关系,理论上能够区分225种拓扑关系,但并不是所有的拓扑关系都有意义。为此,定义了一些规则来排除不符合逻辑的拓扑关系。
规则1:带洞面状对象A与B的外边界外部一定相交,如式(3)所示
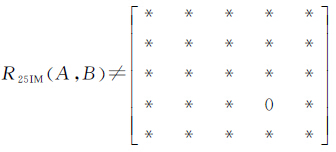 (3)
(3)
证明:设带洞面状对象A和B所在的子空间为X,如果A和B中至少有一个等于子空间X,或者A∪B=X,则空间对象的外部不相交。因为,(Ao∪∂AE∪∂AI∪A-I)∪A-E=X和(Bo∪∂BE∪∂BI∪B-I)∪B-E=X,如果A=X或者B=X或者A∪B=X,则A-E∩B-E=∂。因为,A⊂X,而且B⊂X,并且(A∪B)⊂X,所以A与B的外边界外部一定相交。
规则2:带洞面状对象A的内部、外边界、内边界、外边界外部、内边界外部,至少与B的内部、外边界、内边界、外边界外部、内边界外部的一部分相交,反之亦然,如式(4)所示
 (4)
(4)
证明:设带洞面状对象A和B所在的子空间为X。因为,Ao⊂X、AE⊂X、∂AI⊂X、A-E⊂X、A-E⊂X,所以,Ao∩X≠φ、∂∂AE∩X≠φ、∂∂AE∩X≠φ、A-E∩X≠φ、A-E∩X≠φ。因为,Bo∪BE∪BE∪B-E∪B-E=X,则Ao∩(Bo∪BE∪BE∪B-E∪B-E)≠φ、∂AE∩(Bo∪BE∪BE∪B-E∪B-E)≠φ、∂AE∩(Bo∪BE∪BE∪B-E∪B-E)≠φ、A-E∩(Bo∪BE∪BE∪B-E∪B-E)≠φ、A-E∩(Bo∪BE∪BE∪B-E∪B-E)≠φ,带洞面状对象A的内部、外边界、内边界、外边界外部、内边界外部,至少与B的内部、外边界、内边界、外边界外部、内边界外部的一部分相交。反之,B的内部、外边界、内边界、外边界外部、内边界外部,至少与A的内部、外边界、内边界、外边界外部、内边界外部的一部分相交。
规则3:如果带洞面状对象A的内部与B的外边界外部相交,则A的外边界和B的外边界外部相交;反之亦然。同理,如果带洞面状对象A的内部与B的内边界外部相交,则A的外边界与B的内边界外部相交;反之亦然,如式(5)所示
 (5)
(5)
证明:设带洞面状对象A和B所在的子空间为X。如果Ao∩B-E≠∧,则∃a⊂Ao ∧ a B-E。因为规则1成立,则∃b A-E∧ b⊂B-E。子集a和b位于∂AE的两侧,而a和b是连通的,所以A的外边界与B的外边界外部相交。其他情况,可以类似证明。
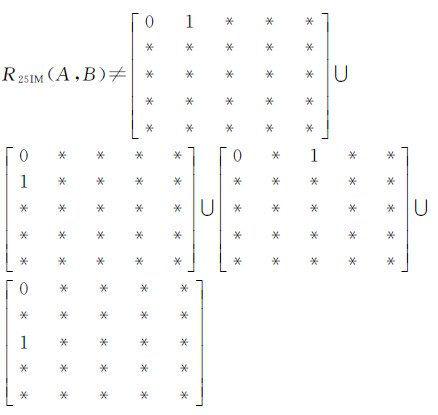
规则4:如果带洞面状对象A的内部与B的内部不相交,则A的内/外边界和B的内部不相交;反之亦然(证明过程类似于规则3的证明),如式(6)所示
 (6)
(6)
规则5:如果带洞面状对象A的内部与B的外边界相交,则A的内部与B的外边界外部相交;反之亦然。同理,如果带洞面状对象A的内部与B的内边界相交,则A的内部与B的内边界外部相交;反之亦然(证明过程类似于规则3的证明),如式(7)所示
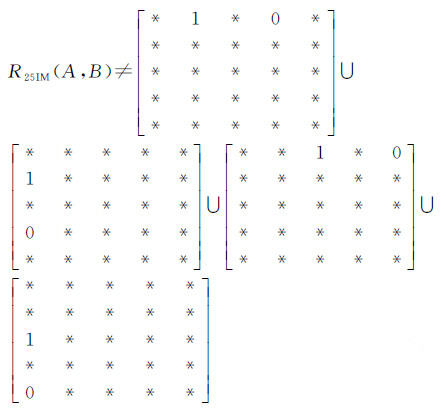 (7)
(7)
规则6:如果带洞面状对象A的内部与B的内部、外边界外部相交,则A的内部与B的外边界相交;反之亦然。同理,如果带洞面状对象A的内部与B的内部、内边界外部相交,则A的内部与B的内边界相交;反之亦然,如式(8)所示
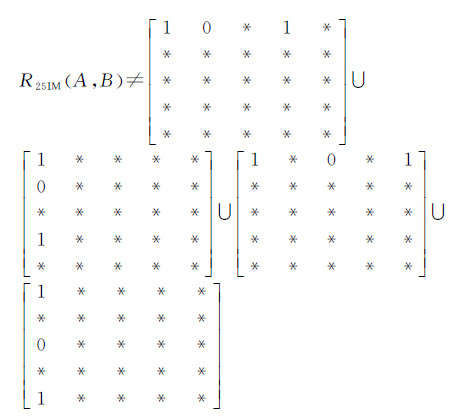 (8)
(8)
证明:设带洞面状对象A和B所在的子空间为X。如果Ao∩Bo≠φ∧Ao∩B-E≠φ,则∃a⊂Ao ∧ a Bo ∧ ∃b Ao ∧ b B-E。子集a和b位于∂BE的两侧,而a与b是连通的,所以A的内部与B的外边界相交。其他情况,可以类似证明。
规则7:如果带洞面状对象A的内/外边界与B的内/外边界均不相交,则至少存在A的内/外边界与B的内/外边界外部相交或者A的内/外边界外部与B的内/外边界相交;反之亦然,如式(9)所示
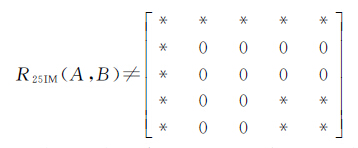 (9)
(9)
证明:设空间目标A和B所在的子空间为X。如果(∂A-E∪∂A-E)∩(∂B-E∪B-E)=φ,则(∂A-E∪∂A-E)∩(Bo∪B-E∪B-E)≠φ ∧ (B-E∪B-E)∩(Ao∪A-E∪A-E)≠φ。如果(∂A-E∪∂A-E)∩(B-E∪B-E)=φ ,则(∂A-E∪∂A-E)∩Bo≠φ,可以推导出:A B,并且(A-E∪A-E)∩(∂B-E∪B-E)≠φ。
规则8:如果带洞面状对象A的内部与B的内部不相交,则至少存在A的内/外边界与B的内/外边界外部相交或者A的内/外边界外部和B的内/外边界相交;反之亦然(证明过程类似于规则7的证明),如式(10)所示
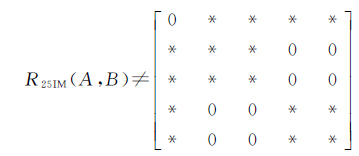 (10)
(10)
基于25IM,可以细致地描述带洞空间对象之间的拓扑关系。在图 6至图 13中,带洞面状对象A和B分别用颜色和网纹进行填充。相离、相接、重叠、覆盖、包含、相等、被覆盖和被包含关系分别表示如下:
2.3.1 相离关系相离关系表示空间对象A与B在空间上是相离的,相离关系的定义为式(11)。基于25IM,可以区分3种不同类型的相离关系(图 6)
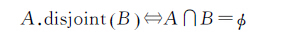 (11)
(11)
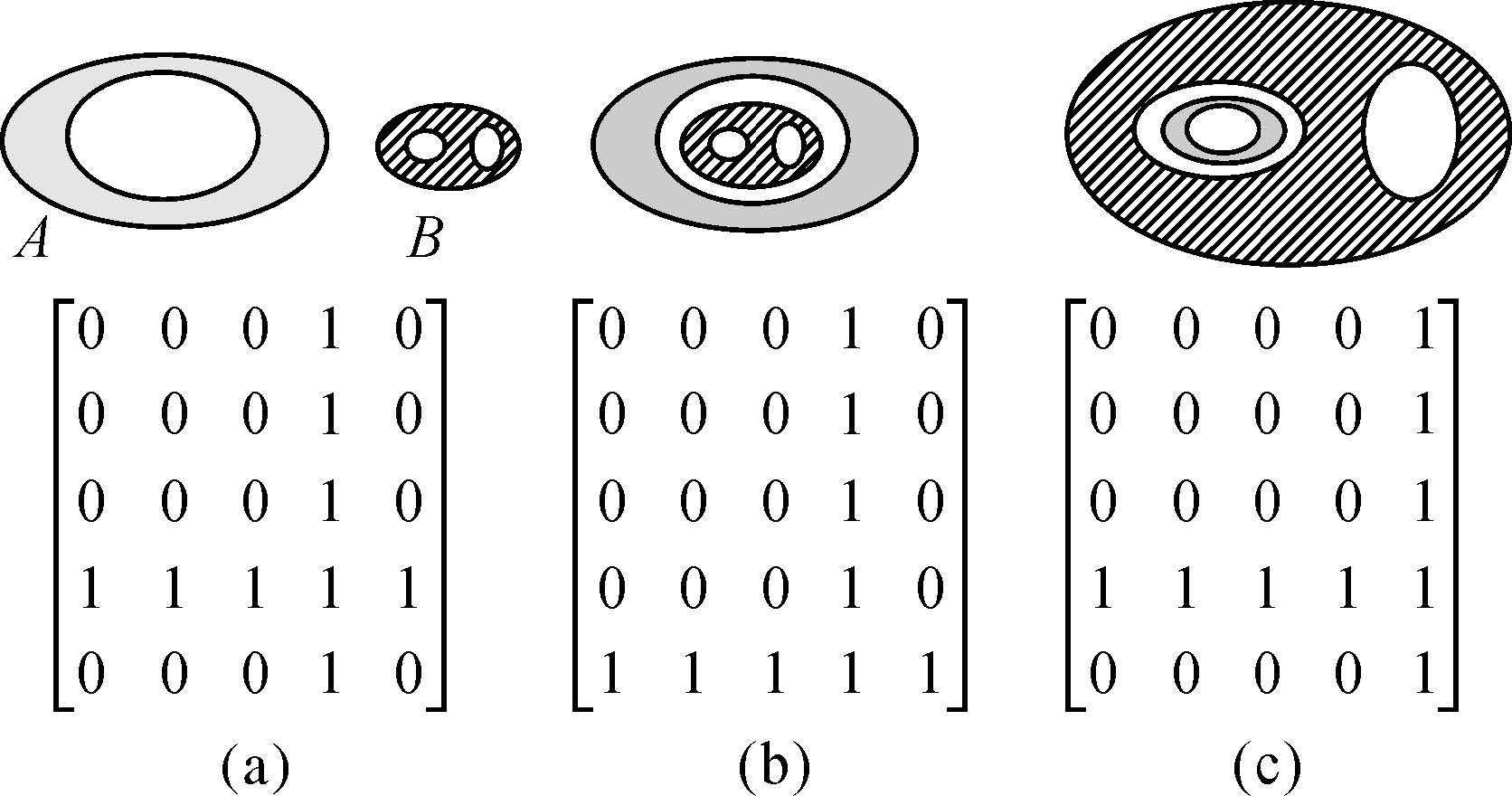
|
| 图 6 带洞面状对象间相离关系的25IM表现形式 Fig. 6 The representation form of the disjoint relation between regions with holes |
2.3.2 相接关系
相接关系表示空间对象A与B在空间上相接,相接关系的定义为式(12)。基于25IM,可以区分3种不同类型的相接关系(图 7)
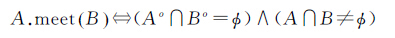 (12)
(12)
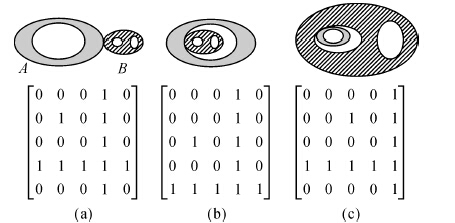
|
| 图 7 带洞面状对象间相接关系的25IM表现形式 Fig. 7 The representation form of the meet relation between regions with holes |
2.3.3 重叠关系
重叠关系表示空间对象A和B的内部相交,并且相交产生的结果不等同于空间对象A或者B。重叠关系的定义为式(13)。基于25IM,可以区分多种不同类型的重叠关系。图 8中列出了4种典型的重叠关系及其25IM的表示形式
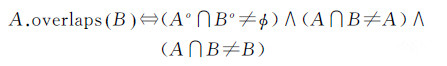 (13)
(13)
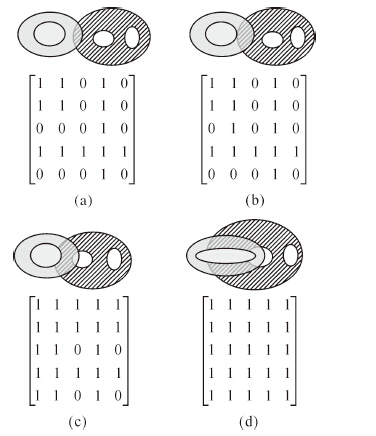
|
| 图 8 带洞面状对象间重叠关系的25IM表现形式 Fig. 8 The representation form of the overlaps relation between regions with holes |
2.3.4 覆盖关系
覆盖关系表示空间对象A的内部包含空间对象B的内部,并且A的边界与B的边界相交,但A与B不相等。覆盖关系的定义为式(14)。基于25IM,可以区分多种不同类型的覆盖关系。图 9中列出了4种典型的覆盖关系及其25IM的表示形式。
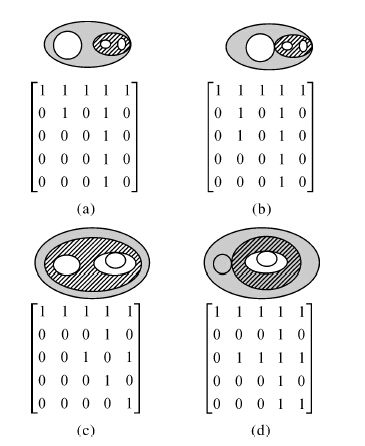
|
| 图 9 带洞面状对象间覆盖关系的25IM表现形式 Fig. 9 The representation form of the covers relation between regions with holes |
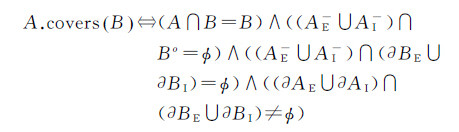 (14)
(14)
包含关系表示空间对象A完全包含空间对象B,包含与被包含是相对的。包含关系的定义为式(15)。基于25IM,可以区分3种不同类型的包含关系(图 10)
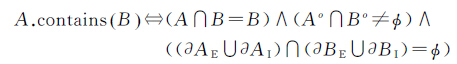 (15)
(15)

|
| 图 10 带洞面状对象间包含关系的25IM表现形式 Fig. 10 The representation form of the contains relation between regions with holesp |
2.3.6 相等关系
相等关系表示空间对象A与空间对象B完全相等。相等关系的定义为式(16)。基于25IM,可以定义相等关系(图 11)

|
| 图 11 带洞面状对象间相等关系的25IM表现形式 Fig. 11 The representation form of the equal relation between regions with holes |
 (16)
(16)
被覆盖关系表示空间对象A的内部完全在空间对象B的内部,并且A的边界与B的边界相交,但A与B不相等,覆盖与被覆盖是相对的,被覆盖关系的定义为式(17)
 (17)
(17)
基于25IM,可以区分多种不同类型的被覆盖关系。图 12中列出了4种典型的被覆盖关系及其25IM的表示形式。

|
| 图 12 带洞面状对象间被覆盖关系的25IM表现形式 Fig. 12 The representation form of the coveredby relation between regions with holes |
2.3.8 被包含关系
被包含关系表示空间对象A完全在空间对象B的内部。被包含关系的定义为式(18)。基于25IM,可以区分3种不同类型的被包含关系(图 13)
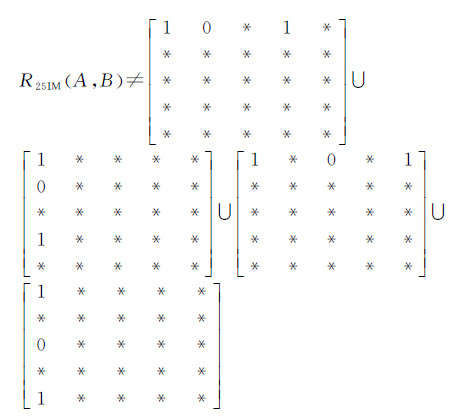 (18)
(18)
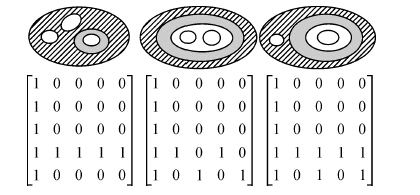
|
| 图 13 带洞面状对象间被包含关系的25IM表现形式 Fig. 13 The representation form of the inside relation between regions with holes |
2.4 实例分析
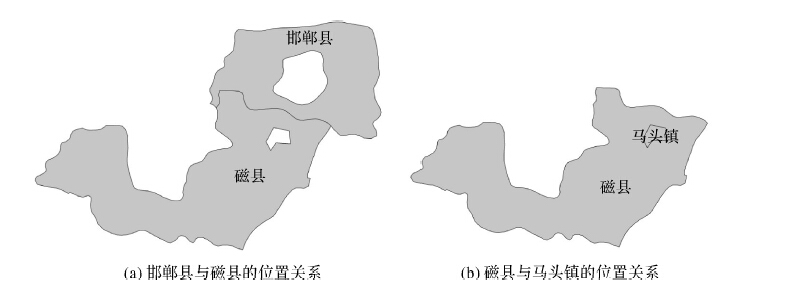
带洞空间对象广泛存在于自然和社会经济现象中,以河北省南部的邯郸县、磁县和马头镇(图 14)的拓扑关系描述为例进行说明。在图 14中,可以发现邯郸县和磁县均为带洞面状对象,马头镇为非带洞面状对象(马头镇可以视为特殊的带洞面状对象,即:内边界、内边界外部为空)。假设邯郸县、磁县和马头镇分别用A、B和C进行表示,A与B、B与C的拓扑关系的9IM表现形式为式(19),A与B、B与C的拓扑关系的25IM表现形式分别为式(20)、式(21)。
|
| 图 14 带洞面状对象的拓扑关系描述实例 Fig. 14 Example of the topological relation representation form between regions with holes |
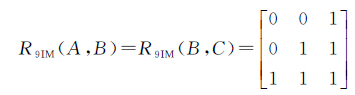 (19)
(19)
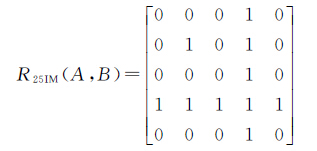 (20)
(20)
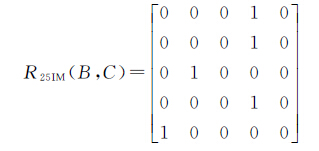 (21)
(21)
式(19)、式(20)和式(21)的对比分析可知:式(19)虽然能够判断上述A与B、B与C的拓扑关系为相接关系,但是无法进一步区分A与B、B与C之间相接关系的差异,而在很多情况下,则需要对这种差异进行描述和认知;相对于9IM,使用25IM的式(20)、式(21)更为详细地表达了A与B、B与C之间的相接关系,其中,A与B属于外部边界相接,B与C属于B的内部边界与C的外部边界相接。
3 结论和展望本文基于点集拓扑理论,提出了一种25IM,对带洞面状对象的拓扑关系进行描述。研究结果表明:①相对于9IM,25IM模型能够区分更多的拓扑关系类型;②提出的8种拓扑关系规则,能够用于排除不符合逻辑的拓扑关系;③基于25IM,对8种基本拓扑关系进行细分描述,进一步验证了25IM的描述能力。
本文研究的下一步工作是将25IM应用于带洞面状对象间的拓扑关系查询、计算、推理等方面,进一步验证和改进25IM模型。此外,基于25IM研究带洞体状对象间的拓扑关系也是下一步的工作重点。
| [1] | CLARKE B L. Individuals and Points[J]. Notre Dame Journal of Formal Logic,1985, 26 (1) : 61 –75 . |
| [2] | CLARKE B L. A Calculus of Individuals Based on “Connection"[J]. Notre Dame Journal of Formal Logic,1981, 22 (3) : 204 –218 . |
| [3] | EGENHOFER M J, FRANZOSAR D. Point-set Topological Spatial Relations[J]. International Journal of Geographical Information Systems,1991, 5 (2) : 161 –174 . |
| [4] | EGENHOFERM J, HERRING J R. Categorizing Binary Topological Relationships between Regions, Lines, and Points in Geographic Databases: Technical Report[R]. Orono: University of Maine, 1991. |
| [5] | CLEMENTINIE, DI F P, VAN O P. A Small Set of Formal Topological Relationships Suitable for End-user Interaction[C]//ABEL D,OOI BC. Advances in Spatial Databases: The 3rd International Symposium on Large Spatial Databases: Lecture Notes in Computer Science. Berlin: Springer, 1993, 692:277-295. |
| [6] | CHEN Jun, LI Chengming, LI Zhilin, et al. A Voronoi-Based 9-intersection Model for Spatial Relations[J]. International Journal of Geographical Information Systems,2001, 15 (3) : 201 –220 . |
| [7] | LONG Zhiguo, LI Sanjiang. A Complete Classification of Spatial Relations Using the Voronoi-based Nine-intersection Model[J]. International Journal of Geographical Information Science,2013, 27 (10) : 2006 –2025 . |
| [8] | EGENHOFER M J, CLEMENTINI E, DI FELICE P. Topological Relations between Regions with Holes[J]. International Journal of Geographical Information Systems,1994, 8 (2) : 129 –144 . |
| [9] | EGENHOFER M, VASARDANI M. Spatial Reasoning with a Hole[C]//WINTER S, DUCKHAM M, KULIK L, et al. Proceedings of the 8th International Conference on Spatial Information Theory:Lecture Notes in Computer Science.Melbourne: Springer, 2007: 303-320. |
| [10] |
邓敏, 李志林, 李光强. 简单面目标与带孔洞面目标间拓扑关系的层次表达方法[J].测绘学报,2008, 37 (3) : 330 –337 .
DENG Min, LI Zhilin, LI Guangqiang. A Hierarchical Approach to Topological Relations between a Simple Area and an Area with Holes[J]. Acta Geodaetica et Cartographica Sinica,2008, 37 (3) : 330 –337 . |
| [11] |
李健, 欧阳继红, 王国伟, 等. 一个带单洞区域和一个简单区域间的拓扑关系表示[J].吉林大学学报(理学版),2012, 50 (6) : 1209 –1213 .
LI Jian, OUYANG Jihong, WANG Guowei, et al. Representation for Topological Relations between a Region with a Hole and a Simple Region[J]. Journal of Jilin University(Science Edition),2012, 50 (6) : 1209 –1213 . |
| [12] |
刘津津. 带洞区域拓扑关系概念邻域图的自动推导研究[D]. 长春: 吉林大学, 2012. LIU Jinjin. Research on Deriving the Conceptual Neighborhood Graphs of Topological Relations between Regions with Holes Automatically[D]. Changchun: Jilin University, 2012. |
| [13] |
李国栋. 带双洞区域与简单区域间拓扑关系的表达推理[D]. 长春: 吉林农业大学, 2011. LI Guodong. Representation and Reasoning to Topological Relations between Region with Double Holes and Simple Region[D]. Changchun: Jilin Agricultural University, 2011. |
| [14] |
李健, 欧阳继红, 王振鑫. 带双洞区域与简单区域间的拓扑关系[J].吉林大学学报(工学版),2012, 42 (5) : 1214 –1218 .
LI Jian, OUYANG Jihong, WANG Zhenxin. Topological Relations between a Region with Two Holes and a Simple Region[J]. Journal of Jilin University(Engineering and Technology Edition),2012, 42 (5) : 1214 –1218 . |
| [15] |
李健, 欧阳继红, 富倩, 等. 凹形区域和带单洞区域间拓扑关系的表示[J].模式识别与人工智能,2013, 26 (3) : 225 –230 .
LI Jian, OUYANG Jihong, FU Qian, et al. Representation of Topological Relations between a Concave Region and a Simple Region with a Hole[J]. Pattern Recognition and Artificial Intelligence,2013, 26 (3) : 225 –230 . |
| [16] |
李健, 欧阳继红, 朱佳斌, 等. 一种双嵌套区域与简单区域间的拓扑关系模型[J].电子学报,2013, 41 (10) : 1988 –1993 .
LI Jian, OUYANG Jihong, ZHU Jiabin, et al. The Topological Relation Model between a Double Nesting Region and a Simple Region[J]. Acta Electronica Sinica,2013, 41 (10) : 1988 –1993 . |
| [17] |
李健, 朱佳斌, 赵慧. 一类带有互相包含洞的区域与简单区域间拓扑关系的表示[J].吉林大学学报(理学版),2013, 51 (6) : 1107 –1110 .
LI Jian, ZHU Jiabin, ZHAO Hui. Representation of Topological Relations between the Region with Holes of Mutual Inclusion and the Simple Region[J]. Journal of Jilin University(Science Edition),2013, 51 (6) : 1107 –1110 . |
| [18] |
王磊. 空间复杂区域间拓扑关系研究[D]. 南京: 南京航空航天大学, 2008. WANG Lei.Research on Topological Relations between Spatial Complex Regions[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008. |
| [19] |
欧阳继红, 霍林林, 刘大有, 等. 能表达带洞区域拓扑关系的扩展9-交集模型[J].吉林大学学报(工学版),2009, 39 (6) : 1595 –1600 .
OUYANG Jihong, HUO Linlin, LIU Dayou, et al. Extended 9-Intersection Model for Description of Topological Relations between Regions with Holes[J]. Journal of Jilin University(Engineering and Technology Edition),2009, 39 (6) : 1595 –1600 . |
| [20] | 霍林林. 复杂空间关系模型及空间描述逻辑中若干问题的研究[J].长春: 吉林大学,2013 . |
| [21] |
熊金城.
点集拓扑讲义[M]. 3版
北京: 高等教育出版社, 2013 .
XIONG Jincheng. Point Set Topology Notes[M]. 3rd ed Beijing: Higher Education Press, 2013 . |



