2. 中国科学院光电研究院计算光学室,北京 100094
2. Key Laboratory of Computational Optics Imaging Technology, Academy of Opto-electronics, Chinese Academy of Sciences, Beijing 100094,China
大孔径静态干涉成像光谱仪[1](large aperture static imaging spectrometer,LASIS)是一种高灵敏度高稳定性的干涉成像光谱仪[2],具有高光通量与高光谱分辨率的优点。依靠对目标的推扫,获取二维空间信息和一维干涉信息[3],再利用傅里叶变换得到地物光谱信息。对于机载和星载的LASIS系统,通过推扫获取完整干涉信息的过程中[4],由于飞机或卫星姿态的不稳定[5-6],会发生偏航、俯仰、横滚等姿态变化,使得获取的图像存在旋转和位移等误差,造成干涉图的提取存在误差,进而造成复原图像和光谱的失真[7]。因此,为了获得正确的光谱图像信息,必须首先对LASIS获取的图像进行配准。
LASIS获取的图像是叠加了干涉条纹的二维图像,由于受到干涉条纹的影响,直接使用常规传统的配准方法[8-12]并不能获得好的效果。针对LASIS的图像特点,文献[13]提出一种基于相位相关与归一化积相关的联合图像校正算法,该方法忽略了LASIS 图像的信息冗余和帧间相关性,因而配准精度不高。文献[14]提出采用归一化的相关系数法对LASIS 图像配准,该方法配准法精度仅为1个像素。文献[15]提出一种单步离散傅里叶变换配准方法对LASIS 图像进行配准,该方法采用互功率谱插值的方法获得亚像素平移,配准精度与插值算法相关,另外该算法虽然只对局部互功率谱进行插值,但配准速度仍然较慢。上述方法为了降低干涉调制的影响,都是选取远离零光程差的局部图像配准,从理论上讲若仪器畸变足够小,在旋转和平移上,局部图像的信息足以替代整幅图像,但LASIS 图像不同于普通图像,即使远离零光程差的位置依然受到干涉调制的影响,之前的文章中验证了选取图像尺寸的大小直接影响了配准精度的高低,图像尺寸越大,配准精度越高。
文献[16-17]提出了基于傅里叶变换互功率谱的Phase Correlation方法。该方法不需要插值,算法简单,能够快速配准位移和旋转误差,并且精度高,能够实现亚像素配准,但在应用于LASIS 图像配准时精度还是受到干涉条纹的影响,使其达不到该算法在普通图像配准时应有的精度,尤其零光程差附近的干涉调制最强的地方,零光程差位置已经看不出目标地物信息,这对Phase Correlation方法的配准精度造成极大影响。针对该问题以及上文提到的LASIS 图像尺寸问题,本文提出了一种利用条纹模板消除LASIS干涉条纹的预处理方法,再利用Phase Correlation方法进行图像配准的方法,算法对于在不同光照下的成像具有很强的鲁棒性。另外,算法可以配准同时包含位移和旋转的图像,由于图像的幅度谱不包含位移信息,所以当同时存在位移和旋转时,可以先配准旋转,再校正位移。仿真结果表明该方法能够很好地消除条纹的影响,实现高精度的配准,而且不需要插值即可实现亚像素级的配准精度。
1 LASIS原理傅里叶变换光谱仪[18]的基本功能是产生两束相干光束,并通过对光程差的控制,使其得到干涉图,再通过对干涉图进行傅里叶变换便可获得目标的光谱
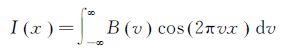 (1)
(1)
式中,Bv是波数为v的光谱强度;Ix是光程差为x的干涉强度,对公式(1)作傅里叶逆变换可得
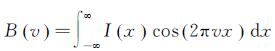 (2)
(2)
以上两个公式便是理想情况下傅里叶变换光谱学的基本关系式。
LASIS也是一种傅里叶变换光谱仪,它的光学系统如图 1所示,不难发现,LASIS实际上是在一个普通照相系统中加入横向剪切干涉仪[19-21]实现的,横向剪切干涉仪使像面上得到的不再是目标的直接像,而是目标的“干涉图像”。
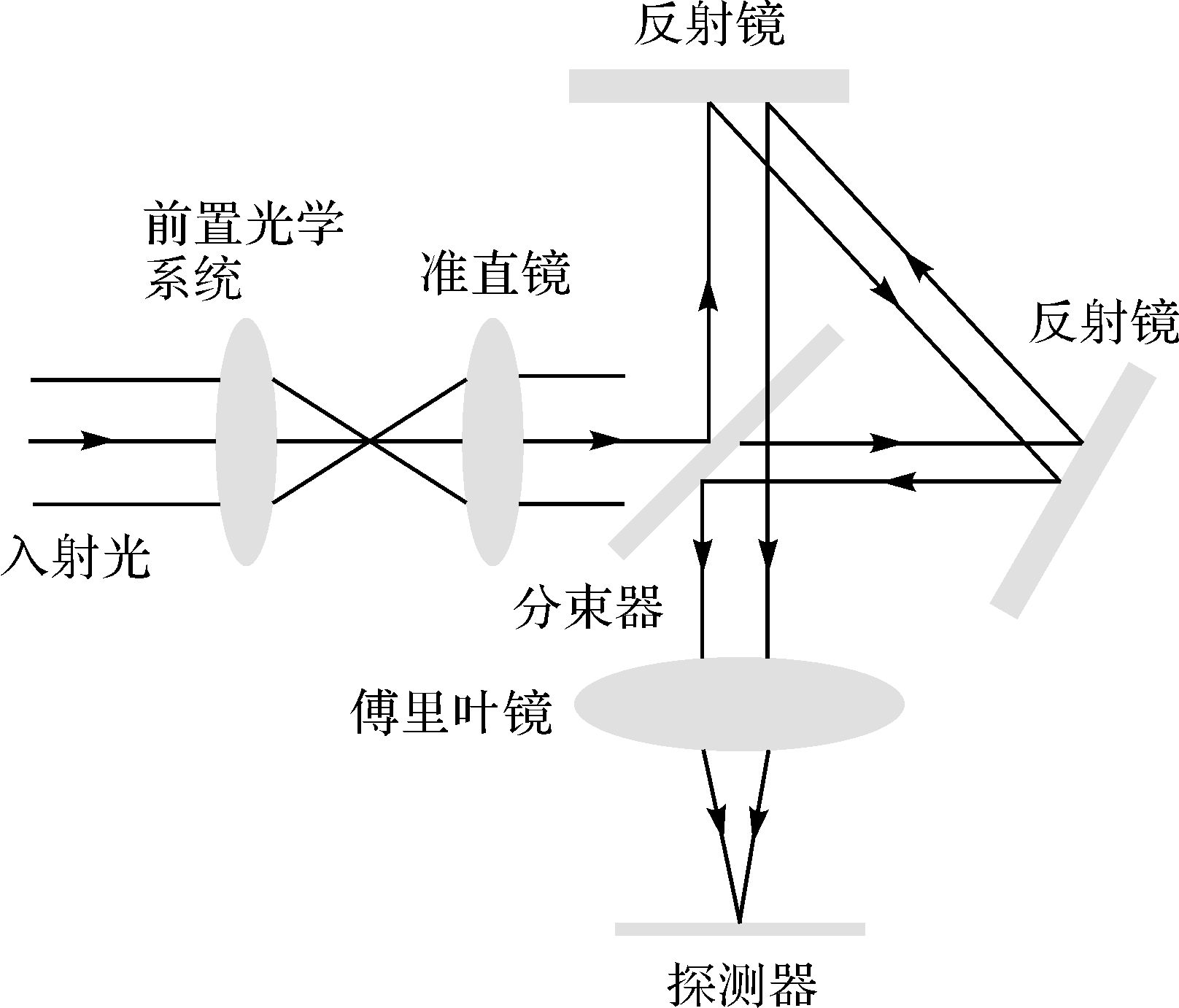
|
| 图 1 LASIS的光学系统 Fig. 1 LASIS optical system |
当物方视场角为ω时,两束相干光束的光程差(OPD)可以表示为
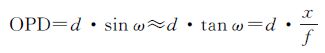 (3)
(3)
式中,d是干涉仪剪切量;f表示傅里叶镜的焦距;x是沿飞行方向某列探测单元的位置。探测单元x位置处的干涉强度为
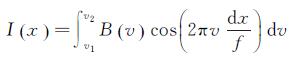 (4)
(4)
提取出某一地物目标点的完整干涉图后,经傅里叶逆变换可以得到该点的光谱信息,L是最大光程差
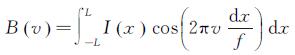 (5)
(5)
由于LASIS 图像受到干涉调制的影响,导致使用常规的配准方法精度较低,为了提高配准的精度,需要先消除干涉条纹对LASIS 图像配准的影响。
2.1 消条纹算法本文假设LASIS 图像由普通图像叠加条纹构成,因此只要寻找到合适的条纹模板,对LASIS 图像消除条纹,即可消除干涉调制对配准精度的影响。LASIS 图像上某点的干涉强度计算公式为
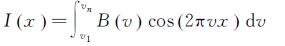 (6)
(6)
式中,B是该点对应的地物光谱信息;v是波数;I(x)是光程差为x的干涉强度,该公式可写成
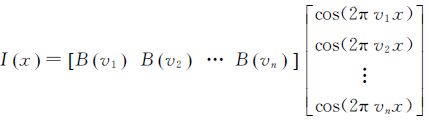 (7)
(7)
假设中的普通图像为
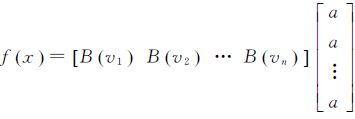 (8)
(8)
由式(7)和式(8)对比可以发现,其实普通图像和LASIS 图像的区别是调制矩阵不同。LASIS 图像相同行中的每个像素点对应的光程差x是相同的,对应的调制矩阵也是一样的;不同行之间的光程差x不同,调制矩阵也不一样。对于同一行的像元,理论上一定存在一个比例因子c,使得该行所有像元的能量强度乘c后最接近普通图像应有的能量强度
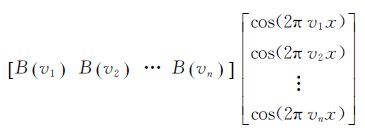 (9)
(9)
LASIS 图像相同行中的每个像素点的光程差x是相同的,对应的调制矩阵hx,y也是一样的,不同行之间的光程差x不同,hx,y也不一样,并且x越小,调制越明显,在图像上则表现为“由普通图像叠加条纹构成”,本文希望能找到一个hx,y使得每行的所有点尽可能满足
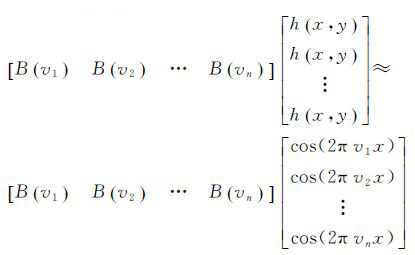 (10)
(10)
即
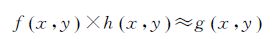 (11)
(11)
式(11)中的gx,y为fx,y对应的LASIS 图像,只要计算出h(x,y),就可通过gx,y和h(x,y)点除计算出没有条纹的fx,y。
为了计算hx,y,首先给定一初始模板h0x,y,h0(x,y)为均匀目标所对应的LASIS 图像,提取未加入误差的仿真图像某一点的干涉曲线,并一维变二维即可得到,该模板就是直接的干涉条纹,不携带LASIS 图像的地物目标信息,该模板的产生与LASIS光学系统设计的参数有关,对同一LASIS光学系统生成的LASIS 图像具有通用性。计算h(x,y)的流程如图 2所示。首先选择一幅LASIS 图像gx,y,计算经过初始模板消条纹之后的图像x,y
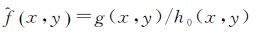 (12)
(12)
通过式(12)计算获得x,y,图像(x,y)是否消条纹成功需要判断标准,包括单个像元是否消除干涉调制成功以及整幅图是否消条纹成功两个事件。对于单个像元,将计算结果(x,y)与fx,y比较,两幅图对应像元位置能量强度相差小于该位置fx,y能量强度的3%时,即认为这个像元消除干涉调制成功;对于整幅LASIS 图像,设定一评估系数∝表征LASIS 图像消条纹成功率,由于LASIS 图像每个像素点对应的地物目标不一样,如果想通过模板将条纹完全去掉,模板必定携带该图像的信息,从而不具备通用性,本文设定∝为0.95,也就是说通过模板可消除每幅LASIS 图像95%的条纹,即认为整幅LASIS 图像消条纹成功,当x,y与fx,y的消条纹成功率≥∝时,获得最终模板hx,y,否则利用式(13)对hx,y进行修正,继续计算x,y,fx,y为不含干涉条纹的普通图像,将未加入误差的序列图像的所有零光程差行提取拼接即可得到。这时通过消条纹的LASIS 图像可能仍有极少数条纹,再通过适当平滑进一步消除条纹
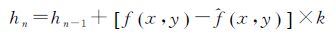 (13)
(13)
式中,k是修正系数,根据修正结果调整k值(0~1),计算流程如图 2所示。

|
| 图 2 计算h(x,y)流程图 Fig. 2 The flow-process diagram for calculating h(x,y) |
需要注意的是,hn的修正需添加限制。首先,每次修正完hn,需要对hn每行的像素点能量强度求平均值替代该行每个像素点的值,保证hn的每一行条纹始终是连续的条纹,避免模板携带了图像的信息,否则用该模板修正其他地物的LASIS 图像时,会使得被修正的图像携带模板信息。另外,在计算模板的过程中,应实时检测模板中是否有不合理的极大值、极小值和零,一经发现便使用邻近像素点的值代替。
最后,由于LASIS的图像每个像素点对应不同的地物,所以修正后的图像零光程差的位置附近还是会有极少断断续续的条纹,因此需要对图像零光程差附近局部图像作适当的平滑,消除剩余条纹。图 3展示了该算法消除条纹的效果,图 3(a)中由于干涉调制的作用,LASIS 图像有些地方的能量被加强,有些地方被减弱,图像看上去明暗对比较高,图 3(b)图像中的条纹信息明显得到了抑制。

|
| 图 3 消除条纹前后LASIS 图像对比 Fig. 3 Image contrast before and after elimination |
2.2 傅里叶变换互功率谱的配准方法[22-23]
傅里叶变换互功率谱方法基于傅里叶位移原理,通过计算两图像的互功率谱实现频域配准。用mx,y和nx,y分别表示两幅图像,(x0,y0)表示两幅图之间的位移量,则
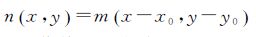 (14)
(14)
将式(14)两边作傅里叶变换
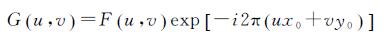 (15)
(15)
则它们的归一化互功率谱可以表示为
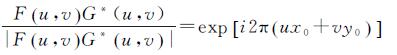 (16)
(16)
式中,G*表示G的复共轭函数。
互功率谱的傅里叶逆变换为
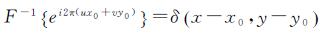 (17)
(17)
F-1{ }表示傅里叶逆变换。
位移理论保证了两幅图像相位差与互功率谱的相位的等效性,通过对互功率谱的傅里叶逆变换可以得到脉冲函数δ(x-x0,y-y0),该函数在偏移位置x0,y0处有明显的尖锐峰值,其余位置的值接近零,通过这个性质即可获取图像的位移。
2.3 Phase correlation算法当图像间存在亚像素位移时,获取的图像等同于图像经过整数位移的降采样图像,图像经过降采样后,相位相关的信号能量不再是单一的峰值,而是多个邻近的峰值,通过几个峰值的简单计算可以获得亚像素图像平移[16-17]。计算公式为
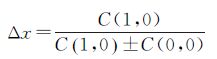 (18)
(18)
式中,Δx是沿X方向上的亚像素平移,C0,0为单位脉冲函数的最大像素值,使用式(18)配准得到亚像素级位移不需要对互功率谱插值,计算速度快,配准精度高。
旋转误差的配准方法与平移基本一致,只不过需要将图像从直角坐标系转换成极坐标系下计算,另外当图像同时存在平移和旋转时,先对旋转量进行配准。需将图像转换成对应的幅度谱进行配准,因为图像的幅度谱不包含位移信息,只有角度信息。校正旋转误差后再配准平移。
3 仿真与结果为了验证算法的有效性,本文共仿真了287帧LASIS 图像。图 4是仿真得到其中4帧LASIS 图像。得到仿真图像后,先对序列图像旋转量进行配准。本文使用了3种方法作了配准:①为了验证LASIS 图像条纹对配准有影响,直接使用Phase Correlation方法(方法1)进行配准;②使用文献[15]的单步离散傅里叶变换配准方法(方法2);③基于条纹消除的Phase Correlation配准方法(方法3)。方法3为本文介绍的方法,将287帧LASIS 图像和之前获得的模板作点除,初步消除条纹之后再作适当平滑,然后再对处理后的图像使用Phase Correlation方法配准。
|
| 图 4 仿真的LASIS 图像 Fig. 4 LASIS images |
表 1中展示了3种配准方法各自的平均误差、方差和最大误差。可以看出,旋转误差配准精度最高,这是因为单位角度的图像分辨率高于单位像素图像分辨率,而X方向配准精度较Y方向低是因为Y方向没有受到干涉调制的影响。方法2在Y方向的配准精度比文献[15]的精度低,有3个可能原因:①其论文只对位移作配准,配准图像不包含旋转误差,本文是通过配准结果校正旋转误差,所以位移配准的图像仍存在旋转误差,从而影响位移配准误差; ②使用图像的尺寸不一样,其论文中配准精度最高用的图像尺寸是256×1024像素,本文是200×500像素;③仿真叠加的误差范围不一样,文献[15]中的误差区间为[-0.5,0.5],本文是[-1,1]。方法3的精度在X方向较方法1和方法2分别提高了64.58%和45.48%,在Y方向上分别提高了61.32%和52.22%,旋转角度上分别提高了39.38%、39.13%。虽然精度有了大幅度的提高,但较文献[16-17]的精度低了10%~20%,经分析有两个原因:经过预处理的图像只是接近普通图像,干涉调制的影响虽然减小,但仍然存在;Shekarforoush只对位移作了配准。在配准速度方面,方法3的速度优于方法2。
| 方法 | XM.E | XE.RMS | XMAX.E | YM.E | YE.RMS | YMAX.E | AngleM.E | AngleE.RMS | AngleMAX.E |
| 方法1 | 0.163 5 | 0.191 0 | 0.355 9 | 0.119 7 | 0.130 0 | 0.467 5 | 0.048 5 | 0.074 8 | 0.312 0 |
| 方法2 | 0.106 2 | 0.117 0 | 0.313 3 | 0.096 9 | 0.147 0 | 0.392 6 | 0.048 3 | 0.073 5 | 0.293 4 |
| 方法3 | 0.057 9 | 0.072 1 | 0.226 5 | 0.046 3 | 0.002 7 | 0.379 9 | 0.029 4 | 0.037 4 | 0.148 0 |
图 5是对真实LASIS 图像进行光谱复原得到的光谱数据立方体,光谱范围914~2549 nm。其中图 5(a)是未经误差矫正直接复原后得到的光谱数据立方体,放大图像的细节不难发现,由于推扫平台的姿态误差,直接提取干涉图复原的光谱图像细节存在明显误差;图 5(b)是矫正误差后提取干涉图复原的结果,相比于图 5(a),图像细节得到明显改善。

|
| 图 5 光谱图像 Fig. 5 Spectral image |
4 总 结
针对LASIS 图像的特点,本文提出了一种基于条纹消除的LASIS干涉图像配准方法。首先利用条纹模板消除LASIS 图像上的干涉条纹,降低干涉条纹对图像配准的影响,然后利用基于傅里叶变换互功率谱的Phase Correlation方法进行图像配准。仿真结果表明:对于同一光学系统获取的LASIS 图像,利用条纹模板可以有效消除序列LASIS 图像叠加的干涉信息,经处理过后的LASIS 图像条纹几乎消失,再结合现有的图像配准算法进行配准处理,相比现有的LASIS 图像配准方法,平移和旋转的配准精度能提高接近一倍,并且不需要插值即可实现亚像素级的配准精度,运行速度快。值得注意的是,本文提出的方法仍有局限性:对于不同的光学系统需要设计不同的模板,并且仅对平移和旋转作了讨论。
| [1] |
袁艳, 成像光谱理论与技术研究[D]. 西安: 中国科学院西安光学精密机械研究所, 2005. YUAN Yan. Theoretical and Technical Study of the Imaging Spectrometry[D]. Xi’an: Xi’an Institute of Optics and Precision Mechanics, the Chinese Academy of Sciences, 2005. |
| [2] | NIEKE J, SCHWARZER H H, NEUMANN A, et al. Imaging Spaceborne and Airborne Sensor Systems in the Beginning of the Next Century[C]//Proceedings of SPIE, Sensors, Systems, and Next-Generation Satellites. London: SPIE, 1997(3221) 581-592. |
| [3] | SHAW G A, BURKE H H. Spectral Imaging for Remote Sensing[J]. Lincoln Laboratory Journal,2003, 14 (1) : 3 –24 . |
| [4] |
相里斌. 干涉成像光谱技术研究[R]. 西安: 中国科学院西安光机所, 1997. XIANG Libin. Study on the Fourier Transform Imaging Spectrometry[R]. Xi’an: Xi’an Institute of Optics and Precision Mechanics, the Chinese Academy of Sciences, 1997. |
| [5] |
蒋永华, 张过, 唐新明, 等. 资源三号测绘卫星多光谱影像高精度谱段配准[J].测绘学报,2013, 42 (6) : 884 –890 .
JIANG Yonghua, ZHANG Guo, TANG Xinming, et al. Research on the High Accuracy Band-to-Band Registration Method of ZY-3 Multispectral Image[J]. Acta Geodaetica et Cartographica Sinica,2013, 42 (6) : 884 –890 . |
| [6] |
花奋奋, 张继贤, 黄国满, 等. 机载重轨干涉合成孔径雷达数据的一种配准方法[J].测绘学报,2014, 43 (3) : 298 –305 .DOI:10.13485/j.cnki.11-2089.2014.0043.
HUA Fenfen, ZHANG Jixian, HUANG Guoman, et al. A Registration Approach for Airborne Repeat Pass InSAR[J]. Acta Geodaetica et Cartographica Sinica,2014, 43 (3) : 298 –305 .DOI:10.13485/j.cnki.11-2089.2014.0043. |
| [7] |
余成伟, 谌德荣, 杨建峰, 等. 卫星姿态抖动对LASIS成像质量的影响[J].光电工程,2004, 31 (5) : 4 –6 .
YU Chengwei, CHEN Derong, YANG Jianfeng, et al. Influence of Satellite Attitude Jitter on LASIS Imaging Quality[J]. Opto-Electronic Engineering,2004, 31 (5) : 4 –6 . |
| [8] | BROWN L G. A Survey of Image Registration Techniques[J]. ACM Computing Surveys,1992, 24 (4) : 325 –376 . |
| [9] | PRATT W K. Digital Image Processing[M]. 2nd ed New York: Wiley & Sons, 1991 . |
| [10] | BARNEA D I, SILVERMAN H F. A Class of Algorithms for Fast Digital Image Registration[J]. IEEE Transactions on Computers,1972 . |
| [11] | MOIGNE J L, CAMPBELL W J, CROMP R F. An Automated Parallel Image Registration Technique Based on the Correlation of Wavelet Features[J]. IEEE Transactions on Geoscience and Remote Sensing,2002, 40 (8) : 1849 –1864 . |
| [12] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision,2004, 60 (2) : 91 –110 . |
| [13] |
李湘滨, 谌德荣, 余成伟, 等. 大孔径静态干涉成像光谱仪图像校正技术[J].光电工程,2004, 31 (8) : 8 –11 .
LI Xiangbin, CHEN Derong, YU Chengwei, et al. Image Correction Techniques for Large-Aperture Static Imaging Spectrometer[J]. Opto-Electronic Engineering,2004, 31 (8) : 8 –11 . |
| [14] |
高莹莹, 杨建峰, 马晓龙, 等. 基于Fourier-Meliin算法的干涉图像配准[J].光学精密工程,2007, 15 (9) : 1415 –1420 .
GAO Yingying, YANG Jianfeng, MA Xiaolong, et al. Interference Image Registration Based on Fourier-Mellin Algorithm[J]. Optics and Precision Engineering,2007, 15 (9) : 1415 –1420 . |
| [15] | ZHANG Xiubao, WANG Qian, ZHOU Zhiliang, et al. Research on the Sequential Images Registration of the Temporally and Spatially Modulated Fourier Transform Imaging Spectrometer[C]//Proceedings of SPIE 7857, Multispectral, Hyperspectral, and Ultraspectral Remote Sensing Technology, Techniques, and Applications III. Incheon: SPIE, 2010. |
| [16] | SHEKARFOROUSH H, BERTHOD M, ZERUBIA J. Subpixel Image Registration by Estimating the Polyphase Decomposition of Cross Power Spectrum[C]//Proceedings of 1996 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 1996: 532-537. |
| [17] | FOROOSH H, ZERUBIA J B, BERTHOD M. Extension of Phase Correlation to Subpixel Registration[J]. IEEE Transactions on Image Processing,2002, 11 (3) : 188 –200 . |
| [18] |
张淳民, 相里斌, 赵葆常, 等. 干涉成像光谱技术研究新进展[J].红外,2000, 3 (3) : 1 –5 .
ZHANG Chunmin, XIANG Libin, ZHAO Baochang, et al. Development of Iamge Interferometry Reseach[J]. Infrared,2000, 3 (3) : 1 –5 . |
| [19] | HORTON R F.Optical Design for a High-Etendue Imaging Fourier-Transform Spectrometer[C]//Proceedings of SPIE, Imaging Spectrometry Ⅱ. Denver: SPIE, 1996(2819): 300-315. |
| [20] | HORTON R F, CONGER C A, PELLIGRINO L S. High Etendue Imaging Fourier Transform Spectrometer: Initial Results[C]//Proceedings of SPIE, Imaging Spectrometry Ⅲ. San Diego, CA: SPIE, 1997(3118): 380-390. |
| [21] | HORTON R F,BYERS T,CONGER C A, et al. HEIFTS Phase Ⅱ: Laboratory and Advanced Simulation Results[C]//Proceedings of SPIE, Imaging Spectrometry Ⅵ. San Diego: SPIE, 2000(4132): 195-205. |
| [22] | KUGLIN C D, HINES D C. The Phase Correlation Image Alignment Method[C]//Proceedings of the IEEE International Conference on Cybernetics and Society. Orlando: IEEE, 1975: 163-165. |
| [23] | REDDY B S, CHATTERJI B N. An FFT-based Technique for Translation, Rotation, and Scale-invariant Image Registration[J]. IEEE Transactions on Image Processing,1996, 5 (8) : 1266 –1271 . |


