近几年无人机受到了人们越来越多的关注,无人机图像拼接方法也随之得到了快速发展。无人机图像拼接是指在无人机平台上对多幅在不同时刻、从不同视角获得的航拍图像经过对齐处理后,然后无缝地融合在一起,从而得到一幅视野更大、分辨率更高的全景图像。目前被广泛应用于数字地图绘制、城市建设规划以及战场态势评估等领域。
航拍图像的拼接一般包括4个步骤:待拼接图像的获取、图像畸变校正、图像配准以及图像融合。其中图像配准是整个图像拼接技术的核心部分,它直接关系到图像拼接的质量[1],其主要目的是得到两幅图像之间的变换矩阵。目前无人机图像配准技术主要是基于特征点匹配的方法,该方法利用图像中提取到的局部特征进行匹配,其关键步骤是图像特征的提取和匹配[2],其中基于SIFT特征点匹配的方法被广泛地应用于航拍图像的配准。该方法能够有效地适应航拍图像间存在的视角和尺度变化,由文献[3-4]在1999年提出,并在2004年又对该算法进行了完善[3-4]。后来又出现了很多改进的SIFT算法应用到图像配准中[5-9]。文献[5]提出的PCA-SIFT方法,采用主成分分析对SIFT算子进行降维操作,大大减少了计算时间。文献[6]提出的尺度和仿射不变量兴趣点检测的GLOH算法,采用一种SIFT变体的描述子,用对数极坐标分级结构替代SIFT使用的4象限,之后再做PCA将其降维,因此保有和SIFT一样精简的表示方法。文献[7]提出的SURF算法,采用快速Hessian方法进行特征点检测,是SIFT算法的加速版。文献[8]提出扩展SURF描述符,采用邻域采样点的局部归一化灰度统计信息以及二阶梯度值细节信息,增强了描述符的约束性与独特性。文献[9]提出的ASIFT算法,通过模拟不同经纬度的图像,克服了SIFT算法的不完全仿射性。但是上述图像配准方法的一个明显不足就是提取特征点比较耗时,从而导致图像拼接速度较慢。为了提高航拍图像的拼接速度,近几年国内外研究者提出了多种拼接方法[10-14, 16-18]。文献[10]中估计变换矩阵以及图像间关系的不确定性,并考虑如何消除图像拼接中的累积误差。文献[11-12]通过预测拼接图像的重叠区域减少拼接的时间消耗。文献[13]提出的F-SIFT图像拼接算法,采用基于子图像块的频域相位相关算法提高图像拼接的速度。文献[14]通过分块Harris角点的方法均匀提取图像中的角点,然后采用金字塔光流算法进行角点配准,缩短了航拍图像的匹配时间。这些方法对于航拍图像的配准和一般图像的配准相同,首先是对航拍图像进行特征点的提取,然后通过相似性度量进行特征点匹配,最后根据得到的两幅图像中对应特征点的坐标关系,采用RANSAC算法[15]计算出最佳匹配的变换矩阵,并没有利用航拍图像特有的优势。文献[16-17]结合了航拍时的参数信息进行图像配准,提高了航拍图像拼接的速度,但是还没有完全发挥航拍参数对图像配准的作用。文献[18]针对机载传感器的精度问题,提出了一种混合的方法,利用基于图像的方法校正由位姿计算带来的拼接误差。本文结合无人机航拍的特点,利用航拍时获得的航拍参数来计算图像间的变换矩阵,然后通过变换矩阵的分解推导出多幅图像连续拼接的变换矩阵,基本不依赖拍摄图像的质量情况,提出了一种快速的航拍图像配准方法。
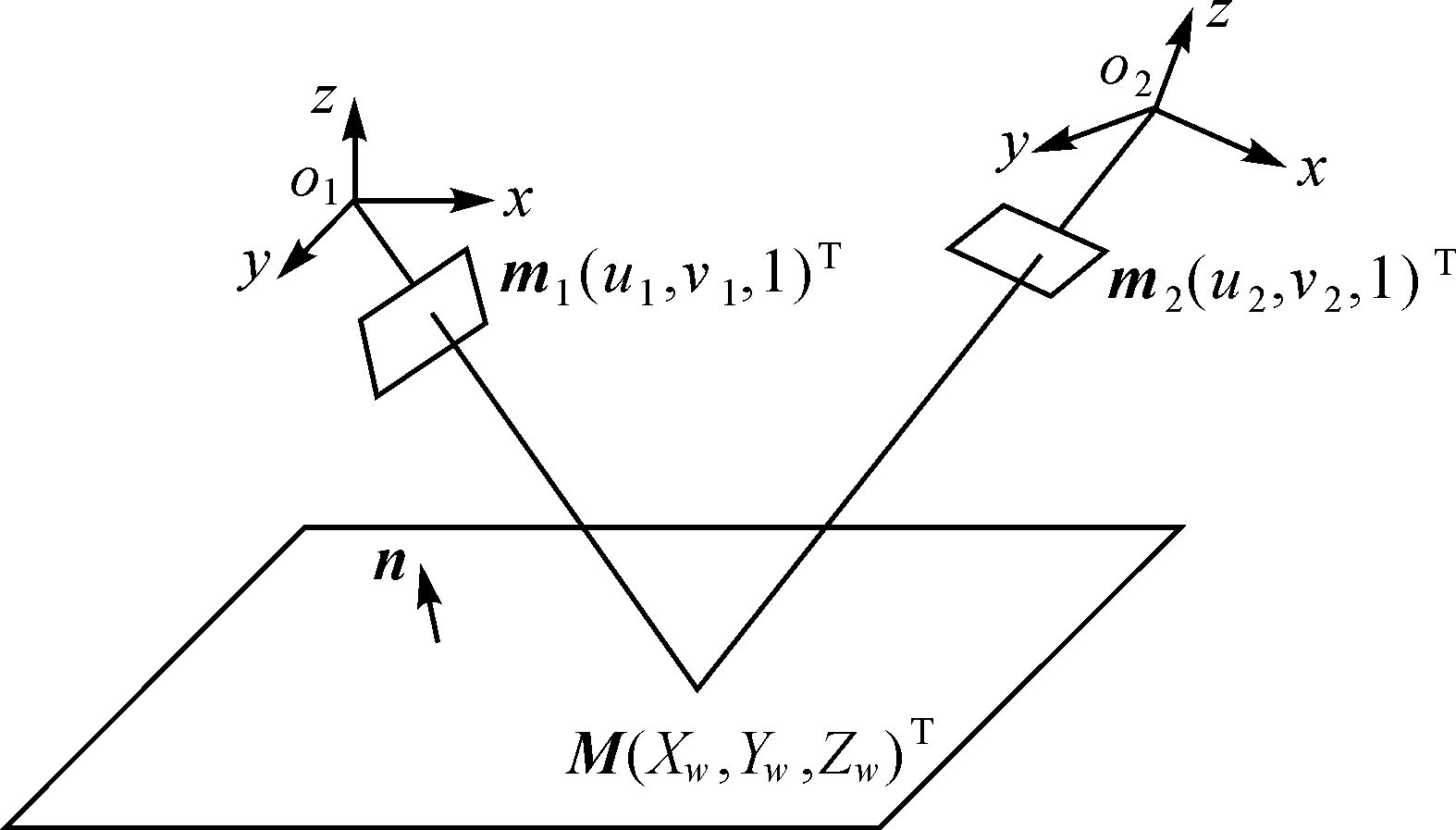
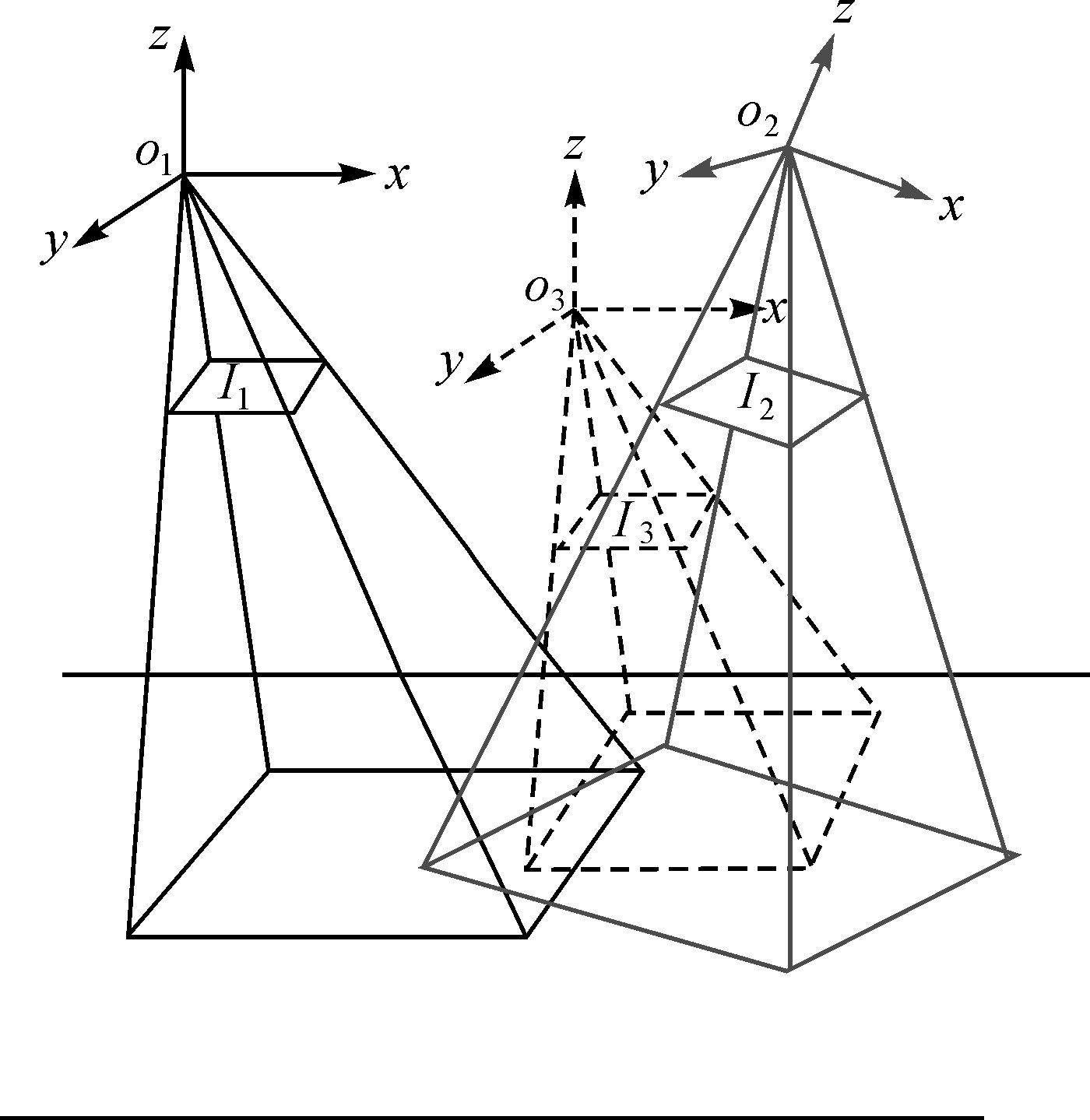
1 两幅航拍图像的配准 1.1 航拍图像间的单应变换矩阵如图 1所示,无人机在位置O1和O2对地面场景进行拍摄,得到图像I1和I2。M(Xw,Yw,Zw)T为场景中的一点,M1(Xc1,Yc1,Zc1)T和M2(Xc2,Yc2,Zc2)T表示M在两个位置的相机坐标。m1(u1,v1,1)T和m2(u2,v2,1)T分别为M在图像I1和I2上对应的点。如果矩阵H能满足
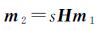 (1)
(1)
|
| 图 1 不同视角的航拍图像 Fig. 1 Aerial image from different angles of view |
则称矩阵H为图像I1到I2的单应变换矩阵。其中s为非零常数项。
将O1点作为世界坐标系原点,则由相机的成像原理可知
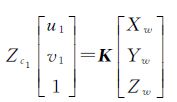 (2)
(2)
式中,K为摄像机的内参数矩阵
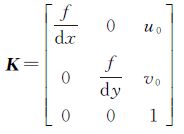 (3)
(3)
式中,K可以通过相机标定得到[19];dx和dy分别表示图像上每一个像素在坐标轴方向的物理尺寸,单位为mm/pixel;(u0,v0)为摄像机光轴与图像平面交点的坐标,一般位于图像的中心处;f表示摄像机的焦距。
由式(2)可得
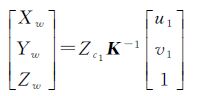 (4)
(4)
若O1和O2之间的运动为R[I,-t],其中R为3×3的旋转矩阵,t为三维平移向量。则有
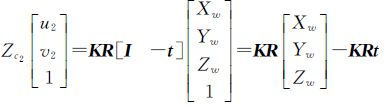 (5)
(5)
设大地平面的方程为
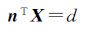 (6)
(6)
式中,X为地面上任意一点;n为地面的单位法向量;d为坐标原点到大地平面的距离。由式(6)可得
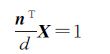 (7)
(7)
综合式(4)、式(5)、式(7)可以得到
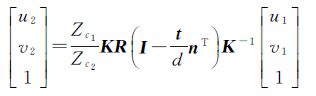 (8)
(8)
而Zc1Zc2是一个非零的常数项,因此两幅航拍图像之间的单应矩阵可表示为
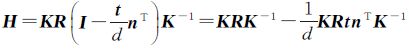 (9)
(9)
至此就得到了航拍图像间的单应变换矩阵。对无人机所在的拍摄位置O可以用6个参数表示,记为Oi(φi,θi,ψi,xi,yi,zi)。无人机上装有惯性导航单元(INU)和GPS,可以实时保存无人机航行时的姿态角和坐标。根据无人机在两个视点间3个姿态角的变化量φ、θ、ψ和两个视点的坐标(x1,y1,z1)、(x2,y2,z2)就可以确定R和t,其中
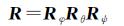 (10)
(10)
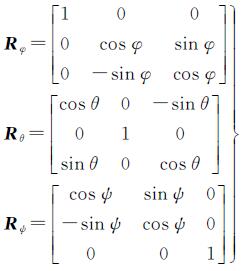 (11)
(11)
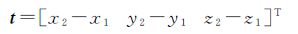 (12)
(12)
从而两幅航拍图像之间的变换矩阵就可以通过这6个参数计算得到。由式(9)中可以看出本文对航拍图像间单应变换矩阵的推导要求图像中所有点的d相同,也就是要保证O1视点下图像里所有的场景都要在一个成像深度中,否则图像之间就不能满足单应变换。
1.2 测量参数的校正由1.1节可知,通过对航拍参数的测量就可以计算得到对应航拍图像间的单应变换矩阵。其中姿态角可以通过无人机上装有的惯性导航单元(IMU)获得,坐标可由GPS获得,飞行高度可由气压计获得。但是一般情况下,得到的测量结果会受到误差的干扰,这对于单应变换矩阵的计算影响较大。因此要得到准确的单应变换矩阵,就需要对测量的参数进行校正。
根据式(9),如果已知两幅图像的单应变换矩阵H和相机的内参数矩阵K,通过奇异值分解的方法就可以计算出摄像机参数[20]。本文首先在离线情况下对测量系统进行校准,得到参数测量误差的补偿量,然后再通过航拍参数进行图像的配准。参数校准的具体步骤如下:
(1) 在离线情况下通过特征点匹配的方法对航拍图像进行配准,得到图像之间的单应变换矩阵H。
(2) 根据文献[20]的方法由H计算出航拍参数。
(3) 将直接测量的航拍参数与参数的计算结果进行对比(试验选择比较80组结果),然后通过多项式拟合的方法得到测量参数的误差补偿量(本文选择3次多项式)。
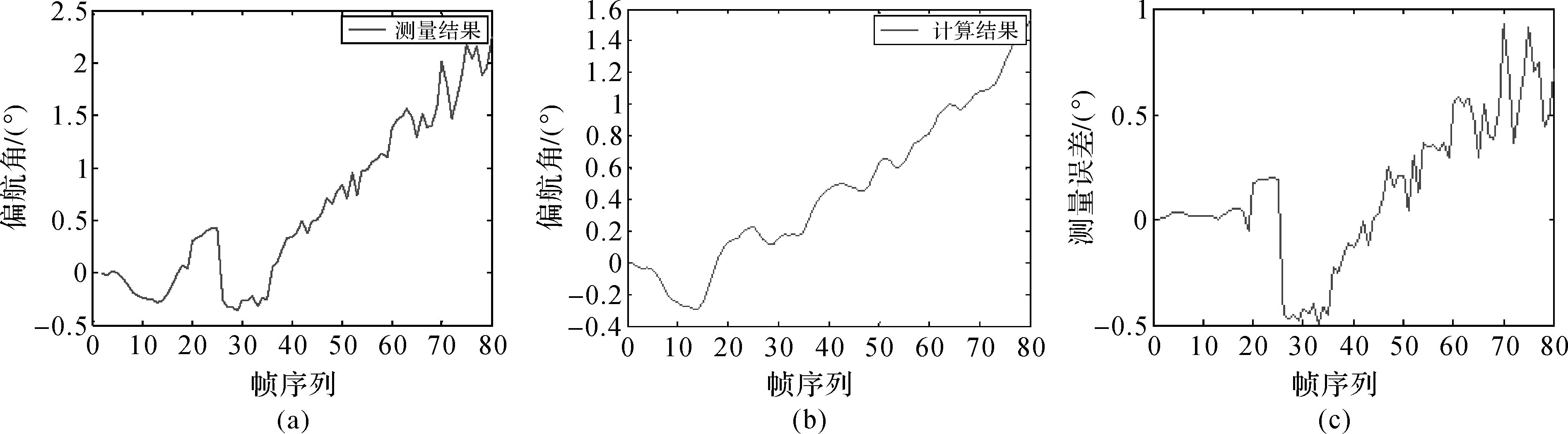
试验结果如图 2所示(以偏航角的校正为例),其中图(a)为直接测量得到的80组结果,图(b)为对应的计算结果,对比这两组结果并计算出测量误差如图(c)所示。由试验结果可以得到测量值与测量误差之间的相关系数为0.902 6,说明这两个量是高度相关的。通过RANSAC算法[15]拟合出测量误差与测量结果的关系为
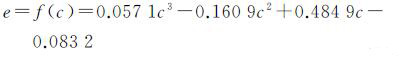 (13)
(13)
|
| 图 2 偏航角的校正 Fig. 2 Correction results of yaw angle |
式中,c为当前的测量结果;e为测量误差。这样就得到了测量结果的误差补偿量,从而就能对测量的航拍参数进行校正,保证了单应变换矩阵计算的精度。
2 多幅图像的拼接 2.1 多幅图像的拼接方法多幅图像的拼接一般就是多次图像的两两拼接。假设有待拼接的图像I1~In,首先拼接图像I1和I2,得到第一次的拼接结果Im1。图像Im1包含两部分内容,一部分是I1变换后的图像I1,2(假设以I2作为基准图像),另一部分则是完整的图像I2,两部分的重叠区域进行加权平均,从而就将I1和I2融合为Im1。然后再拼接Im1和I3得到第2次的拼接结果Im2,直到拼接完所有的图像。这样不断变换基准图的拼接策略可以减少拼接误差的累积[21-22]。
由上节可知根据航拍图像对应的坐标和姿态角可以直接计算出图像间的单应变换矩阵,因此H1,2可直接算出,进而可以得到第1次的拼接结果Im1。但图像Im1并没有对应的航拍参数信息,因此Im1和I3的变换矩阵Hm1,3无法直接得到。所以要实现多幅图像的连续拼接,关键就是要知道上一次的拼接图像与下一幅航拍图像之间的变换矩阵。
2.2 单应矩阵的分解设无人机在位置O1和O2分别拍摄到图像I1和I2,I1到I2的单应变换矩阵为H1,2。从O1到O2可以看作是首先从O1到O3,然后再从O3到O2,如图 3所示。若I3为无人机在O3拍摄到的图像,I1到I3的单应变换矩阵为H1,3,I3到I2的单应变换矩阵为H3,2。
|
| 图 3 单应变换的分解 Fig. 3 Decomposition of homography matrix |
对于图像I1上的任意一点m1(x1,y1),其经过H1,2和H1,3变换后在I2和I3上对应的点分别为m2(x2,y2)和m3(x3,y3)。可以得到
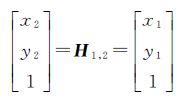 (14)
(14)
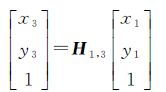 (15)
(15)
而点m3(x3,y3)经过H3,2变换后对应为m2(x2,y2),所以有
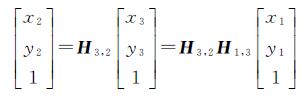 (16)
(16)
因此
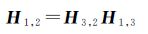 (17)
(17)
这样,就可以将两幅图像的单应变换矩阵分解为两个矩阵,从而可以得到
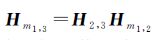 (18)
(18)
式中,H2,3可直接根据图像对应的姿态信息算出,因此只要确定了Hm1,2即可得到Hm1,3。
2.3 推导Hm1,2由于图像Im1是由图像I1和I2拼接得到,其中I1向I2做变换后得到图像I1,2,而图像I2本身没有发生变形。因此I2完整地包含在Im1里面,所以Hm1,2为一个三维平移矩阵。因此设
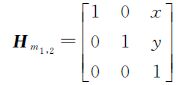 (19)
(19)
式中,平移量x和y可以取图像I2与Im1顶点的平移量。如图 4所示,以A2作为坐标原点,若图像I1和I2的大小分别为m1×n1和m2×n2,则图上各点坐标分别为A2(0,0)、B2(0,n2)、C2(m2,n2)、D2(m2,0),而A1、B1、C1、D1分别可以通过(0,0)、(0,n1)、(m1,n1)、(m2,0)与H1,2运算得到。
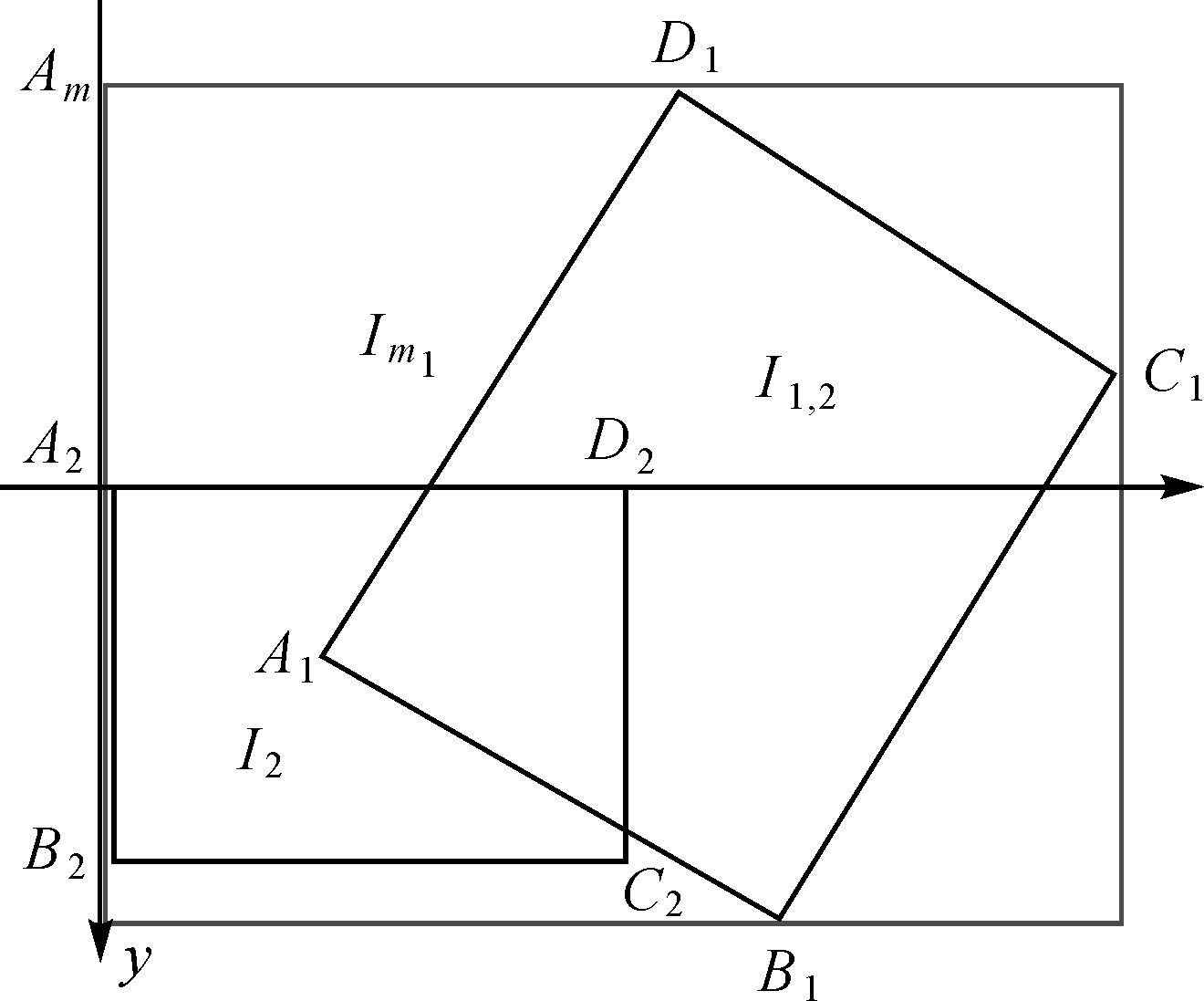
|
| 图 4 两幅图像拼接 Fig. 4 Sample of two images mosaic |
则图像Am(xm,ym)的坐标为
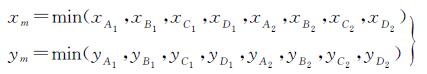 (20)
(20)
因此矩阵Hm1,2的平移分量为
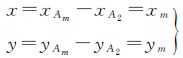 (21)
(21)
这样我们就得到了变换矩阵Hm1,2,进一步由式(18)可以得到矩阵Hm1,3,从而实现多幅图像的连续拼接。
3 相关试验和结果分析试验选取无人机在位置O1-O5所拍摄的5幅图像I1-I5,图像大小为960×540。其中5个视点之间的坐标和姿态角如表 1所示(试验中将O1作为世界坐标原点,测量参数均为校正后的结果)。试验平台为Intel Core(TM) i5-4590 CPU3.30 GHz,16 GB内存,仿真软件为MATLAB7.0。通过相机标定得到相机的内参数矩阵为
| 视点 | 高度(h) | 坐标(x,y,z) | 姿态角(φ,θ,ψ) |
| O1 | 54.48 | (0,0,0) | (1.35,7.61,-6.83) |
| O2 | 54.47 | (-14.76,-1.65,-0.01) | (1.31,7.64,-21.79) |
| O3 | 54.49 | (-19.83,0.45,0.01) | (1.41,7.62,-45.57) |
| O4 | 54.49 | (-20.28,3.29,0.01) | (1.43,7.62,-63.26) |
| O5 | 54.50 | (-16.14,9.49,0.02) | (1.40,7.65,-94.77) |
3.1 图像配准和拼接试验
(1) 利用各视点的坐标和姿态信息,计算各视点与O1之间的单应变换矩阵,然后根据式(17)计算出相邻视点航拍图像之间的变换矩阵。
(2) 根据2.3节计算出Hm1,2,进而由式(18)及H2,3得到Hm1,3。
(3) 同样可以得到Hm2,4与Hm3,5。
为验证本文方法的有效性,选择利用SIFT特征点匹配的方法进行对比,结果如表 2所示。
| 变换矩阵 | 本文的方法 | SIFT特征点匹配法 | ||||
| H1,2 | 0.742 1 | -0.364 7 | 413.306 8 | 0.788 5 | -0.316 2 | 403.943 6 |
| 0.153 0 | 0.778 6 | 12.613 3 | 0.169 9 | 0.837 6 | 0.650 6 | |
| -0.000 2 | -0.000 2 | 1 | -0.000 1 | -0.000 2 | 1 | |
| Hm1,3 | 0.939 3 | -0.194 8 | 261.838 8 | 1.025 4 | -0.188 6 | 264.288 0 |
| -0.153 5 | 0.938 1 | -28.521 1 | -0.206 2 | 1.003 5 | -42.147 9 | |
| 0 | 0 | 1 | 0 | 0.000 1 | 1 | |
| Hm2,4 | 0.985 4 | -0.111 1 | 141.539 4 | 0.966 9 | -0.101 3 | 139.619 2 |
| 0.088 4 | 0.967 4 | -62.830 4 | 0.077 6 | 0.966 4 | -61.947 6 | |
| 0 | 0 | 1 | 0 | 0 | 1 | |
| Hm3,5 | 0.950 6 | -0.210 4 | 267.580 0 | 0.935 7 | -0.168 6 | 263.389 5 |
| 0.173 2 | 0.971 5 | -115.184 0 | 0.165 7 | 1.002 7 | -118.659 | |
| 0 | 0 | 1 | -0.000 1 | 0 | 1 | |
由试验得到的图像间单应变换矩阵进行图像拼接,两种方法的结果如图 5所示。其中Im1~Im4为本文方法的结果,I′m1~I′m4为SIFT方法的结果。

|
| 图 5 拼接结果 Fig. 5 Result of the image mosaic |
3.2 结果分析
图 5(d)、(e)分别为本文方法和用SIFT特征点匹配法的拼接结果,可以看出本文方法与SIFT特征点匹配法的图像拼接效果基本相同,但是在场景细节中还存在一些差距(比如图(d)中篮球场区域的拼接出现错位)。这主要是因为航拍参数测量误差的原因,虽然经过了参数的校正,但是由于校正模型精确度的影响,由航拍参数计算出的单应变换矩阵不可避免地会出现误差。为更好地比较两种方法图像配准的准确程度,定义两幅配准图像中每个匹配特征点的匹配误差和平均配准误差分别为
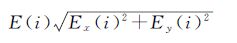 (22)
(22)
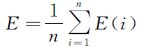 (23)
(23)
式中,Ex(i)与Ey(i)分别表示第i个特征点匹配的坐标误差,定义如下
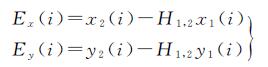 (24)
(24)
x1(i)、x2(i)分别表示第i个特征点在第1幅图像和第2幅图像中的横坐标;y1(i)、y2(i)分别表示第i个特征点在第1幅图像和第2幅图像中的纵坐标。
比较两种方法在4次图像拼接中的配准误差,结果如图 6所示。
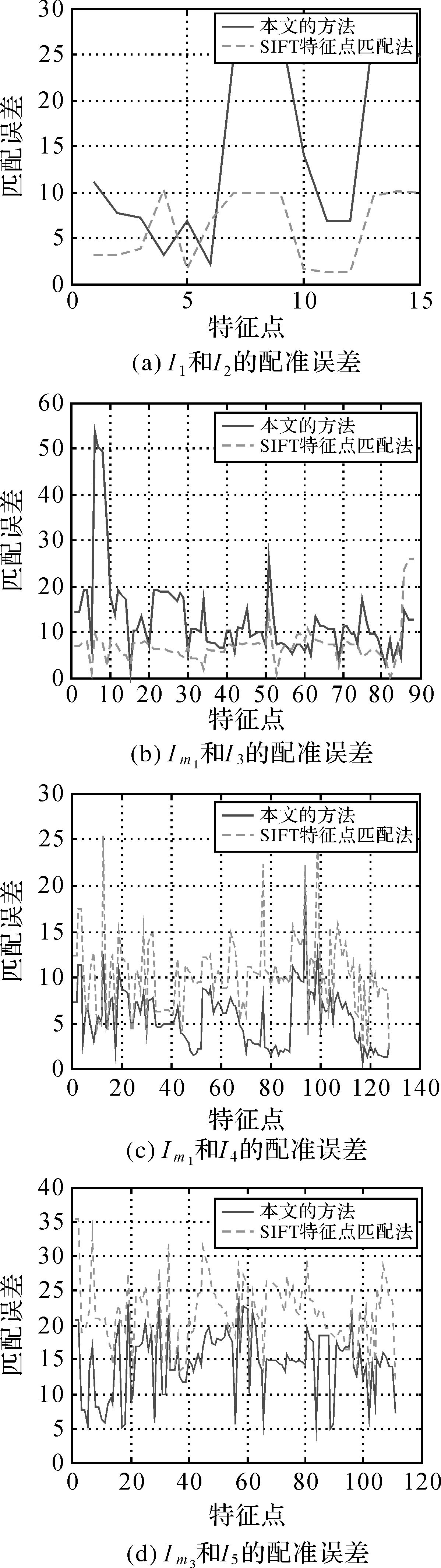
|
| 图 6 图像配准误差结果 Fig. 6 Error result of image registration |
表 3为两种方法的平均匹配误差以及最终的图像拼接时间。可以看出SIFT方法在初始的图像配准中效果好于本文方法,但是随着拼接图像的增加而带来的累积误差,之后该方法的图像配准误差明显增大,而且效果也不如本文的方法。这是因为本文方法通过航拍参数推导图像之间的变换矩阵,连续拼接时拼接图像与航拍图像之间的变换矩阵也是根据航拍图像间的变换矩阵推导而来,因此拼接的累积误差也就只与航拍图像的配准精度相关。也就是说只要得到的航拍图像之间的变换矩阵足够准确,多幅图像连续拼接的误差就不会越来越大。从试验的拼接误差可以发现用特征匹配的方法会导致拼接误差逐渐增大(从6.129增加到21.6),而本文方法的拼接误差基本不随图像的增加而变大。同时可以发现本文方法的拼接速度更快,这是因为该方法只需要进行一些矩阵的运算,而不用提取图像的特征点,因此可以极大地减少图像拼接时间。而对于基于SIFT特征的一类拼接方法,提取图像的SIFT特征极为耗时(提取特征点的耗时占总拼接时间的80%左右)。即便是一些方法采用改进的SIFT描述子(比如SURF等方法)提高特征提取速度,但其拼接耗时仍然大大高于本文的方法。
| 拼接图像 | 特征点数 | 本文方法 | SIFT方法 | |||
| 误差 | 时间/s | 误差 | 时间/s | |||
| Im1 | 15 | 14.895 | 1.007 | 6.129 | 3.565 | |
| Im2 | 88 | 12.715 | 1.144 | 7.039 | 5.244 | |
| Im3 | 129 | 5.483 | 1.228 | 10.229 | 7.043 | |
| Im4 | 111 | 14.519 | 1.333 | 21.600 | 8.679 | |
4 结 论
本文结合无人机航拍的特点,提出了一种利用航拍参数进行图像快速配准的方法。该方法对于航拍图像的质量和场景信息要求不高,主要依赖航拍图像对应的无人机姿态和坐标的测量精度。试验结果显示,本文方法对于低分辨率的航拍视频影像能有效地降低图像拼接的时间,而且对于多幅图像连续拼接产生的累积误差更小。但是对于高分辨率的航拍图像的拼接和几何处理仍需要POS系统提供高精度的测量数据支持。下一步工作是通过建立更好的航拍参数校正模型来提高测量参数的精度,进一步提高航拍图像的拼接效果。
| [1] |
阮芹, 彭刚, 李瑞. 基于特征点的图像配准与拼接技术研究[J].计算机与数字工程,2011, 39 (2) : 141 –144 .
RUAN Qin, PENG Gang, LI Rui. Study on Image Registration and Mosaic Technologhy Based on Surf Feature[J]. Computer &Digital Engineering,2011, 39 (2) : 141 –144 . |
| [2] |
吕金建, 文贡坚, 李德仁, 等. 一种新的基于空间关系的特征匹配方法[J].测绘学报,2008, 37 (3) : 367 –373 .
LV Jinjian, WEN Gongjian, LI Deren, et al. A New Method Based on Spatial Relations for Feature Matching[J]. Acta Geodaetica et Cartographica Sinica,2008, 37 (3) : 367 –373 . |
| [3] |
LOWE D G.Object Recognition from Local Scale-invariant Features[C]//Proceedings of the 7th IEEE International Conference on Computer Vision. Kerkyra: IEEE, 1999: 1150-1157. |
| [4] | LOWER D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision,2004, 60 (2) : 91 –110 . |
| [5] |
KE Yan, SUKTHANKAR R. PCA-SIFT: A More Distinctive Representation for Local Image Descriptors[C]//Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington: IEEE, 2004: 511-517. |
| [6] | MIKOLAJCZYK K, SCHMID C. A Performance Evaluation of Local Descriptors[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2005, 27 (10) : 1615 –1630 . |
| [7] |
BAY H, TUYTELAARS T, VAN GOOL L. SURF: Speeded Up Robust Features[C]//Proceedings of the 9th European Conference on Computer Vision. Berlin: Springer-Verlag, 2006: 404-417. |
| [8] |
罗楠, 孙权森, 耿蕾蕾, 等. 一种扩展SURF描述符及其在遥感图像配准中的应用[J].测绘学报,2013, 42 (3) : 383 –388 .
LUO Nan, SUN Quansen, GENG Leilei, et al. An Extended SURF Descriptor and Its Application in Remote Sensing Images Registration[J]. Acta Geodaetica et Cartographica Sinica,2013, 42 (3) : 383 –388 . |
| [9] | MOREL J M, YU Guoshen. ASIFT: A New Framework for Fully Affine Invariant Image Comparison[J]. SIAM Journal on Imaging Sciences,2009, 2 (2) : 438 –469 . |
| [10] | |
| [11] |
李岩山, 裴继红, 谢维信, 等. 一种新的无人机航拍序列图像快速拼接方法[J].电子学报,2012, 40 (5) : 935 –940 .
LI Yanshan, PEI Jihong, XIE Weixin, et al. A New Fast Automatic Mosaic Method on Unmanned Aerial Vehicle Images[J]. Acta Electronica Sinica,2012, 40 (5) : 935 –940 . |
| [12] |
XIONG Peng, LIU Xianpeng, GAO Chao, et al. A Real-time Stitching Algorithm for UAV Aerial Images[C]//Proceedings of the 2nd International Conference on Computer Science and Electronics Engineering. Paris: Atlantis Press, 2013: 1613-1616. |
| [13] |
何宾, 陶丹, 彭勃. 高实时性F-SIFT图像拼接算法[J].红外与激光工程,2013, 42 (S2) : 440 –444 .
HE Bin, TAO Dan, PENG Bo. High Real-time F-SIFT Image Mosaic Algorithm[J]. Infrared and Laser Engineering,2013, 42 (S2) : 440 –444 . |
| [14] |
杨宇博, 程承旗. 基于分块Harris特征的航拍视频拼接方法[J].北京大学学报(自然科学版),2013, 49 (4) : 657 –661 .
YANG Yubo, CHENG Chengqi. Block Harris Based Mosaic Method for Aerial Video[J]. Acta Scientiarum Naturalium Universitatis Pekinensis,2013, 49 (4) : 657 –661 . |
| [15] | FISCHLER M A, BOLLES R C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Communications of the ACM CACM Homepage Archive,1981, 24 (6) : 381 –395 . |
| [16] |
何贝, 王贵锦, 沈永玲, 等. 结合地理参数的航拍视频实时拼接算法[J].应用科学学报,2012, 30 (2) : 151 –157 .
HE Bei, WANG Guijin, SHEN Yongling, et al. Real-time Mosaicing for Aerial Videos Combined with Geographical Parameters[J]. Journal of Applied Sciences: Electronics and Information Engineering,2012, 30 (2) : 151 –157 . |
| [17] |
徐玉华, 龚文全, 苏昂, 等. 近似平面场景多视点图像拼接算法[J].国防科技大学学报,2014, 36 (2) : 148 –155 .
XU Yuhua, GONG Wenquan, SU Ang, et al. Multi-viewpoint Image Mosaicing Algorithm for Roughly Planar Scenes[J]. Journal of National University of Defense Technology,2014, 36 (2) : 148 –155 . |
| [18] |
YAHYANEJAD S,WISCHOUNIG-STRUCL D, QUARITSCH M, et al. Incremental Mosaicking of Images from Autonomous, Small-scale UAVs[C]//Proceedings of the 2010 Seventh IEEE International Conference on Advanced Video and Signal Based Surveillance. Boston: IEEE, 2010: 329-336. |
| [19] |
朱云芳. 摄像机径向畸变校正和内参估计的单图标定方法[J].光电工程,2012, 39 (9) : 125 –131 .
ZHU Yunfang. Calibration of Radial Distortion and Intrinsic Parameters Using a Single Image[J]. Opto-Electronic Engineering,2012, 39 (9) : 125 –131 . |
| [20] |
丁建华, 姚明海, 赵瑜. 基于单应性矩阵的机器人视觉伺服系统研究[J].机电工程,2012, 29 (12) : 1485 –1489 .
DING Jianhua, YAO Minghai, ZHAO Yu. Study of Visual Servoing System of Robot Based on Homography Matrix[J]. Journal of Mechanical &Electrical Engineering,2012, 29 (12) : 1485 –1489 . |
| [21] |
唐琎, 谷士文, 蔡自兴. 图象拼接误差的理论分析[J].小型微型计算机系统,2003, 24 (12) : 2185 –2189 .
TANG Jin, GU Shiwen, CAI Zixing. Theoretical Analysis on Image Stitching Error[J]. Mini-Micro Systems,2003, 24 (12) : 2185 –2189 . |
| [22] |
李从利, 薛模根, 冷晓艳, 等. 空中侦察序列图像连续拼接的累积误差分析与消除[J].中国图象图形学报,2008, 13 (4) : 814 –819 .
LI Congli, XUE Mogen, LENG Xiaoyan, et al. Analysis and Elimination on Aerial Recon Sequential Image Stitching Accumulative Error[J]. Journal of Image and Graphics,2008, 13 (4) : 814 –819 . |




