遥感图像融合是将不同传感器对同一目标的图像经过一定的处理方式最终综合成一幅图像的技术,同时也可以看作是一幅图像在保留自身有用信息的基础上加入了新的有用信息,其中最典型的应用就是遥感影像中全色图像与多光谱图像的融合,融合后的图像能更加准确和全面地描述所研究的对象[1]。
图像融合的方法众多,不同的融合方法得到的融合效果也各不相同[2-3]。图像融合方法可以分为像素级、特征级和决策级3种类型,这其中像素级的融合方法适应性最强,也是最常用的融合方法,本文中重点讨论像素级的融合方法。像素级的融合方法一般都需要将低分辨率图像进行重采样,使低分辨率图像与高分辨率图像有相同的尺寸大小。像素级的融合方法可以根据其融合的思路进一步分为3类,基于成分替换的融合方法[4-5]、基于模型的融合方法[6-9]和基于多分辨率分析的融合方法[10-11]。不过虽然融合的思路有差异,但最终融合的效果一般都是将高频信息作为新加入的有用信息采用一定的融合方法与低分辨率图像融合在一起[12-13]。这其中对图像中的地物频率进行分析以及定量的确定高频信息是能否得到高质量融合图像的重要步骤,同时图像信号频率与图像分辨率之间有很重要的联系,在用不同分辨率的图像融合时,需要定量的确定融合前后图像中的分辨率从而能够达到最好的融合效果。
目前,人们关注比较多的问题是图像融合的方法和图像融合后的图像质量,而对融合图像中地物频率的变化研究较少。本文结合多种图像融合的方法首先从水平方向对图像融合前后频率的变化进行了分析和公式推导,然后将其扩展到二维,给出了不同分辨率图像进行图像融合后频率的变化规律,最后结合遥感图像对本文中的结论进行了验证。
1 信号频率分析本文中首先采用水平方向的图像信号作为重点研究的对象,使用傅里叶变换将图像信号从空域转化到频域,对图像融合前后的信号频率进行分析。在实际应用中,进行融合的图像频率往往是没有固定范围的,而且融合之前要进行配准和重采样的过程。根据奈奎斯特定理,需要离散系统的奈奎斯特频率高于被采样信号的最高频率或带宽,才能避免混叠现象。本文中根据高采样率奈奎斯特频率、低采样率奈奎斯特频率和信号频率三者之间的关系进行分类讨论。
设正弦信号的表达式为
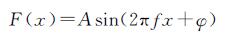 (1)
(1)
式中,A为振幅;f为频率;φ为相位。图像融合中使用不同采样率对信号进行采样,设高采样率为F1,低采样率为F2,高采样率得到的信号为g1(x),低采样率得到的信号为g2(x),融合的过程可以看作是两种不同采样率得到信号的叠加,不同的融合方法使用的叠加方法也不同,这里用下式表示融合的过程
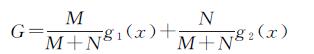 (2)
(2)
式中,MM+N、NM+N分别表示归一化后高采样率信号和低采样率信号对应的系数。不同的融合方法对应有不同的M和N值,从公式可以发现,融合之后高采样率和低采样率得到的信号幅度相对于融合之前会有所降低。
因为信号频率的2倍2f、高采样率F1和低采样率F2三者之间的关系对融合后的频率有很重要的影响,下面分为2f<F2、F2<2f<F1、F1<2f进行讨论。
当2f<F2时,根据采样定律,高采样率和低采样率都能获取信号频率,则g1(x)和g2(x)可以分别表示为
 (3)
(3)
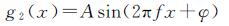 (4)
(4)
融合后的表达式为
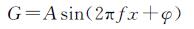 (5)
(5)
当F2<2f<F1时,高采样率能获取信号频率,低采样率则不能准确获取信号频率,g1(x)的表达式为
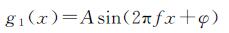 (6)
(6)
g2(x)的表达式为
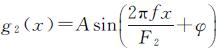 (7)
(7)
式中,x为正整数,公式(7)可以进一步表示为
 (8)
(8)
式中,n为整数;x为正整数。对于低采样率得到的信号,由于不能准确获取信号频率,可以看作是信号频率为f-nF2的信号,其最终得到的信号频率是满足f-nF2<2f的值
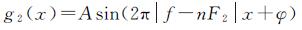 (9)
(9)
式中,n为整数且满足f-nF2<2f,融合后的表达式为
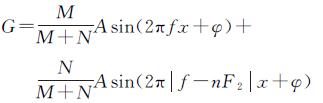 (10)
(10)
式中,n为整数且满足f-nF2<2f。
当F1<2f时,高采样率和低采样率均不能准确获得信号频率,则融合后的表达式为
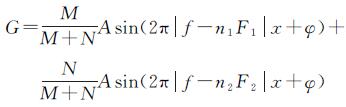 (11)
(11)
式中,n1、n2为整数,f≠F1且满足f-n1F1<2f及f-n2F2<2f。在融合时,低采样率和高采样率往往存在倍数关系,这种倍数关系对最终的信号频率有一定的影响,这种影响主要体现在F1<2f的情况。在F1<2f时如果F1=2F2,则当信号频率满足
| 变化范围 | 高采样率F1得到的频率f1 | 低采样率F2得到的频率f2 | f1和f2的关系 |
| 2f<F2 | f | f | f1=f2 |
| F2<2f<F1 | f | f-nF2(n为整数,且f-nF2<2f) | f1≠f2 |
| F1<2f | f-n1F1(n为整数,且f-n1F1<2f) | f-n2F2(n为整数,且f-n2F2<2f) | 当满足F1=kF2和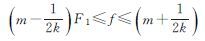 (k、m为正整数,f≠F1)时,f1=f2 (k、m为正整数,f≠F1)时,f1=f2 |
通过表 1可以看到图像融合对图像质量的改变主要体现在F2<2f<F1的情况,在F2<2f<F1时原始信号频率能够在融合图像上得到一定程度的呈现,提升和恢复了低采样率得到的信号频率,不过相比于高采样率图像,由公式(2)可知其得到的信号幅度会有所下降。考虑到图像融合受影响的频率主要集中在F2<2f<F1时,高采样率F1和低采样率F2相差越大,则融合图像与低采样率图像相比信号频率的恢复程度也越大。同时可以发现当高采样率F1和低采样率F2存在两倍关系时,高采样率F1和低采样率F2得到相同信号频率的范围最大,因此在高采样率F1和低采样率F2存在两倍关系时,融合图像与高采样率图像相比信号的恢复程度最为接近。
2 地物的频率分析将地物作为矩形脉冲看待,以水平方向作为研究对象,设非周期矩形脉冲信号的表达式为
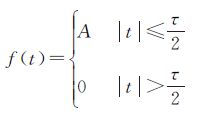 (12)
(12)
由傅里叶变换,可得
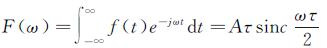 (13)
(13)
考虑到信号的频谱分量主要集中在零频到第一个过零点之间,此宽度一般作为有效带宽,因此对于遥感图像宽度为m的地物,其有效带宽为2π/m,传感器采样距离为H时其对应的采样频率为2π/H。同时由公式(13)可以看到虽然主要地物频率为2π/m,但矩形波在频域是无限延伸的,即表 1中频率变化范围的3种不同情况都会在融合图像中出现。因此由之前的分析可知当对高分辨率图像和低分辨率图像进行融合时,在融合方法和地物相同的情况下,对于同一低分辨率图像,高分辨率图像和低分辨率图像的分辨率相差越大,则融合图像与低分辨率图像相比图像质量的提升程度也越大。对于同一高分辨率图像,当高分辨率图像和低分辨率图像的分辨率存在两倍关系时,融合图像与高采样率图像相比图像质量最为接近。
3 试 验根据高采样率奈奎斯特频率、低采样率奈奎斯特频率和信号频率的关系,分为高采样率奈奎斯特频率和低采样率奈奎斯特频率均大于信号频率、信号频率位于高采样率奈奎斯特频率和低采样率奈奎斯特频率之间,以及高采样率奈奎斯特频率和低采样率奈奎斯特频率均小于信号频率3种情况对水平方向的信号频率变化进行讨论。
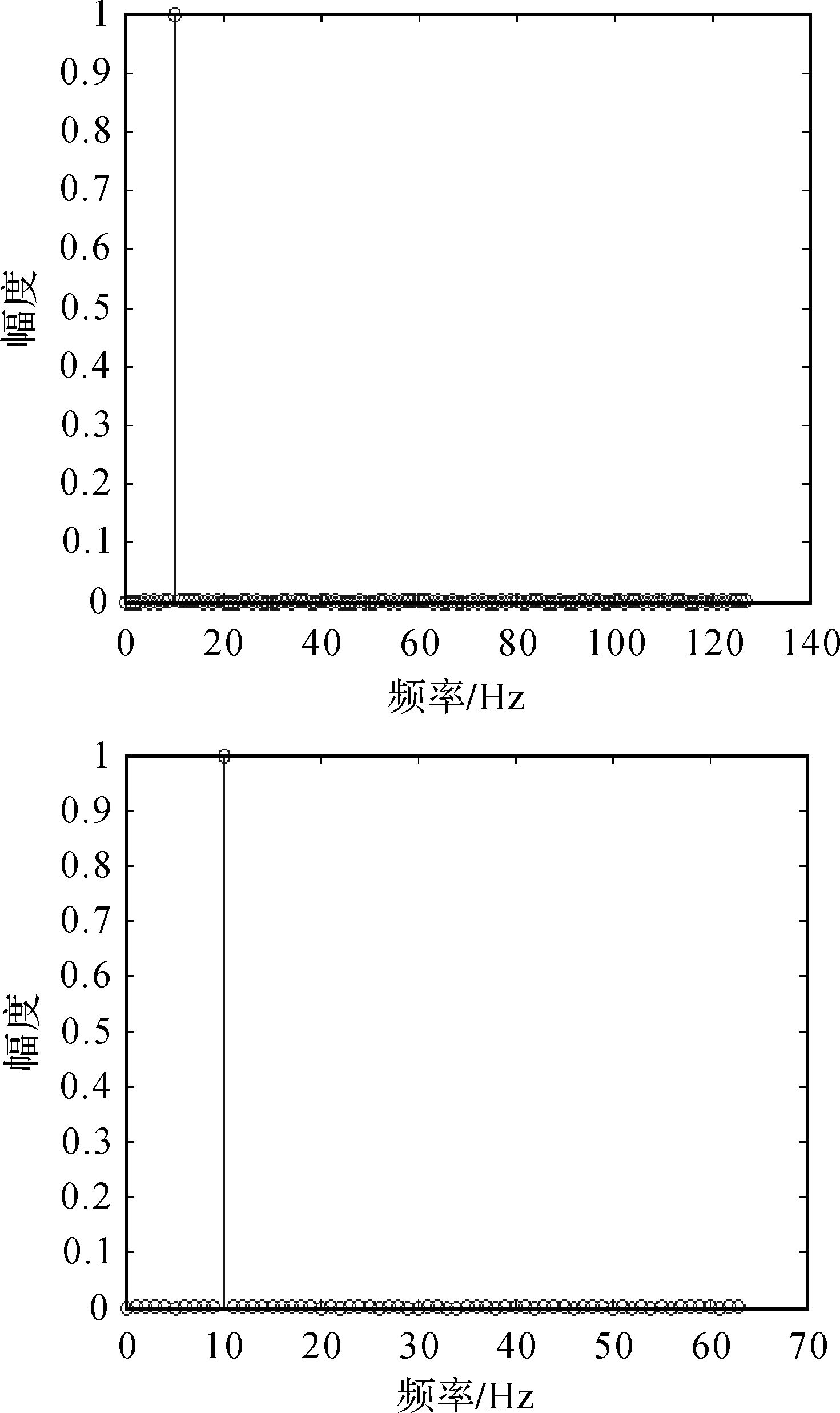
3.1 高采样率奈奎斯特频率和低采样率奈奎斯特频率均大于信号频率设试验中图像信号的频率为10 Hz,幅度为1,相位设为0,信号长度为固定值,高采样频率为256 Hz,低采样频率为128 Hz,如图 1所示,上图为高采样率图像,下图为低采样率图像,其对应的幅度-频率曲线如图 2所示。

|
| 图 1 高采样率图像与低采样率图像 Fig. 1 High sampling rate image and low sampling rate image |
|
| 图 2 融合前的幅度-频率图 Fig. 2 The amplitude-frequency diagram before image fusion |
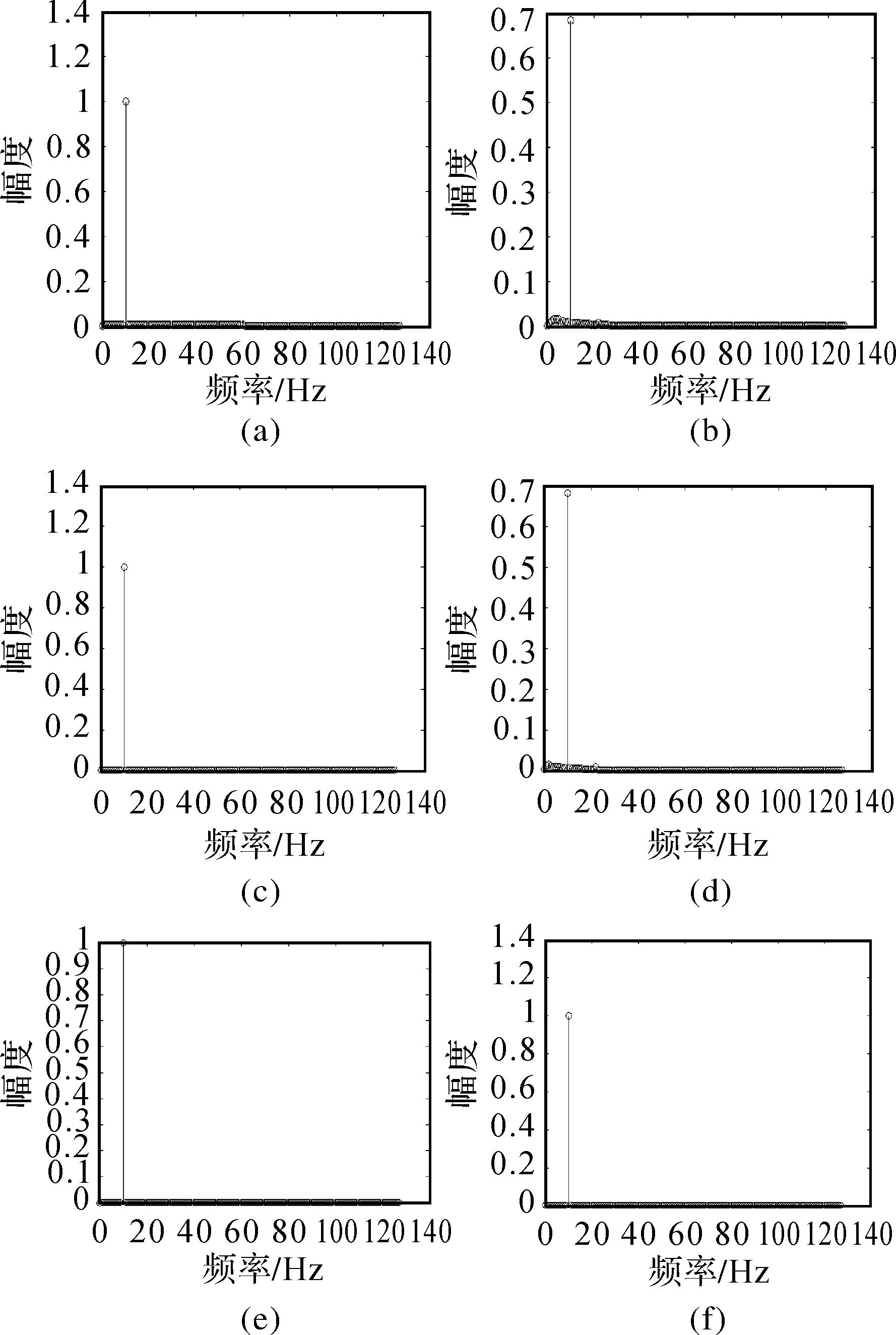
图 2中左图为高采样率图像,右图为低采样率图像,从图中可以看到高采样率图像和低采样率图像中信号频率相同。融合之前要对低采样率图像进行重采样,以达到与高采样率相同的采样率,重采样后的图像频率与重采样前相同。将高采样率图像与重采样后的图像进行haar小波融合[14]、梯度金字塔融合[15]、拉普拉斯金字塔融合[16]、FSD金字塔融合、PCA方法融合[17]、DBSS小波融合[18]得到图像的幅度-频率图如图 3所示。
|
| 图 3 融合后的图像与幅度-频率图 Fig. 3 The amplitude-frequency diagram after image fusion |
图 3(a)为haar小波融合、(b)为梯度金字塔融合、(c)为拉普拉斯金字塔融合、(d)为FSD金字塔融合、(e)为PCA方法融合、(f)为DBSS小波融合。由图 3可以发现融合后信号的频率没有发生变化,即高采样率奈奎斯特频率和低采样率奈奎斯特频率均大于信号频率的情况下图像融合的处理不会影响图像中的信号频率,但不同的融合方法会使融合后的信号幅度有所区别。
3.2 信号频率位于高采样率奈奎斯特频率和低采样率奈奎斯特频率之间设试验中图像信号的频率为100 Hz,幅度为1,信号长度为固定值,高采样频率仍为256 Hz,低采样频率仍为128 Hz,对低采样率的图像进行重采样,将高采样率图像与重采样后的低采样率图像进行haar小波融合、梯度金字塔融合、拉普拉斯金字塔融合、FSD金字塔融合、PCA融合、DBSS小波融合,得到的信号频率见表 2。
| 信号频率 | 高采样率 | 低采样率 | 融合方法 | 融合后的信号频率 |
| 100 | 256 | 128 | haar小波融合 | 100,28 |
| 100 | 256 | 128 | 梯度金字塔融合 | 100,28 |
| 100 | 256 | 128 | 拉普拉斯金字塔融合 | 100,28 |
| 100 | 256 | 128 | FSD金字塔融合 | 100,28 |
| 100 | 256 | 128 | PCA融合 | 100,28 |
| 100 | 256 | 128 | DBSS小波融合 | 100,28 |
由表 2可以发现融合后信号的频率有两个峰值。这是因为虽然高采样率图像能够准确获取信号频率,但是低采样率的图像欠采样导致其不能准确获得信号频率,使本应该在同一频率下进行的图像融合在不同频率的信号之间进行,融合后两种不同的频率都会融合进图像中,同时幅度相较于融合前会有所降低。
3.3 高采样率奈奎斯特频率和低采样率奈奎斯特频率均小于信号频率设试验中图像信号的频率为200 Hz,幅度为1,信号长度为固定值,高采样频率为256 Hz,低采样频率为128 Hz,将高采样率图像与重采样后的图像进行haar小波融合、梯度金字塔融合、拉普拉斯金字塔融合、FSD金字塔融合、PCA方法融合、DBSS小波融合,融合结果见表 3。
| 信号频率 | 高采样率 | 低采样率 | 融合方法 | 融合后的信号频率 |
| 200 | 256 | 128 | haar小波融合 | 56 |
| 200 | 256 | 128 | 梯度金字塔融合 | 56 |
| 200 | 256 | 128 | 拉普拉斯金字塔融合 | 56 |
| 200 | 256 | 128 | FSD金字塔融合 | 56 |
| 200 | 256 | 128 | PCA融合 | 56 |
| 200 | 256 | 128 | DBSS小波融合 | 56 |
由表 3可以发现虽然融合后的频率与信号频率不同,但仍具有唯一的频率,这是因为信号频率满足
| 信号频率 | 高采样率 | 低采样率 | 融合方法 | 融合后的信号频率 |
| 200 | 256 | 120 | haar小波融合 | 40,56 |
| 200 | 256 | 120 | 梯度金字塔融合 | 40,56 |
| 200 | 256 | 120 | 拉普拉斯金字塔融合 | 40,56 |
| 200 | 256 | 120 | FSD金字塔融合 | 40,56 |
| 200 | 256 | 120 | PCA融合 | 40,56 |
| 200 | 256 | 120 | DBSS小波融合 | 40,56 |
由表 4可以看到,当高采样率和低采样率不满足两倍关系时,融合后的图像将同时具有两种信号频率。通过试验可知本文中对于信号频率公式的推导是正确的。
为了进一步验证本文中的结论,使用PCA融合算法对不同来源和背景的全色图像和多光谱图像进行融合,使用图像的来源分别为资源三号图像[19]、DigitalGlobe网站公开的影像产品样例数据和ETM+图像,试验结果如图 4。

|
| 图 4 全色图像、多光谱图像和PCA融合图像 Fig. 4 The panchromatic images,multi-spectral images and fused images by PCA |
图 4(a)图为资源三号全色影像,分辨率为2.1 m;(b)图为资源三号多光谱影像,分辨率为5.8 m;(c)图为PCA融合图像;(d)和(e)为来自于DigitalGlobe网站公开的影像产品样例数据,(d)为全色影像,分辨率为0.5 m,(e)为多光谱影像,分辨率为1.8 m;(f)为PCA融合图像;(g)为ETM+全色影像,分辨率为15 m;(h)为ETM+345波段影像,分辨率为30 m;(i)为PCA融合图像。使用均值、标准差、信息熵、平均梯度[20]对融合前后的图像进行评价,如表 5。
| 图像 | 均值 | 标准差 | 平均梯度 | 信息熵 |
| a | 136.201 5 | 65.398 7 | 16.348 7 | 3.064 1 |
| b | 111.268 4 | 61.661 0 | 5.317 6 | 4.886 0 |
| c | 126.357 4 | 62.068 7 | 11.975 4 | 3.904 5 |
| d | 181.635 2 | 59.348 1 | 28.836 5 | 1.261 5 |
| e | 153.674 0 | 43.268 4 | 21.635 4 | 1.568 4 |
| f | 159.302 5 | 45.654 1 | 23.369 8 | 1.456 7 |
| g | 136.207 4 | 27.746 1 | 11.185 3 | 4.994 1 |
| h | 70.196 2 | 19.652 3 | 6.951 0 | 6.086 9 |
| i | 135.689 6 | 25.001 9 | 9.981 0 | 5.147 7 |
其中,图像均值反映图像的平均亮度,如果均值适中,则表明视觉效果良好。图像方差是图像整体灰度值偏离其均值的程度,是表示图像对比度大小的指标,也能表示图像信息量的大小,图像方差越大,图像的动态范围就越大。图像的信息熵是表达图像信息量大小信息丰富程度的一个主要指标,从图像直方图的角度看,直方图分布越平坦均匀,图像信息熵就越大,当图像所有灰度级分布概率都相同时(即每个灰度级的像素个数都相同时),即直方图为平行于灰度轴的一条直线时,图像信息熵达到最大值。融合图像的信息越大,表明融合图像的信息量就越大越丰富。平均梯度也称为清晰度,一般平均梯度越大,图像层次越丰富,则图像就越清晰。平均梯度反映影像的清晰度,同时也表达图像中的微小细节反差和纹理变化特征。方差、信息熵、平均梯度也是对图像中频率信息的重要体现。
由表 5可知在都使用PCA融合方法的情况下,(c)图相比于(b)图图像质量的提升程度要大于(f)图相比于(e)图,这是因为(b)图与(a)图分辨率的差距相较于(e)图与(d)图分辨率的差距更近。同时也可以发现(i)图与(g)图图像质量的差距相较于其他两组图像更近,这是因为分辨率正好是两倍关系的原因。
4 结 论本文从图像水平方向进行研究,对融合图像的频率变化进行了公式推导和试验分析,通过试验可以得到以下结论:
(1) 当高采样率奈奎斯特频率和低采样率奈奎斯特频率均大于图像信号频率时,融合后图像的信号频率不会发生变化。图像信号频率位于高采样率奈奎斯特频率和低采样率奈奎斯特频率之间时,融合之后图像不再是由单一频率构成,而是由两种不同的频率混合构成,频率中会包含高采样率所获得的原始信号频率f以及低采样率欠采样得到的信号频率f-nF2,其中n为整数且满足f-nF2<2f。高采样率奈奎斯特频率和低采样率奈奎斯特频率均小于图像信号频率时,融合后无法得到图像中的信号频率f,得到的信号频率分别为f-n1F1和f-n2F2其中n1和n2为整数且满足f-n1F1<2f和f-n2F2<2f,当高采样率与低采样率的存在倍数关系时,在满足
(2) 将地物作为矩形脉冲看待,以水平方向作为研究对象,对于遥感图像宽度为m的地物,其有效带宽为2π/m,而矩形波在频域是无限延伸的,2f<F2、F2<2f<F1、F1<2f 3种情况都会出现。图像融合对图像质量的改变主要体现在F2<2f<F1的情况,在F2<2f<F1时原始地物频率能够在融合图像上得到一定程度的呈现,使低采样率得到的地物频率能够提升和恢复,不过相比于高采样率图像,其得到的地物信号幅度会有所下降。
(3) 当对高分辨率图像和低分辨率图像进行融合时,在融合方法和地物相同的情况下,对于同一低分辨率图像,高分辨率图像和低分辨率图像的分辨率相差越大,则融合图像与低分辨率图像相比图像质量的提升程度也越大。对于同一高分辨率图像,当高分辨率图像和低分辨率图像的分辨率存在两倍关系时,融合图像与高采样率图像相比图像质量最为接近。
在实际应用中,应结合人们对融合图像的需要选择合适分辨率的图像和融合方法以达到最佳的融合效果,本文的研究结论对如何通过融合得到更高质量的图像有一定的指导意义。
| [1] | AIAZZI B, BARONTI S, LOTTI F, et al. A Comparison Between Global and Context-Adaptive Pansharpening of Multispectral Images[J]. IEEE Geoscience and Remote Sensing Letters,2009, 6 (2) : 302 –306 . |
| [2] | CHOI J, YEOM J, CHANG A, et al. Hybrid Pansharpening Algorithm for High Spatial Resolution Satellite Imagery to Improve Spatial Quality[J]. IEEE Geoscience and Remote Sensing Letters,2013, 10 (3) : 490 –494 . |
| [3] |
李军, 周月琴, 李德仁. 影像局部直方图匹配滤波技术用于遥感影像数据融合[J].测绘学报,1999, 28 (3) : 226 –232 .
LI Jun, ZHOU Yueqin, LI Deren. A New Fusion Approach Based on Local Histogram Matching Filtering Techniques[J]. Acta Geodaetica et Cartographica Sinica,1999, 28 (3) : 226 –232 . |
| [4] | RAHMANI S, STRAIT M, MERKURJEV D, et al. An Adaptive IHS Pan-sharpening Method[J]. IEEE Geoscience and Remote Sensing Letters,2010, 7 (4) : 746 –750 . |
| [5] | AIAZZI B, BARONTI S, SELVA M. Improving Component Substitution Pansharpening through Multivariate Regression of MS+Pan Data[J]. IEEE Transactions on Geoscience and Remote Sensing,2007, 45 (10) : 3230 –3239 . |
| [6] | LI Shutao, YIN Haitao, FANG Leyuan. Remote Sensing Image Fusion via Sparse Representations over Learned Dictionaries[J]. IEEE Transactions on Geoscience and Remote Sensing,2013, 51 (9) : 4779 –4789 . |
| [7] | JIANG Cheng, ZHANG Hongyan, SHEN Huanfeng, et al. Two-step Sparse Coding for the Pan-sharpening of Remote Sensing Images[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2014, 7 (5) : 1792 –1805 . |
| [8] | ZHU Xiaoxiang, BAMLER R. A Sparse Image Fusion Algorithm with Application to Pan-sharpening[J]. IEEE Transactions on Geoscience and Remote Sensing,2013, 51 (5) : 2827 –2836 . |
| [9] | DURAN J, BUADES A, COLL B, et al. A Nonlocal Variational Model for Pansharpening Image Fusion[J]. Siam Journal on Imaging Sciences,2014, 7 (2) : 761 –796 . |
| [10] | CHOI J, YEOM J, CHANG A, et al. Hybrid Pansharpening Algorithm for High Spatial Resolution Satellite Imagery to Improve Spatial Quality[J]. IEEE Geoscience and Remote Sensing Letters,2013, 10 (3) : 490 –494 . |
| [11] | YIN Haitao, LI Shutao. Pansharpening with Multiscale Normalized Nonlocal Means Filter: a Two-step Approach[J]. IEEE Transactions on Geoscience and Remote Sensing,2015, 53 (10) : 5734 –5745 . |
| [12] |
丰明博, 刘学, 赵冬. 多/高光谱遥感图像的投影和小波融合算法[J].测绘学报,2014, 43 (2) : 158 –163 .
FENG Mingbo, LIU Xue, ZHAO Dong. A Fusion Method of Hyperspectral and Multispectral Images Based on Projection and Wavelet Transformation[J]. Acta Geodaetica et Cartographica Sinica,2014, 43 (2) : 158 –163 . |
| [13] |
窦闻, 陈云浩, 何辉明. 光学遥感影像像素级融合的理论框架[J].测绘学报,2009, 38 (2) : 131 –137 .
DOU Wen, CHEN Yunhao, HE Huiming. Theoretical Framework of Optical Remotely Sensed Image Fusion[J]. Acta Geodaetica et Cartographica Sinica,2009, 38 (2) : 131 –137 . |
| [14] | NUNEZ J, OTAZU X, FORS O, et al. Multiresolution-based Image Fusion with Additive Wavelet Decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing,1999, 37 (3) : 1204 –1211 . |
| [15] | PETROVIC V S, XYDEAS C S. Gradient-based Multiresolution Image Fusion[J]. IEEE Transactions on Image Processing,2004, 13 (2) : 228 –237 . |
| [16] |
陈浩, 王延杰. 基于拉普拉斯金字塔变换的图像融合算法研究[J].激光与红外,2009, 39 (4) : 439 –442 .
CHEN Hao, WANG Yanjie. Research on Image Fusion Algorithm Based on Laplacian Pyramid Transform[J]. Laser &Infrared,2009, 39 (4) : 439 –442 . |
| [17] | SHAH V P, YOUNAN N H, KING R L. An Efficient Pan-sharpening Method via a Combined Adaptive PCA Approach and Contourlets[J]. IEEE Transactions on Geoscience and Remote Sensing,2008, 46 (5) : 1323 –1335 . |
| [18] | LEWIS J J, O’CALLAGHAN R J, NIKOLOV S G, et al. Pixel-and Region-based Image Fusion with Complex Wavelets[J]. Information Fusion,2007, 8 (2) : 119 –130 . |
| [19] |
李德仁. 我国第一颗民用三线阵立体测图卫星——资源三号测绘卫星[J].测绘学报,2012, 41 (3) : 317 –322 .
LI Deren. China’s First Civilian Three-line-array Stereo Mapping Satellite: ZY-3[J]. Acta Geodaetica et Cartographica Sinica,2012, 41 (3) : 317 –322 . |
| [20] | CHU Heng, CHEN Huagang, Zhu Weile. A New Remote Sensing Image Fusion Algorithm in the Decimated Wavelet Domain[J]. Opto-Electronic Engineering,2009, 36 (2) : 91 –95 . |


