2. 武汉大学国家领土主权与海洋权益协同创新中心,湖北 武汉 430079 ;
3. 中铁第四勘察设计院集团有限公司,湖北 武汉430063 ;
4. 渤海大学信息科学与技术学院,辽宁 锦州 121013
2. Collaborative Innovation Center for Territorial Sovereignty and Maritime Rights, Wuhan University, Wuhan 430079, China ;
3. China Railway Siyuan Survey and Design Group CO.,LTD., Wuhan 430063, China ;
4. School of Information Science and Technology,Bohai University, Jinzhou 121013, China
球形全景影像是多台相机通过对360°拍摄的影像进行拼接,形成长方形影像,并投影到球面形成的,可视为以球心为投影中心、半径为焦距、球面为成像面、视场角为360°的虚拟相机拍摄的影像,其位姿估计解求的是类似相机位姿估计的旋转矩阵和平移向量。球形全景影像可全方位地体现场景细节信息,具有场景全覆盖的优势,在街景地图导航服务、景观地图[1]、月球车巡视探测[2]、虚拟现实以及移动机器人视觉[3-5]等领域都有广泛应用。
针对全景影像的研究主要集中在如何实现相机检校[6]、影像拼接缝合[7-10]和影像匹配[11-12]方面,关于球形全景影像位姿估计和三维重建的研究仍处于起步阶段,其中文献[11]利用GPS/IMU提供的位姿初值进行球形全景影像序列光束法区域网平差,解算球形全景影像位姿;文献[13-14]提出了基于相对定向-绝对定向、双球面投影几何的可量测球形立体全景模型,进行球形全景影像位姿估计和三维量测;文献[15]提出了一种针对高噪声环境的蒙特卡罗解法,基于已知地理参考影像实现地面车载全景影像序列的精确定位;文献[16]深入比较了多镜头组合型全景相机的严格成像模型和理想成像模型之间位姿估计和定位精度的差异;文献[17]针对全景相机和定位定姿系统(POS)集成的车载移动测图系统,提出一种外方位元素标定的方法。
上述球形全景影像位姿估计方法大多需要GPS/IMU提供已知的位姿数据,增加了数据采集的成本和复杂性;或者需要进行迭代,虽精度高,但位姿解算精度容易受到迭代初值的影响,算法效率低,鲁棒性差。为解决这个问题,本文引入了Lepetit和Moreno提出的透视成像摄像机高精度快速位姿估计算法EPnP(efficient perspective-n-point)[18],其核心思想是将n(n≥4)个物方点表示为4个虚拟控制点的加权和,通过物方点和像点的对应关系估计虚拟控制点的摄像机坐标,即可求得物方点的摄像机坐标,最后通过Horn绝对定位算法[19]求解旋转矩阵和平移向量。由于Horn绝对定位算法至少需要3个控制点,为提高定位精度至少需要1个多余观测值,故至少需要4个控制点,虚拟控制点取控制点个数范围最小值4。该算法无须迭代求解,时间复杂度为O(n),且能达到较高的精度。
本文采用文献[16]中的理想成像模型,构建了球形全景影像的投影模型和共线条件方程,提出了球形全景影像位姿估计的改进EPnP算法,并与球形全景影像位姿估计的后方交会算法进行比较。仿真试验和实际试验结果表明,本文提出的方法无须迭代求解,更为稳健快速,即使控制点数目较少也能达到高精度,重投影误差可控制在3.00像素左右。
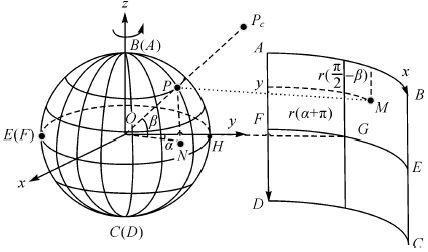
1 球形全景影像的投影模型构建球形全景影像是多台相机通过对360°拍摄的影像进行拼接,形成长方形影像,并投影到球面形成的。如图 1所示,设全景球的半径为r,全景影像ABCD长度方向水平覆盖整个球面,总长度W=2πr,宽度方向竖直覆盖半个球面,总长度H=πr。以点A为原点,指向B为x轴,指向D为y轴,建立像平面坐标系,同时以球心O为原点,指向平面全景影像中心G在全景球上的对应点H为y轴,赤道截面为Oxy平面,建立像空间直角坐标系。长方形全景影像ABCD上任意一点M(x,y),在球形全景影像上存在对应的映射点P(X,Y,Z),其对应的物方点在像空间坐标系中的坐标为Pc(Xc,Yc,Zc)。
|
| 图 1 球形全景影像与平面全景影像的映射关系 Fig. 1 The mapping relationship between spherical panoramic image and plane panoramic image |
如图 1所示,设点P在Oxy平面上的投影为N点,连接ON与Y轴的夹角为α∈[-π,π],与OP的夹角为β∈[-π/2,π/2],顺时针为正,逆时针为负,则根据图 1所示的映射关系,点M和点P的坐标值可表示为如下形式
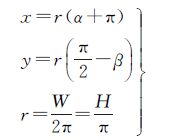 (1)
(1)
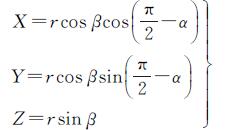 (2)
(2)
由式(1)、式(2)可推导得像平面坐标点M到球形全景像空间坐标点P的映射关系如式(3)
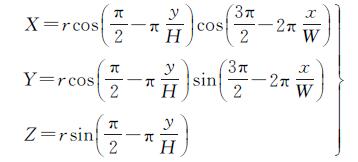 (3)
(3)
同时,点Pc、点P与全景球心O满足共线条件,可列方程如式(4)
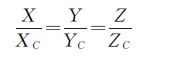 (4)
(4)
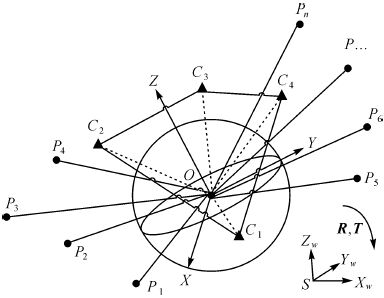
EPnP算法估计的是透视成像摄像机的位姿[20],可将球形全景影像视为以球心为投影中心,半径为焦距,球面为成像面,视场角为360°的虚拟相机拍摄的影像,从而通过EPnP算法求解球形全景影像的位姿。如图 2所示,球形全景影像的位姿由球形全景像空间坐标系OXYZ相对于物方空间坐标系SXwYwZw的旋转矩阵R和平移向量T(全景球心O的物方空间坐标)表示,球形全景影像位姿估计即对R、T进行求解。
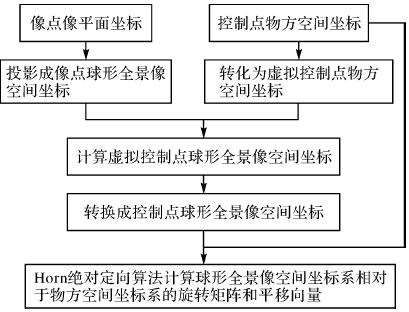
2.2 位姿估计算法图 2中,{P1,P2,…,Pn}为已知的控制点集,C1、C2、C3、C4为虚拟控制点,球形全景影像位姿估计的改进EPnP算法的关键在于以虚拟控制点为桥梁,求解控制点在球形全景像空间坐标系下的坐标,从而利用Horn绝对定位算法解求R、T,其流程如图 3所示。
|
| 图 2 球形全景影像位姿估计图示 Fig. 2 Position and pose obtainment representation of spherical panoramic image |
|
| 图 3 球形全景影像位姿估计流程图 Fig. 3 Position and pose obtainment flow chart of spherical panoramic image |
具体步骤如下:
(1) 确定虚拟控制点的物方空间坐标
设{P1,P2,…,Pn}的物方空间坐标为PWi=[XWiYWiZWi]T(i=1,2,…,n),下标W表示物方空间坐标系下的坐标,通常虚拟控制点C1取控制点集的重心,(C2,C3,C4)取控制点集主分量分解后的3个主分量,其物方空间坐标系下的坐标为CWi=[XWjCYWjCZWjC]T(j=1,2,3,4)。
(2) 求解控制点表示为虚拟控制点的权重
控制点可表示为4个虚拟控制点的加权和,使得求解控制点的球形全景像空间坐标时,可通过求解虚拟控制点的球形全景像空间坐标系实现,简化算法复杂度,这也是虚拟控制点存在的意义。
设控制点的齐次坐标为iW,虚拟控制点的齐次坐标为iW,则二者的转换关系如式(5)
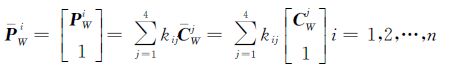 (5)
(5)
由式(5)中PWi最后一个齐次坐标1的转换关系可知,转换系数满足∑j=14kij=1,故称加权和,其中向量[ki1ki2ki3ki4]T为权重,也称为控制点PWi在以虚拟控制点CWi为基的欧氏空间中的坐标,即
 (6)
(6)
(3) 求解虚拟控制点的球形全景像空间坐标
在球形全景像空间坐标系下,n个控制点的坐标为PCi=[XCiYCiZCi]T(i=1,2,…,n),虚拟控制点的坐标为CCj=[XCjCYCjCZCjC]T(j=1,2,3,4),下标C表示球形全景像空间坐标系下的坐标,根据欧氏空间的线性不变性,可知在球形全景像空间坐标系下,控制点PCi和虚拟控制点CCj满足式(7)
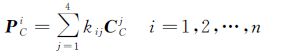 (7)
(7)
根据控制点坐标PCi、像点坐标PCi0=[XCi0YCi0ZCi0]T(i=1,2,…,n)与球心满足共线条件式(4),即可列出3个等式如式(8)
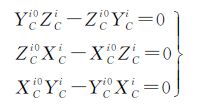 (8)
(8)
n个控制点根据式(8)可列立3n个齐次线性方程,共有3n个控制点坐标未知量,为减少未知量的个数,将式(7)代入式(8)可得
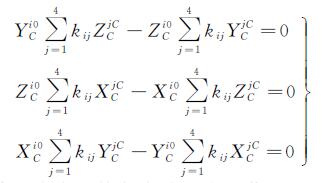 (9)
(9)
令4个虚拟控制点球形全景像空间坐标为
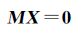 (10)
(10)
则矩阵M的核空间即为未知量X的解
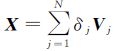 (11)
(11)
式中,Vj为MTM零特征值的特征向量;N是MTM核空间的维数;δj是未知值。根据欧氏变换的保距性,4个虚拟控制点相互间的距离可列式如式(12)
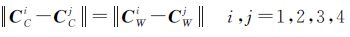 (12)
(12)
将式(11)代入式(12)即可得含6个方程的方程组,利用最小二乘原理可解得未知值δj(为提高精度可以此为初值进行高斯牛顿迭代,δj可快速收敛),即求得4个虚拟控制点的球形全景像空间坐标CCj,从而根据式(6)解算出来的权重向量[kilki2ki3ki4]T获得n个控制点的球形全景像空间坐标PCi。
(4) 求解球形全景像空间坐标系相对于物方空间坐标系的旋转矩阵R和平移向量T
根据PiW、PCi满足式(13),可通过文献[19]提出的绝对定向算法直接解算球形全景像空间坐标系相对于物方空间坐标系的旋转矩阵R和平移向量T(球形全景影像位姿)
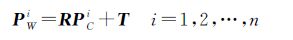 (13)
(13)
首先,将PiW、PCi分别重心化为PW0i=[XW0iYW0iZW0i]T、PC0i=[XC0iYC0iZC0i]T,如式(14)
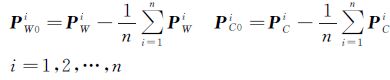 (14)
(14)
然后,通过使∑i=1nPiW0·(RPiC0)=∑i=1n(PiW0)TRPiC0最大化,即最大化Tr[Ri=1T∑nPiW0(PiC0)T],求得旋转矩阵R,进而根据式(13)求得平移向量T。
令矩阵A为式(15),则问题可转化为求解使Tr[RTA]最大化的旋转矩阵R
 (15)
(15)
满足该条件的旋转矩阵R和相对应的平移向量T可表示如式(16)
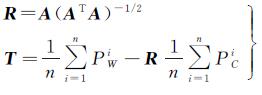 (16)
(16)
为测试球形全景影像位姿估计的改进EPnP算法(EPnP算法)的性能和受控制点数目、噪声水平的影响,首先进行仿真试验,并与球形全景影像位姿估计的后方交会算法(后方交会算法)进行比较。设平面全景影像大小为15 000×7500像素,由于球形全景影像的控制点极少出现在球顶和球底的位置,故设置控制点像点坐标均匀分布在[015 000]×[12506250]的像素区域内,旋转矩阵绕X、Y、Z轴的3个旋转角均匀分布在[0°45°]之间,平移向量在X、Y、Z轴方向上的偏移均匀分布在[-10001000](单位为m)之间,控制点到球形全景影像的球心距离均匀分布在[10100]单位为m)之间。算法求得球形全景影像的位姿后,采用重投影误差来评价算法的精度。
3.1.1 控制点数目试验控制点数目范围为[620]个,步长为1,图像点添加在[0 2]像素范围内的随机整数噪声,每个控制点数目下进行100次独立试验,再对计算时间和重投影误差取平均值,得到重投影误差结果如图 4所示,由于仿真试验像点真实坐标已知,重投影误差为真误差。

|
| 图 4 控制点数目试验重投影误差 Fig. 4 Reprojection error of the experiments changed with the number of control points |
图 4结果显示,在不同的控制点数目下,EPnP算法的重投影误差在[1.701.94]像素之间,波动范围约为0.24像素,波动较小;后方交会算法的重投影误差大部分在[1.041.82]像素之间,精度较高,但在控制点数目为6个、8个、11个、17个的试验中,其重投影误差在[2.402.74]像素之间,大于添加的图像点噪声像素范围。试验表明,EPnP算法的精度受控制点数目变化的影响较小,比后方交会算法稳健。
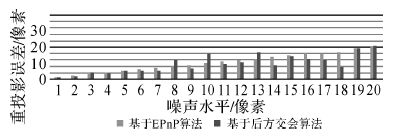
3.1.2 图像噪声试验试验中将控制点数目设为12个,图像点添加均值为0像素,标准差为σ像素的噪声,σ在[120]像素范围内变化,步长为1,进行100次独立试验,再对计算时间和重投影误差取平均值,得到重投影误差结果如图 5所示,由于仿真试验像点真实坐标已知,重投影误差为真误差。
|
| 图 5 图像噪声试验重投影误差 Fig. 5 Reprojection error of the experiments changed with the noise level of image |
图 5结果显示,在不同的图像点噪声水平下,EPnP算法的重投影误差与对应的噪声像素标准差相当,说明该算法的计算精度受图像点噪声水平的影响较大;后方交会算法的重投影误差大部分情况下低于EPnP算法,但在噪声标准差为8像素、10像素、13像素的情况下,明显大于EPnP算法,说明后方交会算法的精度不稳定,波动大,鲁棒性较差。
此外,仿真试验结果中,EPnP算法的计算时间集中在0.45 s左右,后方交会算法的计算时间集中在13 s左右,表明EPnP算法的计算效率比后方交会算法提高了近30倍。
仿真试验结果表明,本文提出的方法具有理论可行性,更为稳健快速,即使控制点数目较少也能达到较高精度。实际应用中可以利用少量均匀分布的控制点,达到较好的位姿估计结果,从而节省成本并提高效率。
3.2 实际影像数据试验仿真试验表明球形全景影像位姿估计的改进EPnP算法具有理论可行性,下面测试其实际可行性。基于球形全景影像的实际数据位姿估计试验在武汉大学信息学部1号楼前进行,采用的相机为ladybug3和ladybug5,每个相机设立两个测站,大小为8000×4000像素,并提供12个控制点数据和96个检查点数据如图 6所示。

|
| 图 6 全景影像实际数据分布 Fig. 6 The distribution of actual data in panoramic image |
图 6中,12个控制点和96个检查点在全景影像中长度方向均匀分布,宽度方向集中在中心位置,这与大部分室外控制点和检查点只能依赖建筑物进行采集以及相机与建筑物的距离有关。用实际数据进行球形全景影像位姿估计的改进EPnP算法(EPnP算法),并与球形全景影像位姿估计的后方交会算法(后方交会算法)进行对比,对比试验中12个控制点的重投影误差(单位为像素)见表 1。
| 点号 | EPnP算法 | 后方交会算法 | |||||||
| ladybug3(测站1) | ladybug3(测站2) | ladybug5(测站1) | ladybug5(测站2) | ladybug3(测站1) | ladybug3(测站2) | ladybug5(测站1) | ladybug5(测站2) | ||
| 像素 | |||||||||
| 1 | 1.47 | 1.48 | 0.28 | 1.31 | 2.27 | 3.19 | 0.50 | 1.51 | |
| 2 | 1.33 | 1.14 | 0.12 | 1.40 | 1.66 | 2.00 | 0.42 | 1.28 | |
| 3 | 5.91 | 0.47 | 0.37 | 0.88 | 6.50 | 0.17 | 0.47 | 1.00 | |
| 4 | 1.97 | 1.32 | 0.14 | 2.95 | 2.01 | 1.40 | 0.50 | 2.88 | |
| 5 | 1.16 | 0.90 | 1.74 | 0.58 | 1.05 | 1.28 | 1.19 | 0.72 | |
| 6 | 1.95 | 0.96 | 2.24 | 1.15 | 1.08 | 1.47 | 2.65 | 1.01 | |
| 7 | 4.34 | 0.48 | 1.39 | 1.23 | 3.30 | 0.45 | 0.74 | 0.76 | |
| 8 | 1.88 | 1.52 | 1.63 | 1.02 | 2.65 | 1.51 | 0.57 | 0.84 | |
| 9 | 1.66 | 3.05 | 0.96 | 1.51 | 1.98 | 3.68 | 0.55 | 1.73 | |
| 10 | 2.57 | 2.51 | 0.06 | 1.25 | 3.42 | 1.20 | 0.11 | 1.00 | |
| 11 | 4.71 | 7.52 | 0.80 | 0.08 | 2.42 | 3.36 | 0.68 | 0.33 | |
| 12 | 4.59 | 5.17 | 1.52 | 0.42 | 1.54 | 2.65 | 1.32 | 0.14 | |
| 均值 | 2.80 | 2.21 | 0.94 | 1.15 | 2.49 | 1.86 | 0.81 | 1.10 | |
如表 1所示,EPnP算法中,ladybug3测站1全景影像控制点重投影误差最大为5.91像素,均值为2.80像素;ladybug3测站2全景影像控制点重投影误差最大为7.52像素,均值为2.21像素;ladybug5测站1全景影像控制点重投影误差最大为2.24像素,均值为0.94像素;ladybug5测站2全景影像控制点重投影误差最大为2.95像素,均值为1.15像素。后方交会算法中,ladybug3测站1全景影像控制点重投影误差最大为6.50像素,均值为2.49像素;ladybug3测站2全景影像控制点重投影误差最大为3.68像素,均值为1.86像素,其中该试验设置Kappa值为0°时,算法无法收敛,设置为90°时,算法才正常收敛;ladybug5测站1全景影像控制点重投影误差最大为2.65像素,均值为0.81像素;ladybug5测站2全景影像控制点重投影误差最大为2.88像素,均值为1.10像素。
此外,试验也得到了96个检查点的重投影误差(单位为像素),其结果见表 2。
| 像素 | |||||||||
| 点号 | EPnP算法 | 后方交会算法 | |||||||
| ladybug3(测站1) | ladybug3(测站2) | ladybug5(测站1) | ladybug5(测站2) | ladybug3(测站1) | ladybug3(测站2) | ladybug5(测站1) | ladybug5(测站2) | ||
| 最大值 | 7.16 | 11.92 | 8.65 | 5.51 | 7.80 | 7.31 | 9.28 | 5.95 | |
| 均值 | 2.81 | 3.66 | 2.67 | 1.70 | 2.44 | 2.72 | 2.86 | 1.10 | |
表 1、表 2试验结果显示,两种球形全景影像位姿估计方法的控制点重投影误差和检查点重投影误差都达到了3.00像素左右的平均精度,说明利用少量均匀分布的控制点数据进行位姿估计可得到较好的检查点重投影精度,即位姿估计结果较好。对于ladybug3,两种球形全景影像位姿估计方法得到的重投影误差差值在0.94像素以内;而对于ladybug5,重投影误差差值则在0.60像素内,说明两种方法位姿估计精度相当,但EPnP算法的计算时间为0.36 s左右,后方交会算法的计算时间为13 s左右。由此可知,本文提出的方法时间效率比后方交会算法提高了30倍多,是一种高精度、快速的球形全景影像位姿估计方法。
由仿真试验和真实数据试验可以得出以下结论:
(1) 本文中EPnP算法计算效率比后方交会算法提高了30倍左右,其中EPnP算法的时间复杂度为O(n),后方交会算法的时间复杂度为O(n*iter),n为控制点个数,iter为迭代次数。
(2) 无须位姿初值迭代求解的EPnP算法精度比后方交会算法略低,但在位姿初值不合适的情况下,后方交会算法将难以收敛到理想值或者不收敛,导致解算精度差,鲁棒性不高。
(3) EPnP算法的重投影误差与图像点噪声水平成正比的规律表明,不宜选用拼接误差过大的全景影像(单相机光心和全景虚拟光心的距离不可忽略)进行位姿估计。
由文献[16]可知,在单相机光心和全景虚拟光心距离可忽略的前提下,单张全景影像拼接误差与控制点到全景虚拟光心的距离有关,近距离控制点成像会引起较大的拼接误差,ladybug相机的最佳拼接半径为20 m,故一般不采用10 m以内的控制点。
本文提出的方法针对的是广泛采用的全景理想成像模型,它是建立在球形全景影像不存在拼接误差或者拼接误差可以忽略不计的前提下的,而对于体型较大的多镜头组合式相机,由于单相机光心和全景虚拟光心的距离不可忽略,球形全景影像存在明显的拼接误差,采用本文建立的球形全景影像投影模型将导致位姿估计误差较大。文献[16]提出的全景严格模型,为解决这一问题提供了方向,全景影像严格模型位姿估计的改进EPnP算法有待于进一步研究。
4 结 论本文构建了球形全景影像的投影模型和共线条件方程,并引入EPnP算法进行改进,提出了一种快速的球形全景影像位姿估计算法,解决了基于球形全景影像进行三维重建需要位姿数据的问题,使其不再依赖GPS/IMU位姿数据,降低了数据采集成本。与球形全景影像位姿估计的后方交会算法对比试验表明,本文提出的方法无须迭代求解,更为稳健快速,重投影误差可控制在3.00像素左右,且即使控制点数目较少也能达到高精度,可在实际应用中实现使用少量控制点进行位姿估计和三维重建,提高效率。
| [1] |
李霖, 于忠海, 李桢, 等. 全景景观地图中地形局部变形研究[J].武汉大学学报(信息科学版),2013, 38 (11) : 1335 –1338 .
LI Lin, YU Zhonghai, LI Zhen, et al. Local Terrain Deformation in Panoramic Maps[J]. Geomatics and Information Science of Wuhan University,2013, 38 (11) : 1335 –1338 . |
| [2] |
张烁, 李群智, 温博, 等. 玉兔号月球车全景相机的正交变换投影模型[J].武汉大学学报(信息科学版),2014, 39 (7) : 804 –808 .
ZHANG Shuo, LI Qunzhi, WEN Bo, et al. Orthogonal Projection Model of Jade Rabbit Lunar Rover Pancam[J]. Geomatics and Information Science of Wuhan University,2014, 39 (7) : 804 –808 . |
| [3] | TONG Guofeng,LIU Ran, TAN Jindong. 3D Information Retrieval in Mobile Robot Vision Based on Spherical Compound Eye[C]//Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics. Karon Beach, Phuket: IEEE, 2011: 1895-1900. |
| [4] | TONG Guofeng, WU Zizhang, WENG Ninglong, et al. An Omni-directional vSLAM Based on Spherical Camera Model and 3D Modeling[C]//Proceedings of the 10th World Congress on Intelligent Control and Automation. Beijing: IEEE, 2012: 4551-4556. |
| [5] | TONG Guofeng, GU Jiuhong. Locating Objects in Spherical Panoramic Images[C]//Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics. Karon Beach, Phuket: IEEE, 2011: 818-823. |
| [6] |
徐芳, 梅文胜, 张利. 线阵全景相机检校模型研究[J].武汉大学学报(信息科学版),2014, 39 (4) : 417 –421 .
XU Fang, MEI Wensheng, ZHANG Li. The Calibration Model of Linear Array Panoramic Cameras[J]. Geomatics and Information Science of Wuhan University,2014, 39 (4) : 417 –421 . |
| [7] |
李晓辉, 周荫清, 王祖林. 基于曲面拼接的球面全景生成算法[J].北京航空航天大学学报,2007, 33 (6) : 668 –671 .
LI Xiaohui, ZHOU Yinqing, WANG Zulin. Spherical Panorama Creating Algorithm Based on Curve Surface Mosaic[J]. Journal of Beijing University of Aeronautics and Astronautics,2007, 33 (6) : 668 –671 . |
| [8] |
龚琪慧, 吴健平, 王洁华, 等. 基于全景图的3维实景制作及其与GIS集成研究[J].测绘与空间地理信息,2012, 35 (6) : 33 –37 .
GONG Qihui, WU Jianping, WANG Jiehua, et al. The Research of the Production of 3D Real Scene and the GIS Integration Thereof Based on Panorama[J]. Geomatics &Spatial Information Technology,2012, 35 (6) : 33 –37 . |
| [9] | TONG Guofeng, PANG Xiaolei, YE Ning, et al. A Precise Spherical Camera Model Based on Multi-camera System[J]. Journal of Computational Information Systems,2013, 9 (3) : 897 –905 . |
| [10] | BROWN M, LOWE D G. Automatic Panoramic Image Stitching Using Invariant Features[J]. International Journal of Computer Vision,2007, 74 (1) : 59 –73 . |
| [11] |
季顺平, 史云. 车载全景相机的影像匹配和光束法平差[J].测绘学报,2013, 42 (1) : 94 –100 .
JI Shunping, SHI Yun. Image Matching and Bundle Adjustment Using Vehicle-based Panoramic Camera[J]. Acta Geodaetica et Cartographica Sinica,2013, 42 (1) : 94 –100 . |
| [12] |
张正鹏, 江万寿, 张靖. 光流特征聚类的车载全景序列影像匹配方法[J].测绘学报,2014, 43 (12) : 1266 –1273 .DOI:10.13485/j.cnki.11-2089.2014.0172.
ZHANG Zhengpeng, JIANG Wanshou, ZHANG Jing. An Image Match Method Based on Optical Flow Feature Clustering for Vehicle-borne Panoramic Image Sequence[J]. Acta Geodaetica et Cartographica Sinica,2014, 43 (12) : 1266 –1273 .DOI:10.13485/j.cnki.11-2089.2014.0172. |
| [13] |
刘帅, 陈军, 孙敏, 等. 一种球形立体全景的三维量测算法与实验[J].地球信息科学学报,2014, 16 (1) : 15 –22 .
LIU Shuai, CHEN Jun, SUN Min, et al. A Three Dimensional Measurement Approach and Experiment Based on Spherical Panorama[J]. Journal of Geo-Information Science,2014, 16 (1) : 15 –22 . |
| [14] |
刘帅, 陈军, 孙敏, 等. 双球面投影几何可量测全景模型的构建[J].计算机辅助设计与图形学学报,2015, 27 (4) : 657 –665 .
LIU Shuai, CHEN Jun, SUN Min, et al. Measurable Panorama Construction Based on Binocular Spherical Projective Geometry[J]. Journal of Computer-aided Design &Computer Graphics,2015, 27 (4) : 657 –665 . |
| [15] |
季顺平, 史云. 高噪声环境下基于参考影像的车载序列影像定位方法[J].测绘学报,2014, 43 (11) : 1174 –1181 .DOI:10.13485/j.cnki.11-2089.2014.0181.
JI Shunping, SHI Yun. Georegistration of Ground Sequential Imagery with Geo-referenced Aerial Images in High Noise Environments[J]. Acta Geodaetica et Cartographica Sinica,2014, 43 (11) : 1174 –1181 .DOI:10.13485/j.cnki.11-2089.2014.0181. |
| [16] |
季顺平, 史云. 多镜头组合型全景相机两种成像模型的定位精度比较[J].测绘学报,2014, 43 (12) : 1252 –1258 .DOI:10.13485/j.cnki.11-2089.2014.0169.
JI Shunping, SHI Yun. Comparison of Two Sensor Models for Multi-camera Rig System in Measurements[J]. Acta Geodaetica et Cartographica Sinica,2014, 43 (12) : 1252 –1258 .DOI:10.13485/j.cnki.11-2089.2014.0169. |
| [17] |
石丽梅, 赵红蕊, 李明海, 等. 车载移动测图系统外方位元素标定方法[J].测绘学报,2015, 44 (1) : 52 –58 .DOI:10.11947/j.AGCS.2015.20130203.
SHI Limei, ZHAO Hongrui, LI Minghai, et al. Extrinsic Calibration for Vehicle-based Mobile Mapping System[J]. Acta Geodaetica et Cartographica Sinica,2015, 44 (1) : 52 –58 .DOI:10.11947/j.AGCS.2015.20130203. |
| [18] | LEPETIT V, MORENO-NOGUER F, FUA P. EPnP: An Accurate O(n) Solution to the Pn P Problem[J]. International Journal of Computer Vision,2009, 81 (2) : 155 –166 . |
| [19] | HORN B K P, HILDEN H M, NEGAHDARIPOUR S. Closed-form Solution of Absolute Orientation Using Orthonormal Matrices[J]. Journal of the Optical Society of America A,1988, 5 (7) : 1127 –1135 . |
| [20] |
王佩军, 徐亚明.
摄影测量学[M]. 武汉: 武汉大学出版社, 2005 .
WANG Peijun, XU Yaming. Photogrammetry[M]. Wuhan: Wuhan University Press, 2005 . |


