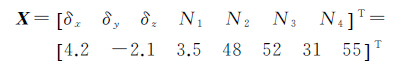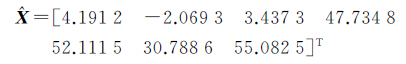2. 桂林理工大学广西空间信息与测绘重点实验室,广西 桂林 541004 ;
3. 精密工程与工业测量国家测绘地理信息局重点实验室,湖北 武汉 430079 ;
4. 闽江学院物理学与电子信息工程系,福建 福州 350108
2. Guangxi Key Laboratory of Spatial Information and Geomatic, Guilin Uninversity of Technology, Guilin 541004, China ;
3. Key Laboratory of Precise Engineering and Industry Surveying of National Administration of Surveying, Mapping and Geoinformation, Wuhan 430079, China ;
4. Department of Physics & Electronic Information, Minjiang University, Fuzhou 350108,China
病态问题广泛存在于GPS快速精密定位、地球物理参数反演、重力场向下延拓等大地测量数据处理领域。病态问题的危害性极大,对观测模型的法方程应用最小二乘估计进行求解时,其解很不稳定,与实际参数真值相差较大。另外当观测值中含有粗差时,此时参数求解的结果更加偏离真值,严重影响了解算成果的质量。为此,需研究既能对病态问题进行有效处理又能抵御观测值粗差影响的稳健解算方法。
病态问题之所以求解结果和真值相差较大,是由于其对应模型法方程系数阵的条件数比较大,对其求逆时放大了误差的影响。目前已有多种方法可对其进行有效解算,总结起来大致可分为两类:一类是通过对法方程的系数阵进行相关处理,以减弱法方程病态性,其常用方法有截断奇异值法[1]与Tikhonov正则化方法[2];一类是不对法方程进行求解,而是直接利用观测模型构造出目标函数进行智能搜索,即将病态问题解算转化为一个函数优化问题,避免了法方程的求逆计算,进而获得近似最优解,当今的主流方法有遗传算法[3]、粒子群优化算法[4]等。但是对于第1类方法中的截断奇异值法,存在对奇异值截断位置比较敏感的问题;而Tikhonov正则化方法存在着正则化参数的选取和正则化矩阵难以确定的缺点。第2类智能搜索方法近些年来研究较多,但在实际应用中,其代表性的遗传算法存在收敛速度慢、易陷入局部最优等问题[5];粒子群优化算法存在进化后期收敛速度降低、局部搜索能力差等缺陷[6]。
对于病态问题中观测值存在粗差的情形,一些学者也对此进行了研究,提出了如抗差岭估计[7]、抗差泛岭估计[8]、抗差主成分估计[9]等比较有效的方法,但解算精度并不太高。
本文不同于以上解算思路,提出在对一种群体智能算法——果蝇优化算法进行有效改进后,将其引入至病态问题解算中来。又考虑到Tikhonov正则化方法本身具有既能克服病态性又可以在一定程度上抑制噪声和误差影响的特点[10],将这两者有机地进行结合,不仅可以提高病态问题的解算精度,还可以在一定程度上抵御观测值粗差对解算结果的影响。本文以实际算例验证该方法在进行病态问题解算中的可行性、有效性与稳健性。
1 病态方程解算的数学模型对于观测方程
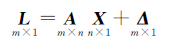 (1)
(1)
式中,L为观测值;A为设计矩阵;X为待估参数;Δ为噪声,Δ~N(0,σ20I)。 其在最小二乘(LS)准则下对应的法方程为
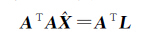 (2)
(2)
当式(2)中的法方程系数阵ATA的条件数非常大时,进行(ATA)-1计算将极不稳定,此时认为法方程病态。式(2)的LS解=(ATA)-1ATL与真值也会相差较远。
2 Tikhonov正则化方法的基本原理Tikhonov正则化方法是当前病态问题解算中应用普遍性最高的一种方法。其估计准则为
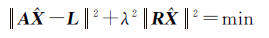 (3)
(3)
式中,λ为正则化参数;R为正则化矩阵;·表示欧氏2范数。
根据Tikhonov估计准则,令R=In,则式(3)的解为
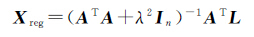 (4)
(4)
从式(4)可以看出,Tikhonov正则化解的关键在于确定正则化参数λ,目前正则化参数的选取准则主要有岭迹法[11]、L曲线法[12-13]、广义交叉检验(GCV)法[14]等。而岭迹法在选择参数时具有一定的主观随意性,GCV法的缺点在于其GCV函数的变化有时较为平缓,此时定位其最小值非常困难[15]。相对而言,L曲线法确定正则化参数的理论非常严密,定位也比较准确[15]。为此,本文将L曲线法选用为Tikhonov正则化参数的确定方法。
L曲线法的基本原理是对不同的正则化参数绘出其残余范数A-L与正则化解范数之间的二维曲线图,由于该曲线形状通常成L形,其拐角即是正则化参数的最优值。对于正则化参数λ,拐角点是通过求解(lgA-L,lg)曲线的最大曲率进行确定。
3 基本果蝇优化算法及其改进算法 3.1 基本果蝇优化算法的原理文献[16]提出一种新的群体智能算法——果蝇优化算法(fruit fly optimization algorithm,FOA),这是一种基于果蝇觅食行为而推演出的搜索全局最优的方法[16]。基本FOA方法寻优的基本步骤如下:
(1) 设置果蝇种群大小与最大迭代次数,并随机初始化果蝇种群的初始位置(Xaxis,Yaxis)。
(2) 赋予果蝇个体利用嗅觉搜寻食物的随机方向η,其位置为:Xi=Xaxis+η,Yi=Yaxis+η。
(3) 由于无法获得食物的具体位置,先确定果蝇个体与原点的距离Di=X2i+Y2i,进而计算气味浓度判定值Si=1/Di。
(4) 将气味浓度判定值Si引入气味浓度判定函数(即需优化问题的目标函数),求取出该位置的气味浓度Si,smell=function(Si)。
(5) 找到果蝇种群中气味浓度最高或最低的果蝇个体(对应目标函数极大或极小值,本文为求极小值),并记录其编号:[Sbestsmell,bbestindex]=min(Si,smell)。
(6) 保留最佳的气味浓度值及该果蝇的位置坐标,此时果蝇群体内的各个体利用视觉向该位置飞去:Ssmellbest=Sbestsmell,Xaxis=X(bbestindex),Yaxis=Y(bbestindex)。
(7) 进入循环迭代过程,此时已保留的果蝇位置坐标成为新一次迭代寻优的果蝇群体初始位置。执行步骤(2)到(5),判断气味浓度值Ssmellbest是否小于所记录最优值,若是,则执行步骤(6)。否则返回步骤(2)进行下一次迭代。 由上述基本FOA方法的寻优过程可以发现,其参数设置非常少(只有种群大小和最大迭代次数两个参数),相应的运算速度也较快并易于程序实现。
3.2 基本FOA算法存在的问题(1) 已有的文献表明基本FOA算法可以有效地处理线性优化问题,但本文进行病态问题解算时,其目标函数都为非线性函数,因此需要进一步了解基本FOA算法在处理非线性函数时的性能。
文献[16]中采用基本FOA算法处理了两种简单的非线性优化函数maxY=2-x2与minY=-5+x2,其寻优结果非常理想,得到了非常好的处理效果。但本文作者将目标函数变为minY=-5+(x+1)2时,却始终不能准确搜索到该函数的极小值。为此,本文又处理两个有代表性的具有非零极值点的非线性测试函数:Shuber函数和Branin函数,经过改变种群数目、迭代次数等处理手段后,始终无法找到正确的极值位置。基于此,可以分析得到:基本FOA算法不能处理极值点为非零的非线性函数,只能对其示例给出的极值点为零的函数有效。
(2) 对基本FOA算法流程进行深入分析,可以发现FOA寻优过程是将气味浓度判定值Si作为极值点(即观测方程中的待估参数xi)代入目标函数进行处理的,而Si作为距离的倒数,始终保持Si0,这也意味着FOA算法不能处理参数为负数的问题[17]。而在大地测量病态问题中,其观测方程中待估参数为负数是极其常见的情况,因此只有解决了这一问题才能将FOA算法应用于本文的病态问题解算中来。
(3) 在FOA算法的步骤(2)中,随机方向η的取值范围是[-1, 1],也就是说其搜索范围为半径为1的区域。这种搜索半径在循环迭代过程由于被固定住而并不能随着迭代的深入而加以变化,这是不合理的。因为随着迭代的进行,果蝇的位置逐渐会向最优值靠近,在搜索早期需要比较大的搜索范围,而在后期搜索范围会逐渐缩小。为此,搜索半径需要加以自适应变化调整[18-19]。
由于上述基本FOA算法存在的诸多问题,可以发现原FOA方法并不能很好地处理目标函数的优化问题,当然也使其在病态问题解算中受到极大的限制。
3.3 改进FOA算法的算法实现流程由于基本FOA算法不能处理非零且非负极值点,本文提出一种改进的FOA算法(IFOA),以对上述问题进行有效处理。其关键技术有以下两点:
(1) IFOA方法在随机搜索方向的选择上不设置两个方向Xi与Yi,而仅仅只对单一的X方向进行搜索处理。为此,IFOA方法将不计算Si=1/Di,即令Si=Xi,此时气味浓度Si,smell=function(Xi)。设待估参数X的搜索区间为[Lbound,Ubound],其中Lbound为搜索下界,Ubound为搜索上界。这样处理的优点在于不论Lbound为正或为负,参数可以在全区域内进行搜索。解决了原FOA算法不能处理极值点为非负和非零的问题。
(2) 设置搜索半径调整系数γ(一般取值可在0.5到1之间),使得迭代次数逐渐增大时,搜索范围逐渐缩小。这样处理的优点在于算法初期可以有较大的搜索半径,以保证其初期具有良好的全局搜索能力。而在算法后期又可以有相对较小的搜索半径,这也保证了在后期有良好的局部搜索能力。可以认为加入的γ平衡了全局搜索与局部搜索之间的关系。
具体IFOA算法的实现流程如下:
(1) 设置果蝇种群大小PopSize与最大迭代次数maxIter,随机初始化果蝇种群的初始位置Xaxis=Lbound+(Ubound-Lbound)×rand( ),其中rand函数产生[0, 1]区间的随机数。
(2) 赋予果蝇个体利用嗅觉搜寻食物的随机方向与距离为:Xi=Xaxis+R×(2×rand( )-1),搜索半径初始值设R=1。
(3) 设置半径调整系数γ,令R=R×γIter,Iter为当前迭代次数,保证迭代次数越大,搜索范围越小。
(4) 令气味浓度判定值Si=Xi;代入目标函数求取出该位置的气味浓度Si,smell=function(Si)。
(5) 找到果蝇种群中气味浓度最低的果蝇个体,并记录其编号:[SbestSmell,bbestindex]=min(Si,smell)。
(6) 保留最佳的气味浓度值及该果蝇的位置坐标:Ssmellbest=SbestSmell,Xaxis=X(bbestindex)。
(7) 进入循环迭代过程,与基本FOA算法一致。 在IFOA算法结束后,其寻优搜索到的Xaxis即为待求解的参数。
4 改进FOA算法结合Tikhonov正则化方法用于病态问题解算IFOA算法在进行寻优过程中,需设置目标函数。一般情况是将式(2)改写为误差方程的形式
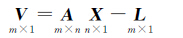 (5)
(5)
可以构造IFOA算法的目标函数为
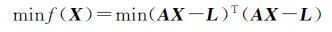 (6)
(6)
通过直接对式(6)中的目标函数进行搜索,可以将病态问题解算转化为一个非线性函数优化问题。而本文在考虑到Tikhonov正则化方法既能克服病态性又可以在一定程度上抑制误差影响的特点,将正则化项引入IFOA算法的目标函数中来,则此时需优化的目标函数变为
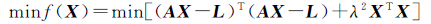 (7)
(7)
式中,λ为第3节所介绍的正则化参数。由此,可以将IFOA算法和Tikhonov正则化方法相结合以处理病态问题,下面以实例对该方法的计算过程进行详细分析。
5 实例分析本实例取自文献[1]的例6-1,为一个GPS快速动态定位算例。历元间隔为2 s,观测了5颗卫星,用4个历元解算整周模糊度。参数的真值为
式中,δx、δy、δz为坐标参数;Ni为模糊度参数。
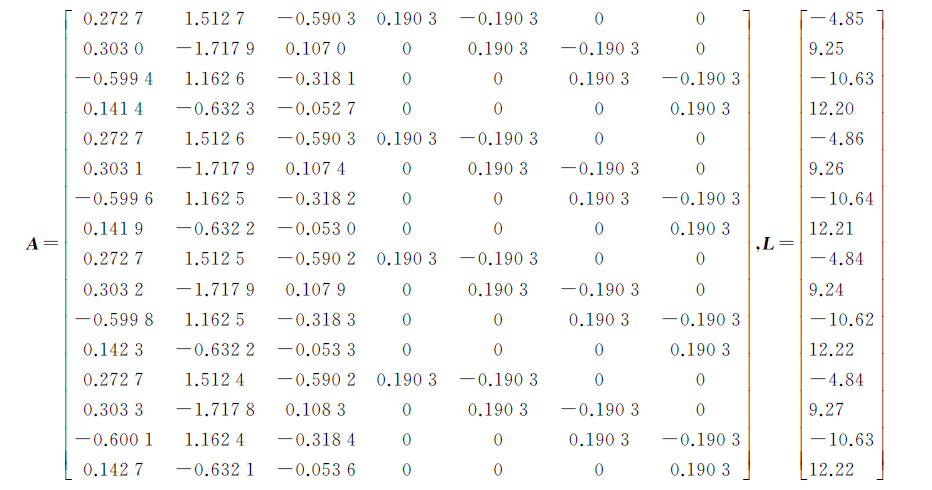
其误差方程的系数阵A和在观测真值中加入微小误差后的观测向量L为
该病态方程的法方程条件数为cond(ATA)=3.212 7×1010,属于严重病态问题。首先利用L曲线法计算出正则化参数λ,如图 1所示。
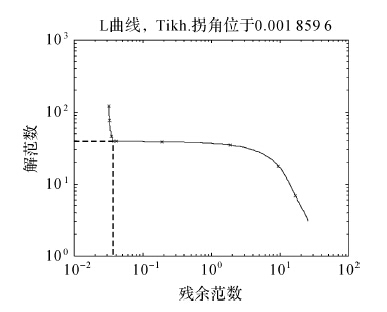
|
| 图 1 L曲线法确定正则化参数 Fig. 1 Regularization parameter determined by L-curve method |
由图 1可知,正则化参数λ=0.001 859 6。在此基础上,设置IFOA算法的参数为:果蝇种群规模PopSize=20,最大迭代次数maxIter=1000,搜索半径调整系数γ=0.9。待求参数的搜索区间设为:δx、δy、δz,取其真值±0.5 m,Ni取其真值±5周。由IFOA算法对目标函数(7)进行搜索。考虑到IFOA算法是一种随机搜索算法,每次计算会有所差异,为此采用运行30次的计算结果的平均值作为最后的计算最终值。其解算最终结果为
以第30次搜索计算为例,其优化迭代过程如图 2所示。
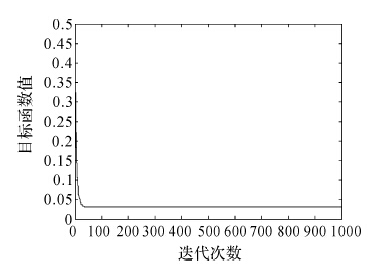
|
| 图 2 IFOA算法的优化迭代过程 Fig. 2 Optimization iterative process of IFOA algorithm |
从图 2中可以看出,在经过很少的迭代次数(36次)后,IFOA算法即可找到目标最优值,表明其收敛速度非常快。如果本实例应用基本FOA算法,由于其参数存在非零和负值,其搜索将不能成功。
本文将IFOA算法搜索目标函数(7)命名为“IFOA+Tikhonov方法”,而IFOA搜索目标函数(6)命名为“IFOA方法”,以对这两种方法加以区分。为了保证这两种方法在计算结果上进行对比时的客观性,本文在程序实现时让其对两种方法在算法的步骤(1)和(2)中生成的随机数相同,即将生成的随机数先赋予一变量,再将该变量加入两种不同的待估参数Xaxis中去。
为了与上述两种方法进行对比,还分别采用了最小二乘法、Tikhonov正则化方法、遗传算法对本实例进行了求解。其中,遗传算法的参数搜索区域、种群数目、迭代次数设置与IFOA算法相同,精英数目设为3,交叉后代比例设为0.9,停止代数设为200,适应度函数值偏差设为1e-10[20],令其目标函数为式(6)。以计算结果与真值的欧氏2范数ΔX作为精度评价指标,各种算法对比结果见表 1。
| 真值 | 最小二乘法 | Tikhonov正则化法 | 遗传算法 | IFOA方法 | IFOA+Tikhonov方法 | |
| δx | 4.2 | 17.661 9 | 1.015 6 | 4.233 4 | 4.187 2 | 4.191 2 |
| δy | -2.1 | -28.373 2 | -8.517 2 | -2.108 6 | -2.067 8 | -2.069 3 |
| δz | 3.5 | 2.060 5 | -10.511 5 | 3.539 8 | 3.430 8 | 3.437 3 |
| N1 | 48 | 78.206 3 | -1.781 6 | 48.384 3 | 47.708 5 | 47.734 8 |
| N2 | 52 | -102.919 8 | -9.947 3 | 52.174 3 | 52.109 9 | 52.111 5 |
| N3 | 31 | 133.878 4 | 13.977 3 | 31.311 1 | 30.760 9 | 30.788 6 |
| N4 | 55 | -42.695 0 | 32.184 7 | 55.015 1 | 55.087 1 | 55.082 5 |
| ‖ΔX‖ | 0 | 214.276 5 | 85.869 8 | 0.527 2 | 0.409 6 | 0.373 1 |
从表 1可以看出,在本实例不含粗差的情况下,本文所提IFOA+Tikhonov方法在所有方法中,其解算结果精度最优,IFOA方法稍微次之;而直接采用最小二乘法解算精度最差,与真值偏离最远。采用Tikhonov正则化方法进行解算其结果也不甚理想。另外本文所提的IFOA方法与遗传算法相对比,不仅解算结果要更优,而且其参数设置较少,整个寻优过程更利于程序的实现,在实际应用中IFOA方法显得更加有利。 需要说明的是,群体智能算法的参数设置对最终求解结果有直接的影响,在设定参数时,种群规模越大,其获得最优解的可能性也越高,但相应的计算时间也会相应增大,一般设置范围在10~100;最大迭代次数一般可以设置在100~5000之间。本文对IFOA算法进行参数设置时,综合考虑了算法计算时间与全局搜索能力之间的平衡,设置种群规模为20,最大迭代次数为1000。而IFOA算法增加的γ系数在设置时,考虑到为使得搜索范围缩小的幅度不至于过快,将其设置为0.9。 为了评价IFOA+Tikhonov方法在病态问题解算中的稳健性能,本文在观测值中加入粗差进行试验。考虑到粗差在观测数据中存在的概率一般不超过10%的原则[21-22],本实例中可加入两个粗差。首先在第2和第5个观测值中加入原观测值20%的粗差,即原有的l2=9.25、l5=-4.86变为l2=11.1、l5=-5.832,此时正则化参数由L曲线法可计算得出λ=0.018 017。保持其余参数的设置不限,重新使用上述所有算法进行计算,其计算结果见表 2。
| 真值 | 最小二乘法 | Tikhonov正则化法 | 遗传算法 | IFOA方法 | IFOA+Tikhonov方法 | |
| δx | 4.2 | -381.950 5 | 0.434 8 | 4.185 1 | 4.154 4 | 4.137 6 |
| δy | -2.1 | -253.173 1 | -8.799 8 | -2.188 1 | -2.189 9 | -2.284 8 |
| δz | 3.5 | -863.582 6 | -11.069 5 | 3.426 2 | 3.384 8 | 3.234 9 |
| N1 | 48 | -3 173.245 2 | -2.321 9 | 49.017 7 | 48.706 5 | 47.754 8 |
| N2 | 52 | -3 027.552 9 | -10.563 3 | 53.761 1 | 53.556 4 | 52.342 7 |
| N3 | 31 | -1 890.142 0 | 12.212 2 | 31.085 7 | 30.867 6 | 30.476 1 |
| N4 | 55 | -732.934 0 | 31.455 6 | 54.697 2 | 54.675 7 | 54.120 1 |
| ‖ΔX‖ | 0 | 5013.549 2 | 87.321 9 | 2.061 4 | 1.751 5 | 1.155 2 |
将加入粗差的位置变为在第8和第11个观测值中,继续加入原观测值20%的粗差,即原有的l8=12.21、l11=-10.62变为l8=14.652、l11=-12.744,计算出正则化参数λ=0.011 079 7。保持其余参数的设置不变,仍然使用上述所有算法进行计算,其计算结果见表 3。
| 真值 | 最小二乘法 | Tikhonov正则化法 | 遗传算法 | IFOA方法 | IFOA+Tikhonov方法 | |
| δx | 4.2 | -231.993 2 | 0.456 4 | 4.262 1 | 4.254 8 | 4.233 6 |
| δy | -2.1 | 564.143 6 | -8.741 4 | -2.095 0 | -2.207 1 | -2.239 7 |
| δz | 3.5 | 275.029 9 | -10.630 7 | 3.446 9 | 3.370 1 | 3.340 2 |
| N1 | 48 | 446.842 2 | -1.187 4 | 48.296 7 | 48.002 4 | 47.830 4 |
| N2 | 52 | 3 770.762 0 | -11.566 9 | 52.536 7 | 51.604 7 | 51.243 6 |
| N3 | 31 | -1 584.492 7 | 13.412 0 | 31.560 4 | 31.615 7 | 31.507 0 |
| N4 | 55 | 2 191.554 7 | 35.003 1 | 58.212 4 | 57.776 2 | 57.609 5 |
| ‖ΔX‖ | 0 | 4 648.988 7 | 86.181 0 | 3.319 1 | 2.876 4 | 2.777 3 |
从表 2和表 3中可以看出,在对原有观测值增加粗差时,最小二乘估计的解算结果已经严重偏离真值;而Tikhonov正则化方法在增加粗差后,解算精度下降并不明显,说明其有一定的抑制粗差的能力。所有算法中,IFOA+Tikhonov方法的解算结果仍然最优,表明其不仅能有效地搜索全局最优解,消除了病态性的影响,也在很大程度上能够抵御粗差,具有一定的稳健性。
6 结 论本文提出了一种改进果蝇优化算法结合Tikhonov正则化的病态问题解算方法,得到如下结论:
(1) 在IFOA算法的目标函数中引入正则化项,将IFOA算法与Tikhonov正则化方法有机地结合,充分发挥了各自的优点,在病态问题的解算中其解算精度要优于普通IFOA算法、遗传算法和单一的Tikhonov正则化方法。
(2) 在观测模型的法方程严重病态的情况下,以最小二乘法进行求解,其结果偏离真值较大。特别是在观测值含有粗差时,这种偏差会迅速增大,而此时采用IFOA+Tikhonov方法具有一定的稳健性,其解算精度与观测值无粗差的情况相比有一定的下降,但仍在可以接受的范围。
(3) IFOA算法可以有效搜索全局最优解,与遗传算法相比,具有参数设置少、计算速度快、寻优过程简单、易于程序实现等特点,在病态问题解算中更具有实用性。
| [1] | HANSEN P C. Truncated Singular Value Decomposition Solutions to Discrete Ill-posed Problems with Ill-determined Numerical Rank[J]. SIAM Journal on Scientific and Statistical Computing,1990, 11 (3) : 503 –518 . |
| [2] | HANKE M, GROETSCH C W. Nonstationary Iterated Tikhonov Regularization[J]. Journal of Optimization Theory and Applications,1998, 98 (1) : 37 –53 . |
| [3] |
曾群意, 欧吉坤. 用遗传算法解算病态方程[J].大地测量学与地球动力学,2003, 23 (3) : 93 –97 .
ZENG Qunyi, OU Jikun. Study on Application of Genetic Algorithms in Solving Ill-conditioned Equations[J]. Journal of Geodesy and Geodynamics,2003, 23 (3) : 93 –97 . |
| [4] |
王建, 张献州, 张勇. 改进粒子群算法求解GPS短基线整周模糊度的研究[J].大地测量学与地球动力学,2012, 32 (4) : 148 –151 .
WANG Jian, ZHANG Xianzhou, ZHANG Yong. Research on Ambiguity Resolution of GPS Short Baseline by Using Improved Particle Swarm Optimization[J]. Journal of Geodesy and Geodynamics,2012, 32 (4) : 148 –151 . |
| [5] |
梁兴建, 詹志辉. 基于双模式变异策略的改进遗传算法[J].山东大学学报(工学版),2014, 44 (6) : 1 –7 .
LIANG Xingjian, ZHAN Zhihui. Improved Genetic Algorithm Based on the Dual-mode Mutation Strategy[J]. Journal of Shandong University (Engineering Science),2014, 44 (6) : 1 –7 . |
| [6] |
赵新超, 刘子阳. 差分和扰动混合的多策略粒子群优化算法[J].计算机科学与探索,2014, 8 (2) : 218 –225 .
ZHAO Xinchao, LIU Ziyang. Hybrid Particle Swarm Optimization with Differential and Perturbation[J]. Journal of Frontiers of Computer Science and Technology,2014, 8 (2) : 218 –225 . |
| [7] |
隋立芬. 抗差岭估计原理及其应用[J].测绘通报,1994 (1) : 9 –12 .
SUI Lifen. The Principle of Robust Rridge Estimation and Its Applications in Geodetic Adjustments[J]. Bulletin of Surveying and Mapping,1994 (1) : 9 –12 . |
| [8] |
归庆明, 黄维彬, 张建军. 抗差泛岭估计[J].测绘学报,1998, 27 (3) : 211 –216 .
GUI Qingming, HUANG Weibin, ZHANG Jianjun. Robust Universal Ridge Estimation[J]. Acta Geodaetica et Cartographica Sinica,1998, 27 (3) : 211 –216 . |
| [9] |
刘雁雨, 隋立芬, 刘青利. 抗差岭型组合主成分估计及误差影响[J].测绘科学,2004, 29 (2) : 50 –52 .
LIU Yanyu, SUI Lifen, LIU Qingli. Robust Ridge Combined Principal Components Estimation and Influence of Errors[J]. Science of Surveying and Mapping,2004, 29 (2) : 50 –52 . |
| [10] |
何然, 黄思训, 周晨腾, 等. 遗传算法结合正则化方法反演海洋大气波导[J].物理学报,2012, 61 (4) : 504 –511 .
HE Ran, HUANG Sixun, ZHOU Chenteng, et al. Genetic Algorithm with Regularization Method to Retrieve Ocean Atmosphere Duct[J]. Acta Physica Sinica,2012, 61 (4) : 504 –511 . |
| [11] |
崔希璋, 於宗俦, 陶本藻, 等. 广义测量平差[M]. 第2版. 武汉: 武汉大学出版社, 2009.
CUI Xizhang, YU Zongchou, TAO Benzao, et al. Generalized Surveying Adjustment[M]. 2nd ed. Wuhan: Wuhan University Press, 2009. |
| [12] | HANSEN P C, O'LEARY D P. The Use of L-curve in the Regularization of Discrete ⅡI-posed Problems[J]. SIAM Journal on Scientific Computing,1993, 14 (6) : 1487 –1503 . |
| [13] | HANSEN P C, JENSEN T K, RODRIGUEZ G. An Adaptive Pruning Algorithm for the Discrete L-curve Criterion[J]. Journal of Computational and Applied Mathematics,2007, 198 (2) : 483 –492 . |
| [14] | GOLUB G H, HEATH M, WAHBA G. Generalized Cross-validation as a Method for Choosing a Good Ridge Parameter[J]. Technometrics,1979, 21 (2) : 215 –223 . |
| [15] |
王振杰. 大地测量中不适定问题的正则化解法研究[D]. 武汉: 中国科学院测量与地球物理研究所, 2003. WANG Zhenjie. Research on the Regularization Solutions of Ill-posed Problems in Geodesy[D]. Wuhan: Institute of Geodesy and Geophysics, CAS, 2003. |
| [16] | PAN W T. A New Fruit Fly Optimization Algorithm: Taking the Financial Distress Model as an Example[J]. Knowledge-based Systems,2012, 26 : 69 –74 . |
| [17] | SHAN Dan, CAO Guohua, DONG Hongjiang. LGMS-FOA: An Improved Fruit Fly Optimization Algorithm for Solving Optimization Problems[J]. Mathematical Problems in Engineering,2013, 2013 : 108768 . |
| [18] | PAN Quanke, SANG Hongyan, DUAN Junhua, et al. An Improved Fruit Fly Optimization Algorithm for Continuous Function Optimization Problems[J]. Knowledge-based Systems,2014, 62 : 69 –83 . |
| [19] | YUAN Xiaofang, DAI Xiangshan, ZHAO Jingyi, et al. On a Novel Multi-swarm Fruit Fly Optimization Algorithm and Its Application[J]. Applied Mathematics and Computation,2014, 233 : 260 –271 . |
| [20] |
雷英杰.
MATLAB遗传算法工具箱及应用[M]. 西安: 西安电子科技大学出版社, 2005 .
LEI Yingjie. MATLAB Genetic Algorithm Toolbox and Its Application[M]. Xi'an: Xidian University Press, 2005 . |
| [21] |
龚循强, 李志林. 稳健加权总体最小二乘法[J].测绘学报,2014, 43 (9) : 888 –894 .DOI:10.13485/j.cnki.11-2089.2014.0140.
GONG Xunqiang, LI Zhilin. A Robust Weighted Total Least Squares Method[J]. Acta Geodaetica et Cartographica Sinica,2014, 43 (9) : 888 –894 .DOI:10.13485/j.cnki.11-2089.2014.0140. |
| [22] | GUI Q, LI X, GONG Y, et al. A Bayesian Unmasking Method for Locating Multiple Gross Errors Based on Posterior Probabilities of Classification Variables[J]. Journal of Geodesy,2011, 85 (4) : 191 –203 . |