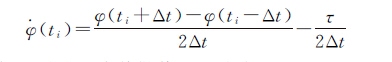2. 国家测绘地理信息局第一大地测量队,陕西 西安 710054
2. The First Geodetic Surveying Brigade of National Administration of Surveying, Mapping and Geoinformation, Xi’an 710054, China
航空重力测量是以飞机为载体,综合应用重力仪(或加速度计)、GPS(Global Position System)和INS(Inertial Navigation System)等多传感器测定近地空中重力加速度的重力测量技术[1]。航线上的重力由重力仪的测量值与载体的惯性加速度求差获得,大量研究表明GPS测得的载体惯性加速度精度是制约高精度航空重力测量的主要因素之一[1-3]。随着DGPS技术的成熟,由其确定的载体加速度精度得到了显著提高,使得航空重力测量步入大规模应用阶段。传统加速度测量主要基于位置差分法,通过对位置序列进行数值差分获得载体加速度,其对位置精度要求很高,在动态长基线的情况下模糊度往往很难固定[2]。因而,文献[3]从载波相位观测方程入手,提出了基于相位变化率的速度与加速度直接求解法,该方法通过站星间双差以及历元间相位差分,消除了模糊度参数以及大部分对流层和电离层误差,但所用卫星数仅为4颗,与位置差分法所得加速度相比,标准偏差约5.18 mGal(1 Gal=10-2 m/s2)。文献[4]指出在卫星分布较好的情况下(DOP≤2),由相位变化率确定的载体速度精度可达3 mm/s。对速度作一次差分可得载体加速度,文献[1]通过实例表明,该方法与位置差分法所得加速度精度相当。此外,载体速度还被应用于厄特弗斯改正,0.1 m/s的速度误差将引起约1 mGal的重力测量误差[5]。由此可见,获取高精度的速度信息对航空重力测量具有重要意义。
在矢量航空重力测量中,为减少姿态误差对重力水平分量的影响,通常要求飞机保持匀速直线飞行。研究表明[6-8],低动态情况下(加速度小于0.5 m/s2),采用一阶相位中心差分法获得的相位变化率(或导出多普勒观测值)即可满足高精度测速要求,然而相位观测值中不可避免会存在周跳和粗差,目前算法利用多频观测数据对大于1周(λ1≈19.03 cm)的大部分周跳或粗差能很好地探测出来,而对小于一周的粗差或小周跳却无能为力,这些误差可使测速精度将至dm/s级。因此,在航空重力测量的GPS数据处理中,需要进行有效的粗差探测等质量控制手段。文献[9]采用经典最小二乘法(least squares,LS)结合IGG Ⅲ抗差方案(robust least squares,RLS),利用验后标准化残差对粗差观测值降权处理,并对动态机载数据进行速度解算,取得了比较理想的结果。然而最小二乘法(LS)的估值不具有抗干扰性[10-11],即某一观测值本身的粗差将会通过多余观测分量矩阵影响其他观测值,从而使标准化残差不能正确定位粗差。文献[12]利用逐个排除法进行多粗差定位,但其计算效率很低。文献[13]结合IGG Ⅲ方案提出了基于中位参数的抗差估计方法,当粗差污染率小于50%时,能较好地定位粗差。
本文在航空重力测量飞行状态平稳条件下,提出了利用观测值验前残差进行粗差探测的思想。根据飞机平稳飞行状态可对其建立较为严密的状态方程,利用常加速度模型[14-15]求得的速度预测值计算本历元观测值的验前残差,并结合IGG Ⅲ抗差方案对观测值权重新分配。由于新方法在平差前进行粗差探测,避免了粗差转移的问题,同时在保证必要观测数的前提下不受粗差污染率(含粗差观测值个数占总观测值个数的百分比)的限制。此外,利用相位时序差分法求解速度,可将周跳等同粗差处理,能在一定程度上降低对GPS数据预处理的要求。
1 粗差探测方法基于多普勒观测值的双差测速模型为[16]
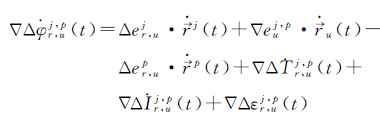 (1)
(1)
式中,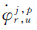
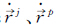
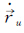
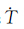
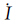
卫星位置、速度可利用广播星历计算获得,其误差对测速影响很小可忽略不计。流动站坐标由标准单点定位获得,其定位精度优于10 m,对站星轨道变化率的影响约为1 mm/s,本文也不予考虑r,u[17-18],对流层延迟采用Saastamoinen模型改正。若载体处于加速度稳定的运动状态,可对其建立较为严密的状态方程,则利用常加速度模型由上历元信息推估得到本历元载体速度的预测值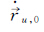
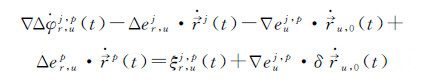 (2)
(2)
式中,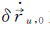
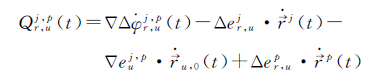 (3)
(3)
式(2)右边根据误差统计特性,可得中误差σ
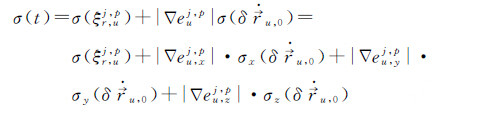 (4)
(4)
式中,“|·|”表示取绝对值,观测误差的方差通常认为与高度角相关,在定位的随机模型中一般采用正弦或余弦函数对其估计,此处采用余弦函数[19]
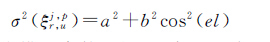 (5)
(5)
式中,a、b为模型参数,需要注意的是本文所谓的观测误差是相对量与定位算法中不同,因此不能直接采用定位算法中的模型参数值。
若Qr,uj,p序列不含粗差,则其应服从N(μ,σ)分布,μ为样本均值。对Qr,uj,p标准化可得
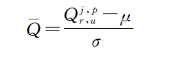 (6)
(6)
给定显著性水平α,则可通过假设检验探测出检验量Qr,uj,p是否包含粗差。本文采用IGG Ⅲ的权函数对观测值权重进行调整,其包含3段,分别是测量误差很小时的正常段,测量误差较大时的可疑段以及测量误差显著异常时的淘汰段[10]。根据值的大小对观测值作降权处理
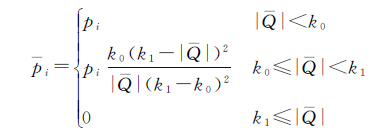 (7)
(7)
式中,pi为第i个观测值的原始权重;i为等价权因子;k0、k1为模型参数,取值范围分别为1~1.5和2.5~8。
由于本文采用一阶相位中心差分法求取导出多普勒值,假设不含粗差的相邻相位观测值计作φ(ti-Δt)、φ(ti)、φ(ti+Δt),若在ti+Δt时刻加入粗差τ,则ti时刻导出多普勒值为
故粗差对导出多普勒值的影响为
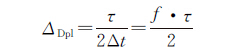 (8)
(8)
式中,f为采样率。参数k0、k1采用经验值k0=1.5,k1=3,结合式(7),认为当检验量进入淘汰段即为本文方法能探测出的最小粗差,故最小可探测粗差为
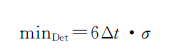 (9)
(9)
可见,采样率越高、检验量中误差越小则粗差探测能力越强。
2 实例分析为验证新方法的可靠性和可行性,分别设计两组试验方案:①利用静态测站的观测条件模拟飞机平稳飞行时段(加速度为常数)的观测条件;②采用实际航空重力测量的GPS观测数据。观测期间,电离层处于平静期,故仅用L1单频相位观测值。
2.1 静态模拟动态试验
采用航空重力测量前仪器检测时段的短基线GPS静态观测数据,数据观测时间为2015年4月24日 07:34:00-08:02:20(UTC),接收机类型为Novatel,数据采样率为5 Hz,观测数据无明显粗差。观测期间卫星高度角变化不大,以G27作为基准星,保证各双差观测序列基准的一致性。由于测站静止,因此认为速度真值为“0”。将载体速度真值“0”代入式(2),则预测值误差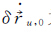
QQ图(quantile-quantile plot)被广泛用于检测序列是否具有正态性,其横坐标为理论分位数,纵坐标为样本分位数,若被检测序列接近直线分布,则说明数据具有很强的正态性[20]。图 1由左至右、由上至下,按高度角从高到低的顺序依次给出了6组观测误差序列的QQ图(本文以非基准星号代表该组双差观测序列),灰色散点为观测误差序列,黑色虚线为拟合直线。由图可见,各误差序列均近似直线型分布,说明具有良好的正态分布性。利用LS对所有观测误差序列拟合,得到式(5)的模型参数值a=1.1 mm,b=2.5 mm。
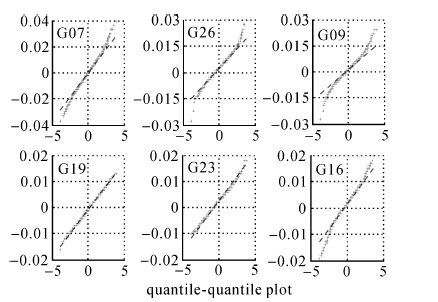
|
| 图 1 观测误差QQ图 Fig. 1 Quantile-quantile plot of measurement noise |
静态情况下,可认为载体作加速度和速度为零的匀速运动。常加速度模型计算的速度预测值与真值之差如图 2所示,可见水平方向速度之差的标准差STD(standard deviation)约为0.004 m/s,垂直方向速度之差的STD约为0.01 m/s,即在载体运动处于理想平稳状态下,常加速度模型可以得到高精度的速度预测值。故取${{\sigma }_{x}}=\left( \delta {{\overset{{\dot{\to }}}{\mathop{r}}\,}_{u,0}} \right)=0.004m/s,{{\delta }_{y}}\left( \delta {{\overset{{\dot{\to }}}{\mathop{r}}\,}_{u,0}} \right)=0.004m/s,{{\sigma }_{z}}\left( \delta {{\overset{{\dot{\to }}}{\mathop{r}}\,}_{u,0}} \right)=0.01m/s$。
|
| 图 2 速度预测值与真值之差 Fig. 2 The difference between the reference velocity and the predicted velocity |
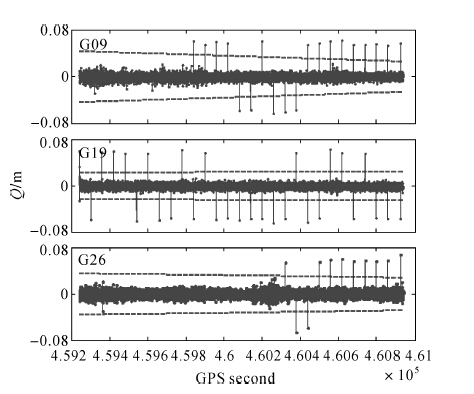
为测试本文粗差探测方法的效果,在原始相位观测值L1中每隔60 s加入2.4 cm大小的粗差,将观测时间分为3段:①GPS second 459 240~459 800,仅对G19卫星增加粗差,粗差污染率为14.3%;②GPS second 459 800~460 300,对G19和G09卫星增加粗差,粗差污染率为28.6%;③GPS second 460 300~460 935,对G19、G09以及G26卫星增加粗差,粗差污染率为42.9%。
图 3由上至下点线分别为G09、G19、G26号卫星Q检验量序列,虚线为最小可探测粗差阈值。可见,粗差被放大了近2.5倍,当观测值不存在粗差的情况下,Q检验量序列变化比较平缓。当有粗差出现时,Q检验量显著增大,利用本文方法能明显探测出粗差。
|
| 图 3 G09、G19、G26号卫星Q检验量 Fig. 3 The priori residual sequenceQ of G09,G19 and G26 |
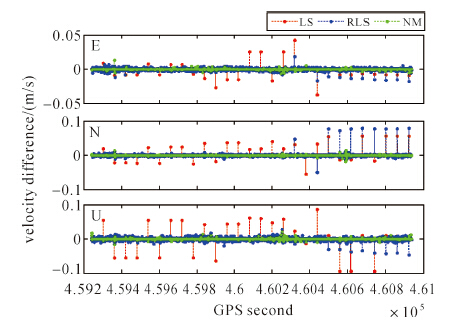
将LS对原始观测数据处理的速度值作为参考值,在含粗差的情况下分别用LS、RLS以及本文方法(new-method,NM)计算的结果与参考值作差,结果如图 4所示。由图可见,在保证必要观测数的前提下,NM方法不受粗差污染率的影响,在3个阶段均表现出良好的抗差性;当粗差污染率小于28.6%时,RLS具有良好的抗差性,当粗差污染率为42.9%时,RLS失去抗差能力。为分析该原因,对包含3个粗差的某一观测历元分别计算RLS和NM的粗差检验量如表 1所示,加粗字体为粗差所在观测值。RLS的检验量为LS解算的验后标准化残差V,只有当参数估值具有可靠的抗差性时,由其计算的残差才能反映观测值的实际分布[21],而LS在观测量较少的情况下,本身即存在不能正确定位粗差的缺陷[11],因此当粗差污染率为49.2%时,由LS解得的残差不能正确定位这些粗差所在的观测值,通过对观测值错误的降权,使得解算结果变得不可靠。而NM检验量能明显反映粗差所在的位置,原因在于利用验前观测值残差来判断观测值是否存在粗差,避免了LS平差时粗差对其余观测量的影响。此外,除粗差所在历元,RLS和NM的计算结果与参考值之差并非完全为“0”,这是因为实测数据虽无明显粗差,但观测质量并不十分理想,利用IGG Ⅲ方案仍可判断出许多可疑段的观测数据,从而造成各方法之间观测值权重的不一致,但并不影响粗差探测性能的评价。
|
| 图 4 E/N/U 3方向飞机飞行速度 Fig. 4 The velocity errors for East/North/Up components in static mode with LS,RLS and NM,respectively |
| RLS检验量 | 迭代次数 | NM检验量 | 参数 | ||
| 0 | 1 | 2 | |||
| V1 | 0.46 | 1.66 | 1.5 | Q 1 | 0.35 |
| V2 | 1.39 | 0.71 | 1.07 | Q2 | 5.5 |
| V3 | 1.04 | 1.31 | 0.28 | Q3 | 0.09 |
| V4 | 0.02 | 1.05 | 0.63 | Q4 | 7.06 |
| V5 | 1.78 | 0.03 | 0.42 | Q5 | 0.08 |
| V6 | 0.15 | 0.27 | 0.45 | Q6 | 5.2 |
| V7 | 0.38 | 0.41 | 1.55 | Q7 | 0.08 |
为分析采样率对NM粗差探测能力的影响,将原数据稀释为1 Hz(即仅保留了整秒观测时刻的观测数据),每隔60 s对G09号卫星增加粗差。由于采样率变为原来的1/5,由误差传播定律可知,观测噪声也降为原来的1/5,即此时a=0.2 mm,b=0.5 mm。虽然速度预测值精度也受观测噪声的影响,利用1 Hz计算的速度预测值精度高达1 mm/s,但实际过程中载体不可能达到完全理想的运动状态,主要误差源自模型误差,考虑到过高的预测精度对实际应用不具有参考价值。故此处仍取
| 粗差大小/cm | 成功率/(%) |
| 2.4 | 0 |
| 5 | 17.2 |
| 6 | 41.4 |
| 7 | 72.4 |
| 10 | 100 |
2.2 机载动态试验
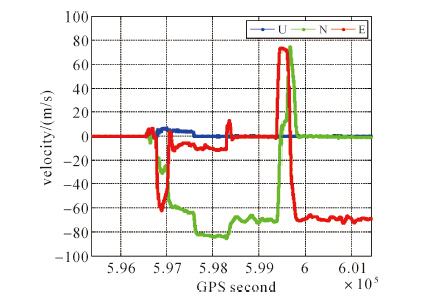
选用西安某次航空重力测量试验数据,接收机类型为Novatel,数据采样率为5 Hz,数据采集时间为当地时间2015年4月26日05:22:40-07:00:00,沿东西方向飞行,历时约100 min,时速约为235 km/h,包含飞机静止、起飞以及进入平稳飞行3个状态。飞机站心坐标系下E/N/U 3个方向速度如图 5所示,大约在起飞后一小时进入测区。截止高度角设为10°,观测期间以G21为基准星。
|
| 图 5 静态模拟动态情况下E/N/U 3方向速度误差 Fig. 5 The aircraft velocity for East/North/Up components |
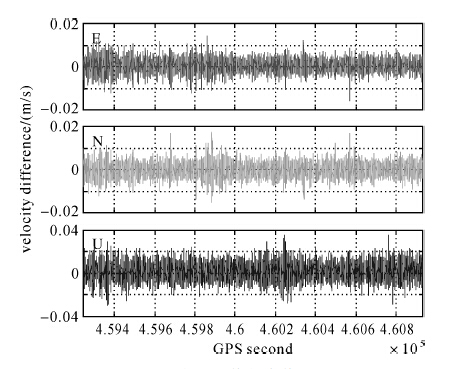
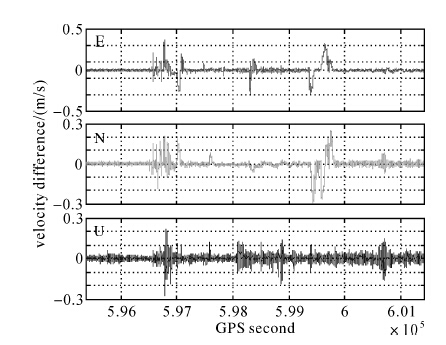
图 6为速度预测值与实测值之差,可见静止阶段(GPS second:595 400~596 480)两者差值均优于4 cm/s,其STD水平方向约为4 mm/s,垂直方向约为9 mm/s,与静态测站模拟结果基本一致。当飞机由起飞至平稳飞行状态阶段(GPS second: 596 480~600 000),两者偏差变化最大,部分历元达到了dm/s级,且主要发生在速度变化较大时期(加速度大小可达1.8 m/s2)原因在于该阶段载体运动状态复杂,用常加速度模型难以较好的估计出下一历元速度预测值。此后,飞机进入平稳飞行阶段(加速度大小保持在0.2 m/s2左右),其中在GPS second: 600 590~600 830时段,出现近50 s的速度偏差峰值,该段时间E/N方向加速度大小分别约为0.2 m/s2和0.4 m/s2,垂直方向加速度最大约为0.8 m/s2,这是由于该时段正值地面气温回升阶段,空中水汽含量急剧增加,使得机翼严重结冰,造成飞行状态不稳定所致。本文仅选用平稳飞行阶段进行分析,其速度预测值与实测值偏差的STD水平方向为1 cm/s,垂直方向为1.7 cm/s。
|
| 图 6 速度预测值与实测值之差 Fig. 6 The difference between the reference velocity and the predicted velocity |
按式(3)计算各卫星的Q 序列如图 7所示,不同颜色散点即代表不同卫星,相应颜色的虚线为其粗差探测阈值。由图可见,除中间时段由飞机震荡引起部分历元Q 值偏大,其余均在5 cm以内,按本文方法设定的阈值,其最小可探测粗差约为7.5 cm,按式(8)换算至相位观测值上,即可探测出约3 cm的粗差。

|
| 图 7 各卫星检验量Q 序列 Fig. 7 The priori residualQ of each double difference observation |
每隔60 s在G24号卫星的L1相位观测值上加入3 cm的粗差,粗差污染率为20%。以不含粗差情况下LS计算的速度作为参考真值,各方法与参考真值之差如图 8所示。红色点线为LS,蓝色点线为RLS,绿色点线为NM。由图可见,若直接采用LS,3 cm的粗差在N和U方向对速度的误差可达8 cm/s,在E方向可达3 cm/s。而用RLS和NM均能很好的探测粗差,进一步说明本文方法的可靠性与可行性。
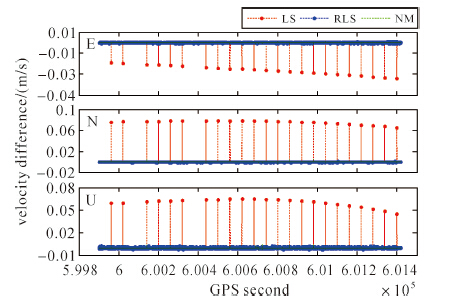
|
| 图 8 动态情况下E/N/U 3方向速度误差 Fig. 8 The velocity errors for East/North/Up components in kinematic mode with LS,RLS and NM,respectively |
3 结 论
针对航空重力测量中飞机处于平稳飞行状态的特性,结合常加速度模型和IGGⅢ抗差方案,提出了基于速度预测值的验前残差粗差探测方法,通过理论和实例分析得出以下结论:
(1) 新方法粗差探测能力主要受观测误差和模型误差的影响。观测误差的影响量级一般在mm/s级;模型误差与载体运动状态紧密相关,由静态试验表明,当载体处于匀速运动的情况下,速度预报精度可达mm/s级,由动态试验可见,当飞机平稳飞行时,速度预报精度在1~2 cm/s左右。
(2) 粗差对一阶中心差分法构造的导出多普勒值的影响大小为f·τ/2。即,当数据采样率大于2 Hz时,粗差被放大,反之则减小。静态试验表明,当f=5 Hz时,新方法可完全探测大小为2.4 cm的粗差;当f=1 Hz时,可完全探测大小为10 cm的粗差。动态试验表明,当载体加速度小于0.4 m/s2时,可完全探测粗差约为3 cm。新方法适用于低动态情况下,相位时序差分法测速的多粗差探测。
(3) 当粗差污染率较高时,利用LS验后标准化残差探测粗差是不可靠的。新方法避免了LS平差造成粗差转移的问题,且在保证必要观测数的前提下不受粗差污染率的影响。同时将周跳等同粗差处理,仅用单频观测数据即可。两组试验均表明,新方法可有效探测出小于1周大小的粗差。
| [1] |
孙中苗. 航空重力测量理论、方法及应用研究[D]. 郑州:信息工程大学, 2004. SUN Zhongmiao. Theory, Methods and Applications of Airborne Gravimetry[D]. Zhengzhou: Information Engineering University, 2004. |
| [2] | BRUTON A M. Improving the Accuracy and Resolution of SINS/DGPS Airborne Gravimetry[D]. Calgary, Alberta: University of Calgary, 2000. |
| [3] | JEKELI C, GARCIA R. GPS Phase Accelerations for Moving-base Vector Gravimetry[J]. Journal of Geodesy,1997, 71 (10) : 630 –639 . |
| [4] |
肖云, 孙中苗, 程广义. 利用多普勒观测值精确确定运动载体的速度[J].武汉测绘科技大学学报,2000, 25 (2) : 113 –118 .
XIAO Yun, SUN Zhongmiao, CHENG Guangyi. Precise Determination of Velocity for Airborne Gravimetry Using the GPS Doppler Observations[J]. Journal of Wuhan Technical University of Surveying and Mapping,2000, 25 (2) : 113 –118 . |
| [5] |
张开东. 基于SINS/DGPS的航空重力测量方法研究[D]. 长沙: 国防科学技术大学, 2007. ZHANG Kaidong.Research on the Methods of Airborne Gravimetry Based on SINS/DGPS[D].Changsha: National University of Defense Technology, 2007. |
| [6] | HEBERT C J, KEITH J, RYAN S, et al. DGPS Kinematic Carrier Phase Signal Simulation Analysis for Precise Aircraft Velocity Determination[C]//Proceedings of the ION GPS-97.Albuquerque: [s.n.], 1997. |
| [7] | BRUTON A M, GLENNIE C L, SCHWARZ K P. Differentiation for High-precision GPS Velocity and Acceleration Determination[J]. GPS Solutions,1999, 2 (4) : 7 –21 . |
| [8] | ZHANG J J.Precise Velocity and Acceleration Determination Using a Standalone GPS Receiver in Real Time[D]. Melbourne: RMIT University, 2007. |
| [9] |
范龙, 翟国君, 白鸽. 基于抗差最小二乘估计的载体速度计算方法[J].测绘学报,2011, 40 (S1) : 95 –99 .
FAN Long, ZHAI Guojun, BAI Ge. Calculating the Carrier Velocity Based on Robust Least Square Estimation[J]. Acta Geodaetica et Cartographica Sinica,2011, 40 (S1) : 95 –99 . |
| [10] |
杨元喜. 等价权原理--参数平差模型的抗差最小二乘解[J].测绘通报,1994 (6) : 33 –35 .
YANG Yuanxi. Theory of Equivalent Weight: The Least Squares Solution of Parameter Adjustment Model[J]. Bulletin of Surveying and Mapping,1994 (6) : 33 –35 . |
| [11] |
彭军还. 非线性M估计研究及其应用[D]. 武汉: 武汉大学, 2003. PENG Junhuan.Research on Non-linear M-estimates and Its Application[D]. Wuhan:Wuhan University, 2003. |
| [12] |
於宗俦, 李明峰. 多维粗差的同时定位与定值[J].武汉测绘科技大学学报,1996, 21 (4) : 323 –329 .
YU Zongchou, LI Mingfeng. Simultaneous Location and Evaluation of Multi-dimensional Gross Errors[J]. Journal of Wuhan Technical University of Surveying and Mapping,1996, 21 (4) : 323 –329 . |
| [13] |
杨玲, 沈云中, 楼立志. 基于中位参数初值的等价权抗差估计方法[J].测绘学报,2011, 40 (1) : 28 –32 .
YANG Ling, SHEN Yunzhong, LOU Lizhi. Equivalent Weight Robust Estimation Method Based on Median Parameter Estimates[J]. Acta Geodaetica et Cartographica Sinica,2011, 40 (1) : 28 –32 . |
| [14] |
林旭, 罗志才, 姚朝龙. 常加速度模型的简化自协方差最小二乘法[J].测绘学报,2014, 43 (11) : 1144 –1150 .DOI:10.13485/j.cnki.11-2089.2014.0143.
LIN Xu, LUO Zhicai, YAO Chaolong. Simplified Autocovariance Least-squares Method for Constant Acceleration Model[J]. Acta Geodaetica et Cartographica Sinica,2014, 43 (11) : 1144 –1150 .DOI:10.13485/j.cnki.11-2089.2014.0143. |
| [15] | SINGER R A. Estimating Optimal Tracking Filter Performance for Manned Maneuvering Targets[J]. IEEE Transactions on Aerospace and Electronic Systems,1970, AES-6 (4) : 473 –483 . |
| [16] | SALAZAR D, HERNANDEZ-PAJARES M, JUAN-ZORNOZA J M, et al. EVA: GPS-based Extended Velocity and Acceleration Determination[J]. Journal of Geodesy,2011, 85 (6) : 329 –340 . |
| [17] | ZHANG Xiaohong, GUO Bofeng, GUO Fei, et al. Influence of Clock Jump on the Velocity and Acceleration Estimation with a Single GPS Receiver Based on Carrier-phase-derived Doppler[J]. GPS Solutions,2013, 17 (4) : 549 –559 . |
| [18] | SERRANO L, KIM D, LANGLEY R B, et al. A GPS Velocity Sensor: How Accurate Can It Be?-A First Look[C]//Proceedings of the ION NTM. San Diego:Institute of Navigation, 2004: 875-885. |
| [19] | JIN Shuanggen, WANG J, PARK P H. An Improvement of GPS Height Estimations: Stochastic Modeling[J]. Earth, Planets and Space,2005, 57 (4) : 253 –259 . |
| [20] | SHUMWAY R H, STOFFER D S. Time Series Analysis and Its Applications: With R Examples. Time Series Analysis and Its Applications: With R Examples[M]. New York: Springer-Verlag, 2011 . |
| [21] |
杨元喜. 自适应抗差最小二乘估计[J].测绘学报,1996, 25 (3) : 206 –211 .
YANG Yuanxi. Adaptively Robust Least Squares Estimation[J]. Acta Geodaetica et Cartographica Sinica,1996, 25 (3) : 206 –211 . |