2. 长安大学地质工程与测量学院,陕西 西安 710054 ;
3. 流域生态与地理环境监测国家测绘地理信息局重点实验室,江西 南昌 330013
2. School of Geological and Surveying Engineering, Chang’an University, Xi’an 710054,China ;
3. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASG, Nanchang 330013,China
粗差是指离群的误差[1]。处理测量中的粗差影响一直是测绘数据处理理论的研究热点。目前主要形成了两种不同的粗差处理模式:将粗差纳入函数模型,沿着巴尔达提出的粗差数据探测(data snooping)[2],该方法将观测值粗差的出现视为观测值的数学期望产生了平移,但方差不变;将粗差纳入随机模型,引进统计学中的抗差估计(robust estimation)[3-4],该方法将粗差观测值看成是观测值的数学期望不变,方差异常。文献[5]在函数模型基础上,根据被观测量的独立观测数判断其观测值能否容忍粗差,提出了一种基于局部分析法的粗差探测法。
随着观测量的不断增多,出现多个粗差观测值的概率将会增大,研究多个粗差的探测、识别和处理具有重要意义[6]。基于统计学原理的粗差探测和定位方法主要包括:数据探测法(data snooping)[2]、多维粗差的同时定位与定值法(the method of simultaneous locating and evaluating multidimensional gross errors,LEGE)[7]、拟准检定法(quasi-detection of gross errors,QUAD)[8-10]、部分最小二乘法或预测残差法(partly least squaes,PLS)[11-12]等。针对上述4种粗差探测和定位方法的异同,文献[13]对均值漂移模型数据探测法和LEGE法的原理、方法和粗差探测过程进行了比较,证明两者在原理上基本等价,探测结果基本相近。文献[14]对独立等精度情形下部分最小二乘法和QUAD法进行了比较,得出其结果具有相同效果。文献[15]讨论了拟准检定法、LEGE法和部分最小二乘法在独立等精度时,粗差估值具有等价性,相关时有一定差异。
本文以粗差观测值定位一致前提下,基于均值漂移模型探讨粗差估值公式,导出观测值统计相关时平移参数的简明表达式。通过对LEGE法、QUAD法和PLS法的进一步分析,证明了LEGE法、QUAD法、PLS法这3种方法与数据探测法在粗差估值方面的异同。理论上给出了4种方法在观测值统计相关、独立(等权和不等权)情形下的估值公式及其差异,揭示了4种方法的理论本质和内在联系。
1 均值漂移模型数据探测法及其参数估计对于线性误差方程式
 (1)
(1)
式中,V为n1维残差向量;A为秩rank(A)=u的nu阶设计矩阵;
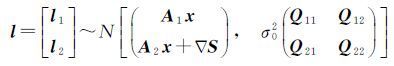 (2)
(2)
则式(1)变为
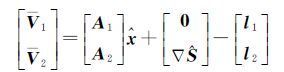 (3)
(3)
设H=[0 E]T,E为n2×n2单位阵。式(3)可表示为
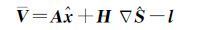 (4)
(4)
根据最小二乘原理得到估值[16]
 (5)
(5)
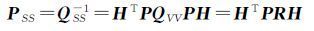 (6)
(6)
式中,QVV=P-1-A(ATPA)-1AT;R=I-A(ATPA)-1ATP[17]。
顾及粗差的未知参数x的估值为[16]
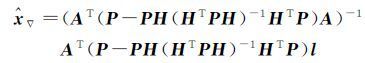 (7)
(7)
由附录的结果代入式(7),可得
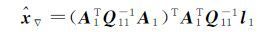 (8)
(8)
顾及附录式(3)′,则式(5)可以表示为
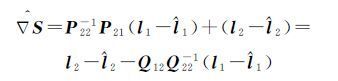 (9)
(9)
式中,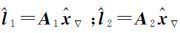
由式(9)可以看出,按照最小二乘原理求解观测值l2数学期望平移参数,实质上是由第1组不含粗差的观测值l1求解未知参数的最小二乘估值
文献[11]将部分最小二乘法应用于粗差的定位与定值,式(1)可表示为
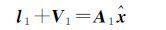 (10a)
(10a)
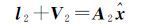 (10b)
(10b)
假设观测值l2含粗差,现仅采用未受粗差污染的观测值l1,根据部分最小二乘准则V1TQ11-1V1=min,得到未知参数估值
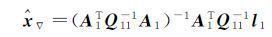 (11)
(11)
受污染的观测值l2对应的预测残差为[19]
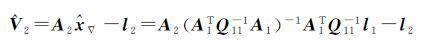 (12)
(12)
比较式(12)和式(9)可以看出,如果两组观测值l1、l2相互独立,则有Q12=Q21T=0,于是
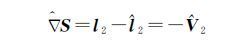 (13)
(13)
因此数据探测法计算的粗差估值与部分最小二乘计算的粗差估值具有等价性。
如果两组观测值l1、l2不独立,则有Q12=Q21T≠0,均值平移模型计算的粗差估值与部分最小二乘计算的粗差估值不相等,两者差值为
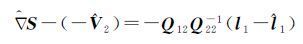 (14)
(14)
应用最小二乘准则VTPV=min对误差方程式求解可以得到[17]
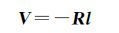 (15)
(15)
R为幂等矩阵,且满足[10]
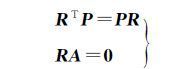 (16)
(16)
对于高斯马尔科夫模型而言,其理论模型为
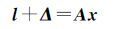 (17)
(17)
式中,Δ为观测值的真误差。
式(17)两边左乘矩阵R得[10]
结合矩阵R的性质得到
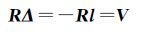 (18)
(18)
如果将Δ视为未知参数,得到秩亏Gauss-Markov模型[6]
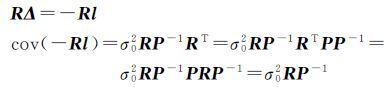 (19)
(19)
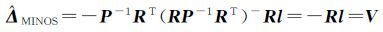 (20)
(20)
注意到PR是RP-1的对称自反g逆[20],易得验证式(20)中(RP-1RT)-=PR[10]。
式(20)两边乘以ATP得
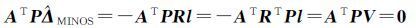 (21)
(21)
因此经典最小二乘法的余差V数值上与方程RΔ=-Rl关于Δ的最小(加权)范数解相同。当存在粗差时,限制
为了求解秩亏方程,选择r(r≥u)个拟准观测值,拟准观测范数极小条件[9-10]
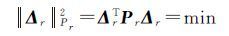 (22)
(22)
选第一组观测值l1为拟准观测值,则有
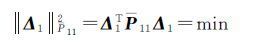 (23)
(23)
式中,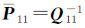
式(23)等价于
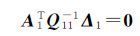 (24)
(24)
于是将式(18)和式(24)联立,得到方程[8]
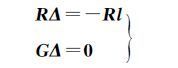 (25)
(25)
式中,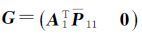
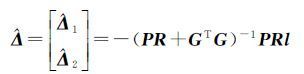 (26)
(26)
式中,
现对前面的部分最小二乘法进行分析,式(11)代入式(12)整理得到[15]
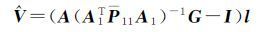 (27)
(27)
式(27)中矩阵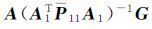
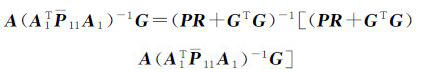 (28)
(28)
由于RA=0,所以式(28)为
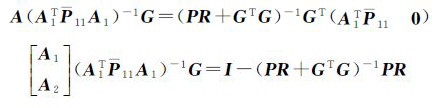 (29)
(29)
于是式(27)可表示为
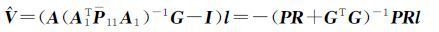 (30)
(30)
比较式(30)和式(26)可知,用QUAD法解算的粗差估值和用部分最小二乘解算的结果一致。
如果两组观测值l1、l2相互独立,则Q12=Q21T=0,所以数据探测法的粗差估值与QUAD法计算的粗差估值等价。如果两组观测值l1、l2不独立,则有Q12=Q21T≠0,数据探测法的粗差估值与QUAD法的粗差估值不相等,两者差值为
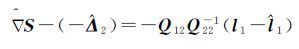 (31)
(31)
将平差因子阵、真误差分为两部分[7],于是式(18)可表示为
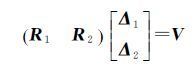 (32)
(32)
假设l2为受粗差污染的观测值,且R2Δ2对于观测值残差V的影响远大于R1Δ1[7]。于是略去式(32)中R1Δ1的影响,得到近似关系[7]
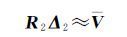 (33)
(33)
从式(33)可以看出,在进行解算时,首先假定Δ1=0,然后按照最小二乘准则,其估值为[7]
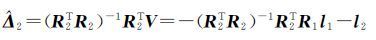 (34)
(34)
式(34)为受粗差污染观测值l2的真误差估值,表现为粗差的影响[7]。
由式(16)可得到[15]
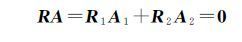 (35)
(35)
所以
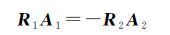 (36)
(36)
于是式(9)可以表示为
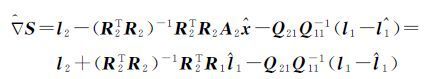 (37)
(37)
由LEGE法的假设Δ1=0可以看出,在解算的过程中,认为第1组观测值
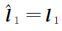
设观测值为独立等权,则Q21=Q12T=0、Q11=Q22=I,于是有[15]
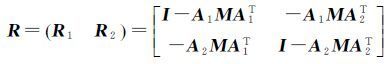 (38)
(38)
式中,M=(A1TA1+A2TA2)-1。
 (39)
(39)
将式(39)代入式(34)得
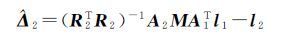 (40)
(40)
对式(37)进一步分析
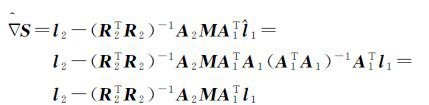 (41)
(41)
比较式(40)和式(41)可以看出,当观测值之间为独立等权时,LEGE法和数据探测法的粗差估值具有等价性。
从而可以得出,对于独立等权观测值而言,4种粗差的估值具有严格的等价关系。
5 算例分析算例1取文献[21]中水准网如图 1所示。设观测值为6个观测高差,设已知点高程为1000m,观测值的协因数矩阵为
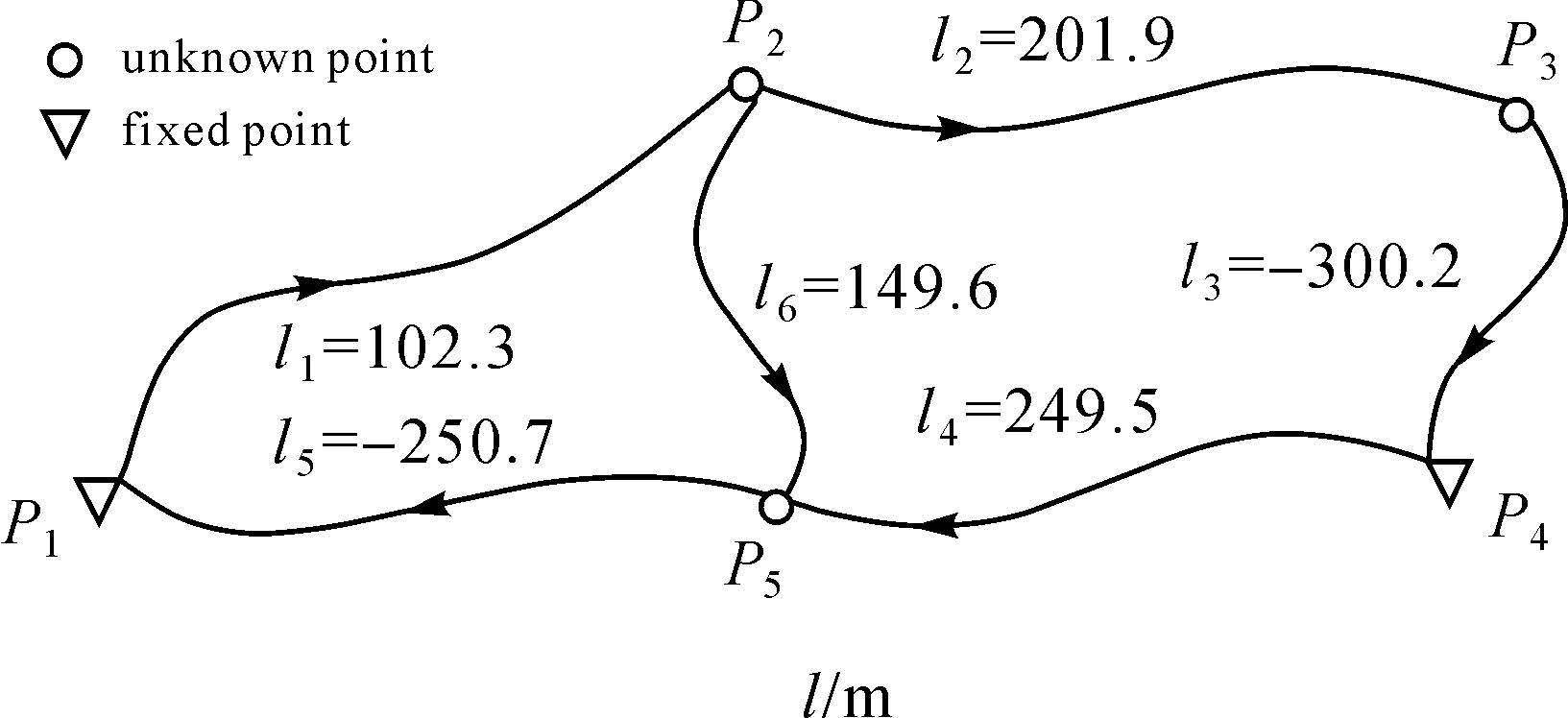
|
| 图 1 水准网 Fig. 1 Levelingnetwork |
假设高差观测值l1中存在粗差,加入不同大小粗差,计算结果如表 1所示。
| i | σli/m | MBDi/m | ri | C0i | w2a | w2b | w2c | w2d | w2e | w2f | w2g |
| 1 | 2.35 | 2.98 | 10.56 | 1.27 | 0.57 | 4.59 | 12.45 | 24.16 | 39.71 | 59.11 | 175.1 |
| 2 | 1.97 | 10.35 | 0.62 | 5.24 | 0.30 | 0.00 | 0.36 | 1.38 | 3.06 | 5.40 | 21.4 |
| 3 | 0.89 | 10.35 | 0.13 | 11.57 | 0.30 | 0.00 | 0.36 | 1.38 | 3.06 | 5.40 | 21.4 |
| 4 | 2.32 | 2.60 | 13.68 | 1.12 | 0.37 | 3.76 | 10.68 | 21.14 | 35.13 | 52.67 | 158.2 |
| 5 | 0.45 | 1.32 | 1.95 | 2.96 | 0.33 | 3.76 | 10.93 | 21.82 | 36.45 | 54.80 | 165.5 |
| 6 | 1.18 | 2.59 | 3.56 | 2.19 | 0.27 | 3.49 | 10.36 | 20.88 | 35.04 | 52.85 | 160.5 |
| 注:表中w上标a、b、c、d、e、f、g表示在高差观测值l1中分别加入1m、2m、3m、4m、5m、10m粗差后计算的检验统计量 | |||||||||||
由于高差观测值l1的MDB(minimal detectable bias)为2.98m,所以对于粗差小于其值的观测值,无法实现粗差的定位,具体讨论详见文献[21],表 1中的MDB、多余观测分量ri和可控性数值C0等计算详见文献 [21-22],限于篇幅,此略。
现设计3种试验方案,方案1为观测值统计相关的情形,其协因数阵Ql为非对角阵;方案2仅取Ql的对角线元素的对角阵,即观测值统计独立不等权;方案3取协因数阵Ql为单位阵,即观测值统计独立等权,试验结果如表 2所示。
| 方案比较 | 观测高差l1中含3m粗差 | 观测高差l1中含4m粗差 | 观测高差l1中含5m粗差 | 观测高差l1中含6m粗差 | 观测高差l1中含10m粗差 | ||||||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||||
| data snooping | 2.54 | 4.94 | 5.74 | 3.54 | 5.94 | 6.74 | 4.54 | 6.94 | 7.74 | 5.54 | 7.94 | 8.74 | 9.54 | 11.94 | 12.74 | ||||
| partly LS | 4.74 | 4.94 | 5.74 | 5.74 | 5.94 | 6.74 | 6.74 | 6.94 | 7.74 | 7.74 | 7.94 | 8.74 | 11.74 | 11.94 | 12.74 | ||||
| QUAD | 4.74 | 4.94 | 5.74 | 5.74 | 5.94 | 6.74 | 6.74 | 6.94 | 7.74 | 7.74 | 7.94 | 8.74 | 11.74 | 11.94 | 12.74 | ||||
| LEGE | 4.80 | 5.20 | 5.74 | 5.80 | 6.20 | 6.74 | 6.80 | 7.20 | 7.74 | 7.80 | 8.20 | 8.74 | 11.80 | 12.20 | 12.74 | ||||
| Q21Q11-1 | -2.20 | 0 | 0 | -2.20 | 0 | 0 | -2.20 | 0 | 0 | -2.20 | 0 | 0 | -2.20 | 0 | 0 | ||||
从表 2计算结果可以看出,①当观测值中含有单个粗差,在能够正确定位粗差的情况下,部分最小二乘粗差估值和拟准鉴定法粗差估值相同,说明两种方法具有等价性和一致性;②从结果可以看出,在观测值统计相关情形下,数据探测法计算的粗差估值与部分最小二乘和拟准检定法的粗差估值结果差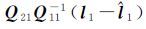
算例2 取文献[6]中的GPS基线向量网,A和B为控制点,C、D、E和F是待定点。总共观测了13条独立基线,多余观测量为27个。控制点A和B的坐标和GPS网中各条基线向量的有关数据见文献[6],在此略。
为比较几种方法在粗差估计方面的情况,将0.4m、-0.3m、-0.2m、0.3m和-0.4m共5个模拟粗差分别加在第5、15、21、31和第37号5个观测值上[20]。不同方法计算的粗差估值比较见表 3。从表 3的GPS网数据解算结果也可以看出几种方法的相互关系,其关系与前面理论分析一致。
| 不同方法 | 粗差估值 | ||||
| 5th | 15th | 21st | 31st | 37th | |
| 粗差真值 | 0.4 | -0.3 | -0.2 | 0.3 | -0.4 |
| data snooping | 0.3911 | -0.2980 | -0.1802 | 0.2978 | -0.3900 |
| partly LS | 0.3915 | -0.2981 | -0.1802 | 0.2979 | -0.3900 |
| QUAD | 0.3915 | -0.2981 | -0.1802 | 0.2979 | -0.3900 |
| LEGE | 0.3933 | -0.2868 | -0.1855 | 0.2938 | -0.3859 |
| Q21Q11-1 | 0.38×10-3 | -0.07×10-3 | 0.002×10-3 | 0.06×10-3 | -0.007×10-3 |
6 结 论
在粗差定位一致的前提下,理论分析表明:①在观测值统计相关时,部分最小二乘法和QUAD法在粗差估值的计算上具有等价性;②在观测值统计相关时,数据探测法和部分最小二乘法、QUAD法两种方法在粗差估值上不一致,其粗差的估值差异均为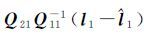
由于本文限于粗差已准确定位,这些方法的粗差探测和定位性能还有待深入研究。
| [1] |
周江文. 经典误差理论与抗差估计[J].测绘学报,1989, 18 (2) : 115 –120 .
ZHOU Jiangwen. Classical Theory of Errors and Robust Estimation[J]. Acta Geodaetica et Cartographica Sinica,1989, 18 (2) : 115 –120 . |
| [2] | BAARDA W. A Testing Procedure for Use in Geodetic Networks[M]. Delft: Netherlands Geodetic Commission, Publication on Geodesy, 1968 . |
| [3] |
杨元喜.
抗差估计理论及其应用[M]. 北京: 八一出版社, 1993 .
YANG Yuanxi. Robust Estimation Theory and Its Applications[M]. Beijing: Bayi Publishing House, 1993 . |
| [4] | YANG Yuanxi, SONG Lijie, XU Tianhe. Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights[J]. Journal of Geodesy,2002, 76 (6-7) : 353 –358 . |
| [5] |
孙海燕, 黄华兵, 王喜娜. 多维平差问题粗差的局部分析法[J].测绘学报,2012, 41 (1) : 54 –58 .
SUN Haiyan, HUANG Huabing, WANG Xi’na. Local Analysis Method on Gross Error of Multidimensional Adjustment Problem[J]. Acta Geodaetica et Cartographica Sinica,2012, 41 (1) : 54 –58 . |
| [6] | WOLF P R, GHILANI C D. Adjustment Computations: Statistics and Least Squares in Surveying and GIS[M]. 3rd ed New York: Wiley, 1997 . |
| [7] |
於宗俦, 李明峰. 多维粗差的同时定位与定值[J].武汉测绘科技大学学报,1996, 21 (4) : 323 –329 .
YU Zongchou, LI Mingfeng. Simultaneous Location and Evaluation of Multidimensional Gross Errors[J]. Journal of Wuhan Technical University of Surveying and Mapping,1996, 21 (4) : 323 –329 . |
| [8] | OU Jikun. A New Method of Identifying and Locating Gross Errors: Quasi-accurate Detection[J]. Chinese Science Bulletin,1999, 44 (23) : 2200 –2204 . |
| [9] |
欧吉坤. 粗差的拟准检定法(QUAD法)[J].测绘学报,1999, 28 (1) : 15 –20 .
OU Jikun. Quasi-accurate Detection of Gross Errors (QUAD)[J]. Acta Geodaetica et Cartographica Sinica,1999, 28 (1) : 15 –20 . |
| [10] | GUO Jianfeng, OU Jikun, WANG Haitao. Quasi-accurate Detection of Outliers for Correlated Observations[J]. Journal of Surveying Engineering,2007, 133 (3) : 129 –133 . |
| [11] |
王爱生, 欧吉坤. 部分最小二乘平差方法及在粗差定值与定位中的应用[J].测绘科学,2005, 30 (2) : 70 –72 .
WANG Aisheng, OU Jikun. Method of Partly Least Squares and Application in Gross Error Location and Estimation[J]. Science of Surveying and Mapping,2005, 30 (2) : 70 –72 . |
| [12] |
徐培亮. 可剔除多个粗差的F-T法[J].武汉测绘科技大学学报,1987, 12 (2) : 41 –46 .
XU Peiliang. A F-T Method for Outliers[J]. Journal of Wuhan Technical University of Surveying and Mapping,1987, 12 (2) : 41 –46 . |
| [13] |
宋力杰, 杨元喜. 均值漂移模型粗差探测法与LEGE法的比较[J].测绘学报,1999, 28 (4) : 295 –300 .
SONG Lijie, YANG Yuanxi. Comparison between Data Snooping and LEGE[J]. Acta Geodaetica et Cartographica Sinica,1999, 28 (4) : 295 –300 . |
| [14] |
刘根友, 郝晓光, 柳林涛. 粗差检定的两种途径[J].大地测量与地球动力学,2005, 25 (3) : 29 –33 .
LIU Genyou, HAO Xiaoguang, LIU Lintao. Two Approaches to Gross Error Detection[J]. Journal of Geodesy and Geodynamics,2005, 25 (3) : 29 –33 . |
| [15] |
王海涛, 欧吉坤, 袁运斌, 等. 估计观测值粗差三种方法的等价性讨论[J].武汉大学学报(信息科学版),2013, 38 (2) : 162 –166 .
WANG Haitao, OU Jikun, YUAN Yunbin, et al. On Equivalence of Three Estimators for Outliers in Linear Model[J]. Geomatics and Information Science of Wuhan University,2013, 38 (2) : 162 –166 . |
| [16] |
李德仁, 袁修孝.
误差处理与可靠性理论[M]. 武汉: 武汉大学出版社, 2002 .
LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory[M]. Wuhan: Wuhan University Press, 2002 . |
| [17] |
周江文, 黄幼才, 杨元喜, 等.
抗差最小二乘法[M]. 武汉: 华中理工大学出版社, 1997 .
ZHOU Jiangwen, HUANG Youcai, YANG Yuanxi, et al. Robust Least Squares Method[M]. Wuhan: Huazhong University of Science and Technology Press, 1997 . |
| [18] |
王金岭, 陈永奇. 粗差数学期望平移模型的理论研究[J].武汉测绘科技大学学报,1995, 20 (2) : 146 –150 .
WANG Jinling, CHEN Yongqi. A Research on the Mean Shift Outlier Models[J]. Journal of Wuhan Technical University of Surveying and Mapping,1995, 20 (2) : 146 –150 . |
| [19] |
宋力杰, 杨元喜. 论粗差修正与粗差剔除[J].测绘通报,1999 (6) : 5 –6 .
SONG Lijie, YANG Yuanxi. Discussion of Outlier Correction Model and Deleting Model[J]. Bulletin of Surveying and Mapping,1999 (6) : 5 –6 . |
| [20] |
郭建锋. 模型误差理论若干问题研究及其在GPS数据处理中的应用[D]. 武汉: 中国科学院测量与地球物理研究所, 2007. GUO Jianfeng. Theory of Model Errors and Its Applications in GPS Data Processing[D]. Wuhan: Institute of Geodesy and Geophysics of Chinese Academy of Sciences, 2007. |
| [21] | KNIGHT N L, WANG Jinling, RIZOS C. Generalised Measures of Reliability for Multiple Outliers[J]. Journal of Geodesy,2010, 84 (10) : 625 –635 . |
| [22] |
王金岭, 陈永奇. 论观测值的可靠性度量[J].测绘学报,1994, 23 (4) : 252 –258 .
WANG Jinling, CHEN Yongqi. On the Reliability Measure of Observations[J]. Acta Geodaetica et Cartographica Sinica,1994, 23 (4) : 252 –258 . |