2. 地理信息工程国家重点实验室,陕西 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi’an 710054, China
卫星导航系统中星载原子钟的钟差预报在维持系统时间同步、优化导航电文中的钟差参数等方面具有重要的作用[1-2]。因此,针对卫星钟差(satellite clock bias,SCB)预报,国内外学者进行了大量的研究,建立起了多种钟差预报模型[2-8],总结起来主要有:二次多项式(QP)模型[2]、灰色系统(GM(1,1))模型[3]、谱分析(SA)模型[4-5]、时间序列(ARIMA)模型[6]、Kalman滤波(KF)模型[7]、小波神经网络(WNN)模型[1]和径向基函数神经网络(RBF)模型[8]等。然而,由于星载原子钟本身复杂变化的时频特性和极易受外界条件的影响,卫星钟差通常表现出复杂的周期变化与随机变化特性,使得已有的钟差预报模型在应用中仍存在一定的局限性:QP预报钟差时其预报误差会随着预报时间的增加而显著变大,GM(1,1)预报精度受模型指数系数影响较大[9],SA的周期函数要根据较长的钟差序列才能可靠确定,ARIMA存在模式识别和模型定阶的困难,KF的优劣取决于对原子钟运行特性和随机先验信息等的认知程度[10],WNN网络拓扑结构的确定比较困难[1],RBF预报中对应的样本长度、样本量以及样本之间间隔的确定缺少理论根据只能依赖经验确定[8]。而在这些模型当中,QP模型和GM(1,1)模型是最为常用且具有代表性的预报模型。
为了更好地反映钟差特性并提高其预报精度,本文同时考虑星载原子钟的物理特性、周期性变化特点与随机变化部分,在钟差二次多项式附加周期项模型的基础上,采用抗差最小二乘配置方法对卫星钟的随机项进行建模,得到一种更加完善的卫星钟差预报模型。钟差预报的结果表明,新方法能够更加全面地描述钟差的特性,并取得较两种常用模型更好的预报效果,同时也说明了针对新模型所提的协方差函数的确定方法是有效的。
1 算法原理 1.1 最小二乘配置模型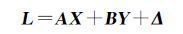 (1)
(1)
式中,L为n维观测向量;Δ为观测误差;X为t维非随机参数;A为n×t阶设计矩阵,rk(A)=t;Y为随机参数,包括n维已测点信号S和g维未测点信号S′;In是n阶单位阵;B=In0、Y=[ST(S′)T]T。对应的随机模型为
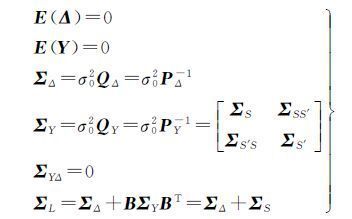 (2)
(2)
通常情况下设σ20=1,此时Σ=Q=P-1。
1.2 顾及卫星钟随机特性的LSC钟差预报算法根据星载原子钟的物理特性,在构造精密的钟差模型时,通常采用包含表征卫星钟时频特性的相位、频率、频率漂移率的二次多项式模型,其具体表达式为[2]
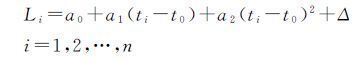 (3)
(3)
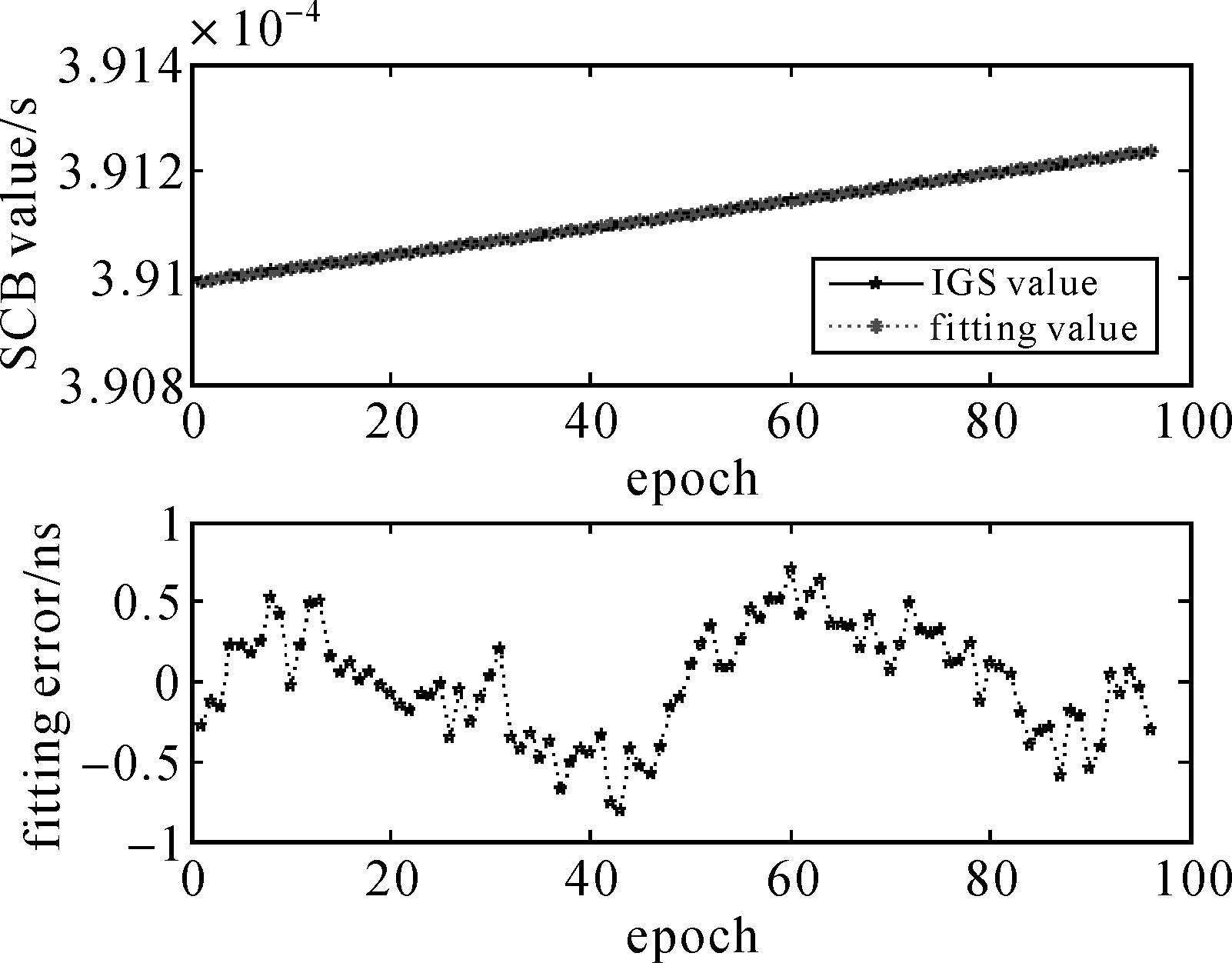
式中,Li是ti时刻的卫星钟差;t0为参考时刻;ti表示历元时刻;待估参数a0、a1和a2分别表示参考时刻t0的相位(钟差)、频率(钟速)及频率漂移率(钟漂);Δ为观测误差。当已知钟差数据不少于3个时,便可拟合求得待估参数。以IGS提供的GPS系统PRN18卫星2015年4月3日15min采样间隔的精密卫星钟差数据为例,使用QP模型对这一天的钟差数据进行拟合,图 1是其对应的拟合情况。
|
| 图 1 PRN18卫星QP模型下的钟差拟合 Fig. 1 Fitting SCB of the satellite PRN18 by QP model |
从图 1中可以看出拟合残差表现出较为明显的周期特性。因此,为了更好地反映钟差的特性,在钟差的预报建模中除了以二次多项式来反映钟差的趋势项部分,还应考虑钟差的周期变化特性。附加周期项的二次多项式(记作MQP)模型表达式为[4]
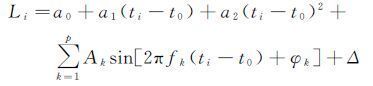 (4)
(4)
式中,p为主要周期函数的个数;Ak、fk、φk分别为对应周期项的振幅、频率和相位;其余符号的含义与式(3)相同。p与fk的值可利用频谱分析的方法来确定。考虑到本文中是以GPS卫星钟差数据进行预报试验,因此基于文献[14]的研究结果,直接取12h、6h作为MQP模型的主周期项。对应于图 1的QP钟差拟合,图 2是基于MQP模型的钟差拟合情况。

|
| 图 2 PRN18卫星MQP模型下的钟差拟合 Fig. 2 Fitting SCB of the satellite PRN18 by MQP model |
对比图 1和图 2可以看出,MQP模型较好地消除钟差周期性变化特性的影响,说明在卫星钟差中除了相位、频率、频率漂移率这些确定的物理特性之外,还有周期性变化的特性,因此在对钟差进行拟合与预报时需要将该特性考虑在内。同时,由图 2可以看出,扣除卫星钟差的趋势项与周期项之后,剩余的残差部分表现为相对平稳的随机序列。为了更全面地反映卫星钟差特性并提高钟差预报精度,在考虑星载原子钟物理特性和周期变化特点的基础上,还应考虑其随机项部分[15]。
钟差随机性变化部分可以看作是一个随时间而连续变化的随机函数,符合最小二乘配置理论的建模条件,因此,本文基于最小二乘配置建立更加全面的钟差预报模型。该模型的表达式可以描述为
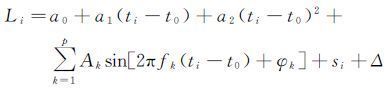 (5)
(5)
式中,si(待估时刻为s′i)表示钟差随机性部分。设ti-t0=δti、Akcosφk=bk、Aksinφk=ck,则式(5)对应矩阵形式的误差方程可以表示为
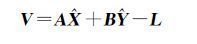 (6)
(6)
式中
根据估值准则
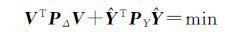 (7)
(7)
求解式(6)可得
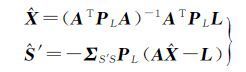 (8)
(8)
式中,
从而得到待求时刻的钟差表达式为
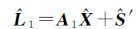 (9)
(9)
式中,1、A1的表达形式类似于L、A,分别表示待求钟差值向量和相应的系数矩阵。
1.3 协方差函数的抗差拟合及其确定合理的协方差函数确定一直是最小二乘配置中的关键问题[11]。同样的,最小二乘配置钟差预报模型的关键也在于其对应协方差函数的确定。对于钟差预报协方差函数的选择,与多数采用最小二乘配置解决实际问题类似,本文也是通过选取可实际应用的经验协方差函数来实现对钟差随机特性(信号)的描述。在已有的经验协方差函数中,高斯函数的应用最为广泛且性能相对较好[11, 13, 16],因此本文选择高斯函数(其表达式为σ(d)=σ2(0)exp(-kd2),式中d为两数据点之间的距离,σ2(0)、k是待求的协方差函数参数)作为最小二乘配置钟差预报模型对应的协方差函数。对于协方差函数参数的确定,可以直接采用两步极小法[17],即根据附有周期项的二次多项式模型的拟合残差确定协方差函数的参数;将该方法确定的最小二乘配置模型记作LSC模型。然而,考虑到在钟差数据中可能存在异常值,因此本文在文献[16—20]的基础上,采用抗差M估计[21]来求取协方差函数参数值的抗差估计解。具体方法如下:
1.3.1 计算抗差迭代的初值对卫星钟差数据进行归化处理,消除趋势项与周期项的影响,得到
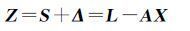 (10)
(10)
式中,X的估值
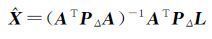 (11)
(11)
归化后得
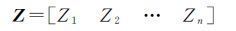 (12)
(12)
式中,n为一定时间段内已知钟差数据的个数。
按照抗差估计原理求Z的中心化值。迭代初值为δZi=Zi-med{Zi};方差因子为σi=med{|δZi|}/0.6745。在最小二乘配置模型中,其协方差阵和权阵间需相互转换;为避免迭代过程中出现过分降权的问题以及使得降权更加平稳,本文选用IGG3权函数[22],得到权因子函数的表达式为
 (13)
(13)
式中,k0和k1为阈值,k0可取值1.0~1.5,k1可取值2.5~3.0,结合钟差预报试验,本文取k0=1.0、k1=2.5。对于钟差预报,通常认为各个钟差数据之间是独立等精度观测的,所以式(13)可直接作为钟差的等价权计算式,即i=wi。通过抗差迭代求取Z的加权平均值
 (14)
(14)
迭代结束,可得钟差等价权=diag{1,2,…,n}和Z的中心化值Zi=Zi-(k),并将等价权较小的钟差数据标定为异常值。
1.3.2 计算样本协方差函数值设m+1个等间距dl=l×τ,式中l0,1,…,m;τ为时间间隔。因为钟差数据分布规则,利用满足|dij-dl|=0的钟差数据点对的Z求协方差函数值σ(dl),其中dl表示相距为l×τ的时间长度;dij为第i时刻与第j时刻的时间差。同时,为减弱异常数据对协方差函数值的影响,在计算中结合降权因子wij=wiwj,得到计算公式如下
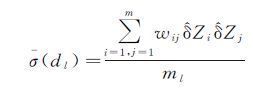 (15)
(15)
式中,ml表示任意两个时间差等于dl的点的对数,该式即为各等间距信号的样本协方差函数值。
1.3.3 拟合协方差函数利用高斯函数作为协方差函数的解析式,即
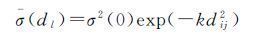 (16)
(16)
等式两边取对数,得到用于拟合计算的公式
 (17)
(17)
将等间距dij及其对应信号的样本协方差(dl)作为样本数据,通过最小二乘原理求得σ2(0)和k。该方法确定的最小二乘配置模型记作RLSC模型。
然而,在钟差预报的试验中发现,不论是采用协方差函数直接拟合的方法还是协方差函数抗差估计拟合的方法,得到的协方差函数参数均不能较为理想地进行钟差预报(参见算例1),这主要是因为要比较可靠地确定信号的协方差函数,必须有大量的数据。然而,这是一个非常困难的问题,实际中,要根据具体问题的性质,通过理论上的研究和对大量已测数据的统计分析才能较好地解决[11]。因此,在最初的试验中,通过改变RLSC模型协方差函数的参数值来观察分析预报结果的变化情况,发现当协方差函数的参数取适当的值时,最小二乘配置钟差预报模型能够取得相对较好的预报结果。最后,基于2015年4月一个月、2013年6月23和24日、2013年7月15和16日、2007年5月25日和6月24日GPS系统15min采样间隔的精密钟差数据进行钟差预报试验(考虑文章篇幅,此处及“试验与分析”部分不详细列出),通过对星载铷钟预报结果的分析总结,最终得到σ2(0)和k较理想的取值范围为:σ2(0)∈{1,5,10,50,100,200,300,400,500},k∈{1.0×10-12~-6,5.0×10-12~-6,9.0×10-12~-6}。将此时确定的最小二乘配置模型记作MRLSC模型。图 3给出了本文所提方法的计算步骤及数据处理流程。需要说明的是,在具体使用这些参数值进行钟差预报时,将σ2(0)与k的取值使得预报结果的均方根误差(RMS,其定义参见式(18))最小的组合数作为MRLSC模型协方差函数参数的最佳取值。例如下文“2.1 试验1”中,在σ2(0)与k的可取数值中,当σ2(0)=500、k=1.0×10-10时,PRN01卫星的钟差预报RMS最小,因此取该组合值作为协方差函数的参数值。而在实际应用中,可以根据所需预报时间段的相邻上一时间段预报确定的协方差函数参数取值作为当前MRLSC模型协方差函数的参数取值,例如下文“2.2 试验2”中4月4日预报4月5日确定的协方差函数参数值,可以作为接下来4月5日预报4月6日、4月6日预报4月7日的协方差函数值进行钟差预报。
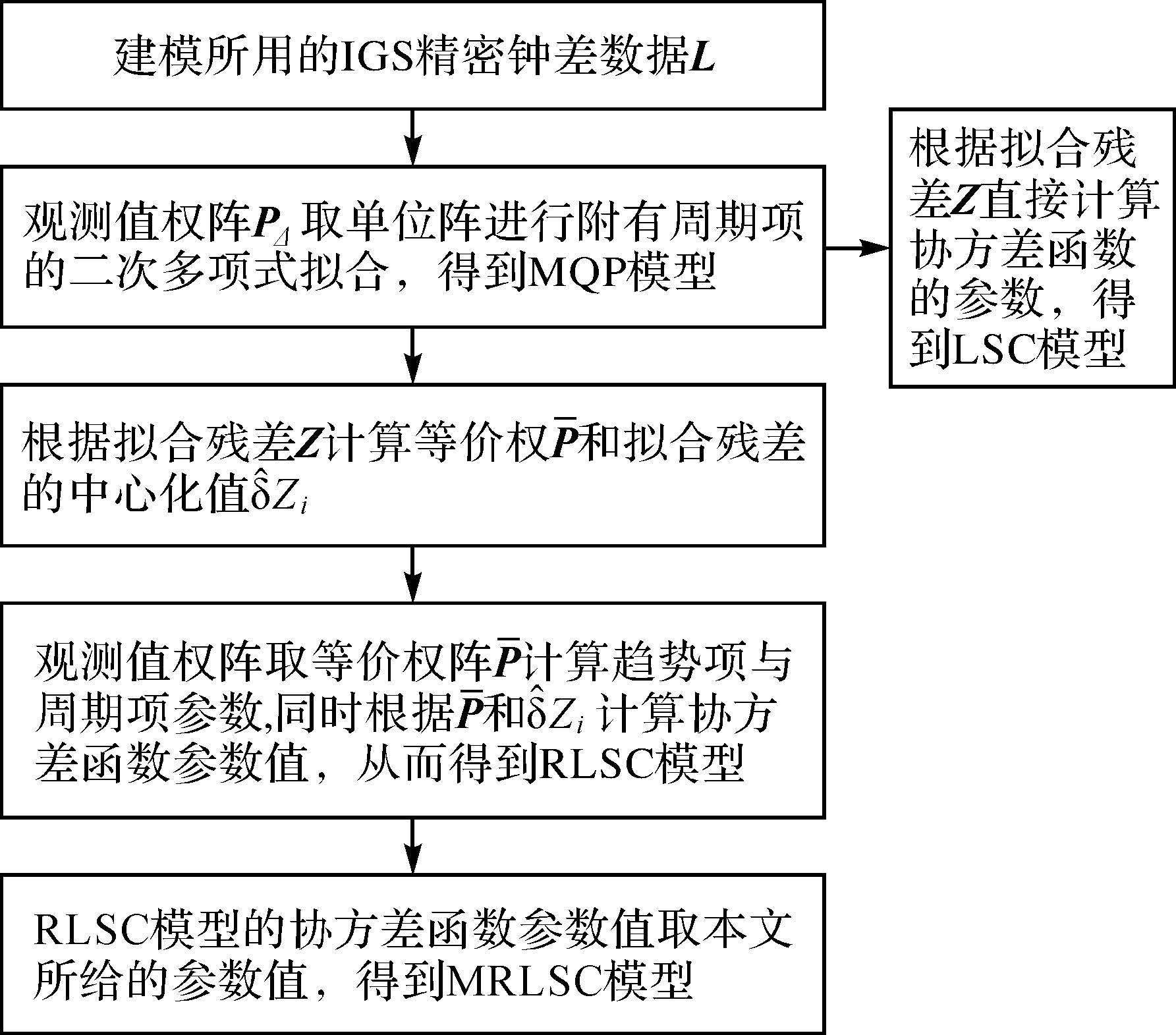
|
| 图 3 新方法的计算步骤及数据处理流程 Fig. 3 Calculation steps and data processing procedures of the proposed method |
2 试验与分析
为了验证所提方法的有效性,采用IGS提供的GPS系统15min采样间隔的精密钟差数据进行试算分析。以2015年4月3日到2015年4月7日的数据为例,考虑当前卫星导航系统在轨运行星载原子钟主要是铷原子钟(Rb钟),因此本文采用该时间段内GPS系统星载Rb钟进行钟差预报试验。该时间段内GPS系统星载Rb钟的信息如表 1所示。表中字体加粗的18颗卫星表示在试验时间段内其钟差数据连续且对应的频率数据[10]相对平稳无跳变。
| 卫星钟类型 | PRN |
| BLOCK ⅡA Rb钟 | 04 08 32 |
| BLOCK ⅡR Rb钟 | 02 11 13 14 16 18 20 21 22 23 28 |
| BLOCK ⅡR-M Rb钟 | 05 07 12 15 17 29 31 |
| BLOCK ⅡF Rb钟 | 01 03 06 09 25 26 27 30 |
另外,以预报时间段对应的已知精密钟差数据为基准值,采用均方根误差(RMS)和极差(最大、最小误差之差的绝对值,记作range)作为预报结果的统计量进行对比与分析,其中RMS表征预报结果的精度,range代表预报结果的稳定性。RMS计算公式为
 (18)
(18)
式中,errori为预报误差;i是i时刻IGS精密钟差值;ti为i时刻钟差预报值。
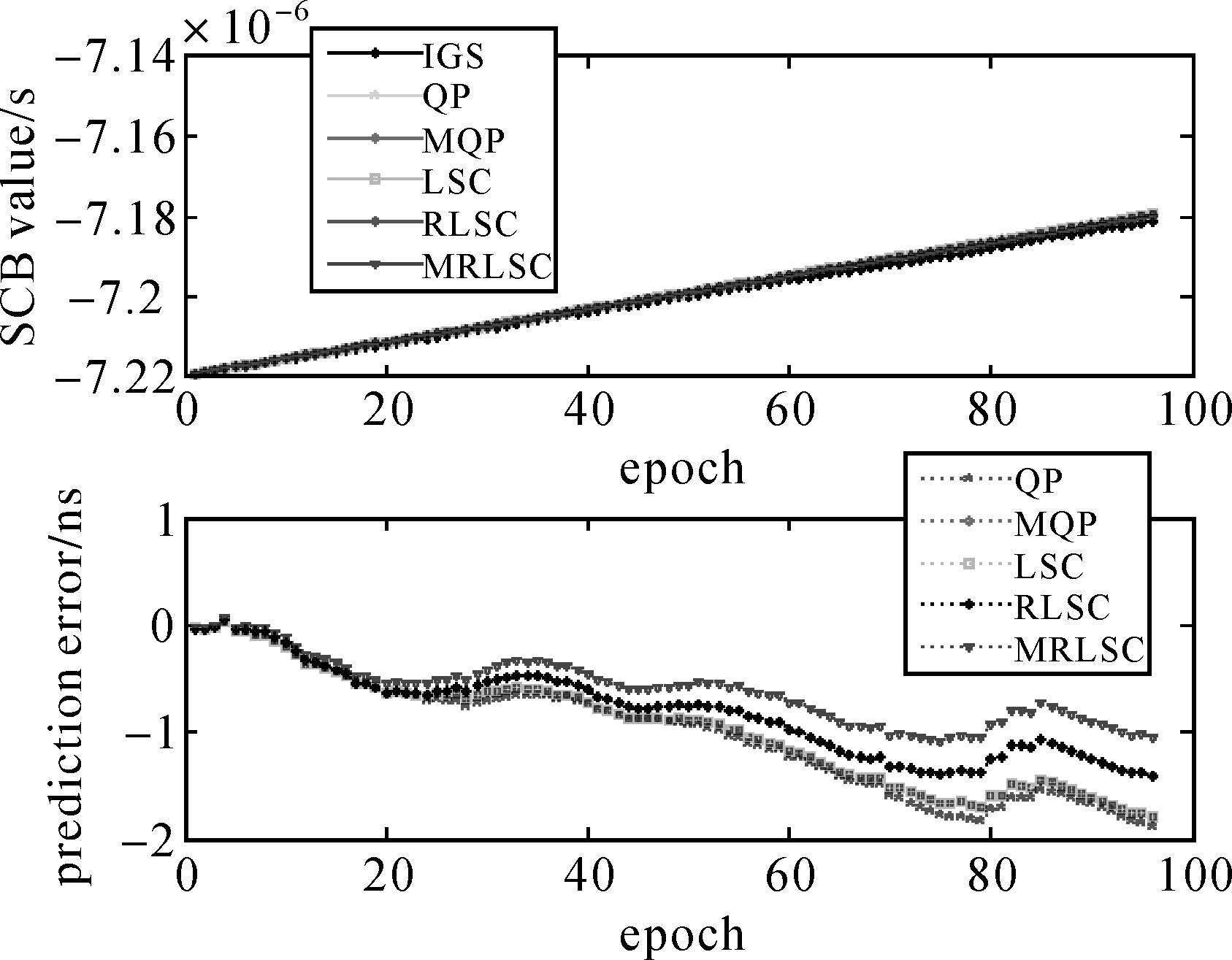
2.1 试验1首先分析新方法的建模过程及协方差函数对预报结果的影响。使用4月3日的卫星钟差数据分别对QP、MQP、LSC、RLSC和MRLSC进行建模,预报接下来4月4日一整天的钟差。此处选取每种类型钟对应的一颗卫星,本文选取的是PRN01、PRN04、PRN18和PRN29共4颗卫星进行试验分析。表 2给出的是4颗卫星进行LSC、RLSC和MRLSC建模时对应协方差函数参数的取值情况。因为是要验证本文所确定的协方差函数的合理性,此处MRLSC对应协方差函数参数的取值是通过使得MRLSC模型4月4日预报误差RMS最小来确定的。图 4—图 7为4颗卫星在5种模型下的预报结果。
| 参 数 | 模 型 | 卫 星 | |||
| PRN01(IIF Rb) | PRN04(IIA Rb) | PRN18(IIR Rb) | PRN29(IIR-M Rb) | ||
| σ2(0) | LSC | 4.240×10-22 | 4.475×10-21 | 1.250×10-21 | 1.515×10-21 |
| RLSC | 2.358×10-24 | 4.475×10-21 | 1.250×10-21 | 4.196×10-22 | |
| MRLSC | 500 | 100 | 200 | 50 | |
| k | LSC | 1.089×10-11 | -2.320×10-10 | -2.527×10-10 | -2.288×10-10 |
| RLSC | -3.728×10-11 | -2.320×10-10 | -2.527×10-10 | -2.019×10-10 | |
| MRLSC | 1.0×10-10 | 5.0×10-11 | 9.0×10-10 | 9.0×10-9 | |
|
| 图 4 PRN01卫星的预报结果 Fig. 4 Prediction results of satellite PRN01 |
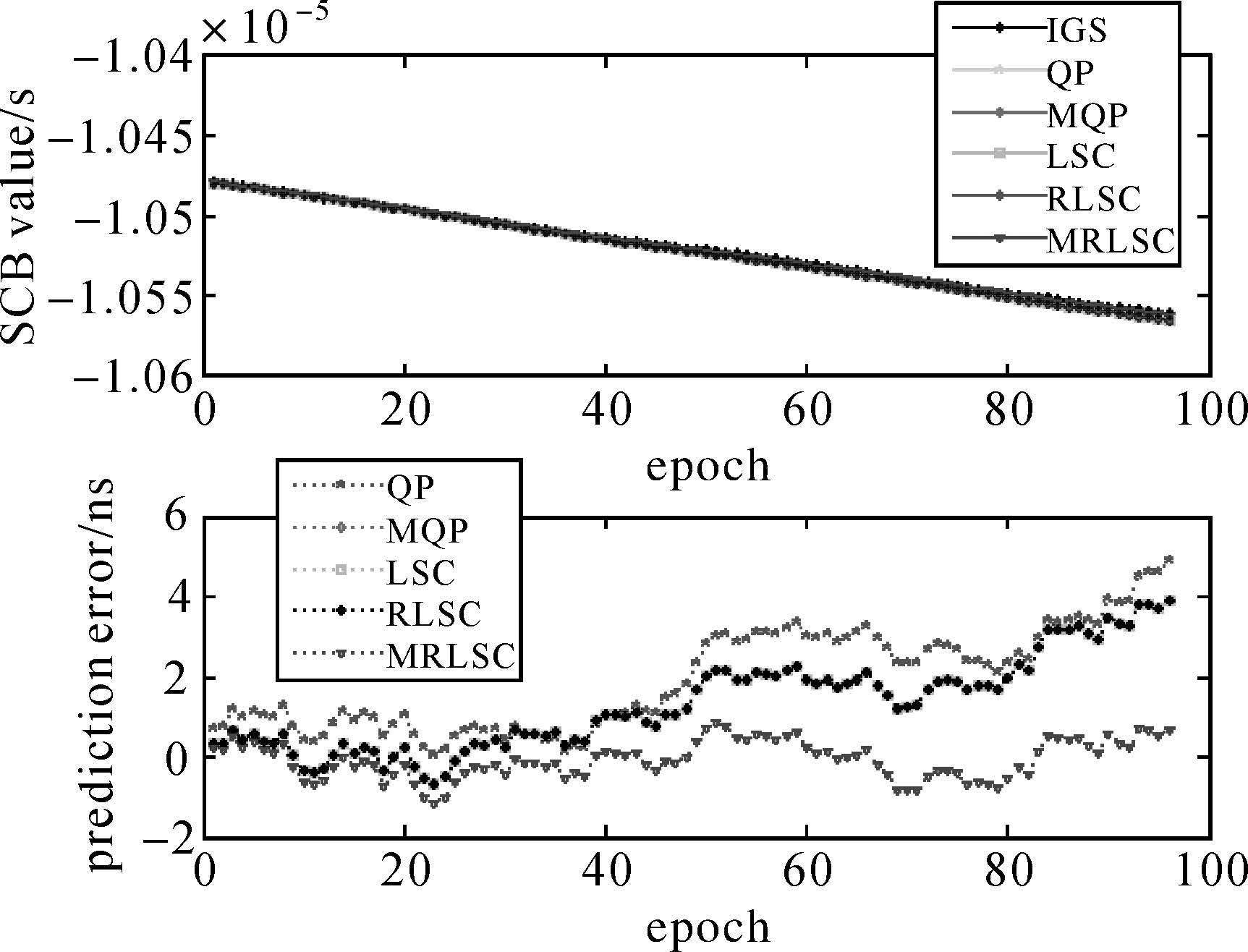
|
| 图 5 PRN04卫星的预报结果 Fig. 5 Prediction results of satellite PRN04 |
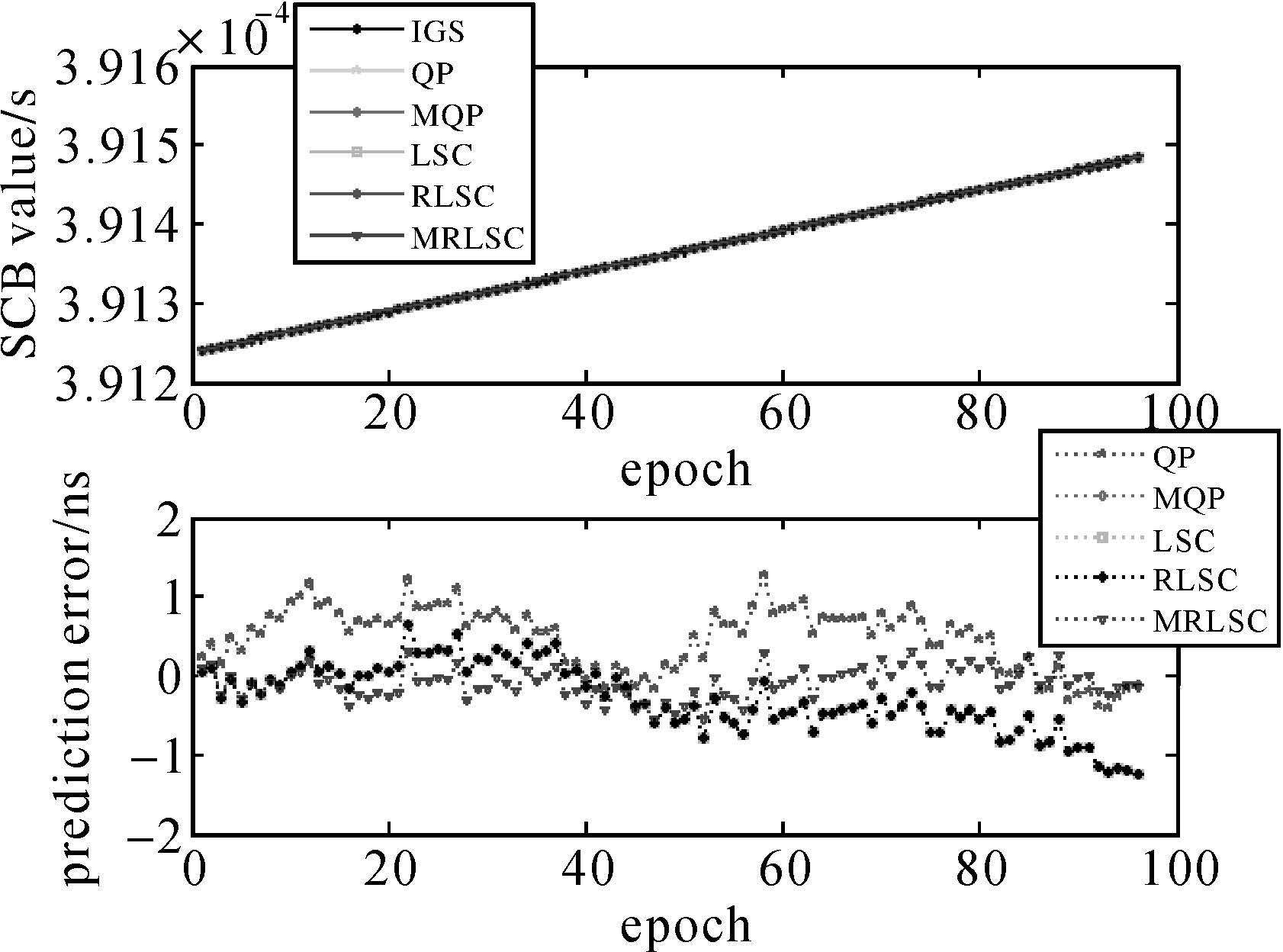
|
| 图 6 PRN18卫星的预报结果 Fig. 6 Prediction results of satellite PRN18 |
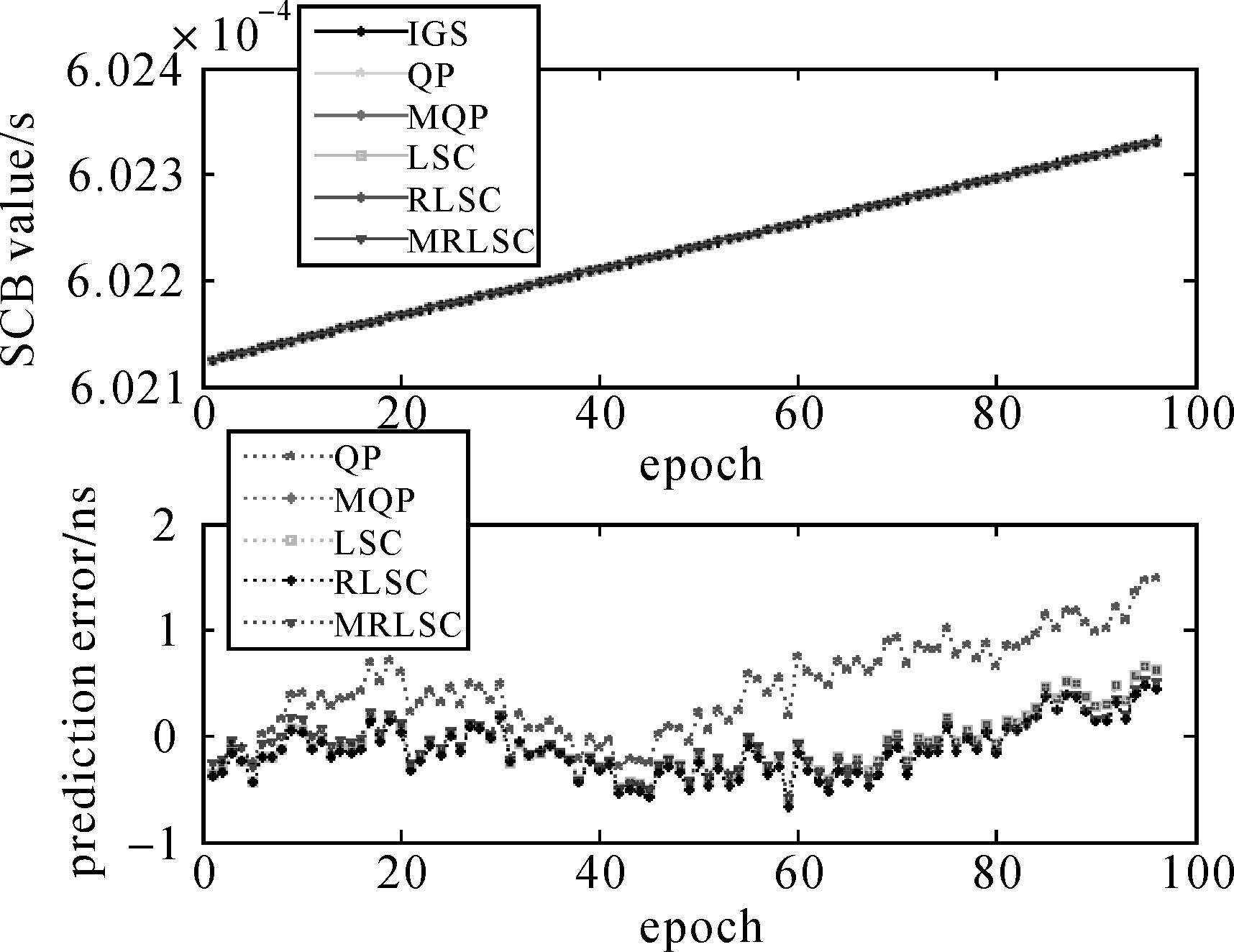
|
| 图 7 PRN29卫星的预报结果 Fig. 7 Prediction results of satellite PRN29 |
对比图中4颗卫星的预报结果可以看出,在5种模型中QP模型的预报误差发散较快且其误差值相对较大,而其他4种模型的预报误差相对较小,说明在钟差预报中考虑卫星钟的周期项与随机变化部分可以一定程度上改善预报效果。为了对预报结果进行定量的分析,表 3给出了4颗卫星预报结果的统计值。
| ns | ||||||||||||||
| 模型 | 卫星 | |||||||||||||
| PRN01(ⅡF Rb) | PRN04(ⅡA Rb) | PRN18(ⅡR Rb) | PRN29(ⅡR-M Rb) | 平均值 | ||||||||||
| RMS | range | RMS | range | RMS | range | RMS | range | RMS | range | |||||
| QP | 1.149 | 1.909 | 2.326 | 4.826 | 0.621 | 1.666 | 0.637 | 1.826 | 1.183 | 2.557 | ||||
| MQP | 1.093 | 1.839 | 1.757 | 4.545 | 0.512 | 1.891 | 0.278 | 1.249 | 0.910 | 2.381 | ||||
| LSC | 1.093 | 1.839 | 1.757 | 4.545 | 0.512 | 1.891 | 0.278 | 1.249 | 0.910 | 2.381 | ||||
| RLSC | 0.901 | 1.460 | 1.757 | 4.545 | 0.512 | 1.891 | 0.287 | 1.150 | 0.864 | 2.262 | ||||
| MRLSC | 0.676 | 1.150 | 0.468 | 1.987 | 0.213 | 0.873 | 0.249 | 1.116 | 0.402 | 1.282 | ||||
对比表中4颗卫星使用MQP和LSC模型的预报结果及其平均值可以看出,两者的结果完全相同,说明直接利用拟合残差得到的协方差函数在进行钟差预报时LSC模型的优势体现不出来。而在同样的条件下,采用协方差函数抗差估计拟合方法的RLSC模型可以取得优于MQP和LSC模型的预报结果,说明采用抗差估计的方法能够一定程度上克服钟差数据中隐含的粗差对LSC模型进行钟差预报时的影响,但是其改善效果仍不显著。在此基础上,当协方差函数的参数使用本文所给范围内的取值时,MRLSC模型的RMS值与range值均明显小于LSC模型和RLSC模型对应的结果值,说明协方差函数的合理确定直接影响钟差预报的结果。而本文所提的在协方差函数抗差估计的基础上协方差函数的参数取本文所给参数是相对有效性的,可以作为最小二乘配置钟差预报模型对应协方差函数确定的方法。
另一方面,从该试验预报结果统计表中可以看出,MQP模型比QP模型的RMS值和range值都小,说明在对卫星钟差进行建模时,考虑钟差的周期项能够加全面地反映卫星钟的特性、提高钟差的预报效果。而MRLSC模型比MQP模型的RMS值和range值都小,说明考虑钟差的随机项可以更进一步反映星载原子钟的特性,从而提高钟差预报的效果。根据每颗卫星的预报结果及其平均值数据可知,MRLSC模型的RMS值与range值最小,说明本文所建模型的预报精度与预报稳定性最好。该模型能够在钟差物理特性及其周期特性的基础上顾及钟差随机特性得到更加完善的钟差模型,从而实现对卫星钟差更加精准的预报。
2.2 试验2将本文所提方法与常用的QP模型和GM(1,1)模型进行对比,进一步分析新方法较两种常用模型的预报特性。对18颗星载铷钟进行连续3d的钟差预报,即分别使用4月4、5、6日一整天的数据进行建模,分别预报接下来4月5、6、7日一整天的钟差。表 4给出了本试验中MRLSC模型中协方差函数对应的参数取值。图 8—图 10是18颗卫星在各模型下预报第1天钟差的预报误差。
| 卫星 | 参数 | |||
| σ2(0) | k | |||
| ⅡA Rb | PRN04 | 500 | 1.0×10-9 | |
| PRN12 | 50 | 5.0×10-11 | ||
| PRN15 | 5 | 9.0×10-10 | ||
| ⅡR-M Rb | PRN17 | 10 | 5.0×10-9 | |
| PRN29 | 5 | 5.0×10-9 | ||
| PRN31 | 5 | 1.0×10-8 | ||
| ⅡR Rb | PRN02 | 1 | 1.0×10-12 | |
| PRN11 | 500 | 1.0×10-10 | ||
| PRN14 | 50 | 5.0×10-8 | ||
| PRN18 | 100 | 5.0×10-11 | ||
| PRN20 | 500 | 5.0×10-7 | ||
| PRN23 | 100 | 5.0×10-9 | ||
| ⅡF Rb | PRN01 | 300 | 9.0×10-10 | |
| PRN03 | 200 | 9.0×10-11 | ||
| PRN06 | 500 | 5.0×10-7 | ||
| PRN09 | 100 | 5.0×10-8 | ||
| PRN27 | 50 | 1.0×10-9 | ||
| PRN30 | 200 | 5.0×10-9 | ||

|
| 图 8 各颗卫星在QP模型下的预报误差 Fig. 8 Prediction errors of QP model for all satellites |
|
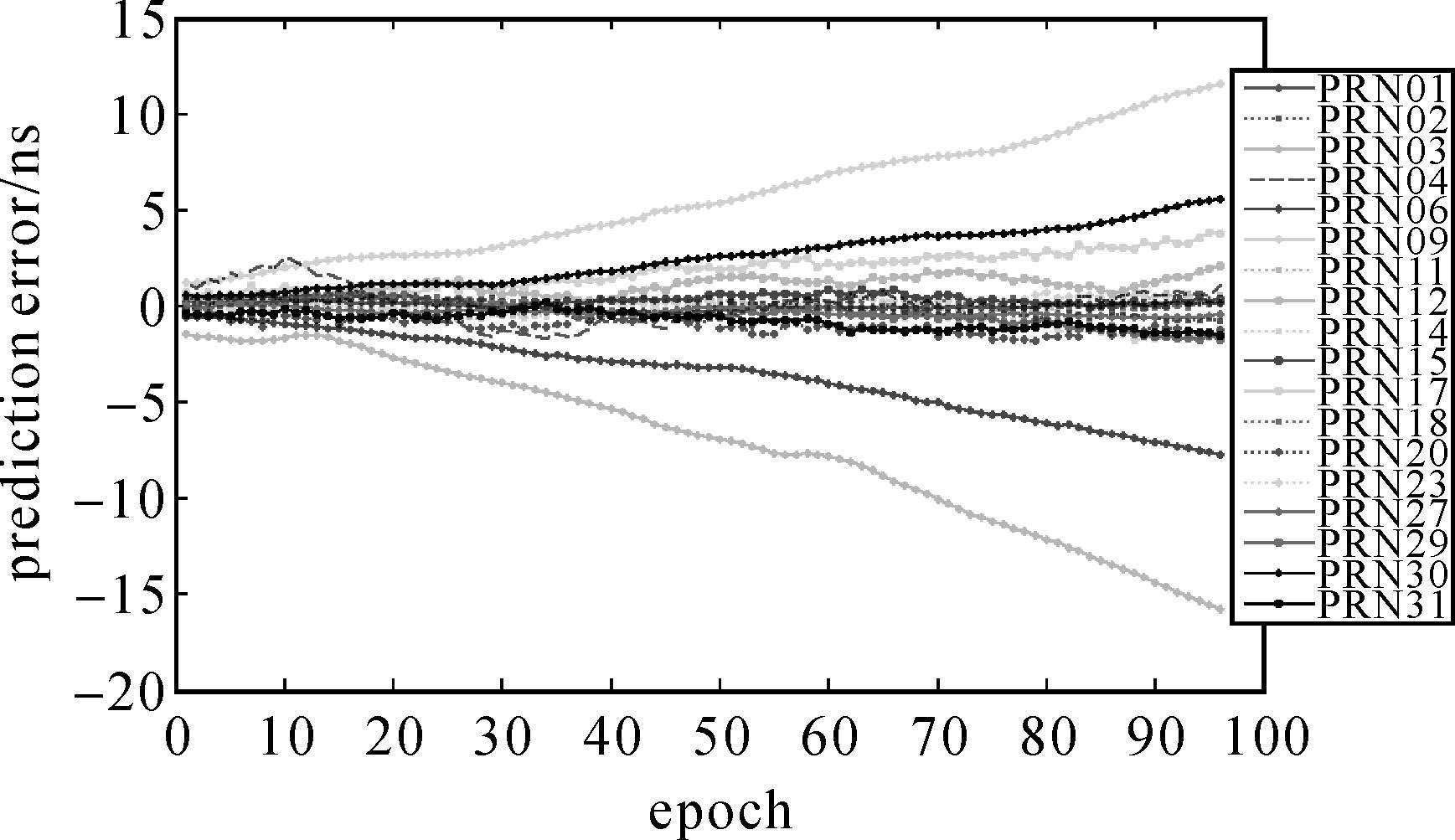
| 图 9 各颗卫星在GM(1,1)模型下的预报误差 Fig. 9 Prediction errors of GM(1,1) model for all satellites |
|
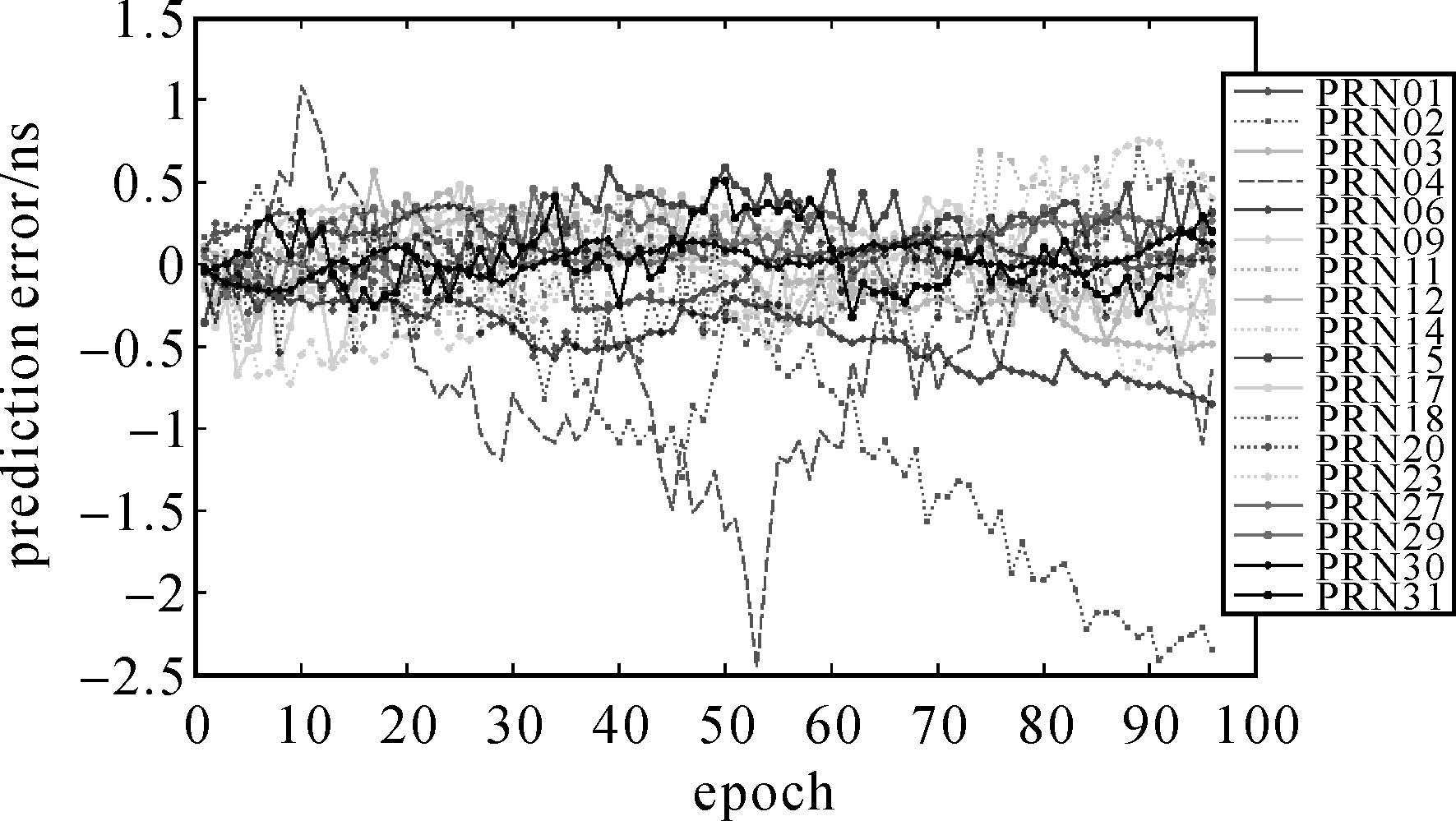
| 图 10 各颗卫星在MRLSC模型下的预报误差 Fig. 10 Prediction errors of MRLSC model for all satellites |
对比3种模型的预报误差图可以看出,本文所提方法的预报误差相对较小且发散较慢,同时误差的波动范围也较小,因此说明新方法的预报效果优于两种常用模型的预报效果,同时也说明了本文所提协方差函数确定方法的有效性。表 5和表 6分别根据卫星的种类给出了各类卫星以及18颗卫星每天预报结果RMS和range平均值的统计情况。
| 星钟类型 | 第1天 | 第2天 | 第3天 | ||||||||
| QP | GM | MRLSC | QP | GM | MRLSC | QP | GM | MRLSC | |||
| ⅡA Rb | 2.946 | 0.985 | 0.840 | 6.691 | 4.027 | 2.916 | 10.224 | 4.289 | 3.904 | ||
| ⅡR Rb | 1.303 | 0.523 | 0.444 | 1.024 | 1.003 | 1.056 | 1.364 | 0.802 | 1.627 | ||
| ⅡR-M Rb | 0.895 | 1.032 | 0.238 | 1.159 | 1.020 | 0.689 | 2.201 | 1.579 | 2.367 | ||
| ⅡF Rb | 1.019 | 3.721 | 0.227 | 0.999 | 3.752 | 0.765 | 1.056 | 3.663 | 1.362 | ||
| all | 1.186 | 1.756 | 0.337 | 1.368 | 2.092 | 0.960 | 1.986 | 2.165 | 1.871 | ||
| 注:all统计值的含义是每天在各模型下18颗卫星预报结果RMS之和的平均值。 | |||||||||||
| 星钟类型 | 第1天 | 第2天 | 第3天 | ||||||||
| QP | GM | MRLSC | QP | GM | MRLSC | QP | GM | MRLSC | |||
| ⅡA Rb | 6.581 | 4.165 | 3.547 | 14.349 | 5.362 | 6.647 | 15.833 | 6.177 | 15.135 | ||
| ⅡR Rb | 2.766 | 1.478 | 1.489 | 2.338 | 2.023 | 2.466 | 2.326 | 1.828 | 3.438 | ||
| ⅡR-M Rb | 1.863 | 2.015 | 0.922 | 2.159 | 1.933 | 1.822 | 4.056 | 3.099 | 4.391 | ||
| ⅡF Rb | 1.922 | 6.448 | 0.625 | 1.898 | 6.347 | 1.327 | 1.839 | 6.353 | 2.428 | ||
| all | 2.446 | 3.458 | 1.158 | 2.809 | 3.625 | 2.140 | 3.395 | 3.931 | 4.016 | ||
| 注:all统计值的含义是每天在各模型下18颗卫星预报结果range之和的平均值。 | |||||||||||
根据表 5和表 6的统计结果可知:每天预报结果的RMS平均值中本文所提方法最小,其精度优于两种常用模型;而每天预报的稳定性(range)平均值,本文方法整体上好于两种常用模型。计算各模型3d预报结果RMS和Range的平均值,分别为
QPRMS=(1.186+1.368+1.986)/3=1.513ns
QPrange=(2.446+2.809+3.395)/3=2.883ns
GMRMS=(1.756+2.092+2.165)/3=2.004ns
GMrange=(3.458+3.625+3.931)/3=3.671ns
MRLSCRMS=(0.337+0.960+1.871)/3=1.056ns
MRLSCrange=(1.158+2.140+4.016)/3=2.438ns
3d的平均预报精度MRLSC模型较QP模型和GM(1,1)分别提高了0.457ns和0.948ns,而3d的平均预报稳定性MRLSC模型较QP模型和GM(1,1)分别提高了0.445ns和1.233ns;因此,进一步说明本文所提方法的合理性、有效性,同时也证明了所给协方差函数确定方法的有效性。对于4类卫星钟的预报,BLOCK ⅡA Rb钟的效果最差,这是因为该类型卫星是GPS系统早期发射,长时间的运行导致卫星上相关设备老化,也致使其钟差预报的效果变差。对比3种模型下不同类型卫星钟的预报结果,特别是前两天的,可以看出MRLSC模型对于新型的BLOCK ⅡF Rb钟的钟差预报能够取得相对更好的效果。此外,在连续3d的预报中,MRLSC模型的协方差函数参数取相同的值,但随着预报时间段的推移,MRLSC模型较两种常用模型的优势明显减弱,特别是预报结果的稳定性,说明本文所提方法对应协方差函数的参数值确定之后,在一定的预报时间段内不改变模型参数值可以进行卫星钟差的连续建模预报,但随着预报长度的增加,预报效果有所下降。这是因为虽然星载原子钟在空间环境中受外界多种不确定因素以及自身频率漂移等的影响,但是在相对较短的时间范围内,这些影响作用于卫星钟差数据的效果可以认为是相同的,因此在使用最小二乘配对卫星钟差随机性变化部分建模时,对应的协方差函数参数可以取相同的数值。另一方面,虽然可以取相同的值,但是这些参数值不一定最佳。
3 总 结为了更全面地反映卫星钟差特性并提高钟差预报精度,本文基于抗差最小二乘配置方法,建立了一种能够同时顾及卫星钟物理特性、钟差周期性变化与随机性变化特点的钟差预报模型。通过试验与分析得出以下结论:
(1) 对于星载原子钟的钟差预报,顾及钟差的周期特性与随机特性能够进一步提高钟差预报的效果。
(2) 采用最小二乘配置对钟差随机变化部分进行建模是合适的,并且本文所给的协方差函数确定方法及其对应的参数取值范围是有效的。
(3) 新方法能够有效地进行钟差预报且能取得优于两种常用模型的预报效果。
最后需要说明的是,协方差函数的合理确定是最小二乘配模型的关键,本文所确定的协方差函数相对有效,接下来还需进行更多的试验与分析来实现进一步的完善。
| [1] |
王宇谱, 吕志平, 陈正生, 等. 卫星钟差预报的小波神经网络算法研究[J].测绘学报,2013, 42 (3) : 323 –330 .
WANG Yupu, LV Zhiping, CHEN Zhengsheng, et al. Research on the Algorithm of Wavelet Neural Network to Predict Satellite Clock Bias[J]. Acta Geodaetica et Cartographica Sinica,2013, 42 (3) : 323 –330 . |
| [2] |
黄观文, 杨元喜, 张勤. 开窗分类因子抗差自适应序贯平差用于卫星钟差参数估计与预报[J].测绘学报,2011, 40 (1) : 15 –21 .
HUANG Guanwen, YANG Yuanxi, ZHANG Qin. Estimate and Predict Satellite Clock Error Using Adaptively Robust Sequential Adjustment with Classified Adaptive Factors Based on Opening Windows[J]. Acta Geodaetica et Cartographica Sinica,2011, 40 (1) : 15 –21 . |
| [3] |
崔先强, 焦文海. 灰色系统模型在卫星钟差预报中的应用[J].武汉大学学报(信息科学版),2005, 30 (5) : 447 –450 .
CUI Xianqiang, JIAO Wenhai. Grey System Model for the Satellite Clock Error Predicting[J]. Geomatics and Information Science of Wuhan University,2005, 30 (5) : 447 –450 . |
| [4] |
郑作亚, 党亚民, 卢秀山, 等. 附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J].天文学报,2010, 51 (1) : 95 –102 .
ZHENG Zuoya, DANG Yamin, LU Xiushan, et al. Prediction Model with Periodic Item and Its Application to the Prediction of GPS Satellite Clock Bias[J]. Acta Astronomica Sinica,2010, 51 (1) : 95 –102 . |
| [5] | HEO Y J, CHO J, HEO M B. Improving Prediction Accuracy of GPS Satellite Clocks with Periodic Variation Behaviour[J]. Measurement Science and Technology,2010, 21 (7) : 073001 . |
| [6] |
徐君毅, 曾安敏. ARIMA(0, 2, q)模型在卫星钟差预报中的应用[J].大地测量与地球动力学,2009, 29 (5) : 116 –120 .
XU Junyi, ZENG Anmin. Application of ARIMA(0, 2, q) Model to Prediction of Satellite Clock Error[J]. Journal of Geodesy and Geodynamics,2009, 29 (5) : 116 –120 . |
| [7] | DAVIS J, BHATTARAI S, ZIEBART M. Development of a Kalman Filter Based GPS Satellite Clock Time-offset Prediction Algorithm[C]//Proceedings of European Frequency and Time Forum (EFTF). Gothenburg: IEEE, 2012: 152-156. |
| [8] |
王国成, 柳林涛, 徐爱功, 等. 径向基函数神经网络在GPS卫星钟差预报中的应用[J].测绘学报,2014, 43 (8) : 803 –807 .DOI:10.13485/j.cnki.11-2089.2014.0078.
WANG Guocheng, LIU Lintao, XU Aigong, et al. The Application of Radial Basis Function Neural Network in the GPS Satellite Clock Bias Prediction[J]. Acta Geodaetica et Cartographica Sinica,2014, 43 (8) : 803 –807 .DOI:10.13485/j.cnki.11-2089.2014.0078. |
| [9] |
郑作亚, 陈永奇, 卢秀山. 灰色模型修正及其在实时GPS卫星钟差预报中的应用研究[J].天文学报,2008, 49 (3) : 306 –320 .
ZHENG Zuoya, CHEN Yongqi, LU Xiushan. An Improved Grey Model for the Prediction of Real-time GPS Satellite Clock Bias[J]. Acta Astronomica Sinica,2008, 49 (3) : 306 –320 . |
| [10] |
郭海荣. 导航卫星原子钟时频特性分析理论与方法研究[D]. 郑州:信息工程大学, 2006. GUO Hairong. Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellites[D]. Zhengzhou: Information Engineering University, 2006. |
| [11] |
黄维彬.
近代平差理论及其应用[M]. 北京: 解放军出版社, 1992 : 92 -118.
HUANG Weibin. Theory of Adjustment and Its Applications in Geodesy[M]. Beijing: The PLA Press, 1992 : 92 -118. |
| [12] | SANS F, VENUTI G. The Convergence Problem of Collocation Solutions in the Framework of the Stochastic Interpretation[J]. Journal of Geodesy,2011, 85 (1) : 51 –63 . |
| [13] |
柴洪洲, 崔岳, 明锋. 最小二乘配置方法确定中国大陆主要块体运动模型[J].测绘学报,2009, 38 (1) : 61 –65 .
CHAI Hongzhou, CUI Yue, MING Feng. The Determination of Chinese Mainland Crustal Movement Model Using Least-squares Collocation[J]. Acta Geodaetica et Cartographica Sinica,2009, 38 (1) : 61 –65 . |
| [14] | SENIOR K L, RAY J R, BEARD R L. Characterization of Periodic Variations in the GPS Satellite Clocks[J]. GPS Solutions,2008, 12 (3) : 211 –225 . |
| [15] | LEI Yu, ZHAO Danning, HU Zhaopeng, et al. Prediction of Navigation Satellite Clock Bias by Gaussian Process Regression[C]//Proceedings of the 6th China Satellite Navigation Conference. Berlin: Springer, 2015: 411-423. |
| [16] |
王海栋, 柴洪洲, 赵东明. 基于抗差最小二乘配置的海底地形生成研究[J].系统仿真学报,2010, 22 (9) : 2091 –2094 .
WANG Haidong, CHAI Hongzhou, ZHAO Dongming. Research on Seabed Terrain Generation Based on Robust Least-squares Collocation[J]. Journal of System Simulation,2010, 22 (9) : 2091 –2094 . |
| [17] |
杨元喜, 刘念. 拟合推估两步极小解法[J].测绘学报,2012, 31 (3) : 192 –195 .
YANG Yuanxi, LIU Nian. A New Resolution of Collocation by Two Minimization Steps[J]. Acta Geodaetica et Cartographica Sinica,2012, 31 (3) : 192 –195 . |
| [18] |
陈西斌, 张波, 鲍国. 基于拟合推估两步极小解法的卫星钟差短期预报[J].大地测量与地球动力学,2014, 34 (5) : 125 –129 .
CHEN Xibin, ZHANG Bo, BAO Guo. Short-term Prediction of Satellite Clock Bias Based on Two-steps Minimization[J]. Journal of Geodesy and Geodynamics,2014, 34 (5) : 125 –129 . |
| [19] |
王宇谱, 吕志平, 陈正生, 等. 一种新的导航卫星钟差预报与内插方法[J].大地测量与地球动力学,2013, 33 (4) : 112 –116 .
WANG Yupu, LV Zhiping, CHEN Zhengsheng, et al. A New Method of Navigation Satellite Clock Bias Prediction and Interpolation[J]. Journal of Geodesy and Geodynamics,2013, 33 (4) : 112 –116 . |
| [20] |
刘念. 协方差函数的抗差拟合[J].测绘科学,2001, 26 (3) : 25 –28 .
LIU Nian. Robust Fitting of Covariance Function[J]. Science of Surveying and Mapping,2001, 26 (3) : 25 –28 . |
| [21] |
周江文, 黄幼才, 杨元喜, 等.
抗差最小二乘法[M]. 武汉: 华中理工大学出版社, 1997 : 71 -158.
ZHOU Jiangwen, HUANG Youcai, YANG Yuanxi, et al. Robustified Least Square Method[M]. Wuhan: Huazhong University of Science and Technology Press, 1997 : 71 -158. |
| [22] |
杨元喜.
抗差估计理论及其应用[M]. 北京: 八一出版社, 1993 : 252 -255.
YANG Yuanxi. Theory of Robust Estimation and Its Applications[M]. Beijing: Bayi Press, 1993 : 252 -255. |



