2. 西安测绘研究所地理空间工程国家重点实验室,陕西 西安 710054 ;
3. 北京卫星导航中心,北京 100094
2. State Key Laboratory of Geo-information Engineering,Xi’an 710054,China ;
3. Beijing Satellite Navigation Center,Beijing 100094,China
北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)已于2012年底完成区域系统建设,正式面向亚太地区提供定位、导航和授时服务[1]。卫星星历的可靠性是卫星航系统提供服务的基础。与其他GNSS一样,除了系统实时播发的广播星历,BDS也有IGS MGEX[2]分析中心公开发布的事后精密星历。卫星星历一般不区分正常轨道和星蚀期的轨道,但是星蚀期卫星轨道精度一般相对较低,将直接影响系统的实时导航和事后精密服务性能。
卫星的星蚀期是指当太阳相对卫星轨道面的夹角(称作β角)小于某个临界值时,卫星在轨道运动周期内将经历地影,直至太阳穿过卫星轨道面、β角大于临界值时地影消失[3]。星蚀期内,BDS的倾斜轨道(IGSO)和中圆轨道(MEO)卫星通过偏航机动(也叫偏航姿态转换)来避免卫星姿态的急速偏航[4-6]。偏航机动期间卫星先由动态偏航模式转换至零偏模式(简称动转零),然后保持零偏航直至β角和偏航角满足零偏转动偏(简称零转动)的条件,再转回动态偏航模式,整个过程持续约7~13d。偏航机动期间,卫星实际姿态与名义姿态不符。这类偏差对卫星精密轨道确定主要有3方面影响[4, 7-9]:①基于名义偏航姿态建立的太阳光压模型不适用,导致非保守摄动力模型误差变大;②相位缠绕误差难以精确修正;③天线相位中心偏差难以精确改正。可见,星蚀期内卫星偏航姿态以及相关摄动力的精确建模水平将直接影响卫星轨道精度。
因而,分析星蚀期间BDS星历的轨道性能,不仅有助于更加全面地了解当前系统的服务性能,还有利于改进北斗卫星轨道确定的函数模型,进而提高北斗精密定轨的精度和可靠性。
卫星轨道精度评估,一方面可以基于定轨解算残差得到内部符合精度,或通过重叠弧段不符值进行统计,得到半外部精度[10],另一方面也可以通过与其他机构发布的精密事后星历比较。但最可靠的方法仍然是采用不同观测技术进行外部检核以得到真正的外部符合精度[10]。卫星激光测距(satellite laser ranging,SLR)[11-12]由于能够提供高精度的距离信息,常作为导航卫星轨道的独立检核手段[13-17],而且北斗所有卫星均装备有激光反射棱镜(laser retroreflector arrays,LRAs),支持地面台站对其进行激光测距。文献[18]采用SLR对2013年前3个月的北斗广播星历进行了评估,得到的轨道径向均方根误差(root mean square,RMS)为0.5~0.8m。文献[19]基于一年的SLR观测值计算了北斗广播星历仅包含轨道部分的空间信号距离误差,分别约为0.7m(不包含GEO时)和1.8m(包含GEO时)。这些研究只对北斗卫星轨道径向精度给出了统计结果,没有对卫星在地影以及偏航机动影响下的轨道精度进行评估和分析。北斗卫星精密定轨研究中,通常也采用SLR观测对事后轨道确定的精度进行检核[20-23],得到的IGSO/MEO卫星轨道径向RMS一般为10cm左右,而对于GEO卫星约为50~70cm。在这些研究中,激光观测值大多仅用于对短期轨道确定结果进行检核验证,并没有基于长时间的激光测距不符值详细分析轨道精度的变化特点。
本文采用一年半的SLR观测资料对BDS的广播星历和精密星历中的轨道进行外部检核,重点分析比较了星蚀期内不同星历中卫星轨道精度的性能。
1 数据与方法 1.1 数据介绍本文采用的北斗广播星历来源于MGEX公布的多系统混合星历,精密星历则来自MGEX中能够较稳定、连续地提供北斗事后精密产品的两家数据分析中心--GFZ和WHU,采用的各星历的起止时间见表 1。
| 星历 | 起止时间 |
| 广播星历 | 2014-01-01-2015-06-10 |
| GFZ精密星历 | 2014-01-28-2015-07-04 |
| WHU精密星历 | 2014-01-01-2015-06-29 |
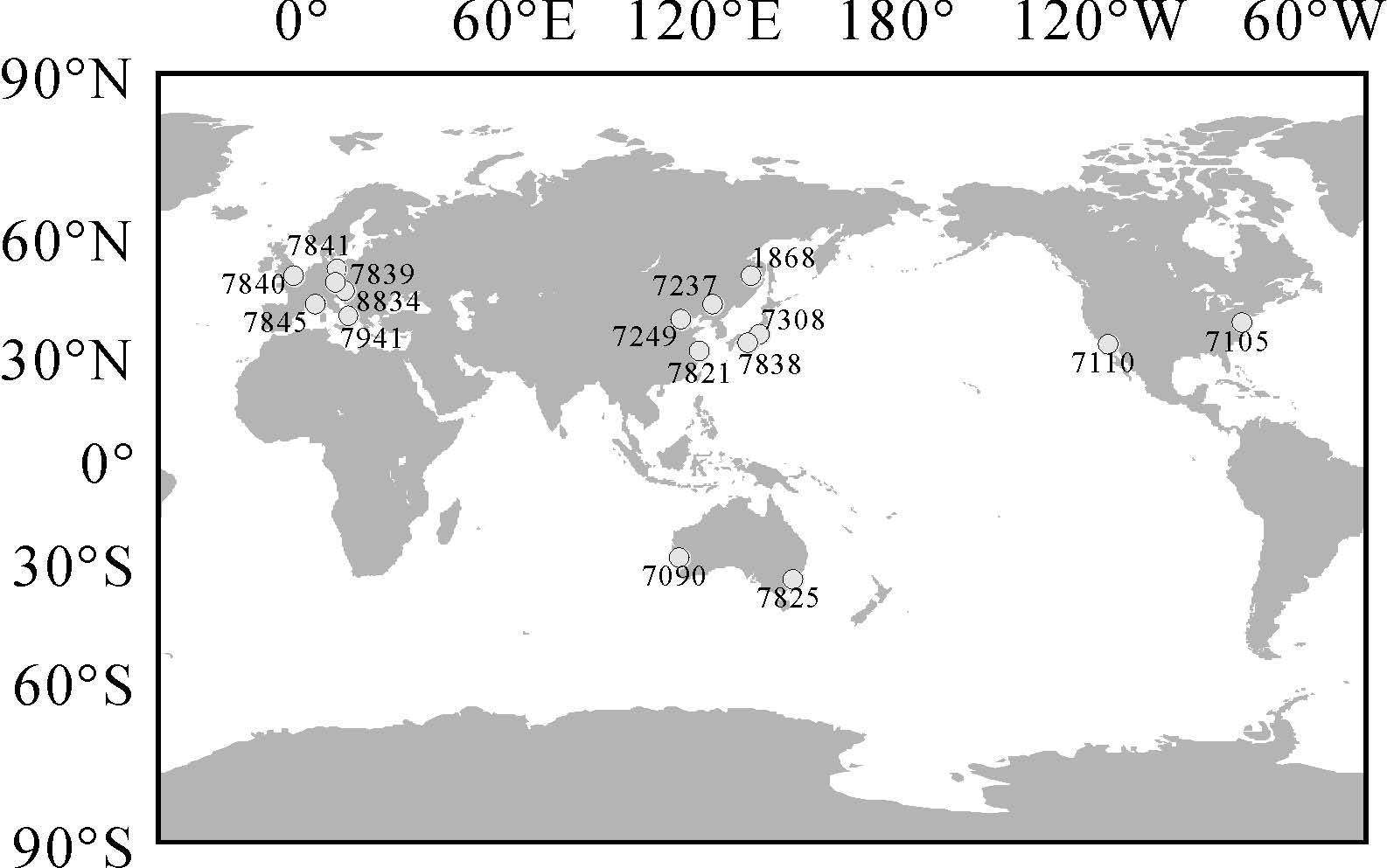
目前,共有4颗北斗卫星参与国际激光测距服务组织(ILRS)[24]的观测任务,本文所采用的SLR观测资料即来自ILRS的16个台站(图 1)于2014年01月-2015年07月间对该4颗北斗卫星--C01(G1)、C08(I3)、C10(I5)和C11(M3)的观测。4颗卫星总的激光标准点(normal point)个数分别为2291、2711、3045和4068。由于广播星历和精密星历均存在少量弧段不连续,因而并不是所有的SLR观测值都参与检核,实际采用的标准点个数约占总数的84%~96%。
|
| 图 1 用于轨道检核的16个SLR台站分布 Fig. 1 Distribution of the 16 SLR stations used for orbit validation |
1.2 方 法
SLR观测量通常为台站发射的激光脉冲经卫星上LRAs反射后再返回台站的整个过程中的双向时延,由此可计算台站至LRAs几何中心的距离。以该距离为外部参考基准与基于星历计算的站星距离作差,由于激光脉冲对卫星的入射角均较小,对于MEO卫星最大仅为14°,而对GEO/IGSO则更小,因而得到的差值序列基本可看作卫星轨道的径向残差序列。另外,由于目前还没有公认的、较为可靠的针对BDS的偏航姿态模型,而且有研究表明[5],北斗偏航姿态误差对几何模型的影响远小于其对动力学模型的影响,因而本文在处理SLR数据时对GEO卫星采用零偏姿态,对IGSO/MEO采用名义(动偏)姿态。
1.2.1 误差修正及粗差剔除根据广播星历可计算卫星在地固系下的位置(参考北斗ICD,http://www.beidou.gov.cn),精密星历则直接以固定间隔提供卫星在地固系下的坐标。本文所有的计算均以J2000.0惯性系为参考,地固系至惯性系的转换遵循IERS 2010协议(http://www.iers.org/iers/publications/tn/tn36),地球自转参数来自IERS提供的EOP文件(ftp://ftp.iers.org /products/eop/rapid/standard finals2000A.all)。任意历元的卫星位置通过8阶Lagrange插值得到。SLR观测值的各项改正均采用IERS 2010推荐的改正模型,主要包括:①台站坐标潮汐改正;②相对论效应修正;③对流层延迟改正;④参照ILRS的建议(http://ilrs.dgfi.badw.de/fileadmin/data_handling/ILRS_Data_Handling_File.snx),对台站的距离偏差与时间偏差进行改正。经过各误差项的改正后,SLR观测量的精度通常优于1~2cm[15],显著高于当前北斗卫星轨道的精度。
此外,广播星历与激光测距不符值超过5.0m、精密星历与激光测距不符值超过1.0m的点(均约占总数的1%)不参与相关统计量的计算。
1.2.2 时间系统与坐标系统BDS广播星历中的星历时为北斗时(BDT),SLR观测值历元通常为UTC,前者通过BDT与GPS时(GPST)的偏差14s、后者通过IERS公布的跳秒文件以及国际原子时(TAI)与GPST的偏差19s均归化至GPST,以便与精密星历的时间系统保持一致。
北斗广播星历(CGCS2000)的参考框架与ITRF略有差别,但目前二者实现之间的差异理论上为几个厘米,相对广播星历的精度可以忽略[19]。而精密星历和SLR台站(SLRF2008)的参考框架与ITRF是一致的,因而认为所有的坐标均基于统一的ITRF参考框架。
1.2.3 LRAs几何中心及卫星天线相位中心SLR观测量为台站与星上激光反射棱镜的几何中心之间的双向时延,精密星历产品中提供的是卫星质心坐标,而基于广播星历计算的卫星轨道通常为卫星天线相位中心位置。因而,在进行轨道检核之前需要统一卫星位置参考点。本文以卫星质心为参考点,对SLR观测数据采用ILRS提供的LRAs几何中心偏差值(http://ilrs.gsfc.nasa.gov/missions/satellite_missions/current_missions/cmg1_com.html)进行改正。由于目前没有官方的北斗卫星天线相位中心改正值公布,而且有学者[19]通过比较广播星历与精密星历发现,广播星历的参考点很可能也是卫星质心(或者至少其相位中心与质心非常接近)。因而,本文也不对北斗广播星历作相位中心改正。
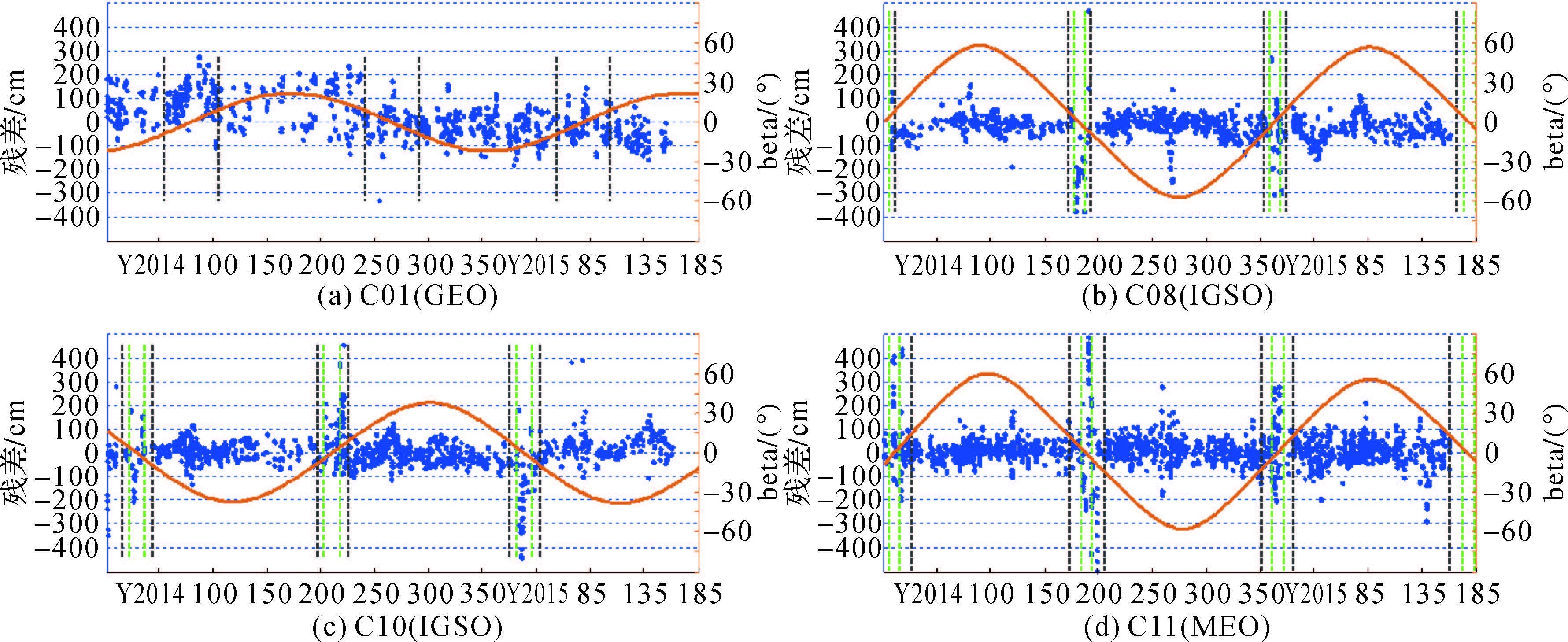
2 结果与分析 2.1 广播星历图 2(a)-(d)依次绘出了4颗卫星广播星历的轨道径向残差序列。由于偏航姿态转换的准确时刻难以确定,本文根据文献中|β|≈4°[4-5]的临界条件粗略确定转换时刻。
|
| 图 2 广播星历轨道径向残差序列 Fig. 2 Orbit radial residuals series of broadcast ephemerides 蓝色圆点表示残差序列;棕黄色曲线为采样期间β角的变化;绿色点画线粗略表示相应时段各卫星进、出地影(黑色点画线)和(IGSO/MEO卫星的)偏航姿态转换时刻。 |
由图 2(b)-(d)可看出,IGSO/MEO卫星的广播星历在星蚀期间轨道精度明显下降,径向误差最大超过4.0m。表明星蚀期对北斗IGSO/MEO卫星轨道确定影响较大,相应轨道动力学模型未能精确描述非保守摄动力的变化。而且,除了C10和C11发生在2014年第200d之后的那次星蚀期外,其他星蚀期内,偏航机动期间的轨道精度(相对非偏航机动期间的轨道精度)再次显著下降。
GEO卫星的轨道面即为地球赤道面,一年经历两次星蚀期(即春、秋分点前后持续约45d)。图 2(a)显示,C01在星蚀期间轨道误差会略微变大,但与其他弧段相比并不显著。这应该主要与GEO卫星普遍较大的轨道误差有关。
表 2中统计了广播星历中4颗卫星在不同情况下的径向误差。“非星蚀期”即指卫星轨道周期内不存在地影的时期;“星蚀期”对于IGSO/MEO卫星包括两个阶段--偏航机动(图 2(b)-(d)中两条相距较近的绿色点画线之间的区域)和正常的动态偏航。
| 卫星 | mean | STD | RMS | ||||||||
| 非星蚀期 | 星蚀期 | 非星蚀期 | 星蚀期 | 非星蚀期 | 星蚀期 | ||||||
| 动偏 | 偏航机动 | 动偏 | 偏航机动 | 动偏 | 偏航机动 | ||||||
| C01 | 10.7 | 30.0 | - | 84.5 | 85.2 | - | 85.2 | 90.3 | - | ||
| C08 | -19.5 | -24.7 | -123.2 | 45.7 | 114.7 | 141.4 | 49.6 | 117.0 | 187.1 | ||
| C10 | 2.1 | 6.4 | -43.4 | 44.4 | 88.7 | 146.4 | 44.4 | 88.7 | 152.4 | ||
| C11 | 9.3 | 1.5 | 55.1 | 45.4 | 97.9 | 190.8 | 46.4 | 97.8 | 198.0 | ||
由表 2可以看出:
(1) 对于IGSO/MEO卫星,非星蚀期间广播星历的径向精度均优于0.5m。
(2) 进入星蚀期但仍为动态偏航时,IGSO/MEO卫星轨道径向误差增大至1.0m左右。
(3) 在偏航机动期间,IGSO/MEO卫星轨道径向误差进一步变大,C08和C11卫星轨道径向RMS甚至接近2.0m。
(4) 对于IGSO/MEO卫星,相比星蚀期内非偏航机动阶段,偏航机动期间轨道精度下降更加显著,与图 2中结果一致。
(5) 对于GEO卫星,非星蚀期间的广播星历轨道径向精度优于0.9m;进入星蚀期,轨道径向精度略微下降,但仍可达0.9m左右。以目前GEO卫星的轨道确定精度,仅从轨道径向残差难以发现星蚀期对于GEO卫星轨道的影响。
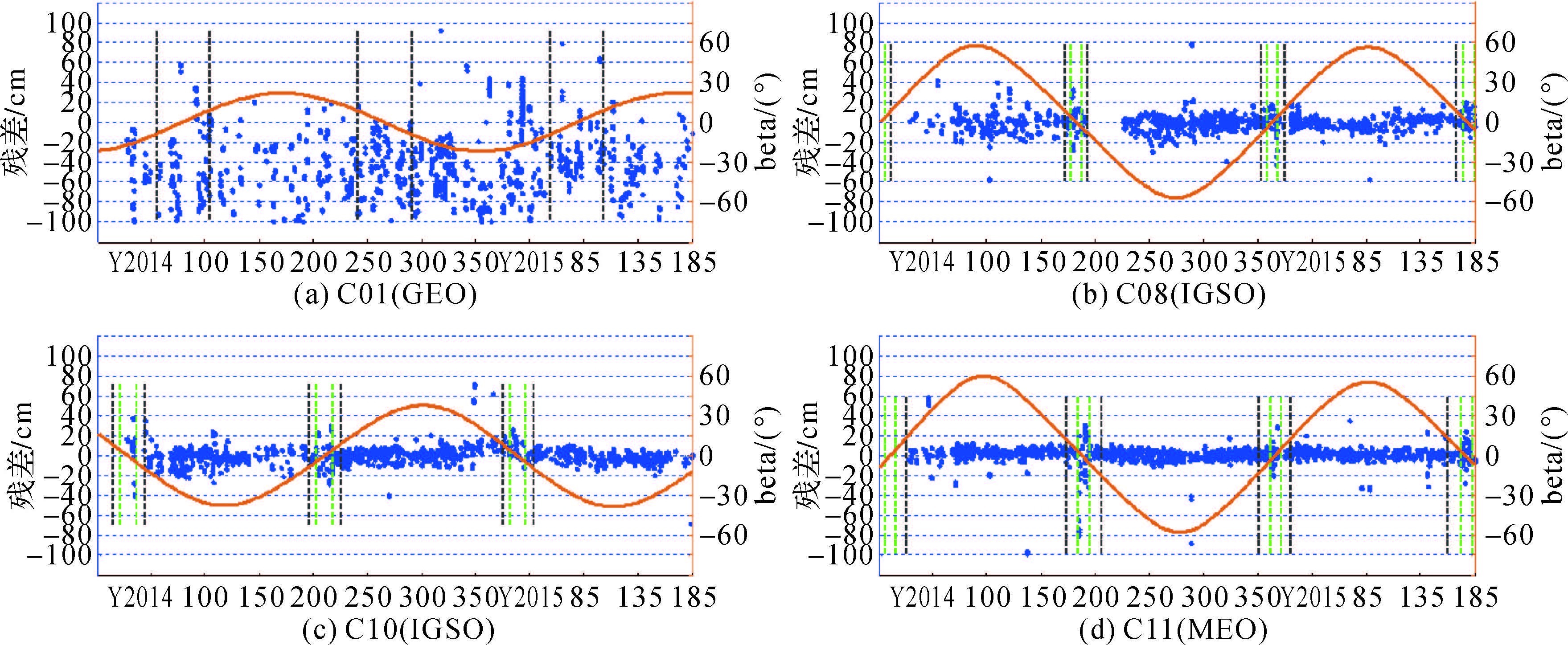
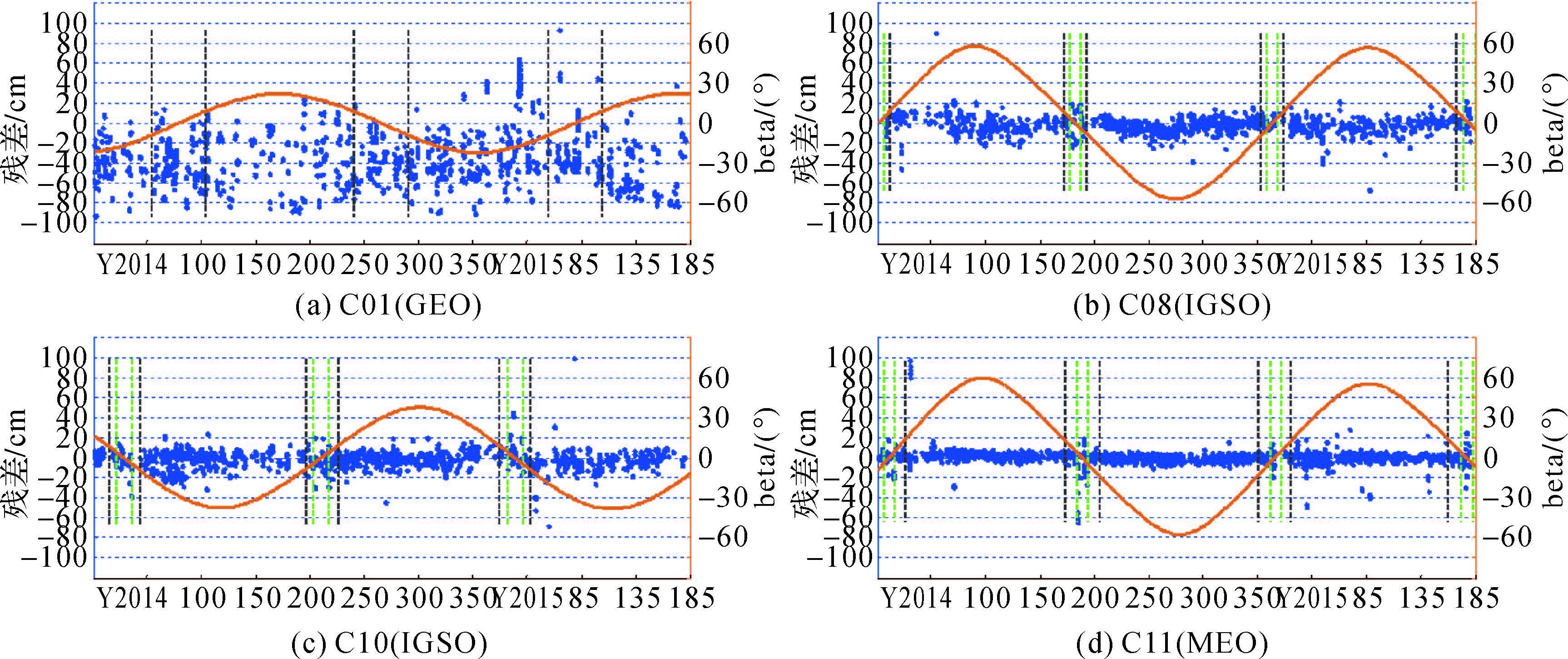
2.2 精密星历图 3、4依次绘出了GFZ和WHU的事后精密星历轨道的径向误差序列,图中有关线条以及数据点的含义同图 2。
|
| 图 3 GFZ精密星历轨道径向残差 Fig. 3 Orbit radial residuals series of GFZ precise ephemerides |
|
| 图 4 WHU精密星历轨道径向残差 Fig. 4 Orbit radial residuals series of WHU precise ephemerides |
由图 3,GFZ发布的精密星历中,C08、C10和C11卫星在星蚀期内(主要在偏航机动期间)同样呈现出明显的精度下降,径向残差最大达0.8m。得益于WHU对IGSO/MEO卫星姿态转换期间偏航姿态模型与非保守摄动力模型作出的有效改进[4-5],与图 3相比,图 4中WHU的精密星历中同一颗卫星在相同星蚀期内的轨道精度衰减不如GFZ的显著。尽管如此,WHU的精密星历在偏航机动期间仍存在轨道精度衰减的现象,如图 4中C10、C11在2014年第200d附近以及C08、C11最后一次(已经开始但还未结束)的星蚀期。表明星蚀期间(主要是偏航机动期间),北斗IGSO/MEO卫星的精密轨道确定仍是一个需要进一步重点研究的问题。
由图 3(a)和图 4(a)均难以看出星蚀期对GEO卫星轨道确定的显著影响。但明显的是,无论GFZ还是WHU提供的BDS事后精密星历中,C01卫星轨道径向均存在一定的系统性偏差。
表 3给出了GFZ和WHU的精密轨道在不同情况下的径向残差统计结果。
| 卫星 | mean | STD | RMS | |||||||||
| 非星蚀期 | 星蚀期 | 非星蚀期 | 星蚀期 | 非星蚀期 | 星蚀期 | |||||||
| 动偏 | 偏航机动 | 动偏 | 偏航机动 | 动偏 | 偏航机动 | |||||||
| GFZ | C01 | -47.3 | -38.9 | - | 31.2 | 27.4 | - | 56.6 | 47.6 | - | ||
| C08 | -0.8 | 1.1 | 2.2 | 9.2 | 5.1 | 11.8 | 9.2 | 5.2 | 12.0 | |||
| C10 | 0.5 | 1.1 | 1.9 | 8.8 | 6.8 | 15.3 | 8.8 | 6.8 | 15.4 | |||
| C11 | 1.8 | 1.7 | -1.0 | 7.3 | 3.6 | 18.4 | 7.5 | 4.0 | 18.4 | |||
| WHU | C01 | -39.4 | -39.0 | - | 27.7 | 20.7 | - | 48.0 | 44.1 | - | ||
| C08 | -2.3 | 0.9 | 0.6 | 8.7 | 6.4 | 10.9 | 9.0 | 6.5 | 10.9 | |||
| C10 | -1.8 | -0.5 | -1.3 | 8.7 | 7.7 | 13.2 | 8.9 | 7.6 | 13.2 | |||
| C11 | 0.8 | 0.9 | -3.0 | 6.0 | 3.3 | 13.6 | 6.0 | 3.4 | 13.9 | |||
由表 3可以看出:
(1) 非星蚀期间,GFZ和WHU的精密星历中IGSO/MEO卫星的轨道径向精度均优于10.0cm,且MEO卫星略优于IGSO卫星,与相关机构的定轨检核结果基本一致[21, 23, 25]。而GEO卫星轨道径向精度约为50.0cm,且均存在40.0cm左右的系统性偏差,这是由GEO卫星相对地面测站几乎不变的几何结构使得定轨中轨道、钟差以及模糊度等参数严重相关导致的。
(2) 星蚀期内,IGSO/MEO卫星在非偏航机动期间轨道径向精度均未见明显下降。偏航机动期间,IGSO/MEO卫星轨道径向误差明显变大,均超过10.0cm。而且与WHU,GFZ相比,精密轨道精度下降更显著,C11卫星径向残差RMS接近20 cm。
(3) 星蚀期对地球静止卫星的轨道确定精度影响不显著,C01卫星进入星蚀期后,两分析中心的轨道精度均未见显著衰减。
(4) 从本文的计算分析看,WHU提供的BDS事后精密星历的精度略优于GFZ提供的相应轨道,尤其是在偏航机动期间。
3 总结与思考本文基于一年半的卫星激光测距观测资料,计算了北斗广播星历、MGEX分析中心GFZ和WHU发布的精密星历中轨道的径向误差,并重点分析比较了星蚀期对不同卫星、不同星历轨道精度的影响,得到如下几点结论:
(1) 非星蚀期间,广播星历中IGSO/MEO卫星和GEO卫星轨道径向精度分别优于0.5m和0.9m。精密星历中IGSO/MEO卫星轨道径向精度优于10.0cm,而GEO的约为50.0cm,且存在40.0cm左右的系统性偏差。
(2) 星蚀期内,广播星历中IGSO/MEO卫星轨道精度下降明显,并且偏航机动期间的轨道精度衰减更加严重,由径向不符值计算的RMS达1.5~2.0m。仅从轨道径向残差看,星蚀期内GEO卫星轨道并未出现明显的精度衰减。
(3) 星蚀期内,精密星历轨道精度在非偏航机动期间未见显著衰减。但在偏航机动期间,IGSO/MEO的轨道径向残差明显变大,且GFZ的比WHU的更加显著。精密星历中同样难以发现星蚀期对GEO卫星轨道的影响。
(4) 总体来看,WHU的精密轨道略优于GFZ提供的精密轨道,尤其是在星蚀期间。
要说明的是,由于目前列入ILRS日常观测计划的北斗卫星仅有4颗,本文研究结果不一定能完全反映整个北斗星座的相关情况。
利用SLR对北斗卫星导航系统轨道精度的检核发现,北斗系统不同星座轨道表现的系统偏差不同,星蚀期对不同星座轨道的影响也不同,因而有必要做进一步的研究,例如SLR检核残差中明显包含卫星轨道相关模型误差信息,深入分析残差的变化特点,可望用于定轨中非保守摄动力模型的改进。
| [1] |
杨元喜, 李金龙, 王爱兵, 等. 北斗区域卫星导航系统基本导航定位性能初步评估[J].中国科学: 地球科学,2014, 57 (1) : 144 –152 .
YANG Yuanxi, LI Jinlong, WANG Aibing, et al. Preliminary Assessment of the Navigation and Positioning Performance of BeiDou Regional Navigation Satellite System[J]. Science China Earth Sciences,2014, 57 (1) : 144 –152 . |
| [2] | MONTENBRUCK O, STEIGENBERGER P, KHACHIKYAN R, et al. IGS-MGEX: Preparing the Ground for Multi-constellation GNSS Science[J]. Inside GNSS,2014, 9 (1) : 42 –49 . |
| [3] | BAR-SEVER Y E. A New Model for GPS Yaw Attitude[J]. Journal of Geodesy,1996, 70 (11) : 714 –723 . |
| [4] | DAI Xiaolei, GE Maorong, LOU Yidong, et al. Estimating the Yaw-attitude of BDS IGSO and MEO Satellites[J]. Journal of Geodesy,2015, 89 (10) : 1005 –1018 . |
| [5] |
郭靖. 姿态、光压和函数模型对导航卫星精密定轨影响的研究[D]. 武汉: 武汉大学, 2014 GUO Jing. The Impacts of Attitude, Solar Radiation and Function Model on Precise Orbit Determination for GNSS Satellites[D]. Wuhan: Wuhan University, 2014. |
| [6] | GUO Jing, ZHAO Qile, GENG Tao, et al. Precise Orbit Determination for COMPASS IGSO Satellites during Yaw Maneuvers[C]//Proceedings of China Satellite Navigation Conference (CSNC). Berlin: Springer, 2013: 41-53. |
| [7] | MONTENBRUCK O, SCHMID R, MERCIER F, et al. GNSS Satellite Geometry and Attitude Models[J]. Advances in Space Research,2015, 56 (6) : 1015 –1029 . |
| [8] | KOUBA J. A Simplified Yaw-attitude Model for Eclipsing GPS Satellites[J]. GPS Solutions,2009, 13 (1) : 1 –12 . |
| [9] | DILSSNER F, SPRINGER T, GIENGER G, et al. The GLONASS-M Satellite Yaw-attitude Model[J]. Advances in Space Research,2011, 47 (1) : 160 –171 . |
| [10] |
杨元喜, 景一帆, 曾安敏. 自适应参数估计与内外部精度的关系[J].测绘学报,2014, 43 (5) : 441 –445 .DOI:10.13485/j.cnki.11-2089.2014.0077.
YANG Yuanxi, JING Yifan, ZENG Anmin. Adaptive Parameter Estimation and Inner and External Precision[J]. Acta Geodaetica et Cartographica Sinica,2014, 43 (5) : 441 –445 .DOI:10.13485/j.cnki.11-2089.2014.0077. |
| [11] |
秦显平, 杨元喜, 焦文海, 等. 利用SLR和伪距资料确定导航卫星钟差[J].测绘学报,2004, 33 (3) : 205 –209 .
QIN Xianping, YANG Yuanxi, JIAO Wenhai, et al. Determination of Navigation Satellite Clock Bias Using SLR and Pseudorange Data[J]. Acta Geodaetica et Cartographica Sinica,2004, 33 (3) : 205 –209 . |
| [12] |
秦显平, 杨元喜, 王刚, 等. SLR资料精密测定GLONASS卫星轨道[J].武汉大学学报(信息科学版),2003, 28 (4) : 440 –443 .
QIN Xianping, YANG Yuanxi, WANG Gang, et al. GLONASS Orbit Determination by Using SLR Data[J]. Geomatics and Information Science of Wuhan University,2003, 28 (4) : 440 –443 . |
| [13] | PAVLIS E C, BEARD R L. The Laser Retroreflector Experiment on GPS-35 and 36[M]//BEUTLER G, MELBOURNEW G, HEING W, et al. GPS Trends in Precise Terrestrial, Airborne, and Spaceborne Applications. Berlin:Springer, 1996: 154-158. |
| [14] | APPLEBY G, OTSUBO T. Comparison of SLR Measurements and Orbits with GLONASS and GPS Microwave Orbits[C]//Proceedings of the 12th International Workshop on Laser Ranging.Matera: NASA, 2000: 13-17. |
| [15] | SOS'NICA K, THALLER D, DACH R, et al. Satellite Laser Ranging to GPS and GLONASS[J]. Journal of Geodesy,2015, 89 (7) : 725 –743 . |
| [16] | URSCHL C, GURTNER W, HUGENTOBLER U, et al. Validation of GNSS Orbits Using SLR Observations[J]. Advances in Space Research,2005, 36 (3) : 412 –417 . |
| [17] | MONTENBRUCK O,STEIGENBERGER P,KIRCHNER G. GNSS Satellite Orbit Validation Using Satellite Laser Ranging[C]//Proceedings of the 18th International Workshop on Laser Ranging.Fujiyoshida: NASA,2013. |
| [18] | MONTENBRUCK O, STEIGENBERGER P. The BeiDou Navigation Message[J]. Journal of Global Positioning Systems,2013, 12 (1) : 1 –12 . |
| [19] | MONTENBRUCK O, STEIGENBERGER P, HAUSCHILD A. Broadcast versus Precise Ephemerides: A Multi-GNSS Perspective[J]. GPS Solutions,2015, 19 (2) : 321 –333 . |
| [20] | STEIGENBERGER P, HUGENTOBLER U, HAUSCHILD A, et al. Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J]. Journal of Geodesy,2013, 87 (6) : 515 –525 . |
| [21] | LOU Yidong, LIU Yang, SHI Chuang, et al. Precise Orbit Determination of BeiDou Constellation Based on BETS and MGEX Network[J]. Scientific Reports,2014, 4 : 4692 . |
| [22] | ZHAO Qile, GUO Jing, LI Min, et al. Initial Results of Precise Orbit and Clock Determination for COMPASS Navigation Satellite System[J]. Journal of Geodesy,2013, 87 (5) : 475 –486 . |
| [23] | LOU Yidong, LIU Yang, SHI Chuang, et al. Precise Orbit Determination of BeiDou Constellation: Method Comparison[J]. GPS Solutions,2016, 20 (2) : 259 –268 . |
| [24] | PEARLMAN M R, DEGNAN J J, BOSWORTH J M. The International Laser Ranging Service[J]. Advances in Space Research,2002, 30 (2) : 135 –143 . |
| [25] | DENG Zhiguo, GE Maorong, UHLEMANN M, et al. Precise Orbit Determination of BeiDou Satellites at GFZ[C]//EGU General Assembly Conference Abstracts. Vienna: EGU, 2014. |


