日月对地球的引潮力,不仅使固体地球产生周期性的形变(固体潮),而且使实际海平面相对于平均海平面产生周期性的涨落(海潮)。固体地球对海潮引起海水质量的重新分布产生的弹性响应,通常称为海潮负荷效应。海潮负荷改正是大地测量精密数据必须要顾及的,在近海地区海潮负荷引起的位移可达数厘米,但海潮模型在海岸附近的精度没有达到国际地球自转服务(IERS)规范的要求,故而有学者提出通过大地测量的手段弥补海潮模型的不足,主要包括超导重力仪(SG)观测技术,甚长基线干涉测量(VLBI)技术和GPS定位技术。其中SG是公认测量精度最高的技术,但由于其实现较困难,难以进行全球范围的测量;而VLBI在全球的测站数目也较少。而GPS定位技术因其具有全球覆盖、测站多、对观测环境要求低且成本低廉的优势,因此利用GPS技术来确定海潮负荷效应引起了广泛关注。
其研究大致可以分为3类。
(1) 基于载波相位的差分GPS(CDGPS)反演海潮负荷位移[1-4]。目前共分为两种方法:一种是通过分别位于内陆和沿海的两个测站的相对坐标时间序列来反演各潮波的相对振幅和相位[1-2, 4];另一种是以一个或多个测站为参考站(对海潮负荷位移进行模型改正),并将其坐标固定在ITRF框架下,再利用CDGPS计算求出其他测站相对这些测站的坐标时间序列,即ITRF框架下的坐标时间序列,再通过调和分析得到绝对的振幅和相位(可以和模型的结果直接进行比较)[3]。两种方法反演得到的M2潮波在垂直方向上的振幅和相位与模型的结果有1.0~4.6mm和6°~10°的差别。但无论采用哪种方法,要想得到绝对的海潮负荷参数必须要引入海潮模型对内陆站或参考站的海潮负荷进行估计,然而实际上海潮模型的结果并不精确,这必然会引入误差,使精度下降。
(2) 利用静态PPP反演海潮负荷位移[5-11];该方法可以直接得到各潮波的绝对振幅和相位,其精度也可与VLBI相媲美[7](在水平和垂直方向上分别达到了0.5mm和1.7mm[12])。然而静态PPP通常是利用GIPSY/OASIS软件处理24小时的观测数据,将位置坐标和海潮负荷位移参数一起进行估计,每天只得到一组估计值,这很有可能平均化了一些海潮信息,还使一些分潮波(例如1/3日潮)信号无法显示出来。
(3) 利用动态PPP确定海潮负荷位移[13-14];同静态PPP一样,该技术也可直接得到各潮波的绝对振幅和相位,但相对来说,动态PPP可以直接反映每个观测间隔海潮负荷位移的变化和一些振幅较小的分潮波信号(见图 3中的1/3日潮)。此外,动态PPP可提供实时动态的海潮负荷位移,为将来建立实时动态的海潮负荷模型提供观测资料。但由于动态PPP的定位精度(厘米级)明显低于静态PPP(毫米级),并且现今关于利用动态PPP反演海潮负荷还没有较为深入研究,只是利用该技术反演了部分潮波,也没有对其有效性以及其结果是否可用于区分海潮模型作详细的探讨。而相对于CDGPS,动态PPP技术只需要利用单个测站的观测值便可进行海潮负荷反演,无须多个测站的同步观测,同时也不需要引入海潮模型就可得到测站上各潮波的绝对振幅和相位。
因此,本文利用动态PPP技术反演获得香港地区的8个潮波(4个半日潮波M2、S2、N2、K2,4个周日潮波K1、O1、P1、Q1)在东北天3个方向的振幅和相位,并同静态PPP的反演结果进行比较来确定该技术反演海潮负荷位移的有效性。相信随着动态PPP定位精度的提高,可以通过处理全球GPS测站的数据,为将来建立高精度的海潮模型提供观测资料(尤其是在海潮模型精度较低的沿海地区)。此外,本文还拟通过与模型结果的比较,找出最适合香港区域的海潮模型。
1 利用GPS反演海潮负荷位移参数的原理根据IERS规范[15]可知,测站在东、北和天(k=1,2,3)方向上的海潮负荷瞬时位移Δck可表示为11个潮波(4个半日潮波M2、S2、N2、K2;4个周日潮波K1、O1、P1、Q1和3个长周期潮波Mf、Mm、Ssa)负荷位移矢量的叠加
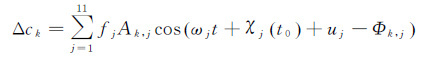 (1)
(1)
式中,Ak,j和Φk,j分别表示潮波j在k方向的振幅和格林尼治相位;ωj和χj分别为潮波j的角频率和天文幅角;t为格林尼治时间,t0为t=0时刻,即参考时刻,本文采用J2000为参考时刻,fj和uj为关于月亮轨道升交点调制作用的参数(周期约为18.6周年),分别为交点因子和订正角。由于8个主要潮波占了总信号的98%左右,并且3个长周期潮波相比8个主潮波在量级上要低数个量级,现在动态PPP的精度很难估计长期波引起的形变,所以本文只考虑周日和半日频段的8个主要潮波。
为了对海潮负荷位移参数建模,将余弦函数展开,把fjAk,j和Φk,j-μj分别看成整体,并忽略3个长周期潮波,式(1)可变成如下形式
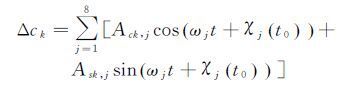 (2)
(2)
式中
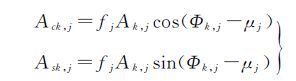 (3)
(3)
各分潮参数具有如下关系
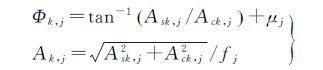 (4)
(4)
由公式(2)可知,估计所采用的观测值为动态精密单点定位所得的坐标相对于该GPS测站真值坐标的站心地平坐标,未知数为8个潮波在E、N、U 3个方向上的Ack和Ask,共48个未知数,利用长时间的动态PPP结果,建立误差方程,采用最小二乘就可以解算出这48个参数。最后根据式(4)便可计算得到各潮波在3个方向上的振幅和相位。
2 数据处理及结果的对比分析 2.1 试验区及数据源由于在内陆海潮负荷位移所引起的位移通常只有毫米级,而动态PPP目前所能达到的精度只有厘米级,故还无法确定动态PPP是否可用来确定内陆GPS测站的海潮负荷位移。与内陆相比,海边测站由海潮负荷引起的位移可达到几厘米甚至十几厘米,故动态PPP的定位精度能满足提取海边测站的海潮信号,故本文选取了香港的12个GPS测站(如图 1所示)来反演海潮负荷位移。为了保证PPP定位的精度,需采用30s的精密钟差文件,而IGS只从2006年11月份才开始提供30s的钟差产品,故本文只采用12个测站2007年以后的数据。Allison等曾指出大于等于1000d的观测数据就可以计算出较好的结果[5],因此本文用2007—2012年的数据足以反演出海潮负荷位移。

|
| 图 1 香港GPS测站和验潮站的分布 Fig. 1 Location of 12 GPS stations and 1 tide gauge station in Hong Kong 圆点为GPS测站,五角星为验潮站 |
2.2 数据处理方法
本文用于数据处理的软件为TriP,该软件是武汉大学测绘学院研发的高精度单点定位软件,通过处理单台GPS双频接收机的非差伪距与相位观测值,可以实现毫米—厘米级的单点静态定位和厘米—分米级的单点动态定位。由式(1)可知,要求得海潮负荷位移参数,最终需要的观测值为GPS测站的站心地平坐标,故数据处理可分为以下3步。
第1步:采用TriP软件的静态处理模式对预处理后的数据进行处理,得到静态坐标(XS,YS,ZS)(由于无法获得测站的真值坐标,故用静态坐标加以替代)。
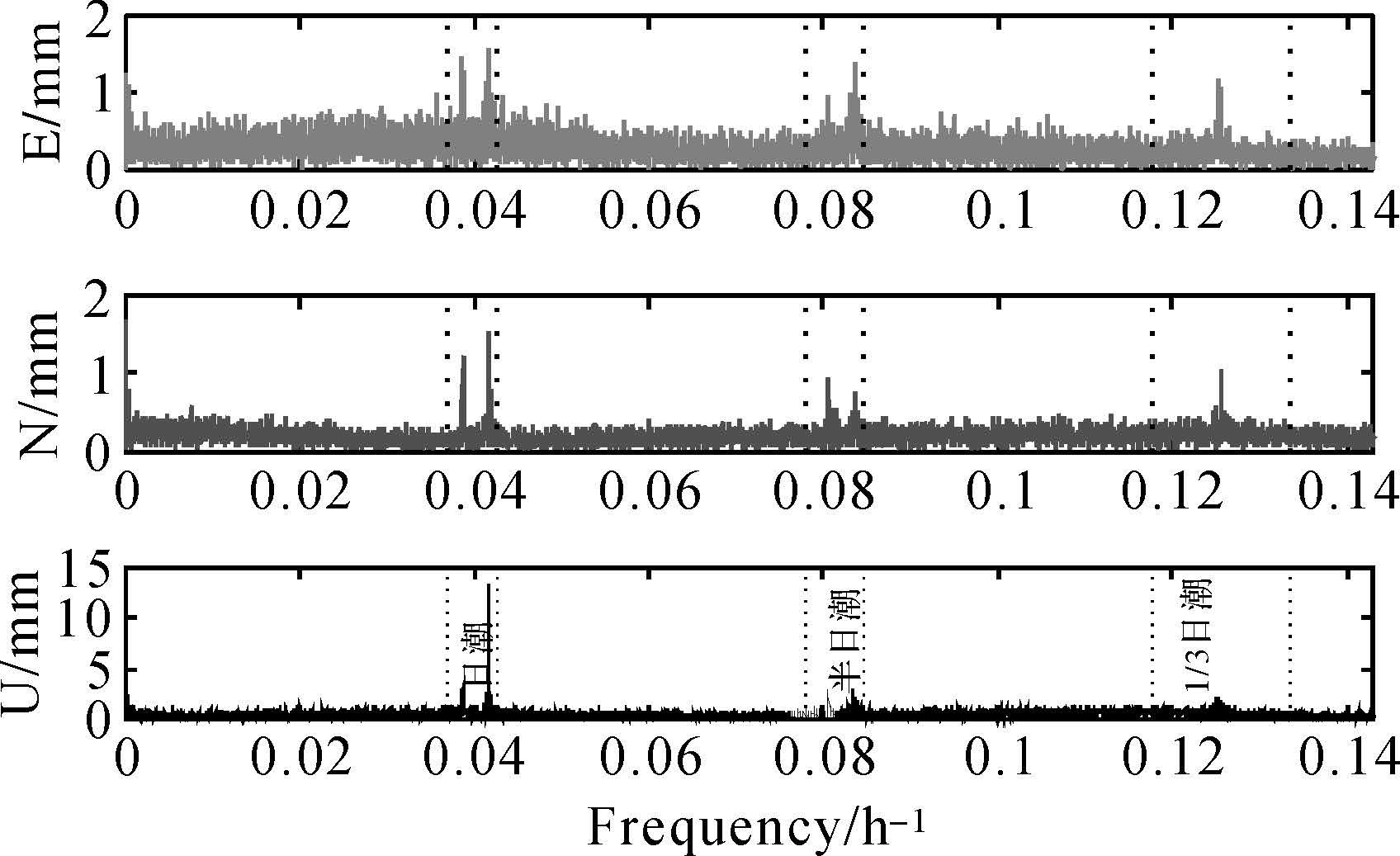
第2步:采用TriP软件的动态处理模式对预处理后的数据进行处理,得到每个历元(时间间隔为300s)的动态坐标(XK,YK,ZK)。利用第1步中的静态坐标,并顾及ITRF参考框架之间的转换和板块运动产生的位移,从而得到测站HKFN在ITRF2000下2007年至2012年的站心地平坐标(N、E、U)序列,如图 2所示。将上面的坐标序列进行频谱分析得到其频谱图,其结果如图 3所示,结合频率和振幅,可看出明显的周日、半日和三分之一潮波信号,可知动态PPP定位结果中含有海潮负荷信号,表明可以用动态PPP来反演海潮负荷位移。

|
| 图 2 HKFN测站6年的PPP动态处理结果 Fig. 2 Results of Kinematic PPP for HKFN station |
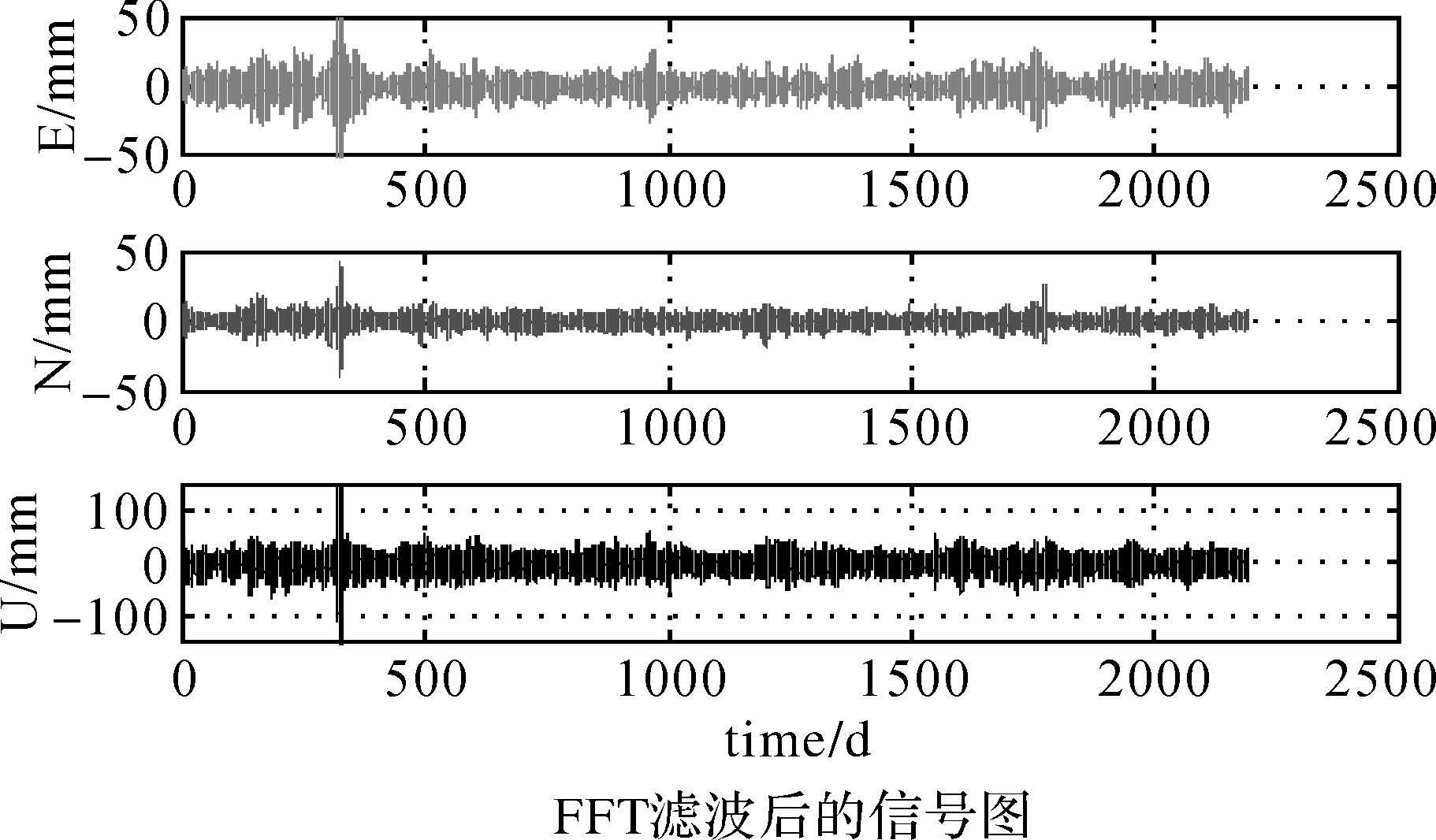
第3步:计算各潮波在E、N、U 3个方向上的振幅Ak,j和格林尼治相位Φk,j。由于PPP动态处理结果中存在一些粗差(如图 2所示),在计算调和参数之前必须对这些粗差进行适当的剔除,本文采用了两种方法:直接剔除法,即直接在水平方向和垂直方向施加0.1m和0.2m的限值,只要其中一个方向上的值大于改限值就将该历元的数据剔除;滤波法,即滤掉除周日潮波和半日潮波附近频率之外的所有频率(即只保留图 3中日潮波和半日潮波虚线内的频率,由于滤掉的频率中所包含的噪声信号和其他潮波的信号,并不是本文所需要研究的信号,将其滤去并不会对周日和半日频段的信号造成影响),再将滤波后的频率进行傅里叶反变换,得到滤波后的观测值序列(如图 4所示),然后再用该观测数据计算各潮波的调和参数。
|
| 图 3 HKFN测站的分潮频谱图 Fig. 3 Spectra analysis for HKFN station |
|
| 图 4 经过滤波处理后HKFN测站的PPP动态结果 Fig. 4 Kinematic PPP results after filtering for HKFN station |
比较以上两种方法的计算结果发现其差别并不大,但通过与后文的模型结果相比较发现,两种方法计算出的K1在U方向的振幅明显比模型估计结果要大,但相对而言滤波法的结果更好,故本文最终采用滤波法。
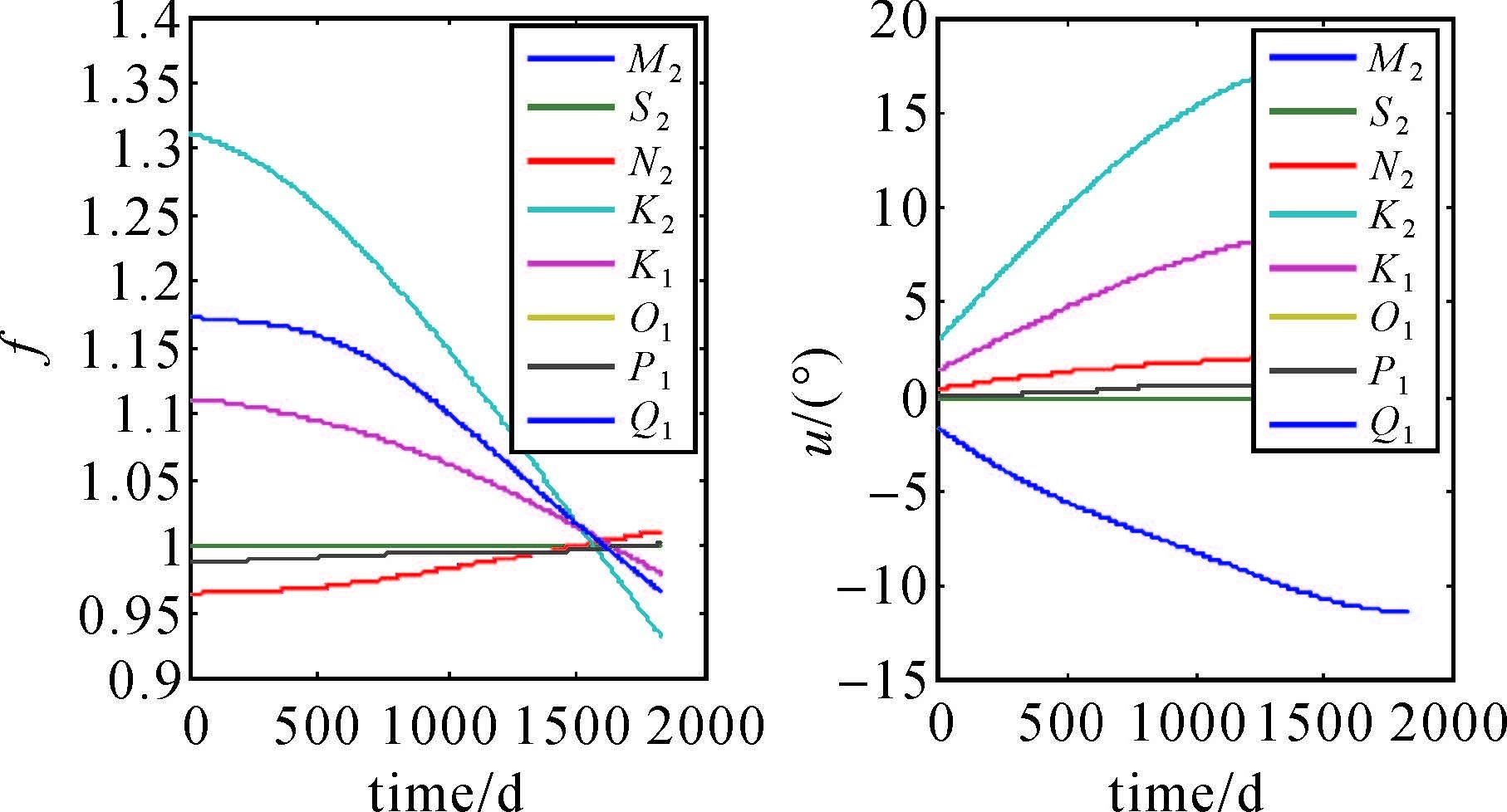
由于8个主潮波只占了所有潮波的小部分,必须对每个潮波进行节点因数改正。图 5给出了交点因子f和订正角u在2007—2012年中的变化。由于M2与N2、O1与Q1潮波的变化一致,故图中只显示了6条曲线。从图中可看出,K2、K1、O1和Q1潮波的交点因子和订正角的变化较大,其中K2的交点因子改正最大可到30%,订正角的改正最大可达18°;其他4个潮波的变化则较小。对于f和u,取最初或最终的值都没有考虑到其随时间的变换,并且会对结果造成一定的误差,故本文取该测量数据时间段内的平均值。
|
| 图 5 交点因子f和订正角u在2007—2012年内的变化 Fig. 5 Variation of argument f and u from 2007 to 2012 |
2.3 潮波的收敛性
为了确定观测时间对动态PPP反演结果的影响,本文分析了不同时间段内各潮波振幅的收敛情况,如图 6所示。

|
| 图 6 测站HKFN各潮波振幅的收敛性 Fig. 6 Convergence of the HKFN station showing the amplitudes in the east (up),north (middle) and vertical (bottom) directions |
由图 6可以看出,除了K1和K2潮波外,其他潮波的3个方向在1000d左右处都基本收敛,只是收敛的速度有所不同,M2和N2在500d时就收敛了。至于K1和K2,在1000d后仍有较大的波动,E、N方向尤为明显,但在2000d后基本趋于稳定。
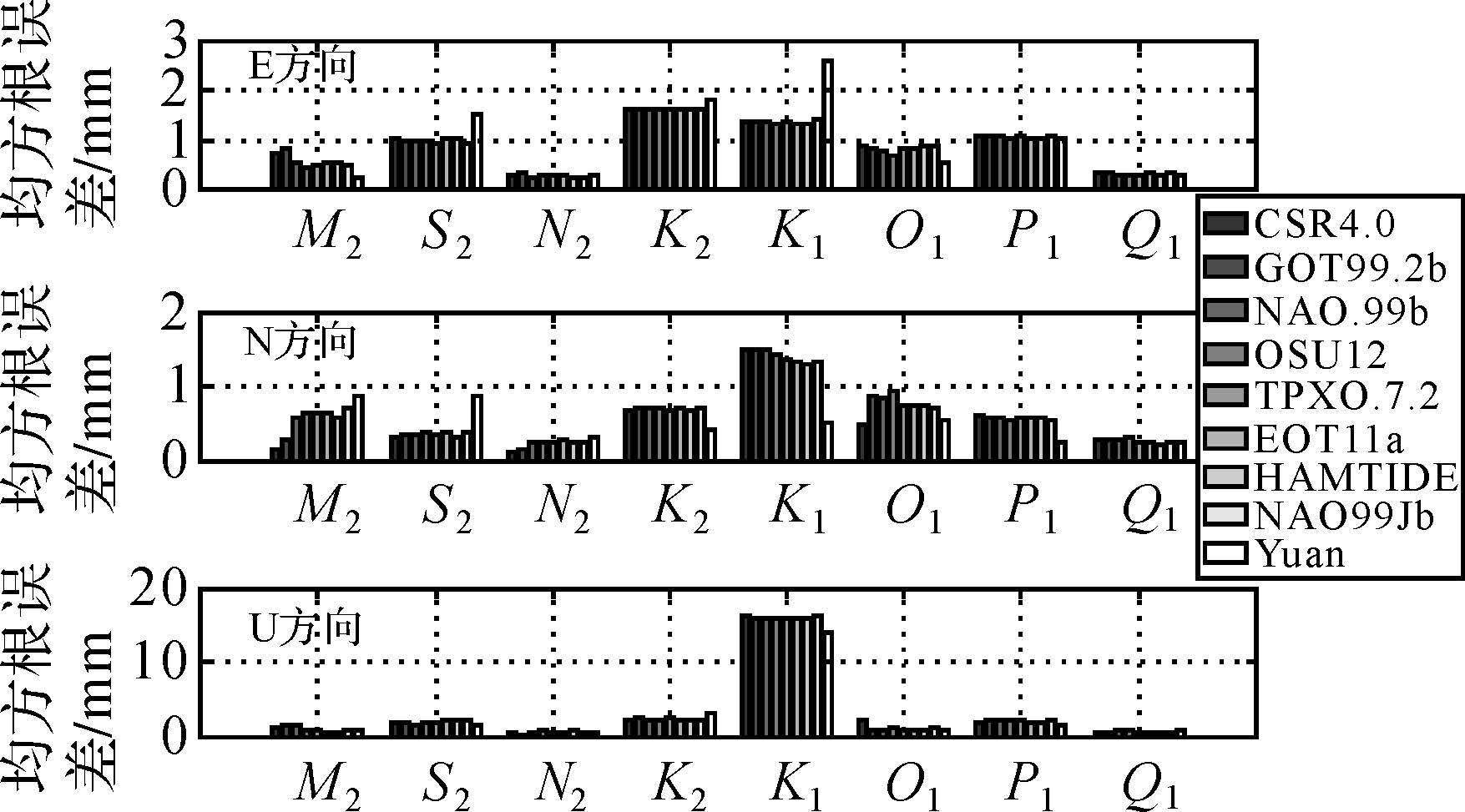
2.4 与模型计算结果和静态PPP结果相比较本文利用HKFN测站滤波后的数据估计48个模型化参数后观测值的残差的中误差在E、N、U 3个方向上分别为7mm、3mm和13mm,这说明利用过滤后的GPS数据反演海潮负荷位移的内符合精度在水平方向上达到了毫米级,在垂直方向上达到了厘米级。为了进一步评定动态PPP确定海潮负荷位移的外符合精度,本文将GPS反演结果与7个全球海潮模型(CSR4.0[16]、GOT99.2b[17]、NAO.99b[18]、OSU12[19]、TPXO.7.2[20]、EOT11a[21]、HAMTIDE[22])、1个区域模型(NAO.99Jb[18])和袁林果2010年静态PPP[10](图 7中由Yuan表示)的结果进行了比较。
|
| 图 7 动态PPP海潮负荷位移估值与模型和静态PPP之间的均方根误差 Fig. 7 RMS misfits between OTL displacements from kinematic PPP and models and static PPP |
7个全球海潮模型的结果都是通过网站http://holt.oso.chalmers.se/loading/给出的,区域模型NAO99Jb的结果由GOTIC2软件[23]得出。本文采用“均方根误差”来评价各个潮波的GPS海潮负荷位移和模型值之间的差异,对于潮波j,坐标分量k,所有测站(n=1,…,N)的GPS估值和模型之间的均方根误差可用式(5)计算
 (5)
(5)
式中
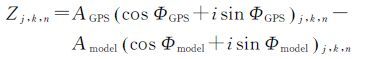 (6)
(6)
式中,A为振幅;Φ为格林尼治相位。
GPS计算的海潮负荷位移和8个海潮模型以及袁林果计算结果[10]之间的均方根误差统计如图 7所示。由图可知,各模型RMS值在整体上的差别并不大,只是在某个潮波的特定方向存在微小的差异。水平方向上,除了K1和K2潮波外,其他潮波的偏差均在1mm左右,有的潮波的偏差甚至小于亚毫米。垂直方向上,仍然是K1和K2的偏差较大,尤其是K1,达到了16mm左右。通过查看数据发现,本文计算的K1潮波的振幅是模型计算结果的两倍多,这可能是由于卫星星座周期,多路径效应以及环境中的某些信号的周期与K1的周期近似,故对K1信号造成了污染,从而导致反演得到的K1的振幅较大。另外K2达到了2.2mm左右,这可能是由于K2的周期与卫星轨道的周期近似,从而引入了一些轨道误差。
与模型的RMS相比较,静态PPP的RMS在垂直方向上比模型整体上要小,水平方向上整体的差别也不大,只是在个别潮波的某个方向上存在较大的差异。其中S2、K1、K2潮波在E方向上,M2和S2潮波在N方向上明显要比模型的RMS大。而在M2的E方向,K1和K2潮波的N方向却又明显要比模型的RMS小。文献[10]的计算的K1在E方向振幅在3mm左右,而本文只有1mm左右,均要小一些。M2潮波在N方也存在较大的差,这是由于本文计算的振幅平均比文献[10]的大了0.3mm。S2潮波在E和N反向存在较大的差别是由于两者计算的结果在振幅和相位都存在一定的差异。另外,从整体上来看,发现与月球有关的潮波(M2、N2、O1和Q1)的RMS明显比太阳有关的潮波(S2、P1、K1和K2)的要小(尤其是垂直方向上),这可能是由于GPS有关的系统误差给太阳频率的潮波造成偏差。
将图 7与文献[10]的图 4进行比较发现,本文GPS估值与模型之间的均方根误差在水平方向上的量级与其近似,但在垂直方向上,除了K1潮波外(大了近10mm),本文在其他潮波上比文献[10]的结果要大1mm左右,这是由于在垂直方向上现在的静态PPP技术的定位精度要比动态PPP要高。此外本文中动态PPP未对某些误差进行处理(例如极潮等),同时也未对模糊度加以固定。另外发现RMS值较大的潮波都是一样的,均是S2、K1和K2,这进一步说明了动态PPP结果的正确性。
文献[10]的结果中发现GPS估值和模型值之间的残差出现明显的区域一致性,故将GPS估值与模型值之间的偏差作为一个常数,从而定义了“观测均方根误差”
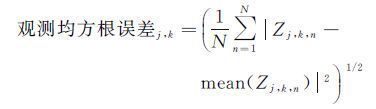 (7)
(7)
本文也对该观测均方根误差进行了计算,并将结果与前面得到的均方根误差进行了比较。图 8给出了基于模型NAO99Jb观测均方根误差统计,发现与均方根误差相比,各潮波在3个方向上都有明显减少,尤其是K1的U方向(从16.4mm减少到了1.3mm),K1和K2的N方向。这进一步说明,一些系统偏差造成了K1和K2潮波反演的误差。这些系统误差一部分可能是海潮模型的误差导致的,而另一部分可能PPP定位过程中引入的。PPP定位引起的误差可分为如下几类:
(2) 由GPS系统引起的误差。由于GPS卫星的轨道周期(11h 58min)和卫星星座的周期(24h)分别与K1和K2潮波接近,致使整两个潮波的振幅偏大。
(3) 模型误差以及环境因素的影响。固体潮未完全模型化,电离层的高阶项以及多路径效应和电离层异常均会导致海潮负荷位移反演的误差。
根据上面的观测均方根误差可知,12个测站与模型的残差存在明显的区域一致性,故选择其中一个测站HKSC(该测站离验潮站最近,便于进一步与验潮站反演结果进行比较)来进一步分析本文计算结果与模型以及静态PPP结果的差异,并探索是否能通过本文计算的结果来区分海潮模型。表 1中给出了HKSC单个测站的RMS值。由上文的分析中可知本文结果在K1和K2潮波与模型偏差较大,故这里没有用这两个潮波来区分海潮模型。
| 方向 | 潮波 | 模型 | ||||||||
| CSR4.0 | GOT99.2b | NAO.99b | OSU12 | TPXO.7.2 | EOT11a | HAMTIDE | NAO99Jb | Yuan | ||
| E方向 | M2 | 0.75 | 0.86 | 0.53 | 0.43 | 0.44 | 0.57 | 0.58 | 0.47 | 0.16 |
| S2 | 0.84 | 0.83 | 0.76 | 0.76 | 0.75 | 0.82 | 0.85 | 0.74 | 1.38 | |
| N2 | 0.27 | 0.31 | 0.17 | 0.25 | 0.22 | 0.22 | 0.21 | 0.17 | 0.19 | |
| O1 | 0.72 | 0.70 | 0.66 | 0.58 | 0.73 | 0.72 | 0.75 | 0.76 | 0.36 | |
| P1 | 1.15 | 1.16 | 1.18 | 1.14 | 1.15 | 1.12 | 1.14 | 1.15 | 1.45 | |
| Q1 | 0.24 | 0.23 | 0.21 | 0.22 | 0.22 | 0.22 | 0.21 | 0.24 | 0.12 | |
| N方向 | M2 | 0.13 | 0.29 | 0.63 | 0.66 | 0.71 | 0.67 | 0.64 | 0.76 | 0.88 |
| S2 | 0.16 | 0.15 | 0.31 | 0.31 | 0.31 | 0.31 | 0.26 | 0.34 | 0.78 | |
| N2 | 0.15 | 0.19 | 0.31 | 0.30 | 0.30 | 0.33 | 0.32 | 0.33 | 0.39 | |
| O1 | 0.48 | 0.86 | 0.82 | 0.92 | 0.72 | 0.72 | 0.72 | 0.67 | 0.50 | |
| P1 | 0.37 | 0.36 | 0.34 | 0.31 | 0.28 | 0.29 | 0.33 | 0.28 | 0.07 | |
| Q1 | 0.29 | 0.27 | 0.28 | 0.30 | 0.25 | 0.25 | 0.23 | 0.25 | 0.21 | |
| U方向 | M2 | 0.95 | 1.44 | 1.52 | 0.93 | 0.72 | 0.37 | 0.26 | 0.49 | 0.75 |
| S2 | 2.13 | 2.08 | 1.89 | 1.91 | 1.99 | 2.30 | 2.16 | 2.32 | 1.94 | |
| N2 | 0.19 | 0.33 | 0.55 | 0.64 | 0.33 | 0.44 | 0.50 | 0.49 | 0.19 | |
| O1 | 2.15 | 0.55 | 0.53 | 0.93 | 0.58 | 0.61 | 0.73 | 1.12 | 0.39 | |
| P1 | 2.24 | 2.30 | 2.35 | 2.31 | 2.30 | 2.19 | 2.29 | 2.30 | 1.90 | |
| Q1 | 0.47 | 0.55 | 0.68 | 0.83 | 0.53 | 0.51 | 0.46 | 0.52 | 0.75 | |
| E方向总和 | 3.97 | 4.09 | 3.51 | 3.39 | 3.50 | 3.67 | 3.73 | 3.52 | 3.67 | |
| N方向总和 | 1.58 | 2.11 | 2.69 | 2.81 | 2.58 | 2.57 | 2.50 | 2.62 | 2.83 | |
| U方向总和 | 8.13 | 7.25 | 7.51 | 7.55 | 6.45 | 6.42 | 6.41 | 7.24 | 5.92 | |
| 3个方向总和 | 13.68 | 13.46 | 13.71 | 13.75 | 12.52 | 12.65 | 12.64 | 13.39 | 12.42 | |
通过分析表 1可知,在E方向上,本文与CSR4.0和GOT99.2b模型符合得最差,而与OSU12和TPXO.7.2模型符合得较好。在N方向上,与CSR4.0和GOT99.2b模型符合得最好,而与NAO.99b和OSU12模型符合得最差。在U方向上,与CSR4.0和OSU12模型符合得最差,而与TPXO.7.2、EOT11a和HAMTIDE符合得较好。但综合3个方向RMS的总和可知,GOT99.2b、TPXO.7.2、EOT11a、HAMTIDE和NAO99Jb 4个模型比另外4个模型要更符合本文的结果。
2.5 与验潮站结果进行比较为了进一步验证动态PPP确定海潮负荷位移的准确性,本文对GPS和验潮站两种不同的观测结果进行了比较。利用调和分析法[24]对香港验潮站(位置如图 1所示)2012年的数据进行了分析,得到了30个潮波的调和参数,在计算过程中f、u均取2012年的平均值。再通过双线性内插或外推得到了上面8个海潮模型的调和参数。验潮站计算结果与模型估计结果之间的均方根误差如表 2所示。
| 模型 | 潮波 | 总和 | 去除K1和K2 | |||||||
| M2 | S2 | N2 | K2 | K1 | O1 | P1 | Q1 | |||
| CSR4.0 | 28.93 | 10.02 | 6.94 | 2.76 | 10.69 | 8.06 | 3.81 | 1.66 | 72.88 | 59.42 |
| GOT99.2b | 15.86 | 3.73 | 3.38 | 0.93 | 9.71 | 7.08 | 3.47 | 1.38 | 45.54 | 34.90 |
| NAO.99b | 15.92 | 7.03 | 3.07 | 1.47 | 8.71 | 7.59 | 3.43 | 1.40 | 48.61 | 38.43 |
| OSU12 | 19.98 | 5.86 | 4.41 | 1.65 | 7.99 | 7.47 | 3.05 | 1.02 | 51.45 | 41.80 |
| TPXO.7.2 | 12.38 | 5.80 | 3.75 | 2.04 | 10.52 | 7.96 | 3.57 | 1.36 | 47.36 | 34.80 |
| EOT11a | 13.44 | 6.70 | 2.97 | 1.51 | 10.63 | 7.27 | 3.54 | 1.55 | 47.61 | 35.46 |
| HAMTIDE | 14.56 | 5.58 | 2.47 | 2.11 | 10.04 | 7.50 | 3.30 | 1.30 | 46.86 | 34.71 |
| NAO.99Jb | 14.23 | 6.08 | 2.72 | 1.21 | 8.21 | 7.72 | 3.30 | 1.38 | 44.85 | 35.43 |
分析表 2可发现,CSR4.0模型与验潮站的结果符合得最差,其次是NAO.99b和OSU12模型,而HAMTIDE模型与验潮在的结果符合得最好,其次是TPXO.7.2、NAO99Jb、GOT99.2b、EOT11a模型。这与上文中HKSC测站的动态PPP估值与模型之间的RMS在除去K1和K2潮波后与模型的符合程度是一致的,故进一步验证了动态PPP确定海潮负荷位移的准确性。
3 结 论本文利用动态PPP对香港12个GPS测站6年的数据进行了海潮负荷位移反演,得到了8个主要潮波的振幅和相位。通过与8个海潮模型和静态PPP的结果进行分析比较,得到如下结论:
(1) HAMTIDE、TPXO.7.2和NAO99Jb 3个模型都比较适合香港区域。
(2) 动态PPP与静态PPP的结果在量级上基本一致,只是在M2、S2、的E、N方向和K1、K2潮波的3个方向上有较大的偏差,可能是由于动态PPP定位精度以及其中某些误差没有改正导致的。
(3) 动态PPP的结果与模型的残差存在明显的区域一致性,当去除平均残差后,各潮波在3个方向上的RMS值都有明显减小,尤其是K1的U方向,从16.4mm减少到1.3mm。
(4) 将验潮站数据反演的结果与模型的结果比较发现,与其符合得较好的模型(HAMTIDE TPXO.7.2、NAO99Jb和GOT99.2b)与动态PPP的结果也都符合得最好,进一步证明了动态PPP反演海潮负荷位移的有效性。
总的来说,除了K1和K2潮波外,利用动态PPP反演得到的其他6个潮波的海潮负荷位移已经达到了模型改正的精度,尤其对于海岸线较为复杂的区域。但动态PPP反演结果与模型结果之间的误差来源还有待进一步分析。另外,香港区域的验潮站只有一个,对于评估海潮模型可能偏少,故可能在以后的研究中进行以下改进:①对于动态PPP中可改正的误差(例如极潮等)进行改正,看反演的结果是否会有改进;②另选一个包含多个并置验潮站的GPS测站区域,进一步来说明可以由验潮站数据反演结果来验证动态PPP反演结果的准确性;③随着动态PPP精度的提高,以后可以用来提供全球的实时动态PPP实测海潮模型。
| [1] | KHAN S A, TSCHERNING C C. Determination of Semi-diurnal Ocean Tide Loading Constituents Using GPS in Alaska[J]. Geophysical Research Letters,2001, 28 (11) : 2249 –2252 . |
| [2] | KHAN S A, SCHERNECK H G. The M2 Ocean Tide Loading Wave in Alaska: Vertical and Horizontal Displacements, Modelled and Observed[J]. Journal of Geodesy,2003, 77 (3-4) : 117 –127 . |
| [3] | YUN H S, LEE D H, SONG D S. Determination of Vertical Displacements over the Coastal Area of Korea Due to the Ocean Tide Loading Using GPS Observations[J]. Journal of Geodynamics,2007, 43 (4-5) : 528 –541 . |
| [4] | RAFIQ M, SANTOS M. Detecting and Mitigating Ocean Tidal Loading Displacements in the Bay of Fundy Using GPS[J]. Journal of Geodetic Science,2011, 1 (2) : 127 –135 . |
| [5] | ALLINSON C R, CLARKE P J, EDWARDS S J. Stability of Direct GPS Estimates of Ocean Tide Loading[J]. Geophysical Research Letters,2004, 31 (15) : 603 –606 . |
| [6] | KING M A, Penna N T, Clarke P J, et al. Validation of Ocean Tide Models around Antarctica Using Onshore GPS and Gravity Data[J]. Journal of Geophysical Research: Solid Earth,2005, 110 (B8) : 401 –421 . |
| [7] | THOMAS I D, KING M A, CLARKE P J. A Comparison of GPS, VLBI and Model Estimates of Ocean Tide Loading Displacements[J]. Journal of Geodesy,2007, 81 (5) : 359 –368 . |
| [8] | THOMAS I D, KING M A, CLARKE P J. A Validation of Ocean Tide Models around Antarctica Using GPS Measurements[M]//CAPRA A, DIETRICH R. Geodetic and Geophysical Observations in Antarctica. Berlin: Springer-Verlag,2008:211-235. |
| [9] | YUAN L G, DING X L, ZHONG P, et al. Estimates of Ocean Tide Loading Displacements and Its Impact on Position Time Series in Hong Kong Using a Dense Continuous GPS Network[J]. Journal of Geodesy,2009, 83 (11) : 999 –1015 . |
| [10] |
袁林果, 丁晓利, 孙和平, 等. 利用GPS技术精密测定香港海潮负荷位移[J].中国科学: 地球科学,2010, 53 (7) : 993 –1007 .
YUAN Linguo, DING Xiaoli, SUN Heping, et al. Determination of Ocean Tide Loading Displacements in Hong Kong Using GPS Technique[J]. Science China Earth Sciences,2010, 53 (7) : 993 –1007 . |
| [11] | YUAN Linguo, CHAO B F. Analysis of Tidal Signals in Surface Displacement Measured by a Dense Continuous GPS Array[J]. Earth and Planetary Science Letters,2012, 355 . |
| [12] | PETROV L, MA C. Study of Harmonic Site Position Variations Determined by Very Long Baseline Interferometry[J]. Journal of Geophysical Research,2003, 108 (B4) : 2190 . |
| [13] | ITO T, OKUBO M, SAGIYA T. High Resolution Mapping of Earth Tide Response Based on GPS Data in Japan[J]. Journal of Geodynamics,2009, 48 (3-5) : 253 –259 . |
| [14] | ZHAO Hong, ZHANG Qin, ZHANG Ming, et al. Extraction of Ocean Tide Semidiurnal Constituents’ Vertical Displacement Parameters Based on GPS PPP and Harmonic Analysis Method[M]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. Proceedings: Volume II China Satellite Navigation Conference (CSNC).Berlin: Springer-Verlag,2014:341-350. |
| [15] | PETIT G, LUZUM B. IERS Conventions (2010)[R]. Frankfurt, 2010. |
| [16] | EANES R J, SHULER A. An Improved Global Ocean Tide Model from TOPEX/Poseidon Altimetry: CSR4.0[C]//EGS 24th General Assembly.The Hague:[s.n.], 1999. |
| [17] | RAY R D. A Global Ocean Tide Model from TOPEX/Poseidon Altimetry: GOT99.2[R].Greenbelt:Goddard Space Flight Center, 1999. |
| [18] | MATSUMOTO K, TAKANEZAWA T, OOE M. Ocean Tide Models Developed by Assimilating TOPEX/Poseidon Altimeter Data into Hydrodynamical Model: A Global Model and a Regional Model Around Japan[J]. Journal of Oceanography,2000, 56 (5) : 567 –581 . |
| [19] | FOK H S.Ocean Tides Modeling Using Satellite Altimetry[R].Columbus,2012. |
| [20] | EGBERT G D, EROFEEVA S Y. Efficient Inverse Modeling of Barotropic Ocean Tides[J]. Journal of Atmospheric and Oceanic Technology,2002, 19 (2) : 183 –204 . |
| [21] | SAVCENKO R, BOSCH W. EOT11A-Empirical Ocean Tide Model from Multi-Mission Satellite Altimetry[R]. DGFI Report No.89.München:Deutsches Geodtisches Forschungsinstitut,2012. |
| [22] | TAGUCHI E, STAMMER D, ZAHEL W. Inferring Deep Ocean Tidal Energy Dissipation from the Global High-Resolution Data-Assimilative HAMTIDE Model[J]. Journal of Geophysical Research: Oceans,2014, 119 (7) : 4573 –4592 . |
| [23] | MATSUMOTO K, SATO T, TAKANEZAWA T, et al. GOTIC2: A Program for Computation of Oceanic Tidal Loading Effect[J]. Journal of the Geodetic Society of Japan,2001, 47 (1) : 243 –248 . |
| [24] |
张凤烨, 魏泽勋, 王新怡, 等. 潮汐调和分析方法的探讨[J].海洋科学,2011, 35 (6) : 68 –75 .
ZHANG Fengye, WEI Zexun, WANG Xinyi, et al. Tidal Harmonic Analysis[J]. Marine Sciences,2011, 35 (6) : 68 –75 . |
| [25] | KOUBA J. A Guide to Using International GNSS Service (IGS) Products[R].Ottawa:Geodetic Survey Division, Natural Resources Canada,2009. |


