2. 地球空间信息技术协同创新中心,湖北 武汉 430079 ;
3. 长江大学地球科学学院,湖北 武汉 430100
2. 2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China ;
3. School of Geosciences, Yangtze University, Wuhan 430100, China
矢量匹配技术是数据融合、变化检测、数据更新等必不可少的关键技术,道路网匹配是矢量匹配的研究热点之一。目前,对道路网匹配方法的研究多集中在相似性度量和匹配策略两个方面。在相似性度量方面,主要以道路实体的几何特征(形状[1]、距离[2-4]、方向[5])、拓扑特征[6-7]、语义特征[8-9]作为相似性特征描述。几何特征中的形状描述多用于面实体整体特征,文献[1]针对线实体进行构面后再采用多级弦长的方式描述,但仅适用于形状变化剧烈的曲线;距离是较好描述线实体的特征,L2距离[2]与改进Hausdorff距离[3-4]在描述道路待匹配对之间距离上有很大进步,但其处理复杂线实体的能力有限;方向描述方法多基于节点或虚拟节点之间的局部角度差异,缺乏整体方向相似性的描述方面的研究;拓扑特征表达实体的拓扑关系,文献[7]提出利用拓扑关系进网状要素匹配算法,该算法中微小的拓扑差异可能致使匹配失败;语义特征的运用依赖于数据质量和属性项的完整情况,普适性受到一定的约束。
在道路匹配策略方面,主要采用特征权值组合与阈值选取[10-11]、概率理论[12]、蚁群算法[13]、概率松弛法[14-15]、最优化[3]和迭代逻辑回归[16]模型等策略获取匹配结果。权值组合与阈值选取法虽能很好的解决匹配问题,但权值、阈值的确定都依赖于经验值,自适应能力偏差;概率理论法避免了阈值的选取问题,但该方法计算量较大,增加了匹配结果对权值选取的敏感度;文献[14-15]均采用概率松弛法求解向量相似性矩阵获得匹配结果,其算法结构复杂且计算量偏大;最优化和迭代逻辑回归模型具有人工干预少的优点,但实际应用于匹配时,需考虑数据分块以控制算法耗时。针对上述问题,本文提出一种道路网多特征优化算法,首先设计了基于面积累积的形状差、综合中值Hausdorff距离和全局加权属性项距离3种相似性特征,然后将此3项特征与SVM算法结合进行模型训练,构建道路网回归匹配模型,实现道路网的有效匹配。
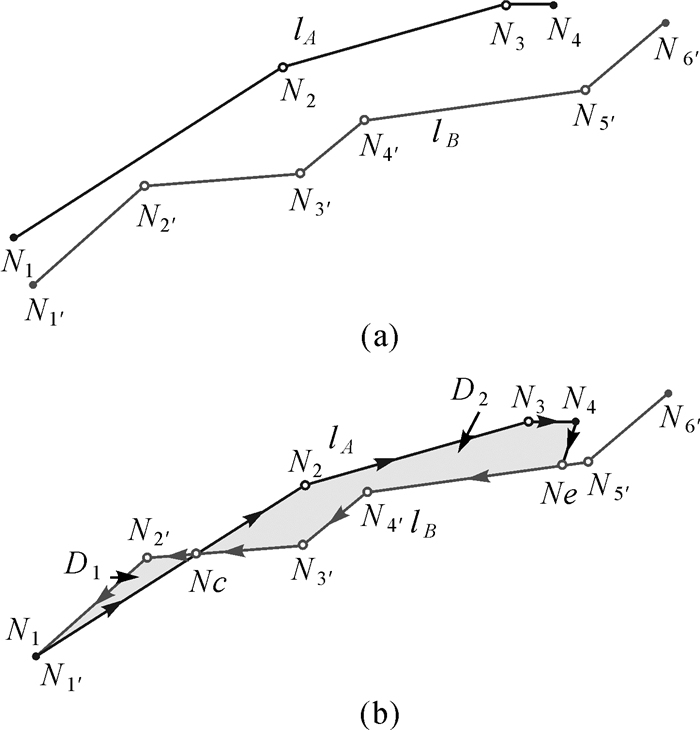
1 道路匹配对相似性描述 1.1 基于面积累积的形状差利用累积计算在差异描述中的作用[5],本文设计了基于面积累积的形状差,即通过线对象之间形成封闭区域的面积累积大小来度量两者形状差异。结合图 1所示,其基本思想:首先较短线对象(lA)向较长对象(lB)平移,使lA、lB的首节点N1和N1′重合(图 1(a)至图 1(b)的过程),以lB首节点N1′为起点,在lB上取等长于lA的点Ne,将lA的尾节点7N4与lB中的Ne连接形成封闭区域(如图 1中阴影区域D1和D2);然后对该区域进行面积累积计算。
|
| 图 1 道路待匹配对之间的形状差示意图 Fig. 1 Diagram of shape differences between road corresponding matching pairs |
lA与lB基于面积累积的形状差Orn(lA,lB)即为封闭区域的多边形面积积分,如下
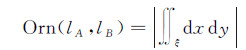 (1)
(1)
式中,ξ表示封闭区域D1和D2;丨∫∫ξdxdy丨表示对ξ进行二元积分。
只需要确保每一线对象及其子对象具有统一的方向走势,且不同线对象走势应相反以形成封闭区域即可,可解除对线方向的约束,加强对整体差异的描述。如图 1所示的箭头方向,设以逆时针方向的积分结果为正,则封闭区域D1和D2的积分结果分别为正和负,两值求和起到一定的抵消作用,与道路形状差异描述中关注整体的描述原则契合。式(1)中直接进行面积积分计算过于复杂,本文引入格林公式将函数的面积分转换为沿封闭区域边界线积分从而降低计算难度。多封闭区域格林公式为
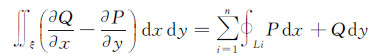 (2)
(2)
式中,n为组成封闭区域ξ的线段数量;Li(i=0,1,2,…n)为组成封闭区域的第i条线段。
将二元积分转化为单元积分,设式(2)中P=y、Q=0,令第i条组成线段Li的斜率为ki,则有直线方程y=kix+bi。将其带入式(2)中并结合式(1)可得道路待匹配对之间封闭区域D1、D2面积累积计算公式为
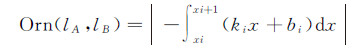 (3)
(3)
式中,xi为Li线段的x坐标。
1.2 综合中值Hausdorff距离Hausdorff距离常用于描述线对象之间的距离相似性,由于其取极值原理,致使无法有效表达线对象之间的平均距离。中值Hausdorff距离能较好表达线对象之间的距离分布主趋势[4],但不适用于线对象之间长度差异较大的情况,而文献[16]提出的较短中值Hausdorff距离(shorted median Hausdorff distance,SM_HD)通过从较短线对象到较长线对象的有向距离解决了这一问题,但其未考虑垂足不在对应的线段上时造成的距离不准确问题。因此,本文提出一种以欧氏距离和垂直距离为基础的综合中值Hausdorff距离(mixed median Hausdorff distance,MM_HD),是通过对较短线对象到较长线对象的有向综合距离取舍、计算、排序,并从中选取中值距离。其基本思想是:做较短线对象中节点到较长线对象的垂线,若垂足点位于长线对象的线段上,则采用垂直距离;若位于其延长线上,则采用欧氏距离。这样可有效避免单纯垂线计算时造成距离错误情况的发生。其计算公式为
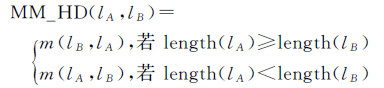 (4)
(4)
式中,length(lA)和length(lB)分别表示道路线对象lA和lB的长度;m(lB,lA)、m(lA,lB)分别为lB到lA、lA到lB的综合中值Hausdorff距离,计算公式分别为
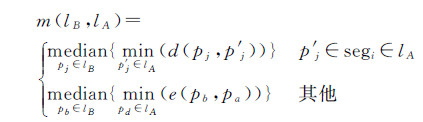 (5)
(5)
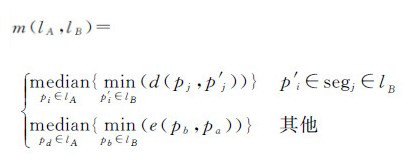 (6)
(6)
式中,pi和pj分别是lA和lB上的节点;p′i和p′j分别是pi和pj在lB和lA上的垂足;pa和pb分别是lA和lB上的任意点;d(pj,p′j)表示pj到p′j的垂直距离;e(pb,pa)表示pb到pa的欧氏距离。以length(lA)≥length(lB)为例,当垂足p′j在lA的第i个子线段对象(一条线对象由若干条子线段对象组成)segi上时,取pj到p′j的垂直距离,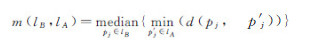
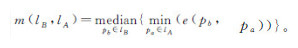
目前,大多数语义相似性度量方法是基于单一属性项进行属性信息相关性匹配[17-18],易导致匹配结果会过于依赖此属性项。因此,本文提出一种全局加权属性项距离,步骤是:选取道路待匹配数据集中所有具有对应关系的属性项,并按显著性等级比例系数对各属性项权值进行分配,再根据属性项内容差异及对应权值计算获得全局加权属性项距离公式为
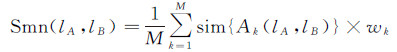 (7)
(7)
式中,M为lA与lB中具有可比性属性项的数量;Ak(lA,lB)表示均存在于lA与lB中的第k个属性项;sim{Ak(lA,lB)}表示第k个属性项的语义相似性,wk表示第k个属性项的权值,Smn(lA,lB)表示lA与lB之间的全局加权属性项距离。
矢量数据属性项类型可归为两类:数字和文本。对于道路矢量数据,数字类型一般包括道路的宽度、长度等;文本类型包括道路的名称、级别、编码等。本文具体采用编辑距离来表达文本类型属性项语义差异,该距离是指从原字符串转换到目标字符串所需要的最少的字符插入、删除和替换的编辑次数[19];并通过数值大小比较表达数字类型属性项的语义差异。属性项语义相似性计算公式为
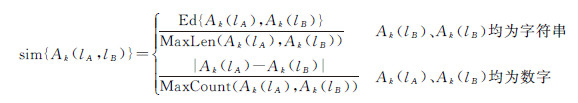 (8)
(8)
式中,Ak(lA)与Ak(lB)分别表示第k个属性项的值,当Ak(lA)与Ak(lB)不为空且为字符串时,Ed{Ak(lA),Ak(lB)}表示两者编辑距离,MaxLen(Ak(lA),Ak(lB))表示获取字符串较长者;当Ak(lA)与Ak(lB)不为空且为数字,|Ak(lA)-Ak(lB)|表示两者差值的绝对值,MaxCount(Ak(lA),Ak(lB))表示获取数值较大者。
2 SVM回归匹配模型判定道路网待匹配对之间是否匹配可被视为一种分类问题,SVM是一种基于统计学习理论的二分类模型,分类是一种特殊的回归。本文求解待匹配对之间的最优分类函数为
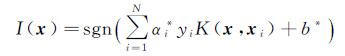 (9)
(9)
式中,N为训练样本总数;b*为分类的阈值;若xi(i=1,2,…,N)为支持向量,则αi*取值不为零;yi为xi对应的分类值;sgn(·)为符号函数;K(x,xi)为核函数;函数I(x)是支持向量机,也是最优超平面的分类规则。
本文将核函数设置为RBF类型,特征维数为3,分别为基于面积累积的形状差、综合中值Hausdorff距离、全局加权属性项距离。通过选取训练样本,统计N条待匹配对的3种相似性特征值,可构建包含N个样本的输入向量(x1,x2,x3,…,xN),通过训练可求取最优解和分类阈值等带入式(9)中确定分类函数,即可构建相应的SVM回归匹配模型。在此模型基础上进行道路匹配判别时,按照SVM最优分类规则进行分类,仅需输入任一道路待匹配对的三维特征数据到分类函数中求解I(x),所得结果只有两种,即为{1,-1},分别表示此测试数据对应的道路匹配对的匹配结果为{匹配,不匹配}。
3 试验与分析本文从相似性特征的描述能力和基于SVM回归模型的道路网匹配两方面进行对比试验验证与分析。
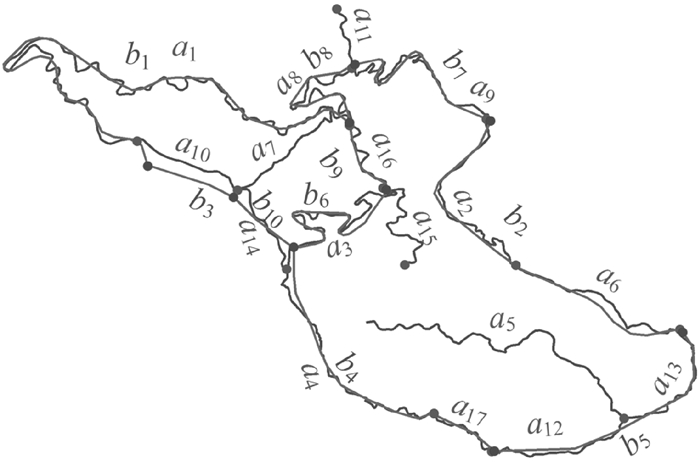
3.1 相似性特征描述能力测试对比分析 3.1.1 基于面积累积的形状差对比试验选取两份形状相对较难分辨的相邻比例尺的乡村道路网数据,如图 2所示两份数据之间存在明显的非线性差异,将面积累积形状差与文献[5]中的角度累积形状差进行对比试验,结果如表 1所示。
|
| 图 2 形状差异测试数据图 Fig. 2 Diagram of shape differences between two data sets |
| 待匹配对 | 面积累积法 | 角度累积法[5] |
| a1:b1 | 0.153 4 | 0.136 5 |
| a8:b8 | 0.073 5 | 0.09 |
| a12:b5 | 0.035 3 | 0.074 7 |
| a13:b5 | 0.025 7 | 0.057 4 |
| a14:b3 | 0.267 8 | 0.174 3 |
| a16:b6 | 1 | 1 |
| a8:b9 | 0.736 2 | 0.487 8 |
| a3:b10 | 0.686 4 | 0.556 7 |
| 注:数据均已归一化处理,粗体显示为不匹配对及其对应值。 | ||
Orn(a,b)和ADir(a,b)分别表示面积累积和角度累积[5]的计算值。从表 1中可以看出,待匹配对a16:b6在4个不匹配对的Orn(a16,b6)和ADir(a16,b6)最大,这符合a16:b6相对于其他不匹配对a14:b3、a8:b9、a3:b10的形状差异最大的事实;在待匹配对中,两对的形状结构相似,但局部特征差异相对较大的a1:b1、a8:b8其面积累积的计算值均小于角度累积的值,说明面积累积在处理锯齿线形状的描述能力要优于文献[5]中的方法。且本文面积累积法形状描述也能够处理1对多的匹配类型(表 1中a12:b5、a13:b5)。表中两组样本的方差分别是0.12和0.09,方差越大说明其描述能力越强,说明其形状描述能力比文献[5]中的角度累积法强。
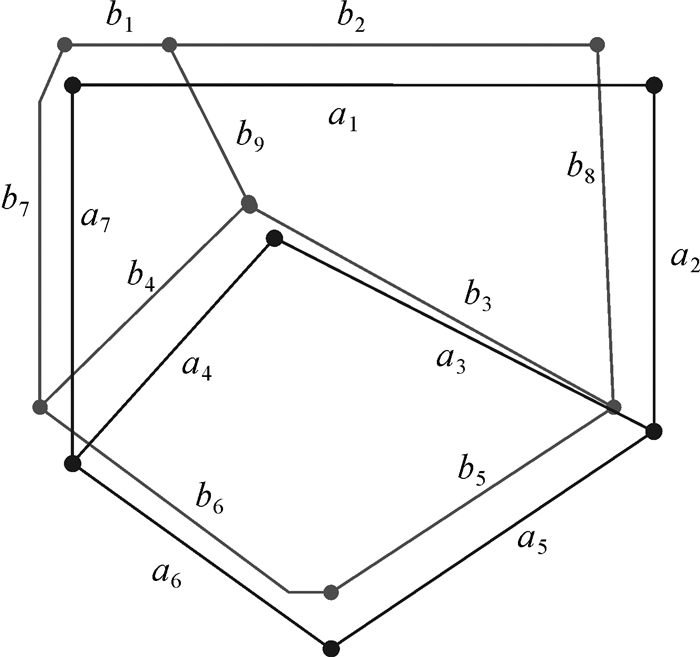
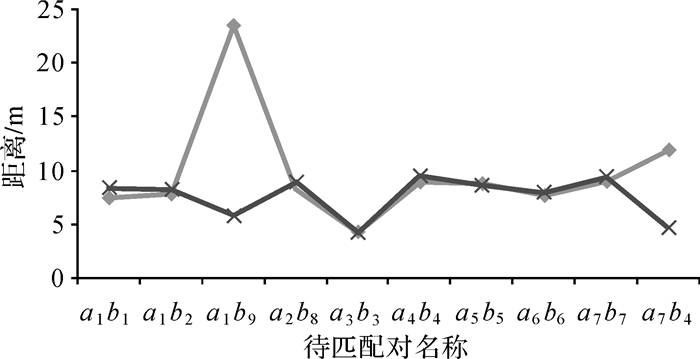
3.1.2 综合中值Hausdorff距离对比试验对如图 3所示的测试数据采用文献[16]中提出的SM_HD与本文提出的MM_HD分别进行距离对比,部分待匹配对结果如图 4所示。可以看出,在图中大部分待匹配对的距离描述上,两者的描述能力相当。但在部分待匹配对上存在明显的差异:从两组不匹配对a1:b9和a7:b4的距离结果MM_HD(a1,b9)=23.42,SM_HD(a1,b9)=5.75;MM_HD(a7,b4)=11.87,SM_HD(a7,b4)=4.64可以得出;其SM_HD和MM_HD的距离表达差异相差较大,相对较小的SM_HD距离的a1:b9和a7:b4可能在匹配预测时被错分为真匹配;而MM_HD可有效避免这种情况的发生,原因是MM_HD顾及了待匹配对中对象A的节点到对象B的线段做垂线在其延长线时可能出现的错分情况,从而使MM_HD在区分错误匹配的能力上要强于SM_HD。
|
| 图 3 距离测试数据图 Fig. 3 Diagram of distances between two data sets |
|
| 图 4 SM_HD与MM_HD的距离特征对比图 Fig. 4 Roads of the distance values between the matching pairs using the SM_HD and MM_HD |
3.1.3 全局加权属性项距离对比试验
本试验数据选自同一地区不同来源的道路网属性数据,表 2、表 3分别是两个对应数据集中部分实体属性数据,本文选取在语义差异描述方面具有代表性的复合编辑距离[20]和语义树距离[10]等两种距离与本文提出的语义距离进行对比试验。前两种距离均选取道路名称“Name”属性进行比较,给定的表 4中属性项权值依次是0.27、0.17、0.27、0.13、0.16,判定是否为同一对象的阈值为0.15。3种距离的对比结果如表 4所示。
| No. | Name | Width | Rank | Length | Way |
| a1 | 机场东路 | 55 | 2 | 0.122 | T |
| a2 | 机场东路 | 55 | 2 | 0.485 | T |
| a3 | 通顺路 | 55 | 3 | 0.333 | F |
| a4 | 通顺路 | 55 | 3 | 0.23 | F |
| a5 | 通顺路 | 55 | 3 | 0.335 | T |
| a6 | 通顺路 | 55 | 3 | 0.227 | T |
| a7 | 四纬路 | 30 | 2 | 0.234 | T |
| a8 | 四纬路 | 30 | 2 | 0.235 | F |
| a9 | 三纬路 | 30 | 2 | 0.213 | T |
| No. | Name | Width | Rank | Length | Way |
| b1 | 机场东路 | 55 | 2 | 0.6 | T |
| b2 | 龙塘路 | 55 | 2 | 1 | T |
| b3 | 通顺路 | 55 | 3 | 0.23 | F |
| b4 | 通顺路 | 55 | 3 | 0.335 | T |
| b5 | 通顺路 | 55 | 3 | 0.227 | T |
| b6 | 五纬路 | 28 | 2 | 0.247 | F |
| b7 | 四纬路 | 28 | 2 | 0.235 | F |
| b8 | 三纬路 | 28 | 2 | 0.21 | F |
| b9 | 二纬路 | 28 | 2 | 0.2423 | F |
| 待匹配对 | 复合编辑距离 | 语义树距离 | 本文 |
| a2:b1 | 0 | 0 | 0.027 |
| a3:b4 | 0 | 0 | 0.16 |
| a3:b5 | 0 | 0 | 0.173 7 |
| a4:b4 | 0 | 0 | 0.174 3 |
| a9:b8 | 0 | 0 | 0.000 5 |
| a9:b9 | 0.333 3 | 1 | 0.253 |
| 注:粗体显示为不匹配对及其对应值。 | |||
从表 4中可看出,待匹配对a9:b9中属性项“Name”的值分别为“三纬路”和“二纬路”,属性项“Way”的值分别为“T”和“F”,3种距离均能成功区分两者为不匹配。而不匹配对a3:b4、a3:b5、a4:b4的复合编辑距离和语义树距离与其他匹配对(如a2:b1)的计算值相同,导致被误判为匹配,原因是两种距离对道路网数据中道路名称相同时情况处理能力不足,未顾及属性项“Way”中信息比较导致匹配错误的发生。而它们的全局加权属性项距离分别为0.16、0.173 7、0.174 3,均大于匹配阈值,能够有效区分为不匹配。原因是本文提出的全局加权属性项距离克服了文献[20]和[10]中两种距离过于依赖单一属性项的问题,且能够综合处理数字、文本类型的属性项信息。试验可得本文提出的全局加权属性项距离的语义差异描述能力从整体上优于其他两种距离。
3.2 SVM回归匹配模型试验 3.2.1 测试数据介绍本文试验选取某省同一地区2014年基础地理数据A和2008年导航数据B进行算法试验(蓝色为数据A),两份数据由于时间跨度较大,大量道路的几何形状和属性信息发生变化,具有较好的匹配意义。数据A中包含2317个要素对象,数据B包含3606个要素对象。缓冲距离设为200 m。通过Microsoft Visual Studio 2010(C#)和ArcGIS Engine 10.1实现道路待匹配对之间的相似性计算;并通过Matlab R2010b实现样本训练、构建SVM回归匹配模型以及预测匹配结果。
首先对相似性特征数据进行格式调整和归一化等预处理;其次将数据划分为训练集和测试集两个子集,通过对训练集数据进行训练以构建SVM回归匹配模型;然后依据此模型对测试集数据的匹配结果进行预测。其中,从相似性特征数据中选取训练集数据时,需考虑被选取样本数据的普遍性、全面性、数量均衡性等方面。从而为构建SVM匹配模型提供最佳训练样本数据,保证分类精度。同样的,测试集也应当包含了各种类型的道路网待匹配对的特征数据,以更为准确的评判匹配模型的区分能力。
如表 5所示,列出了部分数据的3个相似性特征值、实际匹配结果和预测匹配结果。
| MP | Orn | MM_HD | Smn | RMR | PMR | MP | Orn | MM_HD | Smn | RMR | PMR |
| a1:b1 | 0.005 5 | 0.056 9 | 0.241 6 | 1 | 1 | a18:b2 | 0.126 4 | 0.204 3 | 0.256 7 | -1 | 1 |
| a18:b1 | 0.037 5 | 0.058 | 0.142 2 | 1 | 1 | a6:b6 | 0.041 6 | 0.063 7 | 0.268 2 | 1 | 1 |
| a18:b13 | 0.477 4 | 0.739 9 | 0.513 8 | -1 | -1 | a9:b9 | 0.052 1 | 0.073 5 | 0.192 8 | 1 | 1 |
| a2:b2 | 0.096 7 | 0.117 4 | 0.258 1 | 1 | 1 | a9:b11 | 0.540 1 | 0.788 6 | 0.280 4 | -1 | -1 |
| a3:b3 | 0.033 2 | 0.108 7 | 0.241 9 | 1 | 1 | a14:b7 | 0.015 8 | 0.767 9 | 0.467 4 | -1 | -1 |
| a15:b5 | 0.021 4 | 0.091 9 | 0.002 9 | 1 | 1 | a20:b20 | 0.160 8 | 0.290 1 | 0.010 4 | 1 | 1 |
| a4:b5 | 0.041 5 | 0.620 7 | 0.423 6 | -1 | -1 | a20:b21 | 0.790 2 | 0.897 4 | 0.402 9 | -1 | -1 |
| a10:b5 | 0.478 2 | 0.876 7 | 0.695 2 | -1 | -1 | a11:b11 | 0.040 4 | 0.136 4 | 0.120 7 | 1 | 1 |
| 注:待匹配对(matching pairs, MP)、实际匹配结果(real matched result,RMR)、预测匹配结果(predict matched result, PMR),表中特征数据均已归一化处理。 | |||||||||||
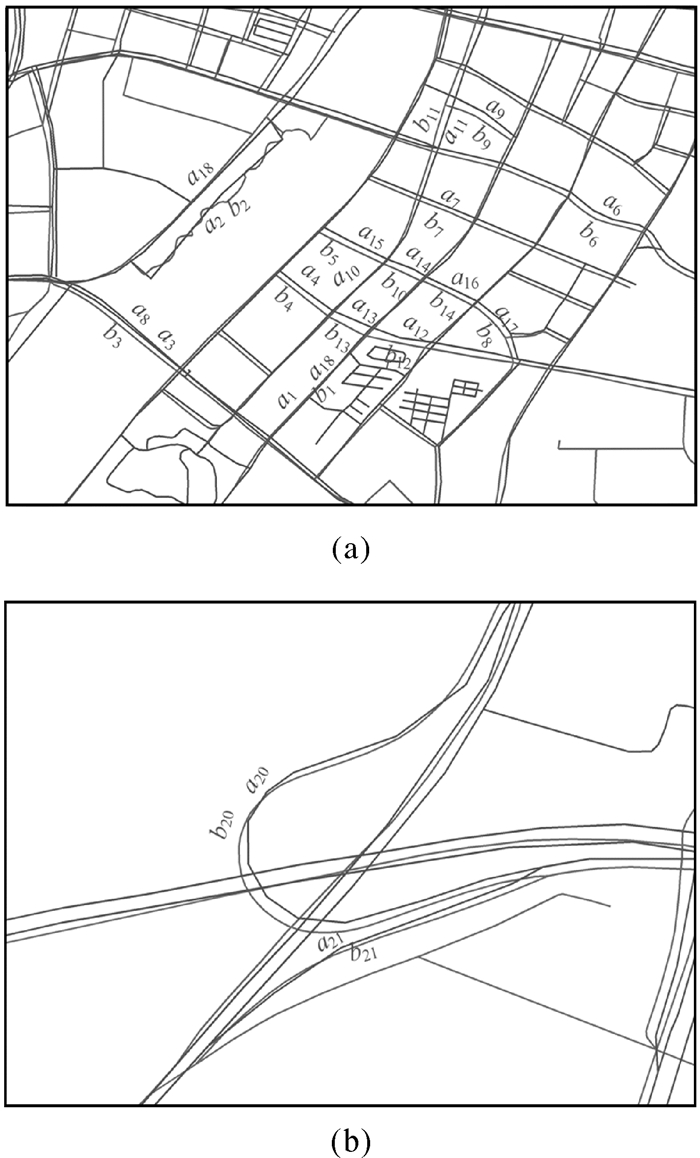
对表 5统计,本文算法的整体匹配准确率是93.0%。从表 5可以看出,除a18:b2以外,其他待匹配对的实际匹配结果与预测匹配结果相同,匹配效果良好。a18:b2匹配错误的原因是形状差和距离值不足以对其进行不匹配的划分。a2:b2的Orn(a2,b2)=0.096 7,相对于形状差异较小的匹配对(如Orn(a1,b1)=0.005 5和Orn(a3,b3)=0.033 2)要大许多,但相对于形状差异巨大的不匹配对(如Orn(a10,b5)=0.478 2和Orn(a9,b11)=0.540 1)要小很多,说明基于面积累积形状差具有良好的区分性。类似的情况还有a20:b21存在一部分的形状很相似的情况(图 5(b)所示),但Orn(a20,b21)=0.790 2很容易区分其形状差异。a11:b11和a18:b1的距离值分别为0.136 4与0.058,可以看出两个待匹配对之间地图偏移距离不同(图 5(a)),说明本文提出的综合中值Hausdorff距离能够很好描述非线性偏差情况下线对象之间的距离。另外,形状差异不大的待匹配对a14:b7,其MM_HD(a14,b7)=0.767 9,Smn(a14,b7)=0.467 4均是较大值,使得综合中值Hausdorff距离和全局加权属性项距离可进一步用于区分仅依据面积累积的形状差无法区分的待匹配对,三者相互补充,以更全面地衡量对象差异。
|
| 图 5 匹配实例 Fig. 5 Matching examples |
3.2.2 算法对比试验分析
本文的道路网匹配算法设计中,在相似性特征和匹配算法两个部分均做了改进,为验证各部分在匹配精度提升上的贡献差异,选取logistic回归模型和文献[16]中的SM_HD特征进行两两组合试验(如表 6中第2、3列所示),测试数据仍然为数据A和数据B,表 6中f(C)、f(W)和f(U)分别表示正确匹配、错误匹配和漏匹配的数量,P、R和耗时分别为准确率、召回率和算法耗时方面的比较结果。
分析表 6可得,本文算法(第3组合)由于对道路网匹配采用了3种较好的相似性描述方法和SVM回归匹配算法,在匹配准确率P和回归率R均优于其他3种组合。其中,第3组合相比于第1组合的优势较小,说明本文提出的相似性特征比匹配模型的贡献大。本文算法相比于文献[16]算法(第2组合)在匹配准确率P和回归率R上有了一定的提升,说明本文算法比文献[16]算法中单纯采用SM_HD特征与logistic回归模型对道路网匹配更加有效。从组合2和组合4可以看出,基于SVM回归匹配模型的匹配结果要优于基于logistic回归匹配模型。原因是SVM寻求最优超平面的原理,虽然使得其复杂度稍高于logistic回归,导致更耗时,但在分类精度要更高,与优化的3种相似性特征结合,在道路网匹配中能实现高精度的匹配。
4 结 论本文通过设计3种有效的道路相似性特征,并结合SVM回归模型构建具有高精度的道路网匹配模型。通过试验论证,得出以下结论:①多特征的优化不仅使得每个相似性特征具有较强的特征差异描述能力,三者结合可实现差异互补,整体具有更强的识别能力。再结合区分能力强的SVM分类算法,使得构建的道路网匹配模型的匹配精度和召回率更高。②无须设定相似性特征之间权值和匹配阈值,使得匹配算法自动化水平得到一定提升。
本文算法仍存在定的不足之处:基于面积累积的形状差方法对局部差异描述的能力相对较弱;SVM回归匹配模型算法复杂度较高,使得耗时较长,降低了匹配效率。这些问题将是下一步研究的重点。
| [1] |
安晓亚, 孙群, 肖强, 等. 一种形状多级描述方法及在多尺度空间数据几何相似性度量中的应用[J].测绘学报,2011, 40 (4) : 495 –501 .
AN Xiaoya, SUN Qun, XIAO Qiang, et al. A Shape Multilevel Description Method and Application in Measuring Geometry Similarity of Multi-scale Spatial Data[J]. Acta Geodaetica et Cartographica Sinica,2011, 40 (4) : 495 –501 . |
| [2] | SAALFELD A. Conflation Automated Map Compilation[J]. International Journal of Geographical Information Systems,1988, 2 (3) : 217 –228 . |
| [3] | LI Linna, GOODCHILD M F. An Optimisation Model for Linear Feature Matching in Geographical Data Conflation[J]. International Journal of Image and Data Fusion,2011, 2 (4) : 309 –328 . |
| [4] | DENG Min, LI Zhilin, CHEN Xiaoyong. Extended Hausdorff Distance for Spatial Objects in GIS[J]. International Journal of Geographical Information Science,2007, 21 (4) : 459 –475 . |
| [5] | YANG Bisheng, ZHANG Yunfei, LUAN Xuechen. A Probabilistic Relaxation Approach for Matching Road Networks[J]. International Journal of Geographical Information Science,2013, 27 (2) : 319 –338 . |
| [6] | SAFRA E, KANZA Y, SAGIV Y, et al. Ad Hoc Matching of Vectorial Road Networks[J]. International Journal of Geographical Information Science,2013, 27 (1) : 114 –153 . |
| [7] |
安晓亚, 孙群, 尉伯虎. 利用相似性度量的不同比例尺地图数据网状要素匹配算法[J].武汉大学学报(信息科学版),2012, 37 (2) : 224 –228 .
AN Xiaoya, SUN Qun, YU Bohu. Feature Matching from Network Data at Different Scales Based on Similarity Measure[J]. Geomatics and Information Science of Wuhan University,2012, 37 (2) : 224 –228 . |
| [8] | RODRÍGUEZ M A, EGENHOFER M J. Comparing Geospatial Entity Classes: An Asymmetric and Context-Dependent Similarity Measure[J]. International Journal of Geographical Information Science,2004, 18 (3) : 229 –256 . |
| [9] | MUSTIÈRE S, DEVOGELE T. Matching Networks with Different Levels of Detail[J]. GeoInformatica,2008, 12 (4) : 435 –453 . |
| [10] |
罗国玮, 张新长, 齐立新, 等. 矢量数据变化对象的快速定位与最优组合匹配方法[J].测绘学报,2014, 43 (12) : 1285 –1292 .DOI:10.13485/j.cnki.11-2089.2014.0191.
LUO Guowei, ZHANG Xingchang, QI Lixin, et al. The Fast Positioning and Optimal Combination Matching Method of Change Vector Object[J]. Acta Geodaetica et Cartographica Sinica,2014, 43 (12) : 1285 –1292 .DOI:10.13485/j.cnki.11-2089.2014.0191. |
| [11] |
栾学晨, 杨必胜, 李秋萍. 基于结构模式的道路网节点匹配方法[J].测绘学报,2013, 42 (4) : 608 –614 .
LUAN Xuechen, YANG Bisheng, LI Qiuping. Pattern-based Node Matching Approach for Road Networks[J]. Acta Geodaetica et Cartographica Sinica,2013, 42 (4) : 608 –614 . |
| [12] | WALTER V, FRITSCH D. Matching Spatial Data Sets: A Statistical Approach[J]. International Journal of Geographical Information Science,1999, 13 (5) : 445 –473 . |
| [13] |
巩现勇, 武芳, 姬存伟, 等. 道路网匹配的蚁群算法求解模型[J].武汉大学学报(信息科学版),2014, 39 (2) : 191 –195 .
GONG Xianyong, WU Fang, JI Cunwei, et al. Ant Colony Optimization Approach to Road Network Matching[J]. Geomatics and Information Science of Wuhan University,2014, 39 (2) : 191 –195 . |
| [14] |
张云菲, 杨必胜, 栾学晨. 利用概率松弛法的城市路网自动匹配[J].测绘学报,2012, 41 (6) : 933 –939 .
ZHANG Yunfei, YANG Bisheng, LUAN Xuechen. Automated Matching Urban Road Networks Using Probabilistic Relaxation[J]. Acta Geodaetica et Cartographica Sinica,2012, 41 (6) : 933 –939 . |
| [15] |
赵东保, 盛业华. 全局寻优的矢量道路网自动匹配方法研究[J].测绘学报,2010, 39 (4) : 416 –421 .
ZHAO Dongbao, SHENG Yehua. Research on Automatic Matching of Vector Road Networks Based on Global Optimization[J]. Acta Geodaetica et Cartographica Sinica,2010, 39 (4) : 416 –421 . |
| [16] | TONG Xiaohua, LIANG Dan, JIN Yanmin. A Linear Road Object Matching Method for Conflation Based on Optimization and Logistic Regression[J]. International Journal of Geographical Information Science,2014, 28 (4) : 824 –846 . |
| [17] | YUAN Shuxin, TAO Chuang. Development of Conflation Components[C]//Proceedings of Geoinformatics’99 Conference. Ann Arbor: [s.n.], 1999: 1-13. |
| [18] | VOLZ S. An Iterative Approach for Matching Multiple Representations of Street Data[C]//Proceedings of the ISPRS Workshop on Multiple Representation and Interoperability of Spatial Data. Hanover: ISPRS, 2006: 101-110. |
| [19] | NAVARRO G. A Guided Tour to Approximate String Matching[J]. ACM Computing Surveys,2001, 33 (1) : 31 –88 . |
| [20] |
刁兴春, 谭明超, 曹建军. 一种融合多种编辑距离的字符串相似度计算方法[J].计算机应用研究,2010, 27 (12) : 4523 –4525 .
DIAO Xingchun, TAN Mingchao, CAO Jianjun. New Method of Character String Similarity Compute Based on Fusing Multiple Edit Distances[J]. Application Research of Computers,2010, 27 (12) : 4523 –4525 . |



