2. 中国测绘科学研究院,北京 100830
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China
与胶片式传统航空摄影测量相比,基于数字相机的航空摄影测量具有成图周期短、精度高、天气要求低等优点,已成为地形测量的主要方法之一。随着计算机和CCD等技术的快速发展,国际市场已出现了多款成熟的大面阵高分辨率数字相机产品。具有实时性和数字化特点的数字相机正逐渐取代传统的胶片式相机成为获取航空摄影测量数据的重要设备。由于地形测量精度的要求,航测相机本身需要较高的精度,但数字相机不是专门为摄影测量而设计制造的,它的内方位元素未知,并存在光学畸变差等缺陷。因此,在开展摄影测量工作前,必须对数字相机进行精确几何标定,这是数字航空摄影测量的基础性工作之一[1-2]。
非量测数字相机的几何标定方法主要有实验场标定法和实验室标定法[3-5]。
实验场标定法分为室内实验场法[6-9]、室外实验场法[10]和飞行实验场法[11-13]。实验场标定法的原理通常建立在共线方程的基础上,实验场可以是三维场、二维场,甚至是纯平液晶显示器等,一般由一定数量已知精确坐标的标志点组成。利用待标定相机获取实验场影像后,可依据直接线性变换、单片空间后方交会、光束法平差、区域网空中三角测量或者自检校等方法来解算内方位元素及几何畸变参数,包括光学畸变差、胶片变形(或CCD器件内部变形)、底片压平(或CCD器件表面不平整)等。
实验室标定法通常基于测角法的原理,并以多筒固定准直仪或可转动的精密测角仪器为基本设备[14]。传统胶片航测相机几何标定时需要在相机的承片框上安置一个精密网格板,调整相机入瞳中心与测角仪器的转轴重合,通过网格板来观测像点位置,并利用网格板上的格值计算像场角,再结合测角仪器测得的入射角就可以计算出相机的内方位元素和畸变。
由于实验室标定法的标定过程中要利用相机标定的专门设备,并且整个标定工作都在实验室内进行,标定条件可控,标定过程标准规范。国内一些科研院所也积极开展了非量测数字相机实验室标定方法的研究[15-17],但尚未有成熟完善实验室标定系统的报道。本文基于测角法的原理以及数字相机的特点,研制出一套实用的非量测数字相机几何标定系统。该系统以精密测角仪器为基本设备,可以实现面阵数字相机的精确几何标定。采用两种典型数字相机进行试验,验证了该系统的正确性以及精度。
1 几何标定系统原理及数据处理 1.1 系统组成及数据获取数字相机实验室几何标定系统主要包括转臂及其控制系统和编码器、相机支架及其控制系统和编码器、计算机系统(工控机)、平行光管等,该系统的主体如图 1所示,对应的结构原理如图 2所示。

|
| 图 1 系统主体 Fig. 1 Principal part of system |

|
| 图 2 系统结构原理 Fig. 2 Structural principle of system |
转臂的编码器位于几何标定系统转臂的内部,工控机通过串口与该编码器通讯,控制转臂的转动并获取转臂的角度值;平行光管位于转臂的内部,用于提供一个无穷远的点目标,通过转臂的旋转就可以提供一系列带有精确角度值的无穷远点目标。此外,工控机通过串口与相机支架的编码器通讯,控制相机支架的水平旋转并获取对应的旋转角度。
该系统具有测量速度快,受环境变化影响小,测量精度高等优点,其技术特点如下:
(1) 标定时,相机镜头朝下,与工作状态一致,标定结果可信。
(2) 转臂由电机驱动,速度快,定位精度好。
(3) 转臂的转动范围可达±45°,可实现视场角达90°的大面阵数字相机的几何标定。
(4) 采用基于数字化测量方式的轴角编码器,角度测量误差小,精度可达1″。
(5) 计算机进行测量过程的控制和数据处理,自动化程度高,使用方便。
面阵数字相机几何标定时,把相机安装固定在相机支架上,使相机的入瞳通过转臂的转轴中心。然后,由相机获取由平行光管形成的无穷远点目标的图像,并通过相机支架调平螺杆的调整和相机支架的旋转,使转臂在转动过程中,目标像始终位于CCD靶面的中心行上,再通过转臂的转动,使得目标像位于CCD靶面中心行的中心像素,并将对应的转臂角度设置为0°。根据被测相机的幅宽及焦距等参数,设置测量时转臂转动的角度范围及间隔,当转臂每转动到一个目标角度时,将相机对无穷远点目标成像,同时,软件记录下相应的转臂角度值。测完一个方向后,将相机旋转90°,按照同样的方法测量中心列方向,进而完成几何标定的数据获取。
1.2 数据处理数字相机几何标定的数据处理主要包括两个部分:目标像的高精度定位与几何标定参数的计算。
1.2.1 目标像的高精度定位数字相机的几何标定,需要精确地测量出目标像在CCD像面上的位置(位置精度一般要求在0.1像素以内),以保证几何标定结果的精度。为实施目标像的亚像素定位,要求目标像不是单个像素点,而是由有明显灰度变化一系列像素点组成,如圆点、角点、十字交叉点等。根据目标图像数据的不同,提高目标像点测量精度的算法主要有形心法、质心法、边缘检测法等[18-19]。
根据本文几何标定系统的特点,本文提出了质心法细分定位与多帧统计法相结合的方案来实现目标像的高精度定位。该方案的流程如下:
(1) 自动确定阈值。为实现目标像的高精度定位,需要首先提取出目标像,将目标像与背景、噪声等区分开来。采用迭代法计算出最佳阈值[19],并将图像中灰度值大于阈值的点作为目标的候选点。
(2) 确定目标像范围。从图像中灰度值最大的像素出发,采用区域增长的算法,搜索出邻域中所有灰度值大于阈值的点,确定出目标像的范围。
(3) 质心法细分定位。为实现目标像的高精度定位,在传统质心法的基础上,一方面采用双线性插值法对原目标像进行插值处理,增加可利用的点,提高目标像中心坐标计算的精度和稳定性。另一方面,为了突出灰度值大的像素对中心定位的作用,提高其权值比重,将传统灰度质心法的线性关系改为非线性关系[20]。
(4) 多帧统计。考虑到数字相机对无穷远点目标成像时可能产生的误差,采用同一位置多次成像的方法获取像点目标的多张图像,对每张图像分别采用(1)-(3)的方法对目标像进行定位,并将其均值作为目标像的最终位置,进一步提高目标像的定位精度。
1.2.2 几何标定参数计算数字相机几何标定的内容是确定相机的内方位元素、镜头的光学畸变参数及CCD面阵内变形系数等[2]。其中,相机的内方位元素包括主距f和主点坐标(x0,y0),镜头的光学畸变参数主要包括径向畸变系数k0、k1、k2、k3和偏心畸变系数p1、p2,CCD面阵内变形系数主要包括比例尺系数b1、修剪系数b2等。
1.2.2.1 内方位元素的计算基于测角法原理的相机内方位元素的计算,就是根据像点坐标数据和对应的角度数据,寻找一种内方位元素的计算方法,使得相机的畸变符合一定的约束条件。不同的计算方法会得到不同的内方位元素和畸变。常用的方法有平均值法、畸变平方和最小算法、威特厂计算方法1和威特厂计算方法2[21]。其中,威特厂计算方法2考虑最为全面,精度最高,但威特厂的两种方法需要镜头的“标准畸变曲线”,而普通数字相机并没有这样的“标准畸变曲线”。由于畸变平方和最小算法的计算结果能保证求得的系统主点、主距能使该系统视场范围内的畸变平方和最小,最有利于测绘精度的提高,因此本文选用畸变平方和最小算法[21-25]。
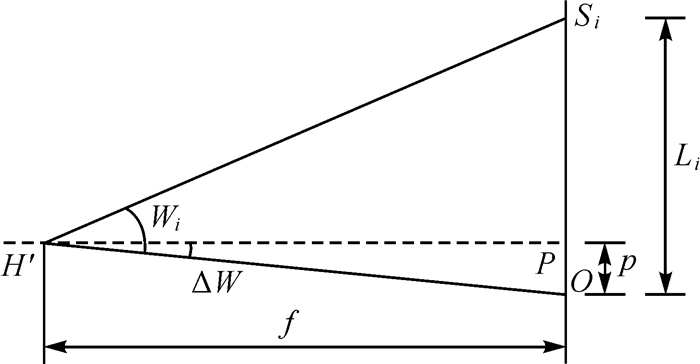
测角法测量数字相机一维畸变和内方位元素的原理如图 3所示,P为像面主点位置,角度ΔW为对应P点的角度,H′为物镜的后节点,O为CCD面阵的中心,f为主距,Si为被测点,Li为Si距像面中心O点的距离,Wi为对应Si点的测角。
|
| 图 3 最小二乘法一维内方位元素和畸变测量原理 Fig. 3 Measurement principle of one-dimensional interior orientation elements and distortions based on the least squares |
根据图 3中的几何关系有
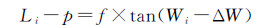 (1)
(1)
根据相机畸变的定义,对应Si点的畸变Di为
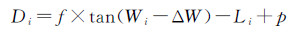 (2)
(2)
式中,ΔW是物镜后节点与主点的连线和物镜后节点与像面中心连线间的夹角,而主点的偏移量一般很小,所以ΔW是小量,近似有
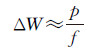 (3)
(3)
因此,tan(Wi-ΔW)项可以用泰勒公式近似
 (4)
(4)
简化后得到相机一维畸变的普遍表达式
 (5)
(5)
由式(5)可知,Li通过对像片进行数据处理得到,Wi由测量得到,而需要求解的未知数有f、p和Di 3个。为了求解这3个未知量,笔者测量像面上一系列的点,按照畸变的平方和最小的约束条件,就可以通过最小二乘法求解出主距f和主点坐标p。欲使畸变的平方和最小∑Di2=min,应有
 (6)
(6)
经整理,最终得到主距、主点的表达式
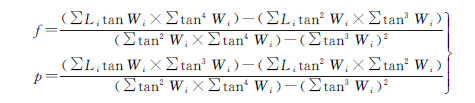 (7)
(7)
根据式(7)以及列方向(X方向)和行方向(Y方向)的量测数据,就可以分别解算出被测相机的主距fx和列方向的主点偏移px以及主距fy和行方向的主点偏移py。考虑到数字相机通常在X和Y方向视场大小的不同,应以视场角较大的方向计算出的主距作为相机最终的主距。
1.2.2.2 畸变参数的计算在1.2.2.1节中计算出内方位元素后,可由式(8)计算出每个测量点的畸变值Di
 (8)
(8)
为达到对畸变校正的目的,采用畸变模型对畸变值进行拟合,本文采用的畸变模型为
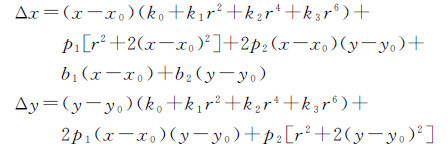 (9)
(9)
根据一系列测量点的畸变值,按照最小二乘原理进行间接平差,计算出各个畸变参数k0、k1、k2、k3、p1、p2、b1、b2。
2 试验与分析本文基于VC++6.0开发了非量测数字相机实验室几何标定软件,主要功能包括硬件控制、目标像的高精度定位、相机的内方位元素和畸变参数的计算等。为验证本文方法的正确性,采用当前国内摄影测量常用的两种典型数字相机--佳能EOS 5D Mark Ⅱ和哈苏H3D,进行试验并对试验结果进行分析。
2.1 试 验 2.1.1 几何标定试验试验相机1的类型为佳能EOS 5D Mark Ⅱ,标称焦距24 mm,像元尺寸0.006 4 mm,像幅尺寸5616×3744像素。试验相机2的类型为哈苏H3D,标称焦距为50 mm,像元尺寸0.006 8 mm,像幅尺寸为7216×5412像素。根据相机的参数信息,设置相机1的测量角度范围为列方向±34°,行方向±24°,步距为2°,设置相机2的测量角度范围为列方向±22°,行方向为±17°,步距为1°,按本文方法采集数据并解算得到两个相机的内方位元素及各畸变参数见表 1。图 4和图 5分别是相机1畸变拟合前、后的畸变,图 6和图 7分别是相机2畸变拟合前、后的畸变,其中,X轴为测量点在以CCD中心为原点的像素坐标系中的列方向或行方向坐标,Y轴为测量点在列方向或行方向上的畸变值。
| 参数 | 试验相机1 | 试验相机2 | ||
| 标定参数 | 中误差 | 标定参数 | 中误差 | |
| f/mm | 23.846 | 0.001 | 50.234 | 0.001 |
| x0/像素 | 14.997 | 0.102 | -35.530 | 0.078 |
| y0/像素 | -9.521 | 0.083 | -13.487 | 0.081 |
| k0 | -1.942 17e-002 | 7.254 6e-004 | -2.123 68e-004 | 6.147 6e-006 |
| k1 | 1.796 01e-004 | 8.193 4e-008 | 2.284 74e-006 | 5.294 3e-009 |
| k2 | -2.435 46e-007 | 4.068 3e-010 | -8.584 07e-009 | 3.450 9e-012 |
| k3 | -1.951 63e-010 | 6.437 6e-013 | 6.437 61e-013 | 4.217 3e-016 |
| p1 | -1.999 95e-005 | 1.631 4e-007 | -9.695 24e-007 | 2.492 5e-009 |
| p2 | 3.573 94e-006 | 1.221 6e-008 | -2.726 21e-008 | 3.178 8e-010 |
| b1 | 7.614 76e-005 | 2.048 7e-007 | 1.797 43-004 | 1.204 6e-007 |
| b2 | 3.127 68e-003 | 2.063 5e-005 | -9.682 28e-004 | 1.648 1e-006 |
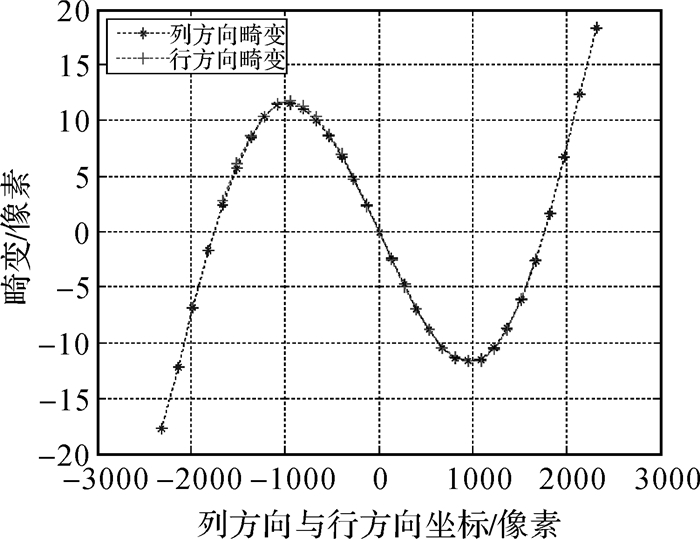
|
| 图 4 相机1内方位计算后列/行方向的畸变 Fig. 4 Distortion in column/line after calculation of interior orientation elements of camera 1 |

|
| 图 5 相机1畸变拟合后列/行方向的畸变 Fig. 5 Distortion in column/line after fitting of camera 1 |
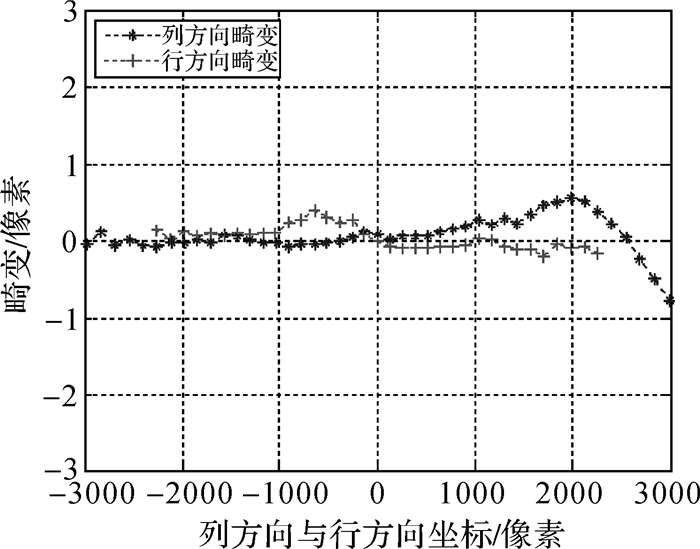
|
| 图 6 相机2内方位计算后列/行方向的畸变 Fig. 6 Distortion in column/line after calculation of interior orientation elements of camera 2 |

|
| 图 7 相机2畸变拟合后列/行方向的畸变 Fig. 7 Distortion in column/line after fitting of camera 2 |
根据最小二乘精度估计方法,畸变拟合结果的标准差为
 (10)
(10)
式中,vi为畸变拟合后的剩余误差;t为未知量个数,这里t=8;n为独立的等精度测量次数,这里相机1试验中n=60,相机2试验中n=80。按式(10)计算,相机1拟合结果的中误差为0.198像素,相机2拟合结果的中误差为0.166像素。
2.1.2 可靠性验证为验证标定结果的可靠性,利用试验相机1作了近景摄影测量试验。试验场选定为某家属楼(图 8),该楼高约30 m,宽约100 m,由电梯、走廊、墙体等构成了多个层次的立体结构。该家属楼上布设有数百个间隔为1.5~2.5 m的控制点标志,用全站仪采用测回法测定了各控制点的坐标,点位精度优于2 mm。利用试验相机1,在拍摄距离约为45 m处(与焦距相比,可视为无穷远),从不同位置、不同高度和不同角度共拍摄了60张影像。数据采集之后,用标定所得参数对影像进行畸变差改正,并将改正后的影像等数据导入到全数字摄影测量工作站JX-4中,在测区范围内选取了9个均匀分布的标志点作为控制点,进行绝对定向。然后选择其中的一个立体像对,在立体模式下采集了影像中137个标志点的三维坐标,并与对应的全站仪测量的坐标作差,利用坐标差Δ,根据公式
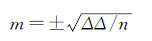 (11)
(11)

|
| 图 8 可靠性验证试验场 Fig. 8 Test field of reliability verification |
计算x、y、z的中误差,结果如下
 (12)
(12)
点位中误差为
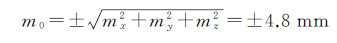 (13)
(13)
(1) 表 1表明,相机几何标定得到的主距、主点位置与标称焦距、主点位置有明显差异,这也说明了数字相机几何标定的必要性。
(2) 图 4中,相机1的两个方向上都存在着明显的畸变,每个方向上的畸变与像点到主点的距离有明显的对称性,而且两个方向上的畸变的规律基本一致,有典型的径向畸变。从图 5可以看出,经过畸变模型拟合后,两个方向上的剩余畸变明显减小,中误差在0.2像素左右,这表明了本文畸变模型的正确性。
(3) 图 6表明,相机2的畸变相对较小,最大偏差约为0.8像素,没有明显的径向畸变。从图 7可以看出,经过本文畸变模型拟合后,两个方向上的残余畸变略有减小。
(4) 从相机1与相机2的畸变拟合前的结果来看,相机1的几何畸变最大值约为20像素,而相机2的几何畸变最大值约为1个像素。因此,相机2的几何成像质量要显著优于相机1。
(5) 可靠性验证试验表明,利用根据标定结果改正后的影像进行近景摄影测量,相对中误差约为1/10 000,结果精度非常高,这进一步验证了相机标定的可靠性。
3 结 论数字相机的几何标定是其在摄影测量中应用的基础。本文构建了一套非量测数字相机实验室几何标定系统,详细介绍了该系统的组成原理及目标像的高精度定位、几何标定参数的计算等数据处理中的关键技术,并采用两种相机进行了试验与分析。试验结果表明:该系统能够实现多种类型面阵数字相机的精确几何标定,结果具有可靠性。
随着科学技术的发展以及多面阵组合数字相机在覆盖面大等方面的优势,越来越多的多面阵组合数字相机应用到摄影测量中,例如DMC、UCD和SWDC4等。这类相机在普通面阵相机几何标定的基础上,还需要标定多面阵相机之间的几何关系。下一步将针对多面阵相机的几何标定开展研究,为多面阵组合数字相机在摄影测量中的应用提供技术支撑。
| [1] |
程效军, 胡敏捷. 数字相机畸变差的检测[J].测绘学报,2002, 31 : 113 –117 .
CHENG Xiaojun, HU Minjie. The Determination of Digital Camera’s Distortion[J]. Acta Geodaetica et Cartographica Sinica,2002, 31 : 113 –117 . |
| [2] |
王留召.小型数字航空摄影测量系统[D].昆明:昆明理工大学, 2006. WANG Liuzhao. Small-scale Digital Aerial Photography Measuring System[D]. Kunming: Kunming University of Science and Technology, 2006. |
| [3] | CLARKE T A, FRYER J G. The Development of Camera Calibration Methods and Models[J]. The Photogrammetric Record,1998, 16 (91) : 51 –66 . |
| [4] |
冯文灏.
近景摄影测量[M]. 武汉: 武汉大学出版社, 2002 .
FENG Wenhao. Close Range Photogrammetry[M]. Wuhan: Wuhan University Press, 2002 . |
| [5] | REMONDINO F, FRASER C. Digital Camera Calibration Methods: Considerations and Comparisons[J]. Institute of Photogrammetry and Remote Sensing,2006, 36 (5) : 266 –272 . |
| [6] | WENG J, COHEN P, HERNIOU M. Camera Calibration with Distortion Models and Accuracy Evaluation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1992, 14 (10) : 965 –980 . |
| [7] | FRASER C S, SHORTIS M R, GANCI G. Multi-sensor System Self-calibration[C]//EL-HAKIM S F. Proceedings of SPIE 2598. Philadelphia: SPIE, 1995: 2-15. |
| [8] | WU Bo, HU Han, ZHU Qing, et al. A Flexible Method for Zoom Lens Calibration and Modeling Using a Planar Checkerboard[J]. Photogrammetric Engineering & Remote Sensing,2013, 79 (6) : 555 –571 . |
| [9] |
詹总谦.基于纯平液晶显示器的相机标定方法与应用研究[D].武汉:武汉大学, 2006. ZHAN Zongqian. Research on Camera Calibration Based on Completely Flat Liquid Crystal Display[D]. Wuhan: Wuhan University, 2006. |
| [10] |
张建霞, 王留召, 刘先林, 等. 数字航空摄影测量的相机检校[J].测绘通报,2005 (11) : 41 –42 .
ZHANG Jianxia, WANG Liuzhao, LIU Xianlin, et al. Camera Calibration for Digital Air Survey[J]. Bulletin of Surveying and Mapping,2005 (11) : 41 –42 . |
| [11] |
王冬红.机载数字传感器几何标定的模型与算法研究[D].郑州:信息工程大学, 2011. WANG Donghong. A Study on the Mathematic Model and Algorithm of the Geometric Calibration of Airborne Digital Sensor[D]. Zhengzhou: Information Engineering University, 2011. |
| [12] |
王涛, 张永生, 张艳, 等. 基于自检校的机载线阵CCD传感器几何标定[J].测绘学报,2012, 41 (3) : 393 –400 .
WANG Tao, ZHANG Yongsheng, ZHANG Yan, et al. Airborne Linear CCD Sensor Geometric Calibration Based on Self-calibration[J]. Acta Geodaetica et Cartographica Sinica,2012, 41 (3) : 393 –400 . |
| [13] |
杨韫澜.摄影测量自检校技术研究[D].西安:长安大学, 2015. YANG Yunlan. Study on the Self-calibration Technology in Photogrammetry[D]. Xi’an: Chang’an University, 2015. |
| [14] | SLY W E. The Calibration of Aerial Survey Cameras[J]. The Photogrammetric Record,1968, 6 (31) : 59 –74 . |
| [15] |
吴国栋, 韩冰, 何煦. 精密测角法的线阵CCD相机几何参数实验室标定方法[J].光学精密工程,2007, 15 (10) : 1628 –1632 .
WU Guodong, HAN Bing, HE Xu. Calibration of Geometric Parameters of Line-array CCD Camera Based on Exact Measuring Angle in Lab[J]. Optics and Precision Engineering,2007, 15 (10) : 1628 –1632 . |
| [16] |
刘金国. 大视场光电测量系统的精密几何标定和畸变校正的研究[J].光学精密工程,1994, 2 (4) : 109 –120 .
LIU Jinguo. Study on High Accurate Geometric Calibration of Precision Photoelectronic Measuring System with Large Field of View and Distortion Correcting[J]. Optics and Precision Engineering,1994, 2 (4) : 109 –120 . |
| [17] |
黄静, 高晓东, 马文礼, 等. 大面阵数字航测相机的精密几何标定[J].光电工程,2006, 33 (2) : 138 –140 .
HUANG Jing, GAO Xiaodong, MA Wenli, et al. Accurate Geometric Calibration of Large Resolution Digital Aerial Survey Camera[J]. Opto-Electronic Engineering,2006, 33 (2) : 138 –140 . |
| [18] |
李玉峰, 郝志航. 星点图像超精度亚像元细分定位算法的研究[J].光学技术,2005, 31 (5) : 666 –668 .
LI Yufeng, HAO Zhihang. Research of Hyper Accuracy Subpixel Subdivision Location Algorithm for Star Image[J]. Optical Technique,2005, 31 (5) : 666 –668 . |
| [19] |
周红锋, 宫爱玲. 图像中CCD光斑中心的亚像素定位研究[J].计量技术,2007 (11) : 21 –23 .
ZHOU Hongfeng, GONG Ailing. Research on Sub-pixel Location of CCD Spot Center in Image[J]. Measurement Technique,2007 (11) : 21 –23 . |
| [20] |
陶珺, 张霞. 光纤传感系统中光斑中心亚像素定位算法[J].计算机工程,2010, 36 (19) : 31 –33 .
TAO Jun, ZHANG Xia. Orientation Algorithm of Light-spot Center Subpiexl in Fiber Sensing System[J]. Computer Engineering,2010, 36 (19) : 31 –33 . |
| [21] |
邹勇平, 徐水平, 李月锋, 等. 实验室检定航摄相机内方位元素和畸变差计算方法的比较[J].测绘技术装备,2006, 8 (1) : 37 –38 .
ZOU Yongping, XU Shuiping, LI Yuefeng, et al. Calculating Approach Comparison of Interior Orientation Elements and Lens Distortion of an Aerial Metric Camera Inspected in Laboratory[J]. Geomatics Technology and Equipment,2006, 8 (1) : 37 –38 . |
| [22] |
邹勇平, 缪剑. 数字航测相机的实验室检定与摄影检校[J].测绘通报,2010 (12) : 4 –6 .
ZOU Yongping, MIAO Jian. Laboratory Calibration and Photographic Calibration of the Digital Airborne Mapping Camera[J]. Bulletin of Surveying and Mapping,2010 (12) : 4 –6 . |
| [23] |
刘波, 贾继强, 丁亚林. 基于测角法的CCD航测相机实验室几何标定[J].激光与红外,2010, 40 (3) : 298 –301 .
LIU Bo, JIA Jiqiang, DING Yalin. Geometric Calibration with Angle Measure for CCD Aerial Photogrammetric Camera in Laboratory[J]. Laser & Infrared,2010, 40 (3) : 298 –301 . |
| [24] |
王之卓.
摄影测量原理[M]. 武汉: 武汉大学出版社, 2007 .
WANG Zhizhuo. Principle of Photogrammetry[M]. Wuhan: Wuhan University Press, 2007 . |
| [25] |
张祖勋, 张剑清.
数字摄影测量学[M]. 武汉: 武汉大学出版社, 2002 .
ZHANG Zuxun, ZHANG Jianqing. Digital Photogrammetry[M]. Wuhan: Wuhan University Press, 2002 . |


