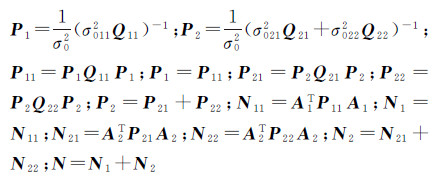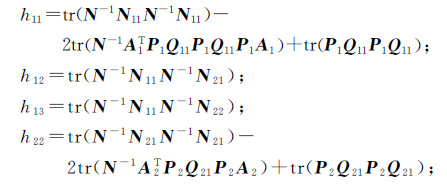2. 中国测绘科学研究院,北京 100039
2. Chinese Academy of Surveying and Mapping,Beijing 100039,China
合成孔径雷达干涉测量(interferometric synthetic aperture radar,InSAR)是一种获取大规模、高精度数字高程模型(digital elevation model,DEM)的有效手段。它利用干涉相位信息能够高精度地反演地形信息,具备全天时、全天候的测量能力,广泛应用于地形测绘领域[1]。
利用InSAR系统进行地形测绘时,需要在干涉处理时采用高精度的干涉参数,干涉参数包括基线长度、基线倾角和相位偏置等,这些干涉参数的标定过程通常称为干涉参数定标。对于大区域的地形测绘,单个像对的InSAR数据干涉参数定标至少需要3个地面控制点。这种单个像对数据逐套处理的方式效率较低,对控制点的需求量较大,并且由于干涉参数定标误差的存在,不同干涉数据会在接边处出现较大的反演高程差异,导致DEM拼接的困难。基于区域网平差的InSAR干涉参数定标,能整体答解整个区域内所有像对的干涉参数,只需要在区域内合理布置少量的控制点,由于平差过程中使用到了重叠处的连接点数据,接边处的反演高程差异能大幅削减[2-3]。正是由于这些原因,基于区域网平差的InSAR干涉参数定标受到了较为广泛的关注。2000年,文献[4]指出利用干涉相位、斜距、多普勒中心频移、轨道参数以及控制点数据可以进行基于最小二乘平差的InSAR地理编码;2002年,文献[5-6]建立了一种交叉轨道数据干涉定标方法,并且推断这种方法能够适用于多条带的干涉SAR数据定标。本课题组先后于2008年和2010年开展了基于区域网平差的InSAR干涉参数定标方法研究,提出了顾及基线长度、基线倾角和相位偏置的InSAR区域网平差干涉参数定标方法[2]。中国科学院电子学研究所和中国测绘科学院等单位在区域网平差干涉参数定标方面也开展了大量研究。2009年,文献[7]进行了大区域稀疏控制条件下的多条带InSAR数据的联合定标研究;2010年,文献[8]通过在联合定标处理中引入加权处理,实现控制点的权重分配,提出了一种基于特征点权重的机载InSAR系统区域网干涉参数定标方法;文献[9]依据相位误差和位置分布不同而导致的各点处高程反演误差的差异对控制点和同名点加权,建立了基于加权最优化模型的机载InSAR联合定标算法;文献[10]通过自动提取连接点,实现了InSAR区域网内多景相互重叠DEM的同时重建;文献[11-12]介绍了一种适用于大区域稀疏控制点下的机载InSAR定标方法并给出了连接点的选取方法;2012年,文献[13]利用区域内稀疏控制点完成了多航带机载InSAR定标;2013年,文献[14]提出了一种稀少控制下机载InSAR区域网联合地理编码方法,文献[15]将PSInSAR中PS点选取的方法引入高程连接点的选取中,设计了一种新的机载双天线InSAR联合定标算法。
InSAR区域网平差定标干涉参数,各误差方程中观测值的权比常常以先验知识给出,设定权值最为简单的方法是均取为1,也可以基于误差传播定律,考虑各个观测值观测分量的误差传播来定权,但是观测分量的方差仍然需要根据先验知识给出,文献[7]和文献[8]给出了利用相位误差和位置分布等先验信息确定权比的方法。由于控制数据以及图像数据本身误差的存在,观测值确定权比时,若只考虑各套干涉数据生成DEM的精度,则各DEM拼接处的高程差异较大,导致DEM拼接精度低;若在区域网平差中过分顾及拼接精度,则生成的DEM精度会下降。上述利用先验知识确定权比的方法具有一定的主观性,并不能保证各观测值权比合理。如果观测值权比不合理,便不能合理顾及DEM的生成精度和拼接精度。
为了研究机载InSAR区域网平差干涉参数定标权值理论,设计相应的InSAR区域网平差干涉参数定标权值确定方法,本文引入验后方差分量估计的思想[16],在利用先验知识给出各方差分量初值的基础上,以提高整体平差精度或者其他约束条件为原则,在平差过程中不断迭代优化方差分量,直到权比合理。验后方差分量估计的方法较多[17-21],在一些特殊条件下各种方法往往是等价的[22-24]。Helmert方差分量估计应用较为广泛[25-26],文献[27-29]分别给出了Helmert方差分量估计的简化公式或近似公式。本文根据InSAR区域网平差干涉参数定标模型的特点,设计了Helmert方差分量估计扩展模型,给出了机载InSAR区域网平差干涉参数定标的定权方案。利用我国机载双天线InSAR数据进行干涉参数定标试验,试验结果表明本文方法能较好给定机载InSAR区域网平差干涉参数定标模型权值,合理顾及DEM的生成精度和拼接精度,验证了机载InSAR区域网平差干涉参数定标权值理论的正确性和可行性。
1 机载InSAR区域网平差干涉参数定标原理机载InSAR区域网平差干涉参数定标是根据InSAR测高原理,利用整个区域内的控制点数据和相邻干涉像对接边处的连接点数据列误差方程式,由最小二乘原理平差答解干涉像对的干涉定标参数(基线长度、基线倾角和相位偏置)和连接点高程值[2]。
根据InSAR测高的原理
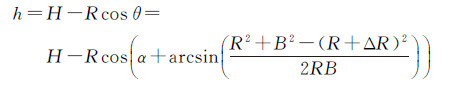 (1)
(1)
式中,h为目标高度;H为主天线高度;R为目标与主天线距离;θ为雷达侧视角;α为基线倾角;B为基线长度;ΔR为目标与主从天线距离差,对于机载双天线InSAR系统,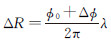
由式(1)可得控制点误差方程式(2)
 (2)
(2)
连接点误差方程式(3)
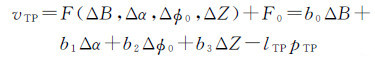 (3)
(3)
式(2)和式(3)中,ΔB、Δα、Δφ0和ΔZ分别为基线长度、基线倾角、相位偏置和地面点高程值的改正数;b0、b1、b2和b3为对应的系数;vGCP、lGCP和pGCP为控制点误差方程式的改正数、观测值和权值;vTP、lTP和pTP为连接点误差方程式的改正数、观测值和权值。
将控制点误差方程式和连接点误差方程式分别表示为矩阵形式,得到InSAR区域网平差误差方程的矩阵形式为
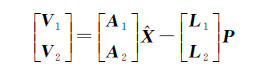 (4)
(4)
式中,V1、A1和L1为控制点误差方程式的改正数向量、设计矩阵和观测值向量;V2、A2和L2为连接点误差方程式的改正数向量、设计矩阵和观测值向量;P为权矩阵。式(4)中各项具体内容参见文献[2]。
2 利用Helmert方差分量估计的InSAR区域网平差权值确定方法在式(4)给出的机载InSAR区域网平差干涉参数定标模型中,控制点观测值可以看作像点距离向坐标y、像点的解缠相位Δφ,两个观测分量的函数;连接点观测值可以认为像点距离向坐标y、像点的解缠相位Δφ以及对应的连接点高程值Z,三个观测分量的函数。基于Helmert方差分量估计原理,可以在区域网平差中估计误差方程观测值的方差,Helmert方差分量估计模型可以参见文献[24],但是利用该模型不能直接估计出观测分量的方差。为了得到每个观测分量的方差分量估计值,需要使用扩展的Helmert方差分量模型。
扩展的Helmert方差分量估计模型[25]仍然遵循Helmert方差分量估计的基本原理,但是在原有模型中考虑各观测分量的误差传播规律。由于Helmert方差分量估计模型中方差分量的估值较容易出现负值,导致方差分量估计无法进行。扩展的Helmert方差分量的模型中,如果考虑InSAR区域网平差函数模型中方差分量的误差传播,像点解缠相位Δφ观测分量的误差传播系数远远大于其他的观测分量,估计过程中将该观测分量纳入估计模型,很容易出现负的方差分量估值,并且控制点和连接点观测值均包含像点距离向坐标y和像点的解缠相位Δφ观测分量,忽略像点的解缠相位Δφ观测分量,能降低计算的复杂度,同时保证整体平差的精度,避免估计的分量过多而出现不收敛的状况。
考虑像点距离向坐标y和连接点高程值Z的观测值的协方差矩阵可以表示为
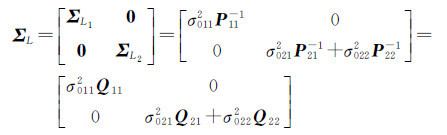 (5)
(5)
式中,第1类观测值包含一个观测分量,第2类观测值包含两个观测分量。ΣLi为两类观测值的协方差矩阵;σ0ij2、Pij、Qij为第i类观测值第j个观测分量的方差分量、权矩阵和权逆阵(i,j=1,2)。
法化误差方程式(4),法方程为
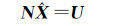 (6)
(6)
式中
误差方程的解为
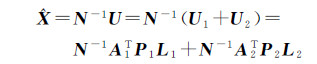 (7)
(7)
带入原始误差方程式(4)中
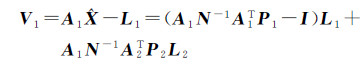 (8a)
(8a)
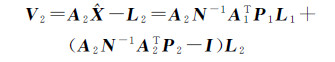 (8b)
(8b)
由协方差的传播定律及式(9a)和(9b)得
 (9a)
(9a)
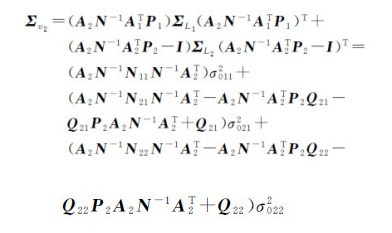 (9b)
(9b)
式中
则有
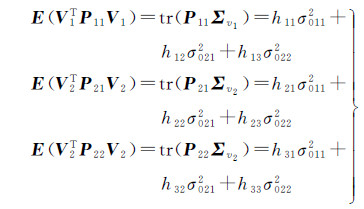 (10)
(10)
式中,hij=hji(i,j=1,2,3),且有
控制点和连接点的像点距离向坐标y是在相同条件下获取的,因此控制点和连接点观测值中,该观测分量的方差分量应该相等,即在式(10)中,有
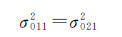 (11)
(11)
则有
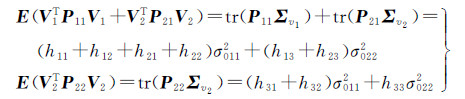 (12)
(12)
式(12)中去掉期望,σ0112和σ0222用其估计值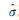
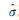
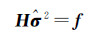 (13)
(13)
即有
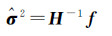 (14)
(14)
简化公式为
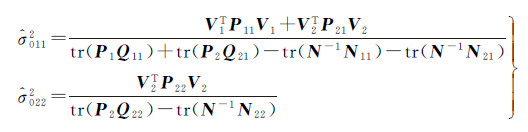 (15)
(15)
利用式(15),并注意σ0112=σ0212,可以对误差方程式中各观测分量的方差分量进行估计。扩展模型能够直接估计像点距离向坐标y和连接点高程值Z的方差分量。
基于扩展Helmert方差分量估计模型的InSAR区域网平差干涉参数定标的一般流程为:
(1) 平差数据的获取,包括控制点和连接点观测数据的获取、待定标的干涉参数初值的确定以及待估计的方差分量初值的确定。
(2) 将间接观测值分为两类,即控制点观测值和连接点观测值,并给定方差分量初值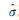
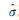
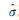
(3) 进行第1次平差解算,求解出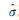
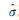
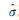
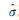
(4) 重复步骤(3),遵循先平差,再进行方差分量估计的步骤,直至各类观测值的方差分量估计值相等为止,即第k次的结果满足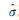
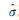
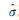
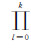
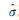
(5) 检查平差计算是否收敛,判断解算的干涉参数改正数和连接点高程改正数是否小于一定的限差,如果满足限差条件,则迭代结束并输出平差结果,否则重复步骤(3)。
3 试 验本文采用中国科学院电子研究所机载InSAR系统获取的多套干涉数据进行干涉参数定标试验。控制数据采用差分GPS实测方式获取,InSAR系统的部分参数如表 1所示。
| 参数类型 | 参数值 |
| 波长/m | 0.031 2 |
| 波段 | X |
| 方位向分辨率/m | 1.1 |
| 距离向分辨率/m | 1.25 |
| 近距延迟/m | 6 699.5 |
| 绝对航高/m | 6 190.0 |
| 多普勒中心频率/Hz | 0 |
| 极化方式 | HH |
试验采用两条相邻航带上的4套InSAR数据,003片和004片为同一航带中的相邻数据块,103片和104片为另一航带中的相邻数据块。表 2所示为各套数据中控制点和连接点的数量。在试验区内,控制点分布较为均匀,连接点则集中分布在多套InSAR数据的接边处,图 1和图 2分别为控制点和连接点在InSAR数据强度图上的分布。

|
| 图 1 控制点分布 Fig. 1 Distribution of ground control points |

|
| 图 2 连接点分布 Fig. 2 Distribution of tie points |
4套InSAR数据的解缠相位如图 3所示。

|
| 图 3 解缠相位 Fig. 3 Phase unwrapping |
从图 3可以看出,在InSAR数据中间部分,数据质量较好,在近距端和远距端,4套数据质量均较差,103片部分区域数据存在明显问题。
采用本文给出的权值确定方法进行InSAR区域网平差干涉参数定标试验,若未进行方差分量估计,一般认为各个观测分量为等精度观测,本文试验中将距离向坐标y的方差分量σ0112(σ0112=σ0212)和连接点高程值Z的方差分量σ0222之比σ0112/σ0222初始设为1。设计如下3种InSAR区域网平差干涉参数定标方案。
方案1:基于扩展的Helmert方差分量估计模型严密公式。
方案2:基于扩展的Helmert方差分量估计模型简化公式。
方案3:不进行方差分量估计。
方案1和方案2的迭代过程如表 3所示,表中数据显示了迭代过程观测值或观测分量的方差分量比。
| 迭代 | σ0112/σ0222 | |
| 方案1 | 方案2 | |
| 1 | 4.780/0.164 | 4.053/0.943 |
| 2 | 4.382/0.564 | 4.083/0.911 |
| 3 | 4.543/0.398 | 4.117/0.875 |
| 4 | 4.515/0.427 | 4.147/0.843 |
| 5 | 4.520/0.422 | 4.174/0.814 |
| 6 | 4.520/0.423 | 4.198/0.789 |
| 7 | 4.519/0.422 | 4.220/0.766 |
| 最终 | 4.519/0.422 | 4.549/0.425 |
| 比值 | 10.708 | 10.703 |
| 迭代次数 | 11 | 260 |
从表 3可以看出,经过多次迭代,Helmert方差分量估计模型和扩展模型的严密公式和简化公式达到最终收敛条件的方差分量比值基本相同,说明了严密公式和简化公式的等效性。
采用上述3种方案计算的干涉参数反演连接点高程,反演的高程值与实测的控制点高程值的差异,即高程误差的情况如表 4和图 4所示,两片重叠处的反演高程差异如表 5和图 5所示,3片重叠处的反演高程差异如表 6和图 6所示。
| m | ||
| 点号 | 连接点高程误差 | |
| 方案1/2 | 方案3 | |
| 1 | 2.819 | 2.814 |
| 2 | 1.249 | 1.245 |
| 3 | 1.217 | 1.214 |
| 4 | 1.121 | 1.118 |
| 6 | 2.435 | 2.430 |
| 7 | 3.735 | 3.730 |
| 8 | 2.686 | 2.681 |
| 9 | 2.913 | 2.908 |
| 10 | 2.819 | 2.814 |
| 11 | 3.478 | 3.472 |
| 12 | 0.991 | 0.988 |
| 13 | 1.358 | 1.354 |
| 15 | -1.460 | -1.457 |
| 16 | 1.343 | 1.310 |
| 18 | 3.876 | 3.832 |
| 19 | 3.971 | 3.931 |
| 20 | 3.485 | 3.452 |
| 21 | 1.595 | 1.581 |
| 23 | 2.204 | 2.215 |
| 25 | 1.215 | 1.226 |
| 26 | -2.192 | -2.207 |
| 27 | -2.568 | -2.585 |
| 28 | -2.656 | -2.673 |
| 31 | 0.264 | 0.270 |
| 33 | -3.958 | -3.942 3 |
| 34 | -4.267 | -4.251 |
| 35 | -3.006 | -2.990 |
| 36 | -5.295 | -5.277 |
| 37 | -4.675 | -4.658 |
| 68 | 5.298 | 5.296 |
| 105 | -4.228 | -4.212 |
| 平均值 | 0.508 | 0.385 |
| 标准差 | 3.025 | 2.816 |

|
| 图 4 连接点高程误差 Fig. 4 Heights’ errors on tie points |
| m | ||
| 点号 | 连接点高程反演差异 | |
| 方案1/2 | 方案3 | |
| 1 | -1.785 | -1.860 |
| 2 | 3.373 | 3.415 |
| 3 | 6.198 | 6.241 |
| 4 | -2.049 | -1.991 |
| 6 | -3.125 | -3.171 |
| 7 | -4.169 | -4.304 |
| 8 | -6.088 | -6.151 |
| 9 | -5.062 | -5.142 |
| 10 | 3.134 | 3.057 |
| 11 | -7.340 | -7.456 |
| 12 | -5.101 | -5.031 |
| 13 | 1.394 | 1.429 |
| 16 | -1.387 | -1.376 |
| 18 | -1.806 | -1.784 |
| 19 | -1.847 | -1.786 |
| 20 | 1.412 | 1.519 |
| 21 | 3.807 | 4.020 |
| 26 | -1.254 | -1.200 |
| 27 | -2.910 | -2.888 |
| 28 | -1.772 | -1.765 |
| 31 | 1.332 | 1.252 |
| 33 | -5.391 | -5.541 |
| 34 | -1.843 | -1.944 |
| 35 | 2.489 | 2.191 |
| 36 | -8.679 | -8.649 |
| 37 | 4.464 | 4.419 |
| 68 | 2.164 | 2.250 |
| 105 | 2.511 | 2.225 |
| 平均值 | -1.040 | -1.072 |
| 标准差 | 3.746 | 3.760 |
|
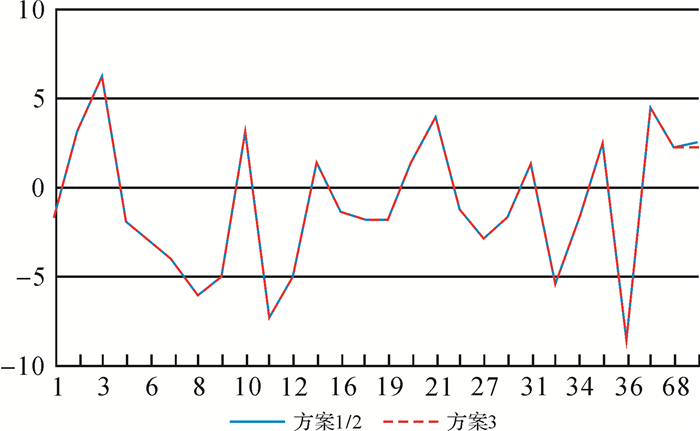
| 图 5 两片重叠处连接点高程反演差异 Fig. 5 Heights’ differences on tie points in overlap of two pairs |
| 点号 | 重叠片号 | 连接点高程反演差异/m | |
| 方案1/2 | 方案3 | ||
| 15 | 003-103 | 15.364 | 15.439 |
| 103-104 | -0.778 | -0.664 | |
| 003-104 | 14.586 | 14.774 | |
| 23 | 003-004 | -0.351 | -0.093 |
| 004-104 | -2.357 | -2.686 | |
| 003-104 | -2.708 | -2.779 | |
| 25 | 003-004 | 7.940 | 8.183 |
| 004-104 | -11.543 | -11.788 | |
| 003-104 | -3.603 | -3.605 | |
| 平均值 | 1.838 | 1.864 | |
| 标准差 | 8.639 | 8.762 | |
|
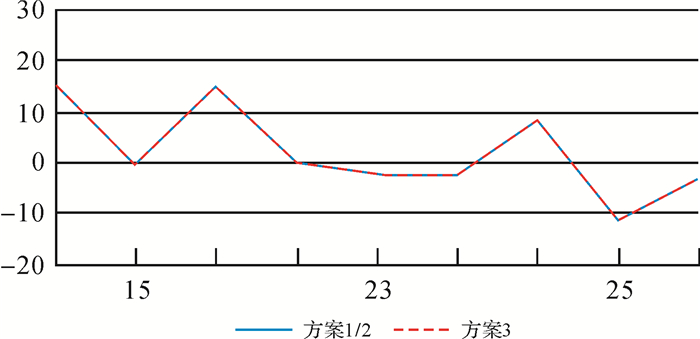
| 图 6 3片重叠处连接点高程反演差异 Fig. 6 Heights’ differences on TPs for three blocks of data overlap |
从表 4-表 6和图 4-图 6可以看出,在方差分量比σ0112/σ0222初始设为1的条件下,相比利用扩展的Helmert方差分量估计定权的方案,未采用方差分量估计的方案连接点处高程误差较小,说明生成DEM的精度较高,但是该方案的连接点反演高程差异较大,会导致DEM拼接困难,因此需要找到合理的方差分量比值,以确定误差方程的权值。
给定不同的初始方差分量比值σ0112/σ0222,连接点处的高程误差标准差如表 7所示,两片重叠处和3片重叠处的反演高程差异标准差如表 8所示。
| 方差分量比 | 方案1/2 | 方案3 |
| 1 | 3.025 | 2.816 |
| 4 | 3.025 | 2.953 |
| 9 | 3.025 | 3.015 |
| 16 | 3.025 | 3.043 |
| 方差分量比 | 方案1/2 | 方案3 |
| 1 | 3.746 | 3.826 |
| 8.639 | 9.093 | |
| 4 | 3.746 | 3.760 |
| 8.639 | 8.762 | |
| 9 | 3.746 | 3.747 |
| 8.639 | 8.654 | |
| 16 | 3.746 | 3.743 |
| 8.639 | 8.610 |
从表 7和表 8可以看出,随着σ0112/σ0222的变化,方案3的高程误差标准差逐渐增大而反演高程差异标准差逐渐减小,方案1和方案2则这两个指标都未发生变化并且保持在适当的数值,说明使用扩展的方差分量估计模型的方案能合理的顾及DEM精度和其拼接处的连接问题,平差的稳定性较好。
4 结 论InSAR区域网平差干涉参数定标过程中,观测方程的权值确定一直以先验的方式给出,若对数据的精度估计不合理,则难以给定适当的平差权值,使平差结果难以同时顾及DEM生成精度和拼接精度。本文基于扩展的Helmert方差分量估计模型,设计了相应的权值确定方案。扩展的Helmert方差分量估计模型,能够估计每类观测分量的方差,并且给定适当的平差权值,合理地考虑了DEM生成精度和DEM拼接精度。
采用扩展的Helmert方差分量估计模型进行估计时,模型的简化计算方法收敛速度较慢,迭代次数较多,造成计算耗时较大,后续的研究需要分析扩展模型中系数矩阵H的结构,设计合理的简化方案,缩短方差分量估计的时间。
| [1] |
靳国旺, 徐青, 张红敏.
合成孔径雷达干涉测量[M]. 北京: 国防工业出版社, 2014 .
JIN Guowang, XU Qing, ZHANG Hongmin. Synthetic Aperture Radar Interferometry[M]. Beijing: National Defense Industry Press, 2014 . |
| [2] |
靳国旺, 吴一戎, 向茂生, 等. 基于区域网平差的InSAR基线估计方法[J].测绘学报,2011, 40 (5) : 616 –622 .
JIN Guowang, WU Yirong, XIANG Maosheng, et al. Baseline Estimation Algorithm of InSAR with Block Adjustment[J]. Acta Geodaetica et Cartographica Sinica,2011, 40 (5) : 616 –622 . |
| [3] | LI Yinwei, XIANG Maosheng, LV Xiaolei, et al. Joint Interferometric Calibration Based on Block Adjustment for an Airborne Dual-antenna InSAR System[J]. International Journal of Remote Sensing,2014, 35 (17) : 6444 –6468 . |
| [4] | HELLWICH O, EBNER H. Geocoding SAR Interferograms by Least Squares Adjustment[J]. ISPRS Journal of Photogrammetry and Remote Sensing,2000, 55 (4) : 277 –288 . |
| [5] | DALL J, CHRISTENSENEL. Interferometric Calibration with Natural Distributed Targets[C]//Proceedings of IEEE International Geoscience and Remote Sensing Symposium. Toronto: IEEE, 2002: 170-172. |
| [6] | DALL J. Cross-Calibration of Interferometric SAR Data[J]. IEEE Proceedings: Radar, Sonar and Navigation,2003, 150 (3) : 177 –183 . |
| [7] |
张薇.机载双天线干涉SAR定标方法研究[D].北京:中国科学院电子学研究所, 2009. ZHANG Wei. Airborne Dual-antenna InSAR’s Interferometric Calibration Method Research[D]. Beijing: Institute of Electrics, Chinese Academy of Sciences, 2009. |
| [8] |
韩松涛, 向茂生. 一种基于特征点权重的机载InSAR系统区域网干涉参数定标方法[J].电子与信息学报,2010, 32 (5) : 1244 –1247 .
HAN Songtao, XIANG Maosheng. A Bundle Adjustment Calibration Method for Airborne InSAR System Based on Weighting of Feature Points[J]. Journal of Electronics & Information Technology,2010, 32 (5) : 1244 –1247 . |
| [9] |
毛永飞, 向茂生. 基于加权最优化模型的机载InSAR联合定标算法[J].电子与信息学报,2011, 33 (12) : 2819 –2824 .
MAO Yongfei, XIANG Maosheng. Joint Calibration of Airborne Interferometric SAR Data Using Weighted Optimization Method[J]. Journal of Electronics & Information Technology,2011, 33 (12) : 2819 –2824 . |
| [10] |
姜丽敏, 陈曙暄, 向茂生. 一种基于连接点的机载InSAR区域网DEM重建方法[J].电子与信息学报,2011, 33 (11) : 2694 –2701 .
JIANG Limin, CHEN Shuxuan, XIANG Maosheng. A Method for Airborne InSAR Block DEM Generation Based on Tie Points[J]. Journal of Electronics & Information Technology,2011, 33 (11) : 2694 –2701 . |
| [11] |
胡继伟, 洪峻, 明峰, 等. 一种适用于大区域稀疏控制点下的机载InSAR定标方法[J].电子与信息学报,2011, 33 (8) : 1792 –1797 .
HU Jiwei, HONG Jun, MING Feng, et al. A Calibration Method for Airborne InSAR Applied to Large Areas with Sparse GCPs[J]. Journal of Electronics & Information Technology,2011, 33 (8) : 1792 –1797 . |
| [12] |
胡继伟, 洪峻, 明峰, 等. 基于模型的稀疏控制点下机载InSAR定标中CP连接点选取方法[J].雷达学报,2012, 1 (4) : 441 –445 .
HU Jiwei, HONG Jun, MING Feng, et al. Model-based CP Selection Method for Calibration of Airborne InSAR with Sparse GCPs[J]. Journal of Radars,2012, 1 (4) : 441 –445 . |
| [13] |
张林涛, 洪峻, 明峰, 等. 利用稀疏GCP的多航摄条带机载InSAR定标方法[J].中国科学院研究生院学报,2012, 29 (3) : 377 –383 .
ZHANG Lintao, HONG Jun, MING Feng, et al. Interferometric Calibration Method of Multi-strip Airborne InSAR Data Using Sparse GCPs[J]. Journal of Graduate University of Chinese Academy of Sciences,2012, 29 (3) : 377 –383 . |
| [14] |
黄国满, 杨书成, 王宁娜, 等. 稀少控制下机载InSAR区域网联合地理编码方法[J].测绘学报,2013, 42 (3) : 397 –403 .
HUANG Guoman, YANG Shucheng, WANG Ningna, et al. Block Combined Geocoding of Airborne InSAR with Sparse GCPs[J]. Acta Geodaetica et Cartographica Sinica,2013, 42 (3) : 397 –403 . |
| [15] |
王萌萌, 黄国满, 花奋奋, 等. 机载双天线InSAR联合定标算法[J].测绘学报,2014, 43 (12) : 1259 –1265 .DOI:10.13485/j.cnki.11-2089.2014.0139.
WANG Mengmeng, HUANG Guoman, HUA Fenfen, et al. Joint Calibration Method of Airborne Dual-antenna Interferometric SAR[J]. Acta Geodaetica et Cartographica Sinica,2014, 43 (12) : 1259 –1265 .DOI:10.13485/j.cnki.11-2089.2014.0139. |
| [16] | HELMERT F R. Die Ausgleichungsrechnung Nach Der Methode Der Kleinsten Quadrate[M]. Leipzig: Zweiteauflage, 1907 . |
| [17] | FORSTNER W. Konvergenzbeschleunigung Bei Der a Posteriori Varianzenschatzung[J]. ZFV,1979, 104 (4) : 149 –156 . |
| [18] | GRAFAREND E. Variance-covariance-component Estimation of Helmert Type in the Gauss-Helmert Model[J]. ZFV,1984, 109 (1) : 34 –44 . |
| [19] | RAO C R. Estimation of Variance and Covariance Components-MINQUE Theory[J]. Journal of Multivariate Analysis,1971, 1 (3) : 257 –275 . |
| [20] | CROCETTON, GATTI M, RUSSO P. Simplified Formulae for the BIQUE Estimation of Variance Components in Disjunctive Observation Groups[J]. Journal of Geodesy,2000, 74 (6) : 447 –457 . |
| [21] | SJÖBERGL E. Unbiased Estimation of Variance-covariance Components in Condition Adjustment with Unknowns: A MINQUE Approach[J]. ZFV,1983, 108 (9) : 382 –387 . |
| [22] | KUBIK K. The Estimation of tWeights of Measured Quantities within the Method of Least Squares[J]. Bulletin Géodésique,1970, 95 (1) : 21 –40 . |
| [23] | YAVUZ E, BAYKAL O, ERSOY N. Comparison of Variance Component Estimation Methods for Horizontal Control Networks[J]. International Journal of the Physical Sciences,2011, 6 (6) : 1317 –1324 . |
| [24] |
于宗俦. 方差-协方差分量估计的统一理论[J].测绘学报,1991, 20 (3) : 161 –171 .
YU Zongchou. The Uniformity Theory of Estimation of Variance-covariance Components[J]. Acta Geodaetica et Cartographic Sinica,1991, 20 (3) : 161 –171 . |
| [25] |
刘长建, 柴洪洲, 吴洪举, 等. 扩展的Helmert型方差分量估计公式[J].测绘学报,2008, 37 (1) : 1 –4 .
LIU Changjian, CHAI Hongzhou, WU Hongju, et al. Extended Formulae of Helmert Type for Estimating Variance Components[J]. Acta Geodaetica et Cartographica Sinica,2008, 37 (1) : 1 –4 . |
| [26] |
张万鹏. 方差分量估计理论及其在边角网平差中的应用[J].武汉测绘科技大学学报,1988, 13 (1) : 9 –21 .
ZHANG Wanpeng. Estimation of Variance Components and Its Application in Direction-distance Network Adjustment[J]. Journal of Wuhan Technical University of Surveying and Mapping,1988, 13 (1) : 9 –21 . |
| [27] |
於宗俦. Helmert型方差—协方差分量估计的通用公式[J].武汉测绘科技大学学报,1991, 16 (2) : 8 –17 .
YU Zongchou. The Goneral Formulas of Helmert Type for Estimating Variance and Covarince Caomponents[J]. Journal of Wuhan Technical University of Surveying and Mapping,1991, 16 (2) : 8 –17 . |
| [28] | WELSCH W. A Posteriori Varianzenschatzung Nach Helmert[J]. AVN,1978, 85 (2) : 55 –63 . |
| [29] | EBNER H. A Posteriori Varianzenschatzungfur Die Koordinat-en Unabhangiger Modelle[J]. ZFV,1972, 97 (4) : 166 –173 . |