2. 湖南科技学院土木与环境工程学院,湖南 永州 425199
2. School of Civil and Environmental Engineering, Hunan University of Science and Engineering, Yongzhou 425199, China
在InSAR数据处理中,干涉图的质量直接关系到数字高程模型的高程精度和地表形变监测[1]的精度,而干涉图往往受到热噪声、时空去相关、多普勒中心频率失相关[2]等因素的影响,含有大量噪声,因此有必要对干涉图相位滤波,为后续相位解缠以及保证地表形变监测精度奠定基础。目前,用于干涉图滤波的方法有很多种,现有的干涉图像滤波方法主要分为频率域滤波、空间域滤波和时频域滤波。经典频率域滤波为Goldstein滤波[3],算法简单,得到了广泛应用。Goldstein算法虽然能滤除大部分噪声,但也会丢失大量边缘信息,给数字高程模型(DEM)和测量形变带来误差。文献[4-6]在Goldstein算法基础上又提出了改进算法,这些算法主要是调整了滤波因子,使干涉图滤波效果有所改善。空间域滤波有代表性的是Lee滤波。Lee滤波[7]通过局部解缠,估计中心像素邻域内的坡度并改善中心像素,但局部解缠计算复杂、费时且目视效果差。此外,空间域滤波还发展了复数空间自适应滤波[8]、最优方向融合滤波[9]、数学形态法[10]、EMD自适应滤波[11]等方法,文献[8]在梯度计算时只考虑了水平和垂直方向,文献[12]进行了改进,有更强的自适应性。文献[9]的最优方向融合滤波结合相干性选择线性方向窗口滤波,增强了Lee算法的稳健性。数学形态法[10]在Lee滤波中进行膨胀腐蚀得到边缘,增强了边缘信息,但强噪区滤波效果有待提高。EMD自适应滤波[11]根据信号和噪声经验模态分解后表现的不同特征再进行自适应滤波,但尺度函数和IMF滤波个数的确定计算复杂。干涉图空间域和频率域滤波是以干涉相位的频率特性时不变或统计特性平稳为前提的,但实际干涉信号经常出现非平稳性[9],因此对其进行空间域或频率域滤波时得不到理想的滤波结果,可以把空间域与频率域分析结合起来,采用时(空)频分析方法对干涉图进行滤波处理,以便于提高精度,增强滤波效果。目前时频分析滤波方法主要小波滤波方法等。文献[13]提出矢量分离式小波软阈值滤波方法,能有效地保持干涉图中的相位信息。文献[14]提出对各个方向高频系数对应方向的边缘位置先平滑后再作中值滤波,很好地保持了图像的边缘特征。文献[15]提出采用小波维纳滤波对相位滤波,能更有效地滤除噪声,然其多次进行的小波维纳滤波,使滤波后的干涉图产生了块状效应。文献[16]将双树复小波用于干涉图去噪,去除了噪声还保持了干涉图的细节纹理信息,但在滤波函数模型中没有考虑复小波系数为复数的情况,丢失了虚部信息,导致信号相位噪声的增加影响滤波效果。
本文用复小波进行干涉图滤波,有其特殊的优越性。首先文献[17]已证明干涉相位噪声是加性的,而含加性噪声的干涉图经小波变换后,小波系数服从高斯分布,这决定了基于小波变换的干涉图滤波具有一定的优越性。其次是双树复小波(DC-CWT)除具有一般小波的优点外,还具有近似平移不变性、有限冗余性、良好的方向选择性和完全重构性等特点,具有提高精度和保留图像细节信息等优点,比实数小波滤波更有优势。
一种好的滤波方法除了变换的方法具备良好的性能外,还应该对变换系数有一个好的统计以及好的系数修改算法,而双变量贝叶斯估计算法正满足此要求。本文将复小波变换与双变量收缩函数相结合,给出了表达复噪声系数实部与虚部的相关性的概率密度函数,推导了复噪声系数概率密度函数、分解系数与其父节点系数的联合概率密度函数、复数域双变量收缩函数过程,给出了含噪信号小波复系数方差、噪声方差等,把双变量模型干涉图滤波函数模型从实数域推广到了复数域,得到了不错的效果。
1 复小波变换和复数域双变量模型干涉图滤波算法 1.1 复小波变换复小波变换是通过两个或多个实小波变换平行对信号处理,一维双树复小波变换表示为[18]
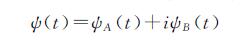 (1)
(1)
对于二维双树复小波变换
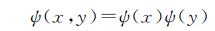 (2)
(2)
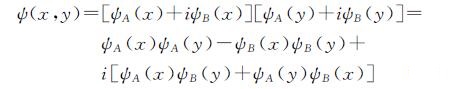 (3)
(3)
双树复小波在分解二维信号时,分别对二维数据的行和列进行变换,每一级分解出两个低频部分和6个高频细节部分,比二维实数小波变换多了3个方向,且由于干涉图中的噪声为加性噪声,含加性噪声的干涉图经小波变换后,其信号小波系数能量主要集中在低频子带,噪声小波系数主要反映在高频子带上,并且高频小波系数服从高斯正态分布,而双变量贝叶斯估计算法针对高频小波系数服从于高斯正态分布,给出了一个好的系数修改方法[19]。因此,将双树复小波变换与双变量贝叶斯估计算法相结合是一种不错的滤波方法,该方法更适用于干涉图滤波,更有利于干涉图干涉条纹边缘等细节信息的保留与检测。
1.2 复数域双变量贝叶斯估计算法经研究发现,图像经小波分解后,不同尺度间有很大的相关性,而双变量模型则在充分挖掘图像小波系数的尺度内、尺度间相关性的基础上,采用非高斯密度函数对“父子”系数分布情况进行建模,通过贝叶斯统计理论可求得原始影像的最大后验估计[19],能很好地刻画小波系数边缘分布形状和局部邻域系数幅值间相关性。该算法首先将含噪InSAR图像经多尺度双树复小波变换后分解成两个低频复数近似子图和若干高频复数方向细节子图,然后对各尺度高频复数方向子图利用双变量贝叶斯模型建模,建立复数双变量贝叶斯模型,并利用该模型对复系数进行贝叶斯最小均方估计,从而达到去噪目的。
对受噪声污染的影像经多尺度双树复小波变换后,得到变换后的复系数
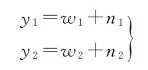 (4)
(4)
设w1是当前小波系数,w2是上一尺度空间位置与w1相同的系数,即w1的“父”系数。用矢量表示为y=w+n,其中
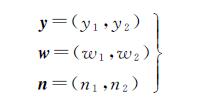 (5)
(5)
式中,y、w、n分别代表含噪影像、原始影像和独立同分布高斯噪声的小波复系数矢量。
由于双树复小波的分解系数是复数,而双变量贝叶斯模型往往是在实数域的范围内使用,以下将实数域双变量滤波模型推广到复数域。
设pw(w)、pn(y-w)分别是真实系数w、噪声系数n的概率密度函数。在贝叶斯统计理论中,最大后验MAP估计即在给定y条件下,使后验概率密度pw|y(w|y)取最大的w
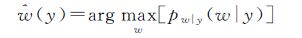 (6)
(6)
利用贝叶斯准则,得到
 (7)
(7)
由于P(Y≤y)=P(w+n≤y)=P(n≤y-w),Y为随机变量,则py|w(y|w)=pn(y-w),进一步可得,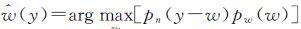
对式(7)取对数可得
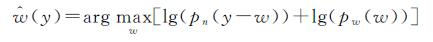 (8)
(8)
从式(8)可知,欲求原始影像复小波系数矢量w的估计值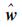
对于原始影像小波系数的概率密度函数Pw(w),Sendur等通过对大量小波系数直方图中“父子”系数间概率分布的统计,提出了一种用非高斯的双变量概率分布函数来刻画小波分解系数与其父节点系数之间的相关性。
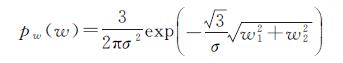 (9)
(9)
式中,w2是w1上一个尺度同位置处父节点系数。
由于w1、w2为复系数,考虑复数虚部的影响,w1、w2的概率密度函数为
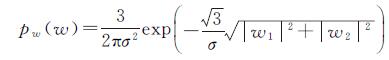 (10)
(10)
干涉图经复小波分解后,复噪声系数n1和n2符合复高斯正态分布,设n1=x1+iy1、n2=x2+iy2,概率密度函数pn1、pn2给出了复噪声系数实部与虚部的相关性。n1、n2的概率密度函数分别为
 (11)
(11)
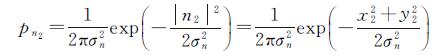 (12)
(12)
利用噪声独立同分布假设,则n1和n2的联合概率密度函数
 (13)
(13)
式中,n2是n1上尺度噪声复系数,σn2复噪声系数方差。
将矢量y、w、n以及式(13)代入式(8),定义f(w)=lg[pw(w)],则
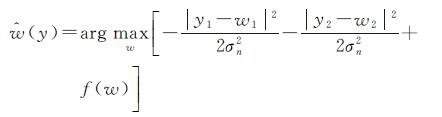 (14)
(14)
对于w(y)的极值,这里是复数的模的极值,即将复数函数取模之后,变成实函数,再用实函数求极值的方法,求出复值函数的极值。
式(14)的等价方程为
 (15)
(15)
 (16)
(16)
式中,
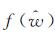
 (17)
(17)
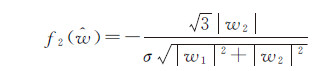 (18)
(18)
将式(17)、(18)代入式(15)、(16),经简单推导
 (19)
(19)
式(19)为复数域双变量收缩函数,考虑了复数的虚部对收缩函数的影响,增强了滤波效果。y1、y2为含噪影像的复小波系数,y2是y1下一级同位置处的父节点复系数。
此处设阈值 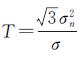
由于含噪信号小波复系数均值为零[20],文献[17]证明符合高斯分布[17]
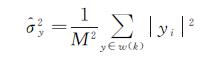 (20)
(20)
M×M为正方形窗口w(k)大小。
噪声标准差在Donoho的鲁棒性中值估计方法的基础上
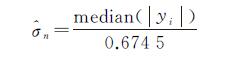 (21)
(21)
|yi|是各层高频子带复系数的模。
则
 (22)
(22)
本文提出的复小波域复数双变量模型干涉图滤波的步骤如下:
(1) 取干涉相位的实部和虚部进行双树复小波分解,每层分解为2个低频子带和6个高频子带,6个高频子带分别对应图像中的6个方向(±15°,±45°,±75°)的复系数。
(2) 对每一个尺度下的6个高频子带的复系数按照式(19)—式(22)进行如下步骤的处理:①计算各尺度下复系数子带的噪声标准差,其算法按照式(21)计算,然后计算噪声方差;②按式(20)计算出各尺度下含噪信号小波复系数的方差,窗口大小为7×7;③按式(22)计算出各尺度下原始影像小波复系数方差;④按式(19)进行复小波系数的收缩,得到高频复信号系数的估计。
(3) 进行复小波逆变换,得到去噪后的复系数并生成干涉图。
2 干涉图试验结果及分析为了验证算法的可靠性和有效性,分别采用模拟干涉图和真实干涉图将本文算法与Goldstein滤波、小波滤波、实数域复小波双变量滤波、最优化融合滤波进行了分析与比较。
2.1 模拟干涉图试验结果采用模拟干涉图比较,相当于知道干涉图的真值,可以更有效的判断本文算法的性能。图 1为模拟干涉图各种方法滤波结果,其大小为592×592像素。Goldstein滤波的滤波参数根据经验选取为0.5,Sym4小波滤波、实数域复小波双变量滤波以及本文算法小波分解尺度皆为3层,实数域复小波双变量滤波(以下简称复小波双变量滤波)只考虑了小波复系数的实部,未考虑虚部,以便于与本文算法比较。其中图 1(d)采用的噪声方差、信号方差估计、双变量收缩函数只考虑复数的实部;图 1(e)该方法考虑了干涉图的相干性。从目视效果看,Goldstein滤波、复小波双变量滤波去噪效果不理想,去噪不均匀,部分区域存在大量噪声,局部地区的细节信息淹没在噪声中;最优化融合方向滤波和Sym4小波滤波去噪效果较好,去除了大部分噪声,细节信息保持较好,但在局部地区还存在明显的噪声斑点;复小波双变量滤波与本文算法相比,复小波双变量滤波由于忽略复小波系数的虚部,未考虑实部与虚部的相关性,导致信号相位噪声的增加影响滤波效果。本文算法考虑了复小波分解后小波系数虚部对干涉图的影响,整体去噪平滑,不存在明显噪声斑点,且细节信息保持良好,与未含噪相位图即真实值相接近。
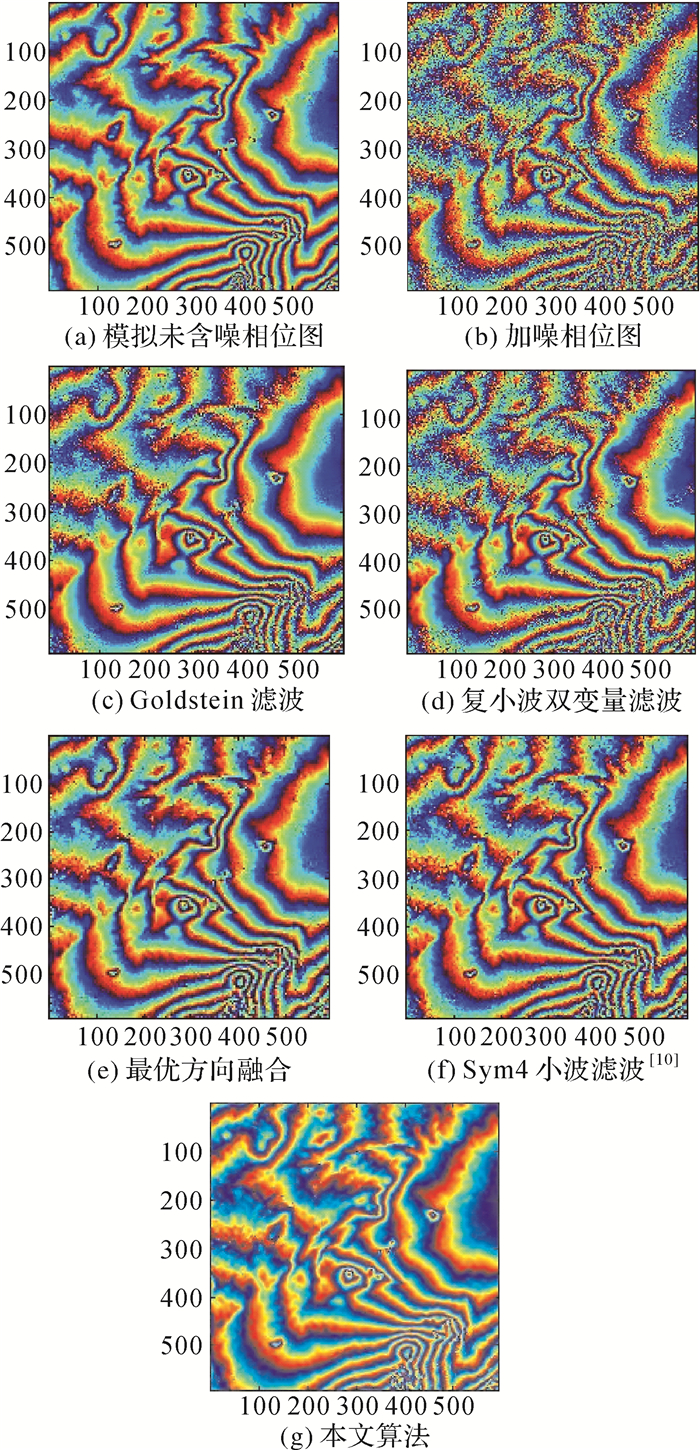
|
| 图 1 模拟干涉图滤波结果 Fig. 1 Filtering results of simulated interferograms |
在模拟的干涉图滤波结果中,选择具有代表性的第510行的相位值进行比较(干涉条纹既有密集的区域,又有疏松的区域)。从图 2中可以看出,Goldstein滤波剖面图和复小波双变量滤波剖面图含有很多毛刺,噪声未滤除干净;效果较好的最优方向融合滤波、Sym4滤波,与未含噪图像的剖面图相比,最优方向融合滤波在图中圆圈处存在剧烈震荡,Sym4滤波由于缺乏平移不变性在图中圆圈处即信号突变点附近存在较大的震荡,即伪吉布斯现象,而本文算法由于复小波具备的优点得到了很好的体现,既保留了细节信息又无离散小波的伪吉布斯现象,与未含噪图像剖面图最接近。
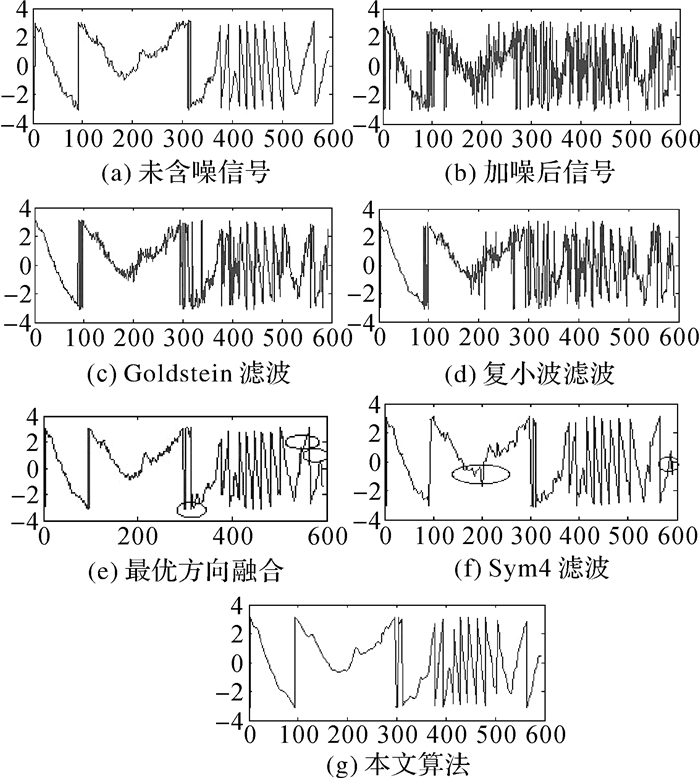
|
| 图 2 模拟干涉图滤波结果第510行剖面图 Fig. 2 Profiles of line 510 of filtering results in simulated interferograms |
2.2 真实干涉图试验结果及分析
采用意大利Etna火山地区的真实干涉图进行研究,该干涉图利用ERS卫星分别于2000年9月6日和10月11日获取,选取范围为400×400像素的区域进行对比分析。从目视效果看,滤波使噪声大量减少,但Goldstein滤波、复小波双变量滤波在局部地区还存在大量明显噪声;效果较好的最优方向融合滤波和Sym4小波滤波去除了大部分噪声,在局部地区出现了纹理断裂现象;效果最好的本文算法,最大程度的消除了图像中的噪声,保持了图像的主要特征,图像纹理更清楚,噪声的抑制最明显,效果最优(图 3)。
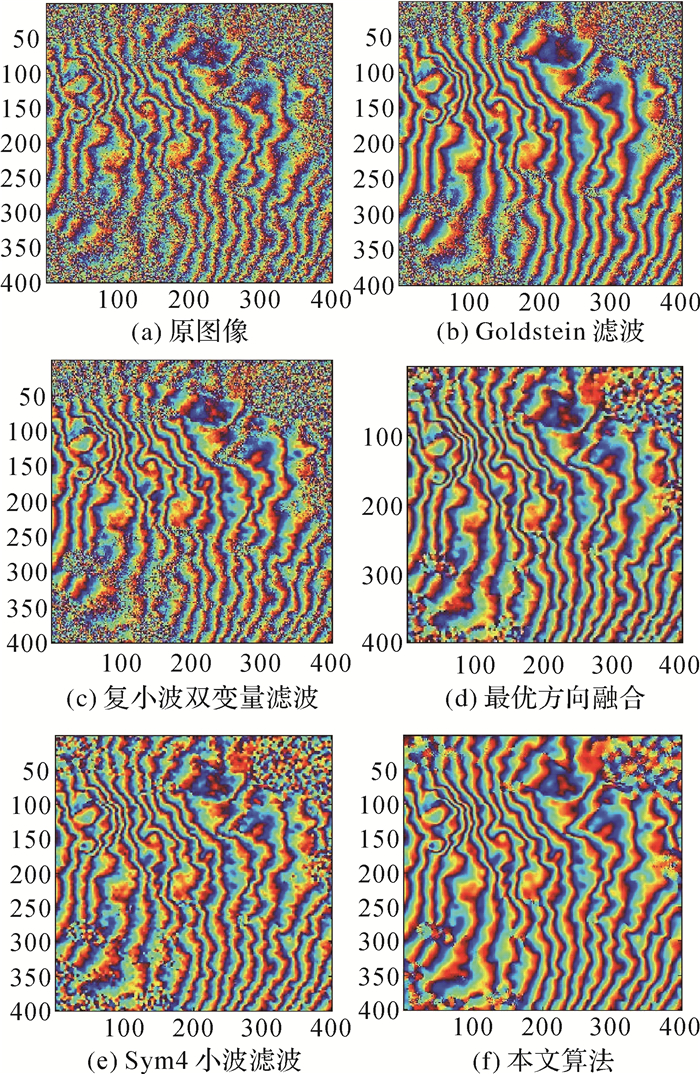
|
| 图 3 意大利Etna火山地区干涉图滤波结果 Fig. 3 Filtering results of interferograms of Etna volcano in Italy |
2.3 干涉图滤波效果定量比较
以上是通过视觉效果定性评定干涉图滤波结果,下面通过残差点数、相位差和值(SPD)、相位标准差(PSD)指标定量评定干涉图滤波效果,在模拟干涉图中,由于知道干涉图真实值,还采用了均方误差(RMS)指标评定。
从表 1模拟干涉图滤波结果中看出,各种方法滤波后各评价指标均有所改善。均方误差(RMS)是利用未加噪的相位图即真值作为参考值,来计算滤波后的相位图和真值之间的偏差,其值越小代表滤波的保真性越好,越接近真值。本文算法RMS最小,滤波效果最好;从残差点的较少数、相位差和值(SPD)以及相位标准差(PSD)等指标来看,本文方法要优于其他算法。从表 2真实干涉图滤波结果看出,Sym4小波滤波和本文算法在各评价指标中表现最优,Sym4小波滤波残差点减少率达到94.31%,本文算法残差点减少率达到95.63%。
| 滤波方法 | 正残差点 | 负残差点 | RMS | SPD | PSD |
| 未含噪信号 | 0 | 0 | - | 1.137 1×105 | 1.217 5×105 |
| 含噪信号 | 16 070 | 16 074 | 3.347 3 | 4.919 6×105 | 6.731 3×105 |
| Goldstein滤波 | 2867 | 2870 | 1.371 5 | 2.588 6×105 | 3.389 5×105 |
| 复小波双变量 | 8774 | 8781 | 1.558 2 | 3.357 1×105 | 4.423 3×105 |
| 最优化融合滤波 | 341 | 343 | 1.146 8 | 1.279 3×105 | 1.454 6×105 |
| Sym4小波滤波 | 358 | 356 | 1.219 6 | 1.305 6×105 | 1.366 2×105 |
| 本文算法 | 125 | 128 | 1.056 8 | 9.363 2×104 | 1.020 5×105 |
| 评价标准 | 越小越好 | 越小越好 | 越小越好 | 越小越好 | 越小越好 |
| 滤波方法 | 正残差点 | 负残差点 | 残差减少率/(%) | SPD | PSD |
| 含噪信号 | 9089 | 9085 | - | 2.434 9×105 | 3.358 8×105 |
| Goldstein滤波 | 5080 | 5074 | 44.13 | 1.714 9×105 | 2.268 6×105 |
| 复小波双变量滤波 | 6000 | 5997 | 33.99 | 1.789 8×105 | 2.340 5×105 |
| 最优化融合滤波 | 406 | 405 | 95.54 | 8.690 2×104 | 9.701 9×104 |
| Sym4小波滤波 | 519 | 516 | 94.31 | 9.481 8×104 | 1.010 7×105 |
| 本文算法 | 399 | 395 | 95.63 | 8.479 3×104 | 9.536 0×104 |
| 评价标准 | 越小越好 | 越小越好 | 越大越好 | 越小越好 | 越小越好 |
3 结 论
本文提出了复数域双变量模型干涉图滤波算法,该算法具有以下特点:①将复小波的双变量去噪模型从实数域推广到复数域,考虑了复数的实部与虚部对信号方差、噪声方差的影响,建立了复小波复数域双变量模型;②从干涉图滤波结果可以看出,二维双树复小波具有的多方向选择性,可提高图像滤波的精度和保留图像细节信息如边缘等,单小波由于缺乏平移不变性在信号突变点附近存在较大的震荡,而复小波由于具有的平移不变性使信号更为平滑;③对各种方法的滤波结果研究对比表明,无论是从目视效果还是定量评价指标来看,本文方法优于其他方法,残差点减少率高达90%以上,均方误差更小,更接近于真实值,达到了滤波的目的。
| [1] | GE Linlin, CHANG H C, RIZOS C. Mine Subsidence Monitoring Using Multi-source Satellite SAR Images[J]. Photogrammetric Engineering & Remote Sensing,2007, 73 (3) : 259 –266 . |
| [2] | ZEBKER H A, VILLASENOR J. Decorrelation in Interferometric Radar Echoes[J]. IEEE Transactions on Geoscience and Remote Sensing,1992, 30 (5) : 950 –959 . |
| [3] | GOLDSTEIN R M, WERNER C L. Radar Interferogram Filtering for Geophysical Applications[J]. Geophysical Research Letters,1998, 25 (21) : 4035 –4038 . |
| [4] | BARAN I, STEWART M P, KAMPES B M, et al. A Modification to the Goldstein Radar Interferogram Filter[J]. IEEE Transactions on Geoscience and Remote Sensing,2003, 41 (9) : 2114 –2118 . |
| [5] | LI Zhiwei, DING Xiaoli, HUANG C, et al. Improved Filtering Parameter Determination for the Goldstein Radar Interferogram Filter[J]. ISPRS Journal of Photogrammetry and Remote Sensing,2008, 63 (6) : 621 –634 . |
| [6] | SUN Qian, LI Zhiwei, ZHU Jianjun, et al. Improved Goldstein Filter for Insar Noise Reduction Based on Local SNR[J]. Journal of Central South University,2013, 20 (7) : 1896 –1903 . |
| [7] | LEE J S, PAPATHANASSIOU K P, AINSWORTH T L, et al. A New Technique for Noise Filtering of SAR Interferometric Phase Images[J]. IEEE Transactions on Geoscience and Remote Sensing,1998, 36 (5) : 1456 –1465 . |
| [8] |
廖明生, 林珲, 张祖勋, 等. InSAR干涉条纹图的复数空间自适应滤波[J].遥感学报,2003, 7 (2) : 98 –105 .
LIAO Mingsheng, LIN Hui, ZHANG Zuxun, et al. Adaptive Algorithm for Filtering Interferometric Phase Noise[J]. Journal of Remote Sensing,2003, 7 (2) : 98 –105 . |
| [9] |
尹宏杰, 李志伟, 丁晓利, 等. InSAR干涉图最优化方向融合滤波[J].遥感学报,2009, 13 (6) : 1092 –1098 .
YIN Hongjie, LI Zhiwei, DING Xiaoli, et al. Optimal Integration-based Adaptive Direction Filter for InSAR Interferogram[J]. Journal of Remote Sensing,2009, 13 (6) : 1092 –1098 . |
| [10] | AHMED S M, ELDIN F A E, TAREK A M. Speckle Noise Reduction in SAR Images Using Adaptive Morphological Filter[C]//Proceedings of the 10th International Conference Intelligent Systems Design and Applications. Cairo: IEEE, 2010, 29: 260-265. |
| [11] |
黄长军, 郭际明, 喻小东, 等. 干涉图EMD-自适应滤波去噪法[J].测绘学报,2013, 42 (5) : 707 –714 .
HUANG Changjun, GUO Jiming, YU Xiaodong, et al. The Study of Interferogram Denoising Method Based on EMD and Adaptive Filter[J]. Acta Geodaetica et Cartographica Sinica,2013, 42 (5) : 707 –714 . |
| [12] |
易辉伟, 朱建军, 陈建群, 等. 一种改进的InSAR干涉图复数空间自适应滤波[J].中南大学学报(自然科学版),2013, 44 (2) : 632 –641 .
YI Huiwei, ZHU Jianjun, CHEN Jianqun, et al. An Improved Adaptive Algorithm for Filtering InSAR Interferogram in Complex Plane[J]. Journal of Central South University (Science and Technology),2013, 44 (2) : 632 –641 . |
| [13] |
靳国旺, 韩晓丁, 贾博, 等. InSAR干涉图的矢量分离式小波滤波[J].武汉大学学报(信息科学版),2008, 33 (2) : 132 –135 .
JIN Guowang, HAN Xiaoding, JIA Bo, et al. Filtering for InSAR Interferograms by Vector Decomposing and Wavelet Transformation[J]. Geomatics and Information Science of Wuhan University,2008, 33 (2) : 132 –135 . |
| [14] |
何儒云, 王耀南. 一种基于小波变换的InSAR干涉图滤波方法[J].测绘学报,2006, 35 (2) : 128 –132 .
HE Ruyun, WANG Yaonan. InSAR Interferogram Filtering Based on Wavelet Transform[J]. Acta Geodaetica et Cartographica Sinica,2006, 35 (2) : 128 –132 . |
| [15] |
蔡国林, 李永树, 刘国祥. 小波-维纳组合滤波算法及其在InSAR干涉图去噪中的应用[J].遥感学报,2009, 13 (1) : 129 –136 .
CAI Guolin, LI Yongshu, LIU Guoxiang. Wavelet-Wiener Combined Filter and Its Application on InSAR Interferogram[J]. Journal of Remote Sensing,2009, 13 (1) : 129 –136 . |
| [16] |
范洪冬, 邓喀中, 庞蕾, 等. 结合边缘信息的DT-CWT干涉图滤波算法[J].武汉大学学报(信息科学版),2012, 37 (7) : 810 –813 .
FAN Hongdong, DENG Kazhong, PANG Lei, et al. Interferogram Filtering Algorithm by Considering Edge Information in DT-CWT Domain[J]. Geomatics and Information Science of Wuhan University,2012, 37 (7) : 810 –813 . |
| [17] |
蔡国林, 刘国祥, 张奥丽, 等. 基于小波域的InSAR干涉图噪声识别与估计[J].遥感学报,2014, 18 (3) : 537 –546 .
CAI Guolin, LIU Guoxiang, ZHANG Aoli, et al. Identification and Estimation of InSAR Interferogram Noise Based on Wavelet Transform[J]. Journal of Remote Sensing,2014, 18 (3) : 537 –546 . |
| [18] | SELESNICK I W, BARANIUK R G, KINGSBURY N C. The Dual-tree Complex Wavelet Transform[J]. IEEE Signal Processing Magazine,2005, 22 (6) : 123 –151 . |
| [19] |
刘帅奇, 胡绍海, 肖扬. 基于复Shearlet域高斯混合模型的SAR图像去噪[J].航空学报,2013, 34 (1) : 173 –180 .
LIU Shuaiqi, HU Shaohai, XIAO Yang. SAR Image De-noising Based on Complex Shearlet Transform Domain Gaussian Mixture Model[J]. Acta Aeronautica et Astronautica Sinica,2013, 34 (1) : 173 –180 . |
| [20] | CHANG S G, YU Bin, VETTERLI M. Adaptive Wavelet Thresholding for Image Denoising and Compression[J]. IEEE Transactions on Image Processing,2000, 9 (9) : 1532 –1546 . |


