2. 青岛农业大学理学与信息科学学院,山东 青岛 266109
2. College of Science and Information, Qingdao Agricultural University, Qingdao 266109, China
2002年,文献[1]提出了短基线集(small baseline subset,SBAS)技术。该技术在一定程度上削弱了传统DInSAR技术的空间基线失相干和大气效应影响,得到了广泛的应用。文献[2]将该技术应用于Mono盆地和Long Valley火山形变监测;文献[3]将其应用于矿区形变监测;文献[4]将其应用于青藏高原季节性冻土形变监测;文献[5-7]将其应用于城市地表形变监测。在上述应用中,当时序干涉对序列属于同一集合时,SBAS形变模型的系数阵是列满秩的,其法方程系数阵满秩,主要采用最小二乘法(least squares,LS)[8-10]解算形变量和形变速率。当时序干涉对序列属于不同集合时,SBAS形变模型的系数阵不是列满秩,其法方程系数阵秩亏,主要采用奇异值分解法(singular value decomposition,SVD)[11-12]进行形变量和形变速率的反演。文献[13]还提出利用加权最小二乘反演算法进行SBAS形变模型求解来提高地表形变监测的能力。文献[14]提出基于L1范数估计准则反演地表形变,通过模拟数据和真实数据说明了基于L1范数估计准则所得到的解比基于L2范数估计准则所得到的解更准确。
对于方程组(1)
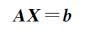 (1)
(1)
式中,A∈Rm×n;b∈Rm为已知量;X∈Rn为待求量。若它的解满足①存在;②唯一;③稳定,则称方程组(1)是适定的。反之,上述3个条件中至少有一个不满足,则称为不适定的。而不适定性是反问题本身固有的一种特性[15]。在SBAS数据处理过程中,干涉对的组合方式在一定程度上决定了模型的设计矩阵。按照事先设置的相干系数、时间基线、空间基线阈值,干涉对自由组合,往往存在某一景影像和多景影像形成干涉像对(如本次试验中第9景数据与其他7景数据形成干涉对),这将会导致模型设计矩阵的列向量间产生近似线性相关,使其法方程的系数阵虽满秩但却产生了病态,即求解短基线集形变模型为不适定问题。求解不适定问题的一般方法是用一组与原不适定问题相“邻近”的适定问题的解去逼近原问题的解,这种方法称为正则化方法。如何建立有效的正则化方法是反问题领域中不适定问题研究的重要内容。通常的正则化方法有基于变分原理的Tikhonov正则化法[16]、各种迭代方法[17-18]以及其他的一些改进方法。
在SBAS处理过程中当时序干涉对序列属于同一个集合,设计矩阵是列满秩,法方程的系数阵满秩但却呈病态,此时最小二乘估计的性质显著变坏,形变量和形变速率反演精度将会变差。本文针对这一问题,将Tikhonov正则化方法引入到短基线集形变模型的求解中。基于Tikhonov正则化理论,将形变速率求解问题转化为极小化问题,根据L-曲线法,选取了合理的正则化参数;考虑最小二乘残差的各个分量间的关系选取了正则化矩阵,实现了SBAS形变模型的稳健解算。在简要介绍短基线集技术原理的基础上,详细分析了Tikhonov正则化算法,并给出正则化参数和正则化矩阵选取的准则;利用ASAR真实数据进行试验,并与LS估计法、岭估计法进行了对比分析,结果表明利用Tikhonov正则化方法反演地表形变,能提高解的稳定性和精确度,可获取更可靠的形变监测结果。
1 短基线集形变模型解算的Tikhonov正则化算法 1.1 短基线集形变模型假设有N+1幅覆盖同一区域且已配准好的单视复(SLC)SAR影像,影像获取时间依次为t0、t1、…、tN。通过限制最大的时间基线和空间基线,生成M个多视的短基线差分干涉图。对这M个差分干涉图进行相位解缠,然后将所有的像元点参考到一个具有高相干性或沉降量已知的点。假设第j幅干涉图是由tA、tB时刻获取的两幅SAR影像进行干涉生成的,那么其高相干像元的差分相位值可表示为
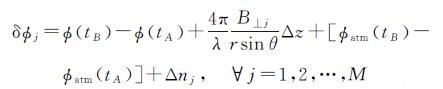 (2)
(2)
式中,λ为雷达波长;φ(tB)和φ(tA)分别为tB、tA时刻相对于t0(设为参考点,即φ(t0)=0)的形变引起的相位;4πB⊥jΔz/λrsin θ是可能的高程误差Δz引起的残余地形相位部分;φatm(tB)-φatm(tA)为获取影像时由于大气不一致而引起大气相位部分;Δnj为包含的失相关影响及其他噪声影响。
忽略大气相位和噪声相位部分,式(2)用矩阵可表示为
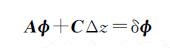 (3)
(3)
式中,A为M×N阶矩阵,它的每一行对应一个干涉图,每一列对应一景影像;φ=[φ(t1)φ(t2)…φ(tN)]T;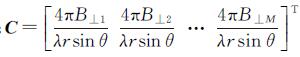
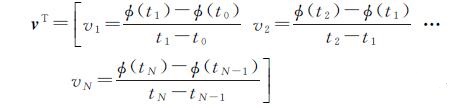 (4)
(4)
将式(4)带入式(3)得
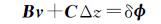 (5)
(5)
式中,B∈RM×N;v∈RN。由文献[1]所提到的方法,借助相位的三次模型,形成一个具有M个方程(这里δφ为解缠的相位值),4个未知量的线性系统,借助最小二乘估计出干涉相位中由DEM误差引起的相位部分CΔz。从解缠的相位减去估计的DEM误差,得到如下线性系统
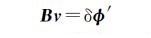 (6)
(6)
式中,δφ′=δφ-CΔz。求出v后,再在时间段上求积分即可得到最后的相位φ。
1.2 形变模型反演的Tikhonov正则化算法对于线性系统(式(6))的典型反演问题,可将其改写成
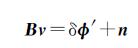 (7)
(7)
式中,n为误差向量,包含残留的DEM误差、大气不均匀引起的误差以及噪声误差等。
若B是列满秩的,可用最小二乘法进行解算,即使误差向量的L2范数最小
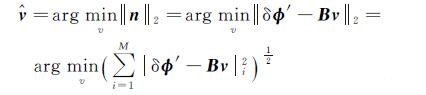 (8)
(8)
从而可得其法方程为
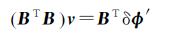 (9)
(9)
由于B是列满秩的,所以BTB是可逆阵,故解式(9)即得式(7)的最小二乘解为
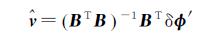 (10)
(10)
最小二乘解在线性无偏估计类中是唯一的具有最小方差的估计。正因为这一点,最小二乘估计在线性系统模型的估计理论与实际应用中占有非常重要的地位。但是在用最小二乘求解反问题时,其结果并不总是令人满意。如文献[19]的47页给出的例子中,所求参数的真值为0,但用LS法求出该参数的估计值是9.363 1,说明在病态情况下,LS法会使某些参数估计值远远偏离真值。研究表明,在有些情况下,LS估计易受数据中的异常值的影响,即系数矩阵或常数项的微小变化可能会引起方程组解的巨大变化,这种方程组称为“病态”方程组。判断方程组是否“病态”或“病态”的程度,通常采用式(11)所示系数矩阵的条件数来衡量
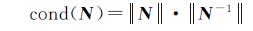 (11)
(11)
式中,N=BTB是满秩的;·表示对矩阵N取某一范数,一般为L2范数。条件数越大,矩阵病态性越严重。由于N为对称正定矩阵,它的条件数还可由下式求得
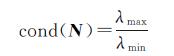 (12)
(12)
式中,λmax、λmin表示矩阵N的最大、最小特征值。
在式(9)中,记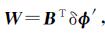
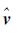
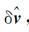
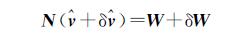 (13)
(13)
则有[20]
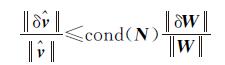 (14)
(14)
式(14)表明方程组解的相对精度不仅取决于观测值相对精度,还依赖于系数矩阵的条件数。当矩阵N的条件数很大时,由式(14)知,观测值很少的扰动都会引起方程组解很大的误差。而在短基线集线性系统中,一般所采用的干涉图组合方式,都会导致法方程的系数矩阵的条件数大于1000,此时式(9)是一个病态方程。在这种情况下,虽然最小二乘估计的方差在线性无偏估计类中最小,但其值却很大,使LS估计的精度较差,表现出相当的不稳定。
为了获取问题的最优稳定解,根据Tikhonov正则化理论,将地面沉降的平均速率求解问题转化为求解下述的极小化问题,即
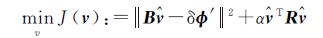 (15)
(15)
式中,α>0为正则化参数;R为正则化矩阵;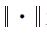
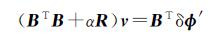 (16)
(16)
Tikhonov正则化的效果主要取决于正则化参数α和正则化矩阵R的选取。正则化参数α的选择对问题的解起着关键的作用。如果α太小,则对问题病态性的改善没有起到什么作用,即解的不稳定性依然存在;反之,如果α太大,则问题(16)虽然可以稳定地求解,但该解与原方程(9)的解相差甚远,是一个相当糟糕的逼近(poor approximation)。所以最优的正则化参数选取应当兼顾这两种情况。通常,参数α的选取有先验(a priori)和后验(a posteriori)两种策略。先验选法是在求正则化解之前,根据正则化参数α具有的数学特性把它确定出来,主要是依据经验进行,这种方法多具有理论上的分析意义,不具有实际应用价值。后验方法是指在计算正则解的过程中根据一定的数学原则确定参数α。常见的后验正则化参数选取准则主要有:①Morozov的偏差原理;②Engl准则;③广义偏差原理;④Arcangeli准则与广义Arcangeli准则;⑤拟最优准则;⑥广义交叉效验(GCV)准则;⑦L-曲线准则,它们的数学理论见文献[21]。本文以L-曲线准则来确定正则化参数α。
令
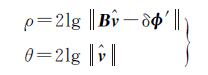 (17)
(17)
则ρ、θ均为正则化参数α的函数。选取不同的α值,得到许多点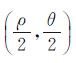
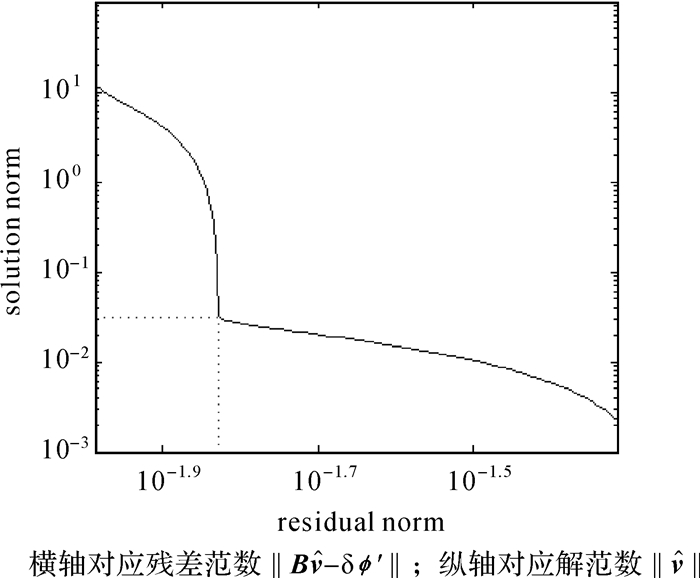
|
| 图 1 L-曲线图 Fig. 1 L-curve image |
该曲线的曲率计算公式为
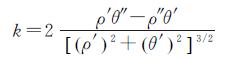 (18)
(18)
式中,ρ′、ρ″、θ′、θ″分别表示ρ、θ的一阶导数和二阶导数。对式(18)求极值,可确定出L-曲线上曲率最大的点,其对应的α值就是所求的正则化参数。由图 1可以从另一个角度诠释该准则选取正则化参数α的含义:L-曲线上曲率最大的点对应正则解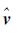
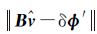
正则化矩阵的选取需根据参数的物理意义来确定,它的适当选取有助于抑制伪目标,增强解的可信性,即合适的正则化矩阵可以降低较小的特征值所对应的模型参数中不可靠的信息对结果的影响。若选取不当,会造成参数的过度平滑。正则化矩阵1
确定正则化参数α和正则化矩阵R后,方程(16)的解为
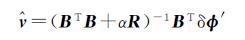 (19)
(19)
其相应的均方误差阵[23]为
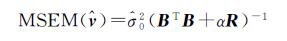 (20)
(20)
式中,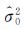
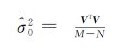
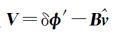
本文所用数据是覆盖北京地区的29景ENVISAT ASAR降轨数据,时间跨度为2007年1月至2010年10月。试验目的是为了比较不同反演算法所得结果的稳定性和可靠性,不讨论研究区的沉降情况。所以在数据覆盖区域,仅选取中心地理坐标为(116.369 8°E、39.914 5°N)面积约为900 km2的一块区域。在数据处理过程中,采用了荷兰Delft大学发布的DORIS精轨数据和SRTM的90 m分辨率的外部DEM数据。
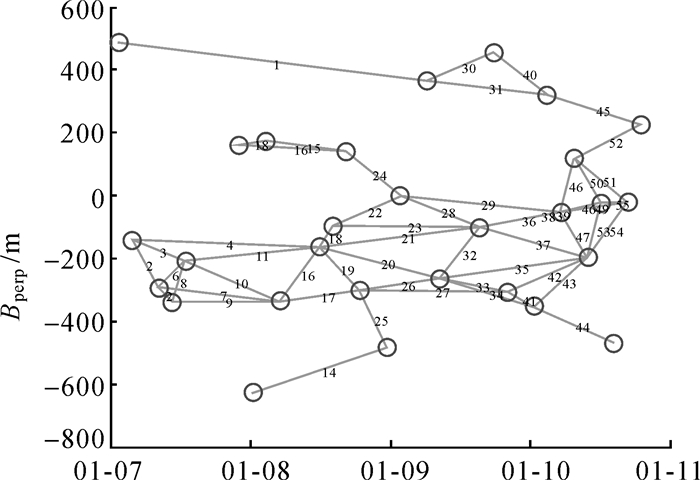
首先根据三基线和最小原则[25],选取2009年1月26日获取的SAR影像为主影像,将其他辅影像配准到主影像系统下。按照选取的最大垂直基线距400 m,最大时间基线距1050 d,最小的相干系数0.5,进行多主影像干涉组合,最终得到55个干涉对,如图 2所示。通过设置0.6的幅度差分离差阈值,最终选取了69 791个高相干点。图 3为短基线集技术所得到的试验区的年平均沉降速率图。
|
| 图 2 干涉图的组合方式 Fig. 2 Combinations of interferograms |
|
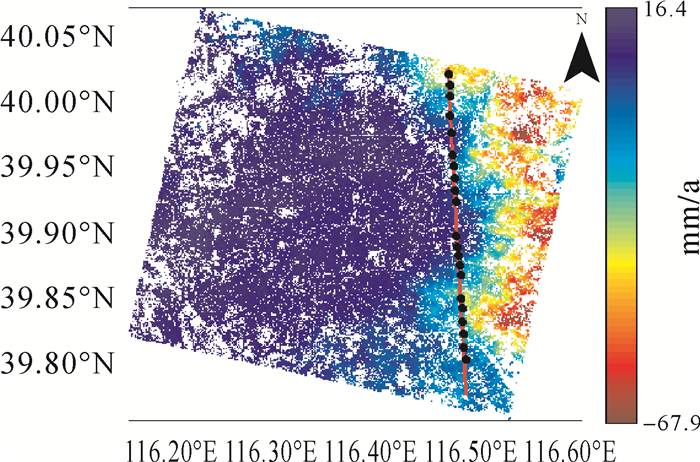
| 图 3 短基线集技术得到的研究区在2007—2010年期间的年平均沉降速率图 Fig. 3 Annual mean subsidence rate of the test area is derived by SBAS approach from 2007 to 2010 |
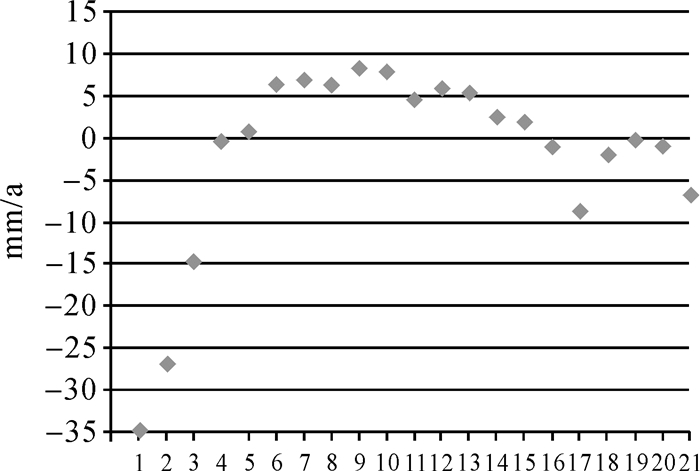
根据上述干涉对的组合方式,得到此时对应式(9)的系数矩阵的条件数为cond(BTB)=3.056 5×103,呈现病态。从图 3中可以看出,经度为116.457 8°的红色直线跨过了试验区的未沉降区、沉降区和抬升区,为了更好验证SBAS形变模型反演的正则化解算方法的有效性,在这条直线上选取了如图 3黑色点所示的21个点,这21个点分别代表了试验区的3种不同沉降情况(未沉降、沉降和抬升),按照由北向南的顺序依次记为1、2、…、20、21。图 4给出了这21个点的年平均沉降速率散点图。
|
| 图 4 21个点的年平均沉降速率散点图 Fig. 4 Scatter diagram of annual mean subsidence rate of the selected 21 points |
对这21个点分别采用最小二乘估计法、岭估计法、Tikhonov正则化估计法进行计算,并比较计算所得估值的均方误差MSE( 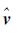
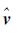
| 点号 | LS估计 | 岭估计 | Tikhonov 正则化估计 |
| 1 | 0.218 4 | 0.203 6 | 0.080 0 |
| 2 | 0.060 4 | 0.029 1 | 0.006 6 |
| 3 | 0.217 4 | 0.115 1 | 0.079 3 |
| 4 | 0.016 7 | 0.015 6 | 0.003 4 |
| 5 | 0.030 8 | 0.024 3 | 0.007 2 |
| 6 | 0.090 3 | 0.067 3 | 0.006 3 |
| 7 | 0.014 1 | 0.013 1 | 0.002 7 |
| 8 | 0.050 4 | 0.036 9 | 0.006 7 |
| 9 | 0.035 6 | 0.033 2 | 0.008 7 |
| 10 | 0.012 3 | 0.011 4 | 0.002 3 |
| 11 | 0.088 6 | 0.071 4 | 0.016 6 |
| 12 | 0.018 5 | 0.017 2 | 0.003 8 |
| 13 | 0.011 6 | 0.010 8 | 0.002 1 |
| 14 | 0.020 2 | 0.018 8 | 0.004 3 |
| 15 | 0.016 4 | 0.013 4 | 0.001 8 |
| 16 | 0.059 0 | 0.055 0 | 0.016 2 |
| 17 | 0.039 8 | 0.037 1 | 0.010 0 |
| 18 | 0.039 6 | 0.037 0 | 0.009 9 |
| 19 | 0.017 8 | 0.016 6 | 0.003 7 |
| 20 | 0.084 1 | 0.078 4 | 0.025 0 |
| 21 | 0.099 3 | 0.092 5 | 0.030 7 |
从表 1可见,岭估计所得结果的均方误差稍微小于最小二乘所得的均方误差,说明岭估计虽然改善了法方程的病态问题,但是所得结果的精确度与最小二乘相差不大。而基于Tikhonov正则化估计法所得结果的MSE远小于LS、岭估计所得结果,图 5直观地显示了这3种算法所得结果的均方误差的大小变化情况。表 1和图 5中3种解算方法均方误差MSE值的大小表明Tikhonov正则化估计法可以改善LS估计和岭估计的结果,提高计算结果的精确度。
|
| 图 5 3种算法所得21个点MSE的曲线图 Fig. 5 Mean squares error calculated by LS, ridge and Tikhonov regularization estimation of the 21 selected points |
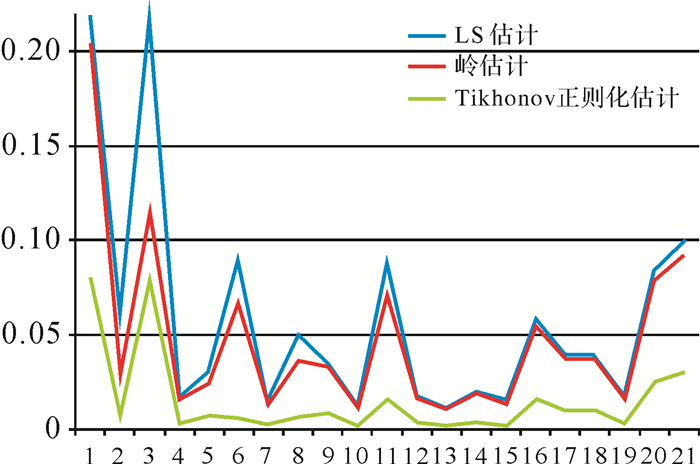
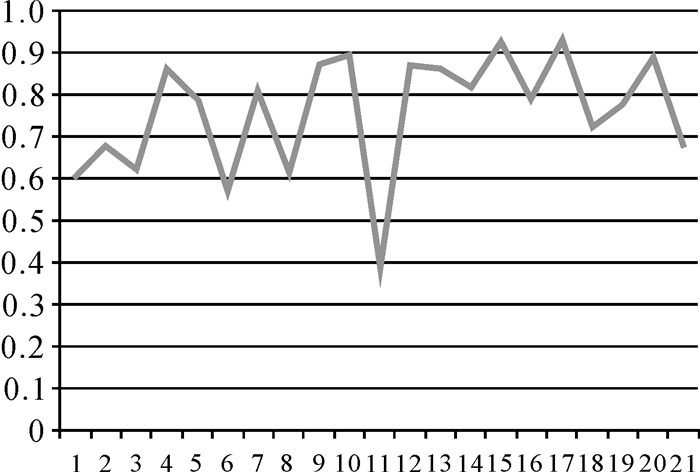
图 6给出了所选取的21个点在短基线集技术处理过程中所获得的相干系数值的曲线图,图 7显示了这21个点基于Tikhonov正则化估计法所得均方误差的曲线图。通过对比图 6和图 7,得到在所选的21个点当中,大部分点具有这样的关系:相干系数值大的点对应的MSE小,相干系数值小的点对应的MSE大。但在个别点如点6、8和11不符合这一关系,是因为病态有Ⅰ、Ⅱ类病态。即使对某一类病态问题,采用不同处理方法如岭估计、正则化等,其结果也会不完全相同。甚至对同一个问题,采用不同的处理方法,其效果也会不相同。
|
| 图 6 21个点的相干系数值 Fig. 6 Coherence image of the selected 21 points |
|
| 图 7 21个点的基于Tikhonov正则化估计法所得均方误差图 Fig. 7 Mean squares errors of the selected 21 points based on Tikhonov regularization estimation |
分析图 4、6、7,发现点1和点2,点2和点3相干系数差别不大,但均方误差相差显著,这主要是因为:①相邻点1、2、3相对于其他18个点的年平均沉降速率相对较大,分别是-35 mm/a、-26 mm/a、-15 mm/a,这3点均处于低相干区,且均基于选定窗口内的灰度(或幅度)值计算出的相干系数,该值的大小会受到窗口内邻近像元灰度值的影响,所以其值相差不大;②在点1、2、3中,点2的相干系数值最大,说明点2受到除沉降以外的大气延迟、植被等的影响最小,其去相干噪声也最小,对噪声反应较敏感的点1、2、3的均方误差值中,点2的均方误差值就最小,且与其他两点(1、3点)相差比较显著。
为了进一步对比Tikhonov正则化法与LS法所得结果,本文引入文献[26]定义的时间相干值(temporal coherence values)
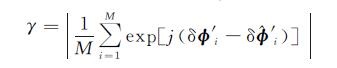 (21)
(21)
式中,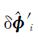
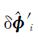
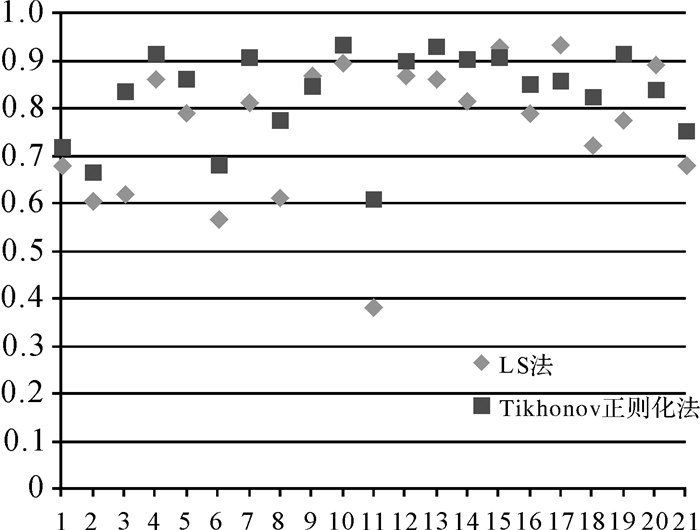
|
| 图 8 所选点的时间相干值散点图 Fig. 8 Temporal coherence values of selected 21 points |
| 点 | LS法 | Tikhonov正则化法 |
| 1 | 0.682 083 | 0.718 3 |
| 2 | 0.604 97 | 0.665 6 |
| 3 | 0.623 387 | 0.837 2 |
| 4 | 0.862 318 | 0.914 7 |
| 5 | 0.790 471 | 0.863 6 |
| 6 | 0.567 301 | 0.681 9 |
| 7 | 0.815 171 | 0.910 2 |
| 8 | 0.613 832 | 0.777 6 |
| 9 | 0.872 514 | 0.849 7 |
| 10 | 0.896 118 | 0.934 5 |
| 11 | 0.383 624 | 0.610 8 |
| 12 | 0.871 657 | 0.901 4 |
| 13 | 0.862 318 | 0.931 3 |
| 14 | 0.819 019 | 0.904 3 |
| 15 | 0.932 27 | 0.910 2 |
| 16 | 0.789 795 | 0.853 1 |
| 17 | 0.935 309 | 0.860 7 |
| 18 | 0.723 35 | 0.825 5 |
| 19 | 0.776 722 | 0.914 3 |
| 20 | 0.892 054 | 0.839 5 |
| 21 | 0.682 083 | 0.754 5 |
虽然对该研究区、相同时间段,缺少相应的GPS、水准等外部数据,但已有学者[10]对北京地区采用类似数据开展过监测。利用与文献[10]研究结果对比和内部精度验证指标(均方误差)这两种方式说明在SBAS形变模型反演中,本文提出的Tikhonov正则化方法优于常用的LS法。
文献[10]中,利用两个相邻轨道的ENVISAT ASAR数据监测北京市地面沉降,得到朝阳区的三间房乡、管庄乡一带在2007年6月至2010年10月期间的沉降速率达到了100 mm/a。而本文借助轨道490的ENVISAT ASAR数据,由LS法解算得到该地区在2007年1月至2010年10月期间的最大沉降速率为82 mm/a,由Tikhonov正则化方法解算得到的最大沉降速率为90 mm/a,这说明在相同数据类型和相同景数的前提下,SBAS处理过程中采用Tikhonov正则化方法解算的结果比采用LS解算的结果更准确。
图 9给出3种方法解算所得到整个研究区的均方误差图。

|
| 图 9 3种方法所得结果的均方误差 Fig. 9 The mean square error calculated by the three methods |
从图 9可以看出,图 9(c)的值在对应点处远小于(a)、(b)的值,说明Tikhonov正则化法所求解的均方误差远小于LS法、岭估计法所求的,进一步说明Tikhonov正则化法求解精度高于其他两种方法。
4 总 结在短基线集技术形变模型的反演中,若时序干涉对序列属于同一集合时,法方程系数矩阵的条件数大于103是存在的,从而呈现病态性。为了克服法矩阵的病态使估计值有较大偏差问题,本文以均方误差为估计准则,根据Tikhonov正则化法将地表形变的平均速率反演问题转化为求目标函数的极小值问题。根据L-曲线准则确定正则化参数α,最小二乘估计的均方误差矩阵的逆的对角线上的元素构成正则化矩阵R,实现SBAS形变模型反演的稳健解算。分别采用LS法、岭估计法和Tikhonov正则化法对覆盖北京地区的29景ENVISAT ASAR数据进行处理,反演出研究区沉降速率图。通过对代表不同沉降情况的21个点的均方误差值和时间相干值、整个研究区的均方误差图等的对比分析,表明基于Tikhonov正则化法估计的解更稳定,具有更高的精确度。
| [1] | BERARDINO P, FORNARO G, LANARI R, et al. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing,2002, 40 (11) : 2375 –2383 . |
| [2] | TIZZANI P, BERARDINO P, CASU F, et al. Surface Deformation of Long Valley Caldera and Mono Basin, California, Investigated with the SBAS-InSAR Approach[J]. Remote Sensing of Environment,2007, 108 (3) : 277 –289 . |
| [3] |
尹宏杰, 朱建军, 李志伟, 等. 基于SBAS的矿区形变监测研究[J].测绘学报,2011, 40 (1) : 52 –58 .
YIN Hongjie, ZHU Jianjun, LI Zhiwei, et al. Ground Subsidence Monitoring in Mining Area Using DInSAR SBAS Algorithm[J]. Acta Geodaetica et Cartographica Sinica,2011, 40 (1) : 52 –58 . |
| [4] |
李珊珊, 李志伟, 胡俊, 等. SBAS-InSAR技术监测青藏高原季节性冻土形变[J].地球物理学报,2013, 56 (5) : 1476 –1486 .
LI Shanshan, LI Zhiwei, HU Jun, et al. Investigation of the Seasonal Oscillation of the Permafrost over Qinghai-Tibet Plateau with SBAS-InSAR Algorithm[J]. Chinese Journal of Geophysics,2013, 56 (5) : 1476 –1486 . |
| [5] |
吴宏安, 张永红, 陈晓勇, 等. 基于小基线DInSAR技术监测太原市2003—2009年地表形变场[J].地球物理学报,2011, 54 (3) : 673 –680 .
WU Hongan, ZHANG Yonghong, CHEN Xiaoyong, et al. Ground Deformation Monitoring Using Small Baseline DInSAR Technique: A Case Study in Taiyuan City from 2003 to 2009[J]. Chinese Journal of Geophysics,2011, 54 (3) : 673 –680 . |
| [6] |
许文斌, 李志伟, 丁晓利, 等. 利用InSAR短基线技术估计洛杉矶地区的地表时序形变和含水层参数[J].地球物理学报,2012, 55 (2) : 452 –461 .
XU Wenbin, LI Zhiwei, DING Xiaoli, et al. Application of Small Baseline Subsets D-InSAR Technology to Estimate the Time Series Land Deformation and Aquifer Storage Coefficients of Los Angeles Area[J]. Chinese Journal of Geophysics,2012, 55 (2) : 452 –461 . |
| [7] |
张永红, 张继贤, 龚文瑜, 等. 基于SAR干涉点目标分析技术的城市地表形变监测[J].测绘学报,2009, 38 (6) : 482 –487 .DOI:10.3321/j.issn:1001-1595.2009.06.003.
ZHANG Yonghong, ZHANG Jixian, GONG Wenyu, et al. Monitoring Urban Subsidence Based on SAR Interferometric Point Target Analysis[J]. Acta Geodaetica et Cartographica Sinica,2009, 38 (6) : 482 –487 .DOI:10.3321/j.issn:1001-1595.2009.06.003. |
| [8] |
张永红, 吴宏安, 孙广通. 时间序列InSAR技术中的形变模型研究[J].测绘学报,2012, 41 (6) : 864 –869 .
ZHANG Yonghong, WU Hongan, SUN Guangtong. Deformation Model of Time Series Interferometric SAR Techniques[J]. Acta Geodaetica et Cartographica Sinica,2012, 41 (6) : 864 –869 . |
| [9] | FERRETTI A, PRATI C, ROCCA F. Nonlinear Subsidence Rate Estimation Using Permanent Scatterers in Differential SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing,2000, 38 (5) : 2202 –2212 . |
| [10] |
李永生, 张景发, 李振洪, 等. 利用短基线集干涉测量时序分析方法监测北京市地面沉降[J].武汉大学学报(信息科学版),2013, 38 (11) : 1374 –1377 .
LI Yongsheng, ZHANG Jingfa, LI Zhenhong, et al. Land Subsidence in Beijing City from InSAR Time Series Analysis with Small Baseline Subset[J]. Geomatics and Information Science of Wuhan University,2013, 38 (11) : 1374 –1377 . |
| [11] | LANARI R, MORA O, MANUNTA M, et al. A Small-baseline Approach for Investigating Deformations on Full-resolution Differential SAR Interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing,2004, 42 (7) : 1377 –1386 . |
| [12] | BONANO M, MANUNTA M, MARSELLA M, et al. Long-term ERS/ENVISAT Deformation Time-series Generation at Full Spatial Resolution via the Extended SBAS Technique[J]. International Journal of Remote Sensing,2012, 33 (15) : 4756 –4783 . |
| [13] | AKBARI V, MOTAGH M. Improved Ground Subsidence Monitoring Using Small Baseline SAR Interferograms and a Weighted Least Squares Inversion Algorithm[J]. IEEE Geoscience and Remote Sensing Letters,2012, 9 (3) : 437 –441 . |
| [14] | LAUKNES T R, ZEBKER H A, LARSEN Y. InSAR Deformation Time Series Using an L1-norm Small-baseline Approach[J]. IEEE Transactions on Geoscience and Remote Sensing,2011, 49 (1) : 536 –546 . |
| [15] |
王家映.
地球物理反演理论[M]. 北京: 高等教育出版社, 2002 .
WANG Jiaying. Inverse Theory in Geophysics[M]. Beijing: Higher Education Press, 2002 . |
| [16] | TIKHONOV A N, ARSENIN V Y. Solutions of Ill-posed Problems. New York: John Wiley and Sons[M]. 1977 . |
| [17] | HE Guoqiang, LIU Linxian. A Kind of Implicit Iterative Methods for Ill-posed Operator Equation[J]. Journal of Computational Mathematics,1999, 17 (3) : 275 –284 . |
| [18] | STEIHAUG T. The Conjugate Gradient Method and Trust Regions in Large Scale Optimization[J]. SIAM Journal on Numerical Analysis,1983, 20 (3) : 626 –637 . |
| [19] |
郭建峰. 测量平差系统病态性的诊断与处理[D]. 郑州: 信息工程大学, 2002. GUO Jianfeng. Diagnostics and Processing of Ill-posed in Surveying Adjustment System[D]. Zhengzhou: Information Engineering University, 2002. |
| [20] |
王松桂, 贾忠贞.
矩阵论中不等式[M]. 合肥: 安徽教育出版社, 1994 .
WANG Songgui, JIA Zhongzhen. Inequality in Matrix Theory[M]. Hefei: Anhui Education Press, 1994 . |
| [21] |
王彦飞.
反演问题的计算方法及其应用[M]. 北京: 高等教育出版社, 2007 .
WANG Yanfei. Computational Methods for Inverse Problems and Their Applications[M]. Beijing: Higher Education Press, 2007 . |
| [22] |
王振杰.
测量中不适定问题的正则化解法[M]. 北京: 科学出版社, 2006 .
WANG Zhenjie. Regularization Solutions of Ill-posed Problems in Geodesy[M]. Beijing: Science Press, 2006 . |
| [23] |
杨文采.
地球物理反演和地震层析成像[M]. 北京: 地质出版社, 1989 .
YANG Wencai. Geophysical Inversion and Seismic Tomography[M]. Beijing: Geological Press, 1989 . |
| [24] |
张方仁, 汪晓庆. 平差参数的岭估计和压缩估计[J].武汉测绘科技大学学报,1989, 14 (3) : 46 –58 .
ZHANG Fangren, WANG Xiaoqing. The Ridge Estimation and the Stein Estimation of Adjustment Parameters[J]. Journal of Wuhan Technical University of Surveying and Mapping,1989, 14 (3) : 46 –58 . |
| [25] |
陶秋香, 刘国林. PS InSAR公共主影像优化选取的一种新方法[J].武汉大学学报(信息科学版),2011, 36 (12) : 1456 –1460 .
TAO Qiuxiang, LIU Guolin. A New Method to Optimize and Select Common Master Images in PS InSAR[J]. Geomatics and Information Science of Wuhan University,2011, 36 (12) : 1456 –1460 . |
| [26] | PEPE A, LANARI R. On the Extension of the Minimum Cost Flow Algorithm for Phase Unwrapping of Multitemporal Differential SAR Interferograms[J]. IEEE Transactions on Geoscience and Remote Sensing,2006, 44 (9) : 2374 –2383 . |



