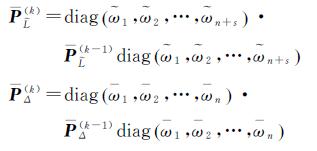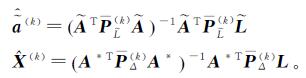2. 信息工程大学理学院,河南 郑州 450001
2. Institute of Science, Information Engineering University, Zhengzhou 450001, China
最近几年,作为变量误差模型(errors-in-variables,EIV)的参数估计方法,整体最小二乘(total least-squares,TLS)或加权整体最小二乘(weighted TLS,WTLS)方法在大地测量领域获得了广泛关注[1, 2],但大多数学者的工作主要集中于WTLS估计的算法研究[3-8]。WTLS估计是在一般的变量误差模型中引入观测误差和系数矩阵误差的方差-协方差矩阵的参数估计方法[3]。事实上,变量误差模型中并不是所有的系数矩阵元素都是随机的。例如,在坐标变换中,一些元素不含误差,可以认为是固定的,而另外一些元素则是由观测值所组成的,可以认为是随机的。顾及这一事实,通常考虑的变量误差模型被推广到更一般的部分变量误差模型[9]。部分变量误差模型的WTLS估计方法,其优势在于不用拉格朗日乘子且法方程未知参数的个数大大减少,因而获得了更多关注[10, 11]。但是,WTLS估计与经典的LS估计一样,对粗差很敏感,不具有抵御粗差影响的能力[12-17]。
如何有效地处理观测数据中的粗差一直是测量领域关注和研究的热点[18, 19],抗差估计是一种处理粗差的有效方法,并且针对Gauss-Markov模型的抗差估计成果较多[20-26]。虽然针对变量误差模型,文献[14-17]提出了为数不多的几个抗差估计,但这些估计均采用残差和验后单位权方差确定降权因子,易受粗差的影响,进而影响其抗差功效。由于部分变量误差模型的系数矩阵也可能含有粗差,所以经典的抗差估计方法并不能直接应用于部分变量误差模型,更为有效的方法值得研究。为此,本文将在提出部分变量误差模型WTLS估计的两步迭代解法的基础上,运用抗差LS估计的等价权方法,提出一种整体抗差最小二乘(TRLS)估计方法,并构建一致最大功效统计量确定降权因子。针对WTLS估计两步迭代解法的特点,设计两个不同的降权方案:第1方案是在估计系数矩阵元素时,不对观测值降权,仅对系数矩阵降权;第2方案是在估计系数矩阵元素时,既对系数矩阵降权,同时也对观测值降权。
1 WTLS估计的两步迭代解法考虑如下部分变量误差模型[9]
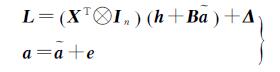 (1)
(1)
式中,L是n×1观测向量;X是t×1未知参数向量;In是n×n单位阵;Δ是n×1随机误差向量;h是由系数矩阵A中零元素和常数元素所组成的nt×1向量;B是给定的nt×s矩阵,s表示A中不同随机元素的个数;a是由A中不同随机元素所组成的s×1向量;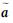
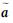
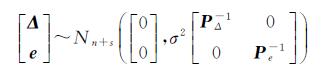 (2)
(2)
式中,σ2为未知的单位权方差。
下面提出部分变量误差模型(1)的WTLS估计的两步迭代解法。首先,将任意给定的X的初值X(0)代入式(1),得到
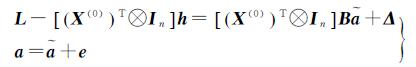 (3)
(3)
令
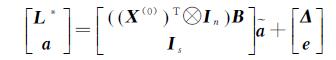 (4)
(4)
再令
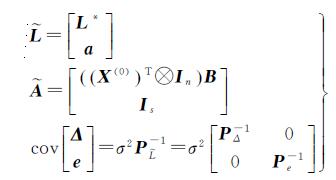 (5)
(5)
并应用LS原理[27],可得向量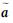
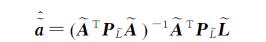 (6)
(6)
对应的残差向量为
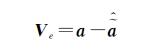 (7)
(7)
然后,将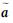
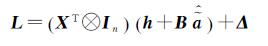 (8)
(8)
应用数学函数invvec,将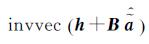
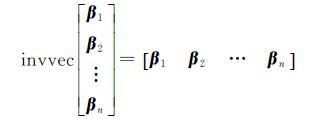 (9)
(9)
式中,βi(i=1,2,…,n)均为t×1列向量。于是式(8)可写为
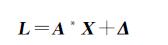 (10)
(10)
再次应用LS原理[19],可得未知参数向量X的估计为
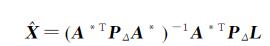 (11)
(11)
对应的残差向量为
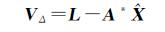 (12)
(12)
最后,可得单位权方差σ2的估计为
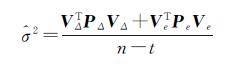 (13)
(13)
值得指出的是,上述WTLS估计的两步迭代解法本质上与现有算法[9]等价。鉴于上述公式是在LS框架下推导得到的,所以经典LS估计和抗差LS估计的相关理论和方法[21-24]都可以直接应用于部分变量误差模型。
2 整体抗差最小二乘(TRLS)方法如上所述,当部分变量误差模型(1)中的观测值和系数矩阵元素同时含有粗差时,对式(6)和式(11)运用抗差LS估计的等价权方法[21-24],可得向量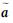
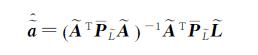 (14)
(14)
和
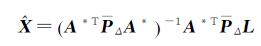 (15)
(15)
式中,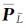
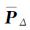
根据基于敏感度分析的抗差估计理论[26],本文将按下列方式确定式(14)、(15)中的等价权阵
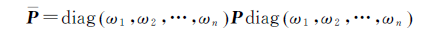 (16)
(16)
式中,ωi为降权因子,可通过Huber权函数[20]进行确定
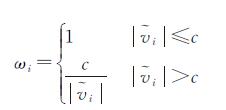 (17)
(17)
式中,
 (18)
(18)
式中,c0和c1的取值区间分别为[1.0,2.0]和[3,5,6.0]。然而,在现有变量误差模型的抗差估计方法[14-16]中,其降权因子是由残差vi和单位权方差的验后估计2共同决定的
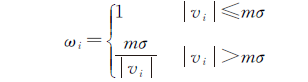 (19)
(19)
式中,m为给定的常数。
众所周知,残差和单位权方差的验后估计易受粗差的影响[26];因此,按式(19)确定降权因子,会造成抗差功效的损失。基于敏感度分析的抗差估计理论表明,基于一致最大功效统计量的抗差估计优于基于残差或标准化残差的抗差估计[26]。令人遗憾的是,通过现有的WTLS估计方法均无法构造此一致最大功效统计量,为此本文利用第1节提出的WTLS估计的两步迭代解法,构造如下统计量,以将基于一致最大功效统计量的抗差估计拓展到部分变量误差模型
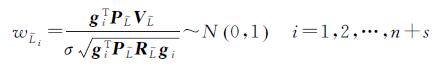 (20)
(20)
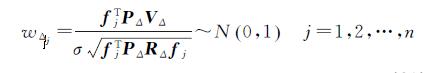 (21)
(21)
式中,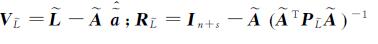
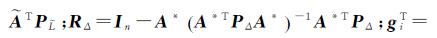
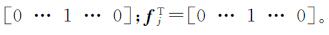
相应的,式(14)、(15)中的等价权阵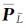
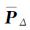
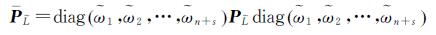 (22)
(22)
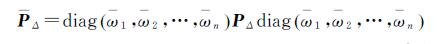 (23)
(23)
对应的降权因子分别为
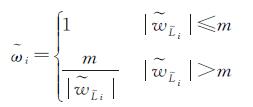 (24)
(24)
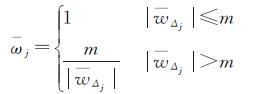 (25)
(25)
式中,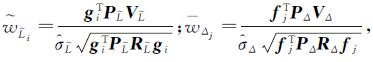
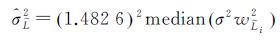 (26)
(26)
 (27)
(27)
注意到式(14)中既包含系数矩阵的权,也包含观测值的权,为此提出如下两个降权方案,以便作比较分析。
方案1,在式(14)中仅对Pe进行降权。
方案2,在式(14)中对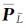
综上所述,计算TRLS估计的迭代算法设计如下:
步骤1,给定初值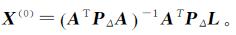
步骤2,构造等价权矩阵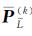
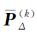
步骤3,计算向量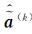
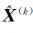
步骤4,如果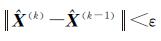
算例1,2D仿射变换的数学模型为
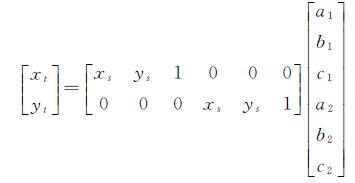 (28)
(28)
式中,(xs,ys)和(xt,yt)分别为同一点在旧坐标系和新坐标系中的坐标;ai、bi和ci(i=1,2)为坐标变换参数。本次试验采用文献[15]提供的部分数据。
假定变换参数的参考值为
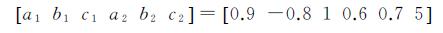 (29)
(29)
而无误差的观测数据如表 1所示。
| 坐标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| xs | 1 | 1 | 1 | 1.5 | 2 | 2.5 | 3 | 3 | 3 | 2.5 | 2 | 1.5 | 1 |
| ys | 1 | 2 | 3 | 3.5 | 4 | 3.5 | 3 | 2 | 1 | 0.5 | 0 | 0.5 | 1 |
| xt | 1.1 | 0.3 | -0.5 | -0.45 | -0.4 | 0.45 | 1.3 | 2.1 | 2.9 | 2.85 | 2.8 | 1.95 | 1.1 |
| yt | 6.3 | 7 | 7.7 | 8.35 | 9 | 8.95 | 8.9 | 8.2 | 7.5 | 6.85 | 6.2 | 6.85 | 6.3 |
根据Monte Carlo策略[15],将协方差矩阵为
 (30)
(30)
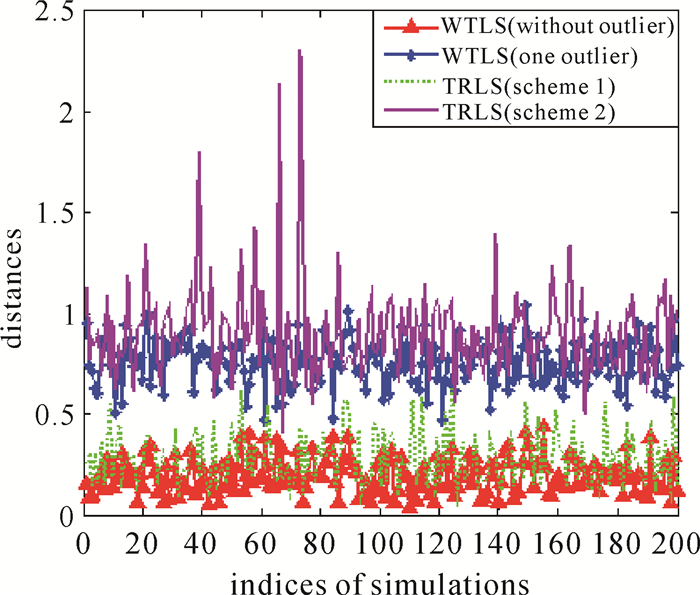
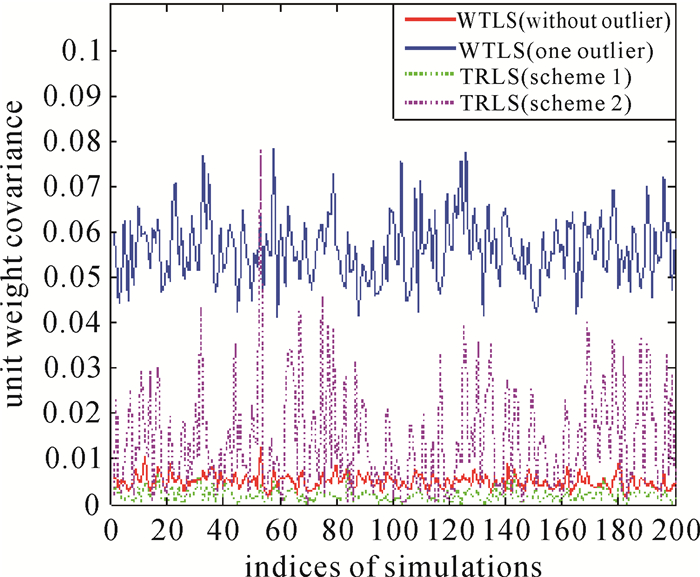
的随机误差分别加在13个点的无误差的原始观测值上,得到模拟观测值,并且在第4个点的旧坐标分量xs上加入大小为2 m的粗差。临界值ε和m分别选为0.000 01和1.5,最大迭代次数为200,权函数取Huber权函数。为消除随机因素的影响,随机模拟运行了200次。单个粗差情形下,由各方案计算得到的变换参数估值与参考值之间的欧氏距离如图 1所示,图 2则给出了单位权方差的估值。
|
| 图 1 各方案计算得到的变换参数估值与参考值之间的欧氏距离(单个粗差情形) Fig. 1 Euclidean distances between estimated transformation parameters by different schemes and reference values with single outlier |
|
| 图 2 单位权方差的估值(单个粗差情形) Fig. 2 Estimate of variance of unit weight with single outlier |
与此同时,对上述200次模拟结果进行了统计分析,其结果如表 2、表 3和表 4所示。从表中不难看出,当系数矩阵元素受到粗差污染时,WTLS估计扭曲得十分厉害,其抗差性很差; 而基于方案1的TRLS估计则较为有效地削弱了粗差对未知参数估值的影响,获得了可靠的参数估值;但方案2并没有达到预期的抗差效果,其稳定性还不如WTLS估计,这说明在估计系数矩阵时,无须进行相应的降权。如果将TRLS估计抵御粗差的成功率定义为
 (31)
(31)
| WTLS (无粗差) |
WTLS (含粗差) |
TIRLS (方案1) |
TIRLS (方案2) |
|
| 平均值 | 0.198 17 | 0.758 51 | 0.281 9 | 0.905 62 |
| 差值 | WTLS(无粗差) | WTLS(含粗差) | TRLS(方案1) | TRLS(方案2) | ||||
| 平均值 | 最大值 | 平均值 | 最大值 | 平均值 | 最大值 | 平均值 | 最大值 | |
| |da1| | 0.057 308 | 0.190 95 | 0.125 6 | 0.334 21 | 0.079 892 | 0.263 15 | 0.261 73 | 0.694 49 |
| |db1| | 0.044 085 | 0.114 08 | 0.314 79 | 0.492 67 | 0.063 138 | 0.237 45 | 0.146 82 | 1.475 9 |
| |dc1| | 0.117 07 | 0.359 11 | 0.538 42 | 0.834 95 | 0.167 1 | 0.553 49 | 0.669 2 | 0.967 26 |
| |da2| | 0.043 539 | 0.166 67 | 0.083 22 | 0.233 73 | 0.064 77 | 0.234 63 | 0.172 1 | 0.416 24 |
| |db2| | 0.029 906 | 0.102 41 | 0.191 7 | 0.310 68 | 0.047 561 | 0.185 88 | 0.117 09 | 1.309 8 |
| |dc2| | 0.097 785 | 0.366 38 | 0.313 44 | 0.583 44 | 0.131 76 | 0.415 86 | 0.415 98 | 0.684 48 |
| WTLS (无粗差) |
WTLS (含粗差) |
TIRLS (方案1) |
TIRLS (方案2) |
|
| 最大值 | 0.012 46 | 0.078 475 | 0.007 461 7 | 0.077 639 |
| 平均值 | 0.005 086 6 | 0.056 165 | 0.002 025 6 | 0.013 959 |
则两种方案的成功率分别为100%和29.5%,这表明方案1的TRLS估计更具稳定性和可靠性。
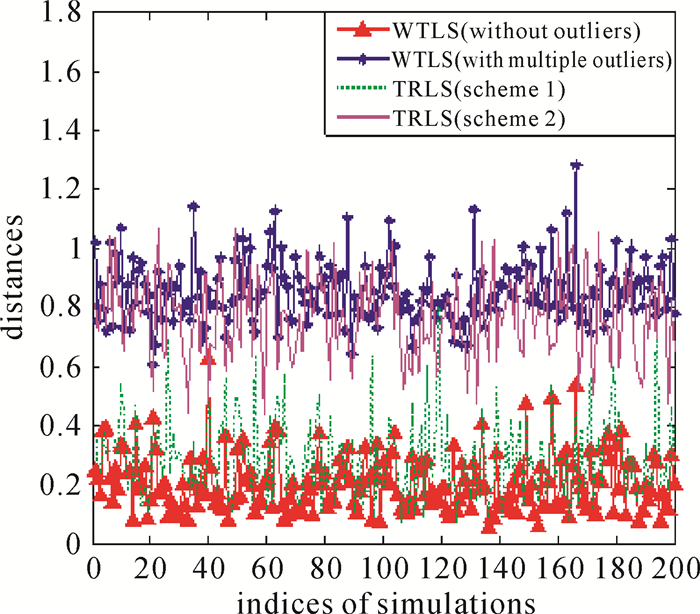
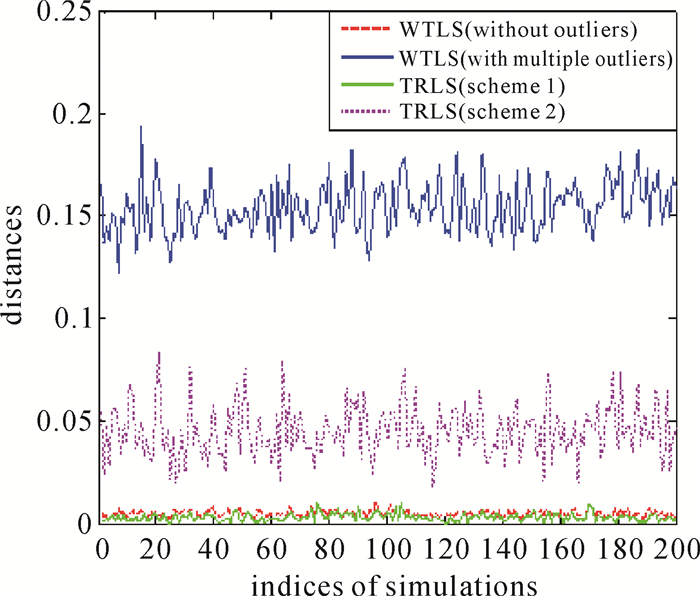
下面考虑多个粗差的情形。为此,继续在第4个点的旧坐标分量ys上加入大小为2 m的粗差,同时在第2个点的新坐标两分量xt和yt上也都加入大小为2 m的粗差。模拟计算200次,其变换参数估值与参考值之间的欧氏距离以及单位权方差估计分别如图 3和图 4所示,而变换参数估值与参考值之间的平均距离如表 5所示。不难看出,方案2的TRLS估计基本上不具有抵御粗差的能力,而方案1的TRLS估计则克服了粗差的影响,并且成功率达到100%。
|
| 图 3 各方案计算得到的变换参数估值与参考值之间的欧氏距离(多个粗差情形) Fig. 3 Euclidean distance between estimated transformation parameters by different schemes and reference values with multiple outliers |
|
| 图 4 200次模拟的单位权方差估值(多个粗差情形) Fig. 4 Estimate of variance of unit weight for 200 simulations with multiple outliers |
| WTLS (无粗差) |
WTLS (含粗差) |
TRLS (方案1) |
TRLS (方案2) |
|
| 平均距离 | 0.200 36 | 0.853 65 | 0.287 07 | 0.768 06 |
综上可知,不论是单个粗差还是多个粗差,方案2的TRLS估计均不具有较强的抗差能力,而方案1的TRLS估计则能够有效削弱单个或多个粗差对未知参数估值的不良影响,这说明在处理部分变量误差模型中的粗差时,应采用方案1的TRLS估计方法。为了显示本文算法的优越性,在相同模拟条件下,仍然应用前面的相关数据,将本文算法与基于残差和验后单位权方差确定降权因子(式(19))的抗差估计进行比较,其计算结果如表 6和表 7所示。相关结果表明本文算法优于现有算法。
| WTLS (无粗差) |
WTLS (含粗差) |
TRLS (方案1) |
TRLS (残差和单位权方差) |
|
| 平均距离 | 0.197 8 | 0.747 7 | 0.281 5 | 0.572 4 |
| 最大距离 | 0.556 1 | 1.110 5 | 0.953 3 | 1.036 0 |
| WTLS (无粗差) |
WTLS (含粗差) |
TRLS (方案1) |
TRLS (残差和单位权方差) |
|
| 平均距离 | 0.193 9 | 0.852 6 | 0.287 2 | 0.419 3 |
| 最大距离 | 0.521 9 | 1.109 8 | 0.870 3 | 0.778 6 |
算例2,考虑如表 8所示的实测数据[29],该数据是关于20个孩子的血液样本中血清中卡那霉素的水平。其中一项数据是通过足跟方式获取,而另外一项则是用导管的方式获取。文献[29]指出表 8中的第2个观测值含有粗差,据此本文将去掉该观测值所得到的WTLS估值作为未知参数的参考值。在计算过程中,迭代终止的条件为相邻迭代估值之间的距离小于0.000 01,或者是迭代次数超过200次,权函数取Huber权函数。分别采用WTLS估计、方案1和方案2的TRLS估计进行解算,并与文献[15]中的结果进行对比,如表 9所示。表 10则给出了由各种方法得到的单位权方差估值。图 5表示的是不同参数估值对应的拟合结果。
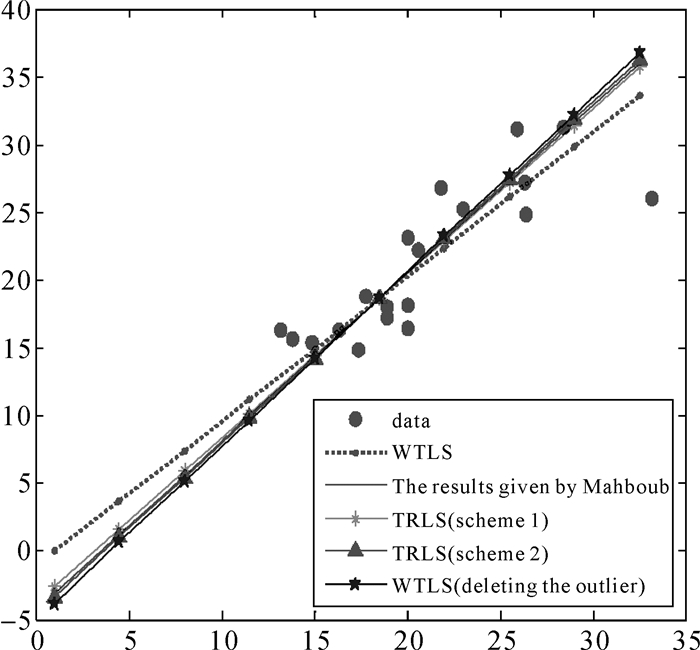
|
| 图 5 线性拟合图 Fig. 5 Linear fitting |
| Heelstick | Catheter | Heelstick | Catheter | ||
| 1 | 23.0 | 25.0 | 11 | 26.4 | 24.8 |
| 2 | 33.2 | 26.0 | 12 | 21.8 | 26.8 |
| 3 | 16.3 | 16.3 | 13 | 14.9 | 15.4 |
| 4 | 26.3 | 27.2 | 14 | 17.4 | 14.9 |
| 5 | 20.0 | 23.2 | 15 | 20.0 | 18.1 |
| 6 | 20.0 | 18.1 | 16 | 13.2 | 16.3 |
| 7 | 20.6 | 22.2 | 17 | 28.4 | 31.3 |
| 8 | 18.9 | 17.2 | 18 | 25.9 | 31.2 |
| 9 | 17.8 | 18.8 | 19 | 18.9 | 18.0 |
| 10 | 20.0 | 16.4 | 20 | 13.8 | 15.6 |
从表 9可以看出,方案1和方案2的TRLS方法均具有一定的抵御粗差的功效,但就未知参数估值与参考值之间的欧氏距离来看,方案1明显优于方案2。与文献[15]中的结果进行比较发现,本文的TRLS估值更稳健。从表 10可以看出,本文算法的计算精度高于文献[15],这也有力地验证了本文方法的有效性和优良性。
4 结 论
(1) 部分变量误差模型的WTLS估计同LS估计一样,对粗差很敏感,即抗差性能很差。
(2) 提出了部分变量误差模型WTLS估计的一种两步迭代解法,该解法的计算公式均是在LS框架下推导得到的,具有易于理解和可操作性强等特点,为构建部分变量误差模型的整体抗差估计奠定了基础。
(3) 利用部分变量误差模型的两步迭代解法,构建了与抗差LS估计相类似的TRLS解式,保持了传统的数据处理方式,并构造了一致最大功效统计量以确定降权因子,其中未知的单位权方差可采用具有高崩溃污染率的LMS方法进行估计。
(4) 结合部分变量误差模型两步迭代解法的特点,设计了两个降权方案:第1个方案是在估计系数矩阵元素时,不对观测值进行降权,仅对系数矩阵降权,而第2个方案则是在估计系数矩阵元素时对观测值和系数矩阵同时降权。
(5) 2D相似变换模拟算例的计算结果表明,单个粗差情形下两种不同降权方案的TRLS估计均具有一定的抗差能力,但方案1的抗差功效更优。多个粗差情形下,方案2的TRLS估计基本上不具有抗差性。因此,处理部分变量误差模型中的粗差时,应采用方案1的TRLS估计。线性拟合实测数据的计算结果表明本文方法优于现有变量误差模型的抗差估计方法。
(6) 需要注意的是,统计量(式(20)、式(21))并非严格意义上的一致最大功效统计量,因此,部分变量误差模型的整体抗差估计及其算法值得进一步研究。
| [1] | FANG X. Weighted Total Least Squares Solutions for Application in Geodesy[D]. Hanover: Leibniz University Hanover, 2011. |
| [2] | SNOW K B. Topics in Total Least-squares Adjustment within the Errors-in-variables Model: Singular Cofactor Matrices and Prior Information[D]. Ohio: Ohio State University, 2012. |
| [3] | SCHAFFRIN B, WIESER A. On Weighted Total Least-squares Adjustment for Linear Regression[J]. Journal of Geodesy,2008, 82 (7) : 415 –421 . |
| [4] | SHEN Yunzhong, LI Bofeng, CHEN Yi. An Iterative Solution of Weighted Total Least-squares Adjustment[J]. Journal of Geodesy,2011, 85 (4) : 229 –238 . |
| [5] | MAHBOUB V. On Weighted Total Least-squares for Geodetic Transformations[J]. Journal of Geodesy,2012, 86 (5) : 359 –367 . |
| [6] | AMIRI-SIMKOOEI A R, JAZAERI S. Weighted Total Least Squares Formulated by Standard Least Squares Theory[J]. Journal of Geodetic Science,2012, 2 (2) : 113 –124 . |
| [7] | FANG Xing. Weighted Total Least Squares: Necessary and Sufficient Conditions, Fixed and Random Parameters[J]. Journal of Geodesy,2013, 87 (8) : 733 –749 . |
| [8] | JAZAERI S, AMIRI-SIMKOOEI A R, SHARIFI M A. Iterative Algorithm for Weighted Total Least Squares Adjustment[J]. Survey Review,2014, 46 (334) : 19 –27 . |
| [9] | XU Peiliang, LIU Jingnan, SHI Chuang. Total Least Squares Adjustment in Partial Errors-in-variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy,2012, 86 (8) : 661 –675 . |
| [10] | SHI Yun, XU Peiliang, LIU Jingnan, et al. Alternative Formulae for Parameter Estimation in Partial Errors-in-variables Models[J]. Journal of Geodesy,2015, 89 (1) : 13 –16 . |
| [11] | ZENG Wenxian, LIU Jingnan, YAO Yibin. On Partial Errors-in-variables Models with Inequality Constraints of Parameters and Variables[J]. Journal of Geodesy,2015, 89 (2) : 111 –119 . |
| [12] | SCHAFFRIN B, UZUN S. Errors-in-variables for Mobile Mapping Algorithms in the Presence of Outliers[J]. Archives of Photogrammetry, Cartography and Remote Sensing,2011, 22 : 377 –387 . |
| [13] | SCHAFFRIN B, UZUN S. On the Reliability of Errors-in-variables Models[J]. Acta et Commentationes Universitatis Tartuensis De Mathematica,2012, 16 (1) : 69 –81 . |
| [14] |
陈义, 陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J].测绘学报,2012, 41 (5) : 715 –722 .
CHENG Yi, LU Jue. Performing 3D Similarity Transformation by Robust Total Least Squares[J]. Acta Geodaetica et Cartographica Sinica,2012, 41 (5) : 715 –722 . |
| [15] | MAHBOUB V, AMIRI-SIMKOOEI A R, SHARIFI M A. Iteratively Reweighted Total Least Squares: A Robust Estimation in Errors-in-variables Models[J]. Survey Review,2013, 45 (329) : 92 –99 . |
| [16] | LU J, CHEN Y, LI B F, FANG X. Robust Total Least Squares with Reweighting Iteration for Three-dimensional Similarity Transformation[J]. Survey Review,2014, 46 (334) : 28 –36 . |
| [17] | TAO Y Q, GAO J X, YAO Y F. TLS Algorithm for GPS Height Fitting Based on Robust Estimation[J]. Survey Review,2014, 46 (336) : 184 –188 . |
| [18] | ROUSSEEUWP J, LEROYA M. Robust Regression and Outlier Detection[M]. New York: John Wiley & Sons, 1987 . |
| [19] | KOCHK R. Parameter Estimation and Hypothesis Testing in Linear Models 2nd ed[M]. New York: Springer, 1999 . |
| [20] | HUBERP J. Robust Statistics[M]. New York: John Wiley & Sons, 1981 . |
| [21] |
周江文. 经典误差理论与抗差估计[J].测绘学报,1989, 18 (2) : 115 –120 .
ZHOU Jiangwen. Classical Theory of Errors and Robust Estimation[J]. Acta Geodaetica et Cartographica Sinica,1989, 18 (2) : 115 –120 . |
| [22] | YANG Y, SONG L, XU T. Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights[J]. Journal of Geodesy,2002, 76 (6-7) : 353 –358 . |
| [23] | YANG Y. Robust Estimation for Dependent Observations[J]. Manuscripta Geodaetica,1994, 19 (1) : 10 –17 . |
| [24] | YANG Y. Robust Estimation of Geodetic Datum Transformation[J]. Journal of Geodesy,1999, 73 (5) : 268 –274 . |
| [25] | XU Peiliang. Sign-constrained Robust Least Squares, Subjective Breakdown Point and the Effect of Weights of Observations on Robustness[J]. Journal of Geodesy,2005, 79 (1-3) : 146 –159 . |
| [26] | GUO Jianfeng, OU Jikun, WANG Haitao. Robust Estimation for Correlated Observations: Two Local Sensitivity-Based Downweighting Strategies[J]. Journal of Geodesy,2010, 84 (4) : 243 –250 . |
| [27] |
黄维彬.
近代平差理论及其应用[M]. 北京: 解放军出版社, 1992 .
HUANG Weibin. Theory and Applications of Modern Adjustment[M]. Beijing: PLA Publishing House, 1992 . |
| [28] |
郭建锋, 赵俊. 粗差探测与识别统计检验量的比较分析[J].测绘学报,2012, 41 (1) : 14 –18 .
GUO Jianfeng, ZHAO Jun. Comparative Analysis of Statistical Tests Used for Detection and Identification of Outliers[J]. Acta Geodaetica et Cartographica Sinica,2012, 41 (1) : 14 –18 . |
| [29] | KELLY G. The Influence Function in the Errors in Variables Problem[J]. The Annals of Statistics,1984, 12 (1) : 87 –100 . |