2. 武汉大学地球空间环境与大地测量教育部重点实验室,湖北 武汉 430079 ;
3. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079 ;
4. 广东工业大学测绘工程系,广东 广州 510006
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China ;
3. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China ;
4. Department of Surveying and Mapping, Guangdong University of Technology, Guangzhou 510006, China
地形起伏反映了局部重力场的高频扰动信息,精确确定地形影响对于局部重力场的精确逼近具有重要的意义[1-2]。残差地形模型(RTM)可逼近地形扰动引起的高频信号,不引入频谱混叠效应,在局部重力场建模中有广泛的应用[3-5]。文献[6]采用残差地形模型改善了重力场模型高频部分的精度,削弱了截断误差的影响;文献[7]联合EGM2008重力场模型和残差地形模型提高了山区大地水准面的精度;文献[8]联合EGM2008和SRTM/DTM2006.0残差地形模型改善了GPS高程转换的精度。残差地形模型仅考虑平滑面与地形面间的质量,平滑面以上的多余质量被移除,以下的缺失质量被填充。经残差地形改正后,重力场逼近的边界面变为该平滑面。若重力点位于平滑面以下,则该点位于质量体内部,不满足重力场逼近中的调和性条件,即为残差地形模型中的非调和性问题[3]。
文献[3]提出调和改正处理非调和性问题。将平滑面内部的重力点与平滑面之间的质量压缩为位于该点以下一个无限薄的质量层,使得测量点重新位于质量体外部,满足调和性条件。基于移去-恢复法,文献[3]提出的方法仅在移去阶段对平滑面以下的重力点施加调和改正,在恢复阶段则忽略了引入调和改正的影响。上述处理方法显然值得讨论,移去阶段改变了重力场观测参量,恢复阶段也需考虑其相应的影响。而如何合理地施加调和改正,综合考虑调和改正在移去及恢复阶段对外部重力场影响的研究尚未有成果发表。此外,文献[9]从理论上比较基于棱柱体与球冠体积分的残差地形模型的差别,认为广泛使用棱柱体模型精度较低,可能引入较大误差,但并未通过实测多源重力数据进行数值分析。本文基于多源重力观测数据,比较棱柱体和球冠体模型的差异,为积分体的选择提供支持。针对非调和性问题,基于解析延拓的思想提出广义残差地形模型,结合基于径向基函数构建局部重力场模型的算例验证该模型的有效性。
1 广义残差地形模型 1.1 质量体模型一般而言,积分质量体可为棱柱体、楔形体及球冠体等几何体,只要基于该质量体的积分公式具有解析形式即可[9]。使用最为广泛的质量体模型为棱柱体[10-12],其引力位模型可以表示为
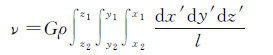 (1)
(1)
式中,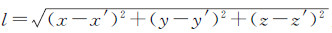
由于地球曲率的影响,即使采用高分辨率的数字地形模型,棱柱体之间也会存在空隙,基于棱柱体的积分质量元逼近真实的地形模型只是较为粗略的近似,可能会影响到残差地形模型逼近重力场高频信号的精度[9]。与棱柱体相比,球冠体模型考虑了地球曲率的影响,能更为准确地描述地形表面,且球冠体之间没有空隙,精度较高,其引力位为
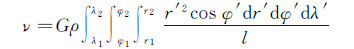 (2)
(2)
式中,λ1、λ2、φ1、φ2、r1、r2为划分球冠体的经圈、纬圈及地心半径的积分上下限。
1.2 广义调和改正模型重力测量点位于高程平滑面以下时,为满足调和性条件,需对其施加调和改正。假设重力点与平滑面间的质量层可视为一个内半径为R,厚度为Δh(外半径为R+Δh),密度为ρ的球层。此球层在其内部任意点x产生的引力位为
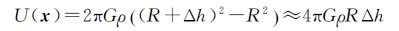 (3)
(3)
该球层对内部任意一点的引力位均为常数,引力位的一阶导数 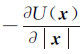
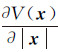
 (4)
(4)
 (5)
(5)
假设将位于平滑面内部的重力点与平滑面间的质量层(当作球层对待)压缩为位于重力点以下一无限薄的质量层,此时μ=ρΔh。移动球层时,对其内部点的引力没有影响。压缩之后,由于薄层质量的影响,引力增加了4πGρΔh,即为调和改正。对比式(3)和式(4)可知,重力点的引力位变化较小,文献[3]认为施加调和改正对高程异常的影响也可忽略,因此调和改正只在移去阶段施加于的重力场观测量,而忽略其在恢复阶段对引力位或高程异常影响。实际情况中,重力点与平滑面之间的质量层不能完全当作球层对待,在移去阶段对重力观测值施加调和改正,必然会对外部引力位产生影响,在恢复阶段需考虑其影响。本文基于解析延拓的思想,将所有位于高程平滑面以下的重力测量点延拓到此平滑面上,综合考虑调和改正在移去及恢复阶段的影响,提出改进的残差地形模型,将其称为基于广义调和改正的残差地形模型,简称为广义残差地形模型(generalized residual terrain model)。
假设P点为残差地形改正后位于地形质量内的重力点,Q点为相应于P点位于高程平滑面上的点,根据泰勒展开式,忽略高阶展开项的影响,Q点的残余扰动位为
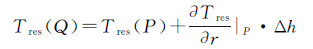 (6)
(6)
式中,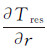
基于式(6),利用移去-恢复法,Q点的残余重力观测值为
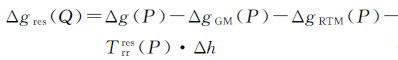 (7)
(7)
式中,Δg为重力异常;ΔgGM为全球重力场模型表示的中长波部分;ΔgRTM表示残差地形模型代表的高频效应;Trrres·Δh表示重力场参量必要的调和改正;Trrres表示残余扰动位径向二阶导数。P、Q两点间存在地形质量的影响,而计算地形质量体内部的扰动位的径向二阶导数较为复杂。实际计算时采用近似计算,即由于P与Q之间地形质量的影响有限,本文忽略两者之间的地形影响,采用下式近似逼近计算Trrres[13]
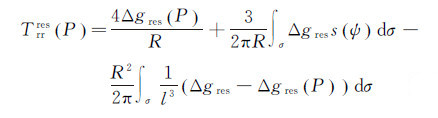 (8)
(8)
式中,ΔgresP为P点的残余重力异常;R为球面半径;σ为单位球面;dσ为球面面元;ψ为计算点与流动点之间的球面角距;s(ψ)为广义Stokes函数;l为计算点与流动面元之间的距离。值得注意的是,计算残余重力参量Δgres时需已知残余扰动位的径向二阶导数Trrres,而计算Trrres同样要已知Δgres,因此实际计算中需迭代逼近计算Δgres和Trrres。
Q点残余高程异常为
 (9)
(9)
式中,γ表示正常重力值,本文以残余重力扰动逼近计算残余扰动位的径向一阶导数 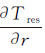
泊松小波径向基函数在空间域和频率域都有较好的局部化特性,可融合多源重力场数据,适合局部重力场建模[14-18]。基于移去-恢复法,残余扰动位Tres可表示为有限个泊松小波基函数之和[17]
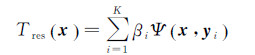 (10)
(10)
式中,x为重力场观测数据的三维坐标;y表示基函数的三维位置,通常位于Bjerhammar球内部;K为基函数的个数;βi表示基函数的未知参数;Ψ(x,yi)表示泊松小波径向基函数,其形式可参见文献[17—18]。
多源重力场观测数据可表示为扰动位的泛函,重力扰动δg、重力异常Δg及高程异常ζ在球面近似条件下分别与扰动位存在如下函数关系
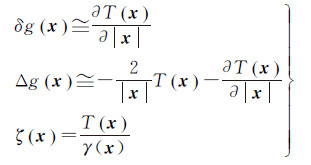 (11)
(11)
结合式(10),对于某一类观测值可以建立观测方程如下
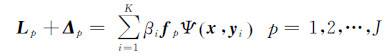 (12)
(12)
式中,Lp表示第p类的重力场信息观测值;Δp表示观测误差;fp表示此类观测值与扰动位之间的泛函关系;J表示观测数据种类的个数。将式(12)改写为误差方程的形式如下
 (13)
(13)
式中,Ap表示mp×K设计矩阵;X表示K×1基函数的未知参数向量;lp表示mp×1误差方程的常数项向量;Vp表示mp×1观测值残差向量,mp表示该类重力场观测值的个数。总的误差方程为
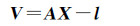 (14)
(14)
式中
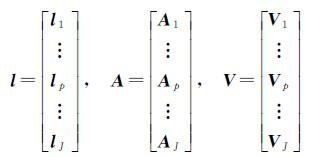 (15)
(15)
假定不同类型的观测值之间互不相关,观测数据的方差-协方差阵为
 (16)
(16)
式中,CJ=σJ2QJ表示第J类观测值的方差-协方差阵,QJ为其协因数阵,σJ2为单位权方差因子。
利用最小二乘原理,基函数的未知参数向量X的估值可表示为
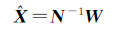 (17)
(17)
式中
 (18)
(18)
 (19)
(19)
采用方差分量估计的方法对各类观测值进行合理地定权,各类观测值的单位权方差因子估计如下[19]
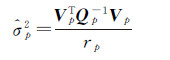 (20)
(20)
式中,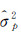
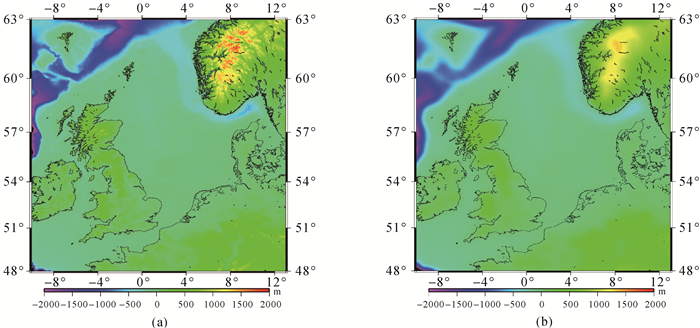
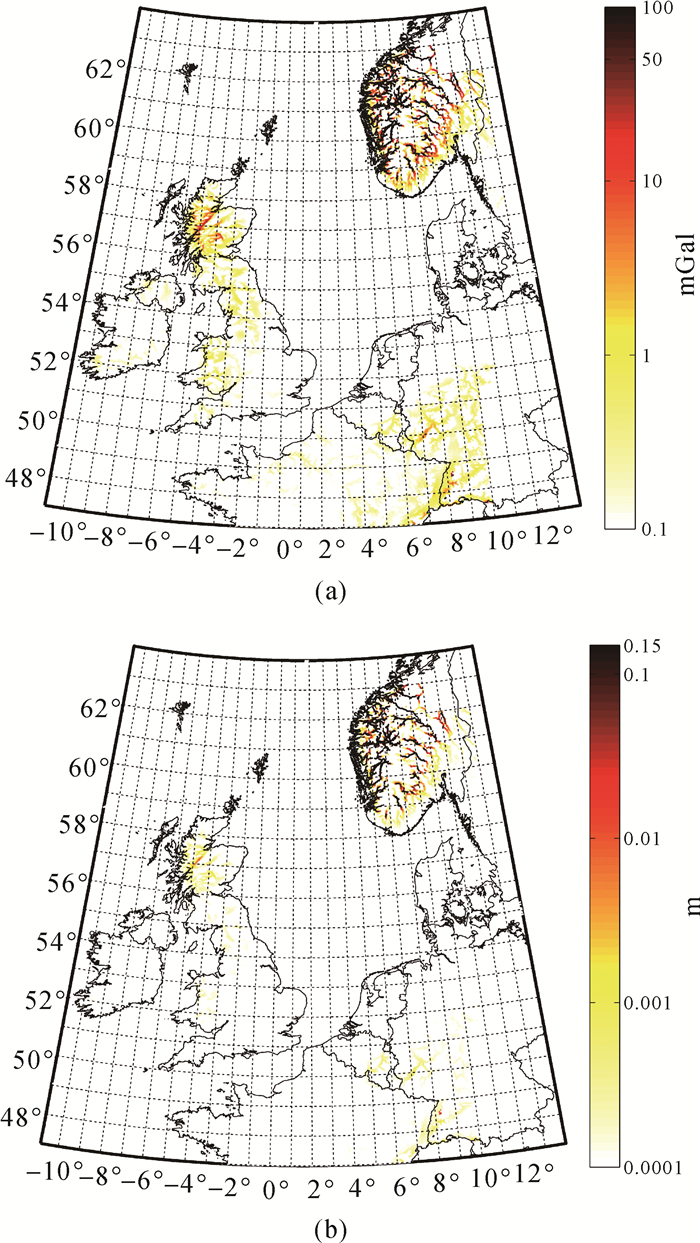
基于Eurodem、SRTM以及GEBCO 3种数字地形模型构建了局部区域高精度、高分辨率(2″×2″)陆海统一的数字地形模型,见图 1(a)。重力场模型采用DGM1S模型,其球谐展开阶数达到250阶[20]。采用移动平均法构建残差地形模型中的高程平滑面[10-11],如图 1(b)所示,其空间分辨率与DGM1S相一致。收集了覆盖整个荷兰、比利时、英国及部分德国、法国、丹麦、挪威和北海区域的多源重力数据。通过交叉点平差完成了船载、航空重力数据中系统偏差的校正;利用阈值法和hampel滤波剔除了多源数据中的粗差;采用低通滤波削弱了船载、航空重力数据中的高频噪声的影响,并将各类重力数据归算到同一参考框架(ETRS89)及垂直基准(EVRF2007)。基于移去-恢复法,利用DGM1S模型和残余地形模型移去重力场的长波和短波信号,计算的残余重力观测数据见图 2,其统计信息见表 1。同时收集了上述国家部分区域的高精度的GPS水准数据,并将其归算到统一的参考框架及垂直基准。
|
| 图 1 局部区域的数字地形模型(a)及高程平滑面(b) Fig. 1 Digital terrain model (a) and mean elevation surface (b) |
|
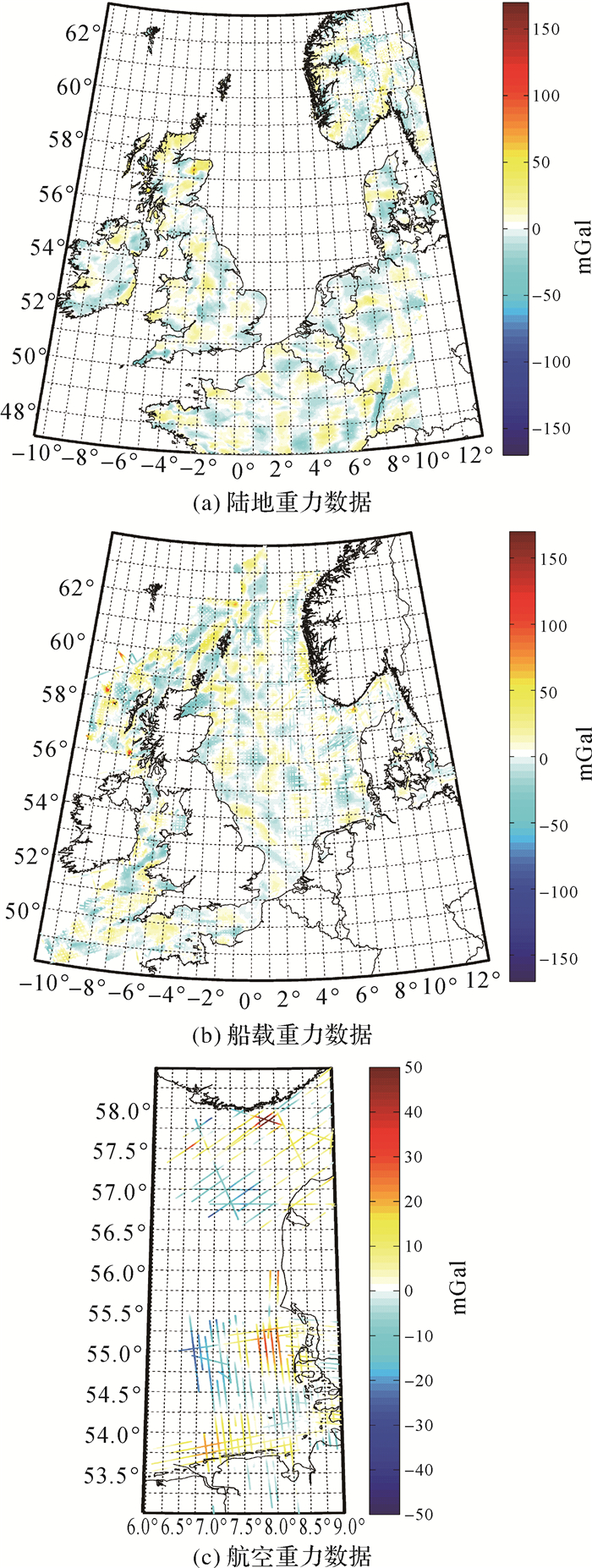
| 图 2 残余重力观测数据 Fig. 2 Residual gravity observations |
| Gal | |||||
| 参数 | max | min | mean | std | rms |
| 陆地重力异常 | 90.474 | -165.521 | -1.086 | 10.652 | 10.707 |
| 船载重力异常 | 158.392 | -78.932 | -0.746 | 12.403 | 12.425 |
| 航空重力扰动 | 49.226 | -25.752 | 2.150 | 10.446 | 10.664 |
3.2 积分体模型的选择
基于不同积分体模型计算的残差地形改正的差异如图 3所示,结合表 2可知,基于棱柱体与球冠体积分的残差地形改正存在差异,其陆地、船载重力异常和航空重力扰动地形改正差异的标准差分别为1.156 mGal、0.390 mGal及0.078 mGal。以陆地重力异常为例,两者的差异主要集中在英国北部、挪威南部及德国和法国的部分多山区域,其量级达到毫伽级。与球冠体积分模型相比,棱柱体模型的求解精度相对较低,特别在地势起伏较大的多山区域,忽略地球曲率的影响可能会引入较大的误差。后续计算中采用基于球冠体积分的残差地形模型用于高频重力场信息的逼近。
| Gal | |||||
| 参数 | max | min | mean | std | rms |
| 陆地重力异常 | 9.286 | -5.810 | 0.177 | 1.156 | 1.169 |
| 船载重力异常 | 4.632 | -3.479 | 0.005 | 0.390 | 0.390 |
| 航空重力扰动 | 0.946 | -0.158 | 0.020 | 0.078 | 0.080 |

|
| 图 3 基于球冠体和棱柱体积分模型计算的残差地形改正的差异 Fig. 3 The difference of the RTM correction computed from prism and tesseroid model |
3.3 基于广义残差地形模型的局部重力场逼近
基于泊松小波基函数,结合广义残差地形模型,融合陆地、船载重力异常及航空重力扰动构建局部重力场模型。试算区域覆盖荷兰、比利时、英国、爱尔兰及部分挪威、德国、法国和北海区域,其纬度范围为47°—63°,经度范围为-11°—13°,基于等间隔格网构建基函数的网络[17],采用约为55 000个泊松小波基函数,其空间分辨率约为7.1 km。图 4(a)表示基于广义残差地形模型计算的重力观测数据的调和改正,其信号主要集中在挪威南部、英国北部及德国西南部的山脉区域。在地形起伏剧烈的多山区域,反映地形中长波段信息的高程平滑面与真实地形起伏差距较大。若重力观测点位于高程平滑面以下,需施加的调和改正较大,局部范围内可达数十毫伽。图 4(b)显示了调和改正在恢复阶段对高程异常的影响。在地形较为平坦的地区,其影响仅达到毫米量级。而在地势起伏较大的英国北部及挪威南部山区,调和改正的影响可达厘米甚至分米级,忽略其影响会引入较大的误差。表 3、表 4分别给出了基于广义残差地形模型和原始模型构建的似大地水准面的检核结果。基于两种模型构建的似大地水准面在地形起伏较为平缓的荷兰、比利时及德国区域精度相当。而在地形起伏较大挪威南部和英国北部山区,结合广义残差地形模型构建的似大地水准面的精度分别提高了约2.1 cm和1.7 mm。
|
| 图 4 基于广义残差地形模型解算的调和改正对重力观测数据和高程异常的影响 Fig. 4 The effect of harmonic corrections on gravity observations and height anomaly computed from the generalized RTM |
| cm | |||||
| 国家 | max | min | mean | std | rms |
| 荷兰 | 8.936 | 0.153 | 3.835 | 1.124 | 3.996 |
| 比利时 | 3.262 | -13.865 | -3.527 | 2.795 | 4.500 |
| 德国 | 6.509 | -11.472 | -3.145 | 2.884 | 4.267 |
| 英国 | 8.122 | -15.980 | -4.696 | 4.926 | 6.806 |
| 挪威 | 11.501 | -18.152 | -8.655 | 5.012 | 10.001 |
| cm | |||||
| 国家 | max | min | mean | std | rms |
| 荷兰 | 8.936 | 0.153 | 3.837 | 1.124 | 3.998 |
| 比利时 | 3.264 | -13.878 | -3.537 | 2.802 | 4.512 |
| 德国 | 6.509 | -11.776 | -3.200 | 2.924 | 4.335 |
| 英国 | 8.122 | -16.972 | -4.778 | 5.092 | 6.983 |
| 挪威 | 18.699 | -27.193 | -10.701 | 7.119 | 12.853 |
4 结 论
本文研究了残差地形模型中的非调和性问题,比较了基于棱柱体和球冠体的积分模型,并基于解析延拓的思想提出了基于球冠体积分的广义残差地形模型。利用径向基函数方法,结合广义残差地形模型,融合实测的陆地、船载重力异常及航空重力扰动数据构建了局部区域陆海统一的似大地水准面模型。结果表明:与球冠体积分模型相比,棱柱体模型的求解精度相对较低,特别在地势起伏较大的多山区域,忽略地球曲率的影响可能会引入毫伽级以上的误差。在地形较为平坦的区域,调和改正对高程异常产生的影响仅达到毫米量级,在厘米级似大地水准面的构建中可忽略其影响。而在地形起伏较大的山区,忽略调和改正的影响可能引入厘米甚至分米级的误差。广义残差地形模型综合考虑了调和改正在移去及恢复阶段的影响,能更为精确地逼近地形因素引起的高频效应。与原始的残差地形模型相比,结合广义残差地形模型构建的似大地水准面的精度在地形起伏较大的英国及挪威山区分别提高了1.7 mm和2.1 cm。
| [1] |
罗志才, 陈永奇, 宁津生. 地形对确定高精度局部大地水准面的影响[J].武汉大学学报(信息科学版),2003, 28 (3) : 340 –344 .
LUO Zhicai, CHEN Yongqi, NING Jinsheng. Effect of Terrain on the Determination of High Precise Local Gravimetric Geoid[J]. Geomatics and Information Science of Wuhan University,2003, 28 (3) : 340 –344 . |
| [2] |
章传银, 晁定波, 丁剑, 等. 厘米级高程异常地形影响的算法及特征分析[J].测绘学报,2006, 35 (4) : 308 –314 .
ZHANG Chuanyin, CHAO Dingbo, DING Jian, et al. Arithmetic and Characters Analysis of Terrain Effects for cm Order Precision Height Anomaly[J]. Acta Geodaetica et Cartographica Sinica,2006, 35 (4) : 308 –314 . |
| [3] | FORSBERG R, TSCHERNING C C. The Use of Height Data in Gravity Field Approximation by Collocation[J]. Journal of Geophysical Research,1981, 86 (B9) : 7843 –7854 . |
| [4] | OMANG O C D, FORSBERG R. How to Handle Topography in Practical Geoid Determination: Three Examples[J]. Journal of Geodesy,2000, 74 (6) : 458 –466 . |
| [5] | HIRT C, MARTI U, BVRKI B, et al. Assessment of EGM2008 in Europe Using Accurate Astrogeodetic Vertical Deflections and Omission Error Estimates from SRTM/DTM2006.0 Residual Terrain Model Data[J]. Journal of Geophysical Research,2010, 115 (B10) : 196 –211 . |
| [6] | HIRT C. RTM Gravity Forward-modeling Using Topography/ Bathymetry Data to Improve High-degree Global Geopotential Models in the Coastal Zone[J]. Marine Geodesy,2013, 36 (2) : 183 –202 . |
| [7] | HIRT C, FEATHERSTONE W E, MARTI U. Combining EGM2008 and SRTM/DTM2006.0 Residual Terrain Model Data to Improve Quasigeoid Computations in Mountainous Areas Devoid of Gravity Data[J]. Journal of Geodesy,2010, 84 (9) : 557 –567 . |
| [8] |
张兴福, 刘成. 综合EGM2008模型和SRTM/DTM2006.0剩余地形模型的GPS高程转换方法[J].测绘学报,2012, 41 (1) : 25 –32 .
ZHANG Xingfu, LIU Cheng. The Approach of GPS Height Transformation Based on EGM2008 and SRTM/DTM2006.0 Residual Terrain Model[J]. Acta Geodaetica et Cartographica Sinica,2012, 41 (1) : 25 –32 . |
| [9] | HECK B, SEITZ K. A Comparison of The Tesseroid, Prism and Point-mass Approaches for Mass Reductions in Gravity Field Modelling[J]. Journal of Geodesy,2007, 81 (2) : 121 –136 . |
| [10] | HIRT C. Prediction of Vertical Deflections from High-degree Spherical Harmonic Synthesis and Residual Terrain Model Data[J]. Journal of Geodesy,2010, 84 (3) : 179 –190 . |
| [11] | TZIAVOS I N, VERGOS G S, GRIGORIADIS V N. Investigation of Topographic Reductions and Aliasing Effects on Gravity and the Geoid over Greece Based on Various Digital Terrain Models[J]. Surveys in Geophysics,2010, 31 (1) : 23 –67 . |
| [12] | NAGY D, PAPP G, BENEDEK J. The Gravitational Potential and Its Derivatives for the Prism[J]. Journal of Geodesy,2000, 74 (7) : 552 –560 . |
| [13] |
宁津生, 李建成, 晁定波. 由地面重力数据确定扰动位径向二阶梯度[J].武汉测绘科技大学学报,1996, 21 (3) : 201 –206 .
NING Jinsheng, LI Jiancheng, CHAO Dingbo. Determination of the 2nd Radial Gradient of Disturbing Potential Using Terrestrial Gravity Data[J]. Journal of Wuhan Technical University of Surveying and Mapping,1996, 21 (3) : 201 –206 . |
| [14] | ANTUNES C, PAIL R, CATALÃO J. Point Mass Method Applied to the Regional Gravimetric Determination of the Geoid[J]. Studia Geophysica et Geodaetica,2003, 47 (3) : 495 –509 . |
| [15] | BENTEL K, SCHMIDT M, GERLACH C. Different Radial Basis Functions and Their Applicability for Regional Gravity Field Representation on the Sphere[J]. GEM-International Journal on Geomathematics,2013, 4 (1) : 67 –96 . |
| [16] | BENTEL K, SCHMIDT M, DENBY C R. Artifacts in Regional Gravity Representations with Spherical Radial Basis Functions[J]. Journal of Geodetic Science,2013, 3 (3) : 173 –187 . |
| [17] | KLEES R, TENZER R, PRUTKIN I, et al. A Data-driven Approach to Local Gravity Field Modelling Using Spherical Radial Basis Functions[J]. Journal of Geodesy,2008, 82 (8) : 457 –471 . |
| [18] | TENZER R, KLEES R. The Choice of the Spherical Radial Basis Functions in Local Gravity Field Modeling[J]. Studia Geophysica et Geodaetica,2008, 52 (3) : 287 –304 . |
| [19] | KUSCHE J. Noise Variance Estimation and Optimal Weight Determination for GOCE Gravity Recovery[J]. Advances in Geosciences,2003, 1 : 81 –85 . |
| [20] | FARAHANI H H, DITMAR P, KLEES R, et al. The Static Gravity Field Model DGM-1S from GRACE and GOCE Data: Computation, Validation and an Analysis of GOCE Mission’s Added Value[J]. Journal of Geodesy,2013, 87 (9) : 843 –867 . |



