2. 海军海洋测绘研究所,天津 300061 ;
3. 海军工程大学导航工程系,湖北 武汉 430033
2. Naval Institute of Hydrographic Surveying and Charting, Tianjin 300061, China ;
3. Department of Navigation, Naval University of Engineering, Wuhan 430033, China
精化大地水准面始终是现代物理大地测量学永恒的研究主题[1-2]。精密确定大地水准面需要联合利用卫星、航空、地面、海洋等多源重力和地形高数据,其计算过程涉及多源数据的融合处理问题。向下延拓是多源重力数据融合处理必不可少的技术环节,在数据准备阶段,需要将卫星和航空重力测量成果延拓到地面作联合处理;在边值问题解算阶段,需要将地面重力数据延拓到大地水准面。由于物理场向下延拓在数学上属于不适定反问题,求解此类问题存在很大的不确定性[3],一直以来国内外诸多学者为解决这一棘手问题付出了不懈的努力[4-28]。目前解决向下延拓问题主要有3种途径,第1种是直接求逆泊松(Poisson)积分方程,是应用比较广泛的主流途径[29],国内外学者主要围绕求逆过程引起的不稳定性问题开展不同形式的正则化方法研究[10, 13, 16, 18-23, 25-26];第2种是间接求逆途径,包括最小二乘配置方法[30-32]、虚拟点质量方法[1-2]和矩谐分析法[24]等,此类方法虽然避开了求逆Poisson方程,但仍涉及矩阵求逆过程,因此也不可避免存在不稳定性问题[33-34];第3种可统称为非求逆途径,文献[17]提出的利用航空重力测量和DEM确定地面重力场的直接代表法,文献[27—28]提出的联合使用超高阶位模型和地形信息确定向下延拓改正数的方法(以下简称差分延拓法)等都属于非求逆途径的范畴,此类方法不受传统求逆过程不稳定性的影响。文献[29]基于带限(band-limited)航空重力测量数据特有的频谱特性,提出了向下延拓的直接积分公式(以下简称频谱截断法),并将其推广应用于大地水准面的直接解算[35],其计算过程也避开了方程求逆问题。文献[13]将频谱截断方法和基于求逆过程的各类正则化方法作了全面的数值比较和分析,得出的结论是,前者的计算精度和效率都明显优于其他方法。
如前所述,困扰向下延拓问题的关键是其本身固有的不适定性。文献[9]曾对向下延拓的稳定性问题做过深入分析,同时提出了改善计算稳定性的地形效应补偿方法;文献[11, 13, 14, 29, 35]专门针对航空重力向下延拓问题,开展了大量有效的数值计算和比对工作,得出了一些极具参考价值的结论。由已有的研究成果得知,虽然向下延拓问题本身是不适定的,但其解算结果的不稳定程度取决于延拓计算高度和数据分辨率(即网格间距大小)两个方面。在一定条件下,向下延拓解算方程可以是良态的,而在超越一定界限以后,即使采用正则化处理技术,也无法取得有效的解算结果[11, 13]。因此,对于实际应用来说,最要紧的是预先掌控前面所指的一定“条件”和“界限”,尽可能在规定的“条件”下开展航空重力测量作业,避免超越已知的“界限”,只有这样才能获得预期的测量成果。另一方面,地形效应对重力向下延拓解算结果具有重要影响,因为求逆过程的稳定性不仅取决于积分方程系数矩阵的结构,还取决于观测向量的频谱特性[9],故可通过地形效应的“移去-恢复”运算来改变重力观测量的频谱特征,从而改善向下延拓解算的稳定性。本文的目的是,通过理论分析、模拟仿真和实际数值计算等手段,对当前国内外最具代表性的3种向下延拓模型进行全面的分析比较和适用性检验,力争为工程应用提供具有可操作性的延拓计算方案。
1 计算模型及稳定性分析 1.1 逆Poisson积分迭代解延拓模型由文献[6]知,Poisson积分向上延拓公式为
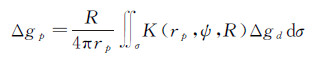 (1)
(1)
 (2)
(2)
式中,Δgp为空中计算点的重力异常;R为地球平均半径;rp=R+H,H为计算点的大地高;D3=r2p+R2-2rpRcos ψ,ψ为rp和R之间的夹角;Δgd为地面重力异常;dσ为单位积分面积元。式(1)把积分面视为球面,忽略了地形高度的影响,因此它只是一个近似的球面解模型。
向下延拓计算是求式(1)的逆问题,即已知Δgp,要求Δgd。对式(1)作离散化处理,可得一线性方程组,用矩阵形式表示为
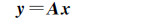 (3)
(3)
式中,y为由航空重力测量获得的已知重力异常向量;x为待求的球面重力异常向量;A为由式(1)积分核函数确定的系数矩阵。可采用如下的Jacobi迭代法解算方程式(3)[9],将A改写为
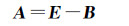 (4)
(4)
代入式(3)有
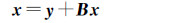 (5)
(5)
 (6)
(6)
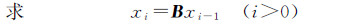 (7)
(7)
当|xi-xi-1|<ε时,结束迭代计算,方程解为
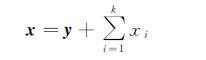 (8)
(8)
式中,E为单位矩阵;ε为给定的某个大于零的限差值;k为迭代次数。
在实际应用中,由于观测数据有限,一般将球面积分区域划分为近区和远区,近区是以计算点为中心、ψ0为半径的球冠区域σ0,近区影响直接由观测数据计算;远区是球面上的剩余部分(σ-σ0),远区影响由位系数模型按下式计算[11, 13]
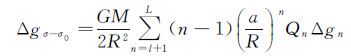 (9)
(9)
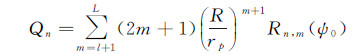 (10)
(10)
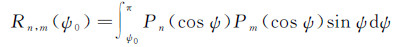 (11)
(11)
式中,GM为地球引力常数;L为位系数模型的最高阶数;l为参考场位模型的最高阶数;a为参考椭球长半轴;Δgn代表重力异常n阶面球谐函数;Qn为Poisson核截断系数;Rn,m(ψ0)可由已知的递推公式计算,具体参见文献[36—37]。此时,对应于式(3)的离散形式为
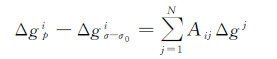 (12)
(12)
式中,N为待求点个数,一般取与已知点个数相同。为了减小中心数据块(即与计算点重合的数据块)离散化误差的影响,可按下式计算系数矩阵A的对角线元素[13]
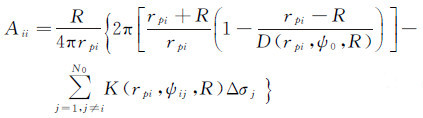 (13)
(13)
矩阵A的非对角线元素为
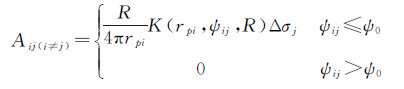 (14)
(14)
式中,N0为位于积分球冠区σ0内的数据点个数;Δσj为数据块面积。
如前所述,式(1)只是近似的球面解模型,式(1)只能反解得到等高度面(即球面或近似为大地水准面)上的重力异常,而非地形面上的重力异常。如果是向下延拓到大地水准面上,那么由于大地水准面外地形质量的存在,使得其延拓解与物理意义上的现实性不相对应,即这里的延拓解只是一组虚拟的重力异常[6]。这类重力异常可单独应用于物理大地测量参数计算,但不宜与其他类型重力异常数据联合使用。为了求得地形面上的重力异常,提出如下位场延拓球面化曲面方法:
(1) 将计算区域的地形高度变化范围(Hmax-Hmin),按整百米间隔(如100 m或200 m)划分为若干个等高度面;
(2) 利用前面的迭代法依次计算出各个等高度面上的重力异常;
(3) 通过内插方法计算得到位于两个等高面之间的地形面上的重力异常。
此外,为了改善向下延拓解算的稳定性,可通过地形效应的“移去-恢复”运算改变重力观测量的频谱特征[9],即首先在航空重力测量成果中移去地形质量对空间点的作用,然后在延拓计算结果中恢复地形质量对地面点的影响。地形效应改正的计算模型可参见文献[1, 28]。
1.2 频谱截断积分延拓模型由于受到飞行环境动态效应的影响,航空重力测量原始观测数据中一般包含上千甚至上万毫伽(mGal=10-5m/s2)的干扰加速度信息[38-39]。为了消除高频干扰噪声的影响,通常需要对航空重力测量数据作低通滤波处理,以获取所需的重力异常信息。但经滤波处理后的重力测量成果必定会损失掉一部分有用的高频重力信息,损失量值大小取决于滤波截断频率的选择,实际应用中需要平衡好测量精度和分辨率两方面的需求。由此可见,航空重力测量成果是经过高频截断后的重力异常场信息,不包含某个频率(L)以上的高频分量。而在对航空重力测量成果作进一步处理(如向下延拓)时,通常还需要引入全球重力场模型(GGM)进行移去-恢复运算,即事先需要从航空重力测量成果中移去GGM的影响,然后在解算结果中作反向的恢复运算。这说明,实际参与向下延拓解算的航空重力测量数据是一类有限带宽的重力场信息(band-limited airborne gravity data)[29]。设GGM的最高阶次为(l-1),则有L=l+b,b称为航空重力测量数据的带宽。如何合理利用航空重力测量数据有限带宽的频谱特性,是有效提高向下延拓解算过程稳定性的关键。文献[9、11、13—14、29、35]全面研究了等高飞行条件下的航空重力测量数据延拓问题,提出了如下相对稳定的频谱截断积分向下延拓公式。
设在恒等高度H的飞行面上获取了一组有限带宽航空重力异常数据Δgb(R+H),飞行面与大地水准面之间已经不存在地形质量,要求确定大地水准面(近似为半径R的球面)上相对应的有限带宽扰动位Tb(R)。理论上可将上述问题表述为如下的伪边值问题[9, 29]
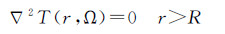 (15)
(15)
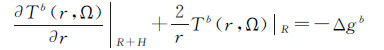 (16)
(16)
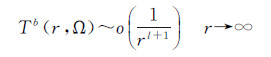 (17)
(17)
对式(16)中的双边值面作近似处理并转换为单边值面后[9],可求得上述问题的扰动位解为[29]
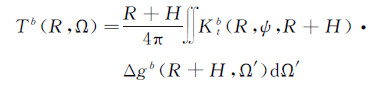 (18)
(18)
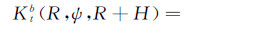 (191)
(191)
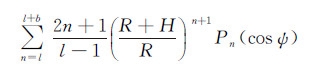 (19)
(19)
式中,Ω=(φ,λ),Ω′=(φ′,λ′),Ktb(R,ψ,R+H)为扰动位的带限核函数。对应于式(18)的重力异常向下延拓计算公式为[13]
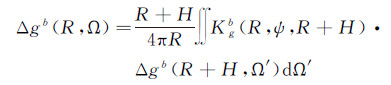 (20)
(20)
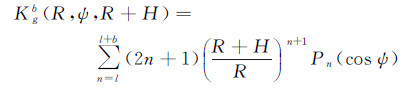 (21)
(21)
式中,Kgb(R,ψ,R+H)为重力异常的带限核函数。使用上述频谱截断延拓模型的前提条件是,观测网格数据必须位于同一个高度面上。当此条件无法严格满足(即测点飞行高度存在一定的差异)时,可考虑采用超高阶重力位模型将不同高度的测点归算到统一的平均高度面上,具体方法和步骤参见文献[27]。此外,对式(20)实施实际计算时,同样需要将全球积分划分为近区和远区,类似于式(9)—式(11),远区效应计算模型如下
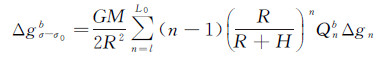 (22)
(22)
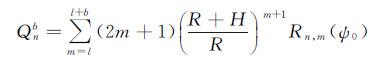 (23)
(23)
式中,L0为位模型最高阶次,且L0≤L,其他符号意义同前。对于近区计算,同样需要对中心数据块作精细化处理,以减小离散化误差的影响。类似于式(13)和式(14),此时对应于积分式(20)的系数矩阵Ab的对角线元素为
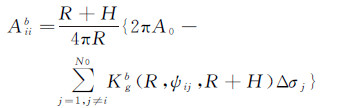 (24)
(24)
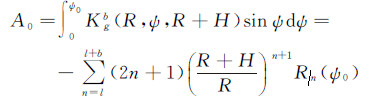 (25)
(25)
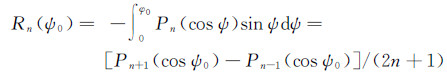 (26)
(26)
矩阵Ab的非对角线元素为
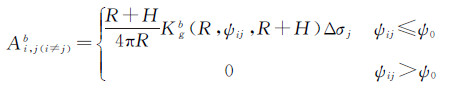 (27)
(27)
式中其他符号意义同前。由式(20)可直接计算得到地形面上的重力异常,故无须作位场延拓平面化曲面处理,此时数据面高度保持不变(r=R+H),计算面高度由R改变为(R+hi),hi代表地面计算点的大地高。类似于前一小节的做法,这里同样需要通过地形效应的“移去-恢复”运算,来消除计算面与数据面之间的地形质量影响,以改善向下延拓解算的稳定性。
1.3 基于位模型和地形改正差分的延拓模型为了规避传统逆Poisson积分向下延拓解算过程的不适定性问题,文献[27—28]借鉴导航定位中的“差分”概念,曾先后提出了利用超高阶位模型和地形高信息,直接实施海域和陆部航空重力测量数据向下延拓计算的新方案。其中,陆部顾及地形效应延拓方案的核心思想是:以飞行高度面与地面对应点的位模型重力异常差分信息表征向下延拓总改正数的中长波分量,以相对应的局部地形改正差分修正量表征总改正数的中高频成分,从而实现航空重力数据向地面点对点的全频段延拓。具体延拓计算模型为[28]
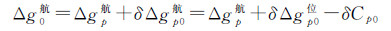 (28)
(28)
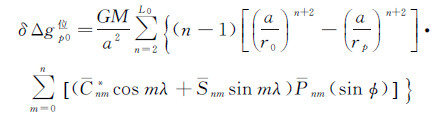 (29)
(29)
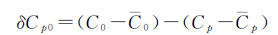 (30)
(30)
式中,Δg0航代表待求的地面重力异常;Δgp航代表空中观测重力异常;δΔgp0航代表向下延拓改正数真值;δΔgp0位为位模型延拓差分改正数;δCp0为局部地形效应差分改正数;Cp代表空中测点P的局部地形改正数; 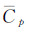
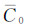
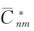
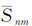
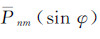
如前言所述,重力场向下延拓计算在数学上属于不适定反问题,其解算过程存在不稳定性是该问题本身固有的一种属性[3]。理论上,由逆Poisson积分公式(1)组成的向下延拓解算方程属于第一类弗雷德霍姆(Fredholm)积分方程,当且仅当满足如下的Picard条件时,该方程存在唯一的收敛解[9]
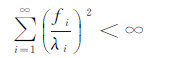 (31)
(31)
式中,fi代表已知航空重力观测量Δgp的傅里叶(Fourier)展开系数;λi代表Poisson核函数的特征值。式(31)说明,要想确保逆Poisson积分方程有解,从某个阶次开始,Fourier系数fi的衰减速度必须快于特征值λi的衰减速度。
对于离散化形式的线性方程组即式(3),通常采用如下的系数矩阵条件数指标来度量方程解的病态性[9, 20]
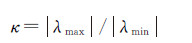 (32)
(32)
式中,λmax和λmin分别代表系数矩阵A之特征值的最大值和最小值。一般认为[20],当0 <κ<100时,方程组是良态的;当100≤κ≤1000时,定义为中等程度病态;当κ>1000时,定义为严重病态。对于在恒等飞行高度H条件下的航空重力向下延拓问题,逆Poisson积分方程系数矩阵的条件数可近似表示为[9, 11]
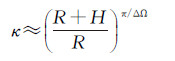 (33)
(33)
式中,π/ΔΩ称为奈奎斯特(Nyquist)频率,ΔΩ为数据网格间距。取ΔΩ=2′,5′,可分别计算得到对应于不同延拓高度H的条件数κ,具体结果如表 1所示。必须指出的是,式(33)给出的条件数只是一种理论上的病态性度量指标,受各种扰动因素影响后,实际问题解的变化特性则要复杂得多,其稳定性除了取决于系数矩阵的结构外,还取决于已知观测量的频谱特性[9]。文献[11]在完成大量的数值计算和分析比较后发现,航空重力数据向下延拓解算的稳定性与数据网格间距和延拓高度的比值(α=ΔΩ/H)密切相关,在受到观测噪声干扰的情况下,只有当比值α>1.1时,直接利用航空重力数据确定的局部大地水准面解才是有效的。而航空重力异常直接向下延拓到地面结果的精度要比前者悲观得多,即使采用一些正则化方法进行优化处理,也无法彻底解决观测噪声的放大问题,要想获得可接受的地面重力异常延拓结果,必须尽可能降低航空重力测量的飞行高度[11]。本文将在第2节继续对此问题进行数值计算和检验。表 1同时列出了数据网格间距分别取ΔΩ=2′,5′时,对应于不同延拓高度的比值α。
| ΔΩ | H/km | 1 | 2 | 3 | 5 | 7 | 10 |
| 2′ | κ | 2.3 | 5.4 | 12.7 | 69.2 | 376.1 | 4 766.0 |
| α | 3.7 | 1.9 | 1.2 | 0.7 | 0.5 | 0.4 | |
| 5′ | κ | 1.4 | 2.0 | 2.8 | 5.4 | 10.7 | 29.6 |
| α | 9.3 | 4.6 | 3.1 | 1.9 | 1.3 | 0.9 |
2 数值计算与分析
为了检验上述各个计算模型的延拓效果,分别采用模拟仿真和实测数据两种方式开展数值计算及分析比较研究。
2.1 模拟仿真计算与分析 2.1.1 试验数据与计算方案以美国本土一个3°×3°区块作为试验区,选用EGM2008位模型作为标准场模拟产生不同高度的2′×2′网格航空和大地水准面(即高度为零)重力异常。之所以选择美国本土作为试验区,是考虑到EGM2008位模型在美国地区具有更高的逼近度[40-41],并与3.2节选用的实测数据试验区取得一致。该区块属于地形变化比较剧烈的大山区,试验效果具有一定的说服力。分别以1 km、3 km和5 km 3个高度的位模型重力异常作为观测量,依次采用逆Poisson积分(简称模型1)和频谱截断积分(简称模型2)两种计算模型,将3个不同高度面上的网格重力异常延拓到零高度面,并将其同由位模型计算得到的零高度面观测量(作为基准值)进行比较,从而获取相应的计算模型精度评估参数。由于基于位模型和地形改正差分的延拓模型(简称模型3)本身就是建立在超高阶位模型之上的,因此该模型暂不参加本阶段的数值计算检验。
为了进一步考察观测噪声对延拓计算结果的影响,特别设计在模拟观测量中分别加入±1 mGal和±3 mGal的随机噪声,生成对应高度面上的带噪声的两组观测量,并重复前面的计算过程和对比分析。上述误差量值与当前国内外航空重力测量的精度水平相当[11, 14, 29, 35, 42],因此其检验结论具有实用意义。本试验统一采用EGM2008位模型的前360阶次作为参考场(GGM),对应于零高度面和3个不同高度面的EGM2008位模型(361~2160阶次)残差重力异常统计结果见表 2。
| 高度/km | 最小值/mGal | 最大值/mGal | 平均值/mGal | 均方根/mGal |
| 0 | -107.09 | 189.19 | -0.44 | 34.28 |
| 1 | -88.22 | 162.05 | -0.39 | 30.26 |
| 3 | -68.34 | 120.33 | -0.33 | 24.07 |
| 5 | -55.22 | 90.66 | -0.28 | 19.56 |
2.1.2 计算结果与分析
本试验在一个高度面上共有网格观测数据30×3×30×3=8100个,对应于模型1,需要求解8100阶线性方程组,采用Jacobi迭代法解算时,迭代终止参数取ε=0.1 mGal;对于模型2,模型参数分别取为l=361、L=L0=2160、b=1799;积分半径统一取为ψ0=1°。按照前面设计的计算方案,对3个高度和两个模型分别解算无误差和有误差干扰条件下的零高度面延拓重力异常,同时将其与零高度面基准值作比较,具体计算结果如表 3所示。为了减小积分边缘效应对统计结果的影响,计算区域边缘1°范围内的数据不参加对比分析。
| 高度/km | 模型 | 误差/mGal | 最小值/mGal | 最大值/mGal | 平均值/mGal | 均方根/mGal |
| 1 | 1 | 0 | -0.61 | 0.44 | -0.01 | 0.14 |
| 1 | -5.49 | 5.09 | -0.057 | 1.74 | ||
| 3 | -19.14 | 16.38 | -0.12 | 5.09 | ||
| 2 | 0 | -0.96 | 1.11 | 0.01 | 0.35 | |
| 1 | -1.61 | 1.41 | -0.00 | 0.51 | ||
| 3 | -3.35 | 4.23 | 0.03 | 1.23 | ||
| 3 | 1 | 0 | -0.36 | 0.24 | -0.01 | 0.08 |
| 1 | -27.39 | 33.40 | -0.08 | 9.63 | ||
| 3 | -99.81 | 88.31 | -0.01 | 28.56 | ||
| 2 | 0 | -1.22 | 1.34 | 0.01 | 0.44 | |
| 1 | -2.50 | 2.18 | -0.00 | 0.77 | ||
| 3 | -6.03 | 6.86 | 0.03 | 1.97 | ||
| 5 | 1 | 0 | -0.25 | 0.28 | -0.01 | 0.09 |
| 1 | -218.81 | 261.87 | -0.24 | 75.35 | ||
| 3 | -700.82 | 680.86 | 0.64 | 230.59 | ||
| 2 | 0 | -1.67 | 1.73 | 0.02 | 0.62 | |
| 1 | -4.11 | 3.47 | 0.00 | 1.25 | ||
| 3 | -11.04 | 12.21 | 0.04 | 3.31 |
从表 3结果可以看出,对于无误差干扰条件下的输入数据,模型1和模型2都能给出比较理想的输出结果,基本不受计算高度大小的影响。但对于有误差干扰条件下的输入数据,模型1和模型2计算效果则表现出非常显著的差异。在3 km以下计算高度,模型2对数据误差具有一定的抑制作用,只有当延拓高度增大到5 km时,模型2才对数据误差产生一定的放大效应,这一结果充分体现了模型2作为正解模型及其截断核函数所具有的超强的抗干扰能力。模型1的解算结果则明显受到数据误差的干扰,在所有计算高度上,模型1对数据误差都有放大作用,计算结果严重失真,当数据误差大于1 mGal,计算高度超过1 km时,模型1的解算结果都是不可靠的。这一结果说明,虽然在理想情况下,通过迭代计算求解逆Poisson积分方程,也能收敛到问题的理论解[6, 9]。但当观测数据存在噪声干扰时,由于反问题自身固有的不适定性,观测噪声将在迭代过程中得到累积和放大,使得较小的噪声干扰也会引起问题解出现较大的变化,最终造成解算结果严重偏离真解。
表 3所列结果也进一步验证了2.4节对逆Poisson积分延拓模型所作的稳定性分析结论,即传统延拓模型在实际应用中明显受到数据分辨率、计算高度和观测噪声等多种因素的制约。虽然使用正则化方法可在一定程度上减弱传统模型向下延拓解算的不稳定性,但要想确定合适的正则化矩阵和正则化参数都不是一件容易的事[18-26]。当正则化参数取的太小时,其应用结果可能达不到抑制观测噪声的作用;而当正则化参数取的过大时,其解算结果会变得过于平滑,也就意味着损失掉了观测量中的一部分有用信息。总之,正则化方法在实际应用中仍存在许多不确定性问题需要研究解决,因此笔者不主张优先选用正则化方法来解决向下延拓解算问题,而是应该设法限制航空重力测量作业高度,以满足实用意义下的稳定性解算要求,或是开辟新的技术途径,寻求更加稳定的解算方法。表 3计算结果表明,模型2在计算稳定性方面具有非常明显的技术优势,因此具有良好的应用前景。
2.2 地面实测数据计算与分析 2.2.1 试验数据与计算方案检验向下延拓计算模型适用性最有效的方法是,直接使用实测航空重力数据完成向下延拓计算,将计算结果与地面实测重力基准值进行比较,由此可得到不同计算模型的精度评价指标。遗憾的是,陆部同时拥有高精度高分辨率航空和地面实际重力观测数据的区域并不多见,目前笔者还缺乏这方面的可靠资料。为此,本文改用向上与向下延拓比对方法对计算模型精度进行外部检核,即首先利用地面网格重力和地形高数据,通过向上延拓方法计算得到一定高度面上的空中重力异常,将其作为航空重力测量的观测量,进而使用不同的计算模型将其向下延拓到地面,求取延拓计算值与地面已知网格重力值的差异,便可获得相应延拓计算模型的精度评价。
这里继续选用与2.1节完全相同的美国本土3°×3°区块作为试验区,开展航空重力向下延拓的实际数值计算和对比分析。该区块同时拥有2′×2′网格地面观测重力异常和30″×30″网格地形高数据,两组数据的变化特征如表 4所示。
| 参量 | 最小值 | 最大值 | 平均值 | 均方根 |
| 重力/mGal | -96.2 | 167.2 | 5.5 | 40.5 |
| 高程/m | 1 056.0 | 4 116.0 | 1 987.3 | 2 034.5 |
使用“先向下后向上”方法[6, 43],首先将地面重力向下延拓到大地水准面,然后将其向上延拓到5 km高度面。为了考察地形效应对向下延拓计算结果的影响,这里采用两种途径完成地面重力向下延拓解算,得到两组大地水准面上的重力值,一种途径是直接采用原始观测重力异常Δg0(1)和式(3)进行纯粹数学意义上的向下延拓计算,得到一组虚拟的重力异常Δg*(1),此方法不扰乱外部重力场[6];另一种途径是首先从地面重力中扣除掉大地水准面以外地形质量引力的影响,得到调整后的重力异常Δg0(2),然后将其向下延拓到大地水准面,得到一组消除地形效应影响后的延拓重力异常Δg*(2)。最后利用Δg*(1)和Δg*(2)可由式(1)向上延拓得到对应5 km高度面的两组航空重力观测量Δgp(1)和Δgp(2),并根据模型1和模型2完成后续的向下延拓计算。但此时需要确定的是地形面上的重力异常,故向下延拓计算高度面是对应于地面网格点高度的等高面。对于模型1,需要利用前面提出的位场延拓球面化曲面方法,将球面上的计算结果内插到地面上的各个测点;模型2可直接计算得到测点上的重力异常;模型3通过局部地形改正差分方式顾及了地形效应的影响,故只需参加由Δg0(1)生成的观测量检验。考虑到本文关注的重点是计算模型的适用性和地形效应的影响,不必过分追求计算结果的绝对精度,故可对向上和向下延拓模型参数设置作统一的近似处理。这里将大地水准面近似为球面,统一取ri=R+hi,rp=R+H,hi为地面点高程,其他符号意义同前。此时模型2的计算参数取为l=361,L=5400,b=5039,L0=2160,即与2′×2′数据分辨率相一致,其他模型参数保持不变。
2.2.2 计算结果与分析按照前面设计的计算方案,分别采用上述3个计算模型完成5 km高度面各两组观测数据的向下延拓解算,将其分别与相对应的地面基准值Δg0(1)和Δg0(2)作比较,具体计算结果如表 5所示。
| mGal | |||||
| 观测量 | 模型 | 最小值 | 最大值 | 平均值 | 均方根 |
| Δgp(1) | 1 | -1.72 | 1.50 | -0.01 | 0.44 |
| 2 | -10.05 | 5.99 | -0.77 | 2.63 | |
| 3 | -5.24 | 4.04 | 0.16 | 1.83 | |
| Δgp(2) | 1 | -1.91 | 1.57 | 0.01 | 0.35 |
| 2 | -7.11 | 4.27 | 0.13 | 1.73 | |
表 5结果显示,模型1的检核效果反而明显好于模型2和模型3,这是由于作为观测量的空中重力异常是由地面重力异常通过Poisson积分向上延拓得到的,它与模型1使用的逆Poisson积分形成闭环关系,其计算模型误差有相互抵消作用,因此该比对结果不能作为评价模型一计算性能的依据,但相应结果至少说明本文提出的位场延拓球面化曲面方法和顾及地形效应策略是可行有效的。由于模型2和模型3的计算原理与Poisson积分向上延拓过程无关,故表 5中对应于模型2和模型3的检核结果是独立有效的。从表 5看出,当不顾及地形效应影响时,模型2的检核精度为±2.63 mGal;而当使用移去-恢复方法顾及地形影响时,模型2的检核精度提高到±1.73 mGal。考虑到使用Poisson积分向上延拓解作为观测量可能存在1~2 mGal的数据误差[44],与新型航空重力测量系统精度水平基本相当[42],对照表 3的仿真检验结果,不难看出,表 5给出的实测数据检核结果完全符合预期,同时说明顾及地形效应对提高模型2的计算精度具有显著成效。模型3的计算输入量与航空重力测量观测量无关,计算过程稳定可靠,且模型自身就具备顾及地形效应的功能,因此具有较高的计算精度,达到±1.83 mGal,与顾及地形效应后的模型2计算精度水平相当。
3 结 论根据前面的模型适用性分析和数值计算比对结果,可得出以下基本结论:
(1) 基于逆Poisson积分的传统向下延拓模型明显受到数据分辨率、计算高度和观测噪声等多种因素的制约,即使在比较理想的数据精度条件下,最大延拓高度也只能达到1 km。使用正则化方法可在一定程度上提高传统延拓模型的稳定性,但其解算过程仍存在较多的不确定性因素,不利于该模型的推广应用。
(2) 基于频谱截断积分的直接向下延拓模型具有良好的计算稳定性,对高频观测噪声干扰具有很好的抑制作用。在当前航空重力测量通常采用的2′分辨率和3 km飞行高度条件下,该模型几乎可以不损失观测数据精度的能力恢复地球表面的重力异常,因此具有良好的应用前景。在实际应用中需要注意把握的问题是积分核函数截断阶数与航空重力测量数据滤波截止频率的匹配关系。解算结果存在一定的边缘效应,同时观测数据网格化处理给测线布设带来的三维空间约束等因素是影响该模型推广应用的主要障碍。
(3) 基于位模型和地形改正差分的直接向下延拓模型具有良好的应用前景,其计算过程完全独立于航空重力观测数据,因此不受观测噪声的干扰。其计算精度取决于超高阶位模型和局部地形改正差分的相对精度,在现有技术条件下,该模型延拓计算精度可达2 mGal,与当前航空重力测量精度水平相当。与模型2相比较,不需要对观测数据作网格化预处理,也不存在积分边缘效应,可实现空中和地面点对点延拓计算是该模型的主要优势。但关于该模型物理意义的严密解释还有待进一步的研究,并通过更多的实际观测数据计算来验证其应用效果。
| [1] |
李建成, 陈俊勇, 宁津生, 等.
地球重力场逼近理论与中国2000似大地水准面的确定[M]. 武汉: 武汉大学出版社, 2003 .
LI Jiancheng, CHEN Junyong, NING Jinsheng, et al. Theory of the Earth’s Gravity Field Approximation and Determination of China Quasi-geoid 2000[M]. Wuhan: Wuhan University Press, 2003 . |
| [2] |
黄谟涛, 翟国君, 管铮, 等.
海洋重力场测定及其应用[M]. 北京: 测绘出版社, 2005 .
HUANG Motao, ZHAI Guojun, GUAN Zheng, et al. The Determination and Application of Marine Gravity Field[M]. Beijing: Surveying and Mapping Press, 2005 . |
| [3] |
王彦飞.
反演问题的计算方法及其应用[M]. 北京: 高等教育出版社, 2007 .
WANG Yanfei. Computational Methods for Inverse Problems and Their Applications[M]. Beijing: Higher Education Press, 2007 . |
| [4] | PELLINEN L P. Accounting for Topography in the Calculation of Quasigeoidal Heights and Plumb-line Deflections from Gravity Anomalies[J]. Bulletin Géodésique,1962, 63 (1) : 57 –65 . |
| [5] | BJERHAMMAR A. Gravity Reduction to a Spherical Surface[R]. Stockholm: Royal Institute of Technology, 1962. |
| [6] | HEISKANEN W A, MORITZ H. Physical Geodesy[M]. San Francisco: Freeman W H and Company, 1967 . |
| [7] | JEKELI C. The Downward Continuation of Aerial Gravimetric Data without Density Hypothesis[J]. Bulletin Géodésique,1987, 61 (4) : 319 –329 . |
| [8] | WANG Y M. The Effect of Topography on the Determination of the Geoid Using Analytical Downward Continuation[J]. Bulletin Géodésique,1990, 64 (3) : 231 –246 . |
| [9] | MARTINEC Z. Stability Investigations of a Discrete Downward Continuation Problem for Geoid Determination in the Canadian Rocky Mountains[J]. Journal of Geodesy,1996, 70 (11) : 805 –828 . |
| [10] | XU Peiliang. Truncated SVD Methods for Discrete Linear Ill-posed Problems[J]. Geophysical Journal International,1998, 135 (2) : 505 –514 . |
| [11] | NOVÁK P, KERN M, SCHWARZ K P. Numerical Studies on the Harmonic Downward Continuation of Band-limited Airborne Gravity[J]. Studia Geophysica et Geodaetica,2001, 45 (4) : 327 –345 . |
| [12] | MUELLER F,MAYER-GUERR T.Comparison of Downward Continuation Methods of Airborne Gravimetry Data[C]//Proceedings of the International Association of Geodesy IAG General Assembly Sapporo. Berlin: Springer, 2005, 128: 254-258. |
| [13] | KERN M. An Analysis of the Combination and Downward Continuation of Satellite, Airborne and Terrestrial Gravity Data[D]. Calgary: University of Calgary, 2003. |
| [14] | ALBERTS B, KLEES R. A Comparison of Methods for the Inversion of Airborne Gravity Data[J]. Journal of Geodesy,2004, 78 (1-2) : 55 –65 . |
| [15] | TZIAVOS I N, ANDRITSANOS V D, FORSBERG R, et al. Numerical Investigation of Downward Continuation Methods for Airborne Gravity Data[C]//GGSM 2004 IAG International Symposium Porto. Berlin Heidelberg: Springer, 2005, 129: 119-124. |
| [16] | ALBERTS B. Regional Gravity Field Modeling Using Airborne Gravimetry Data[C]//Publications on Geodesy 70. Delft: Netherlands Geodetic Commission, 2009. |
| [17] |
石磐, 王兴涛. 利用航空重力测量和DEM确定地面重力场[J].测绘学报,1997, 26 (2) : 117 –121 .
SHI Pan, WANG Xingtao. Determination of the Terrain Surface Gravity Field Using Airborne Gravimetry and DEM[J]. Acta Geodaetica et Cartographica Sinica,1997, 26 (2) : 117 –121 . |
| [18] |
沈云中, 许厚泽. 不适定方程正则化算法的谱分解式[J].大地测量与地球动力学,2002, 22 (3) : 10 –14 .
SHEN Yunzhong, XU Houze. Spectral Decomposition Formula of Regularization Solution for Ill-posed Equation[J]. Journal of Geodesy and Geodynamics,2002, 22 (3) : 10 –14 . |
| [19] |
王兴涛, 石磐, 朱非洲. 航空重力测量数据向下延拓的正则化算法及其谱分解[J].测绘学报,2004, 33 (1) : 33 –38 .
WANG Xingtao, SHI Pan, ZHU Feizhou. Regularization Methods and Spectral Decomposition for the Downward Continuation of Airborne Gravity Data[J]. Acta Geodaetica et Cartographica Sinica,2004, 33 (1) : 33 –38 . |
| [20] |
王振杰.
测量中不适定问题的正则化解法[M]. 北京: 科学出版社, 2006 .
WANG Zhenjie. Regularization Methods for Ill-posed Problem in Survey[M]. Beijing: Science Press, 2006 . |
| [21] |
顾勇为, 归庆明. 航空重力测量数据向下延拓基于信噪比的正则化方法的研究[J].测绘学报,2010, 39 (5) : 458 –464 .
GU Yongwei, Gui Qingming. Study of Regularization Based on Signal-to-noise Index in Airborne Gravity Downward to the Earth Surface[J]. Acta Geodaetica et Cartographica Sinica,2010, 39 (5) : 458 –464 . |
| [22] |
蒋涛, 李建成, 王正涛, 等. 航空重力向下延拓病态问题的求解[J].测绘学报,2011, 40 (6) : 684 –689 .
JIANG Tao, LI Jiancheng, WANG Zhengtao, et al. Solution of Ill-posed Problem in Downward Continuation of Airborne Gravity[J]. Acta Geodaetica et Cartographica Sinica,2011, 40 (6) : 684 –689 . |
| [23] |
邓凯亮, 黄谟涛, 暴景阳, 等. 向下延拓航空重力数据的Tikhonov双参数正则化法[J].测绘学报,2011, 40 (6) : 690 –696 .
DENG Kailiang, HUANG Motao, BAO Jingyang, et al. Tikhonov Two-parameter Regulation Algorithm in Downward Continuation of Airborne Gravity Data[J]. Acta Geodaetica et Cartographica Sinica,2011, 40 (6) : 690 –696 . |
| [24] |
蒋涛, 党亚民, 章传银, 等. 基于矩谐分析的航空重力向下延拓[J].测绘学报,2013, 42 (4) : 475 –480 .
JIANG Tao, DANG Yamin, ZHANG Chuanyin, et al. Downward Continuation of Airborne Gravity Data Based on Rectangular Harmonic Analysis[J]. Acta Geodaetica et Cartographica Sinica,2013, 42 (4) : 475 –480 . |
| [25] |
孙文, 吴晓平, 王庆宾, 等. 航空重力数据向下延拓的波数域迭代Tikhonov正则化方法[J].测绘学报,2014, 43 (6) : 566 –574 .DOI:10.13485/j.cnki.11-2089.2014.0080.
SUN Wen, WU Xiaoping, WANG Qingbin, et al. Wave Number Domain Iterative Tikhonov Regularization Method for Downward Continuation of Airborne Gravity Data[J]. Acta Geodaetica et Cartographica Sinica,2014, 43 (6) : 566 –574 .DOI:10.13485/j.cnki.11-2089.2014.0080. |
| [26] |
刘晓刚, 李迎春, 肖云, 等. 重力与磁力测量数据向下延拓中最优正则化参数确定方法[J].测绘学报,2014, 43 (9) : 881 –887 .DOI:10.13485/j.cnki.11-2089.2014.0160.
LIU Xiaogang, LI Yingchun, XIAO Yun, et al. Optimal Regularization Parameter Determination Method in Downward Continuation of Gravimetric and Geomagnetic Data[J]. Acta Geodaetica et Cartographica Sinica,2014, 43 (9) : 881 –887 .DOI:10.13485/j.cnki.11-2089.2014.0160. |
| [27] |
黄谟涛, 欧阳永忠, 刘敏, 等. 海域航空重力测量数据向下延拓的实用方法[J].武汉大学学报(信息科学版),2014, 39 (10) : 1147 –1152 .
HUANG Motao, OUYANG Yongzhong, LIU Min, et al. Practical Methods for Downward Continuation of Airborne Gravity Data in the Sea Area[J]. Geomatics and Information Science of Wuhan University,2014, 39 (10) : 1147 –1152 . |
| [28] |
黄谟涛, 宁津生, 欧阳永忠, 等. 联合使用位模型和地形信息的陆区航空重力向下延拓方法[J].测绘学报,2015, 44 (4) : 355 –362 .DOI:10.11947/j.AGCS.2015.20130751.
HUANG Motao, NING Jinsheng, OUYANG Yongzhong, et al. Downward Continuation of Airborne Gravimetry on Land Using Geopotential Model and Terrain Information[J]. Acta Geodaetica et Cartographica Sinica,2015, 44 (4) : 355 –362 .DOI:10.11947/j.AGCS.2015.20130751. |
| [29] | NOVÁK P, HECK B. Downward Continuation and Geoid Determination Based on Band-limited Airborne Gravity Data[J]. Journal of Geodesy,2002, 76 (5) : 269 –278 . |
| [30] | MORITZ H. MORITZ H. Advanced Physical Geodesy[M]. Karlsruhe: Herbert Wichmann Verlag, 2009 . |
| [31] | HWANG C, HSIAO Y S, SHIH H C, et al. Geodetic and Geophysical Results from a Taiwan Airborne Gravity Survey: Data Reduction and Accuracy Assessment[J]. Journal Geophysical Research,2007, 112 (B4) : 93 –101 . |
| [32] | FORSBERG R, OLESEN A V. Airborne Gravity Field Determination[M]//XU Guochang. Sciences of Geodesy-I. Berlin: Springer-Verlag, 2010: 83-103. |
| [33] |
黄谟涛, 欧阳永忠, 翟国君, 等. 融合多源重力数据的Tikhonov正则化配置法[J].海洋测绘,2013, 33 (3) : 6 –12 .
HUANG Motao, OUYANG Yongzhong, ZHAI Guojun, et al. Tikhonov Regularization Collocation for Multi-source Gravity Data Fusion Processing[J]. Hydrographic Surveying and Charting,2013, 33 (3) : 6 –12 . |
| [34] |
黄谟涛, 欧阳永忠, 刘敏, 等. 融合海域多源重力数据的正则化点质量方法[J].武汉大学学报(信息科学版),2015, 40 (2) : 170 –175 .
HUANG Motao, OUYANG Yongzhong, LIU Min, et al. Regularization of Point-mass Model for Multi-source Gravity Data Fusion Processing[J]. Geomatics and Information Science of Wuhan University,2015, 40 (2) : 170 –175 . |
| [35] | NOVÁK P, KERN M, SCHWARZ K P, et al. On Geoid Determination from Airborne Gravity[J]. Journal of Geodesy,2003, 76 (9-10) : 510 –522 . |
| [36] | PAUL M K. A Method of Evaluating the Truncation Error Coefficients for Geoidal Height[J]. Bulletin Géodésique,1973, 110 (1) : 413 –425 . |
| [37] |
陆仲连. 球谐函数[R]. 郑州: 测绘学院, 1984. LU Zhonglian. Spherical Harmonic Function[R]. Zhengzhou: Surveying and Mapping Institute, 1984. |
| [38] | OLESEN A V. Improved Airborne Scalar Gravimetry for Regional Gravity Field Mapping and Geoid Determination[D]. Copenhagen: University of Copenhagen, 2002. |
| [39] |
孙中苗. 航空重力测量理论、方法及应用研究[D]. 郑州:信息工程大学, 2004. SUN Zhongmiao. Theory, Methods and Applications of Airborne Gravimetry[D]. Zhengzhou: Information Engineering University, 2004. |
| [40] | PAVLIS N K, HOLMES S A, KENYON S C, et al. The Development and Evaluation of the Earth Gravitational Model 2008 (EGM 2008)[J]. Journal Geophysical Research,2012, 117 (B4) : 531 –535 . |
| [41] |
章传银, 郭春喜, 陈俊勇, 等. EGM 2008地球重力场模型在中国大陆适用性分析[J].测绘学报,2009, 38 (4) : 283 –289 .
ZHANG Chuanyin, GUO Chunxi, CHEN Junyong, et al. EGM 2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica,2009, 38 (4) : 283 –289 . |
| [42] |
欧阳永忠, 邓凯亮, 陆秀平, 等. 多型航空重力仪同机测试及其数据分析[J].海洋测绘,2013, 33 (4) : 6 –11 .
OUYANG Yongzhong, DENG Kailiang, LU Xiuping, et al. Tests of Multi-type Airborne Gravimeters and Data Analysis[J]. Hydrographic Surveying and Charting,2013, 33 (4) : 6 –11 . |
| [43] | MORITZ H. The Computation of the External Gravity Field and the Geodetic Boundary-Value Problem[C]//Proceedings of the Symposium on the Extension of Gravity Anomalies to Unsurveyed Areas. Geophysical Monograph Series Number 9. [S.l.]: American Geophysical Union of the National Academy of Sciences, 1966: 127-136. |
| [44] | ARGESEANU V S. Upward Continuation of Surface Gravity Anomaly Data[C]//Proceedings of the IAG Symposium on Airborne Gravity Field Determination. Boulder: [s.n.], 1995: 95-102. |


