矢量空间数据匹配的困难之一来自数据的多源性、不一致性。长期以来,由于地图数据采集和维护由不同部门完成,导致多源数据在位置精度、数据模型等方面千差万别,给数据集成和更新带来困难。空间数据匹配是空间数据集成与更新的核心技术,是指通过对目标的几何、拓扑和语义进行相似性度量,识别出同一地区不同来源空间数据集中的同一地物[1],从而建立同名目标间的联接,为数据集成共享奠定基础。
线要素是矢量空间数据的常见类型,其匹配也是当前空间数据匹配领域研究的焦点之一。针对线要素匹配的研究已有很多,例如文献[2]采用缓冲区增长方法进行线要素匹配;文献[3]基于道路节点匹配,加入弧段距离、长度、角度、拓扑关系等特征信息进行弧段匹配;部分研究注重与数学方法结合,文献[4]提出了一种基于概率的匹配模型,综合运用多个匹配指标,可有效解决非一对一匹配;也有学者借助形状匹配领域的方法,采用一些形状描述函数,比如傅里叶描述子[5]、转角函数[6]等,对线要素进行形态表达,进而比较其形态相似度以完成匹配。针对多尺度道路网匹配,文献[7]根据道路网折线的匹配特点,提出一种基于格网索引的“折线—节点”距离匹配算法;文献[8]将道路网数据处理成以“节点—弧段”表达的网络数据,通过预匹配、节点匹配、弧段匹配3个步骤,实现最终的匹配运算。
通过以上分析可以发现,目前大多数线要素匹配算法集中在对新技术与新算法的研制、改进等,许多方法已经很成熟,匹配的正确率也已大幅提升。与此同时,突破也越来越困难。为进一步提升空间数据匹配的正确率,本文在已有匹配算法基础上,从其外部出发,将制图综合中的化简技术与线要素匹配方法相结合,通过对线要素化简处理来辅助已有匹配算法从而进一步提高其匹配正确率。
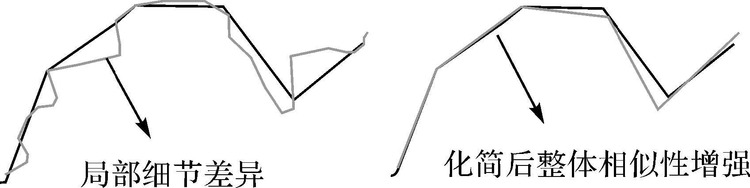
1 动态化简方法及其阈值确定 1.1 基本思想化简的实质,是要删除细节层次,提取其主要形态。现实中,多源数据相互之间在局部细节形态上可能差异较大,给已有匹配算法带来匹配困难。但其整体形态往往是高度一致的,可以充分利用这一特性,完成线要素的匹配。如图 1,同名要素经化简后减少了细节层次和局部位置差异,使得整体形态相似程度增强。因此,若采用化简把线要素局部形态的细节层次删除,只保留主要形态特征,而后利用已有匹配算法对化简后的数据重新进行匹配,其匹配正确率必然会有较大提升。本文基于这一思想展开研究。
|
| 图 1 同名要素化简前后整体形态相似度对比 Fig. 1 Comparison of the integral similarity of corresponding features before and after simplification |
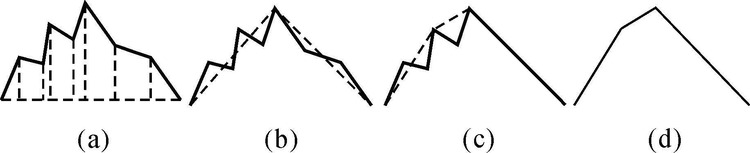
线要素化简算法有很多,如Douglas-Peucker法[14](简称D-P算法,图 2)、垂距法[15]、斜拉式弯曲划分曲线化简方法[16]等。引入化简的作用在于减少要素的复杂度,这是化简的最基本特性,因此本文对各类化简算法是普遍适用的。本文选择具有代表性的D-P算法来验证线要素动态化简方法对提高匹配正确率的作用。
|
| 图 2 D-P算法化简示意图 Fig. 2 The schematic of D-P simplification algorithm |
D-P算法能从整体上有效保持线要素的形态特征,并较好地保持线要素的几何特征和位置精度[9]。其基本思想是:首先连接曲线的端点与末端点;再计算曲线上其他各点至连线的垂距,并找出垂距最大的点;然后将最大垂距点与指定的阈值进行比较,若垂距小于阈值,则将中间所有的点舍去,用连线代替该曲线;否则保留该点,并将原曲线分为两段,分别重复以上步骤,直至无垂距大于阈值的点存在。
1.2.2 化简阈值范围的自动确定由于线要素复杂多样,如何把握化简强度,是一个重要环节[17]。化简有其自身的规则与要求,不能盲目进行,必须要界定化简阈值范围,只允许在此范围内化简。对于多源或多尺度道路数据,其节点个数、结构特征各不相同,如果采取相同的化简阈值进行化简,显然是不科学的。针对这一问题,本文的解决方案区别于把数据源作为一个整体的做法,而采取对每一条线要素都设置不同的阈值范围。主要思想是:待匹配数据一般分为源数据和目标数据,为保证化简的有效性,设定一个比匹配双方数据的比例尺均更小的比例尺,作为化简的极限比例尺Slimit,以化简到该比例尺时线要素的节点数量作为要保留的最少节点数(Nmin),此时对应的化简参数就作为阈值范围的上限。这里涉及依比例选取的问题,采用制图综合中常用的开方根模型来辅助确定Nmin的值。
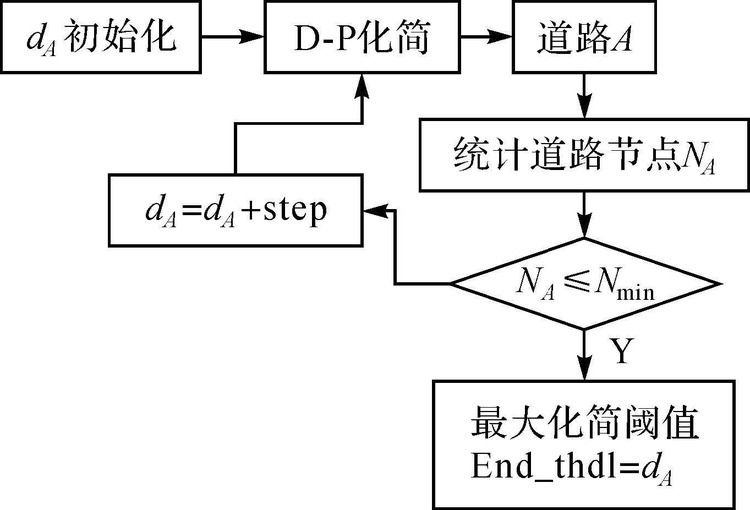
1982年,特普费尔在对分级问题的研究中,发现地物要素的选取数量与地图比例尺之间有着密切的关系,并建立了如下开方根模型的基本公式[10] ${{N}_{2}}={{N}_{1}}\sqrt{({{S}_{1}}/{{S}_{2}})}$ 式中,N1为原图地物数量;N2为新编图上应选取的地物数量;S1为原图比例尺分母;S2为新图比例尺分母。为便于本文表达,这里将式中根号内容作为一个整体,并重新定义其为化简比例系数: $K=\sqrt{({{S}_{1}}/{{S}_{2}})}$ 本文在运用开方根模型的过程中,将线要素的一系列节点作为沿线分布的地物看待,化简到某一比例尺时保留的节点数用开方根规律确定[11, 20]。算法主要步骤如图 3。其中dA表示道路A的化简阈值,NA为A化简某一状态下的剩余节点数,step为阈值变化步长,End_thd1为化简到Slimit时对应的最大化简阈值。 对于同尺度数据匹配和跨尺度数据匹配,确定其化简阈值范围的模式也有所差异: (1) 匹配双方为同尺度数据。匹配双方只有一个共同的比例尺Soriginal,化简模式为:Soriginal—→化简Slimit。 (2) 匹配双方为跨尺度数据。匹配双方数据比例尺分为大比例尺Slarge、小比例尺Ssmall,为保证两化简起点一致,采用的化简模式为①小比例尺:Ssmall—→化简Slimit;②大比例尺:Slarge—→化简Ssmall—→化简Slimit。 由于(2)化简模式相对复杂,本文以跨尺度数据为例并结合图 3加以说明。若要对比例尺1∶10万(Ssmall)的源数据与1∶2.5万(Slarge)的目标数据进行匹配,经大量试验表明,可以往后推一个或两个国家基本比例尺,如选择1∶25万作为Slimit。取1∶10万比例尺的一条道路A,原始节点个数N1=50,当将其化简到比例尺为1∶25万时,首先根据开方根规律确定K=(10/25),计算得到化简后节点Nmin=31。作为匹配数据中比例尺较小的一方,初始化dA=0.0,根据图 3得到最终的dA值即为End_thd1。这样就确定了1∶10万数据中道路A的化简阈值范围(0,End_thd1)。同理,对于1∶2.5万的数据的一条道路B,由于比例尺相对较大,为了较准确地确定dB的范围,本文利用两次开方根规律:第1次初始化dB=0.0,获取化简到1∶10万的dB值作为化简阈值范围的起始值Start_thd2;第2次初始化dB=Start_thd2,获取化简到1∶25万的dB值作为化简阈值范围的终止值End_thd2,得到道路B的阈值范围(Start_thd2,End_thd2)。此方法可降低化简的复杂度,增强化简过程的自动化程度。
|
| 图 3 确定最大化简阈值 Fig. 3 Determination of the maximal simplification threshol |
表 1、2列举出部分道路通过上述方法得到的阈值范围。可看出虽然化简比例相同,但不同线要素的阈值范围差异较大,一方面是由于道路结构本身较复杂,同时也受到制图综合存在较多主观因素的影响。这也说明了对每条道路单独化简的科学性和必要性。
| 道路ID | 原节点数 | 应保留节点数(化简至1∶25万) | 对应化简参数 | 化简阈值范围 |
| 13 | 17 | 10 | 17.4 | (0,17.4) |
| 14 | 10 | 6 | 6.1 | (0,6.1) |
| 17 | 23 | 14 | 26.3 | (0,26.3) |
| 18 | 10 | 6 | 23.3 | (0,23.3) |
| 28 | 26 | 16 | 5.2 | (0,5.2) |
| 32 | 29 | 18 | 4.6 | (0,4.6) |
| 133 | 37 | 23 | 10.3 | (0,10.3) |
| 174 | 29 | 18 | 13.7 | (0,13.7) |
| 175 | 41 | 25 | 15.9 | (0,15.9) |
| 道路ID | 原节点数 | 应保留节点数(化简至1∶10万) | 对应化简参数 | 应保留节点数(化简至1∶25万) | 对应化简参数 | 化简 阈值范围 |
| 7 | 27 | 13 | 12.0 | 8 | 26.6 | (12.0,26.6) |
| 10 | 11 | 5 | 2.7 | 3 | 8.6 | (2.7,8.6) |
| 11 | 24 | 12 | 6.0 | 7 | 18.1 | (6.0,18.1) |
| 18 | 31 | 15 | 3.5 | 9 | 9.1 | (3.5,9.1) |
| 30 | 24 | 12 | 5.2 | 7 | 9.0 | (5.2,9.0) |
| 53 | 49 | 24 | 6.1 | 15 | 15.8 | (6.1,15.8) |
| 130 | 36 | 18 | 6.4 | 11 | 16.9 | (6.4,16.9) |
| 333 | 31 | 15 | 11.3 | 9 | 15.7 | (11.3,15.7) |
| 244 | 62 | 31 | 3.2 | 19 | 9.4 | (3.2,9.4) |
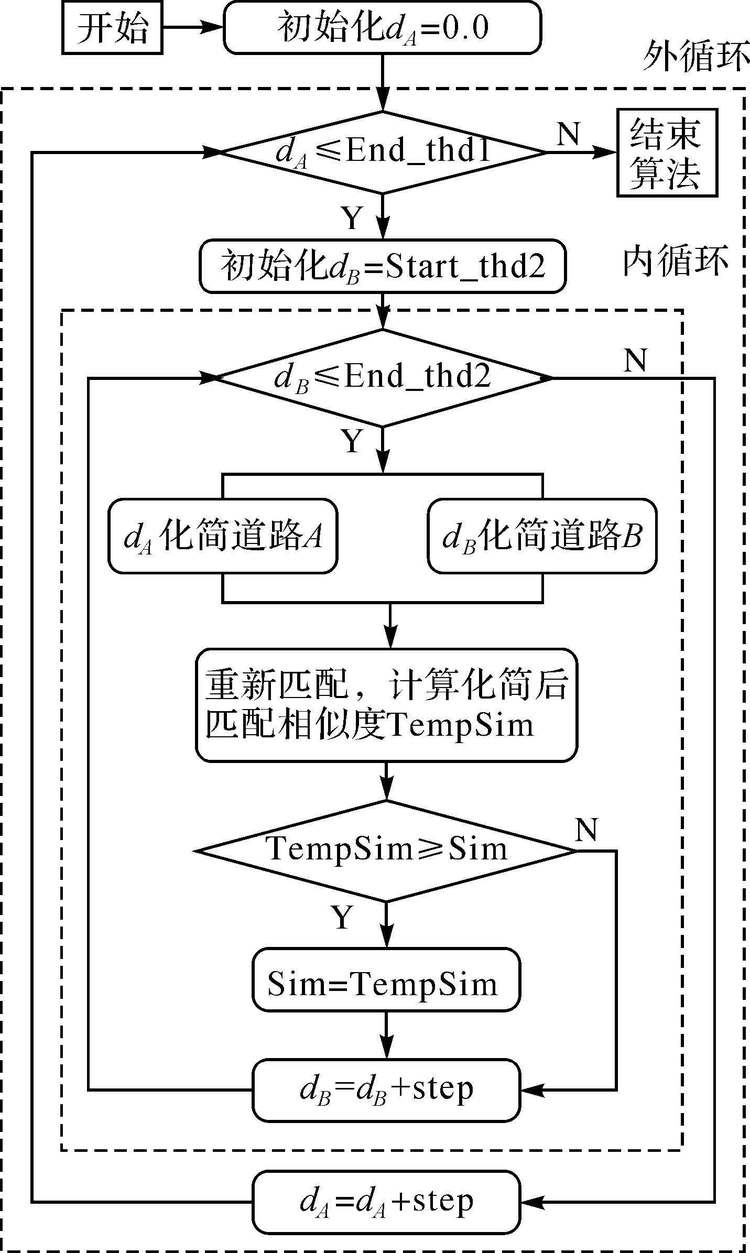
对不同数据源的两条待匹配的同名道路A和B,确定各自的化简阈值dA、dB范围分别为(0,End_thd1)和(Start_thd2,End_thd2),图 4为动态化简算法流程。其中,step为化简阈值变化步长;Sim为最高匹配相似度,TempSim记录化简过程中A和B的相似度值。具体操作步骤如下:
(1) 首先初始化各变量的值,dA=0.0,dB=start_thd2,Sim=0.0,TempSim=0.0,并设置步长step=1.0。
(2) 固定道路A的化简阈值dA,化简后得到道路A′。
|
| 图 4 动态化简算法流程 Fig. 4 Flow chart of the dynamic simplification algorithm |
(3) 道路B的化简阈值dB在(Start_thd2,End_thd2)内以步长step变化,循环对B进行化简,每次化简都将得到的道路B′与A′用已有匹配方法计算其匹配相似度TempSim,并通过比较替换找到该组化简过程中的TempSim的最大值赋值给Sim。
(4) dA=dA+step。如果dA≤End_Thd1,重复步骤(2)和(3),否则结束循环。
(5) 循环结束后,输出此时的最佳匹配相似度Sim值以及最优化简阈值。
1.3.2 动态化简对匹配相似度的影响 不同的匹配方法采用的匹配指标各异,得到的匹配相似度值也各不相同[19],但动态化简对提升每种匹配算法的匹配正确率都具有积极作用。这里以缓冲区法为例,匹配原理为:对源数据建立缓冲区,计算目标数据落入缓冲区内的长度与自身长度之比,得到的数值作为两要素的匹配相似度[12]。如表 3,道路A、B为随机选取的已知同名道路数据,根据1.3.1方法得到最优化简阈值,比较化简前后的缓冲区匹配相似度。| 同名要素ID(A-B) | 最优化简阈值(dA,dB) | 化简前相似度 | 化简后相似度 |
| 26-341 | (19.6,31.8) | 0.791 | 0.927 |
| 38-73 | (12.6,48.1) | 0.692 | 0.808 |
| 147-280 | (0.0,52.4) | 0.810 | 0.870 |
| 159-933 | (8.4,19.8) | 0.797 | 0.876 |
| 55-129 | (6.3,31.3) | 0.836 | 0.894 |
| 109-791 | (4.2,20.8) | 0.782 | 0.833 |
| 203-936 | (16.8,26.1) | 0.863 | 0.992 |
| 28-175 | (23.1,65.3) | 0.704 | 0.953 |
| 70-113 | (10.5,20.1) | 0.791 | 0.890 |
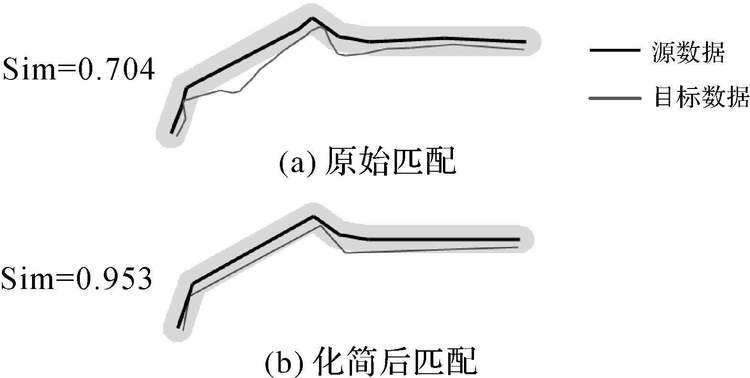
取表中一对同名道路(28-175)作具体分析,如图 5,可直观地看出化简后的数据提取出了道路主要形态,并使得匹配双方整体相似程度明显提升。图 5(a)为原始匹配,目标道路长度L=1392.043,落入缓冲区内长度L_InBuffer=980.165,匹配相似度Sim=0.704;图 5(b)为化简后的匹配状态,此时目标道路长度L′=1360.507,落入缓冲区内长度L_InBuffer′=1296.577,匹配相似度Sim=0.953。因此,化简可以显著提高匹配双方的整体相似度,对进一步提升匹配正确率具有积极意义。
|
| 图 5 最优化简阈值化简前后缓冲区匹配 Fig. 5 Comparison of buffer matching before and after simplification with the optimal threshold |
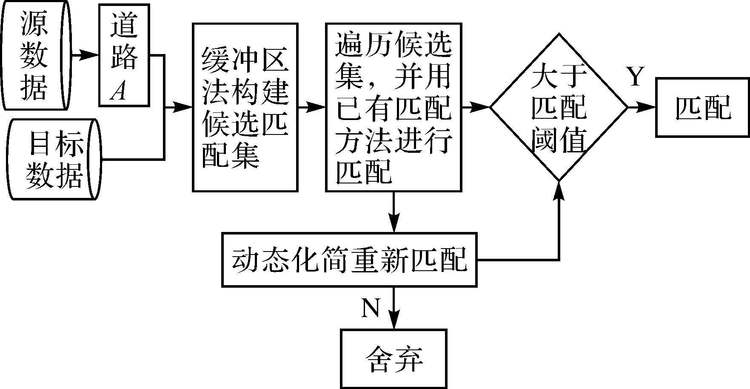
在先化简后匹配的过程中,匹配双方的相似度Sim是动态变化的,当Sim满足设定的匹配阈值时,就可被判定为相互匹配。匹配整体流程如图 6所示。在算法实现的流程中对化简过程作以下优化:①已有匹配方法能够完成匹配的数据,不再作化简处理;②动态化简过程中,当发现Sim值大于匹配阈值时,立即中断化简过程,完成匹配。(注:即此时化简参数不再要求必须是最优化简阈值)。
|
| 图 6 本文方法匹配流程 Fig. 6 Matching flow chart based on dynamic simplification |
整体来说,动态化简与匹配在理论上是正确的。当然,也可能存在少量不确定因素而造成误匹配。误匹配的发生一方面主要是由于化简算法的阈值设置不当造成的,另一方面是由于匹配算法自身采用的指标约束不全面造成的。因此可从上述两个方面最大程度地避免误匹配:①设置极限比例尺的目的是限制化简的比例,在试验过程中,采取动态设置极限比例尺的方式,即初始设置一个较大值,若此时出现误匹配,将比例尺再增大,若未出现误匹配,将初始值减小,依此类推,统计最优匹配结果,将此时的比例尺作为极限比例尺的合适值;②设置较高的匹配阈值,由于匹配算法约束不够全面造成的误匹配,在不改进算法的前提下,采取通过提高匹配标准来尽可能地降低匹配的不确定性,从而进一步减少误匹配发生的概率。
3 试验及对比分析动态化简实质上是一种辅助匹配方法,具有普遍适用性,限于篇幅,仅以常用的缓冲区法和转角函数法为例,验证其整体匹配性能。此外,本文主要针对提高变化要素匹配正确率的问题展开研究,新增要素和消失要素的匹配较为简单(无匹配对象),文中对其进行了过滤处理,只显示变化要素的匹配结果。
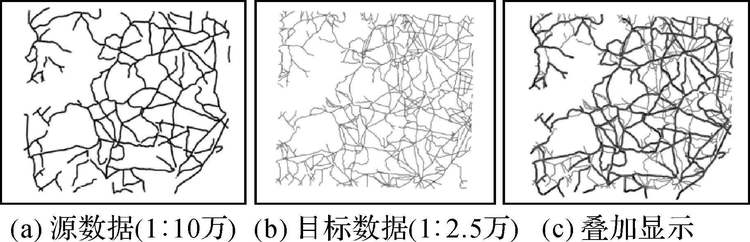
3.1 缓冲区匹配试验图 7为某地1∶10万和1∶2.5万的不同尺度道路网数据。通过对源数据构建缓冲区,依据目标数据落入缓冲区内的长度比率来判断是否匹配。其中,缓冲区半径的设置对匹配结果影响很大,主要根据数据精度等因素来选择合适的缓冲区半径:1∶10万和1∶2.5万的道路网数据,其误差要求分别为±50m和±12.5m。以1∶10万道路为参考数据,取其大者即50m并在该值左右动态设置缓冲区半径值,同时调整匹配阈值,发现当缓冲区半径设置为50m、匹配阈值设为0.8时,既可避免过度匹配,又最大程度地减少了漏匹配,匹配效果达到最佳。因此,在加入动态化简方法进行匹配时,也选用上述同样的参数,以便于比较。
|
| 图 7 不同尺度道路网试验数据 Fig. 7 Experimental road data of different scales |
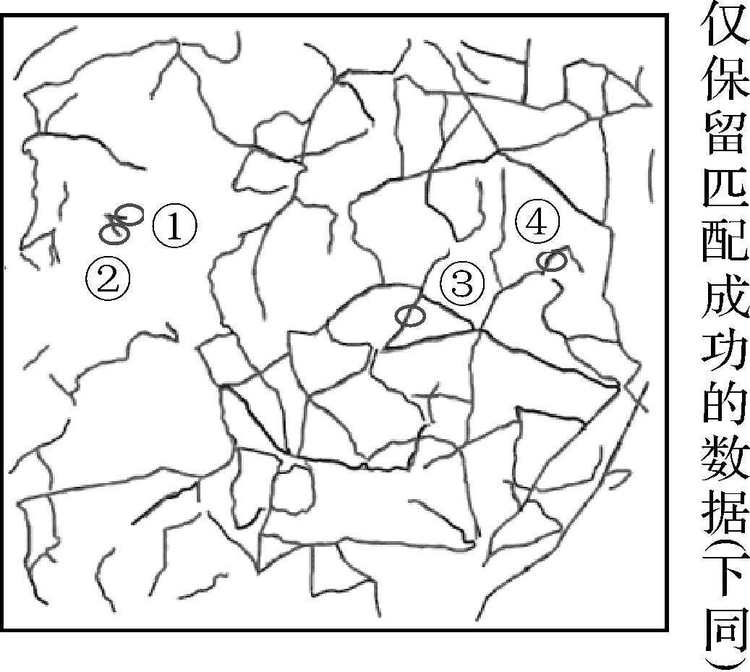
图 8为本文方法辅助Buffer法的匹配结果(包括局部匹配),其中圆圈标记的要素①②③④为一部分新成功匹配的道路,它是指直接采用Buffer法无法匹配、而采用动态化简辅助后匹配成功的变化要素,将其在图 9中放大显示,并对化简前后的缓冲区匹配情况进行了对比,其中连接短线为匹配标识。
|
| 图 8 本文方法辅助Buffer法的匹配结果 Fig. 8 Buffer matching result after dynamic simplification |

|
| 图 9 Buffer法新成功匹配道路化简前后匹配情况对 比(部分) Fig. 9 Buffer matching state comparison of the new successful matches before and afters implification (part) |
由于匹配双方为不同尺度数据,匹配结果比较复杂,存在大量一对多(1∶N)情况[18],为方便对匹配结果进行统计,本文以1∶10万源数据为参考,其中参与匹配道路为198条,匹配道路中,将正确并完整找到匹配对象的情况归为正确匹配,而1∶N匹配中只完成道路部分匹配的称为局部匹配。
表 4数据统计表明,仅使用缓冲区法时正确匹配143条道路,正确率为72.2%(143/198);加入本文方法后,正确匹配道路增加到172条,匹配正确率为86.8%(172/198),匹配正确率提高了14.6%。
对数据作进一步分析:①未匹配道路由17条减少到4条,即新增13条1∶1匹配的道路,说明本文方法能够提高匹配双方的整体相似度;②局部匹配减少了16条,说明本文方法减弱了局部细节层次对缓冲区匹配的影响,弥补了漏匹配,使得一些只完成部分匹配的道路最终实现完全匹配。
| 匹配方法 | 参与匹配 | 匹配道路 | 未匹配道路 | 匹配正确率/(%) | |
| 正确匹配 | 局部匹配 | ||||
| 缓冲区法 | 198 | 143 | 38 | 17 | 72.2 |
| 本文方法 | 198 | 172 | 22 | 4 | 86.8 |
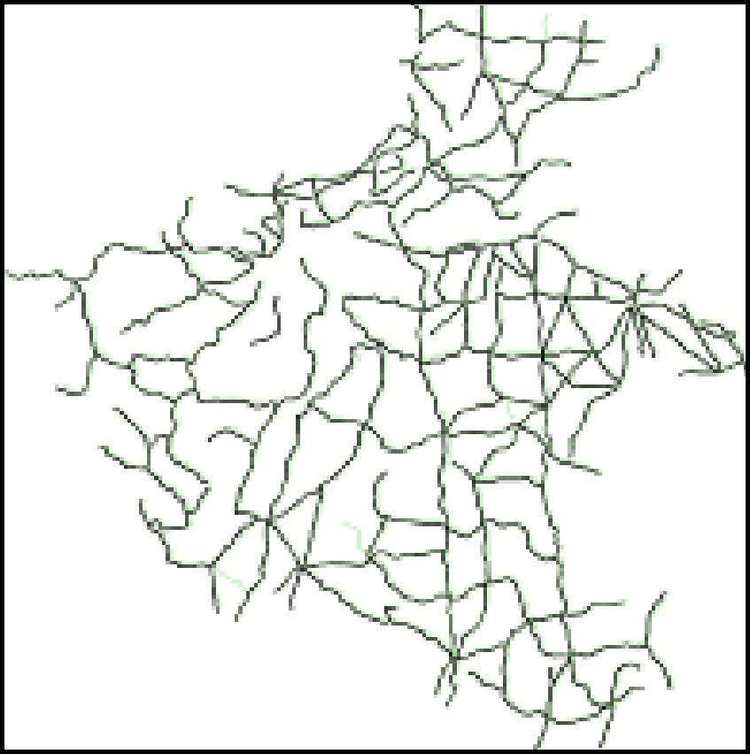
转角函数法是将组成面或线的众多弧段通过其节点处的方位角,表达在直角坐标系中来,由于显示在坐标系的图形类似于正切函数图像,故该方法也称正切空间形状描述法[13]。本文借鉴该方法用于线要素匹配,并加入动态化简方法进行对比。由于转角函数法是顾及线要素整体形态的匹配方法,并不适用于1∶N匹配较多的跨尺度匹配,因此,选取某地不同时期的1∶25万同尺度道路网进行试验验证。如图 10为同尺度匹配试验数据。
|
| 图 10 同尺度不同来源数据叠加 Fig. 10 Road data of the same scale from different sources |
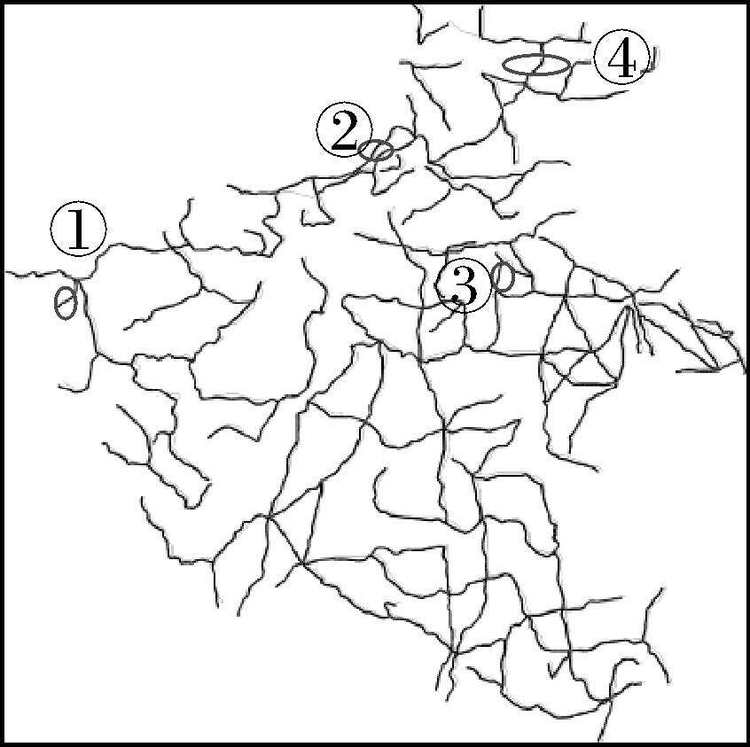
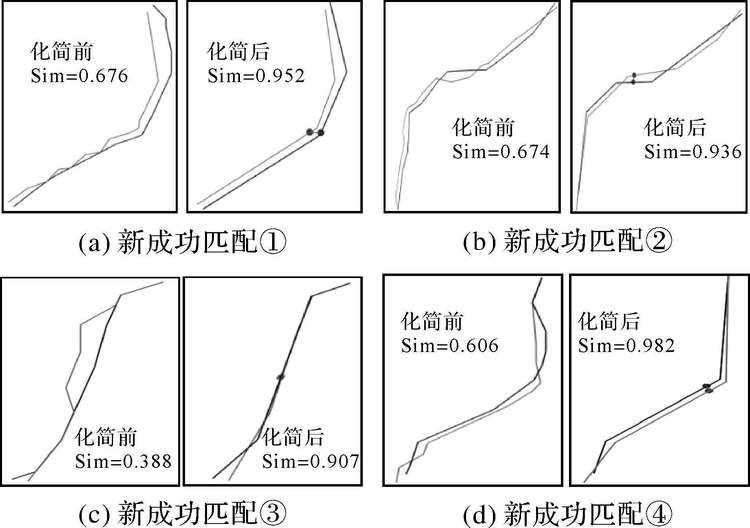
图 11为本文方法辅助转角法的匹配结果,匹配阈值设为0.9,采用与Buffer法类似的表示方法,将其中圈出的新成功匹配要素①、②、③、④在图 12中放大显示,对比了化简前后的匹配情况。
|
| 图 11 本文方法辅助转角法的匹配结果 Fig. 11 Turning function matching result after dynamic simplification |
|
| 图 12 转角法新成功匹配道路化简前后匹配情况对比 (部分) Fig. 12 Turning function matching state comparison of the new successful matches before and after simplification(part) |
分析表 5,转角函数法原始匹配正确率为74.7%(165/226),采用本文方法后正确率为87.2%(197/226),提高了12.5%,说明本文化简方法降低了局部形态差异产生的噪声,从而减少了转角函数描述线要素的不确定性,改善了道路网匹配结果。
| 匹配方法 | 参与匹配 | 正确匹配 | 未匹配 | 匹配正确率/(%) |
| 转角函数法 | 226 | 165 | 61 | 74.7 |
| 本文方法 | 226 | 197 | 39 | 87.2 |
由于本文方法是在原有匹配的基础上,加入动态化简对已有匹配算法未成功匹配的数据重新进行匹配,因此匹配效率降低是必然的。表 6统计了上述两试验化简前后匹配时间的变化。
表 6说明,经动态化简动态匹配后,匹配算法耗时均有所增加,其中缓冲区法的耗时增幅较大,这是因为构建缓冲区本身较为耗时,而动态匹配需要多次构建缓冲区,导致匹配速度降低。转角函数法的匹配时间仅增加了2.9s,在可接受范围之内,能够满足实用。由于本文方法着重在于提高匹配正确率,未能较好地兼顾匹配的效率,匹配效率的研究将作为下一步的重点研究内容。
本文方法为基于已有匹配算法来提高多源线要素匹配正确率提供了一个有效途径。在已有线要素匹配方法的基础上,提出了采用动态化简来辅助已有匹配方法,从而提高了匹配正确率。该方法也可以为面要素匹配提供参考借鉴。其优势在于可有效降低匹配数据的复杂性和可能产生的不确定性,增强已有匹配算法对整体形态相似度的识别与区分能力。
| [1] | 李德仁,龚健雅, 张桥平. 论地图数据库合并技术[J]. 测绘科学, 2004, 29(1):1-4. LI Deren, GONG Jianya, ZHANG Qiaoping. On the Conflation of Geographic Databases[J]. Science of Surveying and Mapping, 2004, 29(1):1-4. |
| [2] | WALTER V, FRITSCH D. Matching Spatial Data Sets:A Statistical Approach[J]. International Journal of Geographical Information Science, 1999, 13(5):445-473. |
| [3] | VOLZ S. An Iterative Approach for Matching Multiple Representations of Street Data[C]//The 3rd Symposium on Location Based Services and Telecartography, Vienna, Austria, 2005. |
| [4] | 童小华, 邓愫愫, 史文中. 基于概率的地图实体匹配方法[J]. 测绘学报, 2007, 36(2):210-217. TONG Xiaohua, DENG Susu, SHI Wenzhong. A Probabilistic Theory-based Matching Method[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2):210-217. DOI:10.3321/j.issn:1001-1595.2007.02.017. |
| [5] | PERSOON E, FU K S. Shape Discrimination Using Fourier Descriptors[J]. IEEE Transaction on Systems, Man and Cybernetics, 1977, 7(3):170-179. |
| [6] | VOLOTĂO C F D S, SANTOS R D C D, ERTHAL G J, et al. Shape Characterization with Turning Functions[C]//Proceedings of the 17th International Conference on Systems, Signals and Image Processing. Rio de Janeiro, Brazil:IWSSIP, 2010. |
| [7] | 陈玉敏, 龚健雅, 史文中. 多尺度道路网的距离匹配算法研究[J]. 测绘学报, 2007, 36(1):84-90. CHEN Yumin, GONG Jianya, SHI Wenzhong. A Distance-based Matching Algorithm for Multi-scale Road Networks[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1):84-90. |
| [8] | 黄蔚, 蒋捷. 多尺度矢量简单几何实体数据几何匹配方法研究[J]. 遥感信息, 2011(1):27-31. HUANG Wei, JIANG Jie. Simple Geometry Matching of Multi-scales Spatial Data[J]. Remote Sensing Information, 2011(1):27-31. |
| [9] | 武芳, 朱鲲鹏. 线要素化简算法几何精度评估[J]. 武汉大学学报(信息科学版), 2008, 33(6):600-603. WU Fang, ZHU Kunpeng. Geometric Accuracy Assessment of Linear Features' Simplification Algorithms[J]. Geomatics and Information Science of Wuhan University, 2008, 33(6):600-603. |
| [10] | 王殷行,李白英, 徐泮林. 基于特普费尔公式的制图综合取舍比例探讨[J]. 山东科技大学学报(自然科学版), 2006, 25(1):40-46. WANG Yinxing, LI Baiying, XU Panlin. Study on the Proportion with Synthetic Acceptance or Rejection on Cartography Based on F.föpfer Formula[J]. Journal of Shandong University of Science and Technology (Natural Science), 2006, 25(1):40-46. |
| [11] | 牛继强, 徐丰. 线状要素多尺度表达不确定性的综合分析与评价研究[J]. 测绘科学, 2007, 32(6):69-71. NIU Jiqiang, XU Feng. General Analysis and Estimate Research on Uncertainty of Multi-scale Representation of Linear Feature[J]. Science of Surveying and Mapping, 2007, 32(6):69-71. |
| [12] | 黄智深, 钱海忠, 王骁, 等. 基于降维技术的面状居民地匹配方法[J]. 测绘科学技术学报, 2012, 29(1):75-78. HUANG Zhishen, QIAN Haizhong, WANG Xiao, et al. Dimension Decrease-oriented Habitation Matching Method[J]. Journal of Geomatics Science and Technology, 2012, 29(1):75-78. |
| [13] | 付仲良, 邵世维, 童春芽. 基于正切空间的多尺度面实体形状匹配[J]. 计算机工程, 2010, 36(17):216-217, 220. FU Zhongliang,SHAO Shiwei,TONG Chunya.Multi-scale Area Entity Shape Matching Based on Tangent Space[J]. Computer Engineering, 2010, 36(17):216-217, 220. |
| [14] | DOUGLAS D H, PEUCKER T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J]. The Canadian Cartographer, 1973, 10(2):112-122. |
| [15] | MCMASTER R B. Automated Line Generalization[J]. Cartographica:The International Journal for Geographic Information and Geovisualization, 1987, 24(2):74-111. |
| [16] | 钱海忠, 武芳, 陈波, 等. 采用斜拉式弯曲划分的曲线化简方法[J]. 测绘学报, 2007, 36(4):443-449. QIAN Haizhong, WU Fang, CHEN Bo, et al. Simplifying Line with Oblique Dividing Curve Method[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4):443-449. |
| [17] | 邓敏, 樊子德, 刘慧敏. 层次信息量的线要素化简算法评价研究[J]. 测绘学报, 2013, 42(5):767-773, 781. DENG Min,FAN Zide,LIU Huimin.Performance Evaluation of Line Simplification Algorithms Based on Hierarchical Information Content[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5):767-773, 781. |
| [18] | 赵东保, 盛业华. 全局寻优的矢量道路网自动匹配方法研究[J]. 测绘学报, 2010, 39(4):416-421. ZHAO Dongbao, SHENG Yehua. Research on Automatic Matching of Vector Road Networks Based on Global Optimization[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4):416-421. |
| [19] | 郝燕玲, 唐文静, 赵玉新, 等. 基于空间相似性的面实体匹配算法研究[J]. 测绘学报, 2008, 37(4):501-506. HAO Yanling,TANG Wenjing,ZHAO Yuxin,et al. Areal Feature Matching Algorithm Based on Spatial Similarity[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4):501-506. |
| [20] | 颜玉龙, 江南. 线性目标多尺度表达的改进内插方法研究[C]//第七届全国地图学与地理信息系统大会. 广州:[s.n.], 2012. YAN Yulong, JIANG Nan. The Study on Improvement Interpolation Method of the Linear Objective Multi-Scale Representation[C]//Proceedings of the 7th National Conference on Cartography and Geography Information System. Guangzhou:[s.n.], 2012. |



