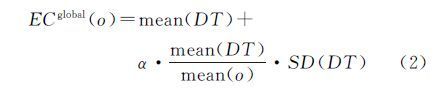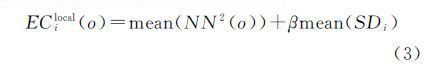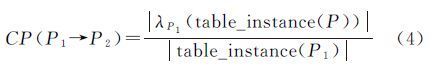伴随着空间数据的爆炸性增长,空间数据挖掘已经引起了国内外学者的广泛关注[1, 2, 3, 4, 5]。空间同位模式挖掘是当前空间数据挖掘领域中的一个研究热点,旨在从包含多个事件类型的空间数据库中发现频繁在邻近位置发生的事件集合,反映事件间的共生规律[6]。当前,空间同位模式挖掘已广泛应用于地球科学、环境管理、公共卫生安全和交通运输等研究领域[7]。现有空间同位模式挖掘研究多是传统的关联规则挖掘方法[8]在空间数据上进行的拓展,与事务型数据库不同,空间数据库中并没有明确定义事务,因此需要将空间数据库离散化为事务数据库。根据是否事务化空间数据,可以将现有方法大致分为两种类型:①事务化的方法,先构建空间事务数据库,再采用传统关联规则挖掘方法(如Apriori算法)挖掘空间同位模式,主要方法包括:参考特征中心模型[9]、窗口中心模型[6]和基于Voronoi的方法[10]等;②非事务化的方法,采用针对实例进行统计的兴趣度量指标挖掘空间同位模式,主要方法包括:实例连接[6]、部分连接[7]、无连接[11]和基于密度[12]的方法。空间事务化的方法存在两个突出问题:一方面对连续空间的离散化,会破坏事务边界实体间的邻近关系,可能导致最终规则的遗漏[7];另一方面,挖掘结果依赖于空间事务化的方法,不同的事务化方法将产生不同的同位模式和规则。非事务化的方法采用实例连接的方法[6]得到每种候选同位模式的实例,进而对实例进行统计,最终得到频繁同位模式,此类方法实例连接计算的开销较大[7, 11]。此外,文献[13]也提出了一种新颖的空间关联模式挖掘工具-地理探测器,也可以从全局上探测空间同位模式。地理探测器通过计算各因子变量对结果变量的决定力指标,发现对特定地理现象起控制作用的环境因子,并可以识别因子间的交互作用。与上述空间同位模式挖掘方法相比,地理探测器具有更严密的统计学基础。
然而,上述方法多从全局视角挖掘空间同位模式,忽略了地理事件的空间异质特性[14],即某些空间同位模式经常仅在某个局部区域是显著的。针对空间同位模式的异质性问题,一些学者进行了初步的研究,主要分为两种策略:①首先将空间数据集划分为一系列子区域,进而在这些子区域内采用全局挖掘方法提取局部的空间同位模式;②对于每个候选同位模式,分别识别出其频繁出现的局部子区域。采取第1种策略的主要工作包括:文献[15]利用四叉树分区的策略发现每个分区中的空间同位模式;文献[16]首先利用格网划分的方法探测出参考事件的热点区域,进而在热点区域内挖掘与参考事件相关的空间关联规则,最后再利用格网划分的方法确定规则的有效区域;文献[17]采用k-邻近图构建不同类型事件的空间邻域,通过将邻域距离相近的邻域图进行合并得到局部子区域,进而在每个子区域内提取空间同位模式。采取第2种策略的主要工作有:文献[18]提出了一种基于划分聚类的方法,即针对每种候选同位模式,依据其兴趣度构造目标函数,进而采用基于划分的聚类算法(如K-Medoids)提取其感兴趣的局部子区域;文献[19]对于每个二元候选同位规则,以前件实体为圆心,人为划定圆形区域,进而在圆形区域内度量二元同位规则的频繁程度;文献[20]提出了一种基于邻接图的方法,将每个候选同位模式连通的邻接子图视为一个聚集位置,进而计算该候选模式在每个聚集位置上的频繁程度。分析上述针对局部空间同位模式挖掘的研究工作可以发现:
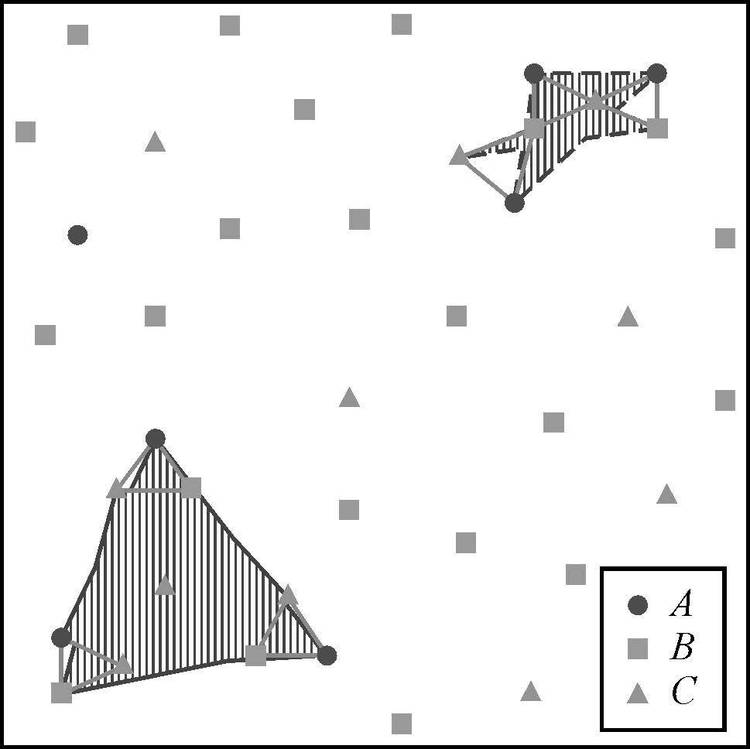
(1) 第1种策略对于子区域的划分严重依赖人为设置参数或分区策略,难以真实反映空间同位模式自然的分布结构。如图 1(a)所示,示例数据集中包含3类事件:A、B和C,每类事件发生在具体位置上的实体称为该事件的实例,图中3类事件分别有7、22和11个实例,图中共有4种空间同位模式{A,B}、{A,C}、{B,C}和{A,B,C},相互连接的实体即满足空间同位关系,空间同位模式中互为空间同位关系的每类事件的实例集合称为该空间同位模式的实例,图 1中4个空间同位模式均有6个实例。如图 1(b)右上角所示,人为设定的子区域划分策略极有可能破坏空间同位模式固有的空间分布结构,导致挖掘结果的误差。
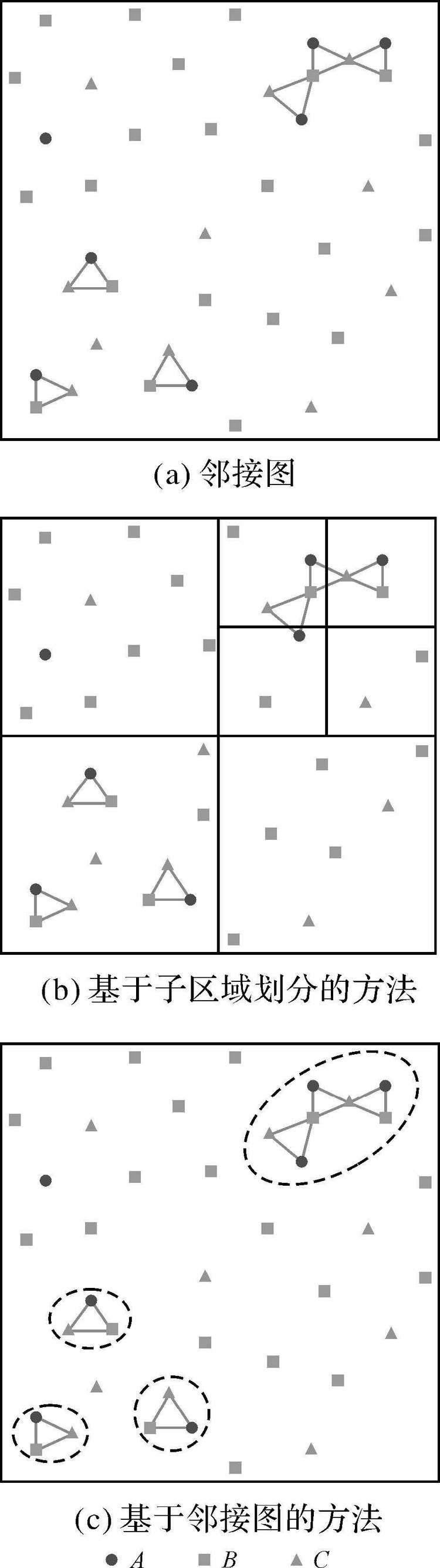
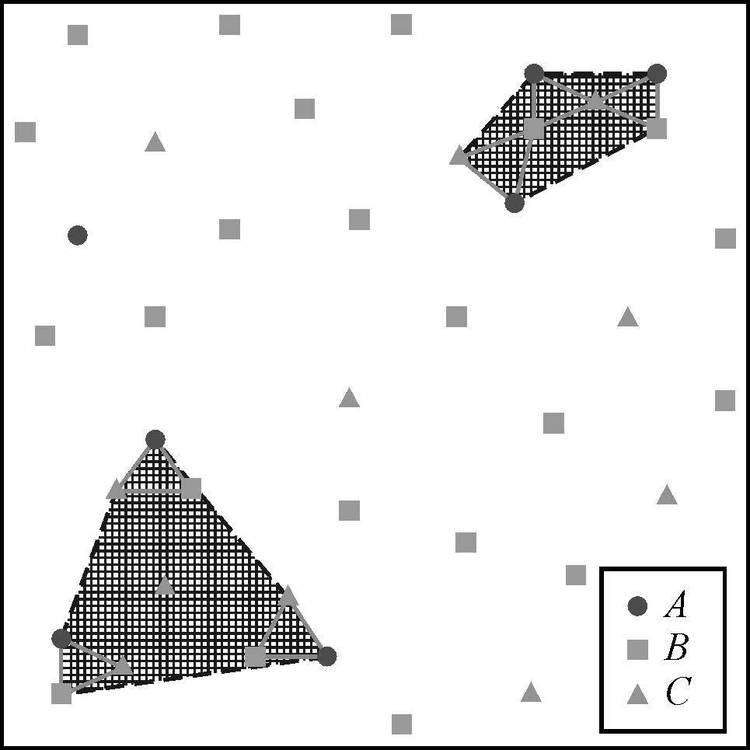
|
| 图 1 示例数据集 Fig. 1 Simulated data set |
(2) 采用第2种策略的方法中,基于划分聚类的方法本质上属于一种空间事务化的方法,且聚类数目确定较为困难;文献[19]的方法仅是为了提取二元空间同位模式的分布结构,且圆形区域半径的设置需较多的先验知识;基于邻接图的方法虽然可以在一定程度上克服基于划分聚类方法的不足,且能够挖掘不同类型的空间同位模式[20],但是采用固定距离构建邻域图难以适应空间同位模式分布的不均匀性[17, 21, 22]。如图 1(c)所示,以空间同位模式{A,B,C}为例,基于邻接图的方法共发现4处聚集位置(即图中虚线圈出的位置),由于该模式在左下角的分布较稀疏,邻接图互不连通,故每个实例位置均视为一个单独的聚集位置,进而导致这些位置上的频繁度较低,难以被发现。此外,基于邻接图的方法中,局部频繁度的计算受全局范围内相关事件实例个数的影响,实际上是采用一个全局的阈值度量空间同位模式的频繁程度,难以真实反映局部视角下的空间同位模式。
因此,为了在提取全局空间同位模式的基础上,能够进一步真正地从局部视角发现空间同位模式,本文提出一种多层次空间同位模式自适应挖掘方法,下面将对本文的研究策略和方法进行阐述。
1 多层次空间同位模式自适应挖掘 1.1 研究策略如前文所述,现有局部空间同位模式挖掘的研究工作中,采用先分区后挖掘的策略的方法难以分别反映不同空间同位模式自然的分布结构;针对每个候选模式提取感兴趣区域的策略难以顾及空间数据分布的不均匀性。然而,空间同位模式作为一种地理现象,其在不同空间层次上的表现各异,本文提出一种由全局到局部的多层次研究策略,首先从全局层次上发现并剔除整体的关联模式,进而借助空间聚类方法提取局部的关联模式,从而能够更全面地发现全局与局部空间同位模式。具体表述如下:
(1) 从全局视角提取空间同位模式,将全局不频繁的同位模式作为局部空间同位模式挖掘的候选集;
(2) 针对候选集合中每类同位模式,将其每个实例视为一个整体,采用自适应空间聚类方法[23]提取这些同位模式的局部感兴趣区域,并在这些区域内对同位模式的频繁程度进行度量;
(3) 发展感兴趣区域的叠置推绎方法,对频繁子模式的局部区域进行叠置分析,生成所有频繁的局部空间同位模式集合及其局部感兴趣区域。 本文方法既可以发现全局视角下的空间同位模式,又可以得到每种局部空间同位模式的自然分布结构,从而能够更全面地反映地理现象间的共生规律。基于上述策略,本文提出方法主要包括两个步骤:基于模式聚类的感兴趣区域探测和基于叠置分析的感兴趣区域推绎,下面将分别进行阐述。
1.2 基于模式聚类的感兴趣区域探测对于k元候选空间同位模式集合,首先在全局范围内借助参与指数
式中,table_instance为空间同位模式的实例集合;λ为删除重复项的关系映射操作。参与指数大于等于所设阈值的候选模式视为全局空间同位模式,否则作为局部视角挖掘的候选空间同位模式集合。对于局部候选集合中每个同位模式,本文提出模式聚类的概念,将空间同位模式的每个实例看成一个整体,其空间位置采用实例中各实体的平均位置表示,作为聚类的基本单元;进而借助空间聚类方法探测出空间同位模式的感兴趣区域;最后,在每个感兴趣区域内采用参与指数度量候选模式的频繁度。由于不同的空间同位模式分布各异,传统空间聚类算法参数设置较为困难,且难以处理空间数据分布不均匀的性质,因此本文采用文献[23]中多层次边长约束的策略自动识别空间同位模式的感兴趣区域:
(1) 对于每个候选模式,计算每个实例的平均位置,并据此构建实例的Delaunay三角网DT;
(2) 针对三角网DT,施加整体边长约束ECglobal,删除整体上过长的边,具体表达如下
式中,mean(DT)为三角网的平均边长值;mean(o)为与实体o直接连接的所有边长的平均值;SD(DT)为三角网所有边长的标准差;α为调节系数,默认设为1。基于以上定义,对于三角网DT的任一顶点o,将与其直接相连的边中长度大于等于ECglobal(o)的边删除,删除整体长边后将得到一系列子图SG={G1,G2,…,Gm}。
(3) 针对每个子图Gi,进一步施加局部边长约束EClocali,删除所有实体二阶邻域内的局部长边,具体表达如下
式中,mean(NN2(o))为子图Gi中实体o二阶邻域内的平均边长值;mean(SDi)为子图Gi中所有实体一阶邻域内边长标准差的平均值;β为调节系数,默认设为1。对于子图Gi中的任一顶点o,将其二阶邻域内长度大于等于EClocali(o)的边删除。
(4) 经过整体和局部约束后,将剩余的每一个子图视为一个空间簇。进而,用同一个簇中候选模式实例中所有实体的最小外接凸多边形表示该模式的感兴趣区域。如果感兴趣区域内该空间同位模式的实例个数较少,则认为该模式在此区域内缺乏代表性。因此,实际应用中需要借助一定的专家知识对感兴趣区域内空间同位模式实例的个数施加约束,剔除小规模区域,以保证结果的实际应用价值。
下面采用如图 1(a)所示的示例数据集,以空间同位模式{A,B}为例,阐述本文提出的基于模式聚类的感兴趣区域探测的具体过程,参与指数阈值设为0.5。数据集中空间同位模式{A,B}的全局参与指数为min(6/7,5/22)≈0.23,故将其作为进一步局部挖掘的候选模式。首先根据同位模式{A,B}实例的整体位置生成如图 2(a)所示的Delaunay三角网,经过整体和局部边长约束条件进行删边后的结果如图 2(b)所示,进而将同一个子图中同位模式{A,B}实例所有实体的最小外接多边形视为该模式的感兴趣区域,如图 2(c)所示,每个局部感兴趣区域中同位模式{A,B}的参与指数均大于0.5,因此可以从局部的视角发现该空间同位模式。
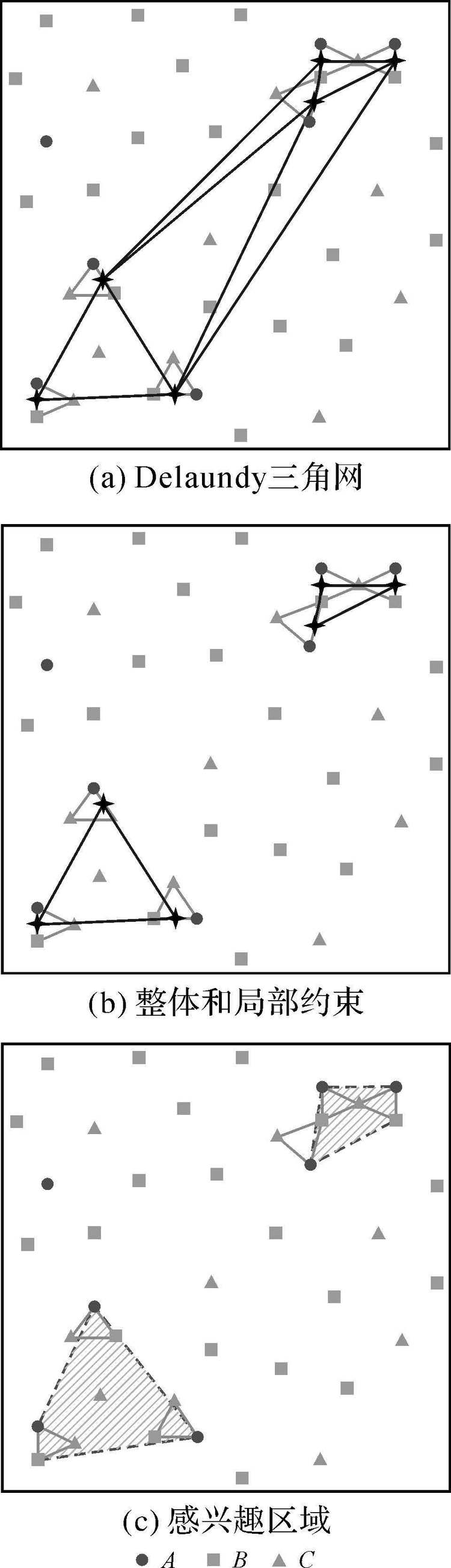
|
| 图 2 基于模式聚类的感兴趣区域探测(以同位模式 {A ,B}为例) Fig. 2 Discovery of there gions of interest based on pattern clustering (taking co-location pattern {A ,B}for example |
对于每个局部候选同位模式,均采用上述模式聚类的方法探测感兴趣区域,当空间数据库中事件类型与数量较多时,将面临巨大的计算开销。为此,本文借助逐长度的产生机制,进一步提出一种叠置推绎的方法,利用k元频繁子模式感兴趣叠置分析得到k+1元候选模式感兴趣区域,以提高较长的空间同位模式感兴趣区域探测的计算效率。该方法首先挖掘k(k≥2)元空间同位模式,后挖掘k+1元空间同位模式,依次上推,直到没有空间同位模式产生为止,因此在探测k+1元候选同位模式的感兴趣区域前,已经得到了其k元子模式的感兴趣区域。如图 3所示,以3元同位模式{A,B,C}为例,其2元子模式为{A,B}、{A,C}和{B,C},已通过上述面向模式聚类的方法找出各自的感兴趣区域。分析发现,只有在子模式感兴趣区域相互有交集时才有可能出现同位模式{A,B,C}。图中列出了4种可能情况:同位模式{A,B,C}的实例中分别有3、2、1、0个实体落在3个区域的交集中,但是这3个实体都不可能出现在3个区域两两交集的并集(即图中黑色实线所包含的区域)之外。因此,对于k+1元候选同位模式,若其存在频繁的局部k元子模式,只需要对子模式的感兴趣区域进行叠置分析,得到各区域两两交集的并集,落在同一个并集中实例的最小外接凸多边形即为该k+1元候选模式的一个感兴趣区域。
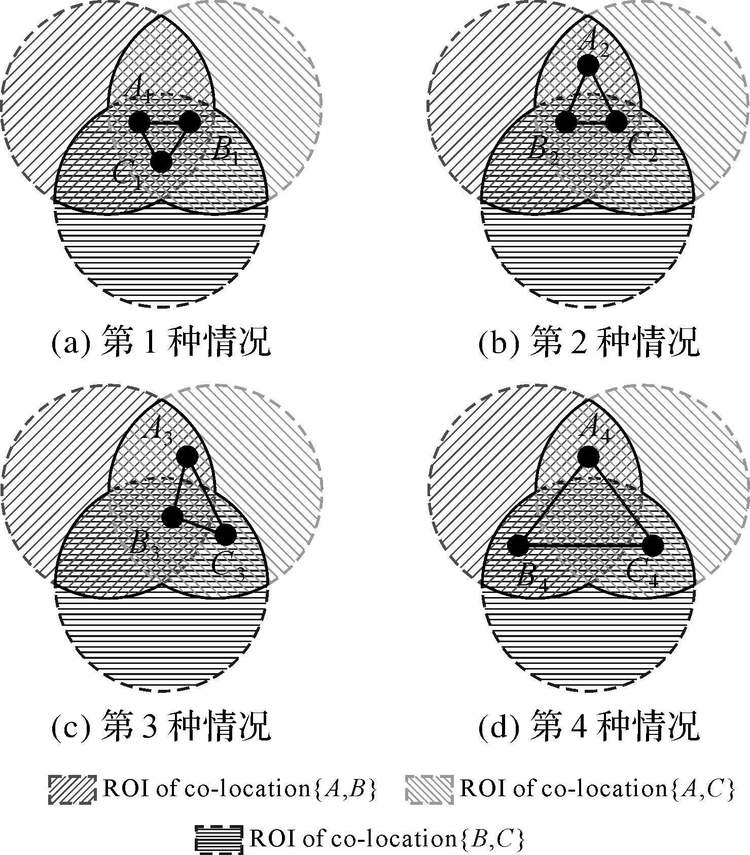
|
| 图 3 感兴趣区域的叠置推绎(以同位模式{A ,B,C}为例) Fig. 3 Overlap method for deducing there gions of interest(taking co-location pattern{A ,B,C} for example) |
同样采用如图 1(a)所示的示例数据集,以空间同位模式{A,B,C}为例,阐述本文提出的基于叠置分析的感兴趣区域推绎的具体过程。图 4和图 5分别为同位模式{A,C}和{B,C}的感兴趣区域,对同位模式{A,B,C}的2元子模式的感兴趣区域进行上述叠置分析操作,得到如图 6所示的两个阴影区域,进而构建各区域内该模式实例中所有实体的最小外接凸多边形,得到如图 7所示的同位模式{A,B,C}的感兴趣区域。
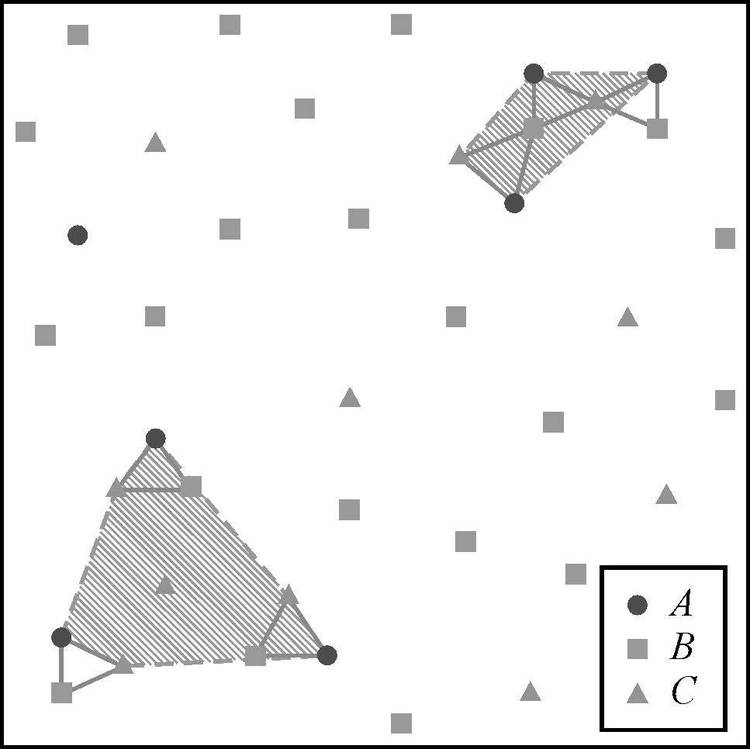
|
| 图 4 同位模式{A ,C}的感兴趣区域 Fig. 4 Regions of interest of co-location pattern{A ,C} |
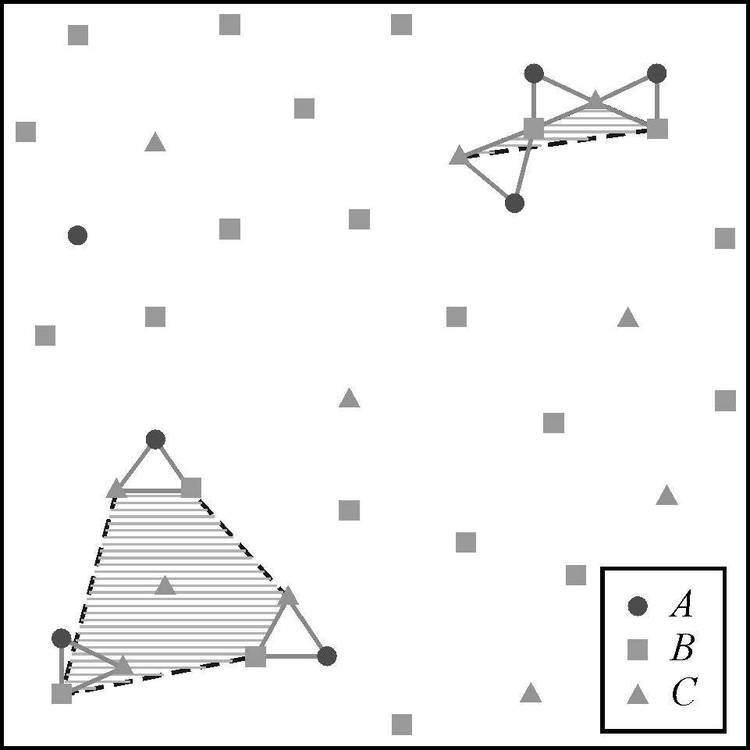
|
| 图 5 同位模式{B,C}的感兴趣区域 Fig. 5 Regions of interest ofco-location pattern{B,C} |
|
| 图 6 子模式感兴趣区域叠置分析结果 Fig. 6 Results obtained by the overlap method |
|
| 图 7 同位模式{A ,B,C}的感兴趣区域 Fig. 7 Regions of interest of co-location pattern{A ,B,C} |
基于以上空间同位模式感兴趣探测的方法,下面进一步介绍本文提出的多层次空间同位模式挖掘算法。对于包含多个事件类型的布尔型空间数据集,算法需要3个输入参数:最小参与指数阈值、最小条件概率阈值和感兴趣区域中空间同位模式的规模阈值,最终输出数据集中所有全局和局部的空间同位模式及规则,及其各自的频繁感兴趣区域。具体步骤如下:
(1) 采用文献[24]的建议,可借助L函数估计合适的邻域距离,构建空间邻域图;
(2) 将所有事件类型两两组合得到2元候选空间同位模式,并由步骤(1)的邻域图得到候选模式的实例;
(3) 对于每个候选模式在全局范围内采用参与指数度量其频繁程度,若大于给定阈值,则视为全局频繁同位模式,否则采用模式聚类的方法探测其感兴趣区域,进而在局部范围内计算参与指数,若大于给定阈值,则视为局部频繁同位模式,并输出相应的频繁感兴趣区域;
(4) 由k元频繁模式及其实例产生k+1元候选模式及其实例;
(5) 对于每个k+1元候选模式,若其k元子模式中存在局部频繁同位模式,根据apriori性质,该k+1元候选模式也不可能为全局频繁同位模式,则采用叠置推绎的方法探测其感兴趣区域,进而在局部范围度量其频繁程度,否则执行步骤(3);
(6) 重复步骤(4)—步骤(5),直到没有频繁空间同位模式产生为止;
(7) 对所有频繁空间同位模式的频繁感兴趣区域中实例个数小于所设阈值的小规模区域进行过滤;
(8) 进一步可以在空间同位模式的基础上获得空间同位规则,用来推测不同类型空间事件间的空间共生规律。对于每个全局或局部频繁同位模式P={f1,f2,…,fk},产生其所有非空子集作为规则的前件P1,相应的补集作为规则的后件P2,得到所有可能的候选同位规则P1→P2,进而在同位模式P的感兴趣区域(全局或局部)内,计算每条候选规则的条件概率[6],具体表达如下
式中,table_instance为空间同位模式的实例集合;λ为删除重复项的关系映射操作。若大于给定阈值,则为强同位规则。
2 试验分析与应用为验证本文方法的有效性,分别采用模拟数据与我国东北某湿地自然保护区的5种生态群落的空间分布数据对本文提出方法进行验证,并与现有的全局和局部空间同位模式挖掘算法[6, 20](分别简称CM和RCMNG),以及地理探测器[13]进行比较。在试验参数设置中,参与指数和条件概率分别用于度量空间同位模式的频繁程度和空间同位规则的可信程度,其取值范围为0~1之间,根据现有研究建议一般认为大于0.5即足够用来度量空间同位模式的有效性[25],因此本文将其阈值均设置为0.5;局部参与指数用于度量空间同位模式在局部位置上出现的频繁度,依据文献[20]的建议,将其阈值设置为一个较小值(0.1)。本文依据文献[26]建议,将空间同位模式规模阈值设置为全部实例个数的2%。
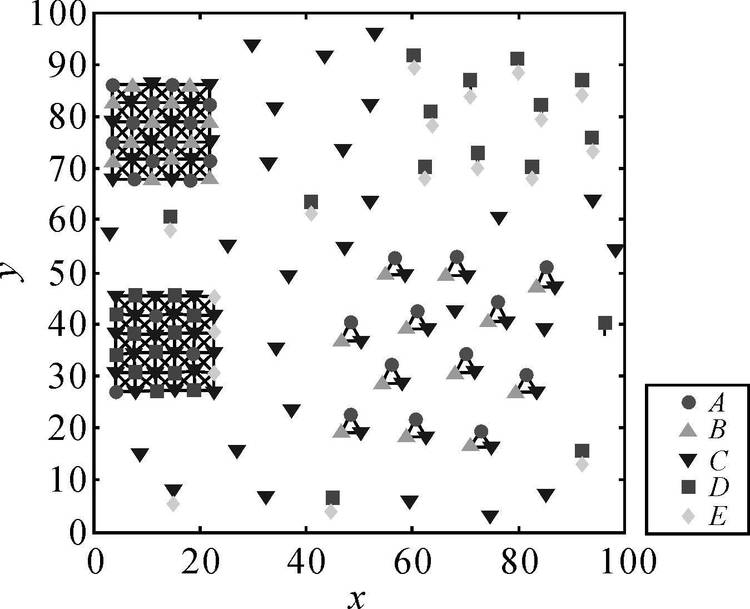
2.1 模拟试验与比较模拟数据集如图 8所示,数据范围为[0, 100]2,一共包含5种事件类型,分别有27、24、68、27、19个实例。邻域距离的L函数估计结果为6,得到如图 9所示的空间邻域图,黑色线段连接的实体即表示其在空间上互为邻域关系。模拟数据集中预设了3个全局同位模式,以及7个局部同位模式。

|
| 图 8 模拟数据集 Fig. 8 Simulated dataset |
|
| 图 9 空间邻域图 Fig. 9 Neighborhood graph |
首先给出3个空间同位模式挖掘算法的试验结果。本文方法的空间同位模式挖掘结果如表 1所示,包含3个全局空间同位模式,以及7个局部空间同位模式,进一步产生了6条全局空间同位规则,以及26条局部空间同位规则(由于篇幅限制,未列出全部试验结果);为了进行比较分析,表 1中第5列给出了CM算法得到的相应同位模式的全局参与指数,仅有3个空间同位模式的全局参与指数大于所设阈值;表 1中6—7列给出了RCMNG算法得到的相应空间同位模式的最小和最大局部参与指数,仅有5个空间同位模式具有局部参与指数大于所设阈值的局部聚集位置,其他同位模式聚集位置上的局部参数指数过小,难以被有效发现。
| 空间同位模式 | 感兴趣范围 | 本文方法 | CM算法 | RCMNG算法 | ||||
| PImin | PImax | GPI | RPImin | RPImax | ||||
| {A,B} | 全局 | 0.89 | 0.89 | 0.89 | 0.04 | 0.44 | ||
| {A,C} | 全局 | 0.50 | 0.50 | 0.50 | 0.01 | 0.18 | ||
| {D,E} | 全局 | 0.63 | 0.63 | 0.63 | 0.04 | 0.04 | ||
| {A,D} | 局部 | 0.83 | 0.83 | 0.11 | 0.04 | 0.07 | ||
| {B,C} | 局部 | 0.86 | 1 | 0.35 | 0.01 | 0.18 | ||
| {C,D} | 局部 | 0.94 | 0.94 | 0.25 | 0.25 | 0.25 | ||
| {C,E} | 局部 | 1 | 1 | 0.10 | 0.01 | 0.09 | ||
| {A,B,C} | 局部 | 0.75 | 0.75 | 0.35 | 0.01 | 0.18 | ||
| {A,C,D} | 局部 | 0.82 | 0.82 | 0.11 | 0.03 | 0.07 | ||
| {C,D,E} | 局部 | 0.83 | 0.83 | 0.07 | 0.03 | 0.04 | ||
| 注:PImin和PImax分别为感兴趣区域内的最小和最大参与指数;GPI为全局参与指数;RPImin和RPImax为最小和最大局部参与指数。 | ||||||||
下面以空间同位模式{B,C}为例,对3个空间同位模式挖掘算法的试验结果进行比较分析。图 10(a)给出了空间同位模式{B,C}的空间邻域图,可以发现在全局范围内有大量的事件C周围不存在事件B,全局的参与指数为0.35,因此全局的空间同位模式挖掘算法CM并不能发现该同位模式;如图 10(b)所示,RCMNG算法借助固定距离的邻域图识别同位模式的局部位置,然而同位模式{B,C}的分布并不均匀,左上角密集,右下角稀疏,因此右下角的实例不能连为一个整体位置,每个局部位置上仅包含一个实例,从而导致局部参与指数小于所设阈值;如图 10(c)所示,本文方法采用自适应的空间聚类算法对同位模式{B,C}的实例进行聚类分析,可以发现不同密度的空间簇,有效地解决了RCMNG算法中固定距离的邻域图不能识别不同密度的局部位置的问题。另外,对于每个局部感兴趣区域,本文方法能够真正从局部区域的视角进行测试,避免了全局事件的实例个数对RCMNG算法中局部参与指数的影响,从而能够有效地提取局部空间同位模式。

|
| 图 10 空间同位模式{B,C} Fig. 10 Spatial co-location pattern{B,C} |
为了与地理探测器进行比较分析,本文首先在数据范围内构建基本单元大小为10×10的格网,统计每个格网中每个事件实例的个数,并对其进行等间距分类(间隔为1),进而得到适用于地理探测器的离散化数据。以事件A为例,将其选为结果变量,其余类型事件为因子变量,各因子对结果的决定力依次为:B(0.49)>C(0.35)>E(0.06)>D(0.04)。从本文结果中筛选出后件为A的空间同位规则,如表 2所示。可以发现,本文方法得到的全局空间同位规则的前件事件,与地理探测器所探测出的具有较高决定力的因子(B和C)相对应,可以说明地理探测器对于发现全局的空间同位规则是有效的。然而,本文方法可以发现局部范围内具有较高可信度的同位规则,但其前件事件的决定力(如事件D)较低,这是由于地理探测器仍然是从全局视角探测各环境因子对地理现象的作用机理。下面将采用本文方法对东北某湿地自然保护区生态群落的空间分布数据进行实际应用分析,揭示湿地植被群落之间的共生规律。
| 空间同位规则 | 感兴趣范围 | 条件概率 |
| B➝A | 全局 | 1 |
| C➝A | 全局 | 0.5 |
| {B,C}➝A | 局部 | 1 |
| D➝A | 局部 | 0.83 |
| {C,D}➝A | 局部 | 0.64 |
植被共生关系是生态学领域的研究热点,对于深入研究生态规律、 改善生态环境和维持生态平衡都具有重要意义[27, 28]。本文选取我国东北地区某湿地作为研究区域(如图 11(a)所示),挖掘毛果苔草、漂筏苔草、狭叶甜茅、小叶章和沼柳等5种生态群落的空间同位模式,其空间分布分别如图 11(b)—图 11(f)所示,研究区域内5种群落分别有7232、9235、11930、6977和21263个实例。生态群落数据集的邻域距离的L函数估计结果为150m。

|
| 图 11 研究区域及5种生态群落的空间分布 Fig. 11 Study area and locations of five plant species |
本文方法挖掘5种生态群落的空间同位模式的结果如表 3所示,包含8个全局空间同位模式以及6个局部空间同位模式,其局部感兴趣区域如图 12所示,进一步产生24条全局空间同位规则,以及24条局部空间同位规则(由于篇幅限制,未列出全部试验结果);为了进行比较分析,表 3第5列给出了CM算法得到的相应同位模式的全局参与指数,仅有8个空间同位模式的全局参与指数大于所设阈值;表 3的6—7列给出了RCMNG算法得到的相应空间同位模式的最小和最大局部参与指数,由于数据本身分布的不均匀性导致同位模式在其连通的固定距离的邻接子图内的实例个数很少,且全局范围内相关事件存在大量实例,因此部分同位模式(如{漂筏苔草,小叶章,沼柳})的局部参与指数很小,难以被有效发现。地理探测器的试验结果与全局空间同位模式的挖掘结果基本吻合,与2.1节中的分析结论基本类似,故不详细列出。
| 空间同位模式 | 感兴趣范围 | 本文方法 | CM算法 | RCMNG算法 | ||||
| PImin | PImax | GPI | RPImin | RPImax | ||||
| {毛果苔草,狭叶甜茅} | 全局 | 0.86 | 0.86 | 0.86 | 8×10-5 | 0.83 | ||
| {漂筏苔草,小叶章} | 全局 | 0.82 | 0.82 | 0.82 | 2×10-4 | 0.82 | ||
| {狭叶甜茅,沼柳} | 全局 | 0.79 | 0.79 | 0.79 | 8×10-5 | 0.65 | ||
| {漂筏苔草,沼柳} | 全局 | 0.64 | 0.64 | 0.64 | 1×10-4 | 0.59 | ||
| {小叶章,沼柳} | 全局 | 0.54 | 0.54 | 0.54 | 5×10-5 | 0.48 | ||
| {毛果苔草,沼柳} | 全局 | 0.53 | 0.53 | 0.53 | 1×10-4 | 0.45 | ||
| {毛果苔草,狭叶甜茅,沼柳} | 全局 | 0.51 | 0.51 | 0.51 | 2×10-5 | 0.34 | ||
| {漂筏苔草,小叶章,沼柳} | 全局 | 0.50 | 0.50 | 0.50 | 5×10-5 | 0.05 | ||
| {漂筏苔草,狭叶甜茅} | 局部 | 0.82 | 1 | 0.36 | 8×10-5 | 0.07 | ||
| {狭叶甜茅,小叶章} | 局部 | 0.70 | 1 | 0.17 | 8×10-5 | 0.10 | ||
| {狭叶甜茅,小叶章,沼柳} | 局部 | 0.50 | 1 | 0.17 | 8×10-5 | 0.13 | ||
| {漂筏苔草,狭叶甜茅,小叶章} | 局部 | 0.71 | 0.97 | 0.14 | 8×10-5 | 0.03 | ||
| {毛果苔草,漂筏苔草} | 局部 | 1 | 1 | 0.07 | 1×10-4 | 6×10-3 | ||
| {毛果苔草,漂筏苔草,狭叶甜茅} | 局部 | 0.8 | 0.8 | 0.06 | 8×10-5 | 6×10-3 | ||
| 注:PImin和PImax分别为感兴趣区域内的最小和最大参与指数;GPI为全局参与指数;RPImin和RPImax为最小和最大局部参与指数。 | ||||||||

|
| 图 12 空间同位模式的局部感兴趣区域 Fig. 12 Regions of interest of the spatial co-location patterns |
分析试验结果,可以发现:①14个空间同位模式中大多都包含沼柳,可见本文研究区域内沼柳属于优势种,对群落结构和环境的形成有着明显控制作用,是其他植被赖以生存的基础;②部分生态群落的空间同位模式具有局部分布的特性。以局部空间同位模式{漂筏苔草,狭叶甜茅}为例,如图 11(c)和(d)所示,漂筏苔草主要分布于研究区域南部,而狭叶甜茅主要分布于研究区域北部,因此从全局视角无法发现该同位模式。本文方法通过对该同位模式进行自适应空间聚类分析,找出其局部聚集区域,进而在局部范围内进行测试,最终保留满足最小参与指数阈值和最小实例个数阈值的局部区域,结果发现该空间同位模式主要分布于研究区域的南部,如图 12(a)所示。可见,本文方法能够有效顾及空间数据的异质特性,从而可以从局部视角提取具有空间分布差异的局部空间同位模式。
进一步可以通过生态物种分布的先验知识对上述挖掘结果的有效性进行评价。针对研究区域的实际调查发现[29]:毛果苔草、狭叶甜茅、小叶章、沼柳均分布在季节性变化的积水沼泽,且主要生态类型为湿生,因此这些生态群落具有类似的生长习性,具备共生的基本条件。从本文的挖掘结果来看,这些生态群落在全局和局部的同位模式表现出了很强的共生性,与现有先验知识是吻合的,也可以说明本文方法的有效性。然而,本文方法挖掘的不同物种间的同位模式在空间上的分布是不均匀的,这极有可能是由于土壤的性质与速效氮含量的差异性造成的,进一步研究这些空间同位模式的分布规律,将为研究植被类型与表层土壤性质的相应关系提供重要的借鉴[30]。
3 总结与展望本文提出了一种多层次空间同位模式自适应挖掘方法,通过由全局到局部的研究策略,借助自适应模式聚类发现地理事件在多个空间层次上的共生规律。通过试验分析和比较发现,本文方法不仅可以提取全局的空间同位模式,还能有效地在空间异质环境下,自适应地提取局部空间同位模式及其自然的空间分布结构,从而能够更全面地反映地理事件间的共生规律。应用本文提出方法成功提取了我国东北某湿地的生态物种的局部共生规律,对于研究该区域的生态物种平衡与环境响应机制具有重要的指导价值。
进一步的研究工作主要集中在两个方面:①本文用聚类分析提取的局部感兴趣区域只是同位模式的热点区域,需要进一步研究空间同位模式由局部向全局扩展过程中有效边界的界定方法;②空间同位模式频繁程度度量还依赖于人为阈值设置,进一步需要研究空间同位模式频繁度的客观判别方法。
| [1] | 李德仁, 张良培, 夏桂松. 遥感大数据自动分析与数据挖掘[J]. 测绘学报, 2014, 43(12):1211-1216. DOI:10.13485/j.cnki.11-2089.2014.0187. LI Deren, ZHANG Liangpei, XIA Guisong. Automatic Analysis and Mining of Remote Sensing Big Data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12):1211-1216. DOI:10.13485/j.cnki.11-2089.2014.0187. |
| [2] | 江冲亚, 李满春, 刘永学. 海岸带水体遥感信息全自动提取方法[J]. 测绘学报, 2011, 40(3):332-337. JIANG Chongya, LI Manchun, LIU Yongxue. Full-automatic Method for Coastal Water Information Extraction from Remote Sensing Image[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3):332-337. |
| [3] | 胡庆武,王明,李清泉. 利用位置签到数据探索城市热点与商圈[J]. 测绘学报, 2014, 43(3):314-321. DOI:10.13485/j.cnki.11-2089.2014.0045. HU Qingwu, WANG Ming, LI Qingquan. Urban Hotspot and Commercial Area Exploration with Check-in Data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(3):314-321. DOI:10.13485/j.cnki.11-2089.2014.0045. |
| [4] | 谢超, 陈毓芬, 王英杰. Apriori算法在ACViS中用户行为监测数据挖掘中的应用研究[J]. 测绘学报, 2010, 39(4):397-403. XIE Chao, CHEN Yufen, WANG Yingjie. Application of Apriori Algorithm in User Action Monitoring Data Mining in Adaptive Cartographic Visualization System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4):397-403. |
| [5] | 田晶, 艾廷华, 丁绍军. 基于C4.5算法的道路网网格模式识别[J]. 测绘学报, 2012, 41(1):121-126. TIAN Jing, AI Tinghua, DING Shaojun. Grid Pattern Recognition in Road Networks Based on C4.5 Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1):121-126. |
| [6] | SHEKHAR S, HUANG Y. Co-location Rules Mining:A Summary of Results[C]//Proceedings of the 7th International Symposium on Spatio and Temporal Databases. Redondo Beach:[s.n.], 2001. |
| [7] | YOO J S, SHEKHAR S, SMITH J, et al. A Partial Join Approach for Mining Co-location Patterns[C]//Proceedings of the 12th Annual ACM International Workshop on Geographic Information Systems. New York:ACM, 2004:241-249. |
| [8] | AGRAWAL R,SRIKANT R.Fast Algorithms for Mining Association Rules[C]//Proceedings of the 20th International Conference on Very Large Data Bases. Santiago:VLDB, 1994:487-499. |
| [9] | KOPERSKI K, HAN Jiawei. Discovery of Spatial Association Rules in Geographic Information Databases[C]//EGENHOFER M J, HERRING J R. Advances in Spatial Databases. Berlin:Springer, 1995:47-66. |
| [10] | 李光强, 邓敏, 朱建军. 基于Voronoi图的空间关联规则挖掘方法研究[J]. 武汉大学学报(信息科学版), 2008, 33(12):1242-1245. LI Guangqiang, DENG Min, ZHU Jianjun. Spatial Association Rules Mining Methods Based on Voronoi Diagram[J]. Geomatics and Information Science of Wuhan University, 2008, 33(12):1242-1245. |
| [11] | YOO J S, SHEKHAR S. A Joinless Approach for Mining Spatial Colocation Patterns[J]. IEEE Transactions on Knowledge and Data Engineering, 2006, 18(10):1323-1337. |
| [12] | XIAO Xiangye, XIE Xing, LUO Qiong, et al. Density Based Co-location Pattern Discovery[C]//Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York:ACM, 2008:29. |
| [13] | WANG Jinfeng, LI Xinhu, CHRISTAKOS G, et al. Geographical Detectors-based Health Risk Assessment and Its Application in the Neural Tube Defects Study of the Heshun Region, China[J]. International Journal of Geographical Information Science, 2010, 24(1):107-127. |
| [14] | MILLER H J, HAN Jiawei. Geographic Data Mining and Knowledge Discovery[M]. 2nd ed. New York:CRC Press, 2009. |
| [15] | CELIK M, KANG J M, SHEKHAR S. Zonal Co-location Pattern Discovery with Dynamic Parameters[C]//Proceedings of the 7th IEEE International Conference on Data Mining. Omaha:IEEE, 2007:433-438. |
| [16] | DING Wei, EICK C F, YUAN Xiaojing, et al. A Framework for Regional Association Rule Mining and Scoping in Spatial Datasets[J]. Geoinformatica, 2011, 15(1):1-28. |
| [17] | QIAN Feng, CHIEW K, HE Qinming, et al. Mining Regional Co-location Patterns with kNNG[J]. Journal of Intelligent Information Systems, 2014, 42(3):485-505. |
| [18] | EICK C F, PARMAR R, DING Wei, et al. Finding Regional Co-location Patterns for Sets of Continuous Variables in Spatial Datasets[C]//Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York:ACM, 2008. |
| [19] | 沙宗尧, 李晓雷. 异质环境下的空间关联规则挖掘[J]. 武汉大学学报(信息科学版), 2009, 34(12):1480-1484. SHA Zongyao, LI Xiaolei. Algorithm of Mining Spatial Association Data under Spatially Heterogeneous Environment[J]. Geomatics and Information Science of Wuhan University, 2009, 34(12):1480-1484. |
| [20] | MOHAN P, SHEKHAR S, SHINE J A, et al. A Neighborhood Graph Based Approach to Regional Co-location Pattern Discovery:A Summary of Results[C]//Proceedings of the 19th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York:ACM, 2011:122-132. |
| [21] | 边馥苓, 万幼. k-邻近空间关系下的同位模式挖掘算法[J]. 武汉大学学报(信息科学版), 2009, 34(3):331-334, 338. BIAN Fuling, WAN You. A Novel Spatial Co-location Pattern Mining Algorithm Based on k-nearest Feature Relationship[J]. Geomatics and Information Science of Wuhan University, 2009, 34(3):331-334, 338. |
| [22] | WAN You,ZHOU Chenghu.QuCOM:K Nearest Features Neighborhood Based Qualitative Spatial Co-location Patterns Mining Algorithm[C]//Proceedings of the IEEE International Conference on Spatial Data Mining and Geographical Knowledge Services. Fuzhou:IEEE, 2011:54-59. |
| [23] | 刘启亮, 邓敏, 石岩, 等. 一种基于多约束的空间聚类方法[J]. 测绘学报, 2011, 40(4):509-516. LIU Qiliang, DENG Min, SHI Yan, et al. A Novel Spatial Clustering Method Based on Multi-constraints[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4):509-516. |
| [24] | YOO J S, BOW M. Mining Spatial Colocation Patterns:A Different Framework[J]. Data Mining and Knowledge Discovery, 2012, 24(1):159-194. |
| [25] | BARUA S, SANDER J. Mining Statistically Significant Co-location and Segregation Patterns[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(5):1185-1199. |
| [26] | ESTIVILL-CASTRO V,LEE I.Argument Free Clustering for Large Spatial Point-data Sets via Boundary Extraction from Delaunay Diagram[J]. Computers, Environment and Urban Systems, 2002, 26(4):315-334. |
| [27] | BOUCHER D H, JAMES S, KEELER K H. The Ecology of Mutualism[J]. Annual Review of Ecology and Systematics, 1982, 13:315-347. |
| [28] | HUBÁLEK Z. Coefficients of Association and Similarity, Based on Binary (Presence-absence) Data:An Evaluation[J]. Biological Reviews, 1982, 57(4):669-689. |
| [29] | 郑明月. 空间聚类规则在洪河湿地植被类型分布梯度变化中的应用[D]. 哈尔滨:哈尔滨师范大学, 2013. ZHENG Mingyue. The Application of Spatial Clustering Rules in the Honghe Wetland Vegetation Form Distribution Change of Gradient[D]. Harbin:Harbin Normal University, 2013. |
| [30] | 娄彦景, 赵魁义. 洪河自然保护区湿地主要植被类型物种多样性与表层土壤性质的相关性研究[J]. 湿地科学, 2008, 6(1):45-50. LOU Yanjing, ZHAO Kuiyi. Correlation between Plant Species Diversity of Main Vegetation Types and Surface Soil Properties in Wetland of Honghe Nature Reserve[J]. Wetland Science, 2008, 6(1):45-50. |