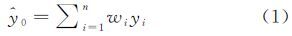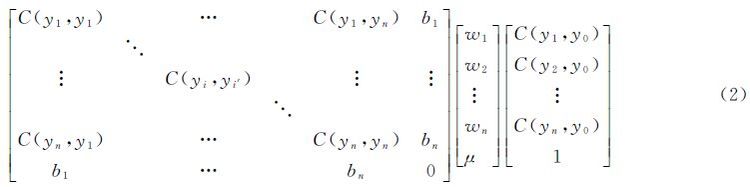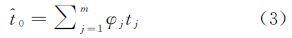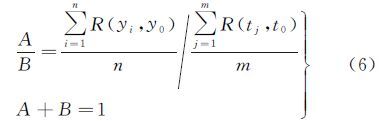2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北武汉 430079;
3. 日电(NEC)中国研究院, 北京 100084
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
3. NEC Labs, Beijing 100084, ChinaAbstract
大自然的演变、人类的生产活动、社会经济的发展都是时空过程,可以用时空数据表示。然而时空数据由于各种原因存在数据缺失的现象[1]。数据缺失降低了时空数据的完整性,可能会导致人们作出不合理的推断和决策。因此时空缺失数据的插值与估计对于时空数据挖掘和建模具有重要意义[2, 3]。
为了解决时空数据的缺失问题,一系列时空数据插值方法被提出用以插值缺失时空数据。其中大多数方法将时空数据简化为连续的空间数据序列进行空间插值[4]。然而,使用空间插值方法处理时空数据会造成数据时间维度信息的丢失[5]。为了解决这一问题,近年来一些学者提出时空插值的方法并广泛应用于时空缺失数据的插值与估计[6, 7, 8]。
目前时空数据的插值方法,主要包括基于回归的方法、时空反距离加权方法以及时空克里金方法等[9, 10, 11, 12, 13, 14, 15]。分析现有时空插值方法,可以发现现有方法插值时空数据时,大都假设时空过程的空间和时间平稳性。由于时空数据存在异质性,现有插值方法的精度仍然不能令人满意。在时空数据插值时,最大程度消除时空异质性的影响,有效融合时空维度数据成为时空插值研究的难点之一。因此,本文提出一种顾及时空异质性的缺失数据时空插值方法解决这一问题。
1 相关研究回顾及本文研究策略基于回归的方法利用周围监测站的记录和相关资料计算回归方程,进而估计缺失的数据。近年来,一些学者顾及空间异质性提出地理加权回归方法并应用于许多领域。例如,文献[16]利用非欧几里德距离地理加权回归估计欧洲房价的分布,文献[17]则利用地理加权回归对我国深圳的房价进行建模分析。然而基于回归的方法处理缺失数据时存在一定的局限性,在数据缺失较多的情况下插值结果不理想[18]。
反距离加权方法通过计算周围监测站点对缺失站点的反距离权重估计站点的缺失数据[19]。一些学者将其扩展至时空,提出时空反距离加权插值方法。时空反距离加权方法计算三维时空距离,并以此距离的倒数为参数定权估计缺失的数据。时空反距离加权方法易于实现,但它是有偏的,精度相比其他方法较低。
另一类广泛应用的插值方法是基于地统计学的克里金方法(Kriging)[20]。克里金方法使用变异函数或协方差函数进行插值估计。克里金方法包括许多扩展,例如简单克里金方法、普通克里金方法、协同克里金方法等。近年来一些学者将克里金方法扩展至时空,耦合时间和空间记录对缺失数据进行插值[21]。在此基础上,文献[9, 22]提出了时空积和协方差模型,并将其成功应用于空气污染物浓度数据的时空插值建模。
此外,文献[23,24]提出了一种时空数据的三明治估计模型。该模型采用层次策略,将研究区域分为采样层、分区层和报告层。三明治模型能够很好地顾及空间异质性,所得结果精度高于其他相关模型。另一种顾及空间异质性的插值方法是点最优线性无偏插值方法(简称P-Bshade)[4, 25, 26]。该方法顾及空间异质性提出了一种站点期望比指标,对比传统克里金方法,P-Bshade方法具有更高的精度和效率。但该算法也具有一定的局限性,未能同时顾及时空异质性融合空间和时间数据对缺失数据进行估计。
分析上述国内外研究方法可以得出:
(1) 现有缺失数据插值方法大都单纯从空间或者时间角度进行插值,主要原因是时空插值对比单纯的空间插值或时间插值计算更复杂。此外,单纯使用时间或空间维度数据估计缺失数据势必会丢失采样数据的部分信息,从而降低插值的精度。
(2) 现有缺失数据时空插值方法,对于异质性的顾及大都只是单独考虑时间或者空间维度。由于时空异质性,即空间和时间非平稳的影响,研究区域不同子区域间可能存在较大的差异,因此有必要同时考虑时空异质性进行插值计算。
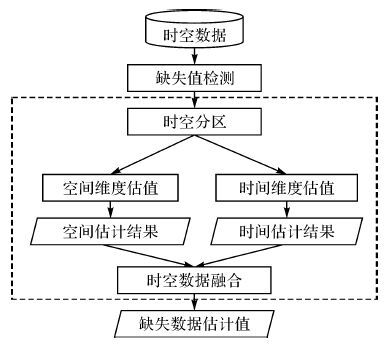
鉴于以上两点,本文提出一种顾及时空异质性的缺失数据时空插值方法。该方法首先对时空数据进行缺失数据检测,进而顾及时空异质性对数据集进行时空分区,在时空子区域内分别选取n个相关性最大的空间周围数据和m个相关性最大的时间周围数据用以估计缺失数据,最后利用相关系数计算时空维度插值结果的贡献权重,融合时空维度插值结果得到缺失数据的最终估计结果。算法的流程图如图 1所示。
|
| 图 1 本文方法流程图 Fig. 1 The flowchart of this method |
本研究首先对时空数据集进行检测,找到缺失数据的位置,进而对时空数据进行异质分区,包括空间聚类分区和时间切片选取两部分。下面分别对其进行介绍。
首先在空间采用聚类分区的策略对数据集进行异质划分,将时空数据按照内部均质划分为不同的子区域,本研究采用REDCAP聚类方法对研究区域进行异质分区[27]。该方法首先按照邻接约束构建研究区域的邻接树,然后计算最小方差增量距离并利用全局邻接约束对整个研究区域按照空间邻接树进行空间划分,最后按照初始规定的聚类数目进行空间聚类分区,聚类的数目由历史经验和聚类评价指标综合确定。
空间异质分区后对时空数据顾及时间异质性进行时间分区。本文采用时间切片的期望值进行时间维度分区,首先对于每个时间切片求期望并排序,进而对排序后的时间切片期望值画图并寻找拐点,以此划分时间切片。时空分区可以有效降低时空异质性对时空插值的影响,使同一子区域内的时空数据相对平稳。在时空子区域中进行时空插值,不仅可以提高插值精度,而且可以缩短计算时间。
数据集进行时空分区处理后,对每个缺失数据选取参与插值计算的空间维度和时间维度采样数据。首先在空间维度选取缺失数据周围空间的n个相关性最大的采样数据,本文选择相关系数R描述站点之间的相关性,具体计算为:对于一个缺失数据,计算其周围空间点的数据序列和缺失数据点的数据序列的相关系数R(yi,y0)。其中,yi表示缺失数据周围空间点的数据序列,y0表示缺失数据点的数据序列。当某一序列中存在其他缺失数据时则去除另一序列中的相应数据继续进行计算。同样对于时间维度,在同一子区域内选取缺失数据前后时间的m个相关性最大的采样数据,其中的相关性计算为:对于一个缺失数据,计算缺失数据周围时间切片的空间点序列和缺失数据所在时间切片的空间点序列的相关系数R(tj,t0)。其中,tj表示缺失数据周围时间切片的空间点序列,t0表示缺失数据所在时间切片的空间点序列。最后,分别在空间维度选择n个、时间维度选择m个相关系数最大的周围数据进行缺失点的插值计算。对于n和m的取值,可以根据现有研究和聚类结果具体设置,文献[4]建议周围站点数目可以设置为5、10、15。
2.2 顾及异质性的时空维度插值选取参与插值计算的空间维度和时间维度采样数据后,分别在时空维度进行缺失数据的插值估计。在空间维度,按照P-Bshade方法[4],利用上述n个相关系数最大的空间周围采样数据,按下式计算缺失数据的空间维度估值${\hat y_0}$
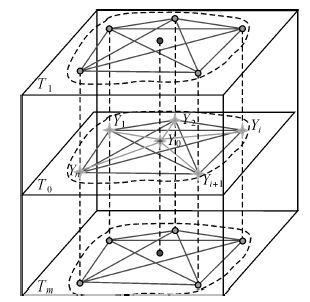
式中,yi表示第i个空间周围采样数据的观测值;wi表示第i个空间周围采样数据对缺失数据的空间贡献权重;wi可以用下式计算求得 式中,方程中间的矩阵为待求矩阵;μ为拉格朗日系数。方程左边的矩阵中C(yi,yi′)表示第i个空间周围采样点的时间序列与第i′个空间周围采样点的时间序列的协方差,bi表示第i个空间周围采样点的时间序列与缺失数据点的时间序列的期望比。方程右边的矩阵中C(yi,y0)表示第i个空间周围采样点的时间序列与缺失数据点的时间序列的协方差,并满足1≤i≤n,1≤i′≤n。空间维度插值算法的思想如图 2所示,其中y0代表缺失数据点,yi代表第i个空间周围采样点数据,T1、T2、…、Ti、…、Tm代表时间层切片,虚线内区域即为一个异质子区域,连接已知点的线表示协方差,上下垂直的虚线表示时间序列,连接缺失点与采样点的线表示采样点对缺失点的空间贡献权重。
|
| 图 2 空间维度插值示意图 Fig. 2 The chart of space dimension interpolation |
同样在时间维度,定义缺失数据周围时间层的空间点序列与缺失数据时间层的空间点序列的期望比这一指标处理时间维度的异质性影响。引入这一指标可以进一步降低时空异质性的影响,提高插值的精度。利用上述m个相关系数最大的时间周围采样数据,按下式计算缺失数据的时间维度估值${\hat t_0}$
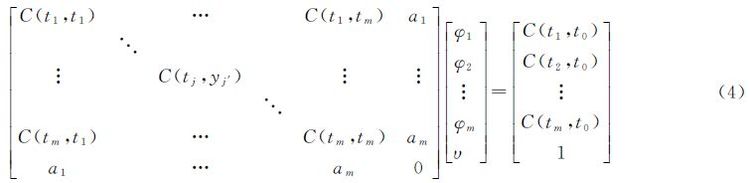
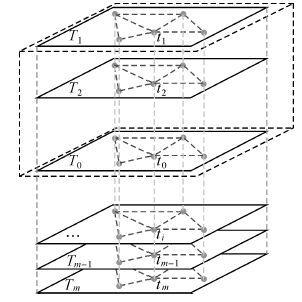
式中,tj表示第j个周围时间采样数据;φj表示第j个周围时间采样数据对缺失数据的时间贡献权重,φj可以用下式计算得出 式中,方程中间的矩阵为待求矩阵,υ为拉格朗日系数。左边矩阵中C(tj,tj′)表示第j个周围时间切片的空间点序列与第j′个周围时间切片的空间点序列的协方差,aj表示第j个周围时间切片的空间点序列与缺失数据时间切片的空间点序列的期望比。右边矩阵中C(tj,t0)表示第j个周围时间切片的空间点序列与缺失数据时间切片的空间点序列的协方差,并满足1≤j≤m,1≤j′≤m。时间维度插值算法的思想如图 3所示,其中t0表示缺失数据点,tj表示缺失数据周围时间维度选择的采样数据点,T1、…、Ti、…、Tm表示时间切片,上下垂直的虚线表示时间序列,虚线矩形框表示选择的异质时间分区,连接采样点的虚线表示协方差。
|
| 图 3 时间维度插值示意图 Fig. 3 The chart of time dimension interpolation |
求得缺失数据在时间和空间维度的估计值后,采用线性加权的方法对其进行融合。由于时空协方差模型分为可分离和不可分离两种,相应时空插值结果的融合也分为可分离和不可分离两种[28, 29]。不可分离时空协方差模型通常计算复杂,例如积和协方差模型需要计算一系列参数拟合时空变异曲面。而可分离时空协方差模型对于时空维度插值结果的融合大多采用线性融合的方法。根据所求缺失数据的空间维度估值和时间维度估值,利用下式(5)计算缺失数据的最终时空估计结果Y0
式中,A表示空间维度权重;B表示时间维度权重。对于权重的确定,本文利用上文中的相关系数进行计算求解公式(6)即可得到时空维度的贡献权重。公式(6)在一定程度上考虑了时间维度和空间维度的贡献率,使得时空维度计算结果的融合更加合理。最后将时空维度估计结果和时空维度权重代入公式(5)即可得到缺失数据的最终时空估计结果。
3 试验分析为了验证本文方法的优越性与适用性,共设计了两组试验。试验1采用我国554个气象监测站点,历时312个月(1984年1月至2009年12月)的气象数据集,包括月平均气温数据和月累计降雨数据。试验数据不存在缺失,使用不同方法对每个时空点进行插值估计,然后采用留一法对不同方法进行交叉验证对比分析,验证本文方法的优越性。试验2采用我国930个气象监测站点,历时53年(1961年至2013年)的年平均气温数据集,数据存在一定的缺失,包括监测的随机缺失和早期未建站点的大量连续缺失。同样使用不同方法对每个时空点进行插值估计,进而采用留一法对不同方法进行交叉验证对比分析,验证本文方法在实际应用中适用性。试验数据集来源于国家气象信息中心。
3.1 试验1:模拟验证对于试验1数据,对比分析本文方法即异质分区时空插值方法、P-Bshade方法、未分区本文方法、时空Kriging方法以及空间Kriging方法。试验选取平均绝对误差(MAE)和均方根误差(RMSE)两个常用指标分析不同插值方法结果的精度。
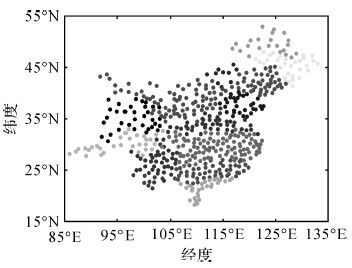
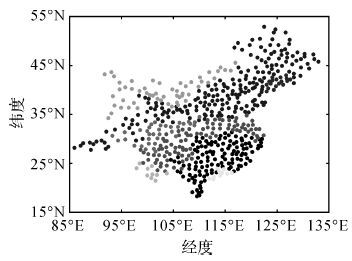
试验中554个气象监测站点及其异质分区如图 4和图 5所示,相同的颜色表示同一空间分区,分区方法为REDCAP聚类方法,聚类分区的数目分别为:气温数据集为12个,降水数据集为8个。聚类分区数目的确定依据我国气温分带及降水分区经验数据和聚类评价指标,并对单点的聚类结果进行合并处理。时空分区处理在一定程度上可以降低时空插值中异质性的影响,然而就分区而言存在两个问题:其一是分区数目的确定,通常需要结合历史数据及经验知识,并且满足聚类的评价指标综合确定。其二是分区后位于区域边界的数据计算精度会下降,而在一些点数较少的分区中,这种区域边界效应更为明显。
|
| 图 4 气温监测点异质分区图 Fig. 4 The chart of temperature observation stations heterogeneity subareas |
|
| 图 5 降水监测点异质分区图 Fig. 5 The chart of precipitation observation stations heterogeneity subareas |
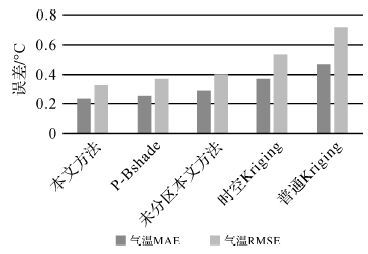
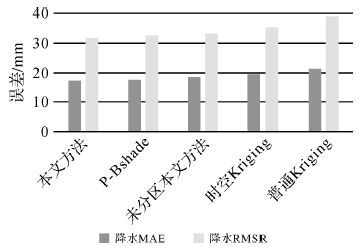
对5种插值方法的结果进行交叉验证得到误差指标MAE和RMSE如表 1所示。其中本文方法和P-Bshade方法的参数n和m,依据聚类结果将其均设置为10,空间Kriging采用普通Kriging方法,时空Kriging方法采用积和模型进行计算。
| 插值方法 | 气温/℃ | 降水/mm | |||
| MAE | RMSE | MAE | RMSE | ||
| 本文方法 | 0.235 | 0.328 | 17.263 | 31.639 | |
| P-Bshade | 0.254 | 0.371 | 17.488 | 32.610 | |
| 未分区本文方法 | 0.290 | 0.401 | 18.370 | 33.284 | |
| 时空Kriging | 0.369 | 0.539 | 19.405 | 35.447 | |
| 普通Kriging | 0.468 | 0.718 | 21.373 | 39.162 | |
将表 1数据展示为直方图形式如图 6和图 7所示。可以看出本文方法在精度上优于其他4种方法。相比于P-Bshade方法,本文方法由于进行时空分区并顾及时间维度信息进行插值,降低了时空异质性的影响,插值精度有所提高。对比未分区的本文方法,分区可以有效降低异质性影响,提高插值精度。但是,未分区本文方法对比P-Bshade方法精度有所下降,这可能是由于在融合时间维度信息时,未分区导致每个时间切片的监测站数量多且数值差异大,使得计算时间维度周围数据的权重精度下降,然而时空分区可以有效解决这一问题。本文方法同样优于时空Kriging和普通Kriging方法,且精度提高较为明显。
|
| 图 6 5种插值方法的气温试验结果 Fig. 6 The results of temperature dataset used |
|
| 图 7 5种插值方法的降水试验结果 Fig. 7 The results of precipitation dataset used |
从试验1可以发现,本文方法的插值精度优于其他几种方法。试验2采用一组具有不同类型缺失的数据进一步对比分析本文方法和P-Bshade方法的精度及适用性。试验数据的缺失情况如图 8所示。图中散点表示缺失数据的位置,折线表示每年缺失数据的变化情况。可以发现,图 8左上角存在连续的数据缺失,这是由于在建站初期一些站点还未建成导致的。数据的最大缺失出现在1968年,共68个站点缺失,并在之后急速减少,在1980年后趋于稳定。
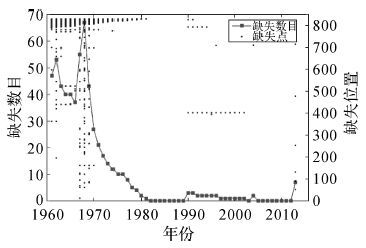
|
| 图 8 数据缺失示意图 Fig. 8 The chart of missing data number and distribution |
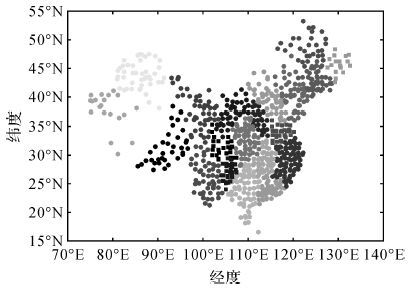
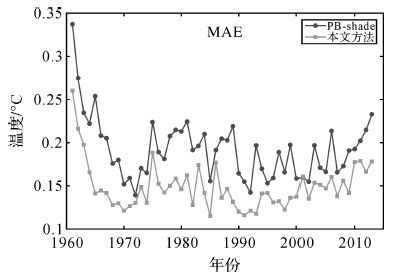
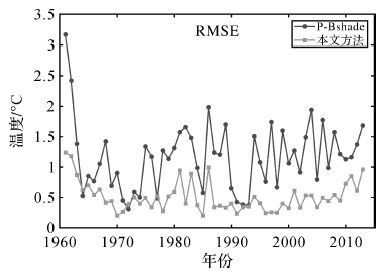
对试验数据2进行异质分区,所得聚类分区的数目为19个,如图 9所示。对实际缺失数据采用本文方法和P-Bshade方法进行插值估计,交叉验证结果为:本文方法的MAE为0.149℃,RMSE为0.531℃;P-Bshade方法的MAE为0.192℃,RMSE为1.164℃。本文方法优于P-Bshade方法。对插值结果进行逐年精度分析如图 10和图 11所示。可以看出本文方法对比P-Bshade方法具有更高的精度和适用性。在1960年至1970年缺失数据较多且存在大量连续缺失的情况下,两种方法都具有较大的误差,而本文方法误差相对更小。在1970年后缺失数目减少并趋于稳定,本文方法精度同样优于P-Bshade方法。
|
| 图 9 气温数据异质分区图 Fig. 9 The chart of temperature observation stations heterogeneity subareas |
|
| 图 10 年均气温插值MAE图 Fig. 10 Yearly MAEs from 1961 to 2013 for two methods |
|
| 图 11 年均气温插值RMSE图 Fig. 11 Yearly RMSEs from 1961 to 2013 for two methods |
本文针对时空数据存在缺失的情况,提出了一种基于时空异质性的缺失数据时空插值方法。该方法顾及时空异质性,首先对时空数据进行异质分区,进而在时间维度和空间维度分别采用异质协方差模型估计缺失数据,最后对时空维度插值结果进行融合。该方法对时空序列缺失数据插值具有良好效果,与已有方法相比提高了插值结果的精度。然而本文方法依然存在一定的局限性,表现在对于时空分区模糊的数据,分区会比较困难。未来研究主要集中在跨分区样本单元分区,以及时空非线性不可分离模型插值等方面,以期进一步提高时空插值的精度。
| [1] | SIMOLO C, BRUNETTI M, MAUGERI M, et al. Improving Estimation of Missing Values in Daily Precipitation Series by a Probability Density Function-Preserving Approach[J]. International Journal of Climatology, 2010, 30(10):1564-1576. |
| [2] | 王劲峰, 葛咏, 李连发, 等. 地理学时空数据分析方法[J]. 地理学报, 2014, 69(9):1326-1345. WANG Jinfeng, GE Yong, LI Lianfa, et al. Spatiotemporal Data Analysis in Geography[J]. Acta Geographica Sinica, 2014, 69(9):1326-1345. |
| [3] | 叶近天, 季世民, 杨勇. 时空地统计学方法研究及进展[J]. 测绘与空间地理信息, 2014, 37(1):38-43. YE Jintian, JI Shimin, YANG Yong. Spatio-Temporal Geotatistics Method Research and Progress[J]. Geomatics & Spatial Information Technology, 2014, 37(1):38-43. |
| [4] | XU Chengdong, WANG Jinfeng, HU Maogui, et al. Interpolation of Missing Temperature Data at Meteorological Stations Using P-BSHADE[J]. Journal of Climate, 2013, 26(19):7452-7463. |
| [5] | DE CESARE L, MYERS D E, POSA D. Estimating and Modeling Space-time Correlation Structures[J]. Statistics & Probability Letters, 2001, 51(1):9-14. |
| [6] | KYRIAKIDIS P C, JOURNEL A G. Geostatistical Space-Time Models:a Review[J]. Mathematical Geology, 1999, 31(6):651-684. |
| [7] | KILIBARDA M, TADIC' M P, HENGL T, et al. Global Geographic and Feature Space Coverage of Temperature Data in the Context of Spatio-Temporal Interpolation[J]. Spatial Statistics, 2015, 14(Part A):22-38. |
| [8] | WANG Jinfeng, XU Chengdong, HU Maogui, et al. A New Estimate of the China Temperature Anomaly Series and Uncertainty Assessment in 1900-2006[J]. Journal of Geophysical Research:Atmospheres, 2014, 119(1):1-9. |
| [9] | DE IACO S,MYERS D E,POSA D.Space-Time Variograms and a Functional Form for Total Air Pollution Measurements[J]. Computational Statistics & Data Analysis, 2002, 41(2):311-328. |
| [10] | LI Lixin, REVESZ P. Interpolation Methods for Spatio-Temporal Geographic Data[J]. Computers, Environment and Urban Systems, 2004, 28(3):201-227. |
| [11] | HUANG Bo, WU Bo, BARRY M. Geographically and Temporally Weighted Regression for Modeling Spatio-Temporal Variation in House Prices[J]. International Journal of Geographical Information Science, 2010, 24(3):383-401. |
| [12] | 杨朝晖, 余洁, 陈江平. 基于聚类与空间自回归模型的缺失数据填补方法[C]//亚太环境科学研究中心. 2010年国际遥感会议论文集.[S.l.]:智能信息技术应用学会, 2010, 3:4. YANG Zhaohui, YU Jie, CHEN Jiangping. A Missing Data Imputation Method Based on Cluster and Spatial Autoregressive Model[C]//Asia Pacific Environmental Science Research Center. Proceedings of 2010 International Conference on Remote Sensing (ICRS 2010).[S.l.]:Application of Intelligent Information Technology Institute, 2010, 3:4. |
| [13] | 李正泉, 吴尧祥. 顾及方向遮蔽性的反距离权重插值法[J]. 测绘学报, 2015, 44(1):91-98. DOI:10.11947/j.AGCS.2015.20130349. LI Zhengquan, WU Yaoxiang. Inverse Distance Weighted Interpolation Involving Position Shading[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(1):91-98. DOI:10.11947/j.AGCS.2015.20130349. |
| [14] | 张锦明, 游雄, 万刚. DEM插值参数优选的试验研究[J]. 测绘学报, 2014, 43(2):178-185, 192. DOI:10.13485/j.cnki.11-2089.2014.0026 ZHANG Jinming, YOU Xiong, WAN Gang. Experimental Research on Optimization of DEM Interpolation Parameters[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(2):178-185, 192. DOI:10.13485/j.cnki.11-2089.2014.0026 |
| [15] | 董箭, 彭认灿, 郑义东, 等. 局部动态最优Voronoi图的NNI算法及其在格网数字水深模型中的应用[J]. 测绘学报, 2013, 42(2):284-289, 303. DONG Jian, PENG Rencan, ZHENG Yidong, et al. An Algorithm of Natural Neighbor Interpolation Based on Local Dynamic Optimal Voronoi Diagram and Its Application in Grid Digital Depth Model[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2):284-289, 303. |
| [16] | LU Binbin, CHARLTON M, HARRIS P, et al. Geographically Weighted Regression with a Non-Euclidean Distance Metric:A Case Study Using Hedonic House Price Data[J]. International Journal of Geographical Information Science, 2014, 28(4):660-681. |
| [17] | WU Bo, LI Rongrong, HUANG Bo. A Geographically and Temporally Weighted Autoregressive Model with Application to Housing Prices[J]. International Journal of Geographical Information Science, 2014, 28(4):1186-1204. |
| [18] | HUBBARD K G, YOU Jinsheng. Sensitivity Analysis of Quality Assurance Using the Spatial Regression Approach-A Case Study of the Maximum/Minimum Air Temperature[J]. Journal of Atmospheric and Oceanic Technology, 2005, 22(10):1520-1530. |
| [19] | LU G Y, WONG D W. An Adaptive Inverse-Distance Weighting Spatial Interpolation Technique[J]. Computers & Geosciences, 2008, 34(9):1044-1055. |
| [20] | 徐爱萍, 圣文顺, 舒红. 时空积和模型的数据插值与交叉验证[J]. 武汉大学学报(信息科学版), 2012, 37(7):766-769. XU Aiping, SHENG Wenshun, SHU Hong. Spatiotemporal Interpolation and Cross Validation Based on Product-Sum Model[J]. Geomatics and Information Science of Wuhan University, 2012, 37(7):766-769. |
| [21] | BILONICK R A. The Space-Time Distribution of Sulfate Deposition in the Northeastern United States[J]. Atmospheric Environment (1967), 1985, 19(11):1829-1845. |
| [22] | DE IACOS S,MYERS D E,POSA D.Space-Time Analysis Using a General Product-Sum Model[J]. Statistics & Probability Letters, 2001, 52(1):21-28. |
| [23] | WANG Jinfeng, HAINING R,LIU Tiejun,et al.Sandwich Estimation for Multi-Unit Reporting on a Stratified Heterogeneous Surface[J]. Environment and Planning A, 2013, 45(10):2515-2534. |
| [24] | WANG Jinfeng, HAINING R, CAO Zhidong. Sample Surveying to Estimate the Mean of a Heterogeneous Surface:Reducing the Error Variance through Zoning[J]. International Journal of Geographical Information Science, 2010, 24(4):523-543. |
| [25] | WANG Jingfeng, REIS B Y, HU Maogui, et al. Area Disease Estimation Based on Sentinel Hospital Records[J]. PLoS One, 2011, 6(8):e23428. |
| [26] | HU Maogui, WANG Jinfeng, ZHAO Yu, et al. A B-SHADE Based Best Linear Unbiased Estimation Tool for Biased Samples[J]. Environmental Modelling & Software, 2013, 48:93-97. |
| [27] | GUO D. Regionalization with Dynamically Constrained Agglomerative Clustering and Partitioning (REDCAP)[J]. International Journal of Geographical Information Science, 2008, 22(7):801-823. |
| [28] | MA Chunsheng. Spatio-temporal Covariance Functions Generated by Mixtures[J]. Mathematical Geology, 2002, 34(8):965-975. |
| [29] | MA Chunsheng. Recent Developments on the Construction of Spatio-Temporal Covariance Models[J]. Stochastic Environmental Research and Risk Assessment, 2008, 22(1):39-47. |