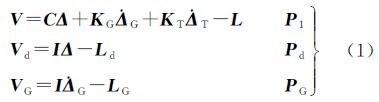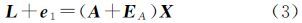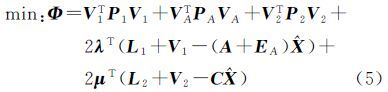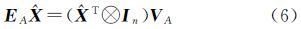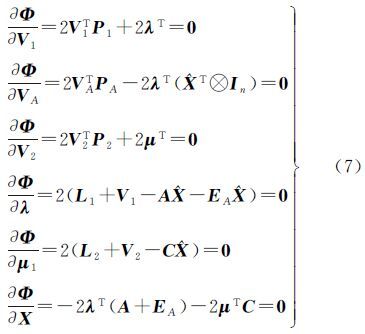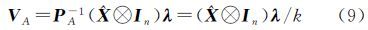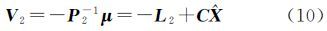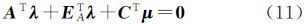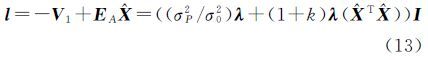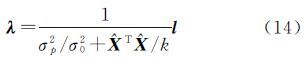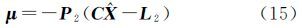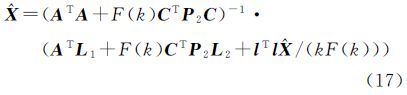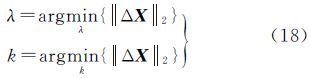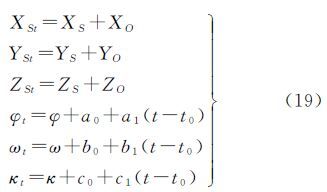2. 西安测绘研究所, 陕西西安 710054;
3. 地理信息工程国家重点实验室, 陕西西安 710054
2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
3. State Key Laboratory of Geo-information Engineering, Xi'an 710054, ChinaAbstract
光束法区域网平差是线阵卫星遥感影像有地面控制条件下几何定位的重要方法。其基本思想是利用地面控制点坐标及其对应像点观测值等测量数据,同时求解成像传感器的外方位元素和地面点的三维坐标[1]。当前,常规的光束法平差方法中均利用Gauss-Markov模型描述像点观测方程的函数模型,即假定函数模型已知、非随机,且观测值中仅含有随机误差。在此基础上引入外方位元素的虚拟观测方程以及控制点误差等方程,利用最小二乘法化迭代求解未知数[2]。但是,在像点观测方程中,观测向量以及描述函数模型的系数矩阵均由观测值组成,即两者均包含随机误差。此时,Gauss-Markov模型并不严格成立,常规的光束法平差计算方法虽在应用中切实可行,但是理论上不够严密。
近些年来,国内外学者针对系数矩阵含有随机误差的函数模型进行了研究,引入了EIV(errors in variables)模型描述随机误差,并研究了基于该模型的总体最小二乘方法[3, 4, 5, 6, 7, 8],已在坐标转换[9, 10, 11]、面阵影像空间后方交会[12]以及影像去噪[13]等方面得到了成功的应用。但是现有加权总体最小二乘难以直接应用于光束法平差计算,主要原因是光束法平差模型中仅有像点观测方程的系数矩阵包含随机误差,虚拟观测方程以及控制条件方程的设计矩阵均为单位阵,二者仍然满足Gauss-Markov条件。现存解决思路是将虚拟观测方程视为含约束条件的总体最小二乘[14],或者将EIV模型转化为方差含参数的Gauss-Markov模型利用自由极值法推导包含虚拟观测方程的总体最小二乘解[16],但是这两种解决思路均假定观测向量随机误差与系数矩阵随机误差为等精度观测量,且后者仅能处理虚拟观测为等精度观测的情形。能否合理给定各类观测值的权值,是线阵卫星遥感影像的光束法平差计算正确与否的重要前提,因而这两类思路难以直接应用于光束法平差计算。
本文拟引入EIV模型描述像点观测的函数模型,结合外方位元素虚拟观测方程与控制点误差方程,利用条件极值原理推导可处理多类虚拟观测值的总体最小二乘方法,基于该方法实现线阵卫星遥感影像的光束法区域网平差计算,之后分别使用模拟平差算例与两地区真实影像对本文方法与现有算法进行对比试验验证。
1 基于总体最小二乘的光束法平差算法 1.1 光束法平差的数学模型光束法平差的误差方程主要包括像点观测方程、外方位元素的虚拟观测方程以及控制点的误差方程。其数学模型可以表示为
式中,Δ表示外方位元素改正数,具体形式随外方位元素模型的变化而不同;C为其对应的系数矩阵;$\dot \Delta $G和$\dot \Delta $T分别为控制点和连接点的坐标改正数;KG和KT分别为对应改正数的系数矩阵;L是常数向量,为像点观测值与计算值之差;Ld与LG分别为虚拟观测向量,通常为零向量;I为单位阵;P1、Pd和PG分别为像点观测方程、外方位元素虚拟观测方程和控制条件方程对应的权矩阵。常规光束法计算方法是直接利用最小二乘估计法化求解式(1),但是式中的像点观测方程是由共线条件方程经线性化得到,且系数矩阵本身由外方位元素、地面控制点坐标和内方位元素共同求得,因此矩阵C、KG和KT中均包含随机误差,直接利用最小二乘进行光束法平差计算并不严密。此时,需要引入EIV模型对像点观测方程进行描述,并在此基础上构建基于总体最小二乘的光束法平差模型。
1.2 基于总体最小二乘的光束法平差模型式(1)中的像点观测方程可利用Gauss-Markov模型表示为
式中,A=[C KG KT];X=[ΔT $\dot \Delta $GT $\dot \Delta $TT]T是未知数向量,其平差值为$\dot X$;e1是像点观测值的随机误差,其平差值为V。当顾及系数矩阵A中的误差时,式(2)可利用EIV模型表示为 式中,EA表示系数矩阵中的误差。当假定系数矩阵A与观测向量L之间为独立观测时,有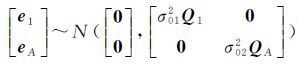 ;矢量eA是将矩阵EA按列拉直后得到的向量,可表示为eA=vec(EA),对应平差值为VA;σ012和σ022为单位权方差;Q1和QA分别为两类观测值的协因数矩阵。
;矢量eA是将矩阵EA按列拉直后得到的向量,可表示为eA=vec(EA),对应平差值为VA;σ012和σ022为单位权方差;Q1和QA分别为两类观测值的协因数矩阵。
式(1)中的外方位元素虚拟观测方程与控制条件方程虽然属两类不同方程,但是在形式上一致,可将两式联立并表示为关于X的方程
式中,L2为虚拟观测向量;e2~N(0,σ22Q2)为虚拟观测的随机误差,对应平差值为V2;Q2为协因数矩阵;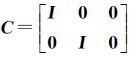 。式(3)与式(4)联立即为基于总体最小二乘的光束法平差模型。
1.3 基于总体最小二乘的光束法平差计算方法
。式(3)与式(4)联立即为基于总体最小二乘的光束法平差模型。
1.3 基于总体最小二乘的光束法平差计算方法
基于总体最小二乘的光束法平差模型中,共包括像点观测误差、虚拟观测误差和系数矩阵误差三类,根据极值条件原理可得如下目标优化函数
根据Kronecker积的性质可知[15]
为使式(5)取得极小值,根据极值定理得到方程组
视A中各元素为独立等精度观测,则可将系数矩阵观测量的权矩阵PA取为m×n阶的对角阵,即PA=kImn,k为正常数。同时顾及到光束法平差中,像点的观测值通常为等权观测,因而可令P1=(σ02/σp2)I,其中,σ02和σp2分别为单位权方差和观测值方差。此时,由方程组(7)可知 式(9)的等价形式为 设l=L1-A$\hat X$,则有 可以解出 由式(10)可知 令F(k)=σp2/σ02+$\hat X$T$\hat X$/k,将式(12)、式(14)和式(15)代入式(11)得到 则未知数向量可计算为注意到式(17)左右两端均包含未知数向量,因而需要通过迭代求解$\hat X$。本文按照如下迭代计算步骤求解未知数:
(1) 给定权初值P1(0)和P2(0),按最小二乘法计算X的初始值为
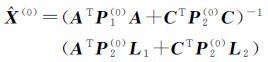
(2) 按方差分量估计法确定各类观测方程的方差[17],并确定P2。其中,P2为分块对角阵,由虚拟观测值类型确定其具体形式。
(3) 计算l(i)=L1-A$\hat X$(i),i为迭代次数;给定参数k;计算F(i)(k)。
(4) 计算
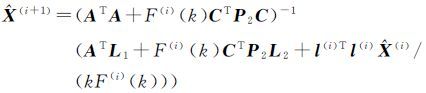
(5) 重复步骤(3)、步骤(4),当‖$\hat X$(i+1)-$\hat X$(i)‖<ε时,停止迭代。
式(17)中,CTP2C是一个对角阵,对角线的非零元素是P2的权值,因而CTP2C与广义岭估计矩阵等价,此时F(k)是一个增益系数,可用于调整P2中各分量的大小以保证病态问题的稳定求解。
2 试验与分析为验证本文方法的正确性与有效性,将利用模拟数据和真实线阵卫星遥感影像对本文方法进行验证。由于式(17)中参数需要确定参数k的取值,因而在试验中将文方法分成两种情况讨论:第1种按照先验信息确定参数,称为本文方法1;第2种从解算病态问题的角度出发,利用岭迹法确定参数k的值,称为本文方法2。
在模拟试验中,将分别对常规最小二乘算法(least squares algorithm,LS)[18]、基于最小二乘的虚拟观测法(least squares based virtual observation method,LSVO)[17]、文献[16]中的基于总体最小二乘的虚拟观测法(total least squares based virtual observation method,TLSVO)方法和本文方法进行试验,用于对比几种方法的单次平差计算精度。
由于TLSVO方法仅能处理单类虚拟观测值的情况,且需要岭迹法确定参数,难以处理对权值依赖较高的光束法平差计算,因而在真实线阵卫星遥感影像试验中,仅将惯用光束法平差方法LSVO和本文方法1进行比较。
2.1 模拟试验本试验用于验证本文方法在单次解算中的性能,试验算例仍然采用文献[16]中的平差算例。该算例在给定系数矩阵、观测向量和未知数真值后,分别在系数矩阵和观测向量中加入随机误差,并进行平差计算,将平差解算得到的未知数估计量与未知数真值进行比较,以二者的偏差平方和作为计算精度的比较依据。原始系数矩阵A0、观测向量L0和真值X0分别为

系数矩阵和常数项中分别加入随机误差e1~N(0,σ02In)和eA~N(0,σ02Imn)(σ02=0.1)后,得到的系数矩阵与观测向量为
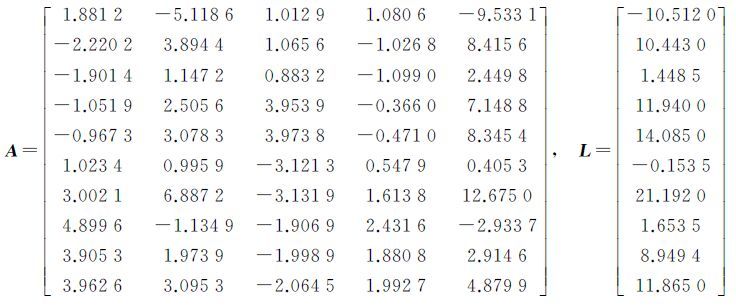
矩阵N=A2TA的条件数cond(N)=2.08×104,求解该方程属病态问题。分别采用最小二乘法、LSVO法、TLSVO法和本文方法对以上问题进行计算,并利用4种方法求得的估计量$\hat X$与真值X0的偏差平方和‖ΔX‖2=‖$\hat X$-X0‖2衡量解算结果与真实值的偏差。
注意到试验中观测向量和系数矩阵中加入的随机误差的方差大小相同,此时系数矩阵与观测向量应为等精度观测,因此在本方方法1中取系数矩阵观测量的权矩阵PA=P1,此时k=σ02/σp2。此外,为减少试验变量的差异,本文沿用文献[16]中试验假设:实际观测向量和虚拟观测向量均为独立、等精度观测。
试验中利用岭迹法确定TLSVO算法中的准则参数λ,并令虚拟观测向量L2=0。LSVO法与本文两类方法试验中,均利用验后方差分量估计方法确定实际观测量与虚拟观测量的方差,进而确定两类观测方程的权值。为减少主观因素对试验的影响,试验中TLSVO算法参数λ和本文方法2的参数k分别在各未知数变化趋于稳定的区间内取为
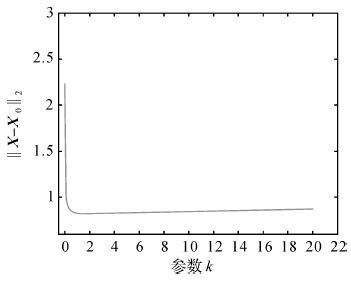
分别利用4种方法估计得到的及对应的偏差平方和的统计结果如表 1所示,本文方法2的岭迹如图 1如所示,图 2为‖ΔX‖2随参数k变化的曲线图。
| X0 | LS | LSVO | TLSVO | 本文方法1 | 本文方法2 | |
| 1 | 1.394 4 | 1.290 1 | 1.156 8 | 1.233 1 | 1.156 2 | |
| 1 | 0.112 3 | 0.277 0 | 0.402 7 | 0.354 2 | 0.402 9 | |
| $\hat X$ | 1 | 0.779 1 | 0.815 5 | 0.777 3 | 0.829 4 | 0.776 5 |
| 1 | 0.262 8 | 0.470 0 | 0.602 9 | 0.574 9 | 0.602 6 | |
| 1 | 1.441 4 | 1.364 0 | 1.298 1 | 1.325 2 | 1.297 9 | |
| 参数 | — | — | — | λ=9.700 0 | PA=P1 | k=2.000 0 |
| ‖Δ$\hat X$‖ | — | 1.308 8 | 1.026 8 | 0.823 1 | 0.887 1 | 0.823 1 |

|
| 图 1 本文方法岭迹图 Fig. 1 Ridge trace of proposed algorithm |
|
| 图 2 估计偏差随参数k变化曲线 Fig. 2 Change curve of bias with parameter k |
由本算例的计算结果可知,引入虚拟观测方程后,LSVO算法的计算精度优于LS算法,主要因为虚拟观测方程的引入改善了原法方程的病态程度,从而提高了平差计算的稳定性与精度。本文方法2与TLSVO算法的平差精度相当,略高于本文方法1;3种方法的计算精度均优于LSVO算法,这是因为这3种方法均顾及了系数矩阵中存在的偶然误差,从而有更高的平差精度,这也体现出EIV模型在平差计算中的优势。本文方法1中F(k)虽由精度确定,但并非处理病态问题时的最优增益值,因而并不能确保处理病态问题时取得最高的估计精度。
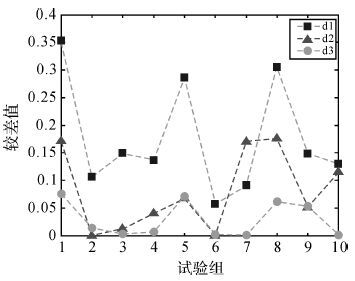
为了进一步比较本文方法1、本文方法2与TLSVO算法之间的差异,在A00和L0中分别加入方差σ02=0.1,0.2,…,0.5的随机误差,共生成10组数据,每个方差对应两组数据,分别利用LSVO算法、TLSVO算法、本文方法1和本文方法2进行平差计算,所得偏差统计如表 2所示,待定参数同样按照式(18)确定。分别用LSVO算法、TLSVO算法和本文方法1计算得到的偏差平方和减去本文方法2得到的偏差平方和,并将10组试验所得到的偏差较差值绘制于图 3。图中任意离散点p(x,y)到x轴的距离表示按该点对应方法进行平差后,计算得到的偏差平方和比本文方法2的偏差平方和高y。若p(x,y)在x轴的上方,则该方法的求解精度低于本文方法2。图中,方块所对应曲线d1=‖ΔXLSVO‖-‖ΔX2‖,三角对应曲线d2=‖ΔXTLSVO‖-‖ΔX2‖,圆对应的曲线d3=‖ΔX1‖-‖ΔX2‖,‖ΔX1‖为本文方法1偏差,‖ΔX2‖为本文方法2偏差。
| ‖ΔX‖2 | ||||||||||
| 试验组 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| σ02 | 0.1 | 0.1 | 0.2 | 0.2 | 0.3 | 0.3 | 0.4 | 0.4 | 0.5 | 0.5 |
| LSVO | 1.408 3 | 1.003 7 | 0.967 2 | 1.117 6 | 1.107 7 | 0.832 2 | 0.940 7 | 1.199 1 | 1.050 4 | 0.955 5 |
| TLSVO | 1.226 9 | 0.898 2 | 0.830 4 | 1.021 2 | 0.888 9 | 0.775 7 | 1.021 1 | 1.070 3 | 0.952 6 | 0.941 2 |
| 本文方法1 | 1.130 4 | 0.911 8 | 0.821 0 | 0.987 7 | 0.892 1 | 0.777 0 | 0.851 0 | 0.955 7 | 0.955 0 | 0.827 1 |
| 本文方法2 | 1.055 1 | 0.898 2 | 0.818 6 | 0.981 3 | 0.821 8 | 0.775 7 | 0.850 6 | 0.894 8 | 0.902 2 | 0.826 1 |
|
| 图 3 4种方法在10组试验中的偏差差值 Fig. 3 The difference of biases from 4 algorithms in 10 experiments |
从表 2与图 3的结果可知,在第3、第6、第7和第10组试验中,本文方法1和本文方法2的计算结果基本相当;本文方法1在大多数情况下精度优于TLSVO算法,部分情况下略低于TLSVO的解算精度;TLSVO算法部分情况下也能达到本文方法2的解算精度,但是结果并不稳定,在第7组试验中解算精度甚至低于LSVO算法;本文方法2在所有试验中均得到最高的参数估计精度,相比于本文方法1,该方法从处理病态问题的角度确定了最优的k值,在处理病态问题时有一定优势。
然而在实际光束法平差的迭代计算中,需快速选择待定参数,减少主观因素对结果的影响,如采用岭迹法确定各次迭代的待定参数,则会造成运算效率的显著下降。实际光束法平差中应依据先验知识确定参数k的取值,即使用本文方法1进行光束法平差计算,适当放宽精度要求,提高计算的效率与自动化水平。
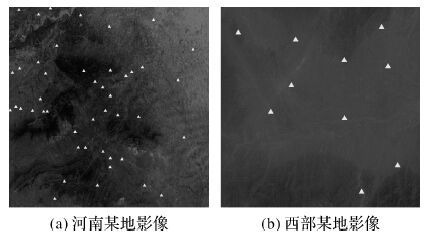
2.2 真实数据试验本试验用于验证本文方法在真实线阵卫星遥感影像光束法平差中的计算精度,将分别采用河南某地(图 4(a))与中国西部某地(图 4(b))的SPOT-5 HRS影像进行验证。河南地区影像以平原地为主,包括部分山区,范围内共包含45个均匀分布的地面控制点。西部某地影像所摄地区以丘陵地形为主,由于地物特征不明显,该影像范围内仅包含10个地面控制点。两幅影像内控制点均由外业测量并通过内业人工量测得到,量测精度在1个像元左右。
|
| 图 4 SPOT-5 HRS影像控制点分布示意图 Fig. 4 Distribution of ground control points for SPOT-5 HRS images |
SPOT-5卫星配备了高精度的定轨和定姿设备,因而可利用卫星辅助数据将成像时刻的瞬时外方位元素XSt、YSt、ZSt、φt、ωt和κt表示为[19, 20]
式中,t0为中心行成像时刻;XS、YS、ZS、φ、ω和κ表示利用辅助数据内插与转化计算得到的t时刻的外方位元素量测值;XO、YO和ZO为外方位线元素偏移量;a0、b0和c0分别为3个角元素的偏移量;a1、b1和c1分别为角元素的漂移改正量。对于由m张影像的构成的区域网而言,式(1)中矩阵C是将每张影像的外方位元素表示为式(19)后,代入线阵影像共线条件方程,经线性化计算得到,改正数Δ中含9m个未知数。在光束法平差迭代计算中,通常取P1=I,并将单位权方差取为像点观测值的方差估计值0[17],即$\hat \sigma _0^2 = \hat \sigma _p^2$。对于外方位元素的虚拟观测值和控制点观测值,通常依据参数的精度给定权初值进行预平差,并将第i类观测值在第n次迭代中的权值计算为[21]
式中,$\hat \sigma _p^2$为像点观测值方差;$\hat \sigma _i^2$为该类观测值在第n-1次迭代后得到的方差估计值。将两组影像数据分别按照式(1)列出像点观测方程、外方位元素虚拟观测方程和控制点的误差方程。由于缺少系数矩阵观测量精度的先验信息,试验中取k=1。分别利用惯用方法(LSVO)和本文方法进行光束法平差运算,所得试验结果如表 3和表 4所示,影像1中的3种试验方案中控制点分布依次为:4个角点、4个角点和1个中心点以及9个标准点位;影像2中控制点数量有限,因此仅比较控制点数为4个、5个和6个3种情况下两种方法光束法平差结果的差异。
| 试验方案 | 平差方法 | 控制 点数 | 检查 点数 | 控制点中误差 | 检查点中误差 | |||||||
| X | Y | 平面 | 高程 | X | Y | 平面 | 高程 | |||||
| 1 | LSVO 本文方法1 | 4 | 41 |
3.198 1.325 | 4.186 3.557 | 5.268 3.796 | 4.499 2.177 | 8.417 7.510 | 5.415 5.289 | 10.009 9.185 | 9.753 8.356 | |
| 2 | LSVO 本文方法1 | 5 | 40 |
3.014 1.231 | 5.271 4.879 | 6.071 5.033 | 6.106 4.426 | 8.509 7.667 | 5.936 5.508 | 10.375 9.440 | 8.762
7.689 | |
| 3 | LSVO 本文方法1 | 9 | 36 |
5.985 5.060 | 4.740 4.280 | 7.635 6.627 | 5.993 4.466 | 7.207 6.792 | 6.001 5.233 | 9.378 8.574 | 8.266
7.386 | |
| 试验方案 | 平差方法 | 控制 点数 | 检查 点数 | 控制点中误差 | 检查点中误差 | |||||||
| X | Y | 平面 | 高程 | X | Y | 平面 | 高程 | |||||
| 1 | LSVO 本文方法1 | 4 | 6 |
6.122 4.443 | 8.921 5.324 | 10.819 6.934 | 5.913 3.889 | 8.767 5.471 | 5.794 6.956 | 10.508 8.850 | 7.531
6.295 | |
| 2 | LSVO 本文方法1 | 5 | 5 |
8.227 7.048 | 13.033 15.048 | 15.412 15.058 | 9.886 8.070 | 5.631 4.308 | 6.958 7.319 | 8.951 8.493 | 6.839 5.882 | |
| 3 | LSVO 本文方法1 | 6 | 4 |
8.220 5.978 | 9.373 6.660 | 10.805 7.852 | 7.556 6.522 | 4.981 4.801 | 5.598 4.836 | 7.493 6.814 | 5.294
4.086 | |
由真实影像试验结果可知:
(1) 在河南地区影像试验中,按本文方法1进行光束法平差计算后,平面精度和高程精度均优于常规平差LSVO算法1 m左右;在西部地区影像试验中,本文方法1的平面精度高于LSVO算法0.5 m左右,高程精度优于LSVO算法1 m以上。这说明了本文所提出方法有更高的平差计算精度,与模拟数据试验的结论一致。
(2) 河南地区影像试验中,当4个角控制点参与平差时,两者平差结果相差最大,随着控制点数量的增加,两种方法平差结果的差距逐渐减小;在西部地区影像试验中,也有相同的结论。这表明控制点数量的增加对常规方法的精度提升更为显著,当控制点数量较少时,本文方法1的优势更为明显。
(3) 在3种控制点布设方案下,河南地区影像的光束法平差计算精度提升并不显著;当增设中心点后,检查点的平面精度略有下降,这表明该试验中的部分控制点精度较低,主要因为对控制点进行量测时,部分地面点难以辨识。尽管误差方程中引入了控制点的误差方程,但是试验未采用选权迭代等方法降低质量较差的控制点对试验结果的影响。如要进一步提高光束法平差计算的精度,需要引入抗差估计法对平差模型进行改进,并引入系统误差参数进行自检校光束法平差,这是需要进一步研究的内容。
3 结 论本文顾及光束法平差中像点观测方程的误差特性,引入EIV模型描述该方程中的观测误差和系数矩阵误差,利用条件极值原理推导了基于总体最小二乘的线阵卫星遥感影像光束法平差计算方法。模拟试验结果表明,相比于传统方法,本文方法在单次平差计算中即可获得较高的平差计算精度。在真实影像试验中,本文方法的光束法平差计算精度优于常规算法,是线阵影像光束法平差计算的一条新的途径。然而,本文方法仍有不足之处需要完善,比如实际光束法平差计算中,参数k的确定存在一定的主观性,而该参数取值直接影响到平差结果,当从系数矩阵观测精度的角度或者改善法方程病态状况的角度出发,对k值的选取进行优化。此外,本文方法未考虑控制点中存在粗差的情况,且未引入系统参数进行自检校光束法平差试验。如要将本文方法进行实际应用,还需要提高算法的计算效率。这些都是今后研究的重点内容。
| [1] | 王任享. 三线阵CCD影像卫星摄影测量原理[M]. 北京:测绘出版社, 2006. WANG Renxiang. Satellite Photogrammetric Principle for Three-line-array CCD Imagery[M]. Beijing:Surveying and Mapping Press, 2006. |
| [2] | 王涛,张永生,张艳,等. 基于自检校的机载线阵CCD传感器几何标定[J]. 测绘学报, 2012, 41(3):393-400. WANG Tao, ZHANG Yongsheng, ZHANG Yan, et al. Airborne Linear CCD Sensor Geometric Calibration Based on Self-calibration[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3):393-400. |
| [3] | GOLUB G H, VAN LOAN C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6):883-893. |
| [4] | SIMA D M,VAN HUFFEL S,GOLUB G H. Regularized Total Least Squares Based on Quadratic Eigenvalue Problem Solvers[J]. BIT Numerical Mathematics, 2004, 44(4):793-812. |
| [5] | BECK A, BEN-TAL A. On the Solution of the Tikhonov Regularization of the Total Least Squares Problem[J]. SIAM Journal on Optimization, 2006, 17(1):98-118. |
| [6] | VAN HUFFEL S,LEMMERLING P.Total Least Squares and Errors-in-variables Modeling:Analysis, Algorithms and Applications[M]. Netherlands:Springer, 2013. |
| [7] | 龚循强, 李志林. 稳健加权总体最小二乘法[J]. 测绘学报, 2014, 43(9):888-894. DOI:10.13485/j.cnki.11-2089.2014.0140. GONG Xunqiang, LI Zhilin. A Robust Weighted Total Least Squares Method[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(9):888-894. DOI:10.13485/j.cnki.11-2089.2014.0140. |
| [8] | 王彬, 李建成, 高井祥, 等. 抗差加权整体最小二乘模型的牛顿-高斯算法[J]. 测绘学报, 2015, 44(6):602-608. DOI:10.11947/j.AGCS.2015.20130704. WANG Bin, LI Jiancheng, GAO Jingxiang, et al. Newton-Gauss Algorithm of Robust Weighted Total Least Squares Model[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(6):602-608. DOI:10.11947/j.AGCS.2015.20130704. |
| [9] | 袁庆, 楼立志, 陈玮娴. 加权总体最小二乘在三维基准转换中的应用[J]. 测绘学报, 2011, 40(S):115-119. YUAN Qing, LOU Lizhi, CHEN Weixian. The Application of the Weighted Total Least-squares to Three Dimensional-datum Transformation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S):115-119. |
| [10] | 陈义, 陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J]. 测绘学报, 2012, 41(5):715-722. CHEN Yi,LU Jue.Performing 3D Similarity Transformation by Robust Total Least Squares[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5):715-722. |
| [11] | TONG Xiaohua, JIN Yanmin, LI Lingyun. An Improved Weighted Total Least Squares Method with Applications in Linear Fitting and Coordinate Transformation[J]. Journal of Surveying Engineering, 2011, 137(4):120-128. |
| [12] | 陈义, 陆珏, 郑波. 总体最小二乘方法在空间后方交会中的应用[J]. 武汉大学学报(信息科学版), 2008, 33(12):1271-1274. CHEN Yi, LU Jue, ZHENG Bo. Application of Total Least Squares to Space Resection[J]. Geomatics and Information Science of Wuhan University, 2008, 33(12):1271-1274. |
| [13] | 许淑华, 齐鸣鸣. 基于多尺度总体最小二乘的图像去噪[J]. 光子学报, 2010, 39(5):956-960. XU Shuhua,QI Mingming.Image Denoising Based on Multi-scales Total Least Squares[J]. Acta Photonica Sinica, 2010, 39(5):956-960. |
| [14] | SCHAFFRIN B. A Note on Constrained Total Least-squares Estimation[J]. Linear Algebra and Its Applications, 2006, 417(1):245-258. |
| [15] | 张贤达.矩阵分析与应用[M].北京:清华大学出版社, 2004. ZHANG Xianda. Matrix Analysis and Applications[M]. Beijing:Tsinghua University Press, 2004. |
| [16] | 王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6):575-581.DOI:10.13485/j.cnki.11-2089.2014.0091. WANG Leyang, YU Dongdong. Virtual Observation Method to Ill-posed Total Least Squares Problems[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6):575-581.DOI:10.13485/j.cnki.11-2089.2014.0091. |
| [17] | 李德仁, 袁修孝. 误差处理与可靠性理论[M]. 2版. 武汉:武汉大学出版社, 2012. LI Deren,YUAN Xiuxiao.Error Processing and Reliability Theory[M]. 2nd ed. Wuhan:Wuhan University Press, 2012. |
| [18] | 隋立芬, 宋立杰, 柴洪洲. 误差理论与测量平差基础[M]. 北京:测绘出版社, 2010. SUI Lifen, SONG Lijie, CHAI Hongzhou. Error Theory and Foundation of Surveying Adjustment[M]. Beijing:Surveying and Mapping Press, 2010. |
| [19] | 刘楚斌, 张永生, 范大昭, 等. 资源三号卫星三线阵影像自检校区域网平差[J]. 测绘学报, 2014, 43(10):1046-1050, 1060. DOI:10.13485/j.cnki.11-2089.2014.0148. LIU Chubin, ZHANG Yongsheng, FAN Dazhao, et al. Self-Calibration Block Adjustment for Three Line Array Image of ZY-3[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10):1046-1050, 1060. DOI:10.13485/j.cnki.11-2089.2014.0148. |
| [20] | 王涛. 线阵CCD传感器实验场几何定标的理论与方法研究[D]. 郑州:中国解放军信息工程大学, 2012. WANG Tao. Study on Theories and Methods of Linear CCD Sensor Geometric Calibration Based on Field[D]. Zhengzhou:The PLA Information Engineering University, 2012. |
| [21] | 袁修孝, 曹金山, 汪韬阳, 等. 高分辨率卫星遥感精确对地目标定位理论与方法[M]. 北京:科学出版社, 2012. YUAN Xiuxiao, CAO Jinshan, WANG Taoyang, et al. Theory and Method of High Resolution Satellite Remote Sensing for Precise Orientation[M]. Beijing:Science Press, 2012. |