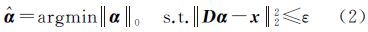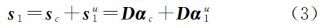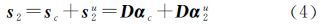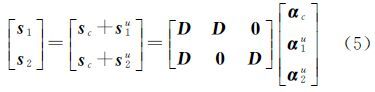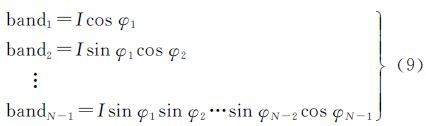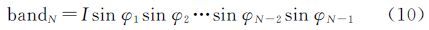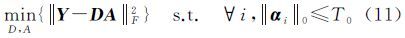2. 中国科学院电子学研究所, 北京 100190;
3. 中国科学院大学, 北京 100049;
4. 中国地质大学(北京)土地科学技术学院, 北京 100083
2. Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. School of Land Science and Technology, China University of Geosciences, Beijing 100083, ChinaAbstract
全色和多光谱影像融合旨在结合全色影像的空间细节和多光谱影像的光谱信息，得到空间分辨率和光谱分辨率兼优的高质量多光谱影像，有利于遥感影像的分类和目标识别等后续处理[1]。迄今为止，学者们提出了很多方法，这些方法可概括为基于组分替换、多分辨率分析以及稀疏表示的融合方法。其中，经典的组分替换融合方法有IHS变换[2]、PCA变换[3]算法，以及改进的组分替换算法GSA[4]、PRACS[5]等，这类算法在变换域内用全色谱段代替多光谱的某一个分量，并通过逆变换得到融合影像，算法计算简单，融合影像空间分辨率高，但是存在一定的光谱失真。而多分辨率分析方法，则是通过提取全色影像的高频信息来弥补多光谱影像缺少的细节，例如经典的WT[6]、AWLP[7]、NSCT[8]、CBD[9]等，这类方法在光谱保持方面得到了提升，但会损失一定的全色高频细节信息。另外，一种用于信号时-频变换的EMD[10]方法在遥感影像融合领域得到了应用，但也需结合IHS变换来获得更好的效果[11]。近年来，基于稀疏表示的遥感影像融合方法[12, 13, 14, 15]得到了快速的发展，其通过大量参考影像进行训练，得到的冗余字典往往具有自适应性，更加符合人眼视觉特性，能够充分地考虑到图像本身的几何正则性，用于彩色图像融合具有较好的光谱特性保持特点。但这类方法通常需要在融合过程中进行冗余字典的训练、稀疏系数解算和数据的重构，计算复杂度高，实时性差。
为了兼顾这3类方法的优点，获取更高质量的融合影像，出现了IHS-WT[16]、DCT-IHS[17]、SVT-APCA[18]、IHS-CS[19]等一系列组合架构的融合方法。这类方法所表现出的良好的融合影像质量，确立了光谱和空间信息保持的遥感影像融合的一个重要研究方向。然而，这种组合架构的融合方法通常需要进行组分替换类方法的参与(如IHS色彩空间变换)，只有部分谱段(通常为3个谱段)用于变换处理，难以利用多光谱数据所有谱段的光谱信息，导致光谱畸变[20]仍然存在于融合影像中，使得这类遥感影像融合方法仍然需要进一步提升光谱信息的保持能力。基于稀疏表示的融合方法虽然在光谱保持上体现了一定优势，但其需要对遥感数据进行逐波段的稀疏求解和重构，对多光谱数据的处理无疑会导致计算复杂度大量增加。针对这些问题，并综合考虑到组合架构融合方法的优势，本文提出了一种基于HCT变换[21]和联合稀疏模型的遥感影像融合方法。HCT变换不仅能实现组分替换类融合方法的良好空间信息保持特性，同时能够对兼顾任意波段的多光谱图像进行处理，而联合稀疏表示方法能够更好地保持多光谱的光谱特性，进一步提升组合架构下遥感影像的融合质量。另外，由于只采用HCT变换的亮度分量参与稀疏表示求解和重构，无须逐波段进行处理
1 稀疏表示和HCT变换 1.1 稀疏表示模型稀疏表示是压缩感知理论的基础之一，其利用字典中少量原子的线性组合来描述信号，图像信息越稀疏，稀疏表示就越准确。假设信号{xi,i=1,2,…，K}，xi∈Rn，字典矩阵D∈Rn×T中的每一列都是一个原子，根据稀疏表示理论[22]，信号可以表示为
式中，α为对应的稀疏系数。由于n≤T，该问题的求解是欠定的，稀疏表示就是寻找其中的最稀疏解，即稀疏系数α中非零元素个数最少的解。通过下面的优化问题[23]，可以实现此目的 式中，‖α‖0为l0范数，表示系数α中的非零元素个数；ε为逼近误差。由于式(2)中的l0范数为N-P难问题，难以进行求解，但在一定条件下[24]，可将其等价为l1范数进行求解。
基于稀疏表示模型和信号特点，文献[25]提出了一种联系多个信号的联合稀疏表示模型(joint sparsity model-1,JSM-1)。该模型认为所有信号可由一个共有的公共成分(common component)和一个各自的差异成分组成(innovation component)。以两个信号为例
式中，sc是信号s1、s2的公共稀疏成分；s1u、s2u是s1、s2各自的差异稀疏成分；αc是公共的稀疏系数；α1u、α2u是s1、s2各自的差异稀疏系数。
将上述公式级联起来，用矩阵的形式表示为
令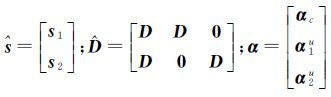
，则式(5)可简化为
对此方程进行求解可以分别得到信号的公共稀疏成分和各自稀疏成分。针对全色和多光谱遥感图像融合，通过联合稀疏表示模型的分析，提出这种利用联合稀疏模型有效提取两类待融合图像之间的冗余信息和互补信息的方法，通过对互补信息的融合，使得影像的融合结果包含更多的信息，以此获得更全面信息量的融合图像的方法。
1.2 HCT变换方法实际遥感卫星在多光谱图像获取过程中，不仅采集RGB谱段数据，还包括近红外等其他波段。但常规的色彩空间变换融合方法只选择RGB 3个谱段进行融合处理，难以有效利用其他谱段的光谱信息，导致融合结果光谱畸变大。超球面色彩变换(hyperspherical color transformation，HCT)[21]将图像从原始笛卡尔空间变换到超球面空间。由于该变换可不限参与变换的波段，可以比对全色数据的光谱响应范围，选择多光谱影像的R、G、B以及近红外波段进行处理，这样可以进一步减小常规三波段变换时近红外波段光谱信息的缺失导致的融合结果的光谱畸变。
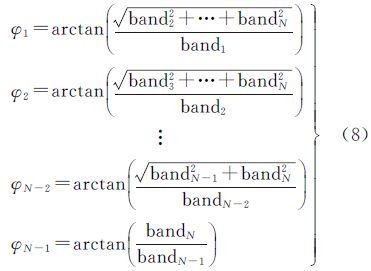
对于一幅具有N波段的图像{bandi}i=1:N，经过该变换，可以得到在超球面空间中的亮度变量I和N-1个角度变量，即
式中，bandi是输入的第i个波段；I是亮度成分；φ1、φ2、…、φN-1是N-1个角度变量，表示颜色或者色度。可以看到，亮度与色度完全独立，这也是基于HCT变换的融合最重要的特征。
对应的HCT变换的逆变换可表示为
与IHS[2]等彩色空间的变换相似，HCT变换参与的遥感图像融合也是一种组分替代的融合方式，但同IHS等彩色空间变换相比，HCT可根据需要选择部分或全部遥感图像波段参与变换，这样可以有针对性地利用所需波段的信息。
2 基于HCT和联合稀疏表示模型的融合方法采用HCT变换可以克服IHS算法由于多光谱数据无近红外谱段参与(全色通常包括近红外光谱范围)，导致植被等地物存在较大光谱畸变的弱点。受到组合架构融合方法的启示，本文在HCT变换基础上引入联合稀疏表示模型，通过分解全色数据和多光谱数据的冗余和本征信息，从而更有效地利用两类数据的差异信息，进一步减小HCT融合处理中光谱的畸变，实现融合影像光谱信息保持的优化。在实际处理流程设计过程中，通过只对HCT变换亮度分量的联合稀疏处理，减小传统稀疏表示融合方法逐波段处理的计算复杂度。因此，本文提出的基于HCT和JSM-1模型的全色与多光谱影像融合方法，旨在综合利用HCT变换和JSM-1模型的优势，实现任意波段的多光谱图像和全色图像的融合处理，以期获得更好的融合效果。
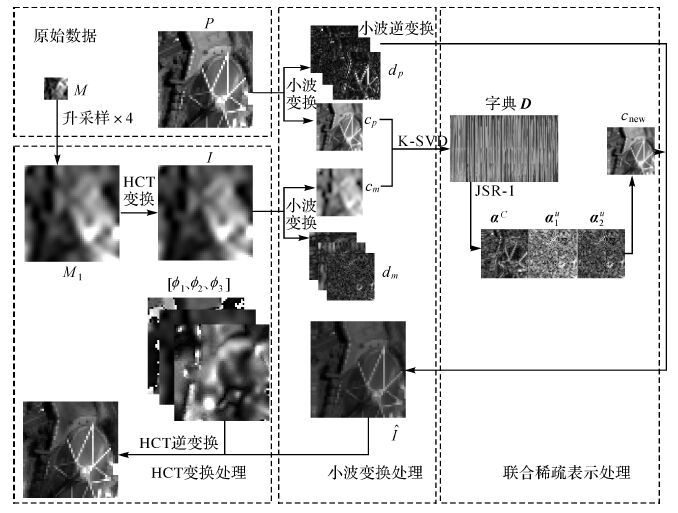
本方法可以分解为4个部分，如图 1所示。第1部分为原始数据的预处理，主要包括完成原始多光谱图像的升采样；第2部分为多光谱数据的HCT变换，得到亮度分量和角度分量；第3部分为小波变换处理，可以分解出低频系数进行处理；第4部分为联合稀疏表示处理，可以获得更好的融合系数。假设全色图像大小为G1×G2，基于HCT和JSM-1模型融合处理的具体实施步骤如下：
|
| 图 1 基于HCT和JSM融合方法流程图 Fig. 1 The flowchart of fusion method based on HCT and JSM |
(1) 多光谱升采样。对N波段低分辨率多光谱图像(M)升采样，采用多项式插值方法进行插值，插值因子是4，得到升采样多光谱图像(M1)。
(2) 多光谱HCT变换。对多光谱图像进行HCT变换，分别得到亮度分量I、角度分量φ1、φ2、…、φN-1。
(3) 多分辨率变换处理。对全色图像(P)依据I进行直方图调整，然后做两层小波变换，得到低频信息cp和高频信息dp以及I分量的低频信息cm和高频信息dm。
(4) 分块处理。对cp和cm分量采用平滑窗进行分块处理。设定平滑窗的窗口大小为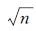
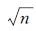×，平滑移动步长为1个像素，将每一个图像块按照列优先的方式重排成长度为n的列向量yi(t)，t∈[1,L]，L=(G1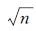－+1)(G2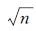－+1)，最后把列向量重新组合成矩阵Y1、Y2和Y=[Y1 Y2]。
(5) 联合稀疏求解。为了获得更加紧致的稀疏表示，本文方法采用KSVD算法[26]进行联合字典训练，得到字典D，所选择的训练样本为Y。
基于Y和D，采用联合稀疏表示模型JSM-1式(11)进行求解，得到公共系数矩阵Ac和差异系数矩阵A1、A2。
(6) 差异稀疏系数的融合。针对融合独特系数矩阵A中的每一列α，本次根据A1、A2中的每一列α1、α2的l1范数权重大小进行融合。具体的计算公式为
则融合后的图像块Y=DAc+DA。
(7) 重建亮度分量$\hat I$。利用小波逆变换重建$\hat I$分量，其中$\hat I$分量的低频为经过联合稀疏得到的Cnew，而高频为全色图像的高频信息dp，低频分量Cnew是由Y按照列优先的方式还原成图像矩阵再除以累加次数得到。
(8) 获取高分辨率多光谱图像。用融合的$\hat I$代替I分量并进行HCT逆变换，从而得到高分辨率多光谱图像HRM。
3 结果与分析针对本文提出的融合方法，采用法国Pleiades-1和美国WorldView-2两种卫星数据进行试验分析(http://www.geosage.com/highview/download.html)。这两型卫星均提供空间分辨率为0.5 m的全色图像和2 m的多光谱图像，并已经完成了影像数据的配准处理。为便于对试验结果进行量化评估，以原始的多光谱图像作为参考影像，而原始的全色数据进行了降采样处理，使其与参考多光谱数据成一致分辨率。而将原始多光谱影像进行低通滤波处理和影像的降采样(采样因子为0.25)，得到用于融合处理输入的低分辨率多光谱影像。而在融合处理过程中，为得到与全色影像同分辨率的多光谱影像，采用多项式插值[27]对低分辨率多光谱进行上采样(在下文用EXP来表示)。
3.1 Pleiades数据试验
Pleiades-1卫星发射于2011年，可获得幅宽达到20 km的0.5 m全色和2 m多光谱数据。为更充分地验证本文方法的有效性，试验采用两幅Pleiades-1卫星多光谱卫星数据的B、G、R、NIR 4个波段和相应的全色波段进行融合，选择影像大小均为400×1000，进行分块的窗口大小为8×8，同时兼顾计算量和试验效果，选择移动步长为4个像素，训练字典大小为64×256。本文采用了4种较新的、效果较好对比算法，即AWLP[7]、GSA[4]、Indusion[28]及PRACS[5]进行对比分析。其中，第1幅图像(Ple-1)5种方法的处理结果如图 2所示。为了突出细节，在图 2中还对影像的局部进行了放大显示。
|
| 图 2 Pleiades卫星数据(Ple-1)融合结果及局部放大显示 Fig. 2 Fusion results of Pleiades images (Ple-1) and partial enlarged views |
从Ple-1的试验结果(图 2)可以看出，在分辨率优化方面，文中采用的所有方法均得到了比参考图像(reference)更好的效果，这是由于为了进行对比分析，采用的参考多光谱图像是原始数据，而与其分辨率相同的全色数据是降采样4倍的数据，因此全色图像在细节方面更优，而这些细节最终通过融合获得了比参考多光谱图像更好结果。在光谱信息保持方面，从图 2中可看出除了Indusion算法有一定的光谱畸变外，其他算法均较接近，从左侧局部放大图的左下角绿色植被色调来看，PRACS算法和本文方法得到了更好的结果。
为了对这5种不同的方法进行量化的比较和分析，本次采用4种量化指标来综合评价这些融合算法，即空间相关系数(sCC)[29]、相对整体维数综合误差ERGAS[30, 31]、光谱角制图SAM[32]、全局质量评价因子Q4[33]。其中，sCC表示融合图像与全色图像的空间相关量，其值越大，说明融合结果的空间细节越多，ERGAS和SAM表征光谱质量，其值越小，表明光谱畸变也越少，Q4则是全局评价因子，其值越大，表明融合图像效果越好。第1幅图像5种算法的综合评价值如表 1所示。可以看出，总体上对于Ple-1场景数据，PRACS算法获得了更好的评价指标值，而本文算法只在SAM值上占优，与其他3种算法相比，本文算法与PRACS的其他指标值相差不大。
| 评价指标 | AWLP | GSA | Indusion | PRACS | 本文算法 |
| sCC | 0.885 2 | 0.873 3 | 0.825 2 | 0.904 8 | 0.893 0 |
| ERGAS | 5.596 4 | 6.263 5 | 7.261 5 | 4.046 8 | 4.538 5 |
| SAM | 4.858 3 | 7.129 6 | 6.314 4 | 4.176 1 | 3.584 6 |
| Q4 | 0.760 8 | 0.683 5 | 0.607 5 | 0.820 4 | 0.797 4 |
另一幅Pleiades-1卫星数据(Ple-2)利用不同评价指标公式得到了定量化评价指标值如表 2所示。可以看出，与Ple-1相似，PRACS方法和本文方法获得了更好的评价值。由于场景的差异，相较Ple-1图像，本文方法在sCC指标上获得了更理想的结果，但与PRACS方法和AWLP差异不大。
| 评价指标 | AWLP | GSA | Indusion | PRACS | 本文算法 |
| sCC | 0.854 1 | 0.832 9 | 0.794 5 | 0.852 1 | 0.855 3 |
| ERGAS | 6.891 5 | 7.752 7 | 8.446 8 | 5.117 2 | 5.791 5 |
| SAM | 4.788 3 | 7.774 1 | 6.812 7 | 4.568 5 | 3.710 7 |
| Q4 | 0.692 6 | 0.612 5 | 0.548 2 | 0.762 7 | 0.735 9 |
WorldView-2卫星是一颗高分辨率商业化运行卫星，由美国DigitalGlobe公司于2009年8月发射。卫星上搭载一个谱段的全色和8个谱段的多光谱传感器，其中全色分辨率达到0.46 m，而多光谱分辨率为1.84 m。试验只采用多光谱卫星数据的B、G、R、NIR 4个波段进行融合，同样，选择两幅大小为400×1000的不同场景的影像数据进行处理。联合稀疏处理时设置的分块大小、移动步长以及训练字典大小与前面Pleiades-1数据试验一致，第1幅影像的试验结果如图 3所示，左右两侧各为一块局部放大图。
|
| 图 3 WorldView-2卫星数据(WV-1)融合结果 Fig. 3 Fusion results of WorldView-2 images (WV-1) and partial enlarged views |
从第1幅WorldView-2图像(WV-1)的融合试验整体结果来看，5种算法均在空间分辨率上取得了改进，从中部区域的植被来看，GSA和Indusion算法在植被色调方面差异较大，显得有些突兀，而其他算法比较柔和。从左侧局部放大图中下部的小绿地可以看出，AWLP、PRACS和本文算法得到的结果较优，而右下部黑红色地物只在PRACS和本文算法中有一定体现。从右侧局部放大图可以看出，右侧红色房顶只有AWLP、PRACS与本文算法和参考图像相似，屋顶红色分布比较平滑；在中下部的植被部分，只有PRACS与本文算法在绿色色调上保持较好。
从WV-1融合结果的量化评价指标来看(表 3)，对于WorldView-2的该场景数据，本文算法在4个指标上均获得了更好的评价指标值，而AWLP算法在sCC指标上也取得了较高值，另外，PRACS算法在ERGAS、SAM以及Q4 3项指标上与本文算法相差不大，这与试验结果在视觉效果上得出的结论一致。
| 评价指标 | AWLP | GSA | Indusion | PRACS | 本文算法 |
| sCC | 0.913 6 | 0.911 5 | 0.858 6 | 0.899 1 | 0.927 4 |
| ERGAS | 6.188 2 | 6.067 6 | 8.304 3 | 5.623 8 | 5.320 4 |
| SAM | 7.126 5 | 11.408 9 | 8.819 4 | 5.741 2 | 5.601 6 |
| Q4 | 0.755 5 | 0.712 3 | 0.623 0 | 0.763 1 | 0.771 4 |
相较WV-1融合图像的评价指标(表 3)，本文算法在第2幅试验数据(WV-2)的评价指标值(表 4)上也取得了较好的结果，只有Q4结果稍逊于PRACS算法。
| 评价指标 | AWLP | GSA | Indusion | PRACS | 本文算法 |
| sCC | 0.887 1 | 0.889 4 | 0.844 7 | 0.888 8 | 0.901 1 |
| ERGAS | 8.283 2 | 8.972 2 | 10.386 1 | 7.295 7 | 7.456 5 |
| SAM | 9.078 0 | 14.521 1 | 10.672 1 | 7.367 5 | 6.989 7 |
| Q4 | 0.745 1 | 0.691 1 | 0.632 1 | 0.756 9 | 0.755 9 |
综合两颗卫星Pleiades-1和WorldView-2的不同场景数据的试验结果，从视觉上的比较来看(图 2和图 3)，PRACS和本文算法都获得了较好的融合图像，空间细节突出，光谱畸变相对较小。从量化评价角度，即从表 1—表 4可以看到，与其他4种算法相比，本文算法在光谱畸变处理上具有一定优势，在第1幅Pleiades-1卫星数据中，SAM值最小，其他3个指标只比PRACS算法稍差，第2幅在sCC和SAM上均最优；而在WorldView-2数据处理结果中，第1幅4个指标都取得了最优值，第2幅只有Q4评价值稍逊于PRACS算法。总体来看，本文提出的算法在Pleiades-1和WorldView-2数据的试验中均得到了较高质量的多波段融合影像。
从表 5中可看出，在融合方法的处理时间方面(运行环境：软件-Matlab7；硬件-Intel(R) Core(TM) 2 Quad CPU (主频2.33 GHz)，4 GB内存)，Indusion方法所需的执行时间最短，经典的GSA方法次之，本文方法采用了组合架构融合方式，处理过程包括HCT和小波变换，并且引入了联合稀疏分解流程，比其他方法需要更长的处理时间。需要指出的是，本文方法由于只对HCT变换的亮度分量进行联合稀疏分解，且分块步长为4，因此在图像大小接近的情况下，相较文献[34]的方法和文献[12]提出的直接稀疏表示融合方法，算法在执行时间上仍然有一定的优势。
| 数据集 | AWLP | GSA | Indusion | PRACS | 本文算法 |
| Ple-1 | 1.354 | 0.600 | 0.471 | 1.456 | 237.280 |
| Ple-2 | 1.382 | 0.591 | 0.480 | 1.451 | 239.448 |
| WV-1 | 1.737 | 0.779 | 0.463 | 1.724 | 217.815 |
| WV-2 | 1.376 | 0.596 | 0.462 | 1.451 | 261.918 |
全色和多光谱遥感影像融合的目的是得到空间分辨率高、光谱畸变小的多光谱影像，但光谱畸变一直是全色与多光谱影像融合的一个难点。本文结合近年来获得良好光谱保持效果的稀疏表示融合方法，引入能支持任意波段处理的HCT变换，提出了一种基于HCT变换和联合稀疏模型的遥感影像融合方法。相较传统的稀疏表示方法，联合稀疏模型充分利用了全色和多光谱的差异成分信息，而HCT则可利用所有的多光谱参与变换，不受传统IHS处理3个谱段的限制，同时处理过程中只对HCT变换的I分量进行联合稀疏处理，有效地提升了处理效率。验证试验分别选取Pleiades-1和WorldView-2两种卫星数据进行了试验。结果表明，本文方法在增强空间细节的同时，更好地保持了多光谱数据的光谱信息，得到了融合质量较好的融合影像。但在融合处理效率上，由于多种变换的参与以及联合稀疏表示分解的引入，导致融合方法所需执行时间长，这是后续需要进一步研究改进的地方。
| [1] | THOMAS C, RANCHIN T, WALD L, et al. Synthesis of Multispectral Images to High Spatial Resolution:A Critical Review of Fusion Methods Based on Remote Sensing Physics[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(5):1301-1312. |
| [2] | CARPER W J, LILLESAND T M, KIEFER R W. The Use of Intensity-hue-saturation Transformations for Merging SPOT Panchromatic and Multispectral Image Data[J]. Photogrammetric Engineering & Remote Sensing, 1990, 56(4):459-467. |
| [3] | CHAVEZ JR P S, KWARTENG A Y. Extracting Spectral Contrast in Landsat Thematic Mapper Image Data Using Selective Principal Component Analysis[J]. Photogrammetric Engineering & Remote Sensing, 1989, 55(3):339-348. |
| [4] | AIAZZI B, BARONTI S, SELVA M. Improving Component Substitution Pansharpening through Multivariate Regression of MS+Pan Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(10):3230-3239. |
| [5] | CHOI J, YU K, KIM Y. A New Adaptive Component-Substitution-based Satellite Image Fusion by Using Partial Replacement[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1):295-309. |
| [6] | GARGUET-DUPORT B,GIREL J,CHASSERY J M,et al. The Use of Multiresolution Analysis and Wavelets Transform for Merging SPOT Panchromatic and Multispectral Image Data[J]. Photogrammetric Engineering & Remote Sensing, 1996, 62(9):1057-1066. |
| [7] | OTAZU X,GONZALEZ-AUDICANA M,FORS O, et al. Introduction of Sensor Spectral Response into Image Fusion Methods:Application to Wavelet-based Methods[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(10):2376-2385. |
| [8] | El-MEZOUAR M C, KPALMA K, TALEB N, et al. A Pan-sharpening Based on the Non-subsampled Contourlet Transform:Application to Worldview-2 Imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(5):1806-1815. |
| [9] | AIAZZI B, ALPARONE L, BARONTI S, et al. Context-driven Fusion of High Spatial and Spectral Resolution Images Based on Oversampled Multiresolution Analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(10):2300-2312. |
| [10] | WANG Jian, XU Changhui, ZHANG Jixian, et al. An EMD-IHS Model for High Resolution Image Fusion[C]//JU Weimin, ZHAO Shuhe. Remotely Sensed Data and Information. Nanjing:[s.n.], 2007, 6752:675209. |
| [11] | DONG Weihua, LI Xia'nen, LIN Xiangguo, et al. A Bidimensional Empirical Mode Decomposition Method for Fusion of Multispectral and Panchromatic Remote Sensing Images[J]. Remote Sensing, 2014, 6(9):8446-8467. |
| [12] | LI Shutao, YANG Bin. A New Pan-sharpening Method Using a Compressed Sensing Technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(2):738-746. |
| [13] | CHEN S S, DONOHO D L, SAUNDERS M A. Atomic Decomposition by Basis Pursuit[J]. SIAM Review, 2001, 43(1):129-159. |
| [14] | ZHU Xiaoxiang, BAMLER R. A Sparse Image Fusion Algorithm with Application to Pan-sharpening[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(5):2827-2836. |
| [15] | CHENG Ming, WANG Cheng, LI Jie, et al. Sparse Representation Based Pansharpening Using Trained Dictionary[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(1):293-297. |
| [16] | ZHANG Yun, HONG Gang. An IHS and Wavelet Integrated Approach to Improve Pan-sharpening Visual Quality of Natural Colour IKONOS and QuickBird Images[J]. Information Fusion, 2005, 6(3):225-234. |
| [17] | 楚恒, 王汝言, 朱维乐. DCT域遥感影像融合算法[J]. 测绘学报, 2008, 37(1):70-76. CHU Heng, WANG Ruyan, ZHU Weile. Remote Sensing Image Fusion Algorithm in the DCT Domain[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1):70-76. |
| [18] | YANG Shuyuan, WANG Min, JIAO Licheng. Fusion of Multispectral and Panchromatic Images Based on Support Value Transform and Adaptive Principal Component Analysis[J]. Information Fusion, 2012, 13(3):177-184. |
| [19] | 夏晓天, 王斌, 张立明. 基于推广的IHS变换和压缩传感的遥感图像融合[J]. 计算机辅助设计与图形学学报, 2013, 25(9):1399-1409. XIA Xiaotian, WANG Bin, ZHANG Liming. Remote Sensing Image Fusion Based on Generalized IHS Transformation and Compressive Sensing[J]. Journal of Computer-Aided Design & Computer Graphics, 2013, 25(9):1399-1409. |
| [20] | 吴连喜, 梁波, 刘晓梅, 等. 保持光谱信息的遥感图像融合方法研究[J]. 测绘学报, 2005, 34(2):118-122, 128. WU Lianxi, LIANG Bo, LIU Xiaomei, et al. A Spectral Preservation Fusion Technique for Remote Sensing Images[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(2):118-122, 128. |
| [21] | PADWICK C, DESKEVICH M, PACIFICI F, et al. World View-2 Pan-sharpening[C]//Proceedings of the ASPRS 2010 Annual Conference. San Diego:[s.n.], 2010:26-30. |
| [22] | CANDES E J, ROMBERG J K, TAO T. Stable Signal Recovery from Incomplete and Inaccurate Measurements[J]. Communications on Pure and Applied Mathematics, 2005, 59(8):1207-1233. |
| [23] | DONOHO D L.For Most Large Underdetermined Systems of Equations, the Minimal-norm Near-solution Approximates the Sparest Near-solution[J]. Communications on Pure and Applied Mathematics, 2006, 59(7):907-934. |
| [24] | BRUCKSTEIN A M, ELAD M, ZIBULEVSKY M. On the Uniqueness of Nonnegative Sparse Solutions to Underdetermined Systems of Equations[J]. IEEE Transactions on Information Theory, 2008, 54(11):4813-4820. |
| [25] | DUARTE M F, SARVOTHAM S, BARON D, et al. Distributed Compressed Sensing of Jointly Sparse Signals[C]//Proceeding of Conference Record of the 39th Asilomar Conference on Signals, Systems and Computers. Pacific Grove:IEEE, 2005. |
| [26] | AHARON M, ELAD M, BRUCKSTEIN A. K-SVD:An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11):4311-4322. |
| [27] | AIAZZI B, BARONTI S, SELVA M, et al. Bi-cubic Interpolation for Shift-free Pan-sharpening[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 86:65-76. |
| [28] | KHAN M M, CHANUSSOT J, CONDAT L, et al. Indusion:Fusion of Multispectral and Panchromatic Images Using the Induction Scaling Technique[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(1):98-102. |
| [29] | ZHOU J, CIVCO D L, SILANDER J A. A Wavelet Transform Method to Merge Landsat TM and SPOT Panchromatic Data[J]. International Journal of Remote Sensing, 1998, 19(4):743-757. |
| [30] | KHAN M M, ALPARONE L, CHANUSSOT J. Pansharpening Quality Assessment Using the Modulation Transfer Functions of Instruments[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(11):3880-3891. |
| [31] | 王慧贤, 江万寿, 雷呈强, 等. 光谱与空间局部相关的SVR影像融合方法[J]. 测绘学报, 2013, 42(4):508-515. WANG Huixian, JIANG Wanshou, LEI Chengqiang, et al. A Robust SVR Image Fusion Method Based on Local Spectral and Spatial Correlation[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4):508-515. |
| [32] | ALPARONE L, WALD L, CHANUSSOT J, et al. Comparison of Pansharpening Algorithms:Outcome of the 2006 GRS-S Data-fusion Contest[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(10):3012-3021. |
| [33] | ALPARONE L, BARONTI S, GARZELLI A, et al. A Global Quality Measurement of Pan-sharpened Multispectral Imagery[J]. IEEE Geoscience and Remote Sensing Letters, 2004, 1(4):313-317. |
| [34] | 刘婷, 程建. 小波变换和稀疏表示相结合的遥感图像融合[J]. 中国图象图形学报, 2013, 18(8):1045-1053. LIU Ting, CHENG Jian. Remote Sensing Image Fusion with Wavelet Transform and Sparse Representation[J]. Journal of Image and Graphics, 2013, 18(8):1045-1053. |