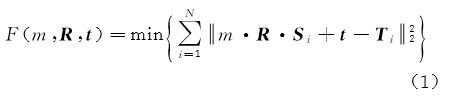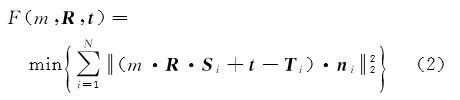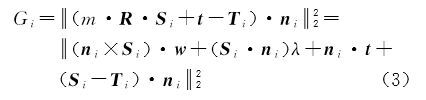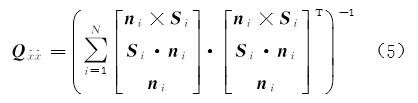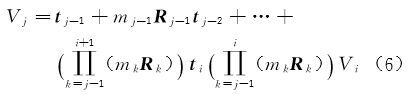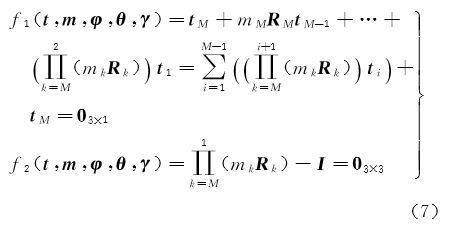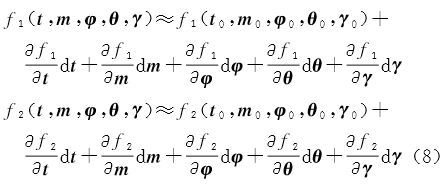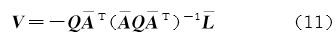2. 成都理工大学地球科学学院, 四川成都 610059
2. College of Earth Sciences, Chengdu University of Technology, Chengdu 610059, ChinaAbstract
三维激光扫描仪能直接、快速地获取物体表面点云3D坐标。为了完整地重构物体表面形状,需要从不同视角进行扫描,每次扫描获得的点云(待配准点云)往往基于独立的局部坐标系统,需要转换至统一的全局坐标系统中,这一过程称为“点云配准”[1]。点云配准是点云处理的重要步骤,配准精度直接影响点云数据处理的整体精度[2]。
根据所处理视角数的不同,点云配准可分两视配准和多视配准。两视配准较为成熟,代表性的算法为迭代最近点(iterative closest points,ICP)配准[3, 4, 5, 6]。而在多视配准方面,起初采用序贯(Sequential)配准[4],即先选择一幅模板点云,然后按点云对应关系依次以前一点云为基准,后一点云为待配准点云,采用两视配准方法进行配准,依此完成配准。该方法直接易行,但前后配准点云之间有误差累积,影响整体配准的精度与可靠性[7, 8]。为避免配准误差累积,提高配准精度,文献 [9, 10, 11] 设计了同时(Simultaneous)配准,该方法按各点云对应关系同时一次性完成多视配准。同时配准的迭代收敛速度慢且会占用大量计算机内存,降低了配准的可靠性和效率[12]。
近些年来,许多学者提出利用平差方法估计全局最优坐标转换参数提高多视配准效率、精度与可靠性的方法。文献 [13, 14, 15, 16] 均使用条件平差法进行简易平差,分别对平移和旋转参数的闭合差进行分配。转换参数不是最原始的观测值,它们之间往往不独立,从这个意义上讲,简易平差方法不严密。文献[17]依据整体平差模型构建误差方程,采用间接平差法获得最小二乘意义下的最优转换参数,但因误差方程复杂而在平差中仅考虑了部分方程,方法也不严密。文献[18]对多视配准的全局一致性进行了研究,但并没有分析转换参数的具体求解方法。点云配准是确定点云的位置和姿态参数的过程,即点云定向[19]。文献 [20, 21]以扫描站射向标靶中心的光束为单元建立平差方程,一次性解算多站地面扫描点云坐标转换参数;文献[22]首先进行初始配准,再采用ICP配准进行优化,实际上它们采用的仍然是同时配准方式。
本文研究一种闭合条件约束的多视配准方法,首先阐述两视配准估计转换参数的具体方法;然后以单站点云为单元,严密推导多视配准的闭合差分配方式;再展示两组代表性的实测数据试验,以验证所提方法的有效性和可行性。
1 两视配准转换参数估计两视点云配准包括初始配准和精确配准两个步骤,初始配准的主要目的是为精确配准提供初始方位,以减少同名点的搜索空间,提高搜索的效率和可靠性[12]。不失一般性,初始配准的方法是在待配准点云S和基准点云T的重叠区域选取不共线且尽量均匀分布的3对近似同名点[23],然后利用单位四元数法[24]计算转换参数,再利用转换参数对S进行转换。
ICP算法是广泛使用的精确配准方法,其算法模型为[1]
式中,Si=[SxiSyiSzi]T是待配准点;Ti=[TxiTyiTzi]T为Si的同名点;t=[txtytz]T为平移向量;m 代表尺度因子;R 表示旋转矩阵,是关于绕 z、x 和y 轴的欧拉旋转角φ、θ 和 γ 的函数;N 为同名点数。ICP算法模型的几何意义为 T 和 S 之间所有同名点间的距离平方和最小。ICP算法主要包括点-点ICP[3]和点-切平面ICP[4]。点-切平面ICP能建立更精确的同名点,收敛速度较快、精度更高[12],它是基于法向量方向上的距离平方和最小为目标,因此笔者将式(1)改进为
式中,ni=[nxinyinzi]T 表示Si 的法向量,其他参数与式(1)一致。经初始配准后,S与T 的相对偏移较小,因此将欧拉旋转角 φ、θ、γ 视为微小量,并且旋转矩阵 R 的值近似为 \[R=\text{ }\left[ \begin{matrix} 1 & \varphi & -\gamma \\ -\varphi & 1 & \theta \\ \gamma & -\theta & 1 \\ \end{matrix} \right]\]
将R带入式(2)得
式中,w=[θ,γ,φ]T,m=1+λ。对转换参数x=[txtytzm φ θ γ]T求导,当导数满足$\sum\limits_{i - 1}^N {\frac{{\partial {G_i}}}{{\partial x}} = 0} $时,目标函数值最小。整理后得到法方程求解(4)即可获得转换参数估计值,并且算得协因数矩阵
式中,${Q_{\hat x\hat x}}$反映的是转换参数之间的相关性大小。 2 多视配准闭合差分配 2.1 闭合环条件方程将扫描获得的 M 个站(或者视角)点云记为V1,V2,…,VM,对应 M 个独立的坐标系。在两两配准求解出转换参数后,对应视角Vi+1与Vi之间存在坐标转换关系,可以表示为Vi+1=Ci,i+1(ti,mi,Ri)Vi。如图 1所示,以单站点云为单元,将V1,V2,…,VM 按照相邻视角依次排列,除第一个视角和最后一个视角外,余下视角均恰好存在两个相邻视角,则这 M 个视角之间的转换参数构成一个视角链;若每个视角均恰好存在两个相邻视角,则这 M 个视角之间的转换参数构成一个视角闭合环。

|
| 图 1 视角链与闭合环示意 Fig. 1 Sketch map of view chain and closed view loop |
在视角链与闭合环中,转换参数被视为随机观测值,视角Vi与Vj(j>i)的转换关系为 ${{\text{V}}_j} = (\prod\limits_{k = j - 1}^i {{C_{k,k + 1}}} ){{\text{V}}_{\text{i}}}$,展开后得到
由${{\text{V}}_M} = (\prod\limits_{k = 1}^{M - 1} {{C_{k,k + 1}}} ){{\text{V}}_{\text{1}}}$ 和V1=CM,1VM 得视角闭合环的条件方程 $\prod\limits_{k = 1}^M {{C_{k,k + 1}} = I} $,进一步得 式中,t=[tT1 tT2…tTM]T;m=[m1 m2…mM]T;φ=[φ1 φ2…φM]T;θ=[θ1 θ2…θM]T;γ=[γ1 γ2…γM]T 表示视角闭合环中的转换参数;I表示单位矩阵。式(7)是非线性的,按泰勒级数展开,取至一次项得 式中,t0、m0、φ0、θ0、γ0分别为转换参数的初始值;${\rm{d}}t = {\left[ {\matrix{ {{\rm{d}}{t_1}^{\rm T}} & {{\rm{d}}{t_2}^{\rm T}} & { \cdot \cdot \cdot } & {{\rm{d}}t_M^{\rm T}} \cr } } \right]^{\rm T}}$;${\rm{d}}m = {\left[ {\matrix{ {{\rm{d}}{m_1}} & {{\rm{d}}{m_2}} & { \cdot \cdot \cdot } & {{\rm{d}}{m_M}} \cr } } \right]^{\rm T}}$;${\rm{d}}\varphi = {\left[ {\matrix{ {{\rm{d}}{\varphi _1}} & {{\rm{d}}{\varphi _2}} & { \cdot \cdot \cdot } & {{\rm{d}}{\varphi _M}} \cr } } \right]^{\rm T}}$;${\rm{d}}\theta = {\left[ {\matrix{ {{\rm{d}}{\theta _1}} & {{\rm{d}}{\theta _2}} & { \cdot \cdot \cdot } & {{\rm{d}}{\theta _M}} \cr } } \right]^{\rm T}}$;${\rm{d}}\gamma = {\left[ {\matrix{ {{\rm{d}}{\gamma _1}} & {{\rm{d}}{\gamma _2}} & { \cdot \cdot \cdot } & {{\rm{d}}{\gamma _M}} \cr } } \right]^{\rm T}}$ 为转换参数的改正数。式(8)用矩阵形式表示为 式中,V=[dtT dmT dφT dθT dγT]T;A 表示系数矩阵 \[A=\left[ \begin{matrix} \frac{\partial {{f}_{1}}}{\partial t} & \frac{\partial {{f}_{1}}}{\partial m} & \frac{\partial {{f}_{1}}}{\partial \varphi } & \frac{\partial {{f}_{1}}}{\partial \theta } & \frac{\partial {{f}_{1}}}{\partial \gamma } \\ \frac{\partial {{f}_{2}}}{\partial t} & \frac{\partial {{f}_{2}}}{\partial m} & \frac{\partial {{f}_{2}}}{\partial \varphi } & \frac{\partial {{f}_{2}}}{\partial \theta } & \frac{\partial {{f}_{2}}}{\partial \gamma } \\ \end{matrix} \right]\] L为常数项 \[L=\left[ \begin{align} & {{f}_{1}}\left( {{t}_{0}},{{m}_{0}},{{\varphi }_{0}},{{\theta }_{0}},{{\gamma }_{0}} \right) \\ & {{f}_{2}}\left( {{t}_{0}},{{m}_{0}},{{\varphi }_{0}},{{\theta }_{0}},{{\gamma }_{0}} \right) \\ \end{align} \right]\] 2.2 闭合差分配在闭合环条件方程中,总的观测值个数为7M,其中必要观测数为 7(M-1),多余观测数为 r=7,即对应7个独立的条件方程。对式(9)的系数阵 A 进行 SVD 分解得A=U·V·D,其中 U、D 为可逆的方阵;V 为对角矩阵,对角线元素不为0的个数恰好等于多余观测数7。式(9)两边同时乘以U 的逆矩阵U-1并取独立的7个方程得
式中,$\bar {\rm A} = {U^{ - 1}}{\rm A},\bar L = {U^{ - 1}}L$。使用条件平差方法求得转换参数的改正数 式中,Q 表示条件平差前转换参数协因数阵,并可计算出转换参数的中误差为${{\hat \delta }_i} = {{\hat \delta }_0}\sqrt {{{\tilde Q}_{ii}}} ({{\hat \delta }_0}$ 代表单位权中误差,${{\tilde Q}_{ii}}$ 表示平差后第 i 个转换参数的协因数)。${{\hat \delta }_i}$ 是衡量配准精度的指标,其值越小,则配准精度越高;反之亦然。在转换参数的条件平差中,平差前转换参数协因数阵和先验权值根据式(5)进行计算。由于各视角之间的两视配准是独立进行的,因此可以认为不同转换关系之间的转换参数具有相互独立的性质,对应的协因数矩阵元素为0,即 Q 为分块对角矩阵。
3 试验结果与分析为验证所提方法的有效性和可行性,试验采用地面三维激光扫描仪FARO FOCUS3D S120获取两组具有不同特征的点云数据。如图 2所示,第1组是孔子像的扫描数据,布设了4个扫描站,采样间隔为毫米级,但相邻点云视角重叠度较小。第2组是结构比孔子像规则的体育馆扫描数据,布设了19个扫描站,采样间隔为厘米级,而相邻视角重叠度较大。

|
| 图 2 点云数据基本情况,百分比表示重叠度,括号里面为采样间隔(单位:cm) Fig. 2 Basic information of the point clouds,where percentages are overlaps and values in the brackets are sampling intervals (unit: cm) |
点云初始配准与ICP配准后的效果如图 3和图 4所示。孔子像相邻点云视角的ICP配准所求转换参数如表 1所示。

|
| 图 3 孔子像数据初始配准和ICP配准后的效果 Fig. 3 Renderings of initial alignment and ICP registration for the Confucius data |

|
| 图 4 体育馆数据始配准和ICP配准后的效果 Fig. 4 Renderings of initial alignment and ICP registration for the gymnasium data |
| C | tx/m | ty/m | tz/m | φ/(°) | θ/(°) | γ/(°) | 尺度因子m |
| C1,2 | 0.0090 | -0.0081 | 0.0005 | 0.0851 | -0.0042 | 0.0026 | 0.99797 |
| C2,3 | 0.0096 | 0.0021 | -0.0028 | 0.1061 | 0.0177 | 0.0671 | 1.00111 |
| C3,4 | -0.0131 | 0.0128 | -0.0016 | -0.1564 | 0.0459 | -0.0575 | 1.00137 |
| C4,1 | -0.0062 | 0.0019 | 0.0007 | -0.1035 | -0.0143 | -0.0188 | 1.00039 |
从两视配准的结果来看,初始配准后各视角点云数据已大致拼合成了一个整体,经过进一步的ICP配准,相邻视角的重叠区域几乎重合。为了评定转换参数的求解精度,并检验求解的可靠性,接下来使用已经求得的转换参数构建闭合环条件方程进行平差计算,对闭合差进行分配。
孔子像的点云V1 至V4 构成视角闭合环,根据式(7)求得转换参数的闭合差为f1=[-0.000588,0.00867,-0.00326]T,并且 \[f2=\left[ \begin{matrix} 0.000837 & -0.001119 & 0.0001179 \\ 0.001199 & 0.000837 & 0.000786 \\ -0.0001189 & -0.000786 & 0.000837 \\ \end{matrix} \right]\]
平差后的单位权中误差为0.7 mm,转换参数及其中误差分别如表 2和表 3所示。体育馆的点云 V1 至 V19 构成视角闭合环,根据式(7)求得转换参数的闭合差为f1=[0.02983,-0.00567,0.01419]T,并且 \[f2=\left[ \begin{matrix} -0.008067 & -0.006512 & -0.007710 \\ 0.006510 & -0.008065 & -0.003649 \\ 0.007713 & 0.003644 & -0.008065 \\ \end{matrix} \right]\]
| C | tx/m | ty/m | tz/m | φ/(°) | θ/(°) | γ/(°) | 尺度因子m |
| C12 | 0.0131 | -0.0123 | 0.0006 | 0.1668 | -0.0091 | 0.0218 | 0.99733 |
| C23 | 0.0104 | 0.0004 | -0.0024 | 0.1172 | 0.0092 | 0.0623 | 1.00075 |
| C34 | -0.0173 | 0.0099 | 0.0010 | -0.1807 | 0.0157 | -0.0639 | 1.00150 |
| C41 | -0.0063 | 0.0020 | 0.0008 | -0.1034 | -0.0156 | -0.0201 | 1.00043 |
| C | δtx/mm | δty/mm | δtz/mm | δφ/(″) | δθ/(″) | δγ/(″) | δm |
| C1,2 | 0.13 | 0.04 | 0.05 | 3.0 | 0.9 | 0.9 | 5.6×10-6 |
| C2,3 | 0.06 | 0.04 | 0.03 | 6.7 | 2.8 | 2.5 | 1.1×10-5 |
| C3,4 | 0.13 | 0.05 | 0.06 | 2.8 | 1.3 | 1.1 | 8.3×10-6 |
| C4,1 | 0.06 | 0.02 | 0.02 | 6.6 | 2.6 | 2.5 | 9.9×10-6 |
平差后的单位权中误差为1.2 mm,转换参数中误差较大的结果如表 4所示。
| C | δtx/mm | δty/mm | δtz/mm | δφ/(″) | δθ/(″) | δγ/(″) | δm |
| C1,2 | 0.03 | 0.02 | 0.01 | 0.18 | 0.12 | 0.14 | 5.9×10-7 |
| C3,4 | 0.03 | 0.06 | 0.05 | 0.13 | 0.31 | 0.24 | 1.2×10-6 |
| C5,6 | 0.05 | 0.08 | 0.05 | 0.18 | 0.12 | 0.17 | 1.8×10-6 |
| C11,12 | 0.09 | 0.09 | 0.08 | 0.18 | 0.29 | 0.30 | 1.7×10-6 |
| C12,13 | 0.09 | 0.11 | 0.06 | 0.47 | 0.23 | 0.19 | 8.1×10-7 |
| C13,14 | 0.03 | 0.05 | 0.04 | 0.21 | 0.12 | 0.15 | 4.8×10-7 |
| C14,15 | 0.03 | 0.04 | 0.02 | 0.20 | 0.14 | 0.13 | 5.0×10-7 |
| C16,17 | 0.04 | 0.04 | 0.04 | 0.23 | 0.32 | 0.22 | 8.5×10-7 |
| C17,18 | 0.06 | 0.02 | 0.04 | 0.16 | 0.14 | 0.24 | 1.3×10-6 |
| C18,19 | 0.03 | 0.04 | 0.02 | 0.34 | 0.20 | 0.13 | 9.3×10-7 |
在精度方面,表 3中平移参数的中误差能够达到0.01 mm级;旋转参数的中误差能够达到s级;缩放参数的中误差为10-6级;相邻视角 V2-V3 和V4-V1 的旋转参数和尺度参数中误差较大。表 4显示,平移参数的中误差能够达到0.01 mm级;旋转参数的中误差能够达到0.1 s级;缩放参数的中误差达到10-7级。
对比表 3和表 4,两组数据的平移参数的中误差几乎是一个数量级,而体育馆数据旋转参数和尺度参数的中误差小一个数量级。结合图 2,两组数据的平均采样间隔分别为毫米级和厘米级,表明点云采样间隔对转换参数中误差的影响很小;但孔子像的V2-V3 和V4-V1 的重叠度仅3%和4%,并且体育馆数据相邻点云视角的重叠度较大,表明重叠度对转换参数中误差的影响较大,对尺度参数和旋转参数中误差的影响大于平移参数中误差。因此,对于采样间隔小的点云数据,为了提高配准精度与可靠性,增大相邻点云的重叠度是一种有效的方式。
4 结 论本文提出了一种闭合条件约束的多视点云配准方法,对坐标转换参数估计进行了严密推导。该方法首先进行ICP配准求解转换参数及其协因数矩阵;再将转换参数作为随机观测值构建视角闭合环,使用行条件平差法分配闭合差,以达到全局最优,并分析了配准精度与可靠性。其中,ICP配准利用七参数相似变换模型作为转换模型,并采用梯度下降法估计转换参数。
通过孔子像和体育馆两组实测扫描数据进行试验,验证了所提方法的有效性和可行性。试验结果表明,对采样间隔为毫米级和厘米级的点云,采样间隔对转换参数中误差的影响很小;重叠度对转换参数中误差,特别是尺度参数和旋转参数的中误差影响较大;增加扫描重叠度能够提高配准精度和可靠性。然而,只对单个视角闭合环的多视点云配准进行了试验,对区域网的的转换参数平差还需进一步分析和研究。
| [1] | GRUEN A, AKCA D. Least Squares 3D Surface Matching[M]. Inst. Für Geodsie Und Photogrammetrie, 2007. |
| [2] | 浦石, 李京伟, 郭四清. 融合语义特征与GPS位置的地面激光点云拼接方法[J]. 测绘学报, 2014, 43(5): 545-550.DOI:10.13485/j.cnki.11-2089.2014.0075 . PU Shi, LI Jingwei, GUO Siqing. Registration of Terrestrial Laser Point Clouds by Fusing Semantic Features and GPS Positions[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(5): 545-550. DOI:10.13485/j.cnki.11-2089.2014.0075. |
| [3] | BESL P J, MCKAY H D. A Method for Registration of 3D Shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256. |
| [4] | CHEN Yang, MEDIONI G. Object Modelling by Registration of Multiple Range Images[J]. Image and Vision Computing, 1992, 10(3): 145-155. |
| [5] | RUSINKIEWICZ S, LEVOY M. Efficient Variants of the ICP Algorithm[C]//Proceedings of the 3rd International Conference on 3D Digital Imaging and Modeling. Quebec City: IEEE, 2001: 145-152. |
| [6] | SALVI J, MATABOSCH C, FOFI D, et al. A Review of Recent Range Image Registration Methods with Accuracy Evaluation[J]. Image and Vision Computing, 2007, 25(5): 578-596. |
| [7] | BERGEVIN R, SOUCY M, GAGNON H,et al. Towards a General Multi-View Registration Technique[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1996, 18(5): 540-547. |
| [8] | GAGNON H,SOUCY M,BERGEVIN R,et al.Registration of Multiple Range Views for Automatic 3D Model Building[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Seattle: IEEE, 1994: 581-586. |
| [9] | BLAIS G, LEVINE M D. Registering Multiview Range Data to Create 3D Computer Objects[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(8): 820-824. |
| [10] | EGGERT D W, FITZGIBBON A W, FISHER R B. Simultaneous Registration of Multiple Range Views for Use in Reverse Engineering[C]//Proceedings of the 13th International Conference on Pattern Recognition. Vienna: IEEE, 1996: 243-247. |
| [11] | NEUGEBAUER P J. Geometrical Cloning of 3D Objects via Simultaneous Registration of Multiple Range Images[C]//Proceedings of International Conference on Shape Modeling and Application. Los Alamitos: IEEE, 1997: 130-179. |
| [12] | PULLI K. Multiview Registration for Large Data Sets[C]//Proceedings of the 2nd International Conference on 3-D Digital Imaging and Modeling. Ottawa: IEEE, 1999: 160-168. |
| [13] | ZHO H, BASAKI R. Reconstructing Urban 3D Model Using Vehicle-borne Laser Range Scanners[C]//Proceedings of the 3rd International Conference on 3-D Digital Imaging and Modeling. Quebec City: IEEE, 2001: 349-356. |
| [14] | 盛业华, 张卡, 张凯, 等. 地面三维激光扫描点云的多站数据无缝拼接[J]. 中国矿业大学学报, 2010, 39(2), 233-237. SHENG Yehua, ZHANG Ka, ZHANG Kai, et al. Seamless Multi Station Merging of Terrestrial Laser Scanned 3D Point Clouds[J]. Journal of China University of Mining & Technology, 2010, 39(2): 233-237. |
| [15] | 徐源强, 高井祥, 张丽, 等. 地面三维激光扫描的点云配准误差研究[J]. 大地测量与地球动力学, 2011, 31(2): 129-132. XU Yuanqiang, GAO Jingxiang, ZHANG Li, et al. Research on Point Cloud Registration Error of Terrestrial Laser Scanning[J]. Journal of Geodesy and Geodynamics, 2011, 31(2): 129-132. |
| [16] | 何朝明. 离散点云处理的关键技术研究[D]. 成都: 西南交通大学, 2007. HE Chaoming. Research on the Key Technologies of Discrete Point Clouds Process[D]. Chengdu: Southwest Jiaotong University, 2007. |
| [17] | 张剑清, 翟瑞芳, 郑顺义. 激光扫描多三维视图的全自动无缝镶嵌[J]. 武汉大学学报(信息科学版), 2007, 32(2), 100-103. ZHANG Jianqing, ZHAI Ruifang, ZHENG Shunyi. Automatic Seamless Registration of 3D Multiple Range Views[J]. Geomatics and Information Science of Wuhan University, 2007, 32(2): 100-103. |
| [18] | LIU Yuan,ZHOU Wen,YANG Zhouwang,et al. Globally Consistent Rigid Registration[J]. Graphical Models, 2014, 76(5): 542-553. |
| [19] | 姚吉利, 马宁, 贾象阳, 等. 球形标靶的固定式扫描大点云自动定向方法[J]. 测绘学报, 2015, 44(4): 431-437. DOI: 10.11947/j.AGCS.2015.20130357. YAO Jili, MA Ning, JIA Xiangyang, et al. An Approach for Automatic Orientation of Big Point Clouds from the Stationary Scanners Based on the Spherical Targets[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 431-437. DOI: 10.11947/j.AGCS.2015.20130357. |
| [20] | 姚吉利, 马宁, 贾象阳, 等. 光束法区域网平差的地面激光扫描多站点云自动定向方法[J]. 测绘学报, 2014, 43(7): 711-716, 723.DOI:10.13485/j.cnki.11-2089.2014.0099 . YAO Jili,MA Ning,JIA Xiangyang,et al. Auto-Registration for Terrestrial Laser Scanning Multi-Stations Point Clouds with Bundle Block Adjustment Method[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 711-716, 723. DOI:10.13485/j.cnki.11-2089.2014.0099. |
| [21] | 姚吉利, 贾向阳, 马宁, 等. 地面激光扫描多站点云整体定向平差模型[J]. 测绘学报, 2014, 43(8): 835-841.DOI:10.13485/j.cnki.11-2089.2014.0023 . YAO Jili, JIA Xiangyang, MA Ning, et al. Overall Orientation Adjustment Model of Terrestrial Laser Scanning Multi-Station Point Clouds[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 835-841.DOI:10.13485/j.cnki.11-2089.2014.0023. |
| [22] | 李彩林, 郭宝云, 季铮. 多视角三维激光点云全局优化整体配准算法[J]. 测绘学报, 2015, 44(2): 183-189. DOI: 10.11947/j.AGCS.2015.20130737. LI Cailin, GUO Baoyun, JI Zheng. Global Optimization and Whole Registration Algorithm of Multi-view 3D Laser Point Cloud[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(2): 183-189. DOI: 10.11947/j.AGCS.2015.20130737. |
| [23] | BERNARDINI F, RUSHMEIER H. The 3D Model Acquisition Pipeline[J]. Computer Graphics Forum, 2002, 21: 149-172. |
| [24] | HORN B K P. Closed-form Solution of Absolute Orientation Using Unit Quaternions[J]. Journal of the Optical Society of America A, 1987, 4(4): 629-642. |