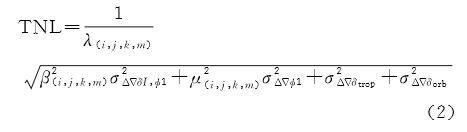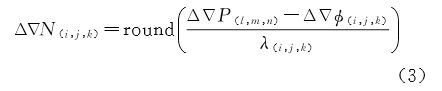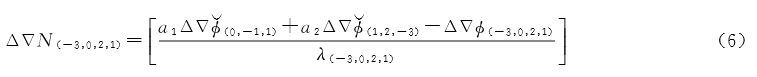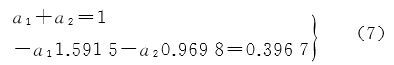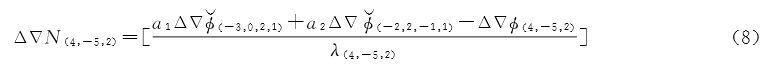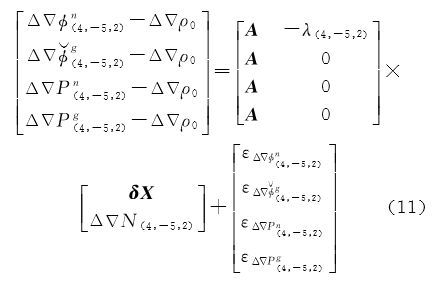整周模糊度解算是高精度定位的关键问题。对于基线较长情况下的模糊度解算,由于电离层误差的空间相关性差,双差测量值中的电离层残差较大[1],导致模糊度解算所需时间长,且解算成功率不高。所以基线较长时模糊度确定的重点问题是如何更好地消除电离层残差的影响。
为了更好地消除电离层误差,模糊度解算一般使用多频测量值,多个频率的测量值可形成一些性能优良的线性组合,有助于模糊度的正确解算。多频模糊度解算的典型方法是三频模糊度解算法(three carrier ambiguity resolution,TCAR)和逐级模糊度解算法(cascade integer resolution,CIR)[2, 3, 4]。这两种方法虽然很容易确定超宽巷模糊度,得到精度优于测距码的超宽巷组合观测值,但对于北斗的3个频率信号,在求解宽巷和窄巷模糊度时受到双差电离层延迟的影响较大,导致模糊度解算效果差。不少学者在这方面进行了相关研究。文献[5]通过固定的超宽巷、宽巷模糊度反求电离层误差,改进了传统的TCAR法,提高了基础载波模糊度解算成功率;文献[6]提出了一种新的TCAR法,以所有误差方差总和最小为原则选取最佳线性组合;文献[7]利用两个超宽巷组合与任一窄巷组合构成几何无关和无电离层延迟(geometry-free and ionosphere-free)的组合,解决了电离层估值精度低的问题[1, 7];文献[8]在计算无电离层组合系数时不仅考虑了消电离层,还尽量使组合噪声最小;文献[9]用两个超宽巷和一个非相关窄巷模糊度反求原始频点模糊度。上述方法均在一定程度上针对目前北斗和GPS的三频信号,对模糊度解算的性能进行了改进,但是由于超宽巷和宽巷测量值受噪声及电离层残差影响较大,窄巷模糊度求解仍需要较长时间的数据才能够正确解算。如果有额外频点的测量信号,则有可能出现性能更优的组合信号,进一步提高模糊度解算的性能。
北斗区域卫星导航系统于2012年12月27日起正式提供区域服务[10]。与其他GNSS系统不同,北斗系统除了提供众所周知的无线电导航业务(radio navigation satellite system,RNSS)外,还提供了卫星无线电测定业务(radio determination satellite service,RDSS)[11, 12]。RNSS和RDSS均可用于民用[12, 13]。RNSS提供了3个L波段频率,RDSS的GEO卫星提供了一个S波段频率。额外的测量值为发展新的模糊度解算方法提供了契机。本文对RNSS+RDSS频率组合进行了分析,在此基础上提出了RNSS与RDSS组合快速模糊度解算方法。该方法利用北斗RDSS服务在GEO卫星上提供的S频段测量值与北斗的RNSS测量值一起形成性能优良的宽巷组合,来求解GEO卫星的窄巷模糊度,再采用有关几何方法用GEO卫星来辅助非GEO卫星的窄巷模糊度求解,从整体上提高了窄巷模糊度解算的效率。最后利用仿真数据验证了算法的有效性。
本文的组织结构如下:第1节分析了RNSS+RDSS频率组合情况;第2节介绍了RDSS+RNSS组合模糊度解算模型,并阐述了算法的具体实施步骤;第3节给出了利用仿真数据对算法进行仿真验证的结果;第4节进行了总结。
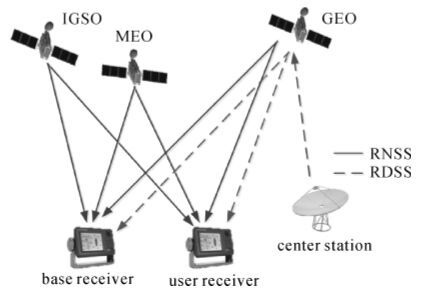
1 RNSS+RDSS频率组合分析如图 1所示,北斗RNSS信号传输路径是从卫星到用户,RDSS无源信号的传输路径是从中心站经卫星转发再到用户[13]。对于RDSS信号的载波相位测量,设从中心站到GEO卫星这段的信号频率为f1,通过GEO卫星对的f1信号进行变频转发后向用户发送频率为f2的信号,则用户接收到的是载波为f2的信号。值得注意的是,此时的f2频率信号含有一定的变频误差和转发时延误差。用户接收到信号后对f2载波信号进行跟踪,并测量其载波相位差。所以,用户端测量的是f2频率信号的载波相位差,与中心站到GEO卫星这段路径无关,用公式可以表示为
式中,${\phi _u}$ 为载波相位测量值;ρs-u 为 GEO 卫星到用户的几何距离;c为光速;δtu、δts 分别为用户钟差和卫星钟差;δu为用户硬件延迟;卫星延迟 δs 表征了转发时延和变频误差时延,故这里的 δs与 RNSS 测量时的硬件时延不同; das-u 为 GEO 卫星到用户的空间延迟,包括电离层延迟和对流层延迟; ${\phi _{0,u}}$和$\phi _0^s$ 分别为卫星和用户端初始相位;N为模糊度;ε为测量误差。在进行站间差分时,卫星钟差δts、转发时延δs 等公共误差可在站间差分时消除。这样,北斗 RDSS 与 RNSS 的单差载波相位具备了一致的观测方程形式,相同的时空基准和传输路径,为 RDSS 与 RNSS 组合高精度定位的研究提供了契机。如果额外的RDSS 测量值能够与 RNSS 测量值一起形成更好的组合观测值,那么将有助于高精度的定位解算。
|
| 图 1 RNSS和RDSS信号传输示意图 Fig. 1 RDSS+RNSS signal transmission path |
根据中国向国际电讯联盟(ITU)提交的文件中,北斗RNSS业务将发送信号的3个频率集中在1 561.089 MHz(B1),1 207.14 MHz(B2)和1 268.52 MHz(B3)[14]。此外,北斗RDSS从卫星到用户段提供的频率为S波段,集中于2 491.75 MHz[15]。这几个频段信号产生的测量值都可用于定位解算。本文首先对北斗的这4个频率信号进行频率组合分析,找到最优的虚拟组合测量值。关于最优频率的组合,很多学者提出了高效实用的筛选方案[16, 17]。本文结合文献 [16, 17]的方法,首先,在短基线(0~20km),中长基线(20~100km)和长基线(100~500km)3种情况下分析了北斗不同频率组合的性能,然后综合考虑波长,电离层延迟系数,测量噪声,并考虑总的噪声与波长的比值(total noise level,TNL),从这些组合中,选择具有弱电离层延迟以及小噪声,并在不同基线长度下具有较小TNL值的组合为最优组合。本文中定义超宽巷的波长范围为:λ>1.7 m,宽巷的波长范围为:0.5 m < λ<1.7 m,窄巷的波长范围为:λ < 0.5 m。对相应组合进行筛选的结果如表 1所示。
| integer coefficients | f(i,j,k,m)/GHz | λ(i,j,k,m)/m | β(i,j,k,m) | μ(i,j,k,m) | TNLshort | TNLmidd | TNLlong | ||||
| B1 | B2 | B3 | S | ||||||||
| EWL | 0 | -1 | 1 | — | 0.0614 | 4.8842 | -1.5915 | 28.5287 | 0.061 | 0.0881 | 0.1439 |
| 1 | 2 | -3 | — | 0.1698 | 1.7654 | -0.9698 | 28.0859 | 0.1622 | 0.1942 | 0.2725 | |
| WL | -3 | 0 | 2 | 1 | 0.3455 | 0.8677 | 0.3967 | 17.0201 | 0.2002 | 0.2197 | 0.2735 |
| -2 | 2 | -1 | 1 | 0.153 | 0.5818 | -0.054 | 9.3862 | 0.168 | 0.1693 | 0.1734 | |
| NL | 4 | -5 | 2 | — | 2.7457 | 0.1092 | -0.0027 | 3.2951 | 0.3913 | 0.3959 | 0.4138 |
表 1中,f(i,j,k,m)为组合测量值的频率;λ(i,j,k,m)为组合测量值的波长;β(i,j,k,m)为组合测量值的一阶电离层延迟系数;μ(i,j,k,m)为组合测量值的观测噪声系数;TNLshort、TNLmidd、TNLlong分别为短基线、中长基线和长基线下的TNL值。对于线性组合系数为i、j、k、m(i、j、k、m均为整数)的虚拟观测值来说,TNL的表达式为
式中,${\sigma _{\Delta \nabla \delta I,\phi 1}}$为B1频点上的一阶双差电离层延迟误差;${\sigma _{\Delta \nabla \phi 1}}$为B1频点上的相位噪声;${\sigma ^2}_{\Delta \nabla {\delta _{trop}}}$为对流层误差,${\sigma ^2}_{\Delta \nabla {\delta _{trop}}}$为轨道误差。 2 RDSS与RNSS组合模糊度解算模型由于北斗系统的RDSS服务只发生在GEO卫星上,也就是只有GEO卫星具有额外的S频点测量值。为了更好地利用额外的观测信息,笔者对GEO卫星和非GEO卫星分别建立模型。在频率组合的选择上,表 1中列出了几组经过筛选的具有合适波长、较小电离层延迟、较小组合误差并且在不同的基线长度下都具有较小TNL值的组合系数。特别是窄巷组合(4,2,-5)的电离层延迟系数非常小,米级的电离层延迟误差对其模糊度解算的影响小于0.1周[17],特别适合模糊度解算。对于GEO和非GEO卫星的组合选择如下:
对于GEO卫星,根据第1节的分析,选择其超宽巷组合为(0,-1,1)和(1,2,-3),宽巷组合为(-3,0,2,1)和(-2,2,-1,1),窄巷组合为(4,-5,2)。对于非GEO卫星,选择其超宽巷组合为(0,-1,1)和(1,2,-3),窄巷组合为(4,-5,2)。即GEO卫星和非GEO卫星选择相同的超宽巷和窄巷组合,由于GEO卫星可发射RDSS信号,故可以形成两个性能优良的宽巷组合。
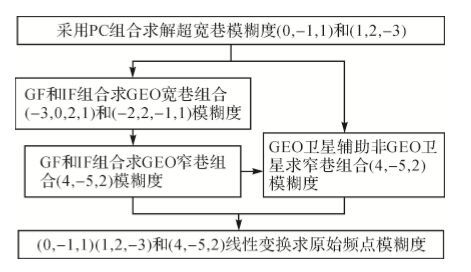
RDSS与RNSS组合模糊度解算流程如图 2所示。
|
| 图 2 RDSS+RNSS模糊度解算流程图 Fig. 2 RDSS+RNSS ambiguity resolution flow chart |
解算时,先解算所有卫星的超宽巷模糊度,对所有卫星直接利用伪距或者采用消电离层PC组合模型解算。然后再解算GEO宽巷模糊度,采用两个超宽巷测量值和待解算的宽巷组合测量值构成几何无关(geometry-free,GF)和电离层无关(ionosphere-free,IF)模型求解。最后解算所有卫星的窄巷模糊度。解算窄巷模糊度时,对于GEO卫星采用两个宽巷组合和窄巷组合形成GF和IF模型解算。对于非GEO卫星,利用已解算模糊度的GEO卫星与未解算模糊度的非GEO卫星一起形成几何有关模型解算。窄巷模糊度解算完成后,采用线性无关的3个组合模糊度进行简单的线性变换即可求出原始频点的模糊度值。具体实施步骤如下。
2.1 超宽巷模糊度解算在中长基线下,为了更好地消除电离层延迟,一般会采用消电离层PC组合(M-W方法)求超宽巷模糊度[18, 19]。对于本文选用的两组超宽巷组合,可以找到相应的PC消电离层组合,如表 2所示。其中,相位组合(0,-1,1)和码组合(0,1,1)形成消电离层PC组合,相位组合(1,2,-3)和P1(即1,0,0)形成近似消电离层PC组合。
| 组合 | B1 | B2 | B3 | β(i,j,k) | μ(i,j,k) |
| 相位组合(i,j,k) | 0 | -1 | 1 | -1.5915 | 28.5287 |
| 1 | 2 | -3 | -0.9698 | 28.0859 | |
| 码组合(l,m,n) | 0 | 1 | 1 | 1.5915 | 0.7073 |
| 1 | 0 | 0 | 1 | 1 |
以周为单位的超宽巷模糊度计算公式为
对于北斗系统,伪距测量精度取σP=0.33 m,载波相位测量精度取${\sigma _\phi }$=0.003 m[11]。可估算利用伪距组合ΔΔP(0,1,1)求超宽巷组合测量值$\Delta \nabla \phi $(0,-1,1)对应的超宽巷模糊度对应的误差为
估算第2个超宽巷组合(1,2,-3)的模糊度解算误差为
设ΔΔI=0.1 m,${\sigma _N}_{_{(1,2, - 3)}} = 0.2728$周。对于超宽巷(0,-1,1)来说,一个历元就正确地解算出模糊度。对于(1,2,-3),则需要少数几个历元的平滑即可正确解算出模糊度。
2.2 GEO卫星宽巷模糊度解算GEO卫星对应的宽巷组合(-3,0,2,1)和(-2,-2,-1,1),其模糊度的求解采用GF和IF组合模型。先求宽巷组合(-3,0,2,1)的模糊度
式中,$\Delta \nabla {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}\to {\phi } }_{(0, - 1,1)}}$和$\Delta \nabla {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}\to {\phi } }_{(1,2, - 3)}}$表示将已固定的模糊度算入之后的无模糊度的组合载波相位测量值,其中,a1、a2满足解出a1=-2.1980,a2=3.1980,σΔΔN(-3,0,2,1)=0.542周。
对于组合(-2,2,-1,1),用同样的方法解出
式中,a1、a2满足 a1=-1.4721,a2=2.4721,σΔΔN(-3,0,2,1)=0.5957周。这一步,通过30个历元左右的平滑即可正确解算出这两个宽巷测量值的模糊度。 2.3 窄巷模糊度解算 2.3.1 GEO卫星窄巷模糊度解算经过平滑解算出(-3,0,2,1)和(-2,2,-1,1)模糊度后,再求解窄巷组合(4,-5,2)的模糊度。
解出a1=0.1258,a2=0.8742,σΔΔN(4,-3,0)=0.2829周。将式(8)的解算结果,通过20个历元左右的平滑即可正确解算GEO卫星的窄巷模糊度。
2.3.2 GEO辅助非GEO窄巷模糊度求解利用RNSS和RDSS频率组合的几何无关方法可以快速地求解出GEO卫星的窄巷模糊度,但是对于非GEO卫星来说,由于没有S频段测量值,无法利用上述快速求解算法。为了利用已解算模糊度的GEO卫星来辅助非GEO卫星窄巷模糊度解算,本文采用几何有关模型。设n为观测卫星总数目,m为观测到的GEO卫星的数目。传统的模糊度解算方程可以表示为
对所有可见卫星列出如式(10)所示的方程联合求解即可解算出所有卫星的窄巷模糊度。若先解算出GEO卫星的窄巷模糊度,那么,将GEO卫星和非GEO卫星观测方程分开表示,式(10)可改写为
式中,$\Delta \nabla {\phi ^n}_{(4, - 5,2)}$和$\Delta \nabla {P^n}_{(4, - 5,2)}$表示非GEO窄巷双差载波相位和双差伪距;$\Delta \nabla {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}\to {\phi } }^g}_{(4, - 5,2)}$和$\Delta \nabla {P^g}_{(4, - 5,2)}$表示GEO卫星的无模糊度的窄巷双差载波相位和双差伪距。再用经典的LAMBDA算法[20]即可求解出非GEO卫星的窄巷模糊度值。显然,对于传统算法,其未知数个数为(n+2)(包括3个位置参数δX和n-1个模糊度参数ΔΔN(4,-5,2))。在窄巷模糊度浮点解求出来之后,需要用LAMBDA算法搜索求解的窄巷模糊度个数为n-1个。对于本文提出的新方法,选择一颗GEO卫星作为参考星,其未知数个数为3+(n-m)(包括3个位置参数δX和n-m个非GEO卫星的模糊度参数ΔΔNn(4,-5,2))。在窄巷模糊度实数解求解出来后,需要用LAMBDA算法搜索求解的窄巷模糊度个数为n-m个。
相对于传统方法,本文方法使得解算方程的未知数个数减少,模糊度搜索的个数减少,这样做的好处是可以提高模糊度解算的效率和成功率。
2.4 原始频点的模糊度解算在解算出两个超宽巷模糊度和一个窄巷模糊度后,由于3个组合是线性无关的,可以通过简单的线性变换求解出原始频点的模糊度
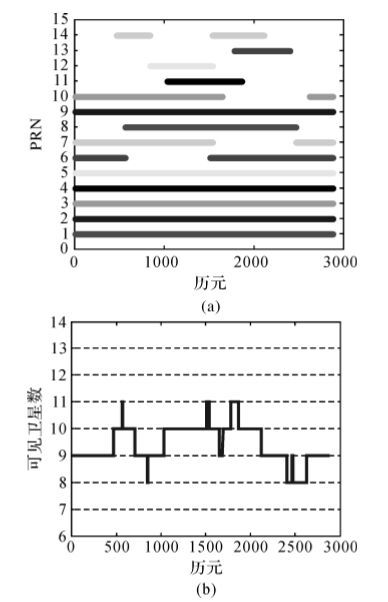
3 算法仿真验证本文提出的RNSS与RDSS组合模糊度解算方法为前沿探索研究,由于缺少实际RDSS测量值,本文利用北斗的实际星历,仿真了不同频率的观测数据,在不同基线下对提出的模糊度解算方法进行静态模糊度解算的仿真验证。由于市场上现在还没有用于接收北斗RDSS载波相位的接收机,故本文在仿真时保守地将RDSS载波相位的测量精度设为与RNSS等同的精度。仿真采用的测站位置和基准站位置如表 3所示。星历数据为2013-11-22 11:08:00至2013-11-23 11:08:00的北斗实际星历数据,设${\sigma _\phi }$=0.003 m,σP=0.33 m,仿真时采用欧洲定轨中心(CODE)提供的高精度电离层格网数据对电离层延迟进行仿真。仿真观测时间段内卫星可见性情况如图 3所示,5颗GEO卫星全部可见,可见卫星总数为8~12颗。
| 观测站 | 站址(经度/(°),纬度/(°),高度/m) | 基线长度/km |
| station 0(reference) | (40.07,116.27,85.01) | — |
| station 1 | (40,116,85) | 24 |
| station 2 | (39.65,116,85) | 52 |
| station 3 | (39.5,115.7,85) | 80 |
| station 4 | (39.4,115.48,85) | 100 |
|
| 图 3 卫星可见情况 Fig. 3 Visible satellites |
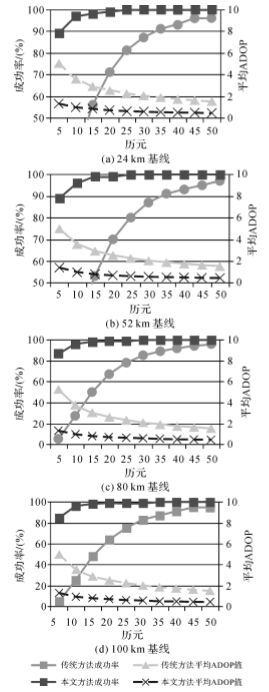
利用本文提出的方法在表 3所示的4组基线长度下解算模糊度,表 3中,Station 0为参考站,Station 1—Station 4为不同的用户观测站位置。在4组不同的基线长度下先求解GEO卫星的模糊度,由于本文提出几何无关GEO模糊度方法对电离层不敏感,在这几组基线长度下,都能利用30个左右历元通过平滑解算出GEO卫星的超宽巷、宽巷和窄巷模糊度。然后,再利用几何有关的方法解算非GEO卫星的模糊度。图 4所示是常规的模糊度解算与GEO辅助非GEO模糊度解算成功率及平均ADOP值对比,其中classical表示用常规的LAMBDA算法解算所有卫星的模糊度,improved表示本文提出的采用已解算的GEO卫星模糊度与非GEO卫星一起求解非GEO卫星模糊度。从图 4可以看出,对于常规方法,由于解算模糊度个数多,ADOP值比较大,并且随着基线长度的增加,模糊度解算效率及成功率都有大幅下降,即使利用40~50个历元也很难得到理想的成功率。对于本文提出的方法,由于几何有关方法解算模糊度个数变少,新方法的平均ADOP值远小于传统方法,并且可以在20~30个历元内得到接近于100%的成功率。显然,新方法能够从整体上提高中长基线下模糊度解算的效率和成功率。
|
| 图 4 不同基线长度下(24~100 km)的模糊度解算成功率及平均ADOP值对比 Fig. 4 The AR success rate and mean ADOP value for different distance baseline (24~100 km) |
本文根据北斗的特殊星座特性和频率特性,提出了一种适用于北斗系统的快速模糊度解算方法,利用RNSS与RDSS测量值组合形成性能优良的虚拟组合观测值,先采用几何无关方法解算GEO卫星的窄巷模糊度,再利用其辅助非GEO卫星的窄巷模糊度解算,以解决模糊度解算受电离层影响大,导致模糊度解算时间长、效率低的问题。由于目前市场上还没有可同时接收RNSS和RDSS载波相位观测量的接收机,无法给出实际观测数据的解算结果,故本文利用北斗实际星历仿真了4组观测数据(24~100 km)对新方法进行了仿真验证,结果表明,新方法能够从整体上提高模糊度解算的效率和成功率。
| [1] | 李博峰,沈云中,周泽波. 中长基线三频GNSS模糊度的快速算法[J]. 测绘学报, 2009, 38(4): 296-301. LI Bofeng, SHEN Yunzhong, ZHOU Zebo. A New Method for Medium and Long Range Three Frequency GNSS Rapid Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 296-301. |
| [2] | FORSSELL B, MARTIN-NEIRA M, HARRIS R A. Carrier Phase Ambiguity Resolution in GNSS-2[C]//Proceedings of the 10th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS). Kansas, MO: ION Publications, 1997: 1727-1736. |
| [3] | VOLLATH U,BIRNBACH S,LANDAU H,et al. Analysis of Three-carrier Ambiguity Resolution (TCAR) Technique for Precise Relative Positioning in GNSS-2[C]//Proceedings of the 11th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS). Nashville, TN: ION Publications, 1998: 417-426. |
| [4] | HATCH R, JUNG J, ENGE P, et al. Civilian GPS: The Benefits of Three Frequencies[J]. GPS Solutions, 2000, 3(4): 1-9. |
| [5] | 伍岳. 第二代导航卫星系统多频数据处理理论及应用[D]. 武汉: 武汉大学, 2005. WU Yue. The Theory and Application on Multi-frequency Data Processing of GNSS 2[D]. Wuhan: Wuhan University,2005. |
| [6] | FENG Yanming. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-reduced Virtual Signals[J]. Journal of Geodesy, 2008, 82(12): 847-862. |
| [7] | LI Bofeng, FENG Yanming, SHEN Yunzhong. Three Carrier Ambiguity Resolution: Distance-independent Performance Demonstrated Using Semi-generated Triple Frequency GPS Signals[J]. GPS Solutions, 2010, 14(2): 177-184. |
| [8] | DAI Zhiqiang, ZHAO Qile, HU Zhigang, et al. COMPASS Three Carrier Ambiguity Resolution[C]//SUN Jiandong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2013 Proceedings. Berlin: Springer-Verlag, 2013: 441-448. |
| [9] | 邓健, 潘树国, 王胜利. 基于最优组合的长基线网络RTK三频载波模糊度快速解算[J]. 中国惯性技术学报, 2012, 20(5): 587-592. DENG Jian, PAN Shuguo, WANG Shengli. Fast Resolution for Three-frequency Carrier Ambiguity of Long-range Network RTK Based on Optimal Combination[J]. Journal of Chinese Inertial Technology, 2012, 20(5): 587-592. |
| [10] | 杨元喜, 李金龙, 王爱兵, 等. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学: 地球科学, 2014, 44(1): 72-81. YANG Yuanxi, LI Jinlong, WANG Aibing, et al. Preliminary Assessment of the Navigation and Positioning Performance of BeiDou Regional Navigation Satellite System[J]. Science China: Earth Sciences, 2014, 57(1): 144-152. |
| [11] | 谭述森. 卫星导航定位工程[M]. 北京: 国防工业出版社, 2007: 12-20. TAN Shusen. The Engineering of Satellite Navigation and Positioning[M]. Beijing: National Defence Industry Press, 2007: 12-20. |
| [12] | 谭述森. 广义卫星无线电定位报告原理及其应用价值[J]. 测绘学报, 2009, 38(1): 1-5. TAN Shusen. Theory and Application of Comprehensive RDSS Position and Report[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 1-5. |
| [13] | DOU Changjiang, ZHANG Binqi, TAN Shusen, et al. A New Three-satellite High-precision RDSS/RNSS Combination Positioning Method[C]//Proceedings of the 2nd International Workshop on Education Technology and Computer Science. Wuhan: IEEE, 2010, 2: 288-290. |
| [14] | SHI Chuang, ZHAO Qile, HU Zhigang, et al. Precise Relative Positioning Using Real Tracking Data from COMPASS GEO and IGSO Satellites[J]. GPS Solutions, 2013, 17(1): 103-119. |
| [15] | QU J, YUAN H, ZHANG X, et al. Single-epoch COMPASS Carrier-phase Ambiguous Resolution Using Three Civil Frequencies and Special Constellations[C]//Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS). Nashville, TN: ION Publications, 2012: 310-316. |
| [16] | FENG Yanming. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-reduced Virtual Signals[J]. Journal of Geodesy, 2008, 82(12): 847-862. |
| [17] | 李金龙, 杨元喜, 何海波, 等. 函数极值法求解三频GNSS最优载波相位组合观测量[J]. 测绘学报, 2012, 41(6): 797-803. LI Jinlong, YANG Yuanxi, HE Haibo, et al. Optimal Carrier-phase Combinations for Triple-frequency GNSS Derived from an Analytical Method[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 797-803. |
| [18] | WVBBENA G. The GPS Adjustment Software Package-GEONAP-concepts and Models[C]//Proceedings of the Fifth International Symposium on Satellite Positioning. Las Cruces, New Mexico: [s.n.], 1989: 452-461. |
| [19] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. Initial Assessment of the COMPASS/BeiDou-2 Regional Navigation Satellite System[J]. GPS Solutions, 2013, 17(2): 211-222. |
| [20] | TEUNISSEN P J G. The Least-squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82. |