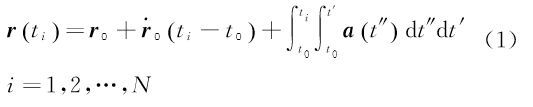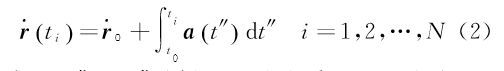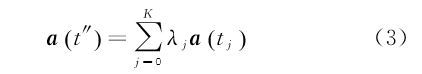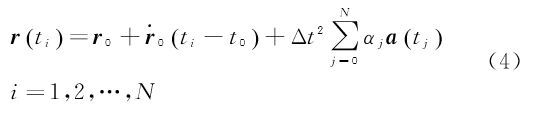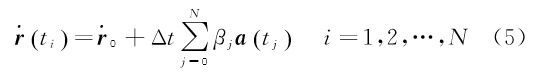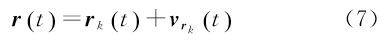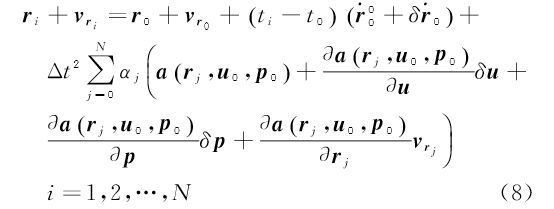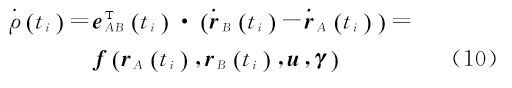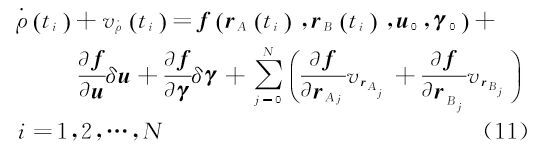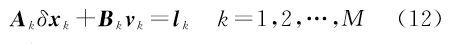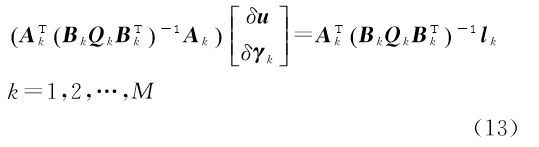2. 香港理工大学土地测量及地理资讯学系, 香港;
3. 同济大学空间信息与可持续发展应用中心, 上海 200092;
4. 广东工业大学测绘工程系, 广东广州 510006;
5. 大地测量与地球动力学国家重点实验室, 湖北武汉 430077
2. Department of Land Surveying and Geo-Informatics, Hong Kong Polytechnic University, Hong Kong, China;
3. Center for Spatial Information Science and Sustainable Development, Shanghai 200092, China;
4. Departments of Surveying and Mapping, Guangdong University of Technology, Guangzhou 510006, China;
5. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, Wuhan 430077, ChinaAbstract
地球重力场的分布源于地球质量、密度分布以及质量的重新分布(包括地球内部运动、大气运动、水循环、潮汐)。地球内部物质的质量分布可划分为稳态分布与非稳态分布,稳态分布决定了静态地球重力场,非稳态的质量重分布决定了时变地球重力场的特性。CHAMP(Challenging Mini-satellite Payload)[1]、GRACE(Gravity Recovery and Climate Experiment)[2]和GOCE(Gravity Field and Steady State Ocean Circulation Explorer)[3]是当今卫星重力探测的3类典型重力卫星。其中,CHAMP主要探测低阶地球重力场[1];GRACE的最大贡献在于探测非稳态地球重力场并用于全球气候时变监测[4];GOCE的主要目标是探测高阶静态地球重力场信号[5],尤其是100阶后的重力场信息。对于探测前100阶的重力场信号,GRACE卫星的优势仍然明显大于GOCE卫星。尽管GARCE卫星的预期寿命为5a,但该卫星自2002年3月发射后,至今仍在运行,已经提供了约12a的观测数据,因此可利用GRACE卫星的长时间数据序列反演高精度的静态地球重力场。目前国际上有多个研究机构利用GRACE卫星长时间观测序列反演静态地球重力场模型。其中,用纯GRACE数据解算的最新无约束重力场模型包括GGM05S[6]、AIUB-GRACE03S[7]、ITSG-Grace2014s[8]以及Tongji-GRACE01[9],约束重力场模型仅仅只有ITSG-Grace2014k[8]。我国很多学者对应用卫星重力数据反演静态地球重力场作出了卓有成效的工作与贡献,取得了许多研究成果[9, 10, 11, 12, 13, 14, 15, 16, 17, 18]。如文献[18]利用经典动力学法恢复了100阶次的GRACE静态重力场模型。
动力学法是卫星重力反演的常用方法[19],其核心思想是根据卫星初始状态参数、先验重力场模型以及其他力模型确定的参考轨道为初值,对卫星重力反演的非线性观测方程进行线性化。动力学法的线性化观测方程的设计矩阵需通过变分方程数值积分,且需多次迭代解算。文献[20]提出以卫星轨道观测值为初值的线性化方法,然而涉及四重积分计算,模型比较复杂。文献[21]采用类似的思想改进加速度法,并利用GRACE卫星轨道数据反演重力场。本文将该线性化方法用于改进动力学法,并利用2003年1月至2010年12月共8a的GRACE卫星轨道、星间距离变率、姿态和非保守力加速度数据,解算一个180阶次的T ongji-Dyn01s 全球静态重力场模型。为改善高阶位系数精度,进一步使用 Kaula 规则约束位系数,解算了一个180阶次的静态重力场模型Tongji-Dyn01k。利用现有的高精度重力场模型,GPS 水准和 DTU13 海洋重力异常数据对Tongji-Dyn01s和Tongji-Dyn01k 静态重力场模型的精度进行了检核,结果表明Tongji-Dyn01s 模型与国际最新的纯 GRACE 重力场模型精度相当,而且Tongji-Dyn01k 模型总体上优于国际最新的纯 GRACE 重力场模型。
1 理论方法对于由N+1个离散点所构成的卫星轨道弧段,根据动力学法,第i个历元时刻ti的位置r(ti)与速度$\mathop r\limits^ \cdot $(ti)方程可描述为
式中,a(t″)为t″时刻卫星单位质量所受合力,可由相邻历元加速度的K阶多项式内插而得 式中,λj为多项式系数。将式(3)代入式(1)和式(2),可将式(1)和式(2)离散化为 式中,${\left( {r_0^{\rm T},\dot r_0^{\rm T}} \right)^{\rm T}}$为卫星初始位置与速度向量;Δt为轨道采样率(5 s);αj和βj为离散化系数;N为弧段观测历元最大下标。a(tj)可表示为保守力ag和非保守力af的关系式[22, 23] 式中,保守力ag是卫星轨道位置r(ti)和重力位系数u的函数;非保守力与卫星姿态qi和星固系下非保守力加速度观测值facc有关;C为星固系到惯性系间的转换矩阵。由于加速度计观测值为有偏观测量,一般需要估计加速度计尺度S和偏差p。由于尺度参数与重力场位系数存在较强相关性,因此本文与GFZ一样,只估计偏差参数p。将式(4)—式(6)中的卫星轨道以几何轨道rk与为初值展开 式中,vrk为几何轨道的改正向量。将式(7)代入式(4)—式(6),并以重力场位系数、初始速度参数和加速度计偏差等参数的先验值u0、r00T和p0为概率值对卫星位置和速度方程式(4)和式(5)线性化,可得若分别记$\gamma = \left[ {r_o^{\rm T}} \right.{\left. {{p^{\rm T}}} \right]^{\rm T}}$,则星间距离变率观测模型可建立为
式中,$\mathop \rho \limits^ \cdot \left( {{t_i}} \right)$为星间距离变率观测值;eAB(ti)为GRACE卫星A至GRACE卫星B的视线向量。顾及GRACE卫星A和B的位置与速度的线性化方程,可将距离变率观测模型式(10)线性化为 式中,${\upsilon _\rho }({t_i})$为星间距离变率观测值改正数。假设有M个弧段,对于第k个弧段,为联合卫星轨道与星间距离变率数据求解重力场,该弧段所有历元的卫星轨道和星间距离变率的观测方程可用矩阵形式表示为
式中,待估参数${x_k} = \left[ {{u^T}} \right.{\left. {\gamma _k^T} \right]^T}$为全局重力场参数u与局部参数γk(包括初始速度参数与加速度偏差参数);Ak为观测方程式(8)和式(11)中关于位系数与弧段局部参数的偏导数矩阵;Bk观测方程式(8)和式(11)中关于轨道与星间距离变率观测值的偏导数矩阵;lk为卫星轨道和星间距离观测向量与参考向量之差。基于最小二乘准则可得到每个弧段关于待估参数的法方程为 式中,Qk为轨道和星间距离变率观测值方差-协方差阵,可根据轨道和星间距离变率观测值先验精度确定(轨道精度约为2 cm;星间距离变率精度约为0.2μm/s)[23]。消去局部参数γk后得到只与位系数有关的法方程,进一步累加各个弧段与位系数有关的法方程并求得重力场参数,具体解算方法可参考文献 [21, 22, 23]。当解算的重力位模型达到180阶次时,其法方程严重病态。为改善法方程的病态性,本文采用Kaula约束的正则化方法进行位系数解算,相关算法参见文献[24]。 2 静态地球重力场模型反演本文采用2003年1月至2010年12月共8a的GRACE卫星A和B的观测数据反演了180阶次的Tongji-Dyn01s静态地球重力场。所用的数据包括由JPL提供的K波段星间距离变率、卫星姿态、非保守力加速度数据以及武汉大学GNSS研究中心提供的约化动力学轨道[25]。几何轨道直接由GNSS观测值确定,不受先验重力场制约,更适合于重力场反演;而约化动力学轨道无疑会受先验重力场模型影响,但若与距离变率数据一起组合求解,先验重力场的影响就大为减少[22],因此本文反演重力场时以约化动力学轨道作为观测值,且在线性化时也以约化动力学轨道为初值。原始观测数据需进行预处理,比如卫星姿态和非保守力加速度数据存在数据间断,尤其是卫星姿态的间断十分频繁,需进行内插处理;距离变率数据为GRACE卫星最重要的观测量,对中长波重力信号十分敏感,然而其存在数据间断和粗差,本文直接忽略掉间断的距离变率数据;约化动力学轨道十分平滑,不存在数据间断和粗差,可用于剔除星间距离变率数据粗差。此外,还需顾及日月等行星三体扰动、海潮、海洋极潮、固体潮、固体极潮、大气与海洋的非潮汐变化和相对论效应等保守力以及非保守力摄动,具体参见文献[23]。
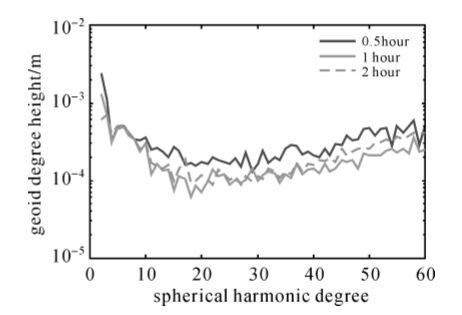
GFZ利用经典动力学法反演高精度的EIGEN6C2模型时并未估计非保守力加速度尺度参数。因此,本文中非保守力尺度并未作为待估参数,其采用Bettadpur推荐值[26]。与GFZ相同[27],本文每小时估计一组非保守力加速度偏差。由于在形成每个弧段法方程时均需计算逆矩阵(BkQkB/Tk)-1,该矩阵规模与弧段长度有关,矩阵规模太大将不利于求逆的稳定性。为了选择较为合适的弧段长度,本文利用2008年1月的GRACE数据,分别以0.5h、1h和2h弧长反演得3组60阶次的重力场解,每个弧段估计一组初始速度参数。图 1为3组重力场解相对于EIGEN6C2[28]的大地水准面误差,结果表明1h的弧长比较适合本文改进的动力学法。因此在解算Tongji-Dyn01s静态地球重力场模型时,本文积分弧长取为1h,每个弧段估计一组加速度偏差参数。
|
| 图 1 不同弧长所得重力场解相对于EIGEN6C2大地水准面阶误差 Fig. 1 Geoid degree errors of solutions computed by using different arc lengths with respect to EIGEN6C2 |
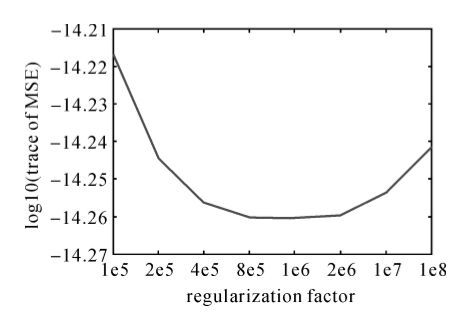
本文以卫星轨道观测值为初值对卫星运动方程进行线性化,其优点在于重力场解算结果不依赖于初始重力场模型,且不需要迭代计算,不同的初始重力场模型仅仅是改变观测方程的常数项向量[21]。然而,以卫星轨道观测值为初值对卫星运动方程进行线性化,其缺点在于每个积分弧段均需计算逆矩阵(BkQkBTk)-1,弧段较长时该求逆运算的工作量比较大。Tongji-Dyn01s模型的法方程条件数达到1.9×1013,显然该法方程严重病态,必定会影响高阶重力位系数的解算精度。因此本文对重力位系数用Kaula规则约束,并采用正则化算法解算了全球静态地球重力场模型Tongji-Dyn01k。正则化因子是以MSE迹最小为准则来确定[10],图 2表明,正则化参数取1.0×106时,MSE迹最小。
|
| 图 2 不同正则化因子所对应的MSE的迹(取对数) Fig. 2 Trace of MSE (log10 scale) from different regularized factors |
为了检核Tongji-Dyn01s和Tongji-Dyn01k模型的精度水平,本文将Tongji-Dyn01s、Tongji-Dyn01k与最新发布的GGM05S、AIUB-GRACE03S、ITSG-Grace2014k、Tongji-GRACE01等纯GRACE重力场模型进行比较分析。其中,GGM05S为美国德克萨斯大学空间中心(CSR)利用经典动力学法基于10a的GRACE数据所解算的180阶次无约束模型;AIUB-GRACE03S为瑞士伯尼尔大学基于天体力学方法(其本质是动力学法,区别在于采用了不同的参数化方法,如采用开普勒轨道根数并引入经验加速度参数)利用6a的GRACE数据所解算的160阶次无约束模型;ITSG-Grace2014k为德国波恩大学基于经典短弧长积分法利用约10.5a的GRACE数据所解算的200阶次正则化约束模型;Tongji-GRACE01为同济大学利用改进的短弧长积分法基于4a GRACE数据所解算的160阶次无约束模型。GFZ推出的EIGEN6C2模型采用多种观测数据求得,包括GRACE、GOCE、Lageos(Laser Geodynamics Satellite)[29]、海洋测高、地面重力以及航空重力数据,具有非常高的精度,本文将其作为基准模型评价不同GRACE重力场模型内符合精度。
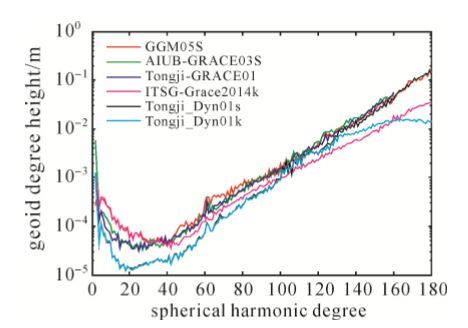
各模型相对于EIGEN6C2的大地水准面阶误差如图 3所示。由图 3可见,Tongji-Dyn01s和Tongji-Dyn01k在前100阶次比当前其他所有的GRACE重力场模型更加靠近EIGEN6C2。尤其是在前60阶,Tongji-Dyn01s和Tongji-Dyn01k的大地水准面误差比GGM05S、AIUB-GRACE03S、ITSG-Grace2014k和Tongji-GRACE01等模型约小一个量级。Tongji-Dyn01s在100阶次后与GGM05S、AIUB-GRACE03S和Tongji-GRACE01等模型非常接近。Tongji-Dyn01k在101到160阶次间大地水准面误差稍大于ITSG-Grace2014k。然而在161到180阶次之间,Tongji-Dyn01k大地水准面误差小于ITSG-Grace2014k。
|
| 图 3 不同模型相对于EIGEN6C2大地水准面阶误差 Fig. 3 The geoid degree errors of different models with respect to EIGEN6C2 |
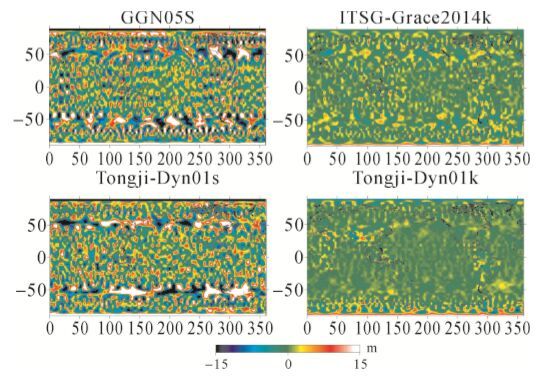
为了进一步比较Tongji-Dyn01s和Tongji-Dyn01k模型与其他GRACE重力场模型间的内符合精度,本文利用这些模型截断到不同阶次计算全球重力异常信号。图 4给出了不同模型扣除EIGEN6C2系数后截断至180阶次的重力异常信号。由于EIGEN6C2使用了GOCE梯度数据,高阶次系数精度优于纯GRACE模型,因此图 4反映不同纯GRACE模型高阶位系数的误差。图 4表明,无约束解GGM05S和Tongji-Dyn01s模型高阶位系数误差均大于正则化解ITSG-GRACE2014k和Tongji-Dyn01k,且高纬度地区的误差明显大于低纬度地区;其主要原因是卫星重力反演模型是病态的,且GRACE轨道在两极存在1°左右空白,导致高阶次位系数和高纬度区域的误差偏大;正则化解能够抑制高阶次位系数的误差,因此正则化解的结果要明显优于无约束解。Tongji-Dyn01k的误差小于所有模型,其180阶次位系数与EIGEN6C2重力异常差值标准差仅为3.6 mGal(1Gal=10-2m/s2)。为了分析Tongji-Dyn01s和Tongji-Dyn01k的外部精度,笔者利用丹麦技术大学发布的DTU13产品(分辨率为2′×2′,精度约为2 mGal)[30, 31]中太平洋中部64980个海洋重力异常数据,对上述不同模型在太平洋中部海洋重力异常进行检核。具体区域为([17°S,23°S],[314°E,326°E])[32],面积约为83.8万km2。各模型分别截断至120、150和180阶次,并由EIGEN6C2填补高阶次系数(完全至1949阶),依次计算太平洋中部重力异常。表 1给出了不同模型截断至不同阶次的重力异常差值统计结果。可以看出,无论是截断到120还是150阶次,不同模型所计算的重力异常与DTU13海洋重力异常差值的标准差均十分接近,可以说这些模型在前150阶次的精度水平相当。对于截断到180阶次的结果,GGM05S精度最差,其次是Tongji-Dyn01s,Tongji-Dyn01k表现最好,其截断到180阶所计算的太平洋中部海洋重力异常与DTU13重力异常之差标准差仅为4.1 mGal,与截断到120和150阶次所计算的标准差差别不大,然而其他模型截断到180阶次与截断到120或150相比,其标准差均发生突变,有力地说明了Tongji-Dyn01k模型180阶次位系数的可靠程度。可以说,截断至180阶次计算重力异常差值能够有效区分GRACE高阶重力位系数的可靠程度。
|
| 图 4 不同纯GRACE模型相对于EIGEN6C2的全球重力异常(截断至180阶次) Fig. 4 The difference of global gravity anomalies between GRACE-only models and EIGEN6C2 (truncated to degree and order 180) |
| 模型 | 阶 | 统计结果 | |||
| 最小值 | 最大值 | 平均值 | 标准差 | ||
| AIUB-GRACE03S | 120 | -26.8 | 19.1 | 0.06 | 3.7 |
| 150 | -23.0 | 21.0 | -0.02 | 4.2 | |
| Tongji-GARCE01 | 120 | -26.7 | 19.4 | 0.03 | 3.7 |
| 150 | -28.6 | 19.9 | 0.02 | 4.0 | |
| GGM05S | 120 | -26.8 | 19.0 | 0.08 | 3.7 |
| 150 | 24.3 | 21.6 | -0.10 | 4.3 | |
| 180 | -73.3 | 78.2 | -0.42 | 25.8 | |
| ITSG-Grace2014k | 120 | -27.0 | 19.0 | 0.04 | 3.7 |
| 150 | -27.3 | 19.6 | -0.02 | 3.7 | |
| 180 | -29.8 | 25.4 | -0.04 | 4.9 | |
| Tongji-Dyn01s | 120 | -27.4 | 19.3 | 0.03 | 3.7 |
| 150 | -29.4 | 22.3 | -0.07 | 3.9 | |
| 180 | -49.9 | 47.7 | -0.31 | 15.4 | |
| Tongji-Dyn01k | 120 | -27.4 | 19.1 | 0.04 | 3.7 |
| 150 | -27.2 | 20.3 | -0.03 | 3.7 | |
| 180 | -31.0 | 21.8 | -0.02 | 4.1 | |
为了进一步客观评价Tongji-Dyn01s与Tongji- Dyn01k模型的精度水平,本文采用美国、墨西哥和江西3个地区的GPS/水准网观测数据进行外部检核。其中美国和墨西哥数据可从网站(http://www.ngs.noaa.gov/GEOID/GEOID12)下载,其水准点数据本文分别选取8006个和536个,江西选取117个。各模型分别截断至90、120、150和180阶,并采用EIGEN6C2填补高阶位系数(完全至1949阶),依次计算美国、墨西哥和江西等地区的大地水准面高程异常。统计计算值与实测值的最大值、最小值与标准差,结果如表 2所示。表 2中,对于截断至相同阶次(90和120),从所计算的模型高程异常与实测结果之差的标准差来看,所有模型在美国、墨西哥和江西的表现相当。对于截断到150阶次,Tongji-Dyn01s的表现仅仅略逊于ITSG-Grace2014k,然而Tongji-Dyn01k优于其他模型。尤其对于截断到180阶次,无论是利用美国、墨西哥还是江西的数据进行外部检核,Tongji-Dyn01k模型精度均远优于其他GRACE重力场模型。
| 模型 | 阶 | 美国 | 墨西哥 | 江西 | ||||||||
| 最小值 | 最大值 | 标准差 | 最小值 | 最大值 | 标准差 | 最小值 | 最大值 | 标准差 | ||||
| AIUB-GRACE03S | 90 | -33.1 | 54.2 | 21.8 | -109.5 | 55.6 | 31.1 | -27.8 | 23.7 | 10.0 | ||
| 120 | -34.0 | 55.3 | 22.0 | -108.8 | 54.9 | 31.1 | -28.3 | 22.3 | 9.6 | |||
| 150 | -56.5 | 77.3 | 23.3 | -117.3 | 58.8 | 31.6 | -35.3 | 26.2 | 12.9 | |||
| Tongji-GARCE01 | 90 | -33.4 | 53.6 | 21.6 | -109.7 | 55.4 | 31.1 | -27.9 | 23.8 | 10.0 | ||
| 120 | -31.9 | 52.6 | 21.7 | -110.4 | 56.7 | 31.1 | -28.3 | 23.6 | 10.0 | |||
| 150 | -40.0 | 66.7 | 24.0 | -109.8 | 66.3 | 31.3 | -32.4 | 23.2 | 9.8 | |||
| GGM05S | 90 | -33.1 | 54.6 | 21.9 | -110.0 | 55.5 | 31.1 | -27.6 | 23.9 | 10.0 | ||
| 120 | -32.8 | 54.9 | 22.1 | -109.8 | 56.6 | 30.9 | -28.4 | 24.1 | 10.0 | |||
| 150 | -47.6 | -66.7 | 23.4 | -114.7 | 58.8 | 31.2 | -38.6 | 23.6 | 12.2 | |||
| 180 | -185.9 | 224.1 | 73.3 | -180.0 | 141.2 | 58.3 | -92.3 | 103.4 | 50.3 | |||
| ITSG-Grace-2014k | 90 | -33.0 | 54.0 | 21.7 | -109.5 | 55.4 | 31.1 | -27.6 | 24.0 | 10.0 | ||
| 120 | -32.6 | 53.1 | 21.8 | -110.6 | 56.4 | 31.0 | -27.7 | 24.6 | 10.0 | |||
| 150 | -35.0 | 55.6 | 23.1 | -105.2 | 60.8 | 31.0 | -27.5 | 26.2 | 10.4 | |||
| 180 | -70.5 | 67.6 | 26.5 | -120.0 | 64.2 | 33.1 | -39.0 | 24.9 | 12.3 | |||
| Tongji-Dyn01s | 90 | 33.2 | 53.7 | 21.7 | -109.4 | 55.6 | 31.1 | -27.8 | 23.8 | 10.0 | ||
| 120 | -34.7 | 53.3 | 21.9 | -109.5 | 58.9 | 31.0 | -27.1 | 24.4 | 10.1 | |||
| 150 | -52.9 | 69.1 | 25.2 | -108.8 | 64.8 | 31.6 | -29.3 | 24.7 | 10.5 | |||
| 180 | -165.5 | 175.5 | 63.4 | -163.1 | 128.7 | 47.0 | -45.9 | 46.1 | 19.1 | |||
| Tongji-Dyn01k | 90 | -33.1 | 53.7 | 21.6 | -109.4 | 55.6 | 31.1 | -27.7 | 24.0 | 9.9 | ||
| 120 | -34.1 | 53.6 | 21.8 | -110.4 | 58.2 | 31.0 | -27.3 | 24.4 | 10.0 | |||
| 150 | -39.8 | 55.8 | 22.6 | -108.3 | 58.9 | 31.1 | -27.6 | 23.9 | 9.6 | |||
| 180 | -39.9 | 58.1 | 23.5 | -104.7 | 61.9 | 31.6 | -35.3 | 28.0 | 12.2 | |||
本文以卫星轨道观测值为初值对经典动力学法卫星重力反演的非线性观测方程进行线性化,建立了卫星轨道和星间距离变率反演地球重力场的线性化观测模型。与传统动力学法相比,本文所建立的动力学法不需要解算变分方程与迭代计算,且不依赖于先验重力场模型。利用2003年1月至2010年12月GRACE卫星的姿态、轨道、星间距离变率和非保守力加速度等观测数据,解算了一个180阶次的Tongji-Dyn01s全球静态重力场模型;进一步对重力位系数进行了Kaula规则约束,通过正则化解法求得了Tongji-Dyn01k模型。利用多种方法与数据对Tongji-Dyn01s和Tongji-Dyn01k模型和国际不同机构最新的纯GRACE重力场模型AIUB-GRACE03S、ITSG-Grace2014k、GGM05S和Tongji-GARCE01的精度进行了分析。
从模型的大地水准面误差看,Tongji-Dyn01s和Tongji-Dyn01k前100阶位系数比国际不同机构的最新GRACE重力场模型更加靠近EIGEN6C2。从全球重力异常看,Tongji-Dyn01s仅次于ITSG-Grace2014k,而Tongji-Dyn01k相比于其他GRACE无约束模型更加靠近EIGEN6C2。DTU13太平洋中部海洋重力异常以及美国、墨西哥和江西区域GPS/水准点的检核结果,证实了Tongji-Dyn01s和Tongji-Dyn01k模型在前150阶次与国际不同机构最新的GRACE重力场模型精度处于同一水平,然而Tongji-Dyn01k在180阶次的位系数精度优于当前所有GRACE数据反演的重力场模型,其所计算的太平洋海洋中部重力异常与DTU13数据之差标准差仅为4.1 mGal。总体来说,本文所建立的轨道与星间距离变率理论模型能够有效地提取重力场信号,Kaula规则约束的正则化解法能够显著改善高阶位系数解算精度。
致谢:感谢美国JPL和德国GFZ所提供的GRACE Level-1b观测数据以及武汉大学GNSS研究中心赵齐乐教授所提供的约化动力学轨道数据。
| [1] | REIGBER C, BALMINO G, SCHWINTZER P, et al. A High-quality Global Gravity Field Model from CHAMP GPS Tracking Data and Accelerometry (EIGEN-1S)[J]. Geophysical Research Letters, 2002, 29(14): 1-4. |
| [2] | TAPLEY B D, BETTADPUR S, WATKINS M, et al. The Gravity Recovery and Climate Experiment: Mission Overview and Early Results[J]. Geophysical Research Letters, 2004, 31(9): 278-282. |
| [3] | DRINKWATER M R, FLOBERGHAGEN R, HAAGMANS R, et al. GOCE: ESA’s First Earth Explorer Core Mission [C]//BEUTLER G, DRINKWATER M R, RUMMEL R, et al. Proceedings of the Earth Gravity Field from Space — From Sensors to Earth Sciences. The Netherlands: Springer, 2006, 6-8. |
| [4] | TAPLEY B D,BETTADPUR S,RIES J C, et al. GRACE Measurements of Mass Variability in the Earth System[J]. Science, 2004, 305(5683): 503-505. |
| [5] | BOUMAN J, FIOROT S, Fuchs M, et al. GOCE Gravitational Gradients along the Orbit[J]. Journal of Geodesy, 2011, 85(11): 791-805. |
| [6] | TAPLEY B D, FLECHTNER F, BETTADPUR S V, et al. The Status and Future Prospect for GRACE after the First Decade[C]//AGU Fall Meeting. [S.l]: AGU, 2013: 9-12. |
| [7] | JGGI A,BEUTLER G,MEYER U,et al. AIUB-GRACE02S: Status of GRACE Gravity Field Recovery Using the Celestial Mechanics Approach[J]. Geodesy for Planet Earth, 2012: 161-169. |
| [8] | MAYER-GVRR T,ZEHENTNER N,KLINGER B, et al. ITSG-Grace 2014: A New GRACE Gravity Field Release Computed in Graz[C]//Oral Presentation at the GRACE Science Team Meeting. Potsdam: [s.n.], 2014, 29. |
| [9] | SHEN Yunzhong,CHEN Qiujie,HSU H,et al. A Modified Short Arc Approach for Recovering Gravity Field Model[C]//Oral Presentation at the GRACE Science Team Meeting. Austin: University of Texas, 2013: 22-25. |
| [10] | 沈云中. 应用CHAMP卫星星历精化地球重力场模型的研究[D]. 武汉: 中国科学院测量与地球物理研究所, 2000. SHEN Yunzhong. Study of Recovering Gravitational Potential Model from the Ephemerides of CHAMP[D]. Wuhan:The Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 2000. |
| [11] | 王正涛. 卫星跟踪卫星测量确定地球重力场的理论与方法[D]. 武汉: 武汉大学, 2005. WANG Zhengtao. Theory and Methodology of Earth Gravity Field Recovery by Satellite-to-Satellite Tracking Data[D]. Wuhan: Wuhan University, 2005. |
| [12] | 徐天河. 利用CHAMP卫星轨道和加速度计数据推求地球重力场模型[D]. 郑州: 信息工程大学, 2004. XU Tianhe. Gravity Field Recovery from CHAMP Orbit and Accelerometer Data[D]. Zhengzhou: The PLA Information Engineering University, 2004. |
| [13] | 肖云. 基于卫星跟踪卫星数据恢复地球重力场的研究[D]. 郑州: 信息工程大学, 2006. XIAO Yun. Analysis of Earth Gravity Field Recovery by Satellite-to-Satellite Tracking Data[D]. Zhengzhou: The PLA Information Engineering University, 2006. |
| [14] | 游为. 应用低轨卫星数据反演地球重力场模型的理论和方法[D]. 成都: 西南交通大学, 2011. YOU Wei. Theory and Methodology of Earth’s Gravitational Field Model Recovery by LEO Data[D]. Chengdu: Southwest Jiaotong University, 2011. |
| [15] | 张兴福. 应用低轨卫星跟踪数据反演地球重力场模型[D]. 上海: 同济大学, 2007. ZHANG Xingfu. The Earth’s Field Model Recovery on the Basis of Satellite-to-Satellite Tracking Missions[D]. Shanghai: Tongji University, 2007. |
| [16] | 周旭华. 卫星重力及其应用研究[D]. 武汉: 中国科学院测量与地球物理研究所, 2005. Zhou Xuhua. Study of Satellite Gravity and Its Application[D]. Wuhan: Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 2005. |
| [17] | 苏勇, 范东明, 游为. 利用GOCE卫星数据确定全球重力场模型[J]. 物理学报, 2014, 63(9): 099101. SU Yong, FAN Dongming, YOU Wei. Gravity Field Model Calculated by Using the GOCE Data[J]. Acta Physica Sinica, 2014, 63(9): 099101. |
| [18] | 肖云, 夏哲仁, 王兴涛. 用GRACE星间速度恢复地球重力场[J]. 测绘学报, 2007, 36(1): 19-25. XIAO Yun, XIA Zheren, WANG Xingtao. Recovering the Earth Gravity Field from Inter-satellite Range-rate of GRACE[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 19-25. |
| [19] | ZHU S, REIGBER C, KNIG R. Integrated Adjustment of CHAMP, GRACE, and GPS Data[J]. Journal of Geodesy, 2004, 78(1-2): 103-108. |
| [20] | XU Peiliang. Position and Velocity Perturbations for the Determination of Geopotential from Space Geodetic Measurements[J]. Celestial Mechanics and Dynamical Astronomy, 2008, 100(3): 231-249. |
| [21] | 陈秋杰, 沈云中, 张兴福. 基于重力卫星几何轨道线性化的地球重力场反演方法[J]. 地球物理学报, 2013, 56(7): 2238-2244. Chen Qiujie, Shen Yunzhong, Zhang Xinfu. Linearization Method of Recovering Earth’s Gravity Field with Respect to Gravity Satellite’s Kinematic Orbits[J]. Chinese Journal of Geophysics, 2013, 56(7): 2238-2244. |
| [22] | CHEN Qiujie, SHEN Yunzhong, ZHANG Xingfu, et al. Global Earth’s Gravity Field Solution with GRACE Orbit and Range Measurements Using Modified Short Arc Approach[J]. Acta Geodaetica et Geophysica, 2014, 50(2): 173-185. |
| [23] | CHEN Qiujie, SHEN Yunzhong, ZHANG Xingfu, et al. Monthly Gravity Field Models Derived from GRACE Level 1B Data Using a Modified Short-arc Approach[J]. Journal of Geophysical Research, 2015, 120(3): 1804-1819. |
| [24] | KUSCHE J, KLEES R. Regularization of Gravity Field Estimation from Satellite Gravity Gradients[J]. Journal of Geodesy, 2002, 76(6-7): 359-368. |
| [25] | ZHAO Qile, GUO Jing, HU Zhigang, et al. GRACE Gravity Field Modeling with an Investigation on Correlation Between Nuisance Parameters and Gravity Field Coefficients[J]. Advances in Space Research, 2011, 47(10): 1833-1850. |
| [26] | BETTADPUR S.Recommendation for A-Priori Bias & Scale Parameters for Level-1B ACC Data (Version 2)[EB/OL]. [2015-05-01]. http://podaac.jpl.nasa.gov/gravity/grace-documentation. |
| [27] | DAHLE C, FLECHTNER F, GRUBER C, et al. GFZ GRACE Level-2 Processing Standards Document for Level-2 Product Release 0005[EB/OL]. [2015-05-01]. http://gfzpublic.gfz-potsdam.de/pubman/item/escidoc:61197:9/component/escidoc:65055/1202. |
| [28] | FRSTE C,BRUINSMA S,FLECHTNER F,et al.EIGEN-6C2-A New Combined Global Gravity Field Model Including GOCE Data up to Degree and Order 1949 of GFZ Potsdam and GRGS Toulouse[C]//EGU General Assembly Conference. Vienna: [s.n.], 2013. |
| [29] | DIEDRICH R, GENDT G. A Gravity Field Model from LAGEOS Based on Point Masses (POEM-L1)[C]//Proceedings of the 6th International Symposium “Geodesy and Physics of the Earth”. Potsdam: GDR, 1989: 22-27. |
| [30] | ANDERSEN O B, KNUDSEN P, KENYON S, et al. Global and Arctic Marine Gravity Field from Recent Satellite Altimetry (DTU13)[C]//76th EAGE Conference and Exhibition 2014, Amsterdam, Netherlands: [s.n.], 2014: 16-19. |
| [31] | ANDERSEN O B, JAIN M, KNUDSEN P. The Impact of Using Jason-1 and Cryosat-2 Geodetic Mission Altimetry for Gravity Field Modeling[J]. International Association of Geodesy Symposia, 2015: 1-6. |