2. 江苏省地理信息资源开发与利用协同创新中心, 江苏 南京 210023
2. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China
硬件加速的地图绘制方法不仅引起了学术界的广泛讨论[1, 2],还得到了商业界和开源社区的积极响应。谷歌公司推出基于硬件加速的WebGL地图测试版以及MapServer发布支持OpenGL绘制的地图服务就是其中的典型。与纯软件绘制方法不同的是,硬件加速绘制的基本单元主要是三角形、四边形以及它们构成的条带(stripe)或扇(fan)[3]。如何对线对象实施高质量三角剖分成为线对象硬件加速绘制的关键问题。
线对象分解方法包括:Minkowski和分解[4]、顶点分解[5]、线段分解[6]、V分解[7]与梯形分解[8]。Minkowski和分解方法属于基于点集理论的分解方法,具有严密的数学基础,但是算法复杂度较高且无法支持宽度渐变、颜色渐变的线型。顶点分解方法首先逐个计算顶点的法向量,然后基于线段的宽度,顺、逆法线方向,构造三角形条带。该方法没有考虑张角较大和顶点比较接近这两种情况,仅适用于绘制光滑曲线。线段分解方法以线对象两个相邻顶点为单位,独立进行三角剖分,线段相交的地方叠加绘制一个弥补视觉缺陷的圆形。该方法绘制效率高,但仅能满足视觉要求,适用于纯色填充的线型绘制,不支持纹理线型和渐变线型。V分解方法对于任意线对象,沿坐标点的顺序,除首末点外,计算任意相邻两个顶点的中点(内插点),内插点—顶点—内插点构成一个V型的折线。该算法以V作为基本单位,V单元之间彼此独立,存在顶点冗余,三角剖分后三角形过多,三角形条带数量大,绘制效率不高。梯形分解方法将扩展多边形的顶点按照y坐标由小到大排序,在不同y坐标处引一条平行于x轴的平行线,所有的平行线将扩展多边形分解为一系列梯形(梯形可退化为三角形)。梯形分解时,需要涉及内外判别、排序等算法,算法复杂度高,三角形条带个数较多,绘制效率不高。综合来看,Minkowski和与梯形分解方法属于全局的分解方法,没有借助顶点本身的顺序信息来辅助三角剖分,导致分解质量不高。顶点分解、线段分解、V分解方法属于局部的分解方法,均是针对线对象的局部几何特征来设计的,三角剖分的质量不高且适应性不强。
文献[9]发现线对象上某些点的信息要比其他点丰富,关键点对于线对象的几何、结构特征描述具有决定性的作用。此后,线对象特征点的提取问题引起了广泛的研究,相继提出了张角探测、多边形拟合、滤波以及混合型的方法[10, 11, 12]。特征点分析已经在曲线形态结构化表达、曲线综合等方面展开应用。但是,尚没有针对线对象三角剖分的特征点提取与应用方法。
从上述线对象三角解剖算法的效率、质量和适应性来看,线对象本身形态复杂,线型较多。现有三角剖分算法没有顾及到线对象的整体结构特征,导致三角剖分质量不高,绘制效率低,影响矢量地图操作体验,难以支持数据量大的矢量制图和高更新率的动态制图[13]。本文在分析线对象渐变与突变特征的基础上提出一种线对象的单调分解与三角剖分方法。
1 线对象单调分解与三角剖分方法 1.1 线对象的单调分解在客观地理世界中,地理对象和地理现象的渐变和突变现象广泛存在。线对象邻近顶点构成的张角作为决定三角剖分的关键因素,也存在渐变与突变现象。图 1(a)为某地区一段河流,包含37个顶点。若Pi、Pi-1构成的向量记为a,Pi、Pi+1构成的向量记为b,则
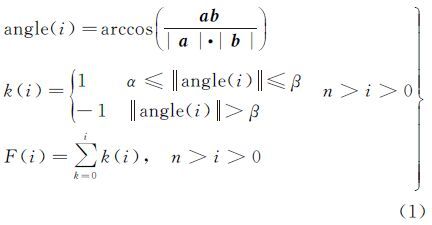
|
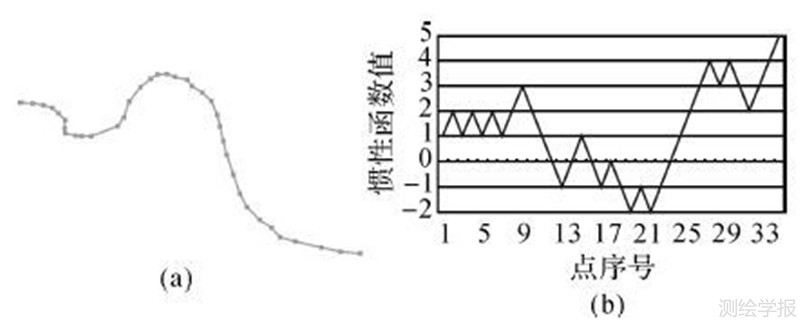
| 图 1 线对象的惯性函数示意图 Fig. 1 Momentum function diagram for polyline |
本文通过定义惯性函数对线对象实施单调分解,以单调区间为单位实施三角剖分。
1.2 基于单调区间的三角剖分方法顶点、三角形、图元个数是三角剖分的3个重点评价指标。下文以这3个指标作为定量分析的依据,从线对象单个顶点和邻近顶点两个角度来论述本文思路。
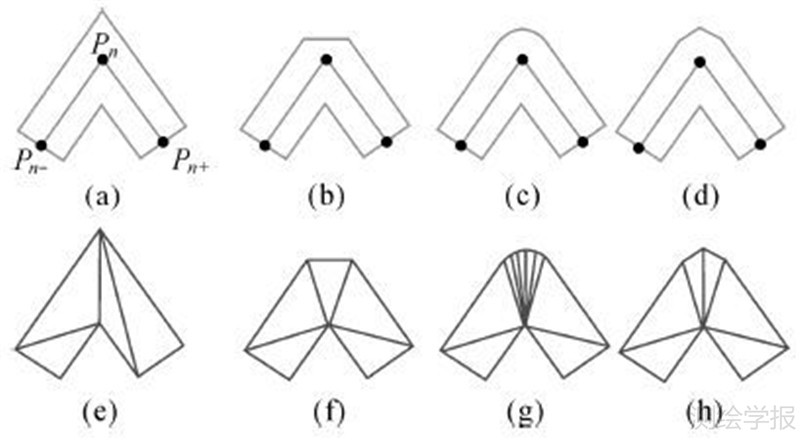
1.2.1 线对象单个顶点的优化剖分文献[14, 15, 16]将线对象顶点分为miter、bevel、round、triangular 4种类型,分别如图 2中(a)、(b)、(c)、(d)所示。现有的三角剖分方法中,Minkowski和分解、顶点分解、线段分解与梯形分解方法均忽略顶点间的顺序关系,剖分时需要内插辅助点,顶点、三角形和三角形条带数据均较大,剖分质量较低。V分解方法利用顶点的顺序关系,剖分质量最高。综合来看,miter类型的最优分解方案是分解为如图 2中(e)所示的一个完整的三角形条带,bevel、round、triangular类型的最优分解方案是如图 2(f)、(g)、(h)所示的一个完整三角形扇。文献[2]更进一步认为当张角接近于平角,后3种情况可退化为第1种情况。
|
| 图 2 线对象的优化三角剖分示意图 Fig. 2 Optimized tessellation for polyline |
从三角形条带和三角形扇的数据结构容易看出,相邻的两个三角形条带是可以合并的,即:位置相同的两个顶点可以合并,两个三角形条带可以合并为一个三角形条带。如果两个三角形扇的起始点不一致,则无法合并。如果一个包含4个顶点的三角形条带和一个三角形扇邻近,则该三角形条带可以合并到三角形扇中。V分解方法虽然能够保证顶点类型的最优剖分,但忽略了分解单元之间连续性,导致整体剖分质量不高。
由上述两方面的分析来看,单调递增区间内的顶点可优化剖分为一个连续的三角形条带;单调递减区间内的顶点,可优化剖分为一个三角形扇。如果单增区间仅包含两个顶点,则该单增区间对应的三角形条带并入邻近的三角形扇中。这种剖分方法不管在整体还是局部上均优于前文所述5种方法。
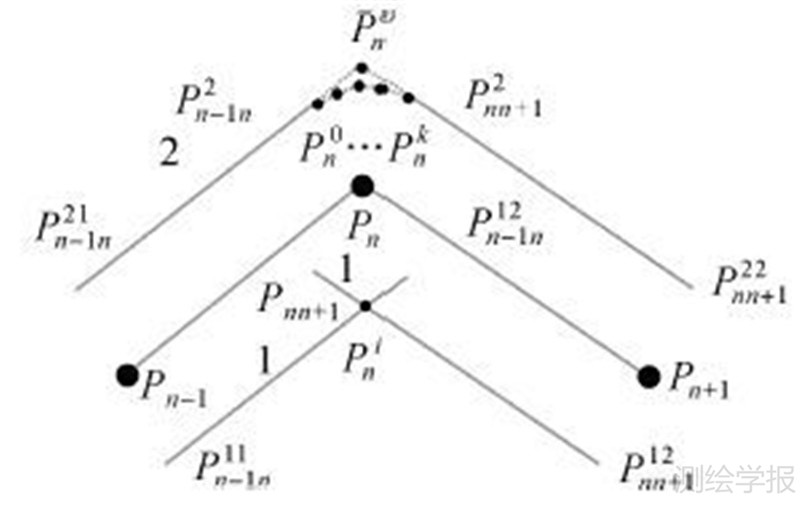
1.3 基于单调区间的三角剖分算法描述本文根据张角是否接近平角,将顶点分为两种类型:V形顶点和扇形顶点。本文将内角方向的顶点平移计算称为内推,相应的点称为内推点。反之,称为外推和外推点。如图 3所示,Pn-1、Pn的内推点为Pn-1n11、Pn-1n12;Pn、Pn+1的内推点为Pnn+111、Pnn+112;Pn-1、Pn的外推点为Pn-1n12、Pn-1n22;Pn、Pn+1的外推点为Pnn+112、Pnn+122。若∠Pn-1PnPn+1接近于[a,b],则计算Pnn-112Pnn-112与Pnn+111Pnn+112的交点Pni以及Pn-1n21Pn-1n22与Pnn+121Pnn+122的交点Pno,Pni与Pno构成的顶点称为顶点对,记为pair〈Pni,Pno〉。若∠Pn-1PnPn+1不接近于[a,b],则计算Pnn-112Pnn-112与Pnn+111Pnn+112的交点Pni以及Pn-1n21Pn-1n22与Pnn+121Pnn+122的交弧Pn0…Pnk,其中k为交弧的顶点个数,k取决于拟合的角度或者长度阈值。Pni与Pn0…Pnk构成的顶点集合称为扇形,记为Triangle_fan〈Pni,Pn0…Pnk〉。
|
| 图 3 顶点内推线、外推线示意图 Fig. 3 Interpolated line and extrapolated line of vertex |
本文采用逐点推进、一次遍历的方法同时完成三角形的单调分解和三角剖分,完整的算法流程如下。
(1) 算法开始。建立一个全局的pair〈Pni,Pno〉的顶点对的缓存。清空该顶点对缓存。
(2) 第1个顶点处理。第1个点作为V形顶点,将pair〈P0i,P0o〉植入顶点对缓存,转入下一个点。
(3) 下一个顶点处理。如果下一个点是V形顶点,首先判断上一顶点是否存在未封闭的Triangle_Fan,有则将pair〈Pni,Pno〉加入Triangle_Fan的后面。否则将pair〈Pni,Pno〉置入顶点对缓存,转入下一个点。
(4) 三角形条带延迟封闭处理。如果下一个点是扇形顶点,首先判断上一顶点是否存在未封闭的Triangle_Fan,有则将pair〈Pni,Pn0〉追加到该Triangle_Fan,立即封闭该Triangle_Fan。再判断顶点对缓存中顶点对的个数,若顶点对的个数大于1,则将pair〈Pni,Pn0〉置入缓存,立即将顶点对缓存转变为一个连续的Triangle_Stripe,清空顶点对缓存。若顶点对的个数等于1,则构造一个fan〈Pni,Pn-1i,Pn-10Pn0…Pnk〉,清空顶点对缓存。若顶点对的个数等于0,则构造一个fan〈Pni,Pn0…Pk〉,该三角形扇不立即封闭,转入下一个点。
(5) 最后一个顶点处理。若是最后一个顶点,如果前一个顶点是扇形顶点,则将pair〈Pni,Pn0〉追加到扇形后面,立即结束该三角形扇;如果前一个顶点是V形顶点,则将pair〈Pni,Pn0〉置入缓存,将顶点对缓存转变为一个连续的三角形条带,清空顶点对缓存。
(6) 算法结束。清空全局顶点对缓存。
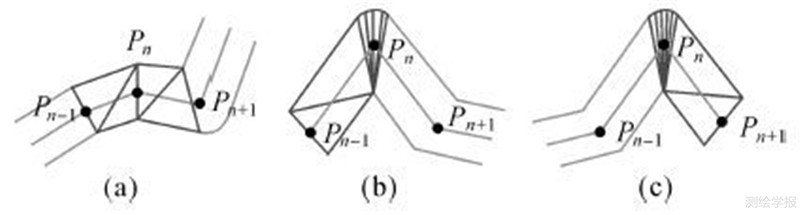
算法步骤(2)—(4)中,建立顶点对缓存对应于一个单增区间开始。顶点对缓存并不立即清空,而是等单增区间结束(下一个顶点为扇形顶点)时才将顶点对缓存变为一个连续的三角形条带。如图 4(a)中,Pn-1、Pn为V型顶点,Pn+1为扇形顶点。Pn-1、Pn对应的三角形条带延迟到Pn+1才封闭。步骤(4)中,需要判断顶点对缓存是否为1,其目的是为了处理单增区间仅包含一个顶点的情况。如图 4(b)所示,当线对象开始于Pn-1,而Pn为扇形顶点,则顶点Pn-1对应的三角形条带可并入Pn对应的Triangle_Fan中。步骤(4)中的Triangle_Fan也不立即封闭的主要原因是,若下一个顶点为V型顶点,则该条带顶点的两个点可并入上一个Triangle_Fan中;如果下下个顶点为扇形顶点,则可减少一个三角形条带。如图 4(c) 所示,如果线对象在Pn结束,也可减少一个三角形条带。本文将上述策略称之为三角形条带的延迟封闭。
|
| 图 4 三角形条带延迟封闭的3种情况 Fig. 4 Three kinds of delayed closure for triangle strip |
由图 1(b)可知,线对象惯性函数的单调递增区间广泛存在且覆盖范围较大。本文算法中的三角形条带的延迟封闭策略,可以将单增区间内的顶点优化剖分为一个连续的三角形条带。单调递增区间中,还包含一些仅包含两个顶点的区间,本文算法中的三角形条带的延迟封闭还可将仅包含一个顶点的区间对应的三角形条带并入到邻近的三角形扇中,可进一步优化三角剖分质量。
2 3种特殊线型的三角剖分本文将具有宽度、颜色等符号信息的线称之为线型。综合文献[17, 18, 19]的讨论,符号化过程中还包括宽度变化的线型、封闭的线型以及光滑的线型等。本文方法适用于封闭线型、变宽线型和光滑线型的绘制。
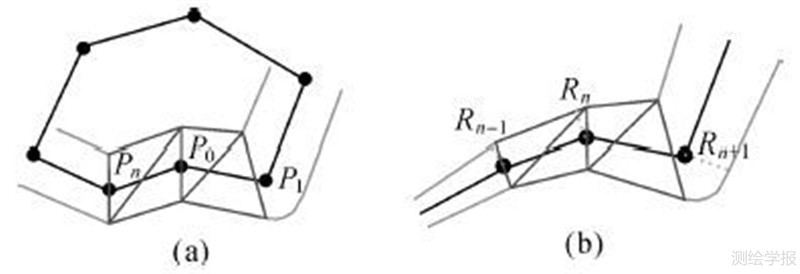
2.1 封闭线型在1.3节描述的三角剖分流程中,起点作为V形顶点处理。如图 5(a)所示,对于封闭的线对象,起点的类型将依据下一顶点P1和最后一个点Pn构成的张角来判断。若为V形顶点,则按照1.3节描述的单调三角剖分流程执行结束后,增加判断Pn的顶点类型:若Pn为V形顶点,则Pn派生的三角形条带和P0派生的三角形条带合并;若为扇形顶点,则跳过P0,判断P1的顶点类型,直到搜索到第一个V形顶点。将中间跳过的扇形顶点,顺序追加到Pn后面。执行单调剖分,完成封闭线型的三角剖分。
|
| 图 5 封闭线、变宽线三角剖分示意图 Fig. 5 Tessellation for closed and mutative width line style |
本文方法支持等宽线型与变宽线型的绘制。如图 5(b)所示,在顶点进行内推线、外推线的计算时,线对象的每个顶点均可以独立赋宽度值。若所有顶点的宽度相同,则为等宽线型。若顶点宽度不同,即为变宽线型。
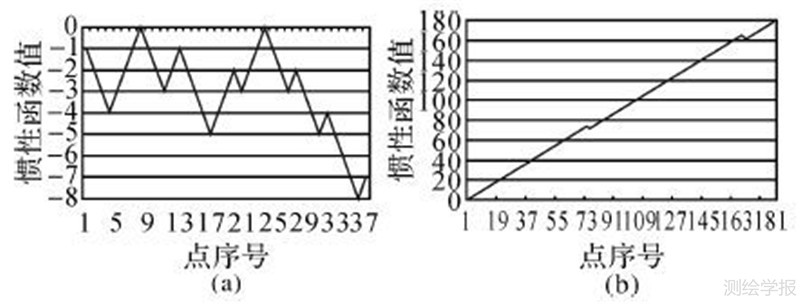
2.3 光滑线型连续参数曲线在栅格化的过程中必须离散化。在连续曲线的栅格化过程中,离散化本身涉及导数、三角函数等计算,为保证离散后参数曲线的光滑特征,离散后数据量显著增大,这两个方面的原因均会降低光滑曲线的绘制效率。本文方法中离散后的线段存在较强的连续性。一段包含39个顶点的等高线数据,对其进行3次B样条曲线拟合,得到257个点,分别绘制离散前后惯性函数,如图 6(a)、(b)所示。由图可知,拟合为光滑曲线后惯性函数表现出的单调递增区间更大,单调递增区间的个数更多。因此,本文算法有利于形成更为连续的三角形条带,得到质量更高的三角剖分结果。
|
| 图 6 等高线光滑前后惯性函数对比 Fig. 6Contrast of momentum function before and after contour smoothing |
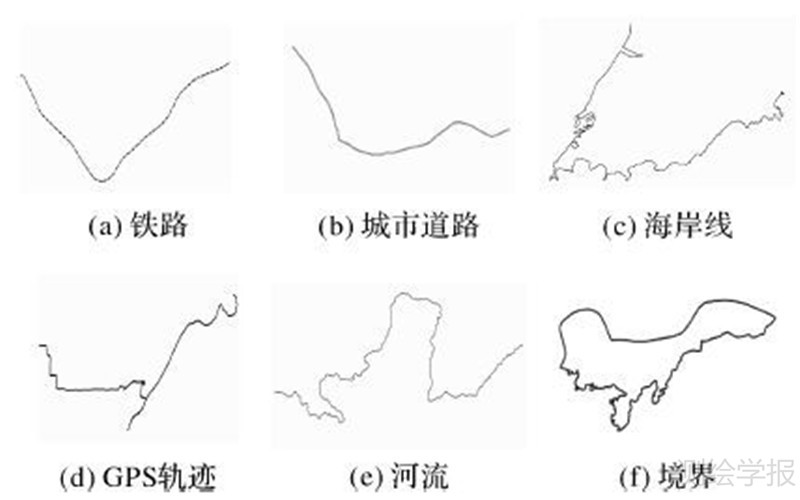
如图 7所示,选择OpenStreetMap数据集(http://www.openstreetmap.org/)中的海岸线、河流、境界线、铁路、城市道路和GPS轨迹6组数据进行对比测试。采用顶点分解和线段分解两类算法与本文算法进行效率与质量对比。顶点分解采用Vase Render(VR)算法(https://github.com/tyt2y3/vaserenderer)。线段分解采用MapServer6.0.0 中线符号绘制代码算法(简写为MS)(http://mapserver.org/zh_cn/download.html)。试验采用C++语言实现本文算法,采用OpenGL作为图形绘制接口。试验中采用开源空间数据读写软件包GDAL1.4(Geospatial Data Abstraction Library)实现对试验数据的读取。测试环境:IBM ThinkPad T410s,Inter(R)core(TM)i5 CPU,3GB内存,Windows 7,32位操作系统。每次绘制100次。运行10次,取平均值作为测试结果。试验结果如表 1所示。
|
| 图 7 6组试验数据 Fig. 7 Six groups of experimental data |
| 数据集名称 | 顶点数 | 顶点,三角形,图元数 | 绘制1000次效率/(10-3s) | |||||
| MS法 | VR法 | 本文算法 | MS法 | VR法 | 本文算法 | |||
| 铁路 | 127 | (3298,2919,253) | (417,748,125) | (260,258,5) | 165 | 96 | 15 | |
| 城市道路 | 321 | (8342,7381,641) | (899,1911,319) | (813,811,83) | 401 | 255 | 46 | |
| 海岸线 | 410 | (10656,9428,819) | (3011,4379,408) | (2182,2180,319) | 503 | 409 | 122 | |
| GPS轨迹 | 730 | (18976,16788,1459) | (3284,4654,728) | (2012,2010,231) | 858 | 595 | 119 | |
| 河流 | 995 | (25866,22883,1989) | (5321,6867,993) | (4045,4043,823) | 1172 | 807 | 263 | |
| 境界 | 1563 | (40634,35947,3125) | (6504,10719,1561) | (5163,5161,766) | 1815 | 1222 | 314 | |
由表 1可知,本文三角剖分方法所得顶点、三角形、图元个数明显小于V分解方法和线段分解方法。其主要原因是:V分解算法中,对于任意线对象,沿着坐标点的顺序,除首末点外,计算任意相邻两个顶点的中点(内插点),按内插点—顶点—内插点顺序构成一个V型的折线,由n个顶点构成的线对象可以分解为n-2个V对象。V对象之间彼此独立,存在顶点冗余,三角剖分后,三角形过多,三角形条带数量大,导致绘制效率不高。线段分解方法以线对象两个相邻顶点为单位,分解为由两个相邻顶点构成的线段,将线段进行内、外推,得到一个矩形,一个矩形分解为一个三角形条带。线段相交的地方叠加绘制一个半径为r的圆形。由于线段之间彼此独立,三角形条带数量大,不考虑Bevel、Round、Triangular 3种情况,任意张角均绘制一个半径为r的圆,也增加了顶点、三角形条带、扇的个数,导致绘制效率不高。本文方法直接以单调链为三角剖分的基本单位,分解中由于避免了中间内插顶点的外推,扩展多边形的顶点数据、三角形的个数、三角形条带的个数均小于V分解和线段分解。因此,绘制效率明显优于V分解方法和线段分解方法
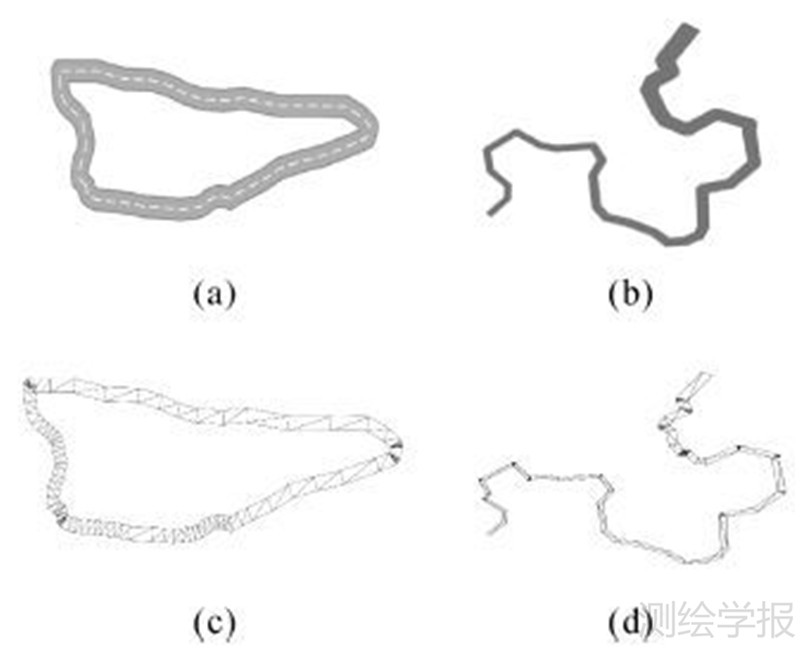
3.2 适应性分析叠加两个不同宽度的线型和一个虚线线型,绘制了封闭的高速公路,如图 8(a);采用宽度渐变填充,绘制了渐变线型的河流,如图 8(b)。其对应的三角剖分结果分别如图 8(c)、(d)所示。
|
| 图 8 算法对线型的支持 Fig. 8 Algorithm support for different line styles |
采用数据量不等的3组等高线数据来验证本文算法对光滑线型绘制的支持。选择MS方法作为比较对象,采用直接绘制和三次B样条光滑曲线绘制。统计本文方法对MS方法的加速比(倍率)。表 2所示的试验结果中,加速比由直接绘制时平均8.6倍增长为光滑绘制时的平均9.4倍。其主要原因是:光滑曲线绘制过程中,本文算法能够充分利用线对象的连续性,得到质量更高的剖分结果,从而提高绘制效率。因此,本文算法针对光滑线型绘制的加速比要高于折线绘制的加速比。
| 数据 | 原始内插 | 顶点数 | 直接绘制 | 光滑绘制 | |||
| MS/10-3 s | 本文方法加速比 | MS/10-3 s | 本文方法加速比 | ||||
| 等高线1 | 39 | 192 | 76 | 9.5 | 257 | 10.3 | |
| 等高线2 | 75 | 372 | 107 | 8.9 | 436 | 10.1 | |
| 等高线3 | 229 | 1143 | 279 | 7.5 | 1311 | 7.9 | |
线对象符号化的效率与质量成为当前地图制图与发布的关键因素[20]。硬件加速绘制成为当前的研究热点。本文认为,现有三角剖分算法中,不管是顶点分解、线段分解还是V分解,均是从线对象的局部几何特征出发来设计的,忽略了线对象的整体形态特征。整体分解方法没有利用线对象本身的结构特征,算法复杂度较高且分解质量差。
本文给出了线对象的惯性函数,提出了一种基于单调区间的三角剖分方法。惯性函数的单调递增区间是线对象张角的渐变区间,可连续剖分为一个优化的三角形条带;惯性函数的单调递减区间是线对象张角的突变区间,可离散剖分为一个优化的三角形扇。本文采用真实数据对本文算法进行了试验,结果表明本文方法的三角剖分质量和绘制效率均优于基于顶点、基于线段的三角剖分方法,能够显著提高线对象的符号化效率。
| [1] | RENHART Y. Fast Map Rendering for Mobile Devices[D]. Gothenburg:University of Gothenburg, 2009. |
| [2] | RÖSSLER L. Rendering Interactive Maps on Mobile Devices Using Graphics Hardware[D]. Vienna:Vienna University of Technology, 2012. |
| [3] | ROUGIER N. Shader-based Antialiased Dashed Stroked Polylines[J]. Journal of Computer Graphics Techniques, 2013, 2(2):91-107. |
| [4] | Category System. A Realistic 2D Drawing System[EB/OL].[2003-06-19]. http://www.keithp.com/. |
| [5] | HERTZMANN A. A Survey of Stroke-based Rendering[J]. IEEE Computer Graphics and Applications, 2003, 23(4):70-81. |
| [6] | WANG Jiechen, CUI Can, PUYingxia, et al. A Novel Algorithm of Buffer Construction Based on Run-length Encoding[J]. The Cartographic Journal, 2010, 47(3):198-210. |
| [7] | TSANG C. Vase Renderer is a Polyline and Curve Renderer on Open GL[EB/OL].[2014-09-18]. https://github.com/tyt2y3/vaserenderer. |
| [8] | KILGARD M J, BOLZ J. GPU-accelerated Path Rendering[J]. ACM Transactions on Graphics(TOG), 2012, 31(6):172. |
| [9] | LI Zhilin. An Examination of Algorithms for the Detection of Critical Points on Digital Cartographic Lines[J]. The Cartographic Journal, 1995, 32(2):121-125. |
| [10] | GUILBERT E, SAUX E. Cartographic Generalisation of Lines Based on a B-spline Snake Model[J]. International Journal of Geographical Information Science, 2008, 22(8):847-870. |
| [11] | 艾廷华, 郭仁忠, 刘耀林. 曲线弯曲深度层次结构的二叉树表达[J]. 测绘学报, 2001, 30(4):343-348. AI Tinghua, GUO Renzhong, LIU Yaolin. A Binary Tree Representation of Curve Hierarchical Structure in Depth[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4):343-348. |
| [12] | 彭东亮, 邓敏, 刘慧敏. 更充分利用独立弯曲结构的线状要素Morphing变换方法[J]. 测绘学报, 2014, 43(6):637-644, 652. DOI:10.13485/j.cnki.11-2089.2014.0100. PENG Dongliang, DENG Min, LIU Huimin. Morphing Transformation of Linear Features by Using Independent Bend Structures More Sufficiently[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6):637-644, 652. DOI:10.13485/j.cnki.11-2089.2014,0100. |
| [13] | SWIENTY O, ZHANG M, REICHENBACHER T, et al. Establishing a Neurocognition-based Taxonomy of Graphical Variables for Attention-guiding Geovisualisation[C]//International Society for Optics and Photonics.Nanjing:SPIE, 2007:675109. |
| [14] | W3C Recommendation. Scalable Vector Graphics(SVG) Full 1.2 Specification[EB/OL].[2010-07-11]. http://www.w3.org/TR/SVG12. |
| [15] | Adobe Systems Incorporated.PDF Reference[EB/OL].[2007-04-11]. http://www.images.adobe.com/content/dam/Adobe/en/devnet/pdf/pdfs/pdf_reference_1-7.pdf. |
| [16] | DANIEL R. Open VG Specification Version 1.0.1[EB/OL].[2005-05-13]. https://www.khronos.org/registry/vg/specs/openvg_1_0_1.pdf. |
| [17] | OGC 02-070. Styled Layer Descriptor Implementation Specification[S].Open GIS Consortium Inc.,2002. |
| [18] | 李丽, 王结臣, 沈定涛, 等. 一种单线河流渐变符号的绘制方法[J]. 测绘通报, 2008(11):64-67. LI Li, WANG Jiechen, SHEN Dingtao, et al. A Method for Plotting Gradual Change Symbol of Single-line Stream[J]. Bulletin of Surveying and Mapping, 2008(11):64-67. |
| [19] | MACEACHREN A M.How Maps Work:Representation, Visualization, and Design[M]. New York:Guilford Press, 2004. |
| [20] | NOGUERA J M, SEGURA R J, OGÁYAR C J, et al. A Scalable Architecture for 3D Map Navigation on Mobile Devices[J]. Personal and Ubiquitous Computing, 2013, 17(7):1487-1502. |


