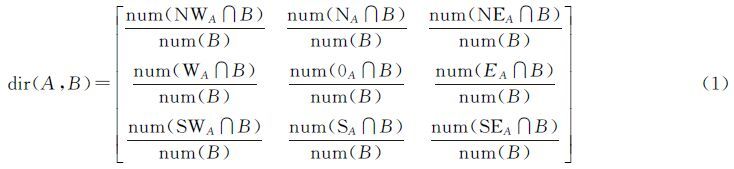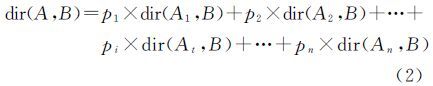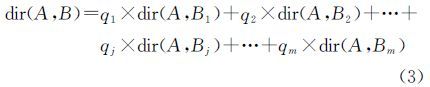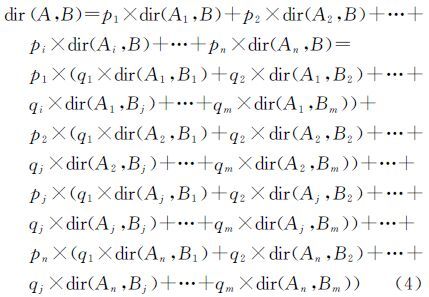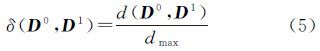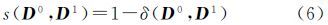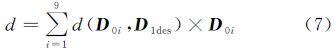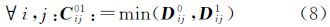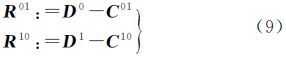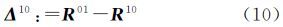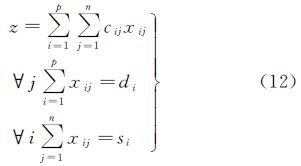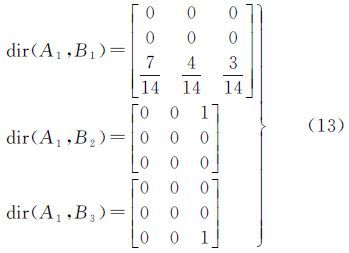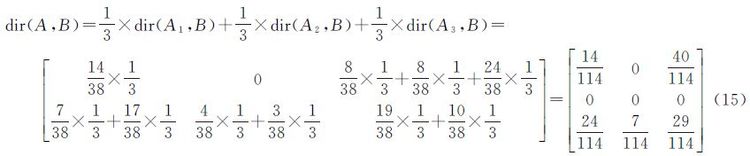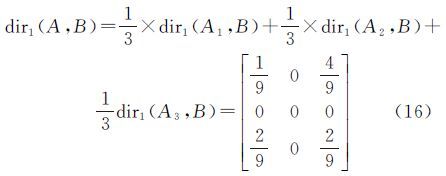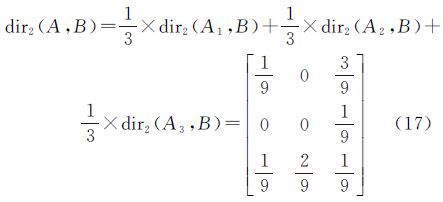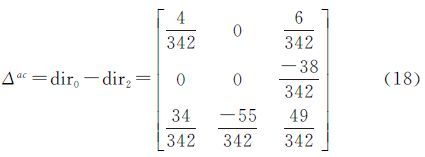2. 地理信息工程国家重点实验室, 陕西 西安 710054;
3. 西安测绘研究所, 陕西 西安 710054
2. State Key Laboratory of Geography Information Engineering, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
在地图制图综合中常将大比例尺地图转换为小比例尺地图,尽管尺度发生变化,但其所表达的信息应该保持一定的相似性,空间相似性可用来评判综合结果是否合理。文献[1]将多尺度地图空间相似关系分为图像相似和属性相似两大类,而方向关系相似是图形相似中重要的组成部分,因此方向关系间的相似度可作为制图综合结果的评判因子。
现阶段很多学者对方向关系模型进行了研究,既有表示方向关系的定性模型[2, 3, 4, 5, 6, 7, 8],亦有用于相似度评估的定量模型,以及既为定性模型亦为定量模型的方向矩阵模型[9, 10] 。如文献[2]提出用三角模型,通过质心替代对象进行方向关系判断;文献[3]提出一维间隔模型用间隔表示了13种独立的关系;文献[4]将二维对象投影到x轴和y轴再分别运用一维间隔模型从而得到了二维间隔模型;文献[5, 6]将一维模型扩展到二维空间,得到描述四边平行于平面直角坐标的空间对象的矩形代数模型。文献[7]提出二维串模型用标志图及空间目标网格来表示空间关系;文献[8]提出MBR模型并用于空间目标间拓扑关系的检索;文献[9, 10]提出既为定性模型亦为定量模型的方向矩阵模型,还有在此基础上进行改进得到一系列可应用于栅格数据或解决分区线与对象重合等问题的模型,如文献[11]提出SK主方向关系模型并设计了相容性复合方法,文献[12, 13]利用栅格数目比例作为量化信息来表达栅格数据对象间的方向关系,文献[14]采用缩小中心分区的方法改进了该模型;此外,根据不同的应用情况产生了各种侧重点不同的方向关系模型,如文献[15]建立基于Voronoi图的空间方向关系形式化描述模型;文献[16, 17, 18]依次提出一种能表达与参照对象外接矩形内部有关信息细节的定性方向关系表达模型,一种模糊的描述空间关系的方法以及一种方向关系粗糙、变精度粗糙表达方法并将其应用到方向关系的粗糙推理方法中;文献[19]提出了方向关系描述的分层多级处理方法并建立了方向描述的3层模式结构;文献[20]在基于Cobb的空间拓扑关系模型的基础上建立了拓扑关系矩阵和方向关系矩阵;文献[21]提出4种不同情况下基于同一参照系的定性方向推理方法。
上述的方向关系模型中定性模型无法进行相似性度度量,且同大部分定量模型一样,都是基于简单空间对象,对复合对象之间的方向关系表达和度量能力不足,因而不能对复合对象之间的方向关系相似度进行度量。而实际应用中,存在大量的复合对象,如由高校校区经常是由多个区构成的多区对象,在河流交汇处由多条河流构成的多线对象,十字路口处是由多条道路构成的多线对象等。同时实际应用中数据繁杂多源,进行相似性比较的数据也常是异源多尺度,如大比例尺中的面对象在小比例尺中变为点对象。而现有的方法大多考量同维几何实体间的方向相似度。因此,本文将顾及空间尺度差异,研究复合空间对象的方向关系表达及其方向相似度度量方法。
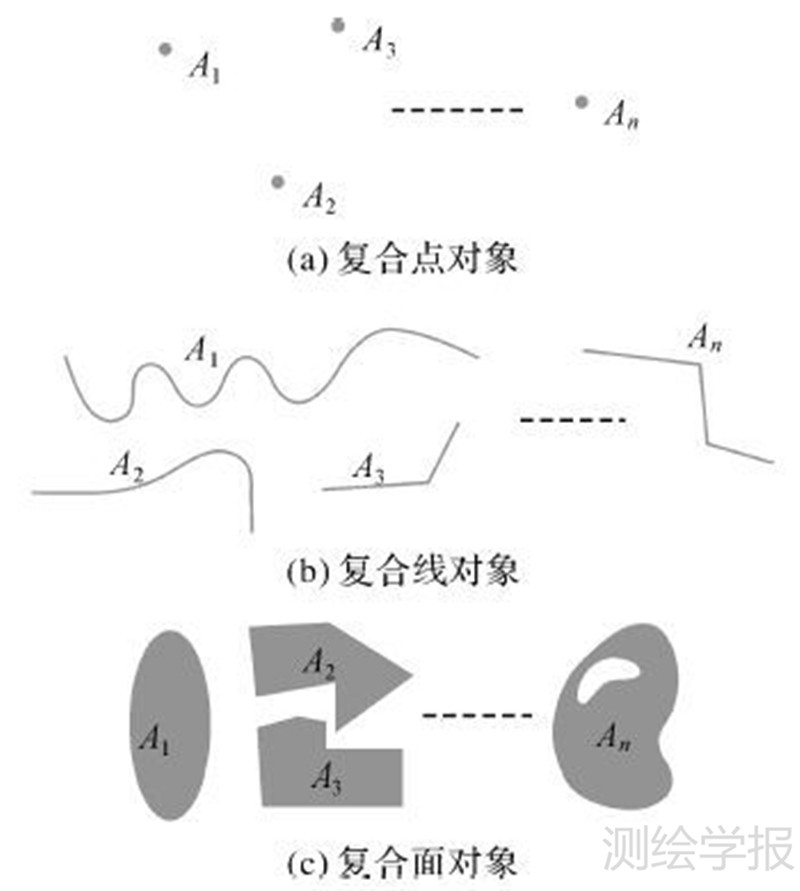
1 复合空间对象及其方向关系描述 1.1 复合对象如图 1所示,复合对象由单一类型的对象构成,有3种类型的复合对象(图 1):复合点对象、复合线对象、复合面对象,它们分别由n(n≥1)个点、线、区构成,点之间、线之间、区之间均不重合,线之间可相交或相邻、区之间不可相交可相邻,即A={A1∪A2∪…∪An }。
|
| 图 1 复合对象 Fig. 1 Composite geometric objects |
本文通过一种格网下的方向关系矩阵来表示单对象之间的方向关系。该方法首先通过参考对象最小外包矩形边所在直线将空间划分成9个分区{N,S,E,W,NE,SE,SW,NW,same},分别对应3×3矩阵的9个元素,再将地图上所涉及的区域划分为固定大小的网格,9个元素值分别为对象在该分区所占的网格数目比例,如式(1)所示
本文方法是在方向关系矩阵上的改良,可简化关系矩阵的计算。方法规定单个点对象所占的网格数记为1,当参考对象为点时以该点所在网格的延长线进行分区。在此基础上,本文结合分解思想,使复合对象间的方向关系也能通过方向格网关系矩阵表示。根据参考对象A和目标对象B是否为复合对象,本文分为3种情况对复合空间对象的格网方向关系矩阵进行介绍。
1.2.1 参考对象为复合对象当参考对象A为由n个单对象组成的复合对象时,则分别以这n个单对象为参考对象,求取每个单参考对象与目标对象的方向关系矩阵,然后按照这n个单对象所占网格数目与对象A所占的网格数目的比值分配权重,将n个单对象与目标对象的关系矩阵相加(式(2)),便得到复合对象与目标对象的方向关系矩阵,式中dir(Ai,B)为复合参考对象中第i个单对象与目标对象的方向关系矩阵,pi为复合参考对象中第i的单对象所占的格网数目比例
1.2.2 目标对象为复合对象当目标对象B为有m个单对象组成的复合对象时,则分别以这m个单对象为目标对象,求取参考对象与每个单目标对象的方向关系矩阵,然后按照这m个单对象所占网格数目与对象B所占的网格数目的比值分配权重,将参考对象与这m个目标对象的关系矩阵相加(式(3)),便得到参考对象与复合目标对象的方向关系矩阵,式中dir(A,Bj)是参考对象A与复合目标对象中第j的单对象的方向关系矩阵,qj为复合目标对象中第j的单对象所占的格网数目比例
1.2.3 参考对象和目标对象都为复合对象当参考对象A与目标对象B分别为n个和m个单对象组成的复合对象时,将参考对象划分为n个对象,逐个以n个单对象为参考对象,求参考对象与复合目标对象的方向关系矩阵,同时将复合目标对象B划分为m个单目标对象后逐个计算当前参考对象与目标对象间的方向关系矩阵,最后将求得的n个单参考对象与复合目标对象之间的方向关系矩阵按单参考对象网格数目的权重值相加,即为最终复合参考对象与复合目标对象之间的方向关系矩阵
式中,dir(Ai,Bj)为复合参考对象A的第i个单对象与复合目标对象B的第j个单对象的方向关系矩阵,pi为A的第i个对象所占的网格比,qj为B的第j个对象所占的网格比。 2 方向相似性度量方法方向关系可通过方向关系矩阵表达,两个方向关系之间的相似度即可通过其对应的方向关系矩阵之间的相似度来反映。如图 2所示,计算方向关系之间的相似度s首先需计算方向关系矩阵之间的距离d,然后将d转换为相异度δ,最后通过δ求相似度s,如下式
式中,D为方向关系矩阵;dmax为邻域图的最大距离。相似度取值范围为[0, 1],取值越大表示两个方向关系越相似,1表示两个方向关系完全相同。本文将任意两个方向关系矩阵之间的距离定义为从源方向矩阵D0转换成目的方向矩阵D1的最小代价,该转换通过将D0中的非零元素从原来的位置沿着邻域图的路径移动到D1中非零元素的位置来实现。距离d的计算需分两种情况讨论:单元素矩阵间的距离与多元素矩阵间的距离。单元素方向矩阵只有一个非零元素,多元素方向关系矩阵中存在多个非零元素,单元素矩阵可看作一种特殊的多元素矩阵。

|
| 图 2 求解相似度的具体过程 Fig. 2 Process for assessing similarity |
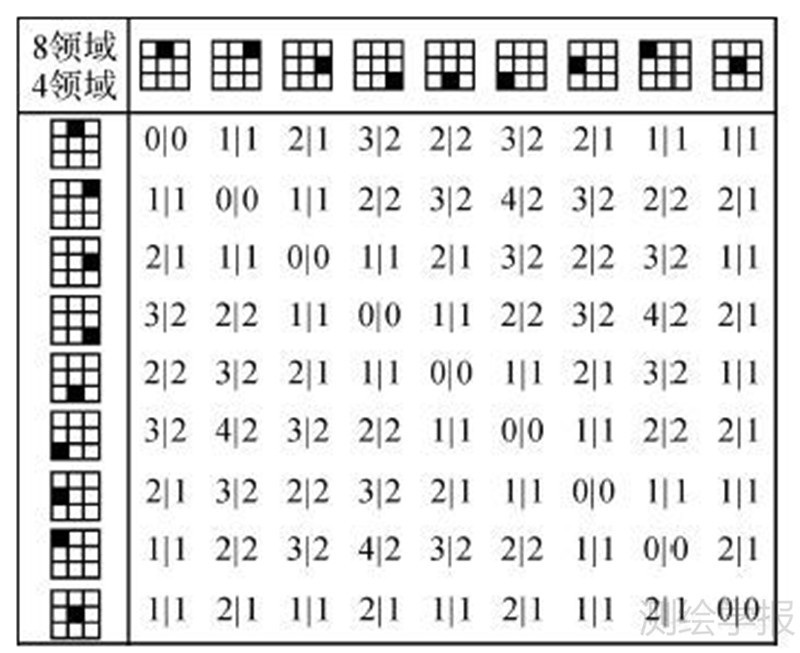
单元素方向矩阵对应九种不同单元素方向关系。单元素矩阵间的最小距离与邻域图有关。在9方向分区上建立合适的邻域图有利于提高距离的计算精确度。邻域图分为4邻域图和8邻域图,4邻域图和8邻域图中各顶点之间的最小距离不同(图 3)。若采用4邻域图,式(2)中dmax取值为4,若采用8邻域图则其取值为2。
|
| 图 3 4邻域图(左侧值)和8邻域图(右侧值)的单元素方向关系矩阵间距离 Fig. 3 4-neighbor distances (left) and 8-neighbor distances (right) between cardinal direction |
这种情况亦分为两种情形,一是从多元素矩阵转换为单元素矩阵;二是从多元素矩阵转换为多元素矩阵。
2.2.1 多元素矩阵转换为单元素矩阵从多元素矩阵转换为单元素矩阵,即将多元素的非零元素移入目的矩阵中唯一的非零元素中,需计算多元素矩阵中每个非零元素按其权重与单元素矩阵中非零元素的距离之和
式中,D0i表示源矩阵D0中的元素值,D1des表示目的矩阵D1中的非零元素,d(D0i,D1des)表示两个元素之间的距离,即两个对应位置非零的单元素矩阵之间的距离。由于距离是对称的,单元素源矩阵与多元素目的矩阵的距离可通过计算目的矩阵到源矩阵的距离获得。 2.2.2 多元素矩阵转换为多元素矩阵由于这种情况下不能明确源多元素矩阵各非零元素转入目的多元素矩阵各非零元素的比例,本文利用方向矩阵间转换的最小代价计算距离。首先,了解几个与矩阵相关的概念。
定义1:矩阵D0和D1的共性矩阵C01(式(8))的每个元素的值取D0和D1相应位置上两个元素的较小值。同理,D1和D0的共性矩阵C10元素的值亦取两个矩阵中元素的较小值,因而C01=C10
定义2:矩阵D0与D1的非对称相异矩阵R01(式(9))为矩阵D0与共性矩阵之差,同理,矩阵D1与D0的非对称相异矩阵R10为矩阵D1与共性矩阵之差
定义3:矩阵D0与D1的方向相异矩阵Δ01(式(10))定义为两个非对称相异矩阵的差值
用式(9)中的值替换到式(10)中,即可用D0与D1表示Δ01(式(11)),Δ01元素的值范围为[-1, 1]
由于方向关系矩阵间的转换与平衡传输问题有一定的共性,借用平衡传输问题的解决方法可求解矩阵间转换的最小代价。
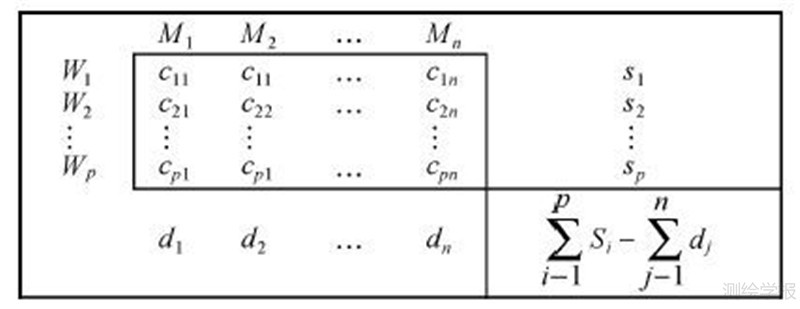
2.2.3 多元素矩阵转换为多元素矩阵首先了解普通的平衡传输问题及其求解思想。平衡传输表(balance transportation tableau,BTT)如图 4所示,已知仓库Wi能供给的货物量为si,市场Mj的需求量为dj,cij为从Wi到Mj运送单位货物的成本,已知仓库的总供给量等于市场的总需求量。如何分配货物才能使得运输成本最低,即平衡运输问题。
|
| 图 4 平衡传输表 Fig. 4 The balance transportation tableau |
假设最终解决方案中从Wi运送到Mj的货物为xij。问题演变成确定特定的x,使得代价z最小,且x需满足仓库供给量和市场需求量的约束(式(12))
一种求解xij的方法为Northwest-Corner方法:从平衡传输表的左上方开始,先清空一个仓库或填满一个市场,将实际运输量记下,并从相应的行列中减去运输量,然后删除已空的仓库(行)或已满的市场(列),如果两者同时满足且该行不是剩下的唯一行,则优先去掉行,直到所有的行列都删除,否则继续回到新表的左上方重新开始,每次记下的运输量即为最终xij的解。
方向关系矩阵间的转换与从仓库(源矩阵非零元素对应的分区)运输货物(非零元素)到市场(目的矩阵非零元素对应的分区)类似,两矩阵若在同一位置都有非零元素,那么部分非零元素(两者中值较小的元素值)是不需运送的,即两者的共性矩阵中的非零元素无须运送,因此非零元素的运送实质是在两个非对称相异矩阵中进行。本文采用的算法对普通简易平衡传输算法结果的优化,以期得到最优结果。该方法需要通过平衡传输表T的子集循环表C来实现,且每一个行\列不含有或有且仅有2个C的单元格。
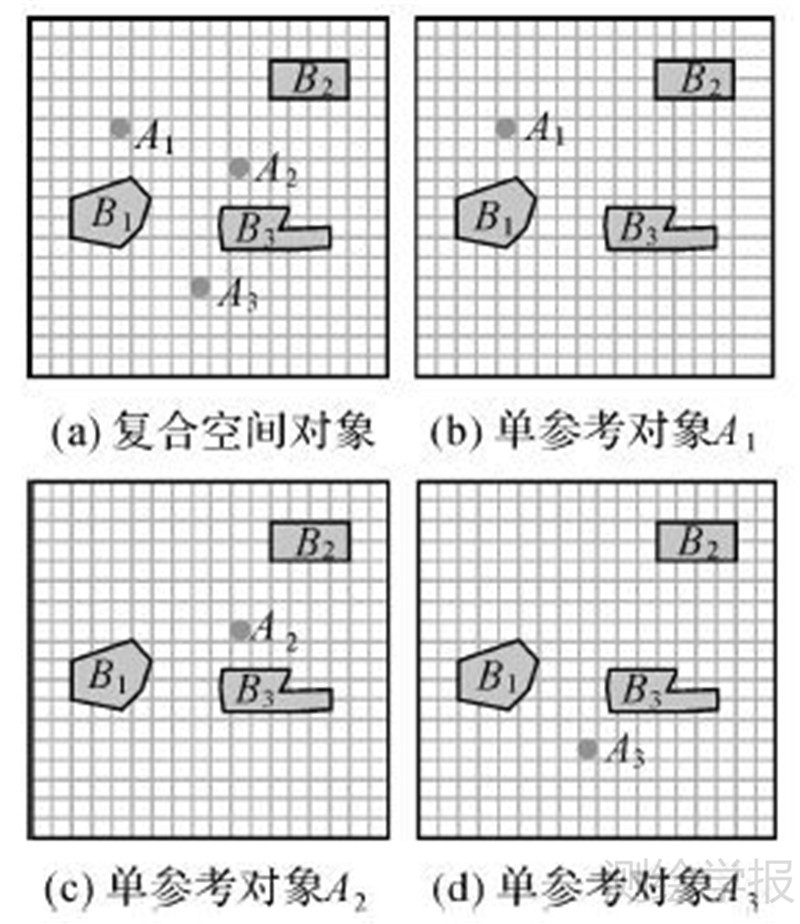
3 算例分析如图 5所示,图 5(a)为大比例尺下的点复合参考对象A和面复合目标对象B,而图 5(b)、(c)为(a)进行综合后的小比例尺地图,其中点复合参考对象A保持点状态不变,但是图 5(a)中的面复合目标对象B在图 5(b)、(c)中变为了点复合目标对象B;图 5(b)、(c)的不同之处在于点复合目标对象的单个点对象间的位置略有差别。先对图 5(b)、(c)进行比较,计算两者与图 5(a)之间的相似度。

|
| 图 5 大比例下点和面转为小比例尺下点和点 Fig. 5 Collapsing a composite point and a composite region at large scale to a pair of point at small scale |
首先,需表示出3种情形下参考对象与目标对象的方向关系矩阵,以图 5(a)为例。如图 6,按照分解的思想,先将复合参考对象A划分为3个单参考对象(图 6(b)—(d))分别求取参考对象与复合目标对象之间的方向关系矩阵。
|
| 图 6 划分复合参考对象A Fig. 6Split the composite reference object A |
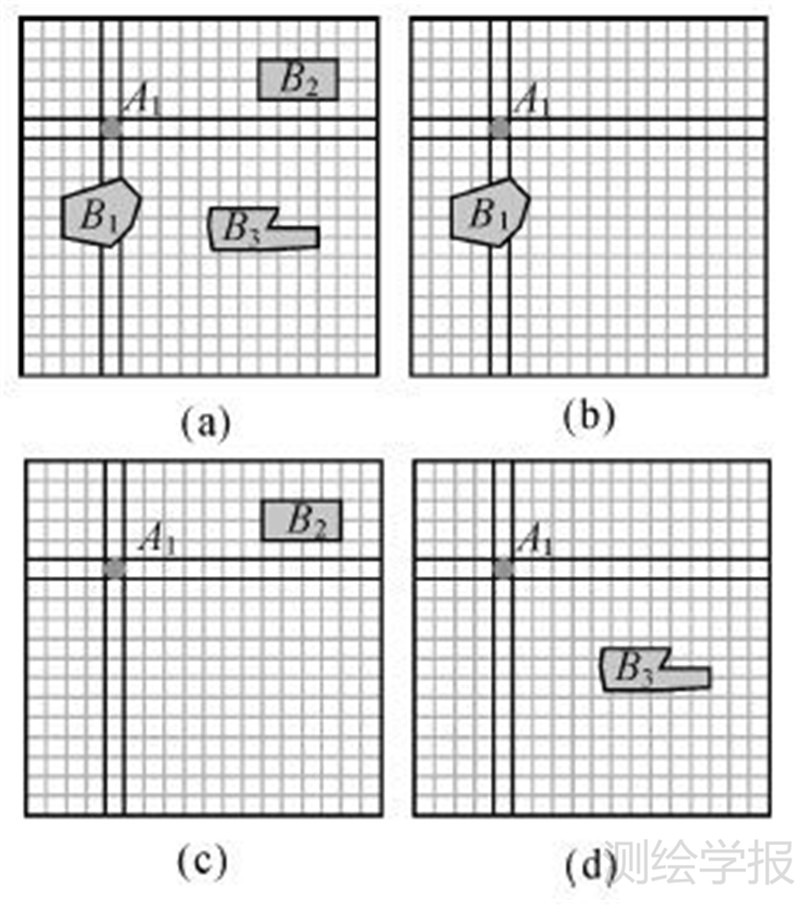
以划分后的A1参考对象为例,再将复合目标对象B为3个单目标对象(图 7)。
|
| 图 7 划分复合目标对象B Fig. 7 Split the composite target object B |
求得单参考对象A1与3个单目标对象的方向关系矩阵如下式
根据目标对象所占网格的权重比值可得A1与目标对象之间的方向关系矩阵如下式
同样的方法可求得单参考对象A2、A3与目标对象之间的方向关系矩阵如式(14)。再通过各单参考对象的所占的网格比例权重,可计算得到复合参考对象A与复合目标对象B之间的方向关系矩阵如式(15)
同理,可得图 6(b)、(c)的方向关系矩阵为
3.2 复合参考对象方向关系相似度计算由于图 5(a)、(b)、(c)的方向关系矩阵均为多元素矩阵,因此通过平衡传输优化算法进行相似度的计算;即首先通过西北角算法得到初始解后再通过传输算法进行优化。以图 5(a)、(b)间的方向相似度计算为例。
首先,得到图 5(a)、(b)与图 5(a)、(c)之间方向关系矩阵的方向相异矩阵(式(18))。得到图 5(a)、(b)之间平衡传输表如图 8,通过西北角算法得到解为:x11=21、x21=11、x11=4

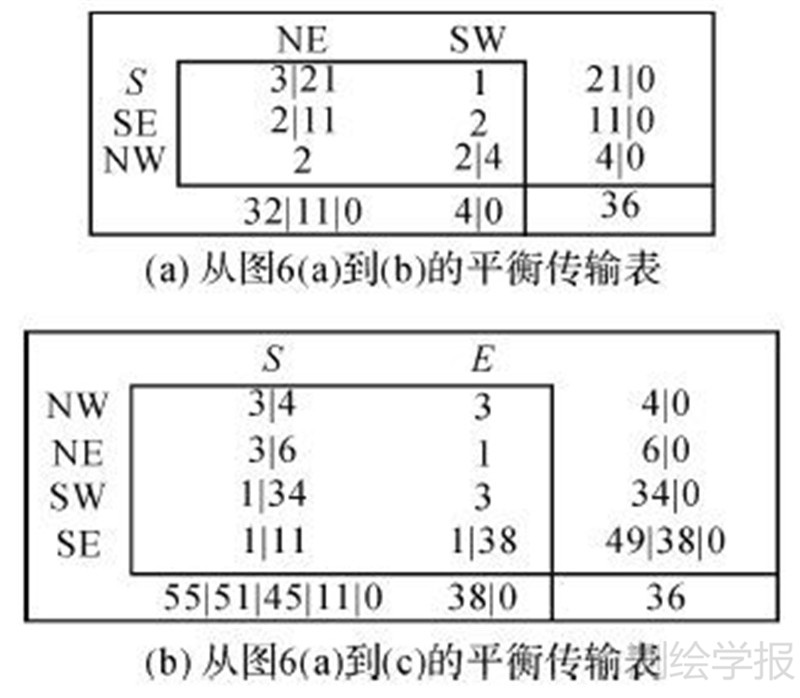
|
| 图 8 实例中的平衡传输表 Fig. 8 TTB in the example |
将这3个解所处的单元格标记为基本单元格(图 9),开始通过传输算法进行优化,首先给所有a、b值赋值;赋值后用cij-ai-bj替代cij;非基本单元格中有负值存在,则还需继续优化,取最小值-4所在单元格为“获取”单元格。

|
| 图 9 优化算法 Fig. 9 Optimum algorithm |
图 9中基本单元格和“获取”单元格所在的单元格不能构成循环表,最后两行行都只有1个可以形成循环表C的单元格,而非0或者2个。因此,当前的解集已是最优。所以图 5(a)、(b)之间的运输代价z1=(3×21+2×11+2×4)/342=0.271 929 825,相似度为s1=1-0.271 929 828/4=0.932 017 543 859 649;
同理,对图 5(a)、(c)的传输表(图 8)进行优化,如图 10先找到基本表的组成单元格;然后对所有的a、b进行赋值;再替换所有的c值;最后找到最小的c值所在的单元格框住作为“获取”单元格并其他基本单元格中找到与该“获取”格可组成循环表的单元格,并找到这些选中的基本单元格中最小的作为选定的“给予”格,将剩余的两个单元格交错的赋为“获取”和“给予”格;最后根据所赋予的符号加上或减去选定的“给予”的解值,并将框格圈入基本格中,将选定的“给予”格剔出基本格中,将最初的c值替换回。
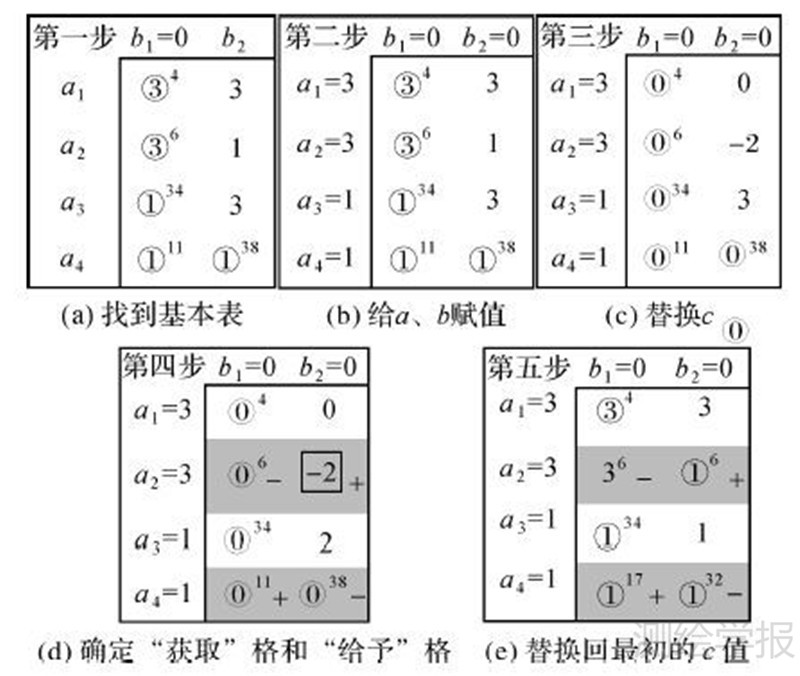
|
| 图 10 优化算法——找到基本表 Fig. 10 Optimum algorithm |
计算得出图 5(a)、(c)之间的运输代价z2=(3×4+1×6+1×34+1×17+1×32)/342=0.295 321 637 426 9,相似度为s2=1-0.295 321 637 426 9/4=0.926 169 590 643 275
而s1=0.932大于s2=0.926 2,亦即图 5(a)、(b)之间的方向相似度大于图 5(a)、(c)之间的方向相似度,结果表明图 5(a)、(b)之间的方向相似度略高于图 5(a)、(c)之间的方向相似度。图 5(a)、(b)中B2都在A1的东北方向,而在图 5(c)中B2在A1的正东方向。因此就这一点而言,从人的主观视觉上判断,图 5(a)、(b)之间的方向相似度也应该是高于图 5(a)、(c)之间的方向相似度的。就图 5(b)、(c)与(a)相似度相关问题,随机对256人进行问卷调查,调查表如表 1所示。从图 11可看出,受访人员给图 5(a)、(b)之间的相似度的打分集中在8~10分,给图 5(a)、(c)之间相似度打分集中在6~8分;调查结果表明,92.58%的受访人员认为图 5(a)、(b)之间的相似度更高,试验结果符合人的认知。
| 问题编号 | 问题内容 | 候选答案 |
| 1 | 与图(a)场景更相似 | 图(a)、(b) |
| 2 | 图(b)与(a)的相似度 | 1~10分 |
| 3 | 图(c)与(a)的相似度 | 1~10分 |
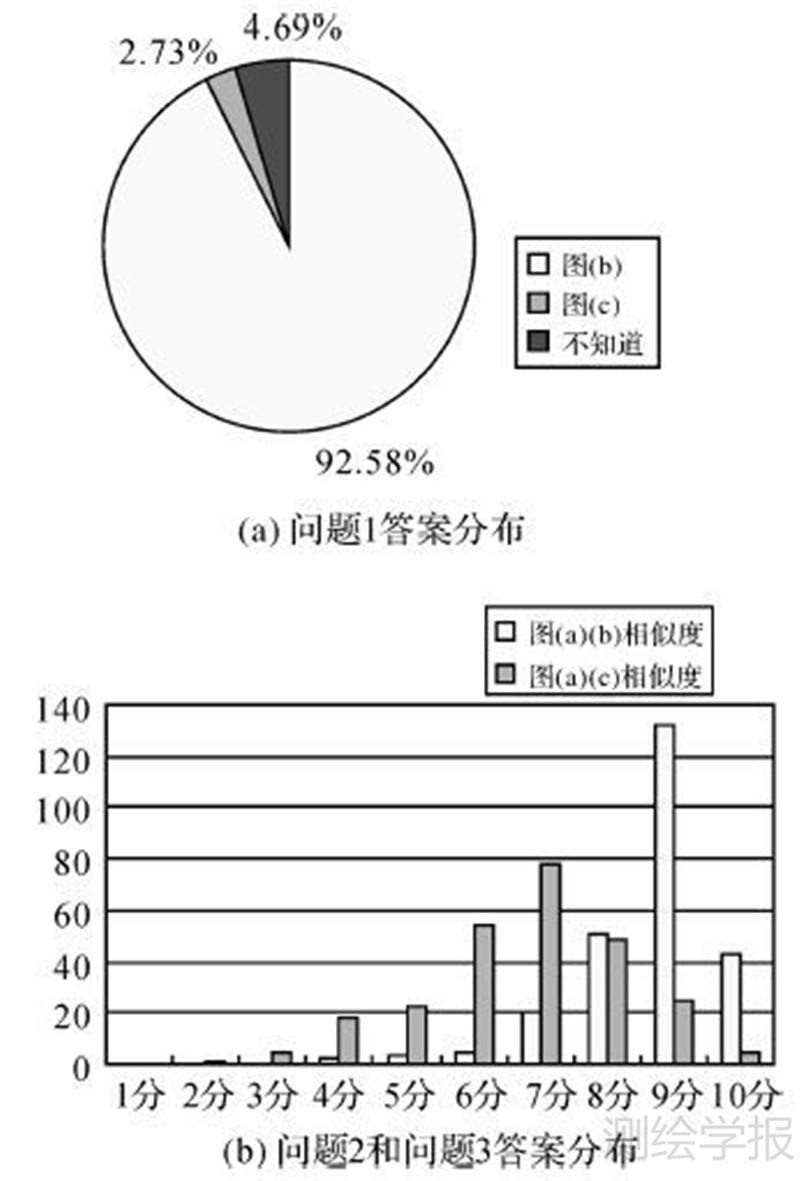
|
| 图 11 调查结果 Fig. 11 Results of questionnaire |
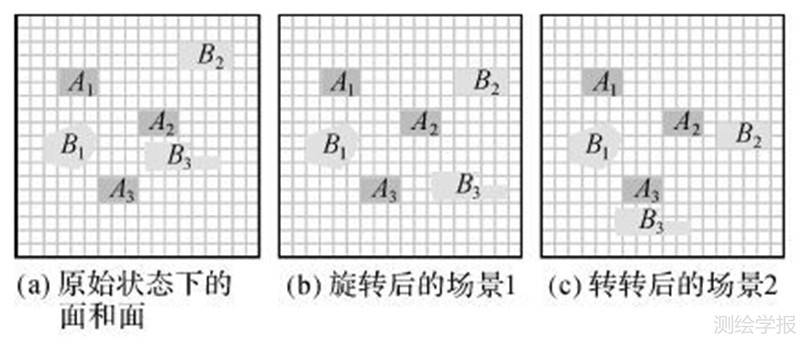
对上面实例进一步扩展,图 12(a)的场景中参考对象和目标对象均为复合面对象,将图 12(a)中目标对象中的两个单对象B2、B3的位置围绕复合对象A进行顺时针旋转,分别得到图 12(b)和(c)状态。
|
| 图 12 旋转目标对象中的部分单对象 Fig. 12 Rotate parts of the complex target object B |
先求出图 12中(a)、(b)、(c)三者的方向矩阵(式(19)),从而得到图 12(a)、(b)与(a)、(c)间的方向相异矩阵(式(20))
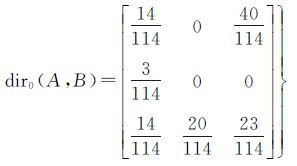
通过优化交通平衡传输算法可以得到图 12(a)、(b)与(a)、(c)传输最小代价以及相似度如下,z1=(1×28+1×6+1×1)/114=0.307 017 543 859 649 1,相似度为s1=1-0.271 929 828/4=0.923 245 614 035 087 7;z2=(4×15+3×7+2×6+1×4)/114=0.850 877 192 982 5,相似度为s1=1-0.271 929 828/4=0.787 280 701 754;由于图 12(b)相较图 12(c),相对图 12(a)旋转的角度较小,因此可以通过视觉直观地判断出图 12(a)、(b)之间的相似度更高,而计算结果s1大于s2,与人的认知一致。现对参考对象进行调整,改变单个参考对象的面积(图 13),先求得图 13(a)、(b)、(c)的方向矩阵(式(21))。

|
| 图 13 改变参考对象面积比例 Fig. 13 Change the area rate of the complex reference object A |
再求得图 13(a)、(b)与(a)、(c)间的方向相异矩阵(式(22))
通过优化交通平衡传输算法可以得到图 13(a)、(b)与(a)、(c)传输最小代价以及相似度。z1=649/798=0.813 283 208 020 050 1,相似度为s1=0.796 679 197 994 987 5;z2=1086/798=1.360 902 255 639 098,相似度为s1=0.659 774 436 090 225 6。由此可见,即使改变参考对象的面积分布,使图 13(a)、(b)与图 13(a)、(c)之间的相似度更接近,本文提出的计算方法仍能准确地判断出正确地方向关系。
4 总 结本文通过方向关系矩阵间的相似度来评判制图综合后复合空间对象结果的合理性。利用方向关系矩阵量化模型的特点,计算多尺度复合空间场景中方向对间的相似度,从而进行比较和评判。
本文模型直接通过网格数目比例分布得到方向关系矩阵,并计算复合对象的方向相似度,简单直观易计算,同时在计算多元素方向关系矩阵间的距离时,采用了传输算法对传统的西北角算法进行优化,使得计算结果更精确。本文的方法解决了复合对象方向关系间的相似性度量问题。下一步工作将优化网格计数方法,顾及多尺度复合对象各个组成部分的几何形状特征优化其计算权重,以提高复合空间对象方向相似度的计算准确度。
| [1] | 闫浩文,褚衍东.多尺度地图空间相似关系基本问题研究[J]. 地理与地理信息科学, 2009, 25(4):42-44, 48. YAN Haowen, CHU Yandong. On the Fundamental Issues of Spatial Similarity Relations in Multi-scale Maps[J]. Geography and Geo-Information Science, 2009, 25(4):42-44, 48. |
| [2] | HAAR R. Computational Models of Spatial Relations[R]. Technical Report:TR-478, MSC-72-03610, Computer Science, University of Maryland, College Park, MD, 1976. |
| [3] | ALLEN J F. Maintaining Knowledge about Temporal Intervals[J]. Communications of the ACM, 1983, 26(11):832-843. |
| [4] | GUESGEN H W.Spatial Reasoning Based on Allen's Temporal Logic[R]. Technical Report:TR-89-049, International Computer Science Institute, Berkley, CA, 1989. |
| [5] | BALBIANI P, CONDOTTA J F, CERRO L F D. A new Tractable Subclass of the Rectangle Algebra[C]//IJCAI '99 Proceedings of the Sixteenth International Joint Conference on Artificial Intelligence. San Francisco:Morgan Kaufmann Publishers Inc., 1999:442-447. |
| [6] | BALBIANI P, CONDOTTA J. A Model for Reasoning about Bidimensional Temporal Relations[C]//Proceedings of Principles of Knowledge Representation and Reasoning(KR). Trento:[s.n.], 1998, 124-130. |
| [7] | CHANG Shikuo, SHI Qingyun, Yan Chengwen. Iconic Indexing by 2-D Strings[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1987, 9(3):413-428. |
| [8] | PAPADIAS D, SELLIS T, THEODORIDIS Y, et al. Topological Relations in the World of Minimum Bounding Rectangles:A Study with R-Trees[C]//Proceedings of the 1995 ACM SIGMOD International Conference on Management of Data. New York:ACM, 1995:92-103. |
| [9] | GOYAL R K.Similarity Assessment for Cardinal Directions between Extended Spatial Objects[D]. Orono:The University of Maine, 2000. |
| [10] | GOYAL R K, EGENHOFER M J. Similarity of Cardinal Directions[M]//JENSEN C S, SCHNEIDER M, SEEGER B, et al. Advances in Spatial and Temporal Databases:Lecture Notes in Computer Science. Berlin Heidelberg:Springer, 2001:36-55. |
| [11] | SKIADOPOULOS S,KOUBARAKIS M.Composing Cardinal Direction Relations[J]. Artificial Intelligence, 2004, 152(2):143-171. |
| [12] | 丁虹. 空间相似性理论与计算模型的研究[D]. 武汉:武汉大学, 2004. DING Hong. A Study on Spatial Similarity Theory and Calculation Model[D]. Wuhan:Wuhan University, 2004. |
| [13] | 郭庆胜, 丁虹. 基于栅格数据的面状目标空间方向相似性研究[J]. 武汉大学学报(信息科学版), 2004, 29(5):447-450. GUO Qingsheng, DING Hong. Similarity for Spatial Directions between Areal Objects in Raster Data[J]. Geomatics and Information Science of Wuhan University, 2004, 29(5):447-450. |
| [14] | 安晓亚. 空间数据几何相似性度量理论方法与应用研究[D]. 郑州:信息工程大学, 2011. AN Xiaoya.Research on Theory,Methods and Applications of Geometry Similarity Measurement for Spatial Data[D]. Zhengzhou:The PLA Information Engineering University, 2011. |
| [15] | 闫浩文, 郭仁忠. 空间方向关系形式化描述模型研究[J]. 测绘学报, 2003, 32(1):42-46. YAN Haowen, GUO Renzhong. Research on Formal Description Model of Directional Relationships[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(1):42-46. |
| [16] | 杜世宏, 王桥, 杨一鹏. 一种定性细节方向关系的表达模型[J]. 中国图象图形学报, 2004, 9(12):1496-1503. DU Shihong, WANG Qiao, YANG Yipeng. A Qualitative Description Model of Detailed Direction Relations[J]. Journal of Image and Graphics, 2004, 9(12):1496-1503. |
| [17] | 杜世宏, 王桥, 杨一鹏, 等. 空间方向关系模糊描述[J]. 计算机辅助设计与图形学报, 2005, 17(8):1744-1751. DU Shihong, WANG Qiao, YANG Yipeng, et al. Fuzzy Description of Spatial Direction Relations[J]. Journal of Computer-aided Design & Computer Graphics, 2005, 17(8):1744-1751. |
| [18] | 杜世宏, 王桥, 魏斌, 等. 空间方向关系粗糙推理[J]. 测绘学报, 2003, 32(4):334-338. DU Shihong, WANG Qiao, WEI Bin, et al. Spatial Orientational Relations Rough Reasoning[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4):334-338. |
| [19] | 曹菡, 陈军, 杜道生. 空间目标方向关系的定性扩展描述[J]. 测绘学报, 2001, 30(2):162-167. CAO Han, CHEN Jun, DU Daosheng. Qualitative Extention Description for Cardinal Directions of Spatial Objects[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(2):162-167. |
| [20] | 何建华, 刘耀林. GIS中拓扑和方向关系推理模型[J]. 测绘学报, 2004, 33(2):156-162. HE Jianhua, LIU Yaolin. An Integrated Model for Topology & Direction Relation Reasoning[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2):156-162. |
| [21] | 吴静, 程朋根, 陈斐, 等. 空间目标的方向关系定性推理[J]. 测绘学报, 2006, 35(2):160-165. WU Jing,CHENG Penggen,CHEN Fei,et al. Qualitative Reasoning for Direction Relation of Spatial Objects[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2):160-165. |