当前对于道路化简采取的方法,原理上基本与曲线化简一致[1]。但在具体制图综合操作中,道路化简并不是简单的曲线化简,而是需要综合考虑道路与道路之间以及道路与要素之间相互影响的操作。化简前后的道路数据,不但要保持一定精度范围内的位置和形态特征,还需要保持内容表达的一致性,即要素间空间关系的一致性。如果歪曲了实体目标之间的空间关系,就可能产生空间冲突,从而无法从不同尺度传递正确的地理空间知识。
在人机交互的道路化简的过程中,制图员不仅考虑了道路自身的形态,而且对于道路与道路之间、道路与其他要素之间的空间关系也进行了综合考虑。比较经典的曲线化简方法有,Douglas-Peucher算法(D-P算法)、垂距法、BLG(binary line generalization tree)、Li-Open-Shaw算法等[2, 3, 4, 5]。近年来随着对曲线本质认识的深入,出现了基于曲线弯曲识别的曲线化简方法,该方法不仅能够有效地避免化简中出现的曲线自相交问题,而且通过建立曲线弯曲二叉树[6]、多叉树等层次结构,为曲线的层次性表达提供了良好的支撑,化简效果也比较符合人类的认知规律。主要的弯曲识别算法有拐点法、单调链法、Delaunay三角网法、斜拉式弯曲识别算法、基于通视性的弯曲识别及塑形法等[7, 8, 9, 10, 11, 12]。现有的方法在对于单条曲线的化简上已经取得了很好的效果,然而在实际应用中由于已有化简方法并未或很少考虑化简前后曲线与曲线之间,曲线与其他要素之间的空间关系一致性,导致化简结果出现要素冲突、空间关系不一致性等情况。因此必须对曲线弯曲化简算法的过程加以约束,使之更为有效地避免化简前后产生的要素自身、要素间冲突。
本文从基本弯曲的角度,首先以弯曲为单元分析道路化简后可能出现的各种空间冲突;然后提出相应的空间冲突判别规则,对化简产生空间冲突的类型进行判定;最后利用弯曲化简的可控性和弯曲组的间接化简策略实现对化简冲突的避免,并对该冲突避免方法的效果进行试验验证。
1 道路化简导致空间冲突原因与类型分析空间冲突可定义为,空间数据所表达的世界与客观世界不一致,导致数据无法正确和有效地表现客观世界所对应地理实体的结构和关系[13]。本文是在原数据本身不存在空间冲突的前提下讨论,因此文中将化简后造成空间关系不一致情况统称为“化简冲突”。针对道路的形态变化特点,对化简冲突的类型归纳如下。
1.1 道路与道路之间的化简冲突道路由于其连通性特征,在地图上往往是以相互交错的网状形式出现,因此在道路化简很可能导致平交道路间连通关系的改变。道路常见的空间关系表现为相交和相离[14, 15, 16, 17, 18, 19],化简后道路的形态改变很容易对道路之间的空间关系造成破坏(如交叉路口断开、网眼结构被破坏等)。因此,道路化简前后节点的位置、道路连通性和网眼完整性是需要重点考虑的问题。本文通过分析道路化简过程中道路间的空间关系变化,列举了4种常见的化简冲突如1所示。
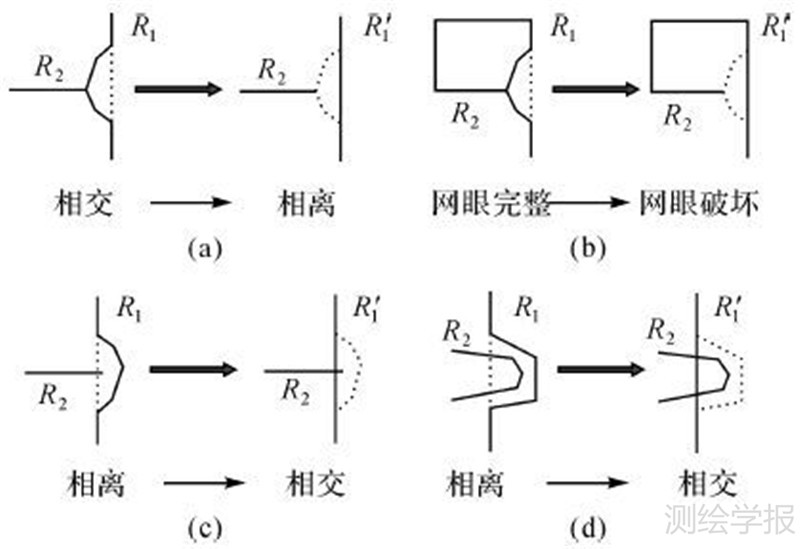
图 1中实线表示道路曲线,虚线表示弯曲的基线,即连接弯曲起止节点的线段。弯曲在删除后的形态简化为弯曲的基线。图 1(a)中道路R1的弯曲化简导致了R1与R2相交节点的消失,本文在图 1(b)中进一步延伸,即节点的消失导致网眼的封闭性遭到破坏;图 1(c)中由于道路R1的弯曲化简导致了一个新节点的产生,这同样也是违背了空间关系的一致性要求;图 1(d)中作了进一步的延伸,即两条道路上的两弯曲出现类似嵌套时,如只对R1进行化简则也会产生道路相交的情况,然而若相交部分的弯曲同时化简则可能不会出现冲突,化简策略在第3节中详细论述。
|
| 图 1 道路间化简冲突 Fig. 1 Simplification conflict between roads |
对于某些地物设施如居民地来说,道路是读图者判断居民地位置的重要参照(例如某重要设施标定在某条道路的右侧、某设施建立在道路之上以及某建筑周围有道路环绕等)[17]。道路与居民地之间的空间关系主要表现为线与点的空间关系以及线与面的空间关系。道路化简过程中弯曲的删除引起道路局部的位置发生了偏移,对于与其邻近要素的空间关系必然会产生一定的影响,从而可能导致化简冲突的产生。本文归纳了以下道路与点状、面状居民地之间的化简冲突,如图 2所示。
|
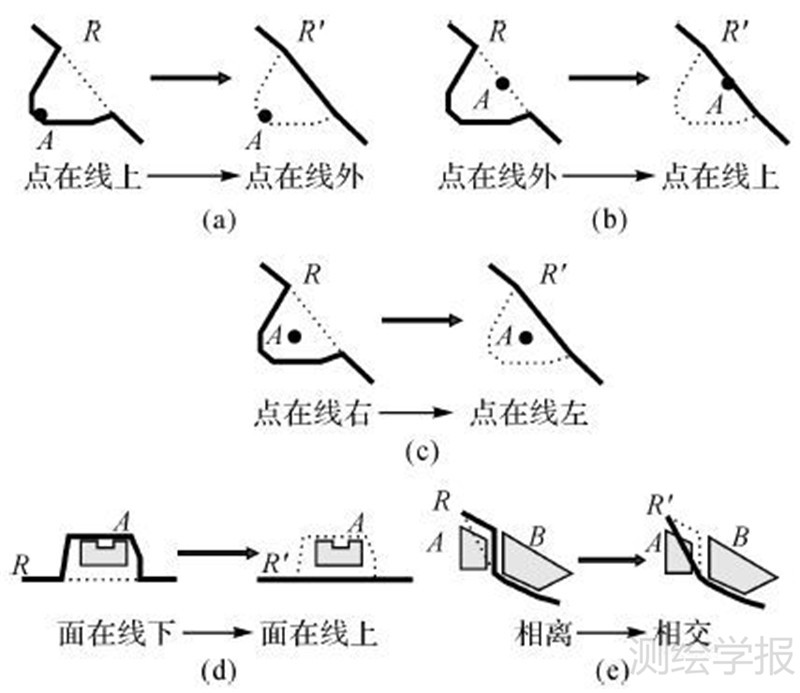
| 图 2 道路与居民地化简冲突 Fig. 2 Simplification conflicts between roads and habitation |
根据点线间的拓扑关系,本文列举了两种互为对偶的典型道路与点状居民地化简冲突,如图 2(a)、(b)所示,道路R在化简后导致点A与R间的拓扑关系发生了改变。图 2(c)中作了进一步延伸,虽然在化简前后点A与R的拓扑关系均是相离,但是A与R的方位关系发生了改变,化简前A在道路的右侧,化简后则A在道路的左侧,从弯曲的角度来看即点A从弯曲与基线围成的弯曲面内变为了A在基线的一侧。
同样的,对于面状居民地来说也存在着与图 2(c)类似的情况,如图 2(d)所示,道路的化简导致了居民地与道路的位置关系发生了改变。图 2(e)中,由于弯曲化简,道路与居民地产生了明显的相交冲突。
1.3 道路与水系之间的化简冲突考虑到水系与人工设施之间关系的特殊性,水系与道路也有着特殊的化简冲突。根据文献[16]中对道路与水系间空间冲突的总结,道路与水系的关系应该满足“道路不能入水”,进一步细分为:道路不能落入并行的河流、湖泊或水库中,单线道路不能与河流小范围、多点或小角度相交等。通过对道路化简后形态变化的分析,本文总结了以下3种道路与水系的化简冲突。
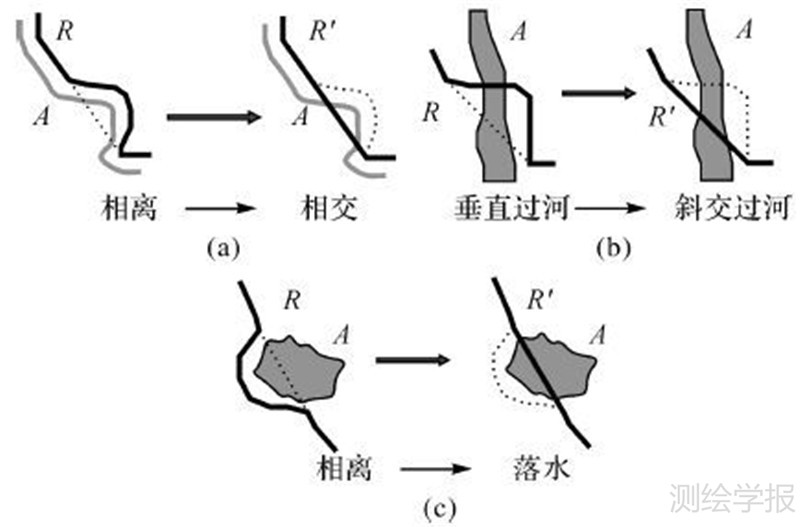
沿河道路在化简后出现了与河流交叉的情况,如图 3(a)所示,道路R在化简后与线状水系出现相交的化简冲突。面状水系与道路的相交形态变化,如图 3(b)所示,道路在化简后,由垂直过河变为斜交过河,因此将其视为化简冲突。图 3(c)所示化简冲突是图 3(a)类型的延伸,即沿面状水系的道路在化简后落水,产生化简冲突。
|
| 图 3 道路与水系之间的化简冲突 Fig. 3 Simplification conflict between roads and waterbodies |
道路与其他要素的化简冲突基本上也是线与点、线与面的化简冲突,因此本文就以上常见的3种要素为例进行讨论,以验证本文方法的可行性。
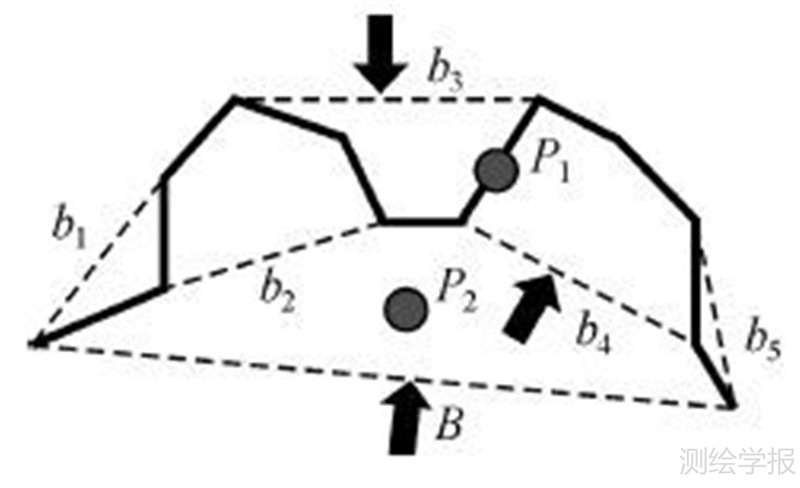
2 基于弯曲的道路化简和冲突判别方法 2.1 基于弯曲的道路化简特点基于弯曲的化简特点总而言之就是独立性和层次性。独立性表现在,基本弯曲是独立的,即一个基本弯曲不再包含其他弯曲,是曲线化简中删除的最小单元,其化简结果在局部可以通过连接基线进行模拟;层次性表现在,复合弯曲是层层嵌套的,一个复合弯曲由多个基本弯曲或低一级的复合弯曲组成,通过建立弯曲的层次结构可以比较容易模拟任意化简尺度上的化简结果。弯曲的这两个特性,使得在道路化简过程中能够很容易地确定化简冲突发生的位置和尺度,如图 4所示。
|
| 图 4 化简冲突发生位置示例 Fig. 4 Position of simplification conflict occurs |
由图 4首先可以推断出化简冲突发生在基本弯曲b3和b4处,即当这两处的弯曲进行化简时将产生图 2(a)所示类型的化简冲突;同时当对复合弯曲B进行化简时也会与点P1、P2产生图 2(a)、(c)类型冲突。由此可见,基于弯曲的化简方法能有效地定位化简冲突发生的位置和尺度,从而能够有效地对冲突进行预判,并根据预判的结果采取相应的避免冲突的化简策略。一般的道路化简方法,如经典的D-P算法,需要在化简结束后对整条道路进行再次的冲突检测才能发现冲突,无法对某一条道路局部位置的化简冲突进行预判和避免,并且冲突的改正过程也比较烦琐。
2.2 基于弯曲的化简冲突判别由第1节的化简冲突归纳可以看出,弯曲化简后是否产生冲突,与弯曲的形态以及弯曲基线的位置有着密切的关系。以弯曲为化简单元的道路化简,在删除某个弯曲后,该弯曲即被其基线所替代。因此,可以通过分析弯曲基线以及基线与弯曲所围成的弯曲面与冲突对象的空间关系,进行化简冲突的预测。依据第1节中归纳的冲突类型,本文设计了以下判断化简冲突的规则(表 1)。这些规则的意义在于,对于满足删除条件的弯曲进行化简冲突规则的判定可以预测出化简后是否存在化简冲突、化简冲突的类型以及冲突对应的弯曲。需要说明的是,在实际的操作中并没有一个确切地判断是否道路与斜交的标准,对于斜交过河的判断本文所选定相交角度(取锐角)的阈值为60°,若与面状河流是否斜交则判断道路与河流两侧线段的相交角度之和是否小于120°,该阈值可以根据制图要求适当调整。
| 类型编号 | 冲突名称 | 判定规则 |
| 1 | 相交—相离(点) | 点在弯曲上∩点不与弯曲起始点重合 |
| 2 | 相交—相离(线) | 线与弯曲相交∩交点不与弯曲起始点重合∩线不与基线相交 |
| 3 | 相离—相交(点) | 点在基线上∩点不与弯曲起始点重合 |
| 4 | 相离—相交(线) | 线与基线相交∩交点不与弯曲起始点重合∩线不与弯曲相交 |
| 5 | 相离—相交(面) | 面与基线相交∩与弯曲曲线不相交 |
| 6 | 弯曲内—弯曲外(点) | 点在弯曲与基线围成的多边形内 |
| 7 | 弯曲内—弯曲外(外) | 面在弯曲与基线围成的多边形内 |
| 8 | 垂直过河—斜交过河(线) | 弯曲与河流(线)相交∩基线与河流角度小于60° |
| 9 | 垂直过河—斜交过河(面) | 河流(面)与弯曲相交∩基线与河流两侧线段相交角度之和小于120° |
冲突类型由上一节中所列举的判定规则进行判断。在定位到化简冲突发生的位置和类型后,需要利用弯曲和“弯曲组”化简的特性对化简冲突进行避免。
3.1 利用弯曲化简特性避免化简冲突首先,对于交叉路口处弯曲化简导致路口的拓扑关系破坏的情况(如图 1(a)、(b)所示),可先对道路进行断链处理,从而将化简操作限制在道路相交节点之间。
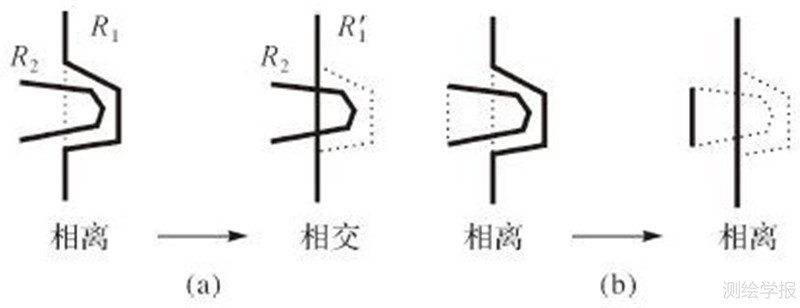
其次,对于弯曲与弯曲之间相离的化简冲突还需考虑一种产生冲突的特殊情况:①如图 5(a)所示,当仅探测到冲突的R1化简时则会产生冲突;②如图 5(b)所示,当R1与R2两个弯曲同时删除时则不会出现冲突。因此针对两弯曲可能存在同时化简的情况,当检测到R1化简存在图 5所示冲突时,判断R2是否也满足化简条件,若满足则两个弯曲同时进行化简;若R2不满足,则同时保留R1、R2。
|
| 图 5 道路之间化简的特殊情况 Fig. 5 Special situation of road simplification |
然后,对道路与其他要素存在化简冲突的弯曲采取保留策略。该部分弯曲的化简是产生化简数据前后不一致的根源,删除会导致化简冲突的产生,因此需要保留。
最后,优化“弯曲组”的化简方法,间接化简存在冲突的道路弯曲。在对产生化简冲突的弯曲进行保留的同时,为了起到间接化简该部分弯曲的目的,需要对其相邻弯曲进行优先化简,这就涉及“弯曲组”的化简策略问题。
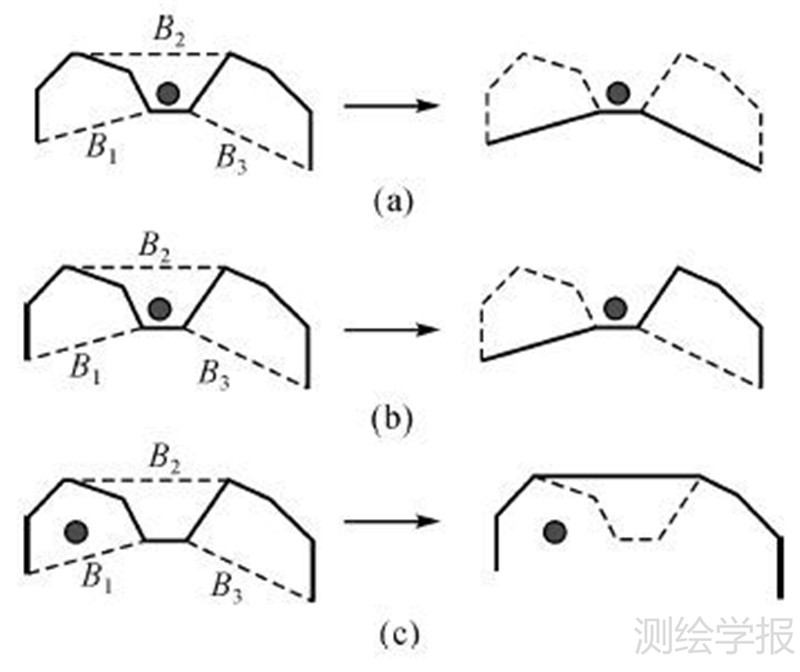
3.2 化简过程中弯曲组的化简弯曲的一个重要特性是连续性,即从曲线的一个方向来看,凹弯曲和凸弯曲交替出现,凹弯曲的相邻弯曲必然是凸弯曲,反之亦然。因此由相邻弯曲的共边关系可知,一个弯曲的化简必然会对它相邻的弯曲产生影响,且影响范围仅限于该弯曲的相邻异侧弯曲。如图 6(a)所示,本文把这种3个相邻的基本弯曲称为一个弯曲组,其化简情况称为弯曲组化简。
|
| 图 6 弯曲组的化简方法示例 Fig. 6 Simplification case of bend |
文献[3]中对弯曲组同时满足化简条件时的化简采用最小位移误差作为判断标准。本文在此基础上讨论弯曲组中存在化简冲突时的化简方式,当弯曲组中遇到有化简冲突的弯曲时按照以下规则进行化简:规则1,小于化简阈值,但存在化简冲突的弯曲对象,则视为需要保留的弯曲,从待删除弯曲对象中剔除;规则2,存在化简冲突的弯曲,若其相邻弯曲小于化简弯曲阈值则优先删除,从而间接化简冲突部分弯曲。
如图 6所示,B1、B2、B3是一个弯曲组。根据以上的两条化简规则,存在以下几种常见的化简情况:
(1) 若存在化简冲突的弯曲在三元弯曲组的中间位置,其相邻弯曲均是待删除弯曲,则对这相邻两个弯曲进行删除。如图 6(a)所示,假设B1、B2、B3均为待删除弯曲,而B2由于存在化简冲突,因此对B2进行保留,同时对B1、B3直接进行删除。
(2) 若存在化简冲突的弯曲在三元弯曲组的中间位置,只有一侧是待删除弯曲,则直接删除该侧弯曲。如图 6(b)所示,假设B1、B2为待删除弯曲,B3为大于删除阈值的弯曲,则只对B1进行删除操作。
(3) 若存在化简冲突的弯曲在三元弯曲组两侧的位置,则直接删除与之相邻的待删除弯曲(若与之相邻的是大于删除阈值的弯曲则不进行操作)。如图 6(c)所示,假设B1、B2、B3均为待删除弯曲,而B1由于存在化简冲突,因此直接删除弯曲B2,达到同时化简B1、B3的效果。
3.3 道路化简流程步骤1:先对道路网进行拓扑预处理。在道路相交的交叉节点处进行断链,使得弯曲化简的节点对象始终在道路交叉节点之间,而不会影响到相交处的道路节点。
步骤2:对道路网进行弯曲提取。道路弯曲在形态上相对于等高线、海岸线等较为简单,因此考虑到道路弯曲的弯曲识别的效率以及循环提取弯曲时的时间成本,本文采用拐点法对道路进行弯曲提取,具体原理请参看文献[9]。
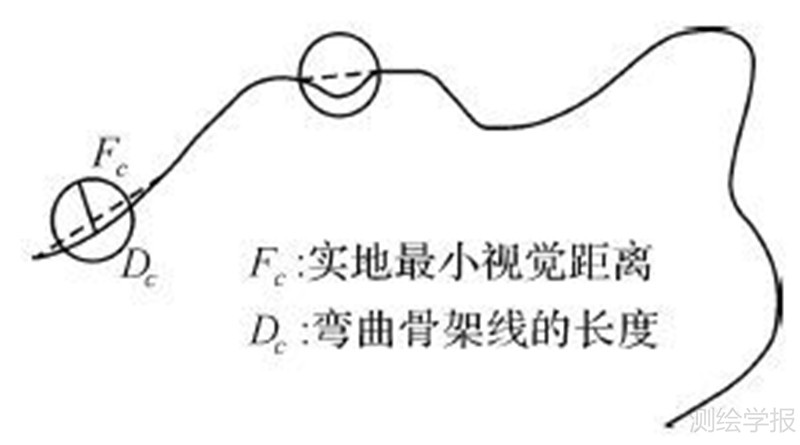
步骤3:基于人的视觉原理设定划分待删除道路弯曲对象。该划分阈值依据人的视觉原理,即人眼在地图上最小的可视目标(SVO),将其表示为具有某一特定直径D的圆[8]。以弯曲基线的中点为圆心,以D 为直径作一个圆(D为图上距离单位mm),若弯曲的所有节点都在圆内则认为该弯曲满足删除条件,列为待删除对象,如图 7所示。
步骤4:对待删除道路弯曲进行基于弯曲的化简冲突检测。对于存在化简冲突的采取相应的冲突消除策略进行化简;对于无化简冲突的弯曲采取一般的弯曲组删除方法进行删除化简。
步骤5:判断步骤4中执行弯曲删除操作的次数,若为0,则表示该当前所得化简结果与上一次化简的结果(第一次时为原图)一致,即满足化简要求,化简结束;若>0则表示所得化简结果与上一次化简结果不一致,因此为了保证化简结果满足化简要求,需要回到步骤2对当前结果提取新的弯曲,并再次执行化简判断。
步骤6:循环步骤2—5,直至化简结束。
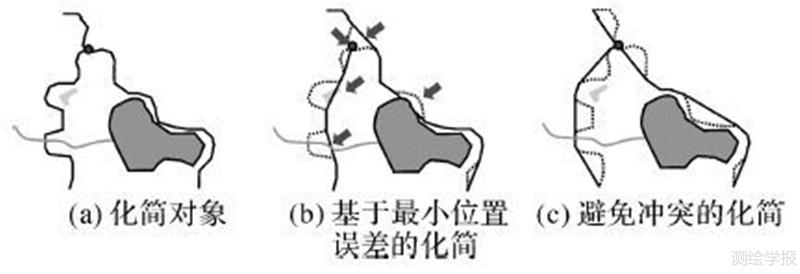
采用冲突避免的策略化简效果如图 8所示,相比于最小位移误差的化简方法,冲突避免的化简方法能够有效地预防化简冲突的产生。
|
| 图 8 冲突避免的道路化简效果示例 Fig. 8 Simplification case of avoid conflict |
同时值得注意的是,理论上避免化简冲突的化简策略会导致化简精度上有所牺牲[18, 20, 21],即在弯曲删除对象的位置误差上(删除弯曲面积除以曲线长度)要略高于最小位置误差原则的化简方法,原因是在对有冲突部分弯曲进行保留的同时优先删除该弯曲相邻的兄弟弯曲。不过一般来说,在制图综合对局部区域的综合处理中避免空间冲突比位置误差的优先级要高,且在实际应用中因避免冲突而产生的位置误差所占比例是比较小的,因此该部分精度上的牺牲处于可接受范围内。
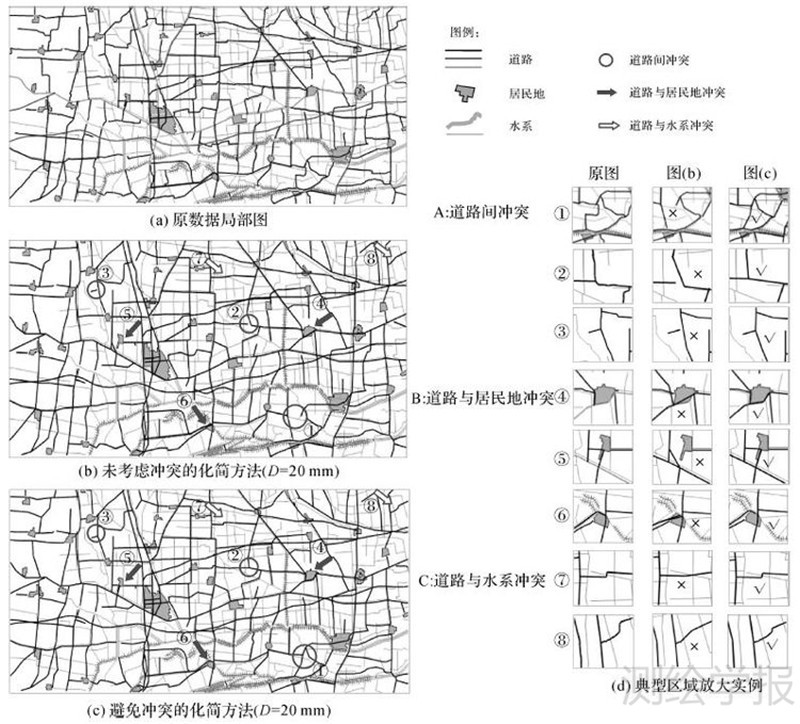
4 结 论本文分别采用基于最小位置误差的一般化简方法和本文提出的避免冲突的化简方法对道路要素进行了化简结果对比。如图 9所示,展示了化简阈值D取20 mm时化简结果的局部截图,图中包含了部分典型的化简冲突,图中标注①—⑧为部分典型的化简冲突对比。由放大图可以看出,未考虑化简冲突的方法在化简后产生了较多的空间冲突,而本文的基于弯曲的化简冲突避免方法能够有效地避免各类化简冲突的产生。本文还分别在不同SVO直径下的化简作对比试验,相关数据统计如表 2所示。其中SVO的直径D分别取值10 mm、20 mm、50 mm。
|
| 图 9 局部化简效果对比 Fig. 9 Comparison between two simplification methods |
| 化简方法 | SVO直径/mm | 避免冲突数量 | 总节点数 | 化简后节点数 | 总连通度 | 化简后连通度 | ||
| 道路间 | 与居民地 | 与水系 | ||||||
| 一般的化简方法 | 10 | — | — | — | 9253 | 4493 | 4597 | 4251 |
| 冲突避免的化简方法 | 10 | 384 | 37 | 259 | 9253 | 5761 | 4597 | 4417 |
| 一般的化简方法 | 20 | — | — | — | 9253 | 2781 | 4597 | 3755 |
| 冲突避免的化简方法 | 20 | 565 | 44 | 407 | 9253 | 4529 | 4597 | 4379 |
| 一般的化简方法 | 50 | — | — | — | 9253 | 1852 | 4597 | 3588 |
| 冲突避免的化简方法 | 50 | 633 | 56 | 481 | 9253 | 4168 | 4597 | 4351 |
结合图 9和统计表 2可以得出以下3个结论:
(1) 随着删除阈值直径D的不断增大,由道路化简而产生的冲突越多,一般的化简方法无法避免冲突的产生,而本文中的化简冲突避免方法,能够有效地识别和避免道路弯曲化简导致的各类冲突,确保了化简前后地图要素间空间关系的一致性。
(2) 两种化简方式在随着化简强度的增大,化简力度即节点数量的变化有明显区别,一般化简方法节点的减少倍数呈现与直径D相同的倍数关系,化简力度在增大,但出现了更多的化简冲突;而本文的化简方法由于对化简冲突部分进行了识别和保留,随着直径D的增大,更多的化简冲突被保留,因此节点数量减少的趋势在逐渐降低,化简力度虽然小于一般的化简方法,但化简的正确性得到了保持。
(3) 通过连通度的对比可以发现,一般的化简方法由于没有考虑道路间节点的特殊性,对道路的连通性造成一定程度的破坏,而本文的方法则能够有效地对道路化简前后的连通性进行保持。
值得一提的是,由于采用了弯曲作为控制化简冲突的对象,明确了冲突发生的范围和化解冲突的操作单元,相比于一般的化简方法需要在化简操作结束后才能对化简冲突进行判断和处理,本文方法的另一个优势是能够实时有效地在化简过程中避免化简冲突的产生,从而确保化简前后道路之间以及道路与其他要素之间空间关系的一致性。
| [1] | 王家耀. 普通地图制图综合原理[M]. 北京:测绘出版社, 1993:78-84. WANG Jiayao.The Principle of Cartographic Generalization for General Map[M]. Beijing:Publishing House of Surveying and Mapping, 1993:78-84. |
| [2] | DOUGLAS D H, PECUCKER T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J].The Canadian Cartographer, 1973, 10(2):112-122. |
| [3] | MCMASTER R B. Automated Line Generalization[J]. Cartographica, 1987, 24(2):74-111. |
| [4] | LI Zhilin,OPENSHAW S. Algorithms for Automated Line Generalization Based on a Natural of Objective Generalization[J]. International Journal of Geographic Information Systems, 1992, 6(5):373-389. |
| [5] | 张青年, 廖克. 基于结构分析的曲线概括方法[J]. 中山大学学报(自然科学版), 2001, 40(5):118-121. ZHANG Qingnian, LIAO Ke. Line Generalization Based on Structure Analysis[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2001, 40(5):118-121. |
| [6] | 艾廷华, 郭仁忠, 刘耀林. 曲线弯曲深度层次结构的二叉树表达[J]. 测绘学报, 2001, 30(4):343-348. AI Tinghua, GUO Renzhong, LIU Yaolin. A Binary Tree Representation of Curve Hierarchical Structure in Depth[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4):343-348. |
| [7] | 翟仁健, 武芳, 朱丽, 等. 曲线形态的结构化表达[J]. 测绘学报, 2009, 38(2):175-182. ZHAI Renjian, WU Fang, ZHU Li, et al. Structured Representation of Curve Shape[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(2):175-182. |
| [8] | 翟仁健, 武芳, 朱丽, 等. 利用地理特征约束进行曲线化简[J]. 武汉大学学报(信息科学版), 2009, 34(9):1021-1024. ZHAI Renjian,WU Fang,ZHU Li,et al.Line Simplification Method Based on Geographic-Feature Constraint[J]. Geomatics and Information Science of Wuhan University, 2009, 34(9):1021-1024. |
| [9] | 朱强, 武芳, 钱海忠, 等. 一种顾及认知规律的曲线弯曲识别方法[J]. 辽宁工程技术大学学报(自然科学版), 2014, 33(4):521-527. ZHU Qiang, WU Fang, QIAN Haizhong, et al. An Identification Method of Line Curves Based on Cognitive Laws[J]. Journal of Liaoning Technical University:Natural Science, 2014, 33(4):521-527. |
| [10] | 操震洲, 李满春, 程亮. 曲线弯曲的多叉树表达[J]. 测绘学报, 2013, 42(4):602-607. CAO Zhenzhou, LI Manchun, CHENG Liang. Multi-way Trees Representation for Curve Bends[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4):602-607. |
| [11] | 彭东亮, 邓敏, 邓慧敏. 更充分利用独立弯曲结构的线状要素Morphing变换方法[J]. 测绘学报, 2014, 43(6):637-644, 652. DOI:10.13485/j.cnki.11-2089.2014.0100. PENG Dongliang, DENG Min, LIU Huimin. Morphing Transformation of Linear Features by Using Independent Bend Structures More Sufficiently[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6):637-644, 652. DOI:10.13485/j.cnki.11-2089.2014.0100. |
| [12] | 钱海忠, 武芳, 陈波, 等. 采用斜拉式弯曲划分的曲线化简方法[J]. 测绘学报, 2007, 36(4):443-449, 456. QIAN Haizhong, WU Fang, CHEN Bo. Simplifying Line with Oblique Dividing Curve Method[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4):443-449, 456. |
| [13] | 詹陈胜, 武芳, 翟仁健, 等. 基于拓扑一致性的线目标空间冲突检测方法[J]. 测绘科学技术学报, 2011, 28(5):387-390. ZHAN Chensheng, WU Fang, ZHAI Renjian, et al. A Method of Spatial Conflicts Detection for Linear Objects Based on Topological Consistency[J]. Journal of Geomatics Science and Technology, 2011, 28(5):387-390. |
| [14] | 刘万增. GIS数据库更新中空间冲突自动检测方法研究[D]. 徐州:中国矿业大学, 2005. LIU WanZeng. An Automatic Method of Spatial Conflict in GIS Database Updating[D]. Xuzhou:China University of Mining & Technology, 2005. |
| [15] | 陈军, 刘万增, 李志林, 等. 线目标间拓扑关系的细化计算方法[J]. 测绘学报, 2006, 35(3):255-260. CHEN Jun, LIU Wanzeng, LI Zhilin, et al. The Refined Calculation Method of Topological Relationships Between Line Objects[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(3):255-260. |
| [16] | 刘万增, 赵仁亮. 水系要素更新中空间冲突的自动检测研究[C]//中国地理信息系统协会第八届年会论文集. 北京:中国地理信息系统协会, 2004. LIU Wanzeng, ZHAO Renliang. Research on Auto Special Conflict Detection in Water Feature Update[C]//China Association for Geographic Information Systems, Proceedings of the Eighth Annual Conference. Beijing:China Association for Geographic Information Systems, 2004. |
| [17] | 郭庆胜, 吕秀琴, 蔡永香. 图形简化过程中空间拓扑关系抽象的规律[J]. 武汉大学学报(信息科学版), 2008, 33(5):520-523. GUO Qingsheng, LU Xiuqin, CAI Yongxiang. Rule of the Spatial Topological Relation Abstraction in Graphic Simplification Process[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5):520-523. |
| [18] | 武芳, 朱鲲鹏. 线要素化简算法几何精度评估[J]. 武汉大学学报(信息科学版), 2008, 33(6):600-603. WU Fang, ZHU Kunpeng. Geometric Accuracy Assessment of Linear Features' Simplification Algorithms[J]. Geomatics and Information Science of Wuhan University, 2008, 33(6):600-603. |
| [19] | NEDAS K A, EGENHOFER M J, WILMSEN D. Metric Details of Topological Line-line Relations[J]. International Journal of Geographical Information Science, 2007, 21(1):21-48. |
| [20] | 邓敏, 樊子德, 刘慧敏. 层次信息量的线要素化简算法评价研究[J]. 测绘学报, 2013, 42(5):767-773, 781. DENG Min,FAN Zide, LIU Huimin. Performance Evaluation of Line Simplification Algorithms Based on Hierarchical Information Content[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5):767-773, 781. |
| [21] | 朱鲲鹏. 线要素化简算法质量评估[D]. 郑州:信息工程大学, 2007. ZHU Kunpeng. Quality Assessment of Linear Features' Simplification Algorithms[D]. Zhengzhou:The PLA Information Engineering University, 2007. |