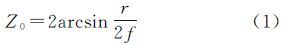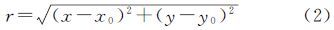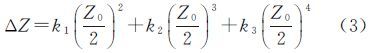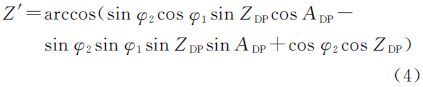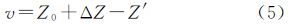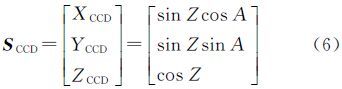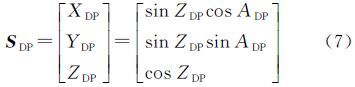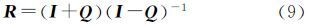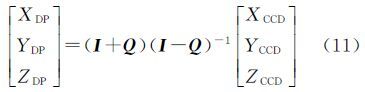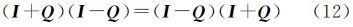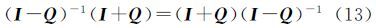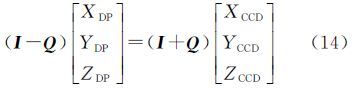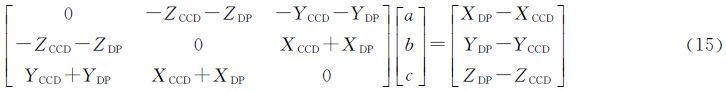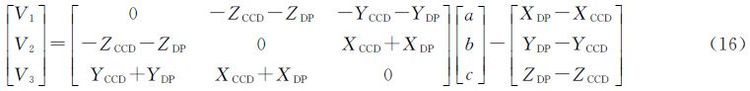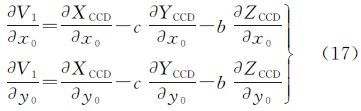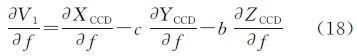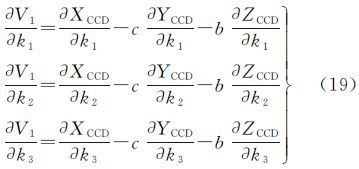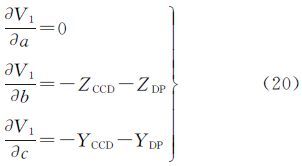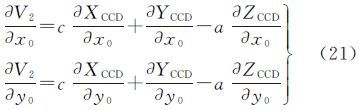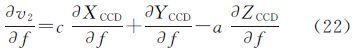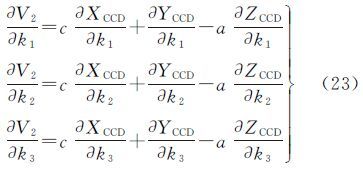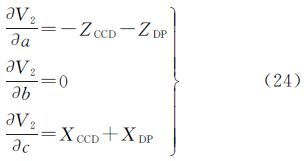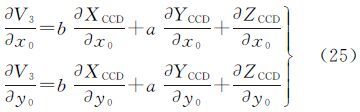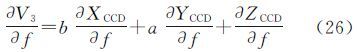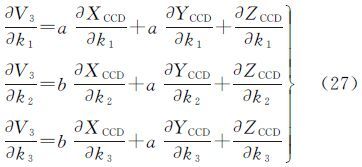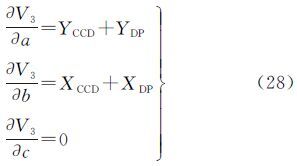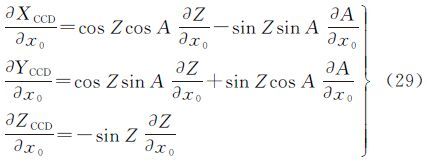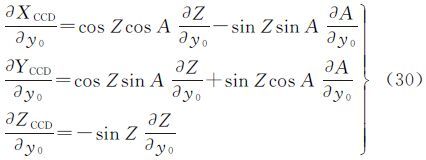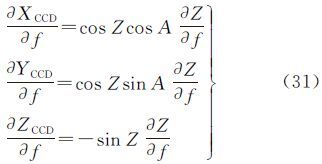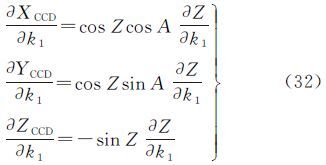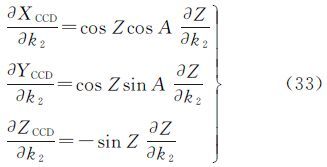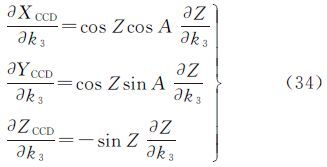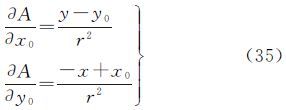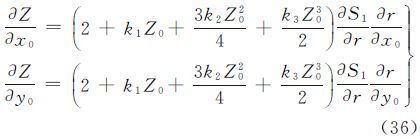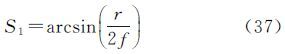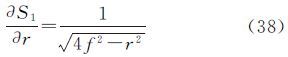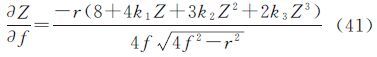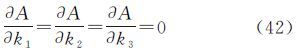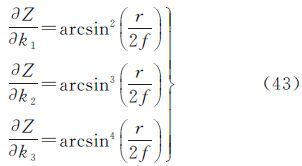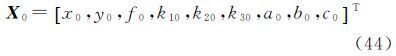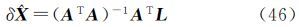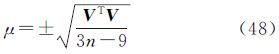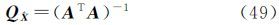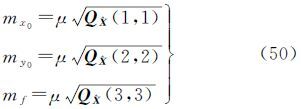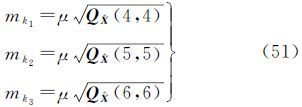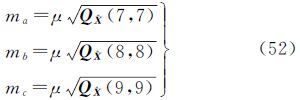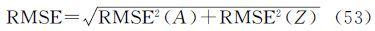2. 郑州大学水利与环境学院, 河南 郑州 450001;
3. 总装备部工程设计研究总院, 北京 100028
2. College of Water Conservancy and Environmental, Zhengzhou University, Zhengzhou 450001, China;
3. Center for Engineering Design and Research under the Headquarters of General Equipment, Beijing 100028, China
鱼眼相机是一种超大视场图像采集设备,能够实现对全天区物体一次成像,在建筑施工[1]、森林监测[2]、行星际漫游车天文导航[3, 4, 5, 6]、天文大地测量[7, 8]等领域有着广泛应用。由于鱼眼相机具有特殊的投影和畸变,因此使用前需要进行严格的检校,相机检校工作显得尤为重要。
1994年,文献[9]开展了鱼眼相机的检校研究,但只考虑了对像主点坐标、焦距和像素尺寸的标定,没有考虑鱼眼镜头的投影和畸变模型,只取得了1°的检校精度。2001年,文献[10]在鱼眼相机检校中考虑了成像模型,发现物方空间直线经鱼眼镜头成像后为椭圆弧,以此对相机进行检校,也取得了1°的检校精度。2005年,文献[11]通过室内标较的方法,采用严格的平差解算对鱼眼相机进行检校,取得了137″的标定精度,但没有给出详细的检校及畸变模型。2008年,文献[12]采用等距投影模型,利用建筑物上的40个标志点对鱼眼相机进行检校,检校精度达到258″。文献[13, 14, 15]也展开了鱼眼相机检校技术研究,但都没有给出明确的检校精度。2012年,文献[16]对恒星法鱼眼相机检校的理论和技术进行了深入研究,发现鱼眼镜头畸变中的径向畸变是最主要的,偏心畸变和平面内畸变非常小,均在10-5~10-6量级,因此提出了基于半视场角约束的等立体角投影多项式畸变模型。模型中的相机参数包括像主点坐标、焦距、径向畸变参数和外方位元素,该方法最终取得了优于100″的检校精度,达到了国际先进水平。需要说明的是,上述相机检校均采用半视场角误差作为精度指标,没有考虑方位角误差。
本文将构建基于矢量观测的相机检校模型,检校模型中的基本观测量不仅包括半视场角,而且包括方位角。通过引入罗德里格矩阵,采用3个独立的罗德里格参数表示外方位元素。本文还将新的检校模型与基于半视场角约束的检校模型进行对比,结果表明新模型可进一步提高相机检校精度。
1 基于半视场角约束的相机检校模型常用的鱼眼镜头投影模型主要有4种,分别为等距投影、等立体角投影、体视投影和正交投影。本文采用的鱼眼相机为等立体角投影模型,不考虑径向畸变时物方点在相机坐标系下的半视场角计算公式为
式中,f为相机的焦距;r为物方点的像点(x,y)相对于像主点(x0,y0)的极距,计算公式为采用4阶多项式描述径向畸变,有[16]
设物方点在测站地平坐标系下的方位角和天顶距为(ADP,ZDP),则其理想的半视场角为[15]
式中,(φ1,φ2)为外方位元素。构建误差方程对误差方程进行线性化,利用最小二乘法即可求解得到相机参数。
基于半视场角约束的相机检校模型只利用了相机观测量中的半视场角,没有用到方位角。下文将从矢量的角度出发,构建全新的相机检校模型。
2 基于矢量观测的相机检校模型 2.1 矢量观测模型设物方空间某点在相机坐标系下的方位角和天顶距(或半视场角)为(A,Z),则物方点在相机坐标系下的直角坐标为
物方点在地平坐标系下的直角坐标为
SCCD与SDP之间存在旋转关系
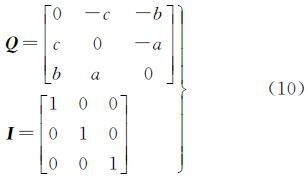
式中,R为旋转矩阵,由外方位元素决定;SCCD与内方位元素有关。当观测量足够多时,进行线性化,利用最小二乘法即可求解相机的内外方位元素,实现相机检校。 2.2 罗德里格矩阵所有旋转矩阵R均可由反对称矩阵Q和单位阵I表示,即[17, 18]
式中 式中,(a,b,c)即为罗德里格参数,用来表示外方位元素。式(8)可表示为Q矩阵具有如下性质
式中,右边和左边同乘以(I-Q)-1得将式(13)代入式(11)并整理得
再将Q矩阵代入式(14)并展开得
构建误差方程
由式(16)可知,采用罗德里格参数表示外方位元素时,避免了复杂的三角函数运算,误差方程的形式及运算更为简单。
2.3 各偏导数表达式V1对(x0,y0,f,k1,k2,k3,a,b,c)的偏导数为
V2对(x0,y0,f,k1,k2,k3,a,b,c)的偏导数为
V3对(x0,y0,f,k1,k2,k3,a,b,c)的偏导数为
SCCD各坐标分量对像主点坐标(x0,y0)的偏导数为
SCCD各坐标分量对焦距f的偏导数为
SCCD各坐标分量对径向畸变参数(k1,k2,k3)的偏导数为
(A,Z)对像主点坐标(x0,y0)的偏导数为
式中(A,Z)对焦距f的偏导数为
(A,Z)对径向畸变参数(k1,k2,k3)的偏导数为
2.4 参数求解及精度估计设未知参数的初值为
误差方程线性化并写为矢量相乘形式
如果有n个物方点及对应的像点,则有3n个误差方程,根据最小二乘法可求解未知参数的改正数为
相机参数估值为
单位权中误差为
未知参数的权逆阵为
相机参数的精度估计公式为[19]
上述精度估计公式只能作为内符合精度估计。在求解未知参数的过程中需要迭代计算,每次迭代计算出新的相机参数后,要根据新的相机参数计算物方点在CCD坐标系下的坐标,然后再构建误差方程进行参数解算。
目前,相机检校领域主要采用3个欧拉角描述外方位旋转元素,三角函数线性化较为复杂。此外,欧拉角通常为大旋转角,初值很难准确确定,致使求解陷入局部最优。本文采用罗德里格矩阵表示外方位旋转元素,不仅避免了复杂的三角函数运算,简化了计算公式,而且容易确定初值。实际应用中,根据内方位元素(主点坐标、焦距和畸变参数),将像点映射到相机坐标系,然后根据式(16)采用最小二乘法,即可直接计算3个罗德里格参数(a,b,c)作为初值。
3 算例分析采用恒星法进行鱼眼相机检校,具有不需要建立专门的检校场,作为控制点的夜空中的恒星数目众多,以及恒星均匀分布于全天区等优点。2012-08-22夜,在登封地区采用自己构建的鱼眼相机拍摄到真实星空进行相机检校。鱼眼镜头采用尼康公司生产的AF DX Fisheye-Nikkor10.5 mm f/2.8GED,CCD采用美国Apogee 仪器公司生产的Alta U9000[20]。经过星点提取及星图识别,匹配得到1080颗高度角大于10°、星等高于5.0的恒星。
约定以下3种相机检校模型:
模型1:基于半视场角约束的相机检校模型,求解(x0,y0,f,k1,k2,k3,φ1,φ2)共8个参数。
模型2:基于矢量观测的相机检校模型,求解(x0,y0,f,k1,k2,k3,a,b,c)共9个参数。
模型3:简化的基于矢量观测的相机检校模型,只求解(x0,y0,f,a,b,c)共6个参数,径向畸变参数(k1,k2,k3)作为已知量由模型1的解算结果提供。
采用的相机固化的较好,CCD具有温控措施,因此相机内方位元素(主点坐标、焦距和畸变参数)变化较小,采用的初值均是先前累积的解算结果,为经验值。而外方位元素涉及相机坐标系与地平坐标系之间的转换,在试验前通过水平仪(徕卡Nivel 230)将相机主光轴大致调为与本地铅垂线重合,因此模型1的外方位元素初值均设置为零。模型2和模型3的3个罗德里格参数a、b、c的初值是这样设定的:视内参数(主点坐标、焦距和畸变参数)初值为已知,将像点映射到相机坐标系下,采用式(16)根据最小二乘法计算a、b、c的初值。
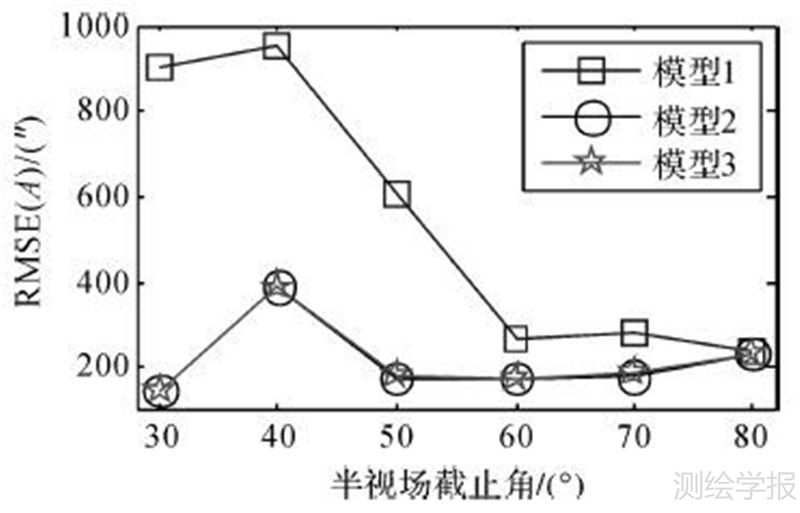
目前的文献均采用方位角和天顶距的均方根误差衡量鱼眼相机的检校精度,即利用求解的外方位元素构造相机坐标系与地平坐标系之间的旋转矩阵R,然后利用R矩阵将相机坐标系下的观测矢量旋转变换到地平坐标系下,最后统计方位角和天顶距的均方根误差,均方根误差越小,说明相机检校的精度越高。图 1、图 2给出了采用不同天顶距截止角以内数据进行相机检校得到的方位角均方根误差RMSE(A)和天顶距均方根误差RMSE(Z)。
|
| 图 1 不同检校模型的方位角均方根误差 Fig. 1 Root mean square errors of azimuth of different calibration models |
|
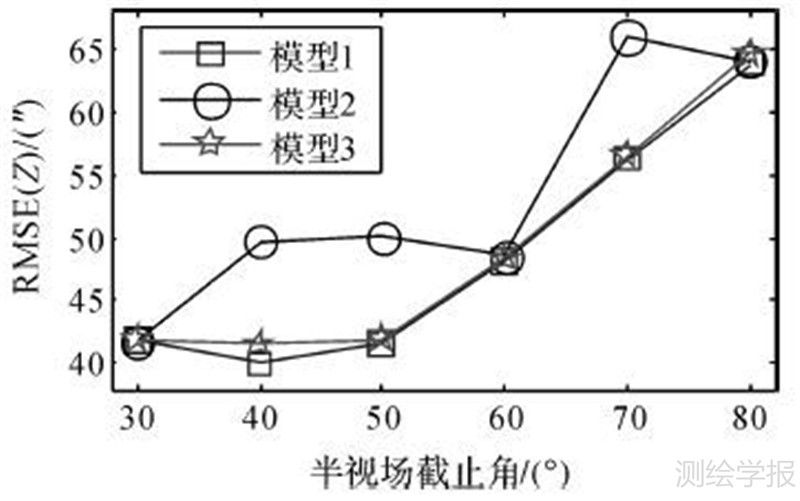
| 图 2 不同检校模型的天顶距均方根误差 Fig. 2 Root mean square errors of zenith distance of different calibration models |
由图 1可知,模型2和模型3的方位角均方根误差要明显小于模型1,而且半视场截止角越小,模型2和模型3的优势越明显。当半视场截止角增大到80°时,3种模型的方位角均方根误差趋于一致。
由图 2可知,模型1和模型3的天顶距均方根误差要明显小于模型2。由于模型3直接采用了模型1的径向畸变参数,因此可以说明模型1求解的径向畸变参数和焦距更准确可靠。而图 1显示模型2的方位角均方根误差要明显小于模型1,说明模型2求解的像主点坐标、焦距和外方位元素更准确。
总体均方根误差计算公式如下
表 1给出了3种模型的总体均方根误差RMSE。
| ± ″ | |||
| 半视场截止角 | 模型1 | 模型2 | 模型3 |
| 30° | 901.49 | 149.42 | 148.12 |
| 40° | 954.57 | 386.47 | 386.66 |
| 50° | 606.29 | 177.18 | 180.93 |
| 60° | 271.18 | 181.05 | 179.39 |
| 70° | 278.89 | 189.56 | 191.43 |
| 80° | 242.85 | 237.37 | 236.53 |
由表 1可知,半视场截止角越小,模型2和模型3的精度相对于模型1优势更明显。当半视场角截止角增大到80°时,3种模型的精度趋于一致。说明本文提出的基于矢量观测的相机检校模型总体要优于基于半视场角约束的相机检校模型。
需要说明的是,模型3的径向畸变参数由模型1给出,但不是将模型1的径向畸变参数当作模型3的初始值,而是已知值,模型3只是改进其他相机参数(主点坐标、焦距、外方位元素)的精度。也就是说,采用模型1+模型3的组合模式,可以最大限度地提高相机检校的精度。
与传统的基于室内人工标志点的鱼眼相机检校方法相比,恒星法鱼眼相机检校具有如下优点:
(1) 作为控制点的恒星数目众多,一次拍摄可获取上千颗恒星影像,且均匀分布于视场内;
(2) 由于恒星具有无穷远的属性,因此在相机检校模型中无须求解外方位元素中的3个平移参数,降低了参数之间的相关性,使求解稳定;
(3) 对于在轨航天器及长时间漫游于月球和火星表面的探测车等设备,由于没有人工控制点,可以考虑采用恒星法进行在轨标定。
4 结 论综合以上分析可以得出以下基本结论:
(1) 基于半视场角约束的相机检校模型在求解径向畸变参数时表现出较为明显的优势,建议在进行鱼眼相机检校时,采用此方法求解径向畸变参数;
(2) 本文提出的基于矢量观测的相机检校模型总体要明显优于基于半视场角约束的相机检校模型,但其在求解径向畸变参数时表现出一定的不足;
(3) 建议在实际应用中,建议采用模型1+模型3的组合方法进行相机检校,即采用基于半视场角约束的相机检校模型求解径向畸变参数,将其作为已知值,然后采用本文提出的算法求解其他相机参数,以提高相机检校的整体精度。
| [1] | 侯文广, 尚涛. 鱼眼镜头在获取建筑物立面影像中的新方法[J]. 武汉大学学报(工学版), 2007, 40(1):105-109. HOU Wenguang, SHANG Tao. A New Method for Obtaining Façade Image of Building by Using Fish-eye Lens[J]. Engineering Journal of Wuhan University, 2007, 40(1):105-109. |
| [2] | 凌飞龙, 李增元, 陈尔学, 等. 青海云杉林叶面积指数半球摄影测量方法研究[J]. 地球科学进展, 2009, 24(7):803-809. LING Feilong, LI Zengyuan, CHEN Erxue, et al. Leaf Area Index Estimation for Qinghai Spruce Forest Using Digital Hemispherical Photography[J]. Advances in Earth Science, 2009, 24(7):803-809. |
| [3] | DEANS M C, WETTERGREEN D, VILLA D. A Sun Tracker for Planetary Analog Rovers[C]//Proceedings of the 8th International Symposium on Artificial Intelligence, Robotics and Automation in Space.Munich, Germany:[s.n.], 2005:1-7. |
| [4] | URGALE P, ENRIGHT J, BARFOOT T. Sun Sensor Navigation for Planetary Rovers:Theory and Field Testing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(3):1631-1647. |
| [5] | THEIN M L, QUINN D A, FOLTA D C. Celestial Navigation(CelNav):Lunar Surface Navigation[C]//Proceedings of the 2008 AIAA/AAS Astrodynamics Specialist Congress and Exposition.Honolulu, Hawaii:[s.n.], 2008:1-19. |
| [6] | 杨鹏. 基于太阳观测图像的月球车天文导航[D]. 杭州:浙江大学, 2011. YANG Peng.Sun Observation Image Based Celestial Navigation for Lunar Rover[D]. Hangzhou:Zhejiang University, 2011. |
| [7] | 李崇辉, 郑勇, 张超, 等. 一种无需精密整平的抗差天文定位方法[J]. 测绘学报, 2013, 42(6):810-816. LI Chonghui, ZHENG Yong, ZHANG Chao, et al. A Robust Celestial Positioning Method without Precise Leveling[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6):810-816. |
| [8] | ZHAN Yinhu, ZHENG Yong, ZHANG Chao. Celestial Positioning with CCD Observing the Sun[C]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al.China Satellite Navigation Conference(CSNC) 2013 Proceedings. Berlin Heidelberg:Springer, 2013:697-706. |
| [9] | SHAH S, AGGARWAL J K. Intrinsic Parameter Calibration Procedure for a(high distortion) Fish-eye Lens Camera with Distortion Model and Accuracy Estimation[J]. Pattern Recognition,1996, 29(11):1775-1788. |
| [10] | BRAUER-BURCHARDT C, VOSS K. A New Algorithm to Correct Fish-eye and Strong Wide-Angle-Lens-Distortion from Single Images[C]//Proceedings of 2001 International Conference on Image Processing.Thessaloniki,Greece:IEEE, 2001,1:225-228. |
| [11] | KEDZIERSKI M, FRYSKOWSKA A. Precise Method of Fish-eye Lens Calibration[C]//Proceedings of the 21th ISPRS Congress.Beijing, China:[s.n.], 2008:765-768. |
| [12] | SCHWALBE E. Geometric Modelling and Calibration of Fisheye Lens Camera Systems[C]//Proceedings of the 2nd Panoramic Photogrammetry Workshop, International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences.Berlin, Germany:[s.n.], 2005, 36:1-6. |
| [13] | 刘兴库, 何东坡, 李兆华. 鱼眼全景像片光束法整体平差解法[J]. 测绘学报, 1993, 22(3):218-222. LIU Xingku, HE Dongpo, LI Zhaohua. A Method of Overall Bundle Adjustment of the Panoramic Photograph by Fish Eye Lens[J]. Acta Geodaetica et Cartographica Sinica, 1993, 22(3):218-222. |
| [14] | 贾云得, 吕宏静, 徐岸, 等. 一种鱼眼镜头成像立体视觉系统的标定方法[J]. 计算机学报, 2000, 23(11):1215-1219. JIA Yunde, LV Hongjing, XU An, et al. Fish-eye Lens Camera Calibration for Stereo Vision System[J]. Chinese Journal of Computers, 2000, 23(11):1215-1219. |
| [15] | 英向华, 胡占义. 一种基于球面透视投影约束的鱼眼镜头校正方法[J]. 计算机学报, 2003, 26(12):1702-1708. YING Xianghua, HU Zhanyi. Fisheye Lense Distortion Correction Using Spherical Perspective Projection Constraint[J]. Chinese Journal of Computers, 2003, 26(12):1702-1708. |
| [16] | 原玉磊. 鱼眼相机恒星法检校技术研究[D].郑州:信息工程大学, 2012. YUAN Yulei. Research on Fish-Eye Camera Stellar Calibration Technology[D].Zhengzhou:The PLA Information Engineering University, 2012. |
| [17] | 曾文宪, 陶本藻. 三维坐标转换的非线性模型[J]. 武汉大学学报(信息科学版), 2003, 28(5):566-568. ZENG Wenxian, TAO Benzao. Non-linear Adjustment Model of Three-Dimensional Coordinate Transformation[J]. Geomatics and Information Science of Wuhan University, 2003, 28(5):566-568. |
| [18] | 姚吉利, 韩保民, 杨元喜. 罗德里格矩阵在三维坐标转换严密解算中的应用[J]. 武汉大学学报(信息科学版), 2006, 31(12):1094-1096. YAO Jili, HAN Baomin, YANG Yuanxi. Applications of Lodrigues Matrix in 3D Coordinate Transformation[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12):1094-1096. |
| [19] | 隋立芬, 宋力杰. 误差理论与测量平差基础[M]. 北京:解放军出版社, 2003. SUI Lifen, SONG Lijie. Basis of Error Theory and Surveying Adjustment[M]. Beijing:PLA Press, 2003. |
| [20] | APOGEE. U9000 High Light[R/OL].(2006-10-16)[2014-12-05] Apogee Instruments, 2006. http://www.Apogee.com. |