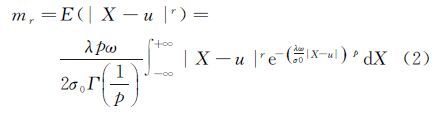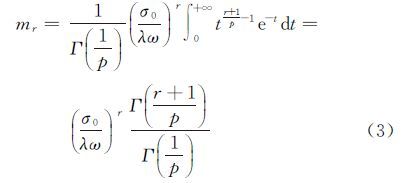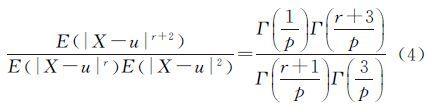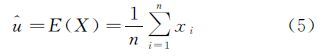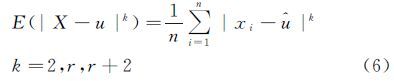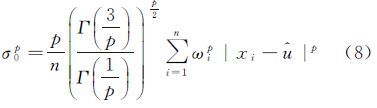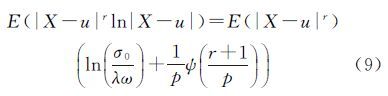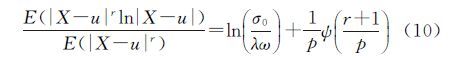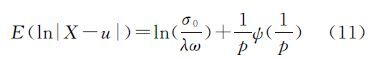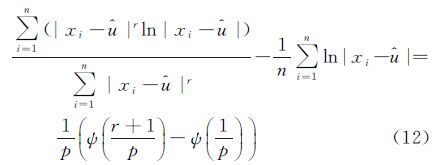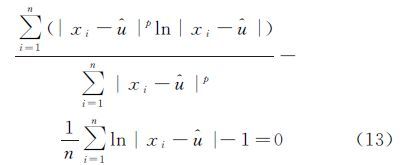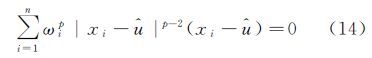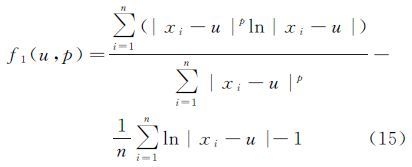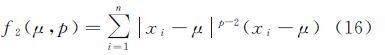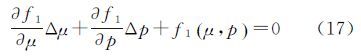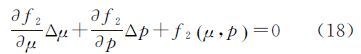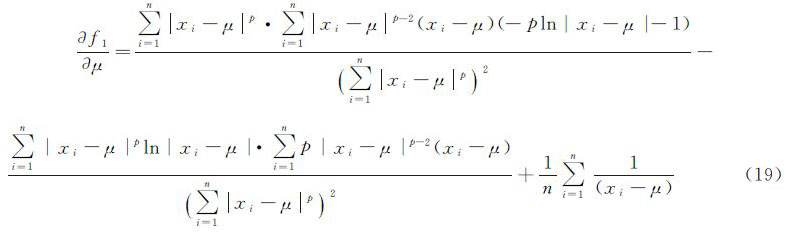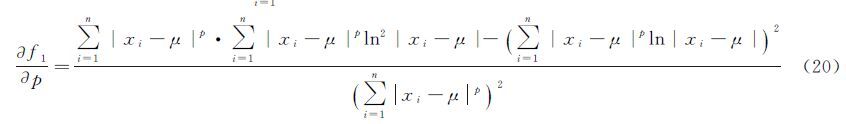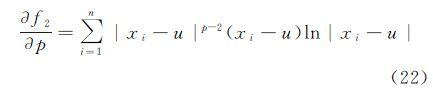随着空间测量技术的发展,对卫星轨道精度的要求越来越高,现有的精密定轨软件程序在解算参数时,都是假设计算误差服从正态分布,采用最小二乘估计进行解算。文献[1]指出,在数据处理过程中,由于观测数据中存在粗差、模型不准确以及计算方法不同等,使得观测误差并不服从正态分布。文献[2]从观测误差的实际分布出发,利用LP估计来确定卫星的精密轨道,通过计算,认为LP估计的p值应该在[1, 2]之间;文献[3]指出,对GPS观测值误差处理时,当p=1.4左右时精度最高,效率最好。
在实际工作中,对于一组给定的观测误差,往往并不知道这个p取什么值最合适,这就需要利用观测数据提供的信息,正确确定p值,进行相应的估计。此前,许多学者采用极大似然估计法对P范分布的多种形式,如从对称到非对称、一元到多元等情况进行了研究,得到了一些有用的结果[4, 5, 6, 7, 8, 9]。当观测样本足够大且分布的形式已知时,极大似然估计是最优估计,其渐近分布为正态分布。文献[10]将半参数回归模型成功地应用到极大似然平差法的参数估计理论中,但形状参数p值的获取是半参数P范极大似然回归的应用前提。然而,P范分布的形状参数值未知,极大似然估计方程是非线性方程,需要迭代计算,迭代计算需要较大的数据量及合适的初值才能保证估计精度,此时自适应LP估计等价于相应的最或然估计[11],而形状参数的不正确估计又会使得LP估计的效率变低[12]。理论证明,当p=1时,LS估计将比L1估计损失效率50%;当p=2时,L1估计又将比LS估计损失效率27%,因此,选择合适的p非常重要[12]。文献[2, 13, 14, 15]以SLR数据处理为例说明了自适应LP估计在应用中的稳健性优势,若能获得更可靠的p值,其优势将更为显著。
合理的p值可以体现观测误差最符合的分布,由于p为小数,常用的矩估计法为整数阶估计,本文引入实数阶和对数矩估计方法,导出了相应估计方法的P范分布的参数解算的基础方程,另外,简化了基础方程,消除了普西函数和伽玛函数的导数的计算误差对参数计算的影响,使得参数计算的复杂度降低。
1 实数阶矩估计法设Li(i=1,2,…,n)是均值μ的一组独立的观测值,服从P范分布i[1],Li的先验方差为σ2=σ02qi,其中σ02为单位权方差,σi2为Li的先验方差,令ωi=σ0/σi=1/$\sqrt {{q_i}} $,则Li的密度函数为
式中,λ=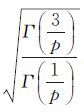 。设x1、x2、…、xn为服从P范分布的一组简单随机样本,样本X的r阶中心绝对矩mr为
。设x1、x2、…、xn为服从P范分布的一组简单随机样本,样本X的r阶中心绝对矩mr为
令t=λ= ,则dX=λ=
,则dX=λ=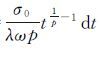 ,将dX和t代入式(2),计算得
,将dX和t代入式(2),计算得
式(3)包含形状参数p、中误差σ0和阶数r,为了减少参数之间的影响,可以构造如式(4)所示的函数,消除中误差σ0对p的影响
式中,总体均值u和r阶绝对中心矩可以通过如下样本估计值计算将式(5)、式(6)代入式(4),化简得到形状参数的估计式为
由式(7)得到形状参数p的估计值后,在式(3)中令r=p,得
确定一个r值后,由式(5)、式(7)、式(8)就可以逐步得到参数的估计值${\hat u}$、 ${\hat p}$、${\hat \sigma }$ 0。从后面的模拟算例可以看出,当阶数r的取值越接近参数p,由实数阶矩估计法计算得到的参数估计量相对偏差越小,其估计精度越高。而r的选取方式比较复杂,一般来说,可以选择多个r值,分别进行平差计算,然后对计算结果进行比较,从中选取一个较好的结果。
从上面的推导过程可知,利用实数阶矩估计法得到的参数估值精度与阶数的选取有较大影响,在实际计算过程中,无法选取合适的阶数r,因此,不能确定参数p的精确取值。在计算过程中,伽玛函数、普西函数的截断误差对参数估计值的计算影响也比较大,为了消除阶数及计算误差对参数估计值精度的影响,采用对数矩估计方法来估计相应参数的估计值${\hat u}$、 ${\hat p}$、${\hat \sigma }$0。
2 对数矩估计法对式(3)求导数得
式中,ψ(·)为普西函数。对式(9)化简得
在式(9)中,令r=0 可得观测值的一阶对数绝对矩为
用样本矩代替总体矩,综合式(10)、式(11),化简得参数p的估计表达式为
为了消除ψ(·)计算误差及阶数对参数计算的影响,在式(12)中,取r=p,由ψ(·)的性质得
由式(8)得到参数u的估计表达式为
求解式(8)、式(13)、式(14),就可得到未知参数的相应估计值${\hat u}$、 ${\hat p}$、${\hat \sigma }$。
3 参数的解算由于式(8)、式(13)、式(14)是非线性方程组,可以用迭代法解算。首先联立求解式(13)、式(14),得${\hat u}$、 ${\hat p}$,然后将得到的估计值代入式(8),直接计算即得到单位权方差的估计值。采用迭代法求解式(13)、式(14)时,一般取ωi=1,实数阶矩估计方法计算得到的参数估计值作为μ、p的初始值,令
将f1(u+Δu,p+Δp)=0,f2(u+Δu,p+Δp)=0在μ、p处展开成泰勒级数,略去二次以上各项,则有
联立求解式(15)—式(18),将μ+Δμ、p+Δp作为新的近似值,即可进行下一次迭代计算。其中,式(15)、式(16)分别对μ、p的偏导数为
令B1=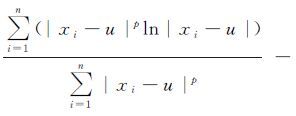
 则式(17)、式(18)变为
则式(17)、式(18)变为
求解方程组(23),如果Δμ、Δp小于给定的迭代阀值εμ及εp,则停止迭代,否则用μ+Δμ、p+Δp作为未知参数的近似值,重新计算式(23)系数阵式及常数项,进而求解该方程。最后可由式(8)求出观测值的单位权方差估计值。
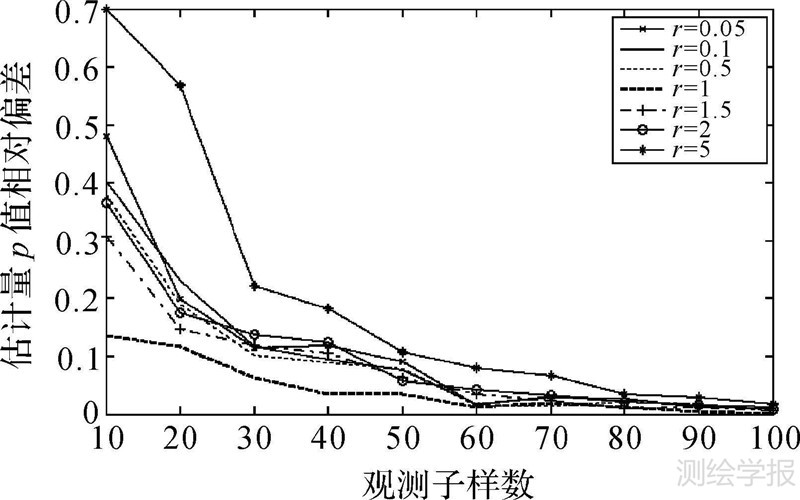
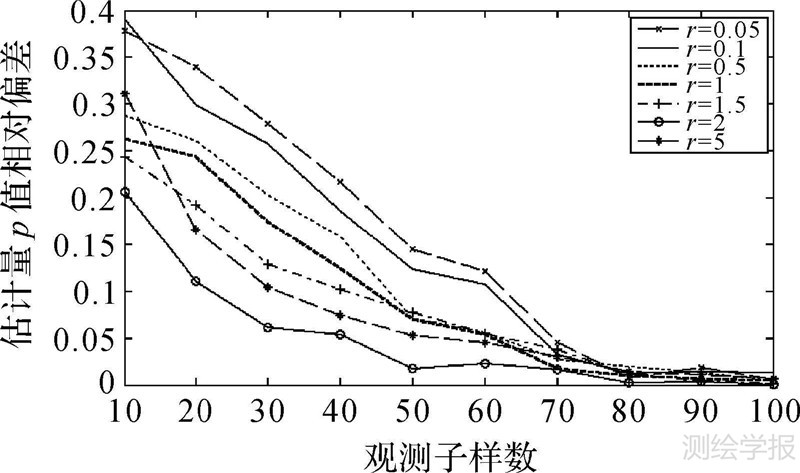
4 算例分析 4.1 阶数对精度的影响为了检验理论的正确性,便于进行对比分析,利用文献[1]的两组来自不同母体的观测数据验证本文方法的估计效果。为了分析阶数对精度的影响,不妨取阶数为0.05、0.1、0.5、1、1.5、2、5,利用估计量的相对偏差(${\hat p}$|-p|/p)表示参数估计的精度,拉普拉斯分布和正态分布的参数估计量的相对偏差曲线如图 1、图 2所示。
|
| 图 1 p=1时,不同r对应估计量p的相对偏差曲线 Fig. 1 The relative deviation curve of estimation p with different r when p=1 |
|
| 图 2 p=2时,不同r对应估计量p的相对偏差曲线 Fig. 2 The relative deviation curve of estimation p with different r when p=2 |
从图中可以看出,阶数r的取值越接近形状参数实际值,参数估计值越接近其真实值,其相对偏差也越小。因此,可以认为当阶数r近似取p值时,实数阶矩估计法的估计精度最高。不妨以拉普拉斯分布为例,其样本个数、阶数及形状参数的关系如表 1所示。
| n | r=0.05 | r=0.1 | r=0.5 | r=1 | r=1.5 | r=2 | r=5 |
| 10 | 1.480 9 | 1.401 9 | 1.377 3 | 0.865 5 | 1.307 7 | 1.364 6 | 1.698 9 |
| 20 | 1.198 5 | 1.231 0 | 0.811 3 | 0.882 6 | 0.854 1 | 0.825 4 | 1.568 8 |
| 30 | 1.114 9 | 0.882 5 | 0.898 9 | 1.062 0 | 0.882 2 | 1.138 0 | 1.220 6 |
| 40 | 0.880 9 | 0.905 5 | 0.911 0 | 1.035 1 | 1.105 0 | 1.124 9 | 1.181 3 |
| 50 | 1.091 3 | 1.075 3 | 0.923 2 | 0.964 7 | 1.062 0 | 0.943 3 | 1.107 2 |
| 60 | 1.015 4 | 0.981 7 | 0.985 8 | 0.987 5 | 1.035 3 | 0.958 0 | 1.078 9 |
| 70 | 1.030 8 | 1.029 1 | 0.986 4 | 1.020 3 | 0.976 6 | 0.967 8 | 1.065 8 |
| 80 | 1.021 0 | 0.972 3 | 1.021 5 | 0.987 7 | 0.989 8 | 1.020 9 | 1.033 9 |
| 90 | 1.016 4 | 0.987 7 | 1.018 4 | 0.996 0 | 1.011 4 | 1.016 8 | 0.970 6 |
| 100 | 0.988 2 | 1.010 1 | 1.006 8 | 1.000 5 | 1.006 4 | 0.991 2 | 1.017 8 |
由表 1可以看出,当子样较少时,无论阶数r取何值,计算得到的参数估值均偏离真实值,阶数与形状参数的差值越大,精度越低。随着参与平差的子样数逐步增多,对应各阶数计算得到的参数估值逐渐趋近于真实值。
4.2 模拟算例对比分析为了分析对数矩和极大似然估计方法[1]的稳定性、收敛速度和精度,利用上述模拟观测数据进行对比分析。由式(23)和式(8),得到不同样本情况下的参数估值${\hat u}$、${\hat p}$和${\hat \sigma }$,并与文献[1]的估计结果进行对比,如表 2、表 3所示。
| n | 对数矩估计法 | 极大似然估计法 | |||||||
| ${\hat p}$ | ${\hat u}$ | ${\hat \sigma }$ | 迭代次数 | ${\hat p}$ | ${\hat u}$ | ${\hat \sigma }$ | 迭代次数 | ||
| 10 | 1.481 5 | -0.204 9 | 1.222 8 | 4 | 1.551 2 | -0.349 7 | 1.300 3 | 9 | |
| 20 | 0.872 0 | -0.101 1 | 0.914 1 | 6 | 1.158 8 | -0.105 4 | 0.846 2 | 11 | |
| 30 | 0.763 4 | -0.128 1 | 1.365 4 | 3 | 0.727 1 | -0.127 7 | 1.395 1 | 6 | |
| 40 | 1.164 2 | 0.024 8 | 1.011 0 | 4 | 1.176 0 | 0.025 0 | 1.009 3 | 7 | |
| 50 | 1.025 9 | -0.025 7 | 1.012 5 | 5 | 1.039 4 | -0.035 7 | 1.021 9 | 12 | |
| 60 | 1.013 3 | 0.115 2 | 1.079 5 | 3 | 1.023 6 | 0.115 5 | 1.088 4 | 3 | |
| 70 | 0.991 7 | -0.051 0 | 0.946 1 | 6 | 0.985 3 | -0.051 8 | 0.925 0 | 10 | |
| 80 | 1.010 2 | 0.015 0 | 1.073 7 | 4 | 0.960 9 | 0.033 0 | 1.090 6 | 8 | |
| 90 | 1.025 8 | 0.016 3 | 1.033 4 | 5 | 1.055 5 | -0.016 3 | 1.026 6 | 7 | |
| 100 | 1.010 2 | -0.008 3 | 1.012 1 | 4 | 1.038 8 | -0.010 4 | 0.961 5 | 9 | |
| n | 对数矩估计法 | 极大似然估计法 | |||||||
| ${\hat p}$ | ${\hat u}$ | ${\hat \sigma }$ | 迭代次数 | ${\hat p}$ | ${\hat u}$ | ${\hat \sigma }$ | 迭代次数 | ||
| 10 | 2.308 3 | -0.406 2 | 0.719 4 | 4 | 3.181 3 | -0.404 9 | 0.699 8 | 6 | |
| 20 | 2.122 4 | -0.268 5 | 1.148 6 | 4 | 1.600 5 | -0.242 0 | 1.249 2 | 10 | |
| 30 | 1.730 7 | -0.390 1 | 0.951 8 | 6 | 1.635 8 | -0.385 0 | 0.953 6 | 8 | |
| 40 | 1.882 8 | 0.051 3 | 0.951 7 | 4 | 2.306 9 | 0.151 7 | 0.930 6 | 6 | |
| 50 | 1.885 1 | 0.044 2 | 1.050 1 | 3 | 1.795 6 | 0.045 6 | 1.059 7 | 5 | |
| 60 | 1.954 1 | -0.048 5 | 0.967 3 | 4 | 1.882 0 | -0.051 2 | 0.984 5 | 8 | |
| 70 | 1.949 3 | 0.009 5 | 0.967 9 | 5 | 1.878 8 | 0.027 3 | 0.953 5 | 8 | |
| 80 | 2.022 8 | -0.043 1 | 0.969 3 | 3 | 1.885 5 | -0.044 1 | 0.960 2 | 4 | |
| 90 | 1.995 4 | 0.002 4 | 1.027 0 | 2 | 2.032 3 | 0.004 4 | 1.041 8 | 4 | |
| 100 | 1.999 4 | 0.005 1 | 0.987 6 | 3 | 2.019 4 | 0.006 5 | 0.976 4 | 5 | |
从表 2、表 3可以看出,当子样较少时,对数矩估计法与极大似然平差法估计结果均与实际值相差较大,随着观测子样的增加,两种方法所得到的参数估计值呈现出越来越接近真实值的趋势。当子样数较小,在估计3个参数时,对数矩估计法在收敛速度、稳定性和精度上明显优于极大似然估计法。
根据表 2、表 3中的计算结果,得出运用对数矩估计法和极大似然估计法获得${\hat p}$的${\hat \sigma }$和参数估计量的相对偏差曲线,如图 3、图 4所示。
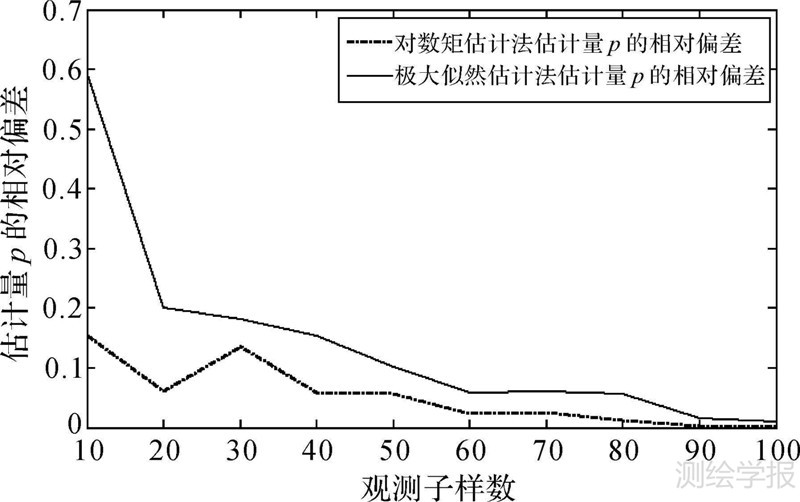
|
| 图 3 p=2时,估计量p的相对偏差曲线 Fig. 3 The relative deviation curve of estimation p when p=2 |

|
| 图 4 p=2时,估计量σ的相对偏差曲线 Fig. 4 The relative deviation curve of estimation when p=2 |
4.3 实际算例1
由文献[16]可知,地图数字化后的数据,经过标准化处理之后得到的误差,经检验得知,该母体服从p=1.6的P范分布。本文数据来自文献[17],利用对数矩估计法计算地图数字化后坐标误差分布的参数估值${\hat u}$、${\hat p}$和${\hat \sigma }$,同时与极大似然估计法得到的估计结果进行对比,计算结果如表 4所示。
| n | 对数矩估计法 | 极大似然估计法 | |||||||
| ${\hat p}$ | ${\hat u}$ | ${\hat \sigma }$ | 迭代次数 | ${\hat p}$ | ${\hat u}$ | ${\hat \sigma }$ | 迭代次数 | ||
| 10 | 2.323 4 | -0.034 7 | 0.124 4 | 13 | 5.412 2 | -0.047 3 | 0.137 7 | 109 | |
| 20 | 1.915 7 | -0.021 3 | 0.075 6 | 3 | 0.999 9 | -0.021 2 | 0.083 1 | 82 | |
| 30 | 1.213 8 | -0.014 5 | 0.081 3 | 4 | 0.999 8 | -0.014 6 | 0.084 4 | 41 | |
| 40 | 1.730 2 | 0.009 8 | 0.097 2 | 4 | 1.456 7 | -0.013 4 | 0.097 7 | 114 | |
| 50 | 1.508 6 | 0.019 9 | 0.098 9 | 7 | 2.124 1 | 0.010 5 | 0.098 3 | 46 | |
| 60 | 1.546 4 | 0.004 7 | 0.089 3 | 5 | 1.884 5 | 0.005 9 | 0.088 5 | 62 | |
| 70 | 1.564 2 | -0.007 5 | 0.099 9 | 4 | 1.341 2 | -0.007 7 | 0.100 9 | 43 | |
| 80 | 1.629 6 | -0.000 9 | 0.109 6 | 5 | 1.803 5 | 0.000 5 | 0.109 1 | 75 | |
| 90 | 1.613 8 | -0.002 7 | 0.107 9 | 12 | 1.875 4 | -0.001 2 | 0.107 3 | 72 | |
| 100 | 1.594 3 | -0.002 6 | 0.104 5 | 8 | 1.740 3 | -0.002 9 | 0.109 0 | 10 | |
通过表 4可以得出结论,当样本服从p=1.6的P范分布时,采用对数矩估计法估计形状参数p值的估计精度要高于极大似然估计法,而对均值u和方差σ的估计效果相当,同时对数矩估计法的迭代次数要远小于极大似然估计法,对数矩估计法的收敛速度较快,表明对数矩估计法能快速定位形状参数p。
4.4 实际算例2由文献[3]可知,经消除GPS观测值中的粗差,完成电离层折射误差、对流层折射误差等多项改正后,GPS输出的最终观测值误差,经检验得知,该母体服从p=1.4的P范分布。
本文算例所用数据来自加拿大Algonquin Park的ALGO测站点,利用TPS NET-G3A接收机,采集获得2013年4月28日全天的观测数据。在获得的32颗卫星数据中,选取某颗卫星伪距的PPP双频无电离层组合观测值残差进行分析。取200个误差值作为原始数据,分别利用对数矩估计法与极大似然估计法对参数u、p和σ进行计算,得到的结果如表 5所示。
| 参数 | ${\hat p}$ | ${\hat u}$ | ${\hat \sigma }$ | 迭代次数 |
| 真实值 | 1.400 000 | 0.000 00 | — | — |
| 对数矩估计法 | 1.381 095 | -0.050 426 | 0.445 228 | 7 |
| 极大似然估计法 | 1.323 699 | -0.050 735 | 0.446 246 | 13 |
从表 5可以看出,针对本组试验数据,当形状参数p为1.4时,两种估计方法的效果均较好,其中对数矩估计法的精度稍高于极大似然估计法,且其迭代次数明显少于极大似然估计,因此采用对数矩估计法能够更快速精确地估计出误差的实际分布参数,再次表明对数矩估计法优于极大似然估计法。
5 结 论本文研究了P范分布的实数阶矩估计方法,利用模拟算例讨论了阶数r与参数估计精度的关系,推导出形状参数、期望和中误差的估计公式,引入对数矩估计方法,消除了伽玛函数、普西函数的截断误差对参数估计值计算造成的影响,给出了相应参数的求解方法和计算过程,用模拟算例和实测数据验证了本文理论的正确性,得到了以下结论:
(1) P范分布能够精确地确定观测数据的最符合分布,本文给出了任意实数阶矩估计公式。利用实数阶矩估计法得到的参数估计值精度与阶数的关系较大。当阶数r的取值越接近p,由实数阶矩估计法计算得到的参数估计量相对偏差越小,其估计精度越高。然而在参数估计过程中,r的选取方式比较复杂,合理的阶数的选取方法值得进一步研究。
(2) 对数阶矩估计方法降低了算法的复杂度,计算简单。从模拟和实测数据可以看出,对数估计方法在参数估计的精度、稳定性和收敛速度以及算法的复杂度等方面优于极大似然估计方法。对于模拟数据,实数阶和对数矩估计法略优于极大似然估计法,对于实测数据,对数矩估计法优势较明显,是一个较好的参数估计方案。
(3) 观测数据的分布受外界因素和样本数量的影响,采用P范分布能够较好地估计参数,接近误差的真实分布。观测样本数越大,计算得到的分布越接近它的真实分布,估计精度也越高。
| [1] | 孙海燕. P范分布理论及其在现代测量数据处理中的应用[D]. 武汉:武汉测绘科技大学, 1995. SUN Haiyan. Theory of P-norm Distribution and Application of Surveying Data Processing[D]. Wuhan:Wuhan Technical University of Surveying and Mapping, 1995. |
| [2] | 李克行. 基于LP估计的SLR数据处理与分析[D]. 上海:中国科学院研究生院, 2005. LI Kexing. SLR Data Processing and Analysis Based on LP Estimation[D]. Shanghai:Graduate School of the Chinese Academy of Sciences, 2005. |
| [3] | 蓝悦明, 贾媛. GPS观测值误差分布的研究[J]. 测绘通报, 2008(4):12-13, 54. LAN Yueming, JIA Yuan. The Study of Error Distribution for GPS Observed Values[J]. Bulletin of Surveying and Mapping, 2008(4):12-13, 54. |
| [4] | 潘雄, 王俊雷, 袁珊丽, 等. 一元P-范分布参数估计的改进方法[J]. 测绘科学, 2011, 36(2):48-49, 52. PAN Xiong, WANG Junlei, YUAN Shanli, et al. An Improvement Method of Parameters Estimation in P-norm Distribution[J]. Science of Surveying and Mapping, 2011, 36(2):48-49, 52. |
| [5] | 胡宏昌, 孙海燕.P-范分布参数σ的估计[J]. 武汉大学学报(信息科学版), 2002, 27(5):483-485. DOI:10.3321/j.issn:1671-8860.2002.05.009. HU Hongchang, SUN Haiyan. Parameter σ Estimation of P-norm Distribution[J]. Geomatics and Information Science of Wuhan University, 2002, 27(5):483-485. DOI:10.3321/j.issn:1671-8860.2002.05.009. |
| [6] | 李博峰, 沈云中. P-范分布混合整数模型极大似然估计[J]. 测绘学报, 2010, 39(2):141-145. LI Bofeng, SHEN Yunzhong. Maximum Likelihood Estimation in Mixed Integer Linear Model with P-norm Distribution[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2):141-145. |
| [7] | 潘雄, 付宗堂. 一元有界P范分布的参数自适应估计[J]. 武汉大学学报(信息科学版), 2007, 32(4):323-325, 335. PAN Xiong,FU Zongtang.Parameter Adaptive Estimation of Bounded P-norm Distribution[J]. Geomatics and Information Science of Wuhan University, 2007, 32(4):323-325, 335. |
| [8] | 潘雄, 赵启龙, 王俊雷, 等. 一元非对称P范分布的极大似然平差[J]. 测绘学报, 2011, 40(1):33-36. PAN Xiong, ZHAO Qilong, WANG Junlei, et al. Maximum Likelihood Adjustment of the Monadic Unsymmetrical P-norm Distribution[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1):33-36. |
| [9] | 於宗俦, 孙海燕, 陈之中. 多元P-范极大似然平差[J]. 测绘学报, 1996, 25(4):241-246. YU Zongchou, SUN Haiyan, CHEN Zhizhong. The Maximum Likelihood Adjustment of the P-norm distribution[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(4):241-246. |
| [10] | 潘雄, 孙海燕. 半参数P-范极大似然回归[J]. 测绘学报, 2005, 34(1):30-34. DOI:10.3321/j.issn:1001-1595.2005.01.006. PAN Xiong, SUN Haiyan. Semiparametric P-norm Maximum Likelihood Regression[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(1):30-34. DOI:10.3321/j.issn:1001-1595.2005.01.006. |
| [11] | 吴杰, 李正心, 王家骥. 自适应LP估计及其在照相天体测量中的应用[J]. 天文学报, 1996, 37(2):132-139. WU Jie, Li Zhengxin, WANG Jiaji. Adaptive LP Estimation and Its Application in the Photographic Astrometry[J]. Acta Astronomica Sinica, 1996, 37(2):132-139. |
| [12] | 潘雄, 程少杰, 赵春茹. 一元P范分布的参数快速估计方法[J]. 武汉大学学报(信息科学版), 2010, 35(2):189-192. PAN Xiong, CHENG Shaojie, ZHAO Chunru. A Fast Parameter Estimation in P-norm Distribution[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2):189-192. |
| [13] | 郑作亚, 卢秀山, 彭军还. LP估计在星载GPS运动学定轨中的应用及精度分析[J]. 天文学报, 2007, 48(2):210-219. ZHENG Zuoya, LU Xiushan, PENG Junhuan. The Application and Precision Analysis of Satellite-borne GPS Kinematic Orbit Determination with LP Estimation[J]. Acta Astronomica Sinica, 2007, 48(2):210-219. |
| [14] | 吴杰, 李正心, 张忠萍. 自适应LP估计及其应用[J]. 测绘学报, 1996, 25(1):31-36. WU Jie, LI Zhengxin, ZHANG Zhongping. Adaptive LP Estimation and its Application[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(1):31-36. |
| [15] | 潘晓刚,李强, 周海银. 基于自适应稳健最小P范数估计的轨道确定方法研究[J]. 天文学报, 2010, 51(3):285-298. PAN Xiaogang, LI Qiang, ZHOU Haiyin. The Research of Orbit Determination Method Based on the Adaptive Robust Least P-norm Estimation[J]. Acta Astronomica Sinica, 2010, 51(3):285-298. |
| [16] | 刘大杰, 史文中, 童小华. GIS空间数据的精度分析与质量控制[M]. 上海:上海科学技术文献出版社, 1999. LIU Dajie, SHI Wenzhong, TONG Xiaohua. Accuracy Analysis and Quality Control of Spatial Data in GIS[M]. Shanghai:Shanghai Science and Technology Literature Press, 1999. |
| [17] | 覃文忠. 地图数字化数据误差的分布检验[D]. 上海:同济大学, 1999. QIN Wenzhong. The Distribution Test of the Digital Map Data Error[D]. Shanghai:Tongji University, 1999. |
| [18] | 胡文琳, 王永良, 王首勇. 基于zrlog(z)期望的K分布参数估计[J]. 电子与信息学报, 2008, 30(1):203-205. HU Wenlin, WANG Yongliang, WANG Shouyong. Estimation of the Parameter of K-distribution Based on zrlog(z) Expectation[J]. Journal of Electronics & Information Technology, 2008, 30(1):203-205. |
| [19] | 胡文琳, 王永良, 王首勇. 基于矩方法的K分布杂波参数估计研究[J]. 雷达科学与技术, 2007, 5(3):194-198. HU Wenlin, WANG Yongliang, WANG Shouyong. Research on Estimation of Parameters of K-Distribution Based on the MOM Approach[J]. Radar Science and Technology, 2007, 5(3):194-198. |
| [20] | ISKANDER D R, ZOUBIR A M. Estimation of the Parameters of the K-distribution Using Higher Order and Fractional Moments[Radar Clutter] [J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(4):1453-1457. |