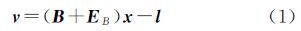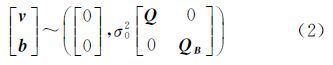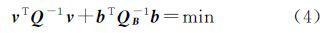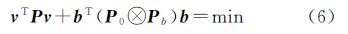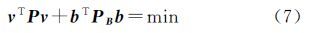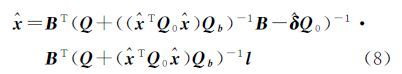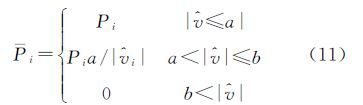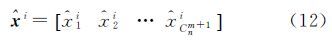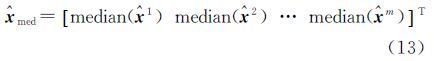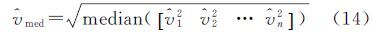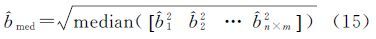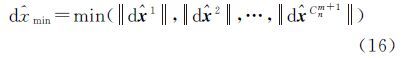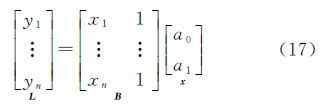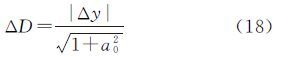2. 中国矿业大学环境与测绘学院, 江苏 徐州 221008
2. School of Environment Science and Spatial Informatics, China University of Mining & Technology, Xuzhou 221008, China
应用总体最小二乘准则(total least squares,TLS)能够解决变量中含有误差(error in variables,EIV)的模型参数估计问题,对其算法的研究在数据处理领域倍受关注[1, 2, 3, 4]。近年来,趋于总体最小二乘算法的成熟,总体最小二乘理论在测绘工作中得到了广泛应用[5, 6, 7, 8]。特别是能够顾及模型随机性质算法的提出[9],使得总体最小二乘模型在测绘数据处理中的应用更加广泛。同时,测绘工作者将经典测量平差模型中广泛存在的参数估计、精度评定、不适定模型的正则化、抗差估计、附有约束条件的模型参数估计等问题系统性地引入总体最小二乘准则下进行讨论[10, 11, 12, 13, 14, 15, 16, 17]:文献[11]对总体最小二乘模型单位权中误差的无偏估计进行研究,并建立单位权中误差无偏估计的迭代算法;文献[13]对病态总体最小二模型的正则化算法进行研究,建立了病态模型的广义正则化算法;文献[15]应用高斯-赫尔墨特模型建立总体最小二乘的抗差估计算法;文献[16]对附有等式约束的总体最小二乘算法进行研究,并应用极值函数解决参数估计问题,文献[17]在此基础上,应用穷举法建立附有不等式约束的总体最小二乘模型迭代算法。
现阶段,总体最小二乘理论在测绘专业的应用中取得丰富研究成果的同时,在抗差总体最小二乘理论方面缺乏适用性的研究成果,具有抗差性的总体最小二乘普遍算法是将经典的等价权函数思想引入总体最小二乘理论[18]。直接将经典的抗差理论应用至总体最小二乘模型,笔者认为存在两个方面的缺陷:①EIV模型的系数矩阵中的元素与观测向量中的元素精度不等,统一根据单位权中误差确定它们的等价权函数的域值并不合理;②应用总体最小二乘理论进行参数估计时,随机模型存在误差,通过调节观测值的权值来实现抗差性,会放大随机模型误差对算法的影响,算法的有效性值得商榷。
针对现有算法存在的不足,提出应用中位数法建立抗差总体最小二乘估计,根据EIV模型的系数矩阵与观测向量的残差分类确定等价权函数的域值,避免随机模型误差与观测元素精度差异等因素对抗差估计的影响。
1 基于等价权函数的总体最小二乘抗差估计 1.1 总体最小二乘模型变量中含有误差的参数估计模型为
式中,l为n×1阶观测向量;v为观测向量中含有的n×1阶误差向量;B为模型的n×m阶系数矩阵;EB为系数矩阵中含有的n×m阶误差矩阵;x为模型m×1阶参数向量。令b=vec(EB),vec(·)为矩阵的拉直符号,表示将矩阵按列拉直所得到的列向量。模型中误差向量的随机模型为 式中,σ02为单位权方差;Q、QB分别为误差向量v、b的协因数阵。与式(3)传统的高斯-马尔可夫模型(Gauss-Markov model,G-M)相比,EIV模型能够顾及系数矩阵中的元素含有的误差。v的计算公式为为实现对模型的观测向量与系数矩阵中含有的误差同时进行最小化的约束,建立总体最小二乘约束准则
当Q、QB为单位矩阵时,式(4)退化为等权估计的总体最小二乘准则。令 式中,⊗表示矩阵的克罗内克积;Q0为m×m阶协因数矩阵;Qb为n×n阶协因数矩阵,并且权矩阵P0=Q0-1、Pb=Qb-1。总体最小二乘准则可以表示为 令PB=P0⊗Pb,则式(6)表示为 1.2 基于等价权函数的抗差估计现阶段,总体最小二乘抗差估计的一般算法是根据参数的总体最小二乘解,求取模型的观测向量和系数矩阵的改正数,根据改正数的大小,应用等价权函数对相应的观测元素进行重新定权,并根据重新定义的权值对参数估值进行迭代求解。以文献[9]提出的基于拉格朗日函数的总体最小二乘迭代算法为例,其参数的总体最小二乘估值${\hat x}$、观测向量改正数${\hat v}$、系数矩阵中含有的误差矩阵${\hat E}$B的估值分别为
式(8)—式(10)中,其他变量的含义与参数的具体求解方法参见文献[9]。根据观测向量与系数矩阵中改正数的估值,应用权函数对其进行重新定权,以IGG权函数为例[19] 式中,Pi为观测元素的权值;${\hat v}$为相应观测元素对应的改正数;域值a、b分别取中误差的σ倍数,a=1.5σ,b=2.5σ。根据重新定义的权值${\bar P}$i迭代求解参数估值,直至收敛。上述算法是现有研究成果中,实现总体最小二乘抗差估计的普遍思路,其优点是理论基础成熟、算法的抗差性容易实现。但是结合总体最小二乘模型的特点,根据上文的分析,直接将经典测量平差抗差理论引用至总体最小二乘平差,其缺点也是显著的。为克服观测向量与系数矩阵中的元素精度不等,以及随机模型误差对总体最小二乘抗差性的影响,基于中位数建立总体最小二乘抗差估计算法。
2 基于中位数法的抗差总体最小二乘估计
假设观测向量的维数为n×1,模型参数的维数为m×1(n>m),在保证能够对参数估值进行精度评定的基础上,可以获得Cnm+1组参数估值。模型参数的第i个元素重新组成Cnm+1×1维向量
求取参数的第i个元素的中位数为median(${\hat x}$i),则模型参数的中位数向量${\hat x}$med为根据模型的中位数参数向量${\hat x}$med,应用式(9)、式(10)计算观测向量与系数矩阵中含有的误差向量的估值${\hat v}$、${\hat b}$,其中${\hat v}$=${\hat v}[$1 ${\hat v}$2…${\hat v}$n],${\hat b}$=[${\hat b}$1 ${\hat b}$2…${\hat b}$n×m]。定义误差向量的中位数为
依据绝对误差中位数与中误差的关系,分类确定观测向量与系数矩阵中的观测元素对应的中误差σL=1.483${\hat v}$med、σB=1.483${\hat b}$med[20]。此时,可以应用抗差权函数重新对观测元素进行分类定权${\bar P}$Li、${\bar P}$Bi。根据重新定义的权值迭代求解Cnm+1组参数估值,并求取其参数的中位数值${\hat x}$med(式(13))。计算各组模型参数的估值与中位参数的差值向量d${\hat x}$i=xi-${\hat x}$med,以Cnm+1组中差值向量的最小范数d${\hat x}$min对应的参数估值作为参数的最终估值
应用中位数法确定参数的估值,可以有效降低含有粗差的观测值对参数估值的影响,相关的研究成果表明,其崩溃污染率可以达到50%[21]。根据模型的观测向量与系数矩阵中观测元素的改正数,应用中位数法分类确定它们的中误差,并进行分类定权的总体最小二乘抗差算法,可以有效避免由于观测向量与系数矩阵中的观测元素实际精度不等,以及随机模型误差对权函数域值确定的影响。
3 算例与分析应用直线方程拟合对论文提出的算法进行验证,并与现有算法进行比较。设直线方程为y=a0x+a1,方程参数的模拟值a0=0.5、a1=10。直线上的点共有10个,其x轴的坐标值列于表 1。根据点的x轴坐标与方程参数的模拟值计算点的y轴坐标,列于表 1。点坐标严格满足模拟参数所确定的直线方程,可以将其作为观测元素的真值。
| 点号 | x | y |
| 1 | 10 | 15 |
| 2 | 15 | 17.5 |
| 3 | 20 | 20 |
| 4 | 25 | 22.5 |
| 5 | 30 | 25 |
| 6 | 35 | 27.5 |
| 7 | 40 | 30 |
| 8 | 45 | 32.5 |
| 9 | 50 | 35 |
| 10 | 55 | 37.5 |
假设有n个观测值时,直线的观测方程表示为
将1号点的x轴坐标、2号点的y轴坐标混入4~5 dm的粗差,点1、2、3、4的其余坐标混入1~6 cm的随机误差,应用混入误差的点1、2、3、4作为观测值求解模型参数,混入误差的点坐标列于表 2。
| m | ||
| 点号 | x | y |
| 1 | 10.45 | 15.03 |
| 2 | 15.06 | 17.9 |
| 3 | 19.95 | 19.98 |
| 4 | 24.95 | 22.47 |
在混入的误差中,x轴方向的误差值高于y轴方向的误差,以模拟总体最小二乘模型的观测向量与系数矩阵中的观测元素精度不等。其余点不混入误差,作为检核点对模型的拟合精度进行检核。
应用提出的中位数法求解模型参数,将选取的观测点1、2、3、4分为4组,即(1、2、3)、(1、2、4)、(1、3、4)、(2、3、4),应用拉格朗日迭代算法分别求解模型参数的初值。最终求解的基于中位数的估值列于表 3。根据传统的总体最小二乘抗差算法,应用点1、2、3、4求解的模型参数列于表 3。模型的观测向量与系数矩阵的权矩阵的初始值均取为单位1,如以4个点同时求解为例,式(8)中协因数阵的取值分别为
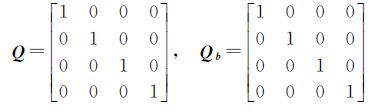
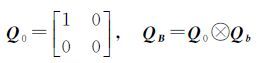
| 算法 | 参数估值 | 观测向量改正数的估值/m | 系数矩阵改正数的估值/m | 中误差的估值 | |||||||
| 1 | 0.504 | 9.969 | -0.166 | 0.269 | -0.039 | -0.064 | 0.084 | -0.136 | 0.020 | 0.032 | 0.257 |
| 2 | 0.510 | 9.849 | -0.117 | 0.295 | -0.033 | -0.080 | 0.060 | -0.151 | 0.017 | 0.041 | 0.146/0.074 |
| 注: 1表示拉格朗日算法,2表示中位数算法;系数矩阵中的常向量改正数为0,故只列出其观测值组成的列向量对应的改正数估值。中误差0.146/0.074分别表示观测向量与系数矩阵对应的中误差。 | |||||||||||
根据表 2中观测点混入误差的特征,此时定义的随机模型存在误差。分别根据拉格朗日算法与中位数法,经过三次迭代计算获得模型参数的估值、改正数的估值、与中误差的估值列于表 3。
由于总体最小二乘准则或者最小二乘准则会对观测值中的误差进行“平摊”,并且应用拉格朗日算法得到的中误差是有偏的[9],表 3的结果表明,如果根据传统算法,应用权函数并不能有效地根据含有粗差的观测值对参数进行抗差估计。应用表 3中由中位数法得到的各类估值,按照本文提出的方法,根据权函数对观测向量与系数矩阵中的观测元素进行分类定权,继续进行迭代计算,并以最小范数解作为模型参数的最终估值(式(16))。
当观测样本有限时,总体最小二乘是一种有偏估计[9],因此,不以中误差为精度的评定标准。根据总体最小二乘的几何意义[22],以检核点(表 1,点5、6、7、8、9、10)到拟合直线垂直距离的真值与拟合值之差ΔD,比较不同算法的拟合精度
式中,Δy为检核点y坐标的真值与拟合值的差值。不同算法拟合的精度列于表 4。结果表明,论文提出的基于中位数的总体最小二乘抗差算法拟合精度高于传统总体最小二乘抗差算法,提出的应用中位数法对模型的观测向量与系数矩阵中的观测元素进行分类定权的思想是可行的。在相同观测样本条件下,本文提出的抗差算法拟合的模型精度更高。| 算法 | 点号 | |||||
| 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | -0.085 9 | -0.104 8 | -0.123 7 | -0.142 6 | -0.161 4 | -0.180 3 |
| 2 | -0.066 3 | -0.078 8 | -0.091 3 | -0.103 8 | -0.116 3 | -0.128 8 |
| 注:1表示拉格朗日算法,2表示中位数算法。 | ||||||
在上述算例中,为了使得应用中位数法求解模型参数时,每组观测值中都含有粗差,分别在不同的点中加入粗差。当应用中位数法求解模型参数时,每组观测样本数小于传统算法,使得样本的粗差污染率变大。如果只在上述观测点中的一个观测点的纵横坐标中加入粗差,论文提出的算法在拟合精度上更有优势。
| [1] | PEARSON K. On Lines and Planes of Closest Fit to Systems of Points in Space[J]. Philosophical Magazine Series 6, 1901, 2(11):559-572. |
| [2] | GOLUB G H, VAN LOAN C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6):883-893. |
| [3] | VAN HUFFEL S, VANDEWALLE J. Analysis and Solution of the Nongeneric Total Least Squares Problem[J]. SIAM Journal on Matrix Analysis and Applications, 1988, 9(3):360-372. |
| [4] | SCHAFFRIN B, FELUS Y A. On Total Least-squares Adjustment with Constraints[J]. International Association of Geodesy Symposia, 2005, 128:417-421. |
| [5] | SCHAFFRIN B, LEE I, CHOI Y, et al. Total Least Squares(TLS) for Geodetic Straight-line and Plane Adjustment[J]. Bollettino di Geodesia e Scienze Affini, 2006, 65(3):141-168. |
| [6] | MAHBOUB V. On Weighted Total Least-squares for Geodetic Transformations[J]. Journal of Geodesy, 2012, 86(5):359-367. |
| [7] | SCHAFFRIN B, FELUS Y A. On the Multivariate Total Least-squares Approach to Empirical Coordinate Transformations:Three Algorithms[J]. Journal of Geodesy, 2008, 82(6):373-383. |
| [8] | KUPFERER S. Application of the Total Least-squares Technology with Geodetic Problem Definitions[D]. Karlsruhe:University of Karlsruhe, 2005. |
| [9] | SCHAFFRIN B, WIESER A. On Weighted Total Least-squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7):415-421. |
| [10] | FULLER W A. Properties of Some Estimators for the Errors-in-Variables Model[J]. The Annals of Statistics, 1980, 8(2):407-422. |
| [11] | TONG Xiaohua, JIN Yanmin, LI Lingyun. An Improved Weighted Total Least Squares Method with Applications in Linear Fitting and Coordinate Transformation[J]. Journal of Surveying Engineering, 2011, 137(4):120-128. |
| [12] | SHEN Yunzhong, LI Bofeng, CHEN Yi. An Iterative Solution of Weighted Total Least-squares Adjustment[J]. Journal of Geodesy, 2011, 85(4):229-238. |
| [13] | 葛旭明, 伍吉仓. 病态总体最小二乘问题的广义正则化[J]. 测绘学报, 2012, 41(3):372-377. GE Xuming, WU Jicang. Generalized Regularization to Ⅲ-posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3):372-377. |
| [14] | SCHAFFRIN B, SNOW K. Total Least-squares Regularization of Tykhonov Type and an Ancient Racetrack in Corinth[J]. Linear Algebra and Its Applications, 2010, 432(8):2061-2076. |
| [15] | 陈义, 陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J]. 测绘学报, 2012, 41(5):715-722. CHEN Yi,LU Jue.Performing 3D Similarity Transformation by Robust Total Least Squares[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5):715-722. |
| [16] | SCHAFFRIN B. A Note on Constrained Total Least Squares Estimation[J]. Linear Algebra and Its Applications, 2006, 417(1):245-258. |
| [17] | ZHANG Songlin, TONG Xiaohua, ZHANG Kun. A Solution to EIV Model with Inequality Constraints and Its Geodetic Applications[J]. Journal of Geodesy, 2013, 87(1):23-28. |
| [18] | TAO Yeqing, GAO Jinxiang, YAO Yifei. TLS Algorithm for GPS Height Fitting Based on Robust Estimation[J] Survey Review, 2014, 46(336):184-188. |
| [19] | 周江文. 经典误差理论与抗差估计[J]. 测绘学报, 1989, 18(2):115-120. ZHOU Jiangwen. Classic Theory of Errors and Robust Estimation[J]. Acta Geodaetica et Cartographica Sinica, 1989, 18(2):115-120. |
| [20] | ROUSSEEUW P J, WAGNER J. Robust Regression with a Distributed Intercept Using Least Median of Squares[J]. Computational Statistics & Data Analysis, 1994, 17(1):65-76. |
| [21] | YANG Yuanxi. Robust Estimation of Geodetic Datum Transformation[J]. Journal of Geodesy, 1999, 73(5):268-274. |
| [22] | 刘经南, 曾文宪, 徐培亮. 整体最小二乘估计的研究进展[J]. 武汉大学学报(信息科学版), 2013, 38(5):505-512. LIU Jingnan, ZENG Wenxian, XU Peiliang. Overview of Total Least Squares Methods[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5):505-512. |