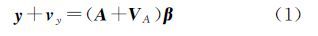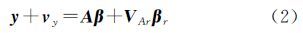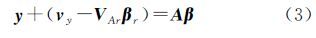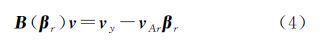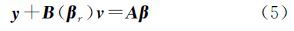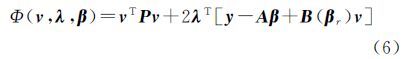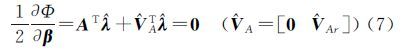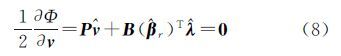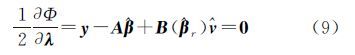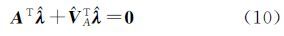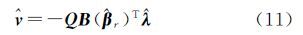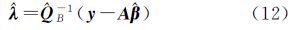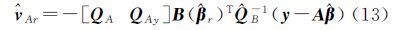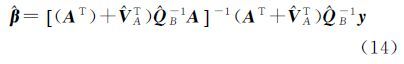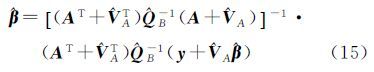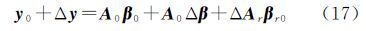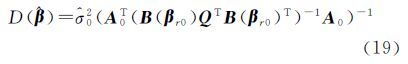2. 武汉大学卫星导航定位技术研究中心, 湖北 武汉 430079;
3. 郑州测绘学校, 河南 郑州 450015
2. Research Center of GNSS, Wuhan University, Wuhan 430079, China;
3. Surveying and Mapping School of Zhengzhou, Zhengzhou 450015, China
高斯-马尔科夫(Gauss-Markov，GM)模型的系数矩阵是固定量(也称非随机量)，最小二乘(least squares，LS)估计可求得GM模型的最优无偏解，LS算法简单、高效，是大地测量领域最常用的估计方法。EIV(errors-in-variables)模型的系数矩阵含随机误差，如果忽略系数矩阵的随机误差采用LS得到的结果有偏[1, 2]，整体最小二乘(total least squares，TLS)估计由于同时顾及了观测向量和系数矩阵中的随机误差，解具有渐近无偏性[3]。文献[4]于19世纪末最早提出整体最小二乘估计准则，但TLS估计的非线性特性致其受制于计算机技术的发展，直到20世纪80年代初，文献[1]提出了著名的奇异值分解算法后，TLS才开始广泛应用于各专业领域。大地测量领域结合测量数据的特性和需求，21世纪初起对TLS进行了深入研究，提出了加权TLS算法[5, 6, 7, 8, 9, 10, 11](weighted total least squares,WTLS)。此外，扩展TLS算法如非线性TLS算法[10, 12]、附有等式和不等式约束的TLS算法[13, 14, 15, 16, 17, 18]等相继得到了研究。
当EIV模型的系数矩阵并非全为随机量，而是同时包含固定量和随机量时，不能简单运用TLS算法求解，需采用混合整体最小二乘(least squares-total least squares,LS-TLS)估计。现有混合LS-TLS算法可分为两类,一类算法仅针对固定列的特殊混合LS-TLS算法，如文献[19, 20]的算法基于矩阵QR分解，文献[3]采用广义奇异值分解方法，这些数值算法并不能得到统计意义上的最优解[2]，文献[21, 22]讨论了固定列混合模型的统计最优解。另一类算法针对结构性系数矩阵情况，提出的结构TLS算法或者加权TLS算法能够解决系数矩阵同时含固定列和随机量的估计问题，如文献[23]采用将权矩阵中对应于固定元素的方差置零，文献[2]将混合模型系数矩阵中的随机量纳入平差的函数模型作为待估参数,文献[16]将系数矩阵表达为独立随机量的函数等。
文献[9, 10]将EIV模型表示为非线性GH模型推导了WTLS算法，但并没有考虑系数矩阵同时包含固定量和随机量的情况。针对这类一般性的EIV模型，本文推导了基于非线性GH模型的混合LS-TLS算法。通过将系数矩阵中的随机量纳入平差的随机模型，从而将平差模型表示为含随机系数矩阵的非线性GH模型形式，提出的算法适用于系数矩阵包含固定列、随机和非随机量的一般情况。同时，本文推导了混合LS-TLS估计的一阶精度评定公式。实例计算结果表明，混合LS-TLS估计结果与现有能够解决混合LS-TLS问题的结构性TLS算法或加权TLS算法估计结果相同，混合LS-TLS算法与参数真值的差异要小于LS或TLS估计结果与真值的差异。当系数矩阵元素全部为固定元素或者全部为随机元素时，混合LS-TLS算法转换为LS或者TLS算法,因此该算法具有一般性。
1 EIV模型的非线性GH模型形式EIV函数模型形式为[3]
式中,y和vy表示n×1的观测向量和改正数向量；β表示t×1的参数向量；A和VA表示n×t的系数矩阵及其改正数矩阵。
系数矩阵A同时包含固定列、随机元素和固定元素，是EIV模型的一般形式，如布尔莎(Bursa—wolf)七参数坐标转换模型，假定式(1)中系数矩阵的前u列为固定列，后t-u列含随机元素和固定元素，对应的(t-u)×1参数向量用βr表示，式(1)可表示为
式中，VAr表示系数矩阵非固定列部分的随机元素对应的n×(t-u)的改正数矩阵(其中固定元素对应0)，将VArβr移到等式左边< 令 式中，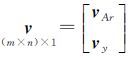
，vAr表示将VAr中的随机元素按列提取出来组成的向量(去掉VAr中固定元素对应的0)，若A中随机元素个数为m，则vAr为m×1列向量；B(βr)表示v的n×(m×n)系数矩阵且含参数βr，模型(2)可表示为如下含随机系数矩阵的非线性GH模型形式
式中，v的协因数阵为
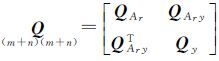；权阵为P，QAr、Qy和QAry分别表示vAr、vy的协因数阵及其互协因数阵。式(5)实质为平差模型的一般形式，GM模型和EIV模型可视为该模型的特殊形式。
2 混合LS-TLS估计
2.1 混合LS-TLS算法
本节在整体最小二乘准则下，导出模型式(5)的混合LS-TLS算法。模型式(5)的目标函数为
式(6)分别对待估计量求一阶偏导并令其为0
式中，变量上加尖号表示模型的估计量，由以上3式可得 式中，$\hat Q$B=B(${\hat \beta }$r)QB(${\hat \beta }$r)T。
式(12)代入式(11)
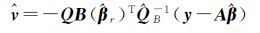
相应的${\hat v}$Ar表达式为
式(12)代入式(10)可导出参数的LS-TLS解如下
等式两边同乘${\hat \beta }$=[(AT+${\hat V}$AT)${\hat Q}$B-1A]，并加上(AT+${\hat V}$AT)${\hat Q}$B-1${\hat V}$A${\hat \beta }$，得到另一种对称的LS-TLS参数解
由式(13)—式(15)，导出混合LS-TLS算法如下：①给出GH模型式(5)的观测向量和系数矩阵y、A，并由式(4)写出B(βr)；②参数初始值取模型的LS估计值：${\hat \beta }$0=(ATQy-1A)-1ATQy-1y，${\hat v}$Ar的初始值取0，用${\hat \beta }$0构建B0(βr)；③根据式(15)(或式(14))迭代计算(${\hat V}$AT由式(13)计算${\hat v}$Ar后更新，B(${\hat \beta }$r)用中的${\hat \beta }$r更新)，直至前后两次计算结果之差小于设定的容许值。
混合LS-TLS算法具有一般性，适用于系数矩阵元素随机和非随机的各种情况，以下给出特殊情况下算法中B(βr)和v的具体形式：①当系数矩阵元素全部为固定量时，B(βr)=In，v=vy，混合LS-TLS算法转换为LS算法；②当系数矩阵元素全部为随机元素时，B(βr)=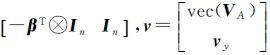
，vec(·)表示矩阵的向量化，混合LS-TLS算法与TLS算法等价；③当系数矩阵仅含固定列和随机元素时，B(βr)=-βrT⊗InIn。
整体最小二乘属于非线性估计，文献[3]证明了整体最小二乘是EIV模型的最优估计，当观测值个数趋于无穷时，估计结果具有弱一致性和渐进无偏性。但是，有限样本情况下整体最小二乘估计结果有偏，文献[2]推导了参数解的偏差估计公式。
目前主要采用线性化方法推导TLS参数估计值的一阶近似精度[2, 24]，模型式(1)可表示为
式中，变量上加“~”表示真值。将式(16)在近似值y0、A0和β0处线性化，并省略二阶项得 式中，ΔAr表示系数矩阵非固定列的随机元素的一阶项对应的n×(t-u)矩阵；βr0表示式(4)中βr对应的近似值，整理式(17)得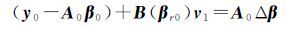
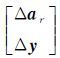，Δar表示将ΔAr中的随机元素按列提取出来组成的向量(去掉ΔAr中固定量对应的0元素)，B(βr0)为式(4)的B(βr)中的参数取近似值βr0。上式是线性化的GH模型形式，参考文献[25]得到混合LS-TLS解的精度评定公式如下
式中，近似值B(βr0)和A0取模型的LS-TLS估计值B(${\hat \beta }$r)和${\hat A}$e。
3 实例分析
本节针对系数矩阵同时包含固定列、随机元素和固定元素的一般情况，设计实例说明本文算法的应用，比较了混合LS-TLS算法结果与文献[2, 23]以及文献[16]中3种算法的结果，并且比较了混合LS-TLS算法与LS算法和TLS算法结果的差异。
布尔莎七参数坐标转换模型是系数矩阵同时含固定列、固定量和随机量的典型EIV模型，但由于坐标转换模型的强非线性特性，该模型要求旋转角度为微小值以避免线性化引起的模型误差过大[26]，加之模型主要用于长距离大地坐标系统间的转换，LS和TLS估计结果相差很小[2]。因此，为了比较混合LS-TLS与LS和TLS估计结果的差异，模拟了与布尔莎模型类似的系数矩阵包含固定列、随机元素和固定元素的EIV模型如下
式中，*符号表示随机元素，系数矩阵前两列为固定列，后两列含固定量和随机量，系数矩阵共含24个元素，固定元素18个，随机元素6个。根据式(2)，式(20)可表示为 式中，符号上加‘-’表示随机元素的观测值，式(21)写成GH模型式(5)的形式，对应的矩阵和向量分别为
| 模拟数据 | ${\tilde A}$ | ${\tilde \beta }$ | ${\tilde y}$ |
| 真值 |  |  |  |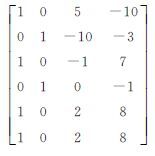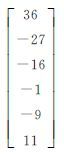
为了比较不同算法的估计结果，避免数据的偶然性的影响，以表 1数据真值为基础，设定A和y中随机量的中误差分别为±0.6和±0.3，且误差均独立，共生成1000组随机误差，计算了混合LS-TLS算法及其他各类算法的估计值，表 2列出了估计结果的平均值，可以看到：
| 算法 | 参数 | ${\hat \beta }$1 | ${\hat \beta }$2 | ${\hat \beta }$3 | ${\hat \beta }$4 | ‖·‖ |
| 混合LS-TLS算法(结构或加权TLS算法) | ${\hat \beta }$ | 1.024 | -3.047 | 3.002 | -2.005 | |
| ${\hat \sigma }$ | 0.029 | 0.037 | 0.003 | 0.004 | 0.047 | |
| ${\hat b}$ | 0.024 | 0.047 | 0.002 | 0.005 | 0.053 | |
| TLS算法 | ${\hat \beta }$ | 1.123 | -3.234 | 2.988 | -2.010 | |
| ${\hat \sigma }$ | 0.032 | 0.040 | 0.005 | 0.004 | 0.052 | |
| ${\hat b}$ | 0.123 | 0.234 | 0.012 | 0.010 | 0.265 | |
| LS算法 | ${\hat \beta }$ | 1.049 | -3.059 | 2.991 | -2.006 | |
| ${\hat \sigma }$ | 0.030 | 0.038 | 0.005 | 0.004 | 0.049 | |
| ${\hat b}$ | 0.049 | 0.059 | 0.009 | 0.006 | 0.077 | |
| 注：${\hat \beta }$表示估计值的均值；${\hat \sigma }$和${\hat b}$为${\hat \beta }$的中误差及偏差；‖·‖表示向量的模，即向量的欧氏长度。 | ||||||
(1) 混合LS-TLS算法与目前能够解决混合LS-TLS问题的文献[2]、[16]和[23]中3种结构或加权TLS算法估计结果相同。与文献[16]和[23]的算法比较，混合LS-TLS算法仅考虑了系数矩阵中随机量的权阵，权阵维数要低于将固定量权置零的处理方法，当系数矩阵的固定量较多时，计算效率显著提高。文献[2]将系数矩阵的随机量提取出来作为待估计参数，与本文算法的计算效率相当。
(2) 整体最小二乘估计具有渐进无偏性，当样本数有限时，估计结果存在偏差。对比混合LS-TLS、LS和TLS的估计结果可以看到，本例中由于LS算法忽略了A中的随机误差，TLS算法将A中全部元素视为随机量，两者与实际模型存在偏差，LS、TLS估计偏差的模(向量的欧氏长度)分别为0.077、0.265，显著大于混合LS-TLS估计偏差的模0.053。A中共24个元素，含18个固定量，仅含6个随机量，因此，将系数矩阵元素全部视为随机量的TLS估计偏差要大于将系数矩阵元素全部视为固定量的LS估计偏差。混合LS-TLS参数估计的中误差要小于LS和TLS参数中误差。
4 结 论EIV模型的整体最小二乘估计被证明具有渐进无偏性，当EIV模型的系数矩阵同时包含固定量和随机量时，需采用混合LS-TLS估计。目前，混合LS-TLS算法可分为两类，一类为直接算法，这些算法仅考虑了系数矩阵为固定列和随机元素的特殊情况，如线性回归模型；另一类为针对结构性系数矩阵的TLS算法，能够解决混合整体最小二乘估计问题，如文献[23]通过将系数矩阵固定量的方差置零,文献[2]将系数矩阵中的随机量纳入平差的函数模型作为待估参数求解，文献[16]将系数矩阵表达为其包含的独立量的函数运用WTLS算法求解。文献[9]和文献[10]研究了将EIV模型改写为高斯-赫尔默特模型形式推导WTLS算法，但并没有考虑系数矩阵固定量与随机量并存的情况，针对EIV模型的这类一般情况，本文通过把系数矩阵随机元素纳入平差的随机模型，从而将模型表示为含系数矩阵随机误差的非线性高斯赫尔默特模型形式，在此基础上提出了混合LS-TLS算法，并推导了一阶近似精度估计公式。与已有的混合LS-TLS直接算法比较，本文算法适用于系数矩阵含固定列、随机元素和固定元素的一般情况。与将固定元素的方差置零的方法比较，本文算法仅提取了随机元素构建相应的方差协方差阵，维数要低于固定元素方差置零的方法，尤其当系数矩阵含有大量固定元素时，本文算法的计算效率显著提高。与将系数矩阵随机元素纳入函数模型的方法比较，本文提出了将系数矩阵随机元素纳入平差的随机模型的一种新思路。模拟实例计算结果表明，本文算法与当前其他能解决混合LS-TLS算法的估计结果相同；此外，由于单纯的LS算法和TLS算法未能顾及系数矩阵固定量和随机量并存的情况，混合LS-TLS估计结果统计上要显著优于LS或者TLS估计结果。本文提出的混合LS-TLS算法具有一般性，适用于系数矩阵包含随机和非随机元素、全部为固定元素或随机元素等各种情况。
| [1] | GOLUB GH, VAN LOAN C F. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6):883-893. |
| [2] | XU Peiliang, LIU Jingnan, SHI Chuang. Total Least Squares Adjustment in Partial Errors-in-variables Models:Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8):661-675. |
| [3] | VAN HUFFEL S,VANDEWALLE J.The Total Least Squares Problem:Computational Aspects and Analysis[M]. Philadelphia:Society for Industrial and Applied Mathematics, 1991. |
| [4] | ADCOCK R J. Note on the Method of Least Squares[J]. The Analyst, 1877, 4(6):183-184. |
| [5] | SCHAFFRIN B, WIESER A. On Weighted Total Least-squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7):415-421. |
| [6] | SHEN Yunzhong, LI Bofeng, CHEN Yi. An Iterative Solution of Weighted Total Least-squares Adjustment[J]. Journal of Geodesy, 2010, 85(4):229-238. |
| [7] | FANG Xing. Weighted Total Least Squares:Necessary and Sufficient Conditions, Fixed and Random Parameters[J]. Journal of Geodesy, 2013, 87(8):733-749. |
| [8] | FANG Xing. A Total Least Squares Solution for Geodetic Datum Transformations[J]. Acta Geodaetica et Geophysica, 2014, 49(2):189-207. |
| [9] | NEITZELF. Generalization of Total Least-squares on Example of Unweighted and Weighted 2D Similarity Transformation[J]. Journal of Geodesy, 2010, 84(12):751-762. |
| [10] | FANG Xing. Weighted Total Least Squares Solutions for Applications in Geodesy[D]. Germany:Leibniz University Hannover, 2011. |
| [11] | TONG Xiaohua, JIN Yanmin, ZHANG Songlin, et al. Bias-Corrected Weighted Total Least-squares Adjustment of Condition Equations[J]. Journal of Surveying Engineering,2014, 141(2):0401-0413. |
| [12] | 胡川,陈义. 非线性整体最小平差迭代算法[J]. 测绘学报, 2014, 43(7):668-674. DOI:10.13485/j.cnki.11-2089.2014.0111. HU Chuan, CHEN Yi. An Iterative Algorithm for Nonlinear Total Least Squares Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7):668-674.DOI:10.13485/j.cnki.11-2089.2014.0111. |
| [13] | ZENG Wenxian, LIU Jingnan, YAO Yibin. On Partial Errors-in-variables Models with Inequality Constraints of Parameters and Variables[J]. Journal of Geodesy, 2015, 89(2):111-119. |
| [14] | 曾文宪, 方兴, 刘经南, 等. 附有不等式约束的加权整体最小二乘算法[J]. 测绘学报, 2014, 43(10):1013-1018. DOI:10.13485/j.cnki.11-2089.2014.0173. ZENG Wenxian, FANG Xing, LIU Jingnan, et al. Weighted Total Least Squares Algorithm with Inequality Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10):1013-1018. DOI:10.13485/j.cnki.11-2089.2014.0173. |
| [15] | FANG Xing. On Non-combinatorial Weighted Total Least Squares with Inequality Constraints[J]. Journal of Geodesy, 2013, 88(8):805-816. |
| [16] | FANG Xing. A Structured and Constrained Total Least-Squares Solution with Cross-covariances[J]. Studia Geophysica et Geodaetica, 2014, 58(1):1-16. |
| [17] | FANG Xing. Weighted Total Least-squares with Constraints:A Universal Formula for Geodetic Symmetrical Transformations[J]. Journal of Geodesy, 2015, 89(5):459-469.DOI:10.1007/s00190-015-0790-8. |
| [18] | ZHANG Songlin, ZHANG Kun. On a Basic Multivariate EIV Model with Linear Equality Constraints[J]. Applied Mathematics and Computation, 2014, 236:247-252. |
| [19] | GOLUB GH, HOFFMAN A, STEWART GW. A Generalization of the Eckart-Young-Mirsky Matrix Approximation Theorem[J]. Linear Algebra and Its Applications, 1987, 88-89:317-327. |
| [20] | DUNNE BE, WILⅡLAMSONGA. QR-based TLS and Mixed LS-TLS Algorithms with Applications to Adaptive ⅡR Filtering[J]. IEEE Transactions on Signal Processing, 2003, 51(2):386-394. |
| [21] | YAN Shijian, FAN Jinyan. The Solution Set of the Mixed LS-TLS Problem[J]. International Journal of Computer Mathematics, 2001, 77(4):545-561. |
| [22] | 胡川, 陈义, 彭友. 混合结构总体最小二乘参数估计[J]. 大地测量与地球动力学, 2013, 33(4):56-60. HU Chuan, CHEN Yi, PENG You.On Mixed Structured Total Least Squares for Parameters Estimation[J]. Journal of Geodesy and Geodynamics, 2013, 33(4):56-60. |
| [23] | MAHBOUB V, SHARIFI MA. On Weighted Total Least-squares with Linear and Quadratic Constraints[J]. Journal of Geodesy, 2013, 87(3):279-286. |
| [24] | 孔建,姚宜斌, 黄承猛. 非线性模型的一阶偏导数确定方法及其在TLS精度评定中的应用[J]. 大地测量与地球动力学, 2011, 31(3):1-5. KONG Jian, YAO Yibin, HUANG Chengmeng. Method for Determining First-order Partial Derivative of Nonlinear Model and Its Application in TLS Accuracy Assessment[J]. Journal of Geodesy and Geodynamics, 2011, 31(3):1-5. |
| [25] | KOCH K R. Parameter Estimation and Hypothesis Testing in Linear Models[M]. Berlin:Springer, 1999. |
| [26] | 曾文宪, 陶本藻. 三维坐标转换的非线性模型[J]. 武汉大学学报(信息科学版), 2003, 28(5):566-568. ZENG Wenxian, TAO Benzao. Non-linear Adjustment Model of Three-dimensional Coordinate Transformation[J].Geomatics and Information Science of Wuhan University, 2003, 28(5):566-568. |