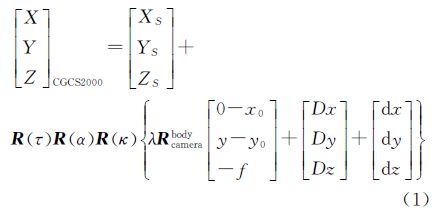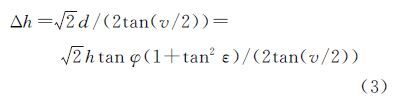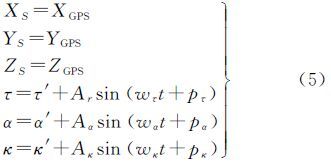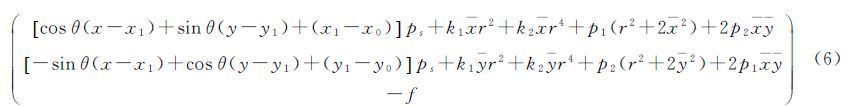2. 中国天绘卫星中心, 北京 102102
2. Center of TH-Satellite of China, Beijing 102102, China
天绘一号卫星是我国第一颗传输型立体测绘遥感卫星,其搭载的5 m分辨率三线阵立体相机的主要任务是实现无地面控制点条件下测制1∶50 000比例尺地形图[1],对几何要求较高。然而,由于受到卫星安装工艺、传感器精度、卫星发射时加速度大、在轨运行温度变化等因素的影响,利用星上辅助数据和实验室标定的几何参数直接定位精度较低[2],因此必须对星上三线阵相机进行在轨几何检校。在这方面国外研究相对成熟,2007年发射的WorldView-1无控定位中误差在10 m以内;2009年发射的WorldView-2无控定位平面中误差为4 m,高程中误差3 m[3];2008年发射的GeoEye-1经检校后精度达到平面中误差2.3 m,高程中误差3.6 m[4];2011年法国发射的Pleiades-1A无控定位中误差为3 m左右[5]。国内方面,大量学者针对2012年发射的资源三号进行了在轨检校研究,资源三号经过检校后,无地面控制定位平面中误差优于15 m,高程中误差优于10 m[6]。
为了减小卫星姿态变化对卫星在轨标定的影响,目前天绘一号卫星所采用的是EFP法进行在轨检校[7],经检校后,利用5个测区114个控制点检查,无控定位平面中误差10.3 m,高程中误差5.7 m,满足20 m等高距下1∶50 000地形图的测绘需求[8]。但是EFP定向片时刻不一定在外方位变化的拐点处,并且只对3个镜头的主距、主点、镜头之间夹角、正视镜头与星敏感器夹角进行检校,并不能很好地改正卫星在轨运行中有可能存在的全部系统误差。
另外,卫星在轨飞行时的几何参数不仅与地面标定的初值不符,而且有低频变化[9],因此严格的检校应分为两步:第1步,利用地面控制点对相机进行在轨几何参数精化;第2步,在全球不同纬度不同季节对卫星相机持续不断地进行在轨几何参数精化,并总结参数的变化规律。本文完成的是检校的第一步工作,对第2步工作不做探讨。
1 三线阵相机在轨几何参数精化模型严格成像模型的建立是在轨几何参数精化的基础[10]。根据推扫式星载光学卫星的成像原理可以建立严格成像模型,即
式中,[X Y Z]CGCS2000T为地面点在CGCS2000坐标系中的坐标;[XSYSZS]T为成像时刻卫星在CGCS2000坐标系中的位置坐标;λ为成像比例系数;R(τ)、R(α)、R(κ)为从CGCS2000坐标系到本体坐标系的3个角元素对应的旋转矩阵;[Dx Dy Dz]T、[dx dy dz]T分别为GPS相位中心相对本体坐标系的偏移与相机坐标系相对于本体坐标系的偏移;Rcamerabody表示的是相机相对于本体的安置矩阵;[0-x0 y-y0 f]T为像元在像空系中的坐标。式(1)可以精确地表示天绘一号卫星三线阵相机的成像几何,但是辅助数据中没有提供[Dx Dy Dz]T、[dx dy dz]T的具体数值,由于线元素与角元素的相关性[11],本文忽略[Dx Dy Dz]T、[dx dy dz]T,但这可能会影响模型的精度。
根据上述原理,三线阵立体交会直接对地定位的结果为:平面中误差49.58 m,高程中误差35.56 m。
1.1 几何参数精化的外方位模型天绘一号卫星三线阵影像共用一组定姿定轨数据,时间从前视成像开始到后视成像结束。其GPS定轨精度为3~4 m[12],定姿方面只配置有3台引进的中等精度星敏感器[13],定姿精度约为2″[14]。
虽然天绘一号卫星定轨精度不高,但实际计算中,将外方位线元素当成真值。不对线元素改正是因为:①线元素与角元素之间强相关,导致最小二乘无法答解;②使用岭估计、虚拟误差方程等方法求解虽然可以收敛,但结果有偏[15],从改正结果来看也不能真正求解出线元素实际存在的误差;③虽然天绘一号卫星定轨精度只有3~4 m,但由于卫星飞行高度高,经角元素改正后对平面和高程定位精度的影响并不很大,如图 1所示。

|
| 图 1 线元素对定位造成的误差 Fig. 1 The positioning error caused by line element error |
以某一高度的地面控制点对外方位角元素改正,得到图上虚线所示改正后的摄影光线,实际摄影光线由实线所示。由于定轨存在3~4 m的误差,卫星飞行高度为500 km,实际摄影光线与改正后的摄影光线之间存在一个较小的角度φ≈arctan(4/500 000),ε为φ角平分线与对应铅垂线方向间的夹角。可以得到在与控制点高度相差h的物方像差d为[16]
当物方像差d出现在核面上时,将对高程定位精度造成最大影响,此时的高程误差Δh的计算公式为[17]
式中,v表示交会角,天绘一号卫星前视后视交会角为25°+25°。由式(3)可知,当φ较小,h在一定范围内时d→0,Δh→0。以地球陆地极限高差9000 m计算地形起伏所引起的物方像差为
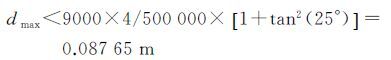
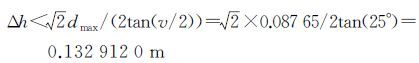
卫星上天后,3个镜头相对于卫星本体存在的安置偏差可归并为常角差,加入安置矩阵Rcamerabody中。Rcamerabody采用如下转角系统
利用31个地面控制点改正后,定位误差为:平面中误差12.63 m,高程中误差26.01 m。相比于直接对地定位虽然平面精度有比较明显的提高,但在高程方向上的定位精度很低,这与通常的结论不符[18]。观察定姿数据可以发现在3个角元素上均存在量级为10-5 rad的抖动,以κ角为例放大显示,如图 2所示。

|
| 图 2 定姿数据中κ角随时间变化情况 Fig. 2The situation of angle κ changes with time |
相较其他卫星的姿态数据这种情况并不正常。为消除抖动影响,仿照低阶多项式模型的原理对定姿数据进行3次多项式拟合后生成一组新的定姿数据,利用这组定姿数据直接对地定位,精度为平面中误差40.66 m,高程中误差45.59 m,利用31个控制点常角差改正后,得到的结果为平面中误差8.98 m,高程中误差4.51 m,这说明卫星实际飞行中并不存在高频的抖动,经过对定姿数据的预处理,可以使定姿数据更接近卫星的实际飞行情况。
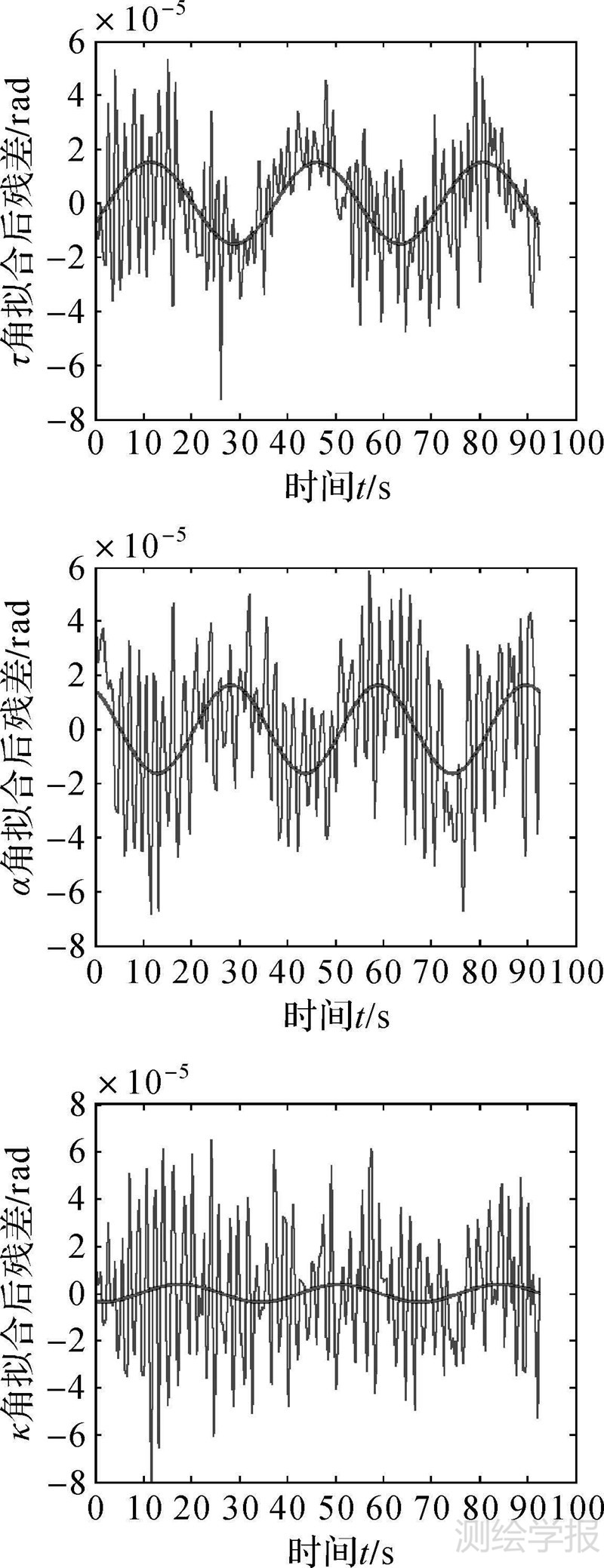
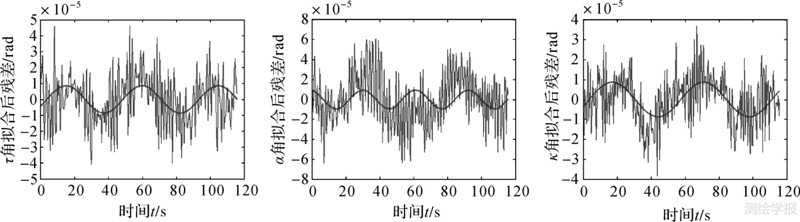
由于天绘一号采用的是小卫星平台,航线并不稳定,采用三阶多项式拟合的定姿数据并不能完全描述卫星的姿态变化情况[19],观察用三阶多项式拟合的定姿数据相对于原始数据的残差可以发现,在残差数据中含有类似正弦函数的低频抖动与不规律的高频抖动,如图 3所示。
|
| 图 3 τ、α、κ拟合后残差情况 Fig. 3 τ、α、κ fitting residual error |
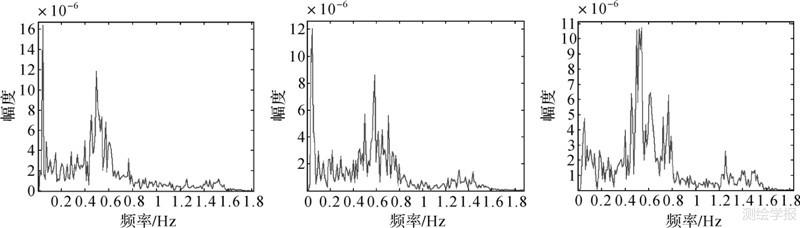
将残差数据转换到频率域观察,如图 4所示。
|
| 图 4 τ、α、κ残差在频率域中的情况 Fig. 4 τ、α、κresidual error in frequency domain |
从图中可以看到τ、α角残差在0~0.2 Hz频率上有极高的能量并且频率相对集中,κ角残差在此波段虽然出现一个峰值但不太明显。3个角元素在0.3~0.8 Hz频率上也有部分的能量,但并不集中,即为之前认为是错误的杂波。由此推断在卫星实际姿态中可能含有低频的抖动误差,经尝试这种低频的抖动很难用更高阶次的多项式拟合,因此仅用低阶多项式模型不能很好地描述天绘一号卫星的姿态变化。由于低频抖动围绕0值波动,且一段时间内频率稳定,振幅量级达到10-5 rad,会对定位产生米级影响,因此采用正弦函数对其补偿。设计卫星本体的外方位模型为
式中,XS、YS、ZS、τ、α、κ为某一影像行成像时刻的外方位元素;XGPS、YGPS、ZGPS、τ′、α′、κ′为由定轨定姿数据内插得到的成像时刻外方位元素;Aτsin(wτt+pτ)、Aαsin(wαt+pα)、Aκsin(wκt+pκ)为随时间变化的正弦函数改正量;Aτ、Aα、Aκ为抖动的振幅;wτ、wα、wκ为抖动的角频率;pτ、pα、pκ为抖动的相位。根据残差可知卫星在κ角的抖动较小,具体情况需要在实际计算时作进一步分析。
1.2 几何参数精化的内方位模型内方位误差改正多采用附加参数模型,其方法是对可能的误差项逐一分析,得到其引起的像点移位(Δx,Δy),从量测的像点坐标上减去相应的移位值,从而改正内方位元素误差造成的影响。其问题是各个误差项是同时对内方位造成影响的,简单的割裂开来分析后再加和并不完全符合实际情况。为解决这一问题,应同时考虑各误差项对内方位造成的影响,直接将像点坐标的改正建立在原始像素观测值上,而非(Δx,Δy)上,可能是更好的选择。为方便通过影像像素坐标描述内方位元素,定义CCD平面直角坐标系oC-xCyC,如图 5所示。

|
| 图 5 CCD平面直角坐标系 Fig. 5 CCD plane rectangular coordinate system |
在与主光轴垂直的像平面内,CCD平面直角坐标系的原点为CCD像元序列的起始位置,yC轴指向CCD线阵序列方向,xC轴依右手法则确定,飞行方向为正。
在CCD平面直角坐标系中综合考虑三线阵相机内方位可能出现的主点偏移、CCD旋转、像元尺寸变化、光学畸变误差,那么像点在像空系中的坐标为
式中,(x,y)、(x0,y0)、(x1,y1)分别为像点、像主点、CCD线阵的转动中心在CCD平面直角坐标系中的像素坐标;ps为CCD像元的尺寸;θ为CCD线阵在像平面内旋转的角度;k1、k2为镜头径向畸变系数;p1、p2为镜头切向畸变系数;x、y为像点与像主点在对应轴向上的距离;r为像点坐标到像主点的辐射距。在平差时只需对上述参数改正即可。不对焦距f进行改正的原因是焦距对像点误差的影响与像元尺寸变化的影响相同,并且在答解时会和像主点坐标的x0分量相互影响,造成解的不准确[20]。由于内方位元素众多,参数之间的相关性会对法方程解算稳定性产生影响,在实际几何参数精化过程中应根据内方位实际存在误差的情况和参数解算中的相关性对参数进行选择。
2 试验与分析为确定几何参数精化模型和求解策略,本文采用单侧有控外推的方式,首先利用河南地区的数据进行试验,之后利用北京-山东、黑龙江两地的数据进行验证。
2.1 试验数据试验使用的河南地区数据为同一轨内的135、136两景天绘三线阵影像、辅助数据和控制点数据。两张影像的范围内包含平原和山地,地形起伏约800 m左右。其中135影像中包含控制点31个,136影像中包含控制点10个。验证使用的北京-山东和黑龙江数据均为300 km以上的长条带影像,其上均匀分布5排控制点,每排控制点位于影像的左、中、右3个点位,每个点位处有两个相邻的控制点。控制点均为野外量测,人工在影像上刺点,像点量测精度约为一个像素。
2.2 外方位模型验证试验及分析在第1节分析的基础上,对3种外方位模型进行了对比试验。为防止控制点布设对结果的影响,135影像的31个控制点全部参与平差,并作为检查点验证模型在单景中的适应性,136影像10个控制点全部作为检查点验证模型外推情况(之后的内方位模型参数选择试验与求解策略试验均采用这种方式),内方位元素为实验室标定的(x0,y0)、ps、f,精度统计值为中误差,统计结果如表 1所示。
| m | |||||||||||
| 外方位模型 | 135景 | 136景 | |||||||||
| 纬度方向 | 经度方向 | 平面 | 高程 | 立体 | 纬度方向 | 经度方向 | 平面 | 高程 | 立体 | ||
| 常角差 | 7.49 | 4.94 | 8.98 | 4.51 | 10.05 | 11.48 | 4.83 | 12.45 | 4.73 | 13.32 | |
| 常角差与τ、α正弦函数 | 6.79 | 4.46 | 8.12 | 3.36 | 8.79 | 8.17 | 3.76 | 8.99 | 3.52 | 9.66 | |
| 常角差与τ、α、κ正弦函数 | 6.78 | 4.39 | 8.08 | 3.34 | 8.75 | 8.13 | 3.76 | 8.96 | 3.51 | 9.63 | |
常角差模型的定位精度最差,外推景精度下降达到32.5%,说明对于天绘一号这样的小卫星,姿态并不稳定,使用常用的姿态角常角差模型并不能很好地消除外方位元素中的系统误差。常角差与τ、α正弦函数改正模型在135景内取得了较好的效果,同时外推景的精度下降只有9.9%,这说明卫星飞行过程当中确实存在抖动,该模型较好地改正了外方位元素中的系统误差,加入κ角的正弦函数改正参数之后精度稍有提高。最后得到的正弦函数拟合参数值见表 2。
| 正弦函数改正参数 | τ角振幅A | τ角角频率w | τ角相位p | α角振幅A | α角角频率w | α角相位p | κ角振幅A | κ角角频率w | κ角相位p |
| 原始数据最小二乘拟合 | -1.52E-05 | 0.18 | -0.52 | -1.38E-05 | 0.20 | -1.07 | 3.73E-06 | 0.19 | -8.05 |
| 常角差与τ、α正弦函数 | -7.33E-05 | 0.18 | -0.52 | -1.54E-05 | 0.20 | -1.07 | — | — | — |
| 常角差与τ、α、κ正弦函数 | -8.17E-05 | 0.18 | -0.52 | -1.30E-05 | 0.20 | -1.07 | 2.44E-05 | 0.19 | -8.05 |
由表 2可知,利用原始数据的残差数据拟合后得到的正弦函数抖动角频率和抖动相位参数非常精确,振幅参数的值出入较大,残差数据中低频抖动的幅度并不可信,因此,在能成功答解的情况下,外方位使用常角差与τ、α、κ正弦函数改正模型更为合理可靠。
2.3 内方位模型参数选择试验及分析为确定天绘一号卫星的内方位元素模型,按照第1节给出的内方位模型形式,选择不同内方位参数,外方位采用常角差与τ、α、κ正弦函数改正模型,内外方位模型统一答解,计算结果列于表 3。
| m | |||||||||||
| 内方位模型 | 135景 | 136景 | |||||||||
| 纬度方向 | 经度方向 | 平面 | 高程 | 立体 | 纬度方向 | 经度方向 | 平面 | 高程 | 立体 | ||
| 原始内方位 | 6.78 | 4.39 | 8.08 | 3.34 | 8.75 | 8.13 | 3.76 | 8.96 | 3.51 | 9.63 | |
| x0、y0、ps | 4.30 | 4.37 | 6.13 | 3.48 | 7.05 | 4.14 | 3.64 | 5.51 | 3.60 | 6.58 | |
| x0、y0、ps、x1、y1、θ | 4.30 | 4.37 | 6.13 | 3.48 | 7.05 | 4.14 | 3.64 | 5.51 | 3.60 | 6.58 | |
| x0、y0、ps、k1、k2、p1、p2 | 4.13 | 4.21 | 5.90 | 3.27 | 6.75 | 4.30 | 3.87 | 5.79 | 3.56 | 6.80 | |
| x0、y0、ps、k1 | 4.13 | 4.35 | 6.00 | 3.47 | 6.93 | 4.35 | 3.73 | 5.73 | 3.73 | 6.76 | |
| x0、y0、ps、p1 | 4.30 | 4.24 | 6.04 | 3.34 | 6.90 | 3.88 | 3.78 | 5.42 | 3.61 | 6.51 | |
| x0、y0、ps、k1、k2 | 4.14 | 4.35 | 6.01 | 3.41 | 6.91 | 4.46 | 3.75 | 5.82 | 3.53 | 6.81 | |
| x0、y0、ps、k1、p1 | 4.13 | 4.22 | 5.90 | 3.33 | 6.78 | 4.07 | 3.85 | 5.60 | 3.60 | 6.66 | |
| x0、y0、ps、p1、p2 | 4.29 | 4.22 | 6.02 | 3.32 | 6.87 | 4.19 | 3.80 | 5.66 | 3.65 | 6.73 | |
| x0、y0、ps、k1、k2、p1 | 4.14 | 4.23 | 5.92 | 3.28 | 6.76 | 4.16 | 3.87 | 5.69 | 3.53 | 6.69 | |
| x0、y0、ps、k1、p1、p2 | 4.15 | 4.32 | 5.99 | 3.39 | 6.88 | 4.63 | 3.72 | 5.94 | 3.54 | 6.91 | |
| x0、y0、ps、x1、y1、θ、k1、k2、p1、p2 | 4.13 | 4.21 | 5.90 | 3.27 | 6.75 | 4.30 | 3.87 | 5.79 | 3.56 | 6.80 | |
在只对像主点(x0,y0)、像元大小ps进行改正后,无论是在135景还是外推的136景精度均有提高,这说明模型很好地补偿了内外方位元素中的系统误差。模型加入线阵CCD在像平面内的旋转参数后定位结果没有变化,这是因为线阵CCD的旋转中心基本与像主点重合,外方位角元素改正已经把这类系统误差完全吸收,因此CCD旋转参数可以省略。再加入光学畸变参数后由于有更多参数来吸收残存的系统误差,135景中误差有所减小,但是在136景中定位精度又有所下降,这说明模型并不完全符合传感器的实际情况。对光学畸变参数的不同组合进行试验也都呈现出类似的情况,但在加入参数p1后两景的精度都有所提高,由于试验中共使用了31个控制点,并不具有普遍性,所以利用布设在沿轨方向两侧的6个控制点对两种候选模型进行试验,得到结果见表 4。
| m | |||||||||||
| 内方位模型的确定 | 135景 | 136景 | |||||||||
| 纬度方向 | 经度方向 | 平面 | 高程 | 立体 | 纬度方向 | 经度方向 | 平面 | 高程 | 立体 | ||
| x0、y0、ps、p1 | 5.26 | 5.68 | 7.74 | 16.97 | 18.65 | 3.94 | 4.01 | 5.63 | 14.31 | 15.38 | |
| x0、y0、ps | 5.03 | 5.40 | 7.38 | 3.6 | 8.21 | 4.02 | 3.62 | 5.40 | 3.90 | 6.67 | |
由表 4可知,加入参数p1后的模型在较少控制点时并不稳定,因此内方位只需对像主点(x0,y0)和像元大小ps进行改正,同时说明除了内参数误差被外参数吸收的原因,也可能天绘一号三线阵相机的光学系统本身质量很高,光学畸变误差很小。
2.4 求解策略试验及分析通过之前试验确定的几何参数精化模型参数众多,这可能会出现“过参数化”现象,影响结果的正确性和稳定性,解决的方法一般为内外参数分开求解,但分别对部分参数求解又会造成结果的有偏[21]。为比较哪种策略在解算中更有优势,分3种情况试验,结果如表 5所示。
| m | |||||||||||
| 求解策略 | 135景 | 136景 | |||||||||
| 纬度方向 | 经度方向 | 平面 | 高程 | 立体 | 纬度方向 | 经度方向 | 平面 | 高程 | 立体 | ||
| 先外后内 | 4.59 | 4.29 | 6.29 | 3.34 | 7.12 | 5.34 | 3.51 | 6.39 | 3.51 | 7.29 | |
| 先内后外 | 4.3 | 4.37 | 6.13 | 3.48 | 7.05 | 4.21 | 3.64 | 5.57 | 3.60 | 6.63 | |
| 统一答解 | 4.30 | 4.37 | 6.13 | 3.48 | 7.05 | 4.14 | 3.64 | 5.51 | 3.60 | 6.58 | |
先外后内的方式会让外方位元素错误地吸收内方位元素含有的系统误差,得到的内外方位元素都与真实值有较大偏差,因此在135景和136景所取得的定位精度均不理想。先内后外的方式道理也一样,但因为相机中心投影的结构能一定程度上减小内方位元素对外方位误差的吸收,定位结果比较理想。由于几何参数精化模型设置合理,内方位模型比较简单,统一答解并没有出现明显的“过参数化”现象,在两景取得的定位精度都很理想。
2.5 实际在轨几何参数精化结果采用本文最终确定的几何参数精化模型和求解策略,从河南135影像上选取一定数量分布合理的控制点参与在轨几何参数精化计算,其余点作为检查点,136景所有控制点作为检查点,平差结果列于表 6。
| m | |||||||||||
| 控制点数量 | 135景 | 136景 | |||||||||
| 纬度方向 | 经度方向 | 平面 | 高程 | 立体 | 纬度方向 | 经度方向 | 平面 | 高程 | 立体 | ||
| 6 | 5.03 | 5.40 | 7.38 | 3.61 | 8.21 | 4.02 | 3.62 | 5.40 | 3.90 | 6.67 | |
| 7 | 4.99 | 4.85 | 6.96 | 3.52 | 7.80 | 3.96 | 3.38 | 5.21 | 3.53 | 6.29 | |
| 8 | 5.14 | 5.03 | 7.19 | 3.51 | 8.01 | 3.97 | 3.40 | 5.22 | 3.53 | 6.30 | |
可以看到在控制点合理分布的情况下,控制点数量达到7个时精化结果就较为理想,这说明该方法比较可靠,天绘一号三线阵影像数据和辅助数据的内部相对精度很高。
利用北京-山东和黑龙江的两景长条带影像对本文方法的推广性进行验证。以北京-山东地区影像为例,其定姿残差图如图 6所示。
|
| 图 6 北京-山东地区影像定姿残差图 Fig. 6 Beijing-Shandong image attitude residual plots |
从图中可以看到,有和河南地区影像类似的变化规律,两个地区正弦函数拟合得到的参数如表 7所示。
| 正弦改正系数 | τ角振幅A | τ角角频率w | τ角相位p | α角振幅A | α角角频率w | α角相位p | κ角振幅A | κ角角频率w | κ角相位p |
| 北京-山东原始数据最小二乘 | 8.58E-06 | 0.14 | -0.52 | -9.37E-06 | 0.20 | -1.33 | 8.73E-06 | 0.11 | -0.42 |
| 黑龙江原始数据最小二乘 | 6.23E-06 | 0.20 | 2.60 | 2.86E-06 | 0.15 | -0.21 | 7.16E-06 | 0.16 | -0.86 |
结合表 2可以看到卫星抖动的频率并非是一成不变的。
从长条带影像上半区的3排控制点中挑选出平差点,其余点作为检查点,结果列于表 8、表 9。
| m | |||||||||||
| 控制点数量 | 控制点 | 检查点 | |||||||||
| 纬度方向 | 经度方向 | 平面 | 高程 | 立体 | 纬度方向 | 经度方向 | 平面 | 高程 | 立体 | ||
| 6 | 5.989 4 | 5.32 | 8.01 | 3.64 | 8.80 | 5.54 | 5.13 | 7.55 | 4.05 | 10.68 | |
| 7 | 5.222 4 | 5.15 | 7.33 | 3.58 | 8.16 | 5.12 | 4.95 | 7.12 | 3.72 | 10.07 | |
| 8 | 5.176 | 5.05 | 7.23 | 3.59 | 8.07 | 5.02 | 4.96 | 7.05 | 3.68 | 9.98 | |
| 上半区全部控制点 | 4.539 2 | 4.41 | 6.33 | 3.50 | 7.23 | 4.49 | 4.41 | 6.29 | 3.61 | 8.90 | |
| m | |||||||||||
| 控制点数量 | 控制点 | 检查点 | |||||||||
| 纬度方向 | 经度方向 | 平面 | 高程 | 立体 | 纬度方向 | 经度方向 | 平面 | 高程 | 立体 | ||
| 6 | 6.22 | 5.47 | 8.28 | 3.85 | 9.13 | 6.17 | 5.52 | 8.28 | 4.11 | 11.71 | |
| 7 | 5.39 | 5.28 | 7.55 | 3.65 | 8.39 | 5.57 | 5.40 | 7.75 | 3.72 | 10.97 | |
| 8 | 5.14 | 5.11 | 7.24 | 3.62 | 8.10 | 5.62 | 4.93 | 7.48 | 3.68 | 10.58 | |
| 上半区全部控制点 | 4.90 | 4.97 | 6.98 | 3.41 | 7.77 | 5.03 | 4.87 | 7.00 | 3.53 | 9.90 | |
由于影像跨度、控制点分布、控制点转刺精度等原因,相比河南地区的精度稍有下降,但属于合理范围之内,可以认为本文的方法是有效的。
3 结论及展望通过本文的分析与试验可知:①在外方位线元素中包含一定系统误差的情况下,仅经过角元素的改正后仍能有比较高的定位精度,因此在在轨几何精化的过程中应忽略线元素误差,换取计算方法的简便与求解的稳定;②天绘一号卫星的姿态数据中包含有0.3~0.8 Hz的杂波,应采用低阶多项式拟合的方法预处理,消除杂波的影响,同时对卫星在轨姿态的抖动采用正弦函数进行补偿,还原出卫星在轨飞行时更为真实的姿态;③本文提出相较传统附加参数模型更为直观的以像素坐标为观测值的内方位元素模型,在比较不同参数组合的试验结果后认为,天绘一号卫星三线阵相机几何质量很高,光学畸变误差很小;④由于最终确定的模型较为简单合理,采取统一答解的方式,利用较少控制点就可以得到较好的精化结果。
本文的相机在轨几何参数精化是在轨检校的第一步,其得到的参数是之后在摄影区域进行平差及外推定位的重要依据,也是总结低频误差规律的先决条件,在实际作业中需要多地多次地精化,得到更为稳定的精化结果,提高精化参数的可靠性。
| [1] | 王任享, 胡莘, 王新义, 等. "天绘一号"卫星工程建设与应用[J]. 遥感学报, 2012, 16(S):2-5. WANG Renxiang, HU Xin, WANG Xinyi, et al. The Construction and Application of Mapping Satellite-1 Engineering[J]. Journal of Remote Sensing, 2012, 16(S):2-5. |
| [2] | 刘楚斌. 高分辨率遥感卫星在轨几何定标关键技术研究[D]. 郑州:信息工程大学, 2012. LIU Chubin.Study on Crucial Technique of the On-orbit Geometric Calibration of High Resolution Satellite[D]. Zhengzhou:The PLA Information Engineering University, 2012. |
| [3] | BECKETT K, RAMPERSAD C, PUTIH R, et al. Rapideye Product Quality Assessment[C]//Proceedings of SPIE. Berlin:SPIE, 2009, 7474:1-10. |
| [4] | CRESPI M, COLOSIMO G, DE VENDICTIS L, et al. GeoEye-1:Analysis of Radiometric and Geometric Capability[J]. Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering,2010, 43(7):354-369. |
| [5] | PANEM C, BIGNALET-CAZALET F, BAILLARIN S. Pleiades-HR System Products Performance after In-orbit Commissioning Phase[C]//International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences.Melbourne:ISPRS, 2012, 39-B1:567-572. |
| [6] | 李德仁. 我国第一颗民用三线阵立体测图卫星——资源三号测绘卫星[J]. 测绘学报, 2012, 41(3):317-322. LI Deren. China's First Civilian Three-line-array Stereo Mapping Satellite:ZY-3[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3):317-322. |
| [7] | 李晶, 王蓉, 朱雷鸣, 等. "天绘一号"卫星测绘相机在轨几何定标[J]. 遥感学报, 2012, 16(S):35-39. LI Jing, WANG Rong, ZHU Leiming, et al. In-flight Geometric Calibration for Mapping Satellite-1 Surveying and Mapping Camera[J]. Journal of Remote Sensing, 2012, 16(S):35-39. |
| [8] | 付勇, 邹松柏, 刘会安. "天绘一号"01星立体影像定位精度检测[J]. 遥感学报, 2012, 16(S):94-97. FU Yong, ZOU Songbai, LIU Huian. Evaluation of the Location Accuracy of the Mapping Satellite-1 Stereo Image[J]. Journal of Remote Sensing, 2012, 16(S):94-97. |
| [9] | 王任享, 王建荣. 无地面控制点卫星摄影测量探讨[J]. 测绘科学, 2015, 40(2):3-12. WANG Renxiang,WANG Jianrong.Discussion on Satellite Photogrammetry without Ground Control Point[J]. Science of Surveying and Mapping, 2015, 40(2):3-12. |
| [10] | 刘楚斌, 张永生, 范大昭, 等. 资源三号卫星三线阵影像自检校区域网平差[J]. 测绘学报, 2014, 43(10):1046-1050, 1060.DOI:10.13485/j.cnki.11-2089.2014.0148. LIU Chubin, ZHANG Yongsheng, FAN Dazhao, et al. Self-calibration Block Adjustment for Three Line Array Image of ZY-3[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10):1046-1050, 1060. DOI:10.13485/j.cnki.11-2089.2014.0148. |
| [11] | 蒋永华, 张过, 唐新明, 等. 资源三号测绘卫星三线阵影像高精度几何检校[J]. 测绘学报, 2013, 42(4):523-529, 553. JIANG Yonghua, ZHANG Guo, TANG Xinming, et al. High Accuracy Geometric Calibration of ZY-3 Three-line Image[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4):523-529, 553. |
| [12] | 王任享. 天绘一号卫星无地面控制点摄影测量关键技术及其发展历程[J]. 测绘科学, 2013, 38(1):5-7, 43. WANG Renxiang.Key Photogrammetric Progress of TH-1 Satellite without Ground Control Point[J]. Science of Surveying and Mapping, 2013, 38(1):5-7, 43. |
| [13] | 李松明, 李岩, 李劲东. "天绘一号"传输型摄影测量与遥感卫星[J]. 遥感学报, 2012, 16(S):10-16. LI Songming, LI Yan, LI Jindong. Mapping Satellite-1 Transmission Type Photogrammetric and Remote Sensing Satellite[J]. Journal of Remote Sensing, 2012, 16(S):10-16. |
| [14] | 王任享, 胡莘, 王建荣. 天绘一号无地面控制点摄影测量[J]. 测绘学报, 2013, 42(1):1-5. WANG Renxiang,HU Xin,WANG Jianrong.Photogrammetry of Mapping Satellite-1 without Ground Control Points[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1):1-5. |
| [15] | 郭海涛, 张保明, 归庆明. 广义岭估计在解算单线阵CCD卫星影像外方位元素中的应用[J]. 武汉大学学报(信息科学版), 2003, 28(4):444-447. GUO Haitao,ZHANG Baoming,GUI Qingming.Application of Generalized Ridge Estimate to Computing the Exterior Orientation Elements of Satellite Linear Array Scanner Imagery[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4):444-447. |
| [16] | 唐新明, 张过, 祝小勇, 等. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报,2012, 41(2):191-198. TANG Xinming, ZHANG Guo, ZHU Xiaoyong, et al. Triple Linear-array Imaging Geometry Model of Ziyuan-3 Surveying Satellite and Its Validation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2):191-198. |
| [17] | TOUTIN T. Geometric Processing of Remote Sensing Images:Models, Algorithms and Methods[J]. International Journal of Remote Sensing, 2004, 25(10):1893-1924. |
| [18] | 袁修孝, 余俊鹏. 高分辨率卫星遥感影像的姿态角常差检校[J]. 测绘学报, 2008, 37(1):36-41. YUAN Xiuxiao, YU Junpeng. Calibration of Constant Angular Error for High Resolution Remotely Sensed Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1):36-41. |
| [19] | 秦绪文, 蒋永华, 杜锦华, 等. 光学一号高分辨率卫星在轨几何检校及精度验证[C]//第19届中国遥感大会论文集.西安:中国遥感委员会, 中国宇航学会, 2014, 1:120-127. QIN Xuwen,JIANG Yonghua,DU Jinhua,et al.On-orbit Geometric Calibration of Optics-1 High Resolution Satellite[C]//Proceedings of the 19th China Remote Sensing Conference. Xi'an:Remote Sensing Committee of China,Chinese Society of Astronautics, 2014, 1:120-127. |
| [20] | 余岸竹. 遥感卫星摄影测量参数动态检测关键技术研究[D]. 郑州:信息工程大学, 2014. YU Anzhu. Research on the Key Technology of Dynamic Calibration of Photogrammetric Parameters for Spaceborne Sensors[D]. Zhengzhou:The PLA Information Engineering University, 2014. |
| [21] | 李德仁, 袁修孝.误差处理与可靠性理论[M]. 第2版. 武汉:武汉大学出版社, 2012:5-9. LI Deren,YUAN Xiuxiao.Error Processing and Reliability Theory[M]. 2nd ed. Wuhan:Wuhan University Press, 2012:5-9. |